2. 南京邮电大学地理与生物信息学院,南京市文苑路9号, 210023;
3. 山东省国土测绘院,济南市经十东路2289号,250013
现有解缠方法大致可以分为路径引导和优化逼近2种类型。路径引导类方法的基本原理是根据某些规则,从数据内部获得相关信息,制定出规避不连续边界的相位计算路线,这类方法包括支切法[1]、质量图引导法[2-4]、Flynn最小不连续法[5]、基于网络流的方法[6-7]等,属于局部方法。优化逼近类方法主要是通过设定的全局目标函数的极值优化过程,实现向最优解的逼近,这类方法常采用范数形式定义代价函数,也称最小范数方法,包括最小二乘法、Lp范数法[8]等,属于全局方法。
最小范数解缠方法使用解缠相位与缠绕相位的梯度差的范数作为代价函数进行全局统计,通过目标函数的最小化过程获得全局最优解。最经典的方法是采用L2范数的最小二乘方法。该方法最终转化为泊松方程,具有计算方便的优点,但同时也存在L2范数过度平滑、无法恢复数据细节信息的缺点。在最小二乘方法的基础上,加权最小二乘方法[9]通过引入权重进行改进。Ghiglia[8]等引入一个概括的Lp范数框架,将范数类的模型进行归纳。Liu等[10]提出使用多种范数方案混合的解缠方法。也有学者将卡尔曼滤波[11]和蚁群算法[12]等应用于解缠问题的研究。
最小范数解缠方法的研究难点在于如何选择合适的代价函数模型,实际应用时还有迭代处理低效的问题,这使得最小范数类解缠方法在实用方面不够理想。本文在前人研究的基础上,对代价函数的特征进行分析,提出一种符合L0范数代价函数的二维相位解缠方法,并结合数据分块方案,解决线性微分方程中低频误差收敛慢的问题,以提高解缠处理的效率。
1 最小范数解缠方法的代价函数假定二维相位ψ是相位φ经过相位缠绕之后的结果:
| $ \psi = W\left( \varphi \right) $ |
式中,W为缠绕函数。相位解缠是实现由ψ恢复φ的过程。当解缠结果和真实值之间符合某种准则时,可以认为解缠处理达到理想状态。解缠处理准则一般转化为梯度差相关的优化问题,如:
| $ \mathop {\inf }\limits_\varphi \int\limits_\mathit{\Omega } {g\left( {\left| {\nabla u} \right|} \right){\rm{d}}x} $ | (1) |
式中,u=ϕ-φ,ϕ为解缠结果,φ为相位真实值,Ω⊂R2为定义域,函数g描述不同梯度在统计之中的影响程度,称为代价函数。这种梯度上的约束使解缠结果在相位变化上保持某种程度的一致性。
假定函数g连续且一阶可导,由欧拉-拉格朗日方程[13]可以得到满足最小化的方程:
| $ {\rm{div}}\left( {\frac{{g'\left( {\left| {\nabla u} \right|} \right)}}{{\left| {\nabla u} \right|}}\nabla u} \right) = 0 $ | (2) |
式中,div为散度算子,g′为函数g的一阶导数。在相位数据满足奈奎斯特采样定理的条件下,ψ和φ之间满足:
| $ \nabla \varphi = W\left( {\nabla \psi } \right),\nabla u = \nabla \phi - \nabla \varphi = \nabla \phi - W\left( {\nabla \psi } \right) $ |
则式(2)可以重写为:
| $ {\rm{div}}\left( {\frac{{g'\left( {\left| {\nabla \phi - W\left( {\nabla \psi } \right)} \right|} \right)}}{{\left| {\nabla \phi - W\left( {\nabla \psi } \right)} \right|}}\left| {\nabla \phi - W\left( {\nabla \psi } \right)} \right|} \right) = 0 $ | (3) |
式(3)的形式取决于函数g的具体描述。相位解缠最主要的问题在于相位数据出现不符合采样定理条件的相位不连续,这种不连续可能是由目标的特殊特征或者外界观测噪声等引起的。针对出现的相位不连续问题,代价函数g除了在相位连续位置的数据一致外,还要克服相位不连续的异常影响。
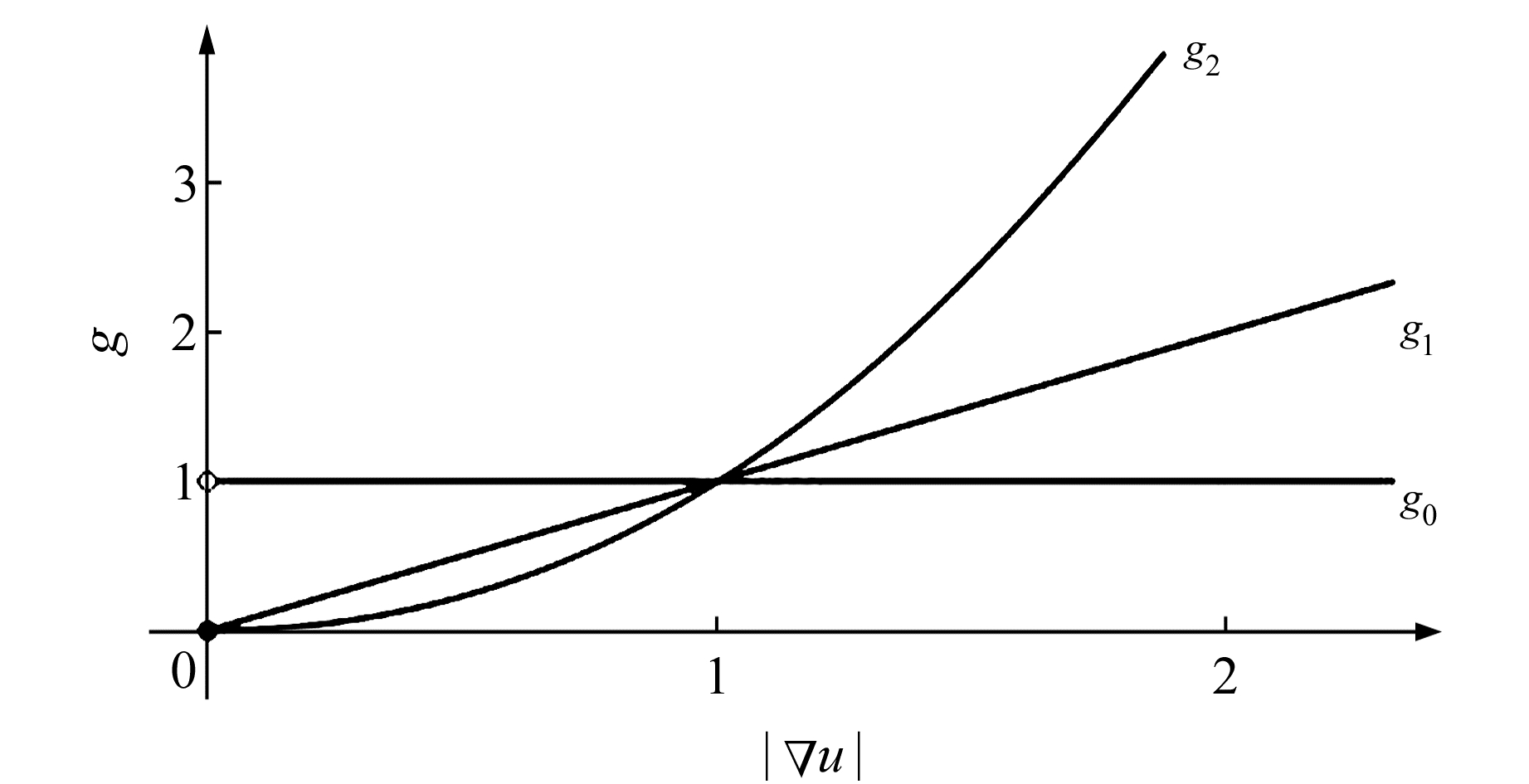
代价函数g的具体形式对于解缠处理具有决定性的作用,例如当函数分别取梯度的L0、L1和L2范数形式时,3种范数对应的图形如图 1所示[14]。不同的范数形式在解缠处理时分别对应不同的策略。如果存在相位不连续的情况,L0范数方法将相位连续和不连续的情况区别对待,而L2范数方法具有较强的平滑作用,L1范数方法则容易出现台阶效应。比较理想的方法是采用L0范数形式的代价函数[11],但是L0范数的定义不满足代价函数连续可导的要求,为此需要寻求一种符合L0范数形式的代价函数表达方式。
|
图 1 代价函数的3种范数形式 Fig. 1 Cost function of three norm forms |
在二维情况下,可以将与∇u相关的表达式分解为u等值线的切向分量uTT和法向分量uNN2个部分。根据文献[15],将式(3)重写为:
| $ \frac{{g'\left( {\left| {\nabla u} \right|} \right)}}{{\left| {\nabla u} \right|}}{u_{TT}} + g''\left( {\left| {\nabla u} \right|} \right){u_{NN}} = 0 $ |
当|∇u|取值较小时,不存在相位不连续的情况,切向分量uTT和法向分量uNN对应的约束应该同时发挥作用。假定此时两项约束作用相当,其系数取值相同,且系数在|∇u|=0处极限取相同正值,这就要求:
| $ \begin{array}{*{20}{c}} {\mathop {\lim }\limits_{\left| {\nabla u} \right| \to {0^ + }} \frac{{g'\left( {\left| {\nabla u} \right|} \right)}}{{\left| {\nabla u} \right|}} = }\\ {\mathop {\lim }\limits_{\left| {\nabla u} \right| \to {0^ + }} g''\left( {\left| {\nabla u} \right|} \right) = g''\left( 0 \right) > 0} \end{array} $ | (4) |
当|∇u|取值较大时,可能出现相位不连续的情况,为降低相位不连续的影响,需要削弱等值线法向分量uNN的比重,保持切向的约束作用,即有条件:
| $ \mathop {\lim }\limits_{\left| {\nabla u} \right| \to + \infty } \frac{{g'\left( {\left| {\nabla u} \right|} \right)}}{{\left| {\nabla u} \right|}} > 0,\mathop {\lim }\limits_{\left| {\nabla u} \right| \to + \infty } g''\left( {\left| {\nabla u} \right|} \right) = 0 $ |
但是这2个条件无法同时成立。针对L0范数的定义,将上式修改为:
| $ \begin{array}{l} \mathop {\lim }\limits_{\left| {\nabla u} \right| \to + \infty } \frac{{g'\left( {\left| {\nabla u} \right|} \right)}}{{\left| {\nabla u} \right|}} = 0\\ \mathop {\lim }\limits_{\left| {\nabla u} \right| \to + \infty } g''\left( {\left| {\nabla u} \right|} \right) = 0\\ \frac{{g'\left( {\left| {\nabla u} \right|} \right)}}{{\left| {\nabla u} \right|}} > g''\left( {\left| {\nabla u} \right|} \right) \end{array} $ | (5) |
即梯度较大时,2个分量的系数都会趋近于0,但是切向分量uTT的约束影响会超过法向分量uNN。
2 基于L0范数准则的代价函数根据式(5)对代价函数g的要求,设计符合L0范数的函数模型。代价函数的具体形式为:
| $ g\left( {\left| {\nabla u} \right|} \right) = \frac{{{{\left| {\nabla u} \right|}^2}}}{{1 + {{\left| {\nabla u} \right|}^2}}} $ | (6) |
该函数在|∇u|=0处为0,并随着|∇u|的变大趋近于常数,图形与L0范数基本一致,且
| $ \frac{{g'\left( {\left| {\nabla u} \right|} \right)}}{{\left| {\nabla u} \right|}} = \frac{1}{{{{\left( {1 + {{\left| {\nabla u} \right|}^2}} \right)}^2}}} $ |
| $ g''\left( {\left| {\nabla u} \right|} \right) = \frac{{1 - 3{{\left| {\nabla u} \right|}^2}}}{{{{\left( {1 + {{\left| {\nabla u} \right|}^2}} \right)}^3}}} $ |
符合式(5)的要求。
将式(6)的代价函数代入式(2)及式(3),可以得到基于新的代价函数的解缠方程式:
| $ {\rm{div}}\frac{{\nabla \phi - W\left( {\nabla \psi } \right)}}{{{{\left( {1 + {{\left| {\nabla \phi - W\left( {\nabla \psi } \right)} \right|}^2}} \right)}^2}}} = 0 $ |
为了消除相位值域的尺度问题,将上式修改为:
| $ {\rm{div}}\frac{{\nabla \phi - W\left( {\nabla \psi } \right)}}{{{{\left( {\alpha + {{\left| {\nabla \phi - W\left( {\nabla \psi } \right)} \right|}^2}} \right)}^2}}} = 0 $ | (7) |
其中,α为一正常数,当相位ψ尺度较大时,α可以稍微调大一些,反之亦然。其代价函数如图 2所示,具体取值可以视情况而定。

|
图 2 不同尺度系数的代价函数 Fig. 2 Cost function of different scale coefficients |
直接解算椭圆微分方程式(7)并不容易,令b=
求解微分方程算法的数值实现,一般先要将微分关系转换成离散数据对应的差分关系,再进行差分方程迭代求解。迭代处理时,每一步处理都是在前一步处理结果的基础上进行的,两步处理结果之间的差异δϕ则成为解算的重要内容。第n步和第n+1步的解缠结果满足方程:
| $ {\rm{div}}\left( {{b_n}\nabla {\phi _{n + 1}}} \right) = {\rm{div}}\left( {{b_n}W\left( {\nabla \psi } \right)} \right) $ |
| $ {b_n} = \frac{1}{{{{\left( {\alpha + {{\left| {\nabla {\phi _n} - W\left( {\nabla \psi } \right)} \right|}^2}} \right)}^2}}} $ |
则待解方程可以重新写为:
| $ {\rm{div}}\left( {{b_n}\nabla \delta {\phi _{n + 1}}} \right) = {\rm{div}}\left( {{b_n}W\left( {\nabla \psi } \right) - \nabla \delta {\phi _n}} \right) $ |
| $ \delta {\phi _n} = {\phi _{n + 1}} - {\phi _n} $ |
此时方程右边项是原始缠绕相位信息扣除掉已知解的部分,求得差异δϕn,更新解缠结果,检测结果鉴定后再决定是否进行下一步迭代。
迭代终止条件主要以缠绕相位解缠残量中残差点的检测为判断依据,解缠残量表示为:
| $ \delta {\psi _n} = \psi - {\phi _n} $ |
当数据δψn中不存在残差点时,即可终止迭代,将δψn进行任意路径积分解缠,并汇入ϕn组成最终解缠结果,否则继续迭代。
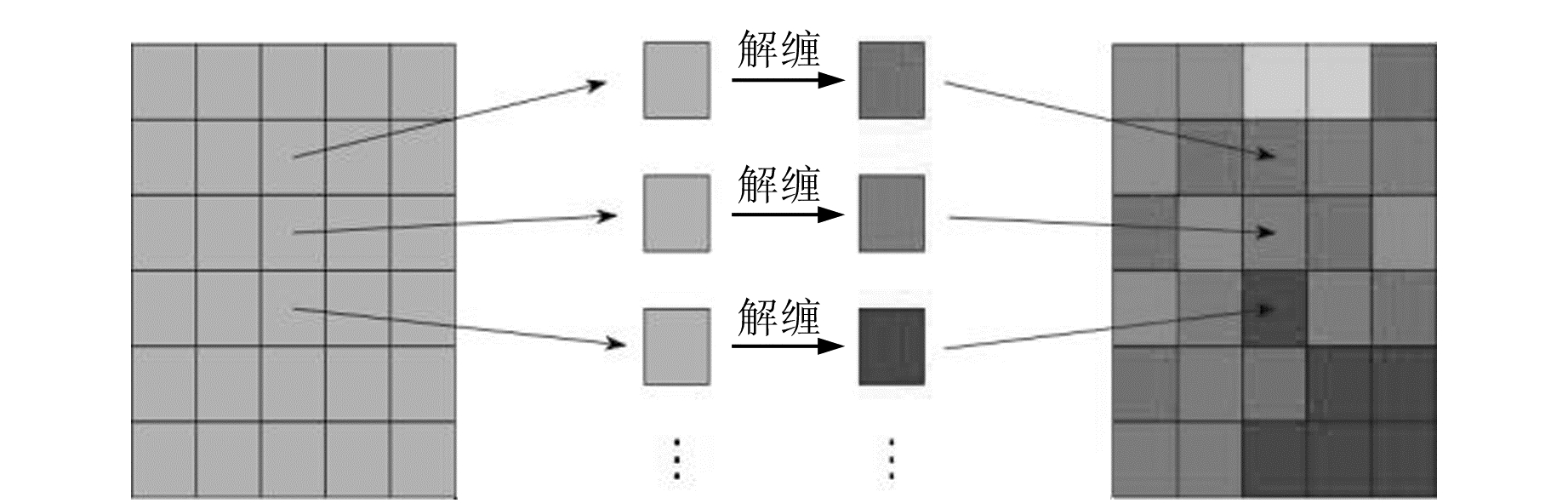
在解算线性方程时,如果数据量比较大,则会遇到低频误差衰减慢的问题,这将导致迭代收敛慢,计算费时。本文采用数据分块处理的策略,解缠处理只在各分块小区域内的相位数据上进行,完成后再进行数据拼接,过程如图 3所示。由于进行了数据分块,分块区域内的高频误差在迭代处理中衰减迅速,迭代计算速度加快,解缠处理效率提高。分块区域之间存在的低频误差可以在数据拼接时通过计算邻接区域间的偏移量进行补偿,从而避免低频误差带来的不利影响。
|
图 3 数据分块解缠 Fig. 3 Unwrapping with data partitioning |
此外,数据分块处理时,因为各分块数据的操作没有依赖关系,可以分别独立进行,因此能够采用并行计算模式,充分发挥处理器的运算能力,提高对大数据量相位解缠处理的效率。需要注意的是,分块区域尺寸的设定不应该破坏相位不连续边界的完整性,否则解缠结果可能会出现区域性的错误。
结合数据分块处理策略,相位解缠的基本过程可以用伪代码方式表示。给定缠绕相位ψ,依次进行如下步骤:1)缠绕相位分块ψi, j,初始解缠相位ϕ0i, j=0;2)计算bni, j;3)计算方程右边项;4)用PCG方法解算方程,得到δϕni, j;5)更新相位ϕn+1i, j=ϕni, j+δϕni, j;6)计算缠绕相位残量δψn+1i, j=ψi, j-ϕn+1i, j;7)残差点检测,不存在则终止计算,否则回到2);8)缠绕相位残量解缠,加入ϕn+1i, j,完成本块处理;9)各分块都完成后,进行邻接周期偏移计算和数据拼接。其中,1)~8)部分在分块处理时各自相互独立,可以实现并行处理。
本文算法主要通过C++编码,其中PCG处理部分采用开源的线性求解工具Hypre实现,并行处理采用支持CPU多核处理的OpenMP方案,数据IO部分借助CImg工具提供的强大接口,源码经过编译生成可高效运行的可执行程序。
4 数据实验与分析处理数据使用的机器配置为:2.7 GHz逻辑8核CPU,双通道1 600 MHz、8 GB DDR3内存,64位操作系统。使用共享内存的多核并行处理模式,线性方程解算采用稳定性较好的半粗化多重网格预条件的共轭梯度算法。
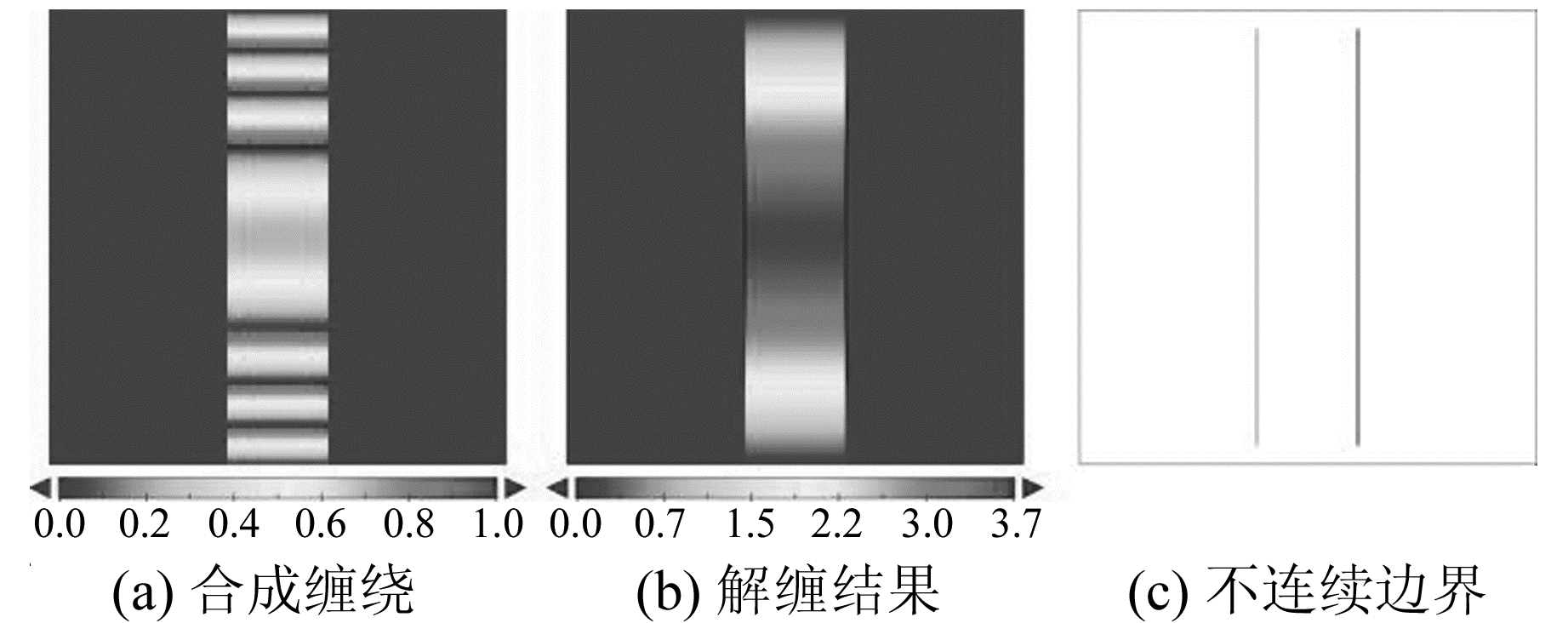
实验数据包括合成缠绕相位和真实InSAR干涉相位数据,合成数据尺寸为513像素×513像素,是在平面背景中央叠加一根竖直的上半周期正弦条带,然后经过相位缠绕处理,将连续的正弦条带经过6次截断变成7段。该数据的解缠处理难度主要在于不连续相位差超过3个周期,对于主要依赖相位数据间微分关系控制解缠结果的方法有一定难度。取α=0.003,不分块整体进行解缠处理,迭代计算8次后,成功恢复正弦条带的连续性,条带数据与背景间的不连续边界也探测出完整的信息。原始合成数据和解缠结果及其对应的不连续边界分布数据的二维显示如图 4所示,数据单位为相位周期(2π)。
|
图 4 合成缠绕相位、解缠结果及其对应的不连续边界 Fig. 4 Artificial wrapped phase, unwrapping results and its discontinuous boundary |
迭代计算过程也是一个按照给定方程的约束条件,由缠绕相位向解缠结果向进行吸引拉伸的过程,作用的强弱则完全由系数b决定。图 5给出了前4次和最后1次系数b的取值(图 5(a)~(e))以及对应的各次缠绕相位残量δψ的变化(图 5(f)~(j))。

|
图 5 前4次和最后1次方程系数以及对应的相位残量 Fig. 5 First four and last coefficients and the corresponding phase residue |
由图 5可以看出,系数b在缠绕相位残量有较大绝对值以及不连续边界位置处的取值较小,在缠绕相位残量绝对值较小的位置取值较大。原始相位信息在取值较大的区域则有较强的引力,吸引解向其靠近,逐次趋近,最后稳定于最终解缠结果附近,此时的残量不再含有残差点,可直接由路径积分获得。
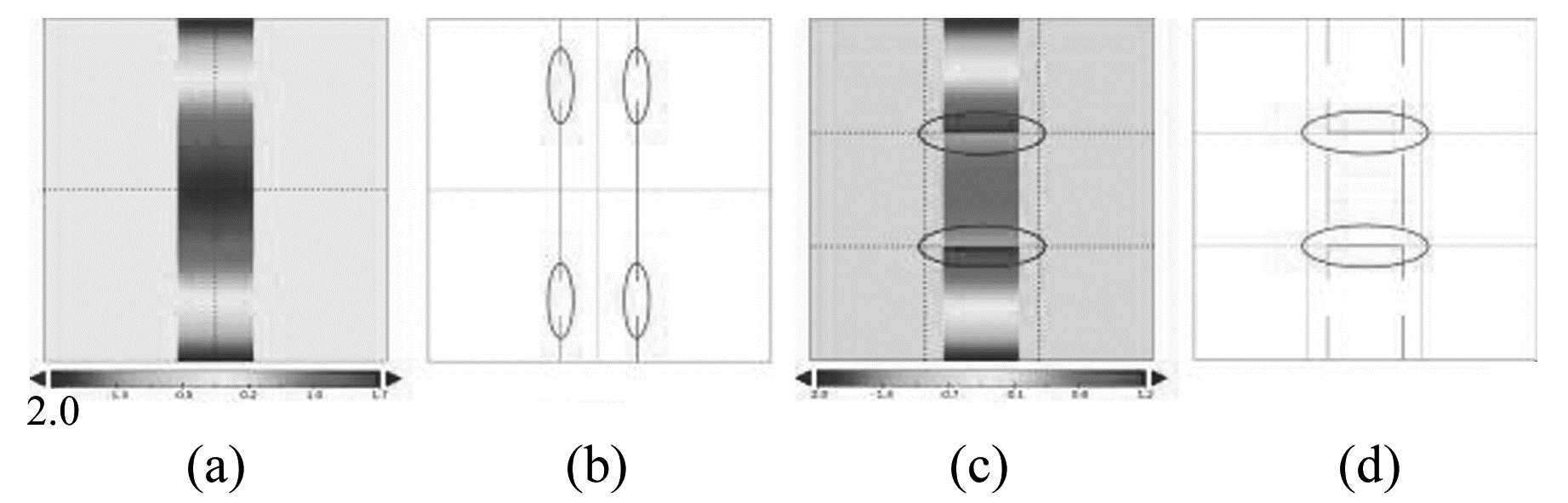
数据分块处理可以降低处理难度、提高数据收敛速度,但使用不当也可能带来问题。对合成缠绕相位数据分别进行2×2和3×3的数据分块,分块解缠处理完再拼接合并。得到的解缠结果和对应的不连续边界分布如图 6所示。可以看出,这2种分块方案都将不连续边界进行了分割,解缠后恢复的边界线不再完整,出现断裂的情况(图 6 (b)中圈示的位置),但是2×2分块的解缠结果(图 6 (b))仍然可以恢复正弦条带的连续性,也是可以接受的解缠结果。使用3×3分块的处理结果(图 6(c))中,中间分块区域的条带具有较大的不连续相位差,无法恢复,致使该区域的条带出现正周期的错位,这种错位无法在分块拼接时补偿,使得解缠结果中出现正弦条带断裂的情况,最终导致解缠处理失败。
|
图 6 使用2×2和3×3分块获得解缠结果和不连续边界分布 Fig. 6 Unwrapping results and discontinuous boundaries of 2×2 and 3×3 partitions |
因此,在进行数据分块处理时,需要注意分块尺寸的设定,虽然尺寸越小计算越快,但是需要避免出现上述不连续边界截断导致块内局部数据周期错位的情况。一般来讲,缠绕相位中的相位不连续常常是由于信号噪声或者观测目标局部特征异常所致,很少出现大范围的不连续边界,所以这个问题并不是很严重。
采用真实InSAR干涉相位作为实验数据,大小为1 398×622像素。数据整体带有平缓的变化趋势,在几处位置上的噪声干扰比较严重,而且有些位于数据边界位置上,这部分噪声的影响仅能利用一侧数据的约束进行消除,在较大区域内的迭代可能比较耗时。现将数据按照200像素和100像素级别尺度(即分别采用7×3和14×6的方案)进行分块,然后分别进行解缠处理。由于分块区域内相位数据质量的差异,在没有残差点的分块内无需进行迭代计算,在残差点较多的分块则可能需要多次迭代才能完成解缠。因此,并行计算的任务分配适合采用动态分配模式,以便更充分地利用资源。
在完成所有分块数据的解缠处理之后,需要将其结果进行拼接合成。在数据拼接之前,包含在缠绕相位中的低频信息在分块区域内无法呈现,在解缠处理时被忽略,但在分块拼接时表现为数据块间的整周期相位偏移,因此需要进行偏移值的补偿。由于解缠结果的相位连续性特征,在分块邻接位置对分块间的相位差值进行统计,偶然混入的不连续边界数据很容易被连续的相位数据湮没,简单的统计分析即可以得到分块间的相位偏移值。选定一块为基准块,按照邻接关系依次计算偏移值,再按照偏移值进项补偿后,进行数据拼接,便可得到完整的相位解缠结果。由图 7可见,即便是数据分解为100像素大小的数据块,解缠结果依然能够保持较好的完整性。

|
图 7 InSAR干涉相位数据14×6分块解缠处理 Fig. 7 Unwrapping process of InSAR phase of 14×6 partitions |
采用Goldstein支切法、基于方差的质量图引导法(quality guided)、Flynn最小不连续法、基于网络流的SNAPHU法、PUMA法以及本文所提出的解缠方法分别对InSAR干涉相位进行解缠处理。将解缠结果的质量、解缠处理的效率分别用量化指标进行统计,包括解缠结果进行缠绕后与原缠绕相位数据间差值的均值和中误差统计、相位不连续边界长度以及运行时间长度,统计结果见表 1。
|
|
表 1 不同方法解缠结果相关指标统计 Tab. 1 Statistics indicators of the results from different unwrapping methods |
需要指出的是,实验处理的数据类型采用8位浮点型数据,其有效数字不超7位,所以相关精度指标达到10-6以上时,可以认为没有误差。从表 1可以看出,再缠绕相位差值的均值统计均达到10-6以上,而中误差指标的统计值中Goldstein支切法比较突出,主要是因为支切法在数据质量较差区域可能会造成孤岛或空洞的情况。不连续边界长度指标的统计结果中,Flynn最小不连续法最优,这也是这种解缠方法最重要的原则;其次是本文所提的符合L0范数准则的方法,在兼顾数据连续性的同时,也可以得到较小的不连续边界;其他如Goldstein支切法、质量图引导法稍差,最差的则是SNAPHU法,主要是因为数据中的噪声造成边角上相位偏差而产生不连续边界。最后是关于运行时间的统计值,Goldstein支切法最快,质量图引导法次之,PUMA法最慢,而本文所提的方法在2种分块方案下,所需的运行时间也稍有差异。数据块尺寸越小处理速度越快,但要避免破坏解缠结果中不连续边界的完整性,使用14×6分块方案耗时优于SNAPHU法,与Flynn最小不连续法相当,即使7×3分块方案耗时也比SNAPHU法稍短,效率整体优于PUMA法。
综合各项统计指标可以看出,本文方法可以得到较好的解缠结果和较小的不连续边界;采用合适的分块方案以及并行处理技术,可以达到较高的处理效率,这种质量和效率兼备的优点是经典的最小范数类方法所不具备的。
5 结语本文提出一种符合L0范数准则代价函数的全局最优二维相位解缠方法,采用的代价函数在相位不连续区域对不连续边界的切方向和法方向采用不同的约束强度,使得在解缠处理时获得连续相位的同时,还能够保证不连续边界不受影响。采用数据分块处理的方法,避免了线性微分方程中大区域内低频误差收敛慢的问题,将低频信息的处理转移到数据块间的偏移量计算中,提高了迭代收敛速度。实验结果表明,本文所提方法可靠,效率较高。
| [1] |
Huang Q, Zhou H Q, Dong S C, et al. Parallel Branch-Cut Algorithm Based on Simulated Annealing for Large-Scale Phase Unwrapping[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(7): 3833-3846 DOI:10.1109/TGRS.2014.2385482
(  0) 0) |
| [2] |
Gao D P, Yin F L. Mask Cut Optimization in Two-Dimensional Phase Unwrapping[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(3): 338-342 DOI:10.1109/LGRS.2011.2168940
(  0) 0) |
| [3] |
Zhong H P, Tang J S, Zhang S, et al. A Quality-Guided and Local Minimum Discontinuity Based Phase Unwrapping Algorithm for InSAR/InSAS Interferograms[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(1): 215-219 DOI:10.1109/LGRS.2013.2252880
(  0) 0) |
| [4] |
钟何平, 唐劲松, 张森. 一种基于质量引导和最小不连续合成的InSAR相位解缠算法[J]. 电子与信息学报, 2011, 33(2): 369-374 (Zhong Heping, Tang Jinsong, Zhang Sen. A Combined Phase Unwrapping Algorithm Based on Quality-Guided and Minimum Discontinuity for InSAR[J]. Journal of Electronics & Information Technology, 2011, 33(2): 369-374)
(  0) 0) |
| [5] |
Flynn T J. Phase Unwrapping Using Discontinuity Optimization[C]. Geoscience and Remote Sensing IEEE International Symposium, Seattle, 1998 https://www.researchgate.net/publication/3760930_Phase_unwrapping_using_discontinuity_optimization
(  0) 0) |
| [6] |
陈强, 杨莹辉, 刘国祥, 等. 基于边界探测的InSAR最小二乘整周相位解缠方法[J]. 测绘学报, 2012, 41(3): 441-448 (Chen Qiang, Yang Yinghui, Liu Guoxiang, et al. InSAR Phase Unwrapping Using Least Squares Method with Integer Ambiguity Resolution and Edge Detection[J]. Acta Geodaeticaet Cartographica Sinica, 2012, 41(3): 441-448)
(  0) 0) |
| [7] |
陆军, 李积江, 王成成, 等. 基于构造边的精确快速相位解缠算法[J]. 光电子·激光, 2015, 26(1): 122-129 (Lu Jun, Li Jijiang, Wang Chengcheng, et al. An Accurate and Fast Phase Unwrapping Algorithm Based on Constructed Edge[J]. Journal of Optoelectronics·Laser, 2015, 26(1): 122-129)
(  0) 0) |
| [8] |
Ghiglia D C, Romero L A. Minimum Lp-Norm Two-Dimensional Phase Unwrapping[J]. Journal of the Optical Society of America A, 1996, 13(10): 1999-2013 DOI:10.1364/JOSAA.13.001999
(  0) 0) |
| [9] |
Ghiglia D C, Romero L A. Robust Two-Dimensional Weighted and Unweighted Phase Unwrapping That Uses Fast Transforms and Iterative Methods[J]. Journal of the Optical Society of America A, 1994, 11(1): 107-117 DOI:10.1364/JOSAA.11.000107
(  0) 0) |
| [10] |
Liu H T, Xing M D, Bao Z. A Novel Mixed-Norm Multibaseline Phase-Unwrapping Algorithm Based on Linear Programming[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(5): 1086-1090 DOI:10.1109/LGRS.2014.2381666
(  0) 0) |
| [11] |
刘国林, 郝华东, 陶秋香. 卡尔曼滤波相位解缠及其与其他方法的对比分析[J]. 武汉大学学报:信息科学版, 2010, 35(10): 1174-1178 (Liu Guolin, Hao Huadong, Tao Qiuxiang. Kalman Filter Phase Unwrapping Algorithm and Comparison and Analysis with Other Methods[J]. Geomatics and Information Science of Wuhan University, 2010, 35(10): 1174-1178)
(  0) 0) |
| [12] |
魏志强, 金亚秋. 基于蚁群算法的InSAR相位解缠算法[J]. 电子与信息学报, 2008, 30(3): 518-523 (Wei Zhiqiang, Jin Yaqiu. InSAR Phase Unwrapping Algorithm Based on Ant Colony Algorithm[J]. Journal of Electronics & Information Technology, 2008, 30(3): 518-523)
(  0) 0) |
| [13] |
Aubert G, Kornprobst P. Mathematical Problems in Image Processing[M]. New York: Springer, 2006
(  0) 0) |
| [14] |
Chen C W. Statistical-Cost Network-Flow Approaches to Two-Dimensional Phase Unwrapping for Radar Interferometry[D]. Palo Alto: Stanford University, 2001 http://citeseerx.ist.psu.edu/showciting?cid=488208
(  0) 0) |
| [15] |
Aubert G, Kornprobst P. Mathematical Problems in Image Processing[M]. New York: Spinger, 2006
(  0) 0) |
| [16] |
Kahan W M. Numerical Linear Algebra[M]. Lincoln: Mathematics & Computer Education, 2013
(  0) 0) |
| [17] |
Demmel J W. Applied Numerical Linear Algebra[M]. USA: Society for Industrial and Applied Mathematics, 1997
(  0) 0) |
2. School of Geographic and Biologic Information, Nanjing University of Posts and Telecommunications, 9 Wenyuan Road, Nanjing 210023, China;
3. Shandong Provincal Institute of Land Surveying and Mapping, 2289 East-Jingshi Road, Ji'nan 250013, China
 2019, Vol. 39
2019, Vol. 39

