灰色模型(grey model, GM)能根据少量信息建模和预测，杂乱无章的数据经过灰色系统处理后可以表现出规律性，因而受到广泛关注，被应用于很多领域。陈明东等^[1]将GM(1, 1)用于滑坡变形监测中。汪凡等^[2]将灰色关联模型和主成分分析相结合应用于公司绩效评价。然而在实际工程中，很难保证原始序列是等时间间隔采集的，因此需要采用非等间距GM(1, 1)模型进行预测。关于非等间距GM(1, 1)模型及其拓展研究已有许多。王钟羡等^[3]将等间距GM(1, 1)模型推广到非等间距GM(1, 1)模型，给出非等间距GM(1, 1)模型的基本理论和方法。李克昭等^[4]将加权非等间距GM(1, 1)模型与线性回归相结合，提出灰线性加权非等间距GM(1, 1)模型。陈鹏宇等^[5]探讨了3种非等间距GM(1, 1)模型在沉降预测中的应用。以上研究均采用最小二乘求解，忽略了系数矩阵的误差。然而实际上系数矩阵是由原始序列组成的，原始序列中的元素一般是通过观测和计算得到的，所以不可避免地带有误差，即系数矩阵也是有误差的。因此有学者将同时考虑系数矩阵和观测向量误差的总体最小二乘(total least squares, TLS)平差用于GM(1, 1)模型中。冯健等^[6]采用TLS求解GM(1, 1)模型，并用于高速铁路监测，但没有顾及系数矩阵中含有无误差的常数项。袁豹等^[7]同样将TLS用于GM(1, 1)模型，并考虑到了系数矩阵和观测向量的权阵，可以保证系数矩阵中常数项的改正数为0，但没有考虑到系数矩阵中各随机项的相关性，不能保证不同位置的相同元素有相同的改正数。为此，陶武勇等^[8]针对GM(1, 1)模型推导了一种TLS算法，可以保证相同元素有相同的改正数。显然，对于非等间距GM(1, 1)模型，同样需要采用TLS求解，但关于TLS在非等间距GM(1, 1)模型的应用还没有报道过。

邓聚龙等^[9]早已提出GM(1, 1)模型中存在病态问题，采用不同的计算精度会导致不同的计算结果。因为当系数矩阵病态时，其解不稳定，数据的微小变化会引起解的巨大变化。吴正鹏等^[10]分析了GM(1, 1)模型产生病态的原因，并提出用数乘变换的方法解决病态问题。郑照宁等^[11]认为，所有的灰色模型都存在严重的病态问题，并且这种病态性来源于模型本身，很难克服。王钟羡等^[3]提出将序列的间距作为乘子，建立的非等间距序列的GM(1, 1)模型方法与等间距序列相同，由于序列的间距往往都是大于1的，因此将其作为乘子会加重病态程度，即对于同一组数据，非等间距GM(1, 1)模型病态问题比等间距GM(1, 1)模型病态问题严重。

考虑到系数矩阵中含有误差，本文采用TLS求解非等间距GM(1, 1)模型，而Golub等^[12]指出，TLS的求解过程是降正则化的过程，因此更需要解决病态问题。唐利民等^[13]提出通过调整计量单位的方式来改善病态问题，然后通过一系列复杂的推导得到新的GM(1, 1)模型，并证明调整实测数据的计量单位不会影响灰参数的求解以及模型的预测精度。该方法实际上与吴正鹏等^[10]提出的数乘变换法一样，如将实测数据的单位从mm改为cm，则实测数据乘上了0.1。本文从平差函数模型入手，对系数矩阵的常数列乘以常数c，通过调节c的大小来改变法方程系数矩阵的条件数，选择合适的c值可以改善病态问题。然后，综合考虑系数矩阵中含有无误差的常数项、有误差的随机项和重复元素时，按照PEIV模型加权总体最小二乘算法^[14]构建平差的函数模型，在算法上又有所差异，推导了一种适合非等间距GM(1, 1)模型求解的TLS算法。

1 非等间距GM(1, 1)模型的病态问题 1.1 非等间距GM(1, 1)模型

设有非负原始序列为:

$ {\mathit{\boldsymbol{X}}^{\left( 0 \right)}} = {\left[ {{x^{\left( 0 \right)}}\left( {{t_1}} \right),{x^{\left( 0 \right)}}\left( {{t_2}} \right), \cdots ,{x^{\left( 0 \right)}}\left( {{t_n}} \right)} \right]^{\rm{T}}} $

(1)

式中，t_i(i=1, 2, …, n)为观测时刻，x⁽⁰⁾(t_i)为t_i时刻的观测值。

进行一次累加得到累加序列^[3]：

$ {\mathit{\boldsymbol{X}}^{\left( 1 \right)}} = {\left[ {{x^{\left( 1 \right)}}\left( {{t_1}} \right),{x^{\left( 1 \right)}}\left( {{t_2}} \right), \cdots ,{x^{\left( 1 \right)}}\left( {{t_n}} \right)} \right]^{\rm{T}}} $

(2)

其中, x⁽¹⁾(t_i)$\sum\limits_{j = 1}^i {{x^{\left( 0 \right)}}} $(t_j)Δt_j(i=1, 2, …n)，Δt_j为时间间隔，Δt_j=t_j-t_j-1，令Δt₁=1。则可以得到白微分方程的系数矩阵和观测向量:

$ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} { - {z^{\left( 1 \right)}}\left( {{t_2}} \right)}&1\\ { - {z^{\left( 1 \right)}}\left( {{t_3}} \right)}&1\\ \vdots&\vdots \\ { - {z^{\left( 1 \right)}}\left( {{t_n}} \right)}&1 \end{array}} \right],\mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} {{x^{\left( 0 \right)}}\left( {{t_2}} \right)}\\ {{x^{\left( 0 \right)}}\left( {{t_3}} \right)}\\ \vdots \\ {{x^{\left( 0 \right)}}\left( {{t_n}} \right)} \end{array}} \right] $

(3)

式中, z⁽¹⁾(t_i)为背景值，z⁽¹⁾(t_i)=$\frac{1}{2}$(x⁽¹⁾(t_i-1)+x⁽¹⁾(t_i))。

若忽略系数矩阵误差，可采用最小二乘解得:

$ \mathit{\boldsymbol{\hat \xi }} = {\left[ {\begin{array}{*{20}{c}} {\hat a}&{\hat u} \end{array}} \right]^{\rm{T}}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}} $

(4)

则法方程系数矩阵为:

$ {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {\sum\limits_{i = 2}^n {{{\left( {{z^{\left( 1 \right)}}\left( {{t_i}} \right)} \right)}^2}} }&{ - \sum\limits_{i = 2}^n {{z^{\left( 1 \right)}}\left( {{t_i}} \right)} }\\ { - \sum\limits_{i = 2}^n {{z^{\left( 1 \right)}}\left( {{t_i}} \right)} }&{n - 1} \end{array}} \right] $

(5)

1.2 病态问题

吴正鹏等^[10]总结了等间距GM(1, 1)模型产生病态的原因，认为引起矩阵A^TA条件数变大的原因只有2个：原始数据过大或数据病态(即近似为首项不为0、其他项为0的常数序列)。对于后一类问题没有现实意义，不必深究，因此产生病态的原因主要是前者。因为原始数据过大，导致$\sum\limits_{i = 1}^n {{{\left( {{z^{\left( 1 \right)}}\left( {{t_i}} \right)} \right)}^2}} $的值很大，与A^TA的另一对角元素n-1相差过大，则A^TA的条件数也会很大。比较非等间距GM(1, 1)模型与等间距GM(1, 1)模型的构建过程可以发现，其区别在于非等间距GM(1, 1)模型在构建累加序列X⁽¹⁾时乘上了时间间隔Δt_j，而Δt_j往往是大于1的值，因此与等间距GM(1, 1)模型相比，其计算得到的X⁽¹⁾会更大，导致$\sum\limits_{i = 2}^n {{{\left( {{z^{\left( 1 \right)}}\left( {{t_i}} \right)} \right)}^2}} $与n-1相差更大，病态程度加深。以文献[4]前12期数据为原始序列数据，计算得到等间距GM(1, 1)模型的法方程系数矩阵条件数为9.770 4×10³，非等间距GM(1, 1)模型的法方程系数矩阵条件数为8.704 9×10⁵，可见非等间距GM(1, 1)模型病态问题更为严重。

采用TLS求解非等间距GM(1, 1)模型，同样受病态的影响，导致计算结果不稳定，因此本文提出对系数矩阵A的常数列乘以常数c，则系数矩阵变为：

$ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} { - {z^{\left( 1 \right)}}\left( {{t_2}} \right)}&c\\ { - {z^{\left( 1 \right)}}\left( {{t_3}} \right)}&c\\ \vdots&\vdots \\ { - {z^{\left( 1 \right)}}\left( {{t_n}} \right)}&c \end{array}} \right] $

(6)

对应的参数估值变为$\mathit{\boldsymbol{\hat \xi = }}{\left[ {\hat a\;\;\frac{{\hat u}}{c}} \right]^{\rm{T}}}$，令$\hat b = \frac{{\hat u}}{c}$，则有$\hat u = c\hat b$，$\mathit{\boldsymbol{\hat \xi = }}{\left[ {\hat a\;\;\hat b} \right]^{\rm{T}}}$。

法方程系数矩阵变为：

$ {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {\sum\limits_{i = 2}^n {{{\left( {{z^{\left( 1 \right)}}\left( {{t_i}} \right)} \right)}^2}} }&{ - c\sum\limits_{i = 2}^n {{z^{\left( 1 \right)}}\left( {{t_i}} \right)} }\\ { - c\sum\limits_{i = 2}^n {{z^{\left( 1 \right)}}\left( {{t_i}} \right)} }&{{c^2}\left( {n - 1} \right)} \end{array}} \right] $

(7)

通过调节c值，可以通过减小$\sum\limits_{i = 2}^n {{{\left( {{z^{\left( 1 \right)}}\left( {{t_i}} \right)} \right)}^2}} $与c²(n-1)的相对大小，达到改善病态问题的目的。而唐利民等^[13]则通过调整计量单位的方式来减小原始数据，从而减小$\sum\limits_{i = 2}^n {{{\left( {{z^{\left( 1 \right)}}\left( {{t_i}} \right)} \right)}^2}} $与n-1的相对大小。所以2种方法的本质是一样的，都是使A^TA的2个主对角线元素相互接近。但唐利民等^[13]的方法推导繁琐，本文的方法更简单、直观。

2 总体最小二乘算法推导

将z⁽¹⁾(t_i)=$\frac{1}{2}$(x⁽¹⁾(t_i-1)+x⁽¹⁾(t_i))代入式(6)中，并顾及x⁽¹⁾(t_i)=$\sum\limits_{j = 1}^i {{x^{\left( 0 \right)}}\left( {{t_j}} \right)\Delta {t_j}} $得:

$ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} { - {x^{\left( 0 \right)}}\left( {{t_1}} \right)\Delta {t_1} - \frac{1}{2}{x^{\left( 0 \right)}}\left( {{t_2}} \right)\Delta {t_2}}&c\\ { - {x^{\left( 0 \right)}}\left( {{t_1}} \right)\Delta {t_1} - {x^{\left( 0 \right)}}\left( {{t_2}} \right)\Delta {t_2} - \frac{1}{2}{x^{\left( 0 \right)}}\left( {{t_3}} \right)\Delta {t_3}}&c\\ \vdots&\vdots \\ { - {x^{\left( 0 \right)}}\left( {{t_1}} \right)\Delta {t_1} - {x^{\left( 0 \right)}}\left( {{t_2}} \right)\Delta {t_2} - \cdots - \frac{1}{2}{x^{\left( 0 \right)}}\left( {{t_n}} \right)\Delta {t_n}}&c \end{array}} \right] $

(8)

可以发现，系数矩阵A和观测向量L的误差均来源于原始序列，它们误差同源，不同位置有重复元素存在，并且系数矩阵中有常数项存在。为此，本文按照PEIV模型加权总体最小二乘构建函数模型，因为PEIV模型加权总体最小二乘综合考虑了系数矩阵的常数项、随机项和重复元素^[14]。

函数模型如下：

$ \left( {{\mathit{\boldsymbol{\xi }}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_{n - 1}}} \right)\left( {\mathit{\boldsymbol{h}} + \mathit{\boldsymbol{Ma}}} \right) = \mathit{\boldsymbol{L}} $

(9)

式中，⊗表示Kronecker积，$\mathit{\boldsymbol{h}} = \left[ \begin{array}{l} {\mathit{\boldsymbol{h}}_1}\\ {\mathit{\boldsymbol{h}}_2} \end{array} \right]$，$\mathop {{\mathit{\boldsymbol{h}}_1}}\limits_{\left( {n - 1} \right) \times 1} = {\left[ {0\;0\; \cdots \;0} \right]^{\rm{T}}}$，$\mathop {{\mathit{\boldsymbol{h}}_2}}\limits_{\left( {n - 1} \right) \times 1} = {\left[ {c\;c\; \cdots \;c} \right]^{\rm{T}}}$，$\mathit{\boldsymbol{M}} = \left[ \begin{array}{l} {\mathit{\boldsymbol{M}}_1}\\ {\mathit{\boldsymbol{M}}_2} \end{array} \right]$，$\mathop {{\mathit{\boldsymbol{M}}_1}}\limits_{\left( {n - 1} \right) \times n} = \left[ \begin{array}{l} - \Delta {t_1}\;\; - \frac{1}{2}\Delta {t_2}\;\;\;\;\;0\;\;\;\;\;\;\; \cdots \;\;\;\;\;\;0\\ {\rm{ - }}\Delta {t_1}\;\;\;\; - \Delta {t_2}\;\;\; - \frac{1}{2}\Delta {t_3}\;\;\; \cdots \;\;\;\;\;\;0\\ \;\; \vdots \;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\; \ddots \;\;\;\;\;\; \vdots \\ - \Delta {t_1}\;\;\; - \Delta {t_2}\;\;\;\; - \Delta {t_3}\;\;\;\; \cdots \;\;\; - \frac{1}{2}\Delta {t_n} \end{array} \right]$，M₂=0_(n-1)×n，a为原始序列组成的列向量，即a=X⁽⁰⁾，I_n-1为(n-1)×(n-1)的单位矩阵。

因为原始序列含有误差，则式(9)变为：

$ \left( {{\mathit{\boldsymbol{\xi }}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_{n - 1}}} \right)\left( {\mathit{\boldsymbol{h}} + \mathit{\boldsymbol{M}}\left( {{\mathit{\boldsymbol{X}}^{\left( 0 \right)}} - \Delta {\mathit{\boldsymbol{X}}^{\left( 0 \right)}}} \right)} \right) = \mathit{\boldsymbol{L}} - \mathit{\boldsymbol{N}}\Delta {\mathit{\boldsymbol{X}}^{\left( 0 \right)}} $

(10)

式中，$\mathop {\mathit{\boldsymbol{N}}}\limits_{\left( {n - 1} \right) \times n} = \left[ {\begin{array}{*{20}{c}} 0&1&0& \cdots &0\\ 0&0&1& \cdots &0\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0&0& \cdots &0&1 \end{array}} \right]$，ΔX⁽⁰⁾为原始序列误差组成的列向量。

由于原始序列一般是独立等精度观测的，所以此时的平差准则为(ΔX⁽⁰⁾)^TΔX⁽⁰⁾=min，与式(7)构建Lagrange目标函数：

$ \begin{array}{*{20}{c}} {\mathit{\Phi }\left( {\Delta {\mathit{\boldsymbol{X}}^{\left( 0 \right)}},\mathit{\boldsymbol{\xi }},\mathit{\boldsymbol{\lambda }}} \right) = {{\left( {\Delta {\mathit{\boldsymbol{X}}^{\left( 0 \right)}}} \right)}^{\rm{T}}}\Delta {\mathit{\boldsymbol{X}}^{\left( 0 \right)}} + }\\ {2{\mathit{\boldsymbol{\lambda }}^{\rm{T}}}\left( {\mathit{\boldsymbol{L}} - \left( {{\mathit{\boldsymbol{\xi }}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_{n - 1}}} \right)\mathit{\boldsymbol{h}} - \left( {{\mathit{\boldsymbol{\xi }}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_{n - 1}}} \right)\mathit{\boldsymbol{M}}{\mathit{\boldsymbol{X}}^{\left( 0 \right)}} + } \right.}\\ {\left. {\left( {{\mathit{\boldsymbol{\xi }}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_{n - 1}}} \right)\mathit{\boldsymbol{M}}\Delta {\mathit{\boldsymbol{X}}^{\left( 0 \right)}} - \mathit{\boldsymbol{N}}\Delta {\mathit{\boldsymbol{X}}^{\left( 0 \right)}}} \right)} \end{array} $

(11)

式中，λ为Lagrange乘常数向量。对上式求偏导数，并令其等于0得：

$ \begin{array}{*{20}{c}} {\frac{1}{2}\frac{{\partial \mathit{\Phi }\left( {\Delta {\mathit{\boldsymbol{X}}^{\left( 0 \right)}},\mathit{\boldsymbol{\xi }},\mathit{\boldsymbol{\lambda }}} \right)}}{{\partial \left( {\Delta {\mathit{\boldsymbol{X}}^{\left( 0 \right)}}} \right)}} = }\\ {\Delta {\mathit{\boldsymbol{X}}^{\left( 0 \right)}} + {{\left( {\left( {{\mathit{\boldsymbol{\xi }}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_{n - 1}}} \right)\mathit{\boldsymbol{M}} - \mathit{\boldsymbol{N}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\lambda }} = 0} \end{array} $

(12)

$ \begin{array}{*{20}{c}} {\frac{1}{2}\frac{{\partial \mathit{\Phi }\left( {\Delta {\mathit{\boldsymbol{X}}^{\left( 0 \right)}},\mathit{\boldsymbol{\xi }},\mathit{\boldsymbol{\lambda }}} \right)}}{{\partial \left( \mathit{\boldsymbol{\xi }} \right)}} = }\\ { - \left( {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{h}}_1}}&{{\mathit{\boldsymbol{h}}_2}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_1}{\mathit{\boldsymbol{X}}^{\left( 0 \right)}}}&{{\mathit{\boldsymbol{M}}_2}{\mathit{\boldsymbol{X}}^{\left( 0 \right)}}} \end{array}} \right] - } \right.}\\ {{{\left. {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_1}\Delta {\mathit{\boldsymbol{X}}^{\left( 0 \right)}}}&{{\mathit{\boldsymbol{M}}_2}\Delta {\mathit{\boldsymbol{X}}^{\left( 0 \right)}}} \end{array}} \right]} \right)}^{\rm{T}}}\mathit{\boldsymbol{\lambda }} = 0} \end{array} $

(13)

$ \begin{array}{*{20}{c}} {\frac{1}{2}\frac{{\partial \mathit{\Phi }\left( {\Delta {\mathit{\boldsymbol{X}}^{\left( 0 \right)}},\mathit{\boldsymbol{\xi }},\mathit{\boldsymbol{\lambda }}} \right)}}{{\partial \left( \mathit{\boldsymbol{\lambda }} \right)}} = }\\ {\mathit{\boldsymbol{L}} - \left( {{\mathit{\boldsymbol{\xi }}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_{n - 1}}} \right)\mathit{\boldsymbol{h}} - \left( {{\mathit{\boldsymbol{\xi }}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_{n - 1}}} \right)\mathit{\boldsymbol{M}}{\mathit{\boldsymbol{X}}^{\left( 0 \right)}} + }\\ {\left( {{\mathit{\boldsymbol{\xi }}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_{n - 1}}} \right)\mathit{\boldsymbol{M}}\Delta {\mathit{\boldsymbol{X}}^{\left( 0 \right)}} - \mathit{\boldsymbol{N}}\Delta {\mathit{\boldsymbol{X}}^{\left( 0 \right)}} = 0} \end{array} $

(14)

由式(12)得：

$ \Delta {{\mathit{\boldsymbol{\hat X}}}^{\left( 0 \right)}} = - {\left( {\left( {{{\mathit{\boldsymbol{\hat \xi }}}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_{n - 1}}} \right)\mathit{\boldsymbol{M}} - \mathit{\boldsymbol{N}}} \right)^{\rm{T}}}\mathit{\boldsymbol{\hat \lambda }} $

(15)

将式(15)代入式(14)得：

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat \lambda }} = {{\left( {\left( {\left( {{{\mathit{\boldsymbol{\hat \xi }}}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_{n - 1}}} \right)\mathit{\boldsymbol{M}} - \mathit{\boldsymbol{N}}} \right){{\left( {\left( {{{\mathit{\boldsymbol{\hat \xi }}}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_{n - 1}}} \right)\mathit{\boldsymbol{M}} - \mathit{\boldsymbol{N}}} \right)}^{\rm{T}}}} \right)}^{ - 1}}}\\ {\left( {\mathit{\boldsymbol{L}} - \left( {{{\mathit{\boldsymbol{\hat \xi }}}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_{n - 1}}} \right)\mathit{\boldsymbol{h}} - \left( {{{\mathit{\boldsymbol{\hat \xi }}}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_{n - 1}}} \right)\mathit{\boldsymbol{M}}{\mathit{\boldsymbol{X}}^{\left( 0 \right)}}} \right) = }\\ {{\mathit{\boldsymbol{D}}^{ - 1}}\left( {\mathit{\boldsymbol{L}} - \left( {{{\mathit{\boldsymbol{\hat \xi }}}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_{n - 1}}} \right)\mathit{\boldsymbol{h}} - \left( {{{\mathit{\boldsymbol{\hat \xi }}}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_{n - 1}}} \right)\mathit{\boldsymbol{M}}{\mathit{\boldsymbol{X}}^{\left( 0 \right)}}} \right) = }\\ {{\mathit{\boldsymbol{D}}^{ - 1}}\left( {\mathit{\boldsymbol{L}} - \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{h}}_1}}&{{\mathit{\boldsymbol{h}}_2}} \end{array}} \right]\mathit{\boldsymbol{\hat \xi }} - \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_1}\Delta {\mathit{\boldsymbol{X}}^{\left( 0 \right)}}}&{{\mathit{\boldsymbol{M}}_2}\Delta {\mathit{\boldsymbol{X}}^{\left( 0 \right)}}} \end{array}} \right]\mathit{\boldsymbol{\hat \xi }}} \right)} \end{array} $

(16)

式中，$\mathit{\boldsymbol{D}} = (({\mathit{\boldsymbol{\hat \xi }}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_{n - 1}})\mathit{\boldsymbol{M}} - \mathit{\boldsymbol{N}}){(({\mathit{\boldsymbol{\hat \xi }}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_{n - 1}})\mathit{\boldsymbol{M}} - \mathit{\boldsymbol{N}})^{\rm{T}}}$，符号“^”表示最佳估值。

将式(16)代入式(13)得：

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat \xi }} = \left[ {\left( {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{h}}_1}}&{{\mathit{\boldsymbol{h}}_2}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_1}{\mathit{\boldsymbol{X}}^{\left( 0 \right)}}}&{{\mathit{\boldsymbol{M}}_2}{\mathit{\boldsymbol{X}}^{\left( 0 \right)}}} \end{array}} \right] - } \right.} \right.}\\ {{{\left. {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_1}\Delta {{\mathit{\boldsymbol{\hat X}}}^{\left( 0 \right)}}}&{{\mathit{\boldsymbol{M}}_2}\Delta {{\mathit{\boldsymbol{\hat X}}}^{\left( 0 \right)}}} \end{array}} \right]} \right)}^{\rm{T}}}{\mathit{\boldsymbol{D}}^{ - 1}}\left( {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{h}}_1}}&{{\mathit{\boldsymbol{h}}_2}} \end{array}} \right] + } \right.}\\ {{{\left. {\left. {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_1}{\mathit{\boldsymbol{X}}^{\left( 0 \right)}}}&{{\mathit{\boldsymbol{M}}_2}{\mathit{\boldsymbol{X}}^{\left( 0 \right)}}} \end{array}} \right]} \right)} \right]}^{ - 1}}\left( {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{h}}_1}}&{{\mathit{\boldsymbol{h}}_2}} \end{array}} \right] + } \right.}\\ {{{\left. {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_1}{\mathit{\boldsymbol{X}}^{\left( 0 \right)}}}&{{\mathit{\boldsymbol{M}}_2}{\mathit{\boldsymbol{X}}^{\left( 0 \right)}}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_1}\Delta {{\mathit{\boldsymbol{\hat X}}}^{\left( 0 \right)}}}&{{\mathit{\boldsymbol{M}}_2}\Delta {{\hat X}^{\left( 0 \right)}}} \end{array}} \right]} \right)}^{\rm{T}}}{\mathit{\boldsymbol{D}}^{ - 1}}\mathit{\boldsymbol{L}}} \end{array} $

(17)

由式(9)的构建过程可以看出，A=[h₁  h₂]+[M₁X⁽⁰⁾  M₂X⁽⁰⁾]，M₂=0_(n-1)×n，代入式(16)、(17)得：

$ \mathit{\boldsymbol{\hat \lambda }} = {\mathit{\boldsymbol{D}}^{ - 1}}\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A\hat \xi }}} \right) $

(18)

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat \xi }} = {{\left( {{{\left( {\mathit{\boldsymbol{A}} - \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_1}\Delta {{\mathit{\boldsymbol{\hat X}}}^{\left( 0 \right)}}}&{{\mathit{\boldsymbol{0}}_{\left( {n - 1} \right) \times 1}}} \end{array}} \right]} \right)}^{\rm{T}}}{\mathit{\boldsymbol{D}}^{ - 1}}\mathit{\boldsymbol{A}}} \right)}^{ - 1}}}\\ {{{\left( {\mathit{\boldsymbol{A}} - \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_1}\Delta {{\mathit{\boldsymbol{\hat X}}}^{\left( 0 \right)}}}&{{\mathit{\boldsymbol{0}}_{\left( {n - 1} \right) \times 1}}} \end{array}} \right]} \right)}^{\rm{T}}}{\mathit{\boldsymbol{D}}^{ - 1}}\mathit{\boldsymbol{L}}} \end{array} $

(19)

因为n个原始序列构成n-1个方程，而要求解的未知数为2个，因此自由度为n-3，单位权方差为:

$ \hat \sigma _0^2 = \frac{{\Delta {\mathit{\boldsymbol{X}}^{\left( 0 \right){\rm{T}}}}\Delta {\mathit{\boldsymbol{X}}^{\left( 0 \right)}}}}{{n - 3}} = \frac{{{{\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A\hat \xi }}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{D}}^{ - 1}}\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A\hat \xi }}} \right)}}{{n - 3}} $

(20)

总结计算步骤如下：

1) 按最小二乘计算初值${\mathit{\boldsymbol{\hat \xi }}_{(0)}}$；

2) $\mathit{\boldsymbol{D}} = ((\mathit{\boldsymbol{\hat \xi }}_{\left( i \right)}^{\rm{T}} \otimes {\mathit{\boldsymbol{I}}_{n - 1}})\mathit{\boldsymbol{M}} - \mathit{\boldsymbol{N}}){((\mathit{\boldsymbol{\hat \xi }}_{\left( i \right)}^{\rm{T}} \otimes {\mathit{\boldsymbol{I}}_{n - 1}})\mathit{\boldsymbol{M}} - \mathit{\boldsymbol{N}})^{\rm{T}}}, $$\mathit{\boldsymbol{\hat \lambda }} = {\mathit{\boldsymbol{D}}^{ - 1}}(\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{\hat \xi }}_{(i)}}), \Delta {\mathit{\boldsymbol{\hat X}}^{(0)}} = - {((\mathit{\boldsymbol{\hat \xi }}_{\left( i \right)}^{\rm{T}} \otimes {\mathit{\boldsymbol{I}}_{n - 1}})\mathit{\boldsymbol{M}} - \mathit{\boldsymbol{N}})^{\rm{T}}}\mathit{\boldsymbol{\hat \lambda }}$，${\mathit{\boldsymbol{\hat \xi }}_{(i + 1)}} = {\left( {{{\left( {\mathit{\boldsymbol{A}} - \left[ {{\mathit{\boldsymbol{M}}_1}\Delta {{\mathit{\boldsymbol{\hat X}}}^{(0)}}\;\;{\mathit{\boldsymbol{0}}_{(n - 1) \times 1}}} \right]} \right)}^{\rm{T}}}{\mathit{\boldsymbol{D}}^{ - 1}}\mathit{\boldsymbol{A}}} \right)^{ - 1}}{\left( {\mathit{\boldsymbol{A}} - \left[ {{\mathit{\boldsymbol{M}}_1}\Delta {{\mathit{\boldsymbol{\hat X}}}^{(0)}}\;\;{\mathit{\boldsymbol{0}}_{(n - 1) \times 1}}} \right]} \right)^{\rm{T}}}{\mathit{\boldsymbol{D}}^{ - 1}}\mathit{\boldsymbol{L}}$;

3) 重复步骤2)，直至$\left\| {{{\mathit{\boldsymbol{\hat \xi }}}_{(i + 1)}} - {{\mathit{\boldsymbol{\hat \xi }}}_{(i)}}} \right\| \le \varepsilon $(ε为一极小值)，迭代结束；

4) 按式(20)计算单位权方差。

3 工程应用

采用文献[4]中某居民楼CJ1沉降点的沉降累计观测数据。如表 1所示，利用前12期沉降数据预测13期沉降数据。

3.1 确定c值

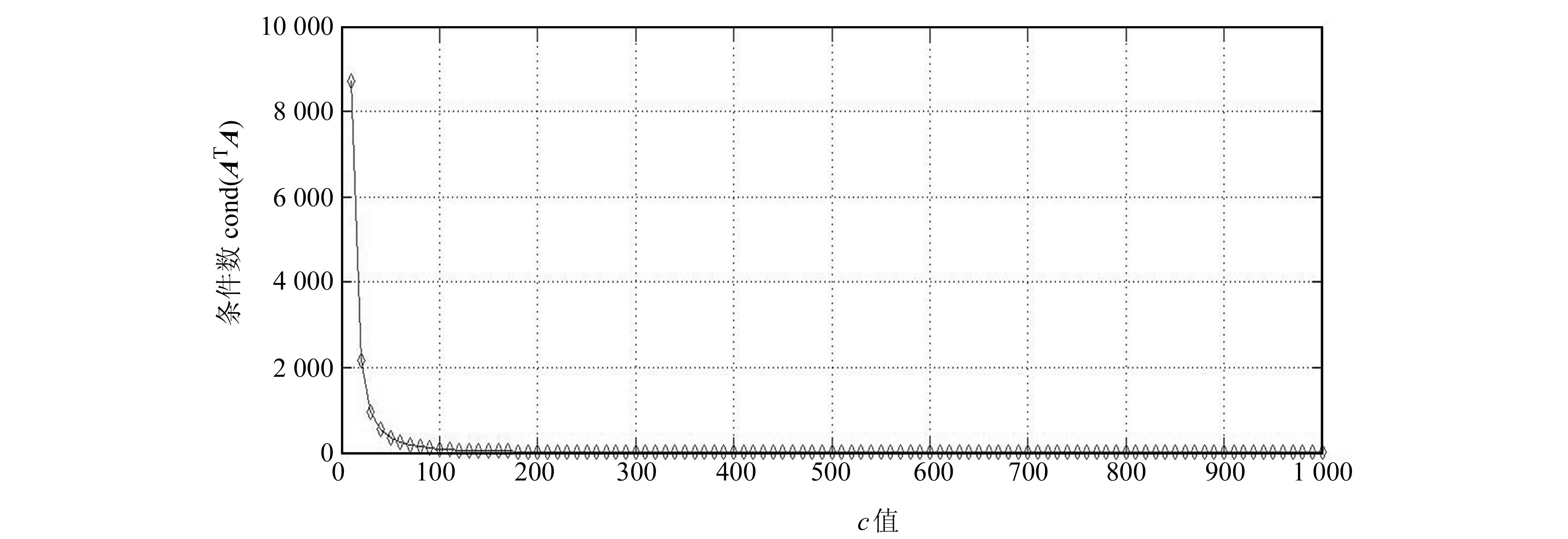
为了改善病态问题，保证TLS计算结果的稳定性，需要确定合适的c值，而病态程度是通过条件数cond(A^TA)来判断的^[15]，因此绘制出c值与cond(A^TA)的曲线图。c取值范围为10到1 000，步长为10，计算每次c值对应的条件数cond(A^TA)，得到的曲线图如图 1所示。

从图 1可以看出，随着c值的增大，条件数先是急速下降，然后趋于平缓，病态性得到极大改善。当c值取100时，条件数为90.917 4，小于100，此时法方程系数矩阵轻度病态；当c值取450时，条件数为9.926 5，小于10，此时法方程系数矩阵是良态的，模型已经稳定，可以放心利用非等间距GM(1, 1)模型建模。因此本文TLS计算时取c值为450即可。

3.2 改变c值对计算结果的影响

唐利民等^[13]通过推导证明了调整计量单位不会改变GM(1, 1)模型的相对残差、平均残差和预测精度。荆科等^[16]通过算列证明了数乘变换不会改变GM(1, 1)模型的相对残差、平均残差和预测精度。为此，此节将分析改变c值对TLS求解非等间距GM(1, 1)模型的影响。分别取c为1(此时即为未处理的非等间距GM(1, 1)模型)、10、100、200和450，采用本文的TLS算法求解，并按式(21)进行预测^[3]：

$ \begin{array}{*{20}{c}} {{{\hat X}^{\left( 0 \right)}}\left( {{t_{i + 1}}} \right) = \frac{1}{{\Delta {t_{i + 1}}}}\left( {1 - {{\rm{e}}^{a\Delta {t_{i + 1}}}}} \right)}\\ {\left( {{x^{\left( 0 \right)}}\left( {{t_1}} \right) - u/a} \right){{\rm{e}}^{ - a\left( {{t_{i + 1}} - {t_1}} \right)}}} \end{array} $

(21)

计算实测数据与预测数据的相对残差Δ_i，然后计算平均残差${\rm{RMS}} = \sqrt {\frac{1}{n}\sum {\Delta _i^2} } $，不同c值计算的相对残差均为(0，-0.634 0，-1.185 2，-1.305 7，-0.739 8，0.369 6，0.733 8，1.114 1，0.089 1，1.835 0，1.418 1，-2.653 1，-1.038 1)，平均残差均为0.339 5。可见对系数矩阵常数列乘以常数c不会改变非等间距GM(1, 1)模型的预测精度，同时能够极大地降低模型的条件数，提高模型的稳定性。

3.3 总体最小二乘算法验证

根据前面的分析结果，取c值为450，这样保证了TLS计算结果的稳定性。为了比较分析，设计如下计算方案：

1) 最小二乘(LS)；

2) 总体最小二乘(TLS)；

3) 加权总体最小二乘^[17](WTLS)，系数矩阵协因数为Q_A=MM^T，观测向量协因数阵为Q_L=NN^T=I_n-1；

4) 本文TLS算法。

计算得到的参数估值和平均残差见表 2。

由表 2可知：

1) LS和TLS计算结果最差，其计算得到的平均残差要大于WTLS和本文TLS，LS忽略了系数矩阵的误差，而TLS则将系数矩阵的常数项也参与了误差分配，因此采用LS和TLS求解非等间距GM(1, 1)模型都是不合理的。

2) 比较WTLS和本文TLS计算结果可以看出，本文TLS计算得到的平均残差都要小于WTLS结果，预测结果与实测数据最相符。WTLS通过协因数传播定律确定系数矩阵的协因数阵，因此确定的协因数阵顾及了系数矩阵各随机项的相关性，可以保证系数矩阵A中相同的元素有相同的改正数，但不能保证系数矩阵A与观测向量L中相同元素有相同的改正数，这与实际理论不符，因为系数矩阵A与观测向量L误差同源。而本文TLS算法则可以保证这一点，因此本文TLS更加合理。

4 结语

在非等间距GM(1, 1)模型中，系数矩阵中含有无误差的常数项和有误差的随机项，并且系数矩阵A与观测向量L不同位置有相同元素存在，这些相同的元素应该有相同的改正数，因此本文推导了一种适合非等间距GM(1, 1)模型求解的总体最小二乘算法。另外，考虑到非等间距GM(1, 1)模型中存在病态问题，为了保证TLS求解的稳定性，提出对系数矩阵常数列乘以常数c的方法来改善病态问题。实验结果表明，本文的TLS算法是可行的，适合非等间距GM(1, 1)模型求解。并且选择合适的c值可以极大降低法方程系数阵的条件数，改善病态问题。