2. 东莞市测绘院,广东省东莞市东城大道268号,523660
随着GPS应用的不断拓展,使用GPS探测水汽中可降水量PWV[1-3]的技术趋于成熟。与传统技术(如卫星辐射计、微波辐射计以及无线探空仪)相比,其具有精度高、时间分辨率高、实时连续、可实现大范围高密度的水汽监测等优势,可以为相关课题的研究提供丰富的水汽资料[4]。应用高效的数据资料分析方法对GPS/PWV时间序列进行分析,可以挖掘出其中蕴含的特征信息并细致地了解水汽演变过程,对与水汽相关的气候建模等研究具有重要参考价值。
GPS/PWV时间序列具有非线性非平稳的特性。Huang等[5]提出一种自适应的时间序列处理的经验模态分解方法(empirical mode decomposition, EMD)。应用EMD方法可以将非线性非平稳的时间序列分解为有限个本征模态分量(intrinsic mode function, IMF)。基于EMD的滤波降噪法与小波分析的效果相当,但EMD是自适应的,且不受小波基选取的影响,也不受傅里叶变换和测不准原理的限制[6]。然而,EMD却存在由间歇信号和噪声造成的模态混叠现象。为了解决这个问题,Wu等[7]利用白噪声尺度均匀及其零均值的特性,提出集成模态分解(ensemble empirical mode decomposition, EEMD)。由EEMD得到的IMF分量不可避免地会被添加的噪声污染。为此,Yeh等[8]提出完全集成经验模态分解方法(complementary ensemble empirical mode decomposition, CEEMD),该方法将随机高斯白噪声以正、负成对的方式加入,能有效消除残余辅助噪声的影响。但EEMD和CEEMD方法都是高耗时的,特别是在数据量较大的时候。另外,由EEMD和CEEMD得到的IMF分量有时是错误的和无意义的。为了克服上述缺陷,Zheng等[9]提出部分集成经验模态分解方法(partly ensemble empirical mode decomposition, PEEMD)。PEEMD方法的本质是对前j个IMF分量以CEEMD的方式得到,并应用排列熵的方法对间歇信号和噪声进行探测,对通过排列熵探测的剩余信号直接应用EMD进行分解。PEEMD方法避免了对所有IMF分量进行不必要的集成和平均次数,极大地缩短了计算时间,并提高了IMF分量的精度。然而,对于所添加白噪声的振幅大小和集成次数这2个关键参数的取值,并没有在PEEMD中给出很好的方法。
本文提出滤波辅助的PEEMD方法,结合滤波辅助的PEEMD和Hilbert谱分析,对GPS/PWV时间序列进行特征提取,并与传统的小波分析进行对比。
1 PWV时间序列特征提取方法对使用PEEMD方法得到的IMF分量进行Hilbert变换之后,再对时间积分可得到Hilbert包络谱[10]。Hilbert包络谱可以提供每个频率对总体幅值(能量)的测量,是一种能量关于频率变化的直接信息,可反映出信号中包含的特征频率。因此,可以应用结合PEEMD方法和Hilbert谱分析对GPS/PWV时间序列进行分析。下面介绍GPS/PWV时间序列特征提取的基本理论。
1.1 滤波辅助的PEEMD在PEEMD方法中,添加白噪声的幅值εn和集成次数N是2个最关键的参数,然而如何确定这2个参数却很困难。Chen等[11]提出,在EEMD中所添加的高斯白噪声应既不影响信号中有效高频成分极值点的分布特性,同时又能改变中低频成分的极值点分布特性。在EEMD中添加白噪声的准则为[12]:
| $ 0 < \alpha < \frac{\sigma }{2} $ | (1) |
式中,α=εn/ε0,σ=εh/ε0,其中εn为加入的高斯白噪声的幅值标准差,ε0为原始信号中有效高频成分的幅值标准差。陈略等[12]建议,在通常情况下,α=σ/4就能有效避免信号分解中的模态混叠现象。
Wu等[7]给出确定集成次数N的公式:
| $ e = \alpha /\sqrt N $ | (2) |
式中,e为信号分解的标准差, 即原始信号与所有相关IMF分量的差值。
参考EEMD方法中确定这2个参数的过程,本文提出一种滤波辅助的PEEMD方法,该方法通过对原始信号进行滤波来确定这2个参数,具体步骤为:1)通过带通或高通滤波器对原始信号进行滤波,获得有效高频成分的幅值标准差εh;2)获得原始信号的幅值标准差ε0;3)确定σ值和α值;4)确定集成次数N;5)基于参数α和N进行PEEMD分解。
滤波器的通带可根据待分析信号的分布特性确定,例如通带选择可采用[3fs/8, fs/2],即包含分析信号的高频段成分,fs为采样率。这样就得到了滤波辅助的PEEMD方法(图 1)。
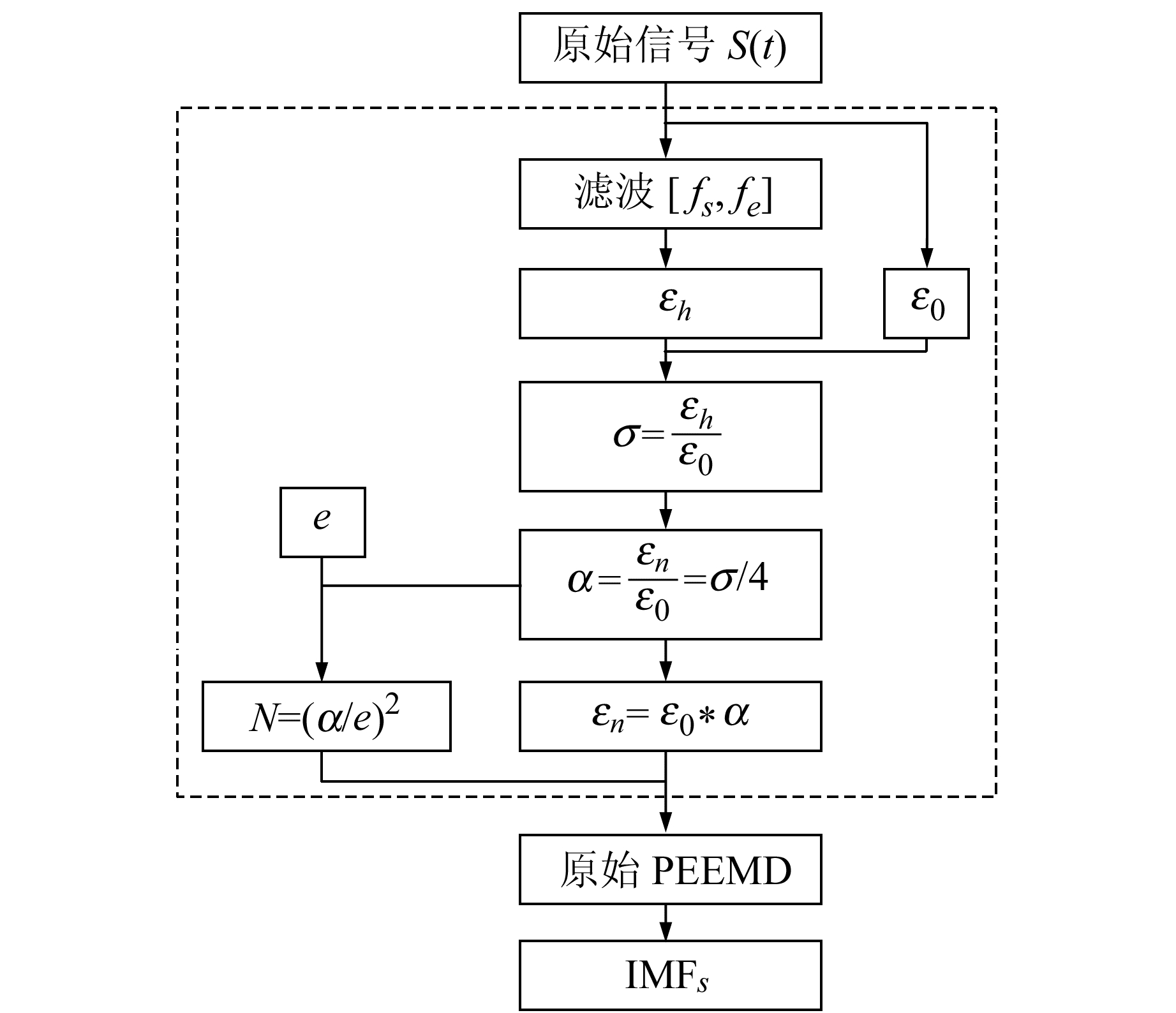
|
图 1 滤波辅助的PEEMD方法流程 Fig. 1 Flow chart of the filter-assisted PEEMD |
在结合滤波辅助的PEEMD方法和Hilbert谱分析的基础上,本文提出GPS/PWV时间序列的特征提取方法,其算法流程见图 2。

|
图 2 GPS/PWV特征提取方法流程 Fig. 2 Flow chart of GPS/PWV feature extraction method |
滤波辅助的PEEMD方法可以将GPS/PWV时间序列分解成有限个IMF分量IMFj(t),j=1, …, n,以及一个剩余项rn(t)。每个IMF分量都是从原始信号中提取出的不同时间尺度的本征能量。对特征IMF分量进行Hilbert变换即可得到GPS/PWV时间序列中的特征频率, 这样就可以在频率域上对特征信息进行进一步的细致分析。
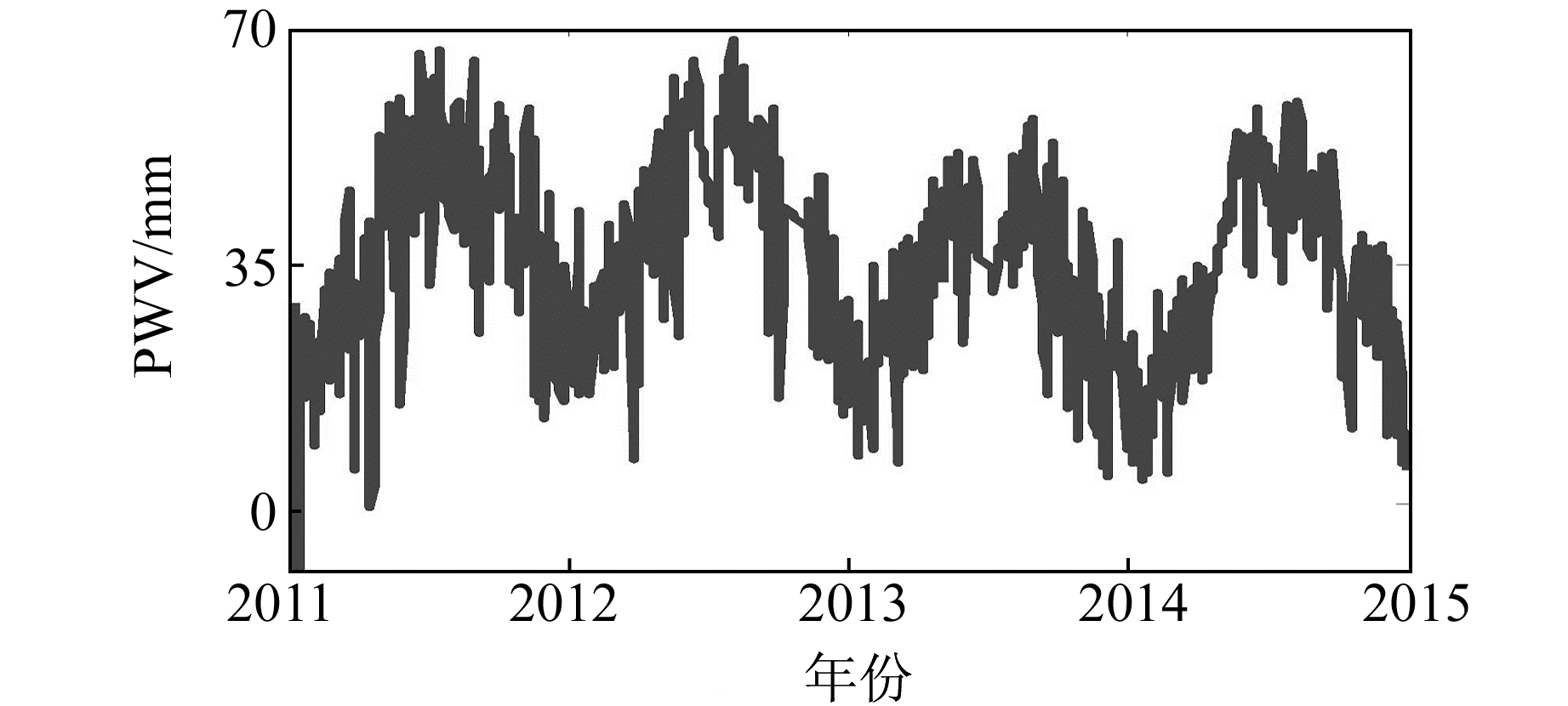
2 实验数据获取和分析 2.1 GPS/PWV时间序列的获取为了获取长时间、高分辨率、高精度的GPS/PWV时间序列,选取中国台湾TNML站点2011-01-01~2014-12-31的观测数据,使用GAMIT/GLOBK软件包解算得到时间跨度为4 a、分辨率为1 h的PWV。图 3为TNML站的GPS/PWV时间序列。
|
图 3 TNML站PWV时间序列 Fig. 3 Time series of PWV at TNML station |
由图 3可以看出,TNML站PWV的范围为0~70 mm。解算得到的GPS/PWV中都含有明显的上升峰值和下降峰值,说明GPS/PWV时间序列中含有可提取的特征信息,提取出这些特征信息可帮助研究GPS/PWV中的变化规律。
2.2 GPS/PWV时间序列特征提取运用本文提出的滤波辅助的PEEMD和Hilbert包络谱分析方法,对TNML站GPS/PWV时间序列分别按长时间(2011-01-01~2014-12-31)和短时间(2014-02-08~02-15)进行分析。选择FIR滤波器,滤波通带设置为[3fs/8, fs/2],其中fs=(1/3 600) Hz,即采样率为1 h,期望的信号误差e设置为0.002。根据Zheng等[9]的实验结果,本文取排列熵阈值θ0=0.5。在以上的参数设置基础上,就可以确定本文提出的滤波辅助的PEEMD参数。表 1为TNML站GPS/PWV时间序列的滤波辅助PEEMD参数。
|
|
表 1 滤波辅助PEEMD的关键参数 Tab. 1 Key parameters of filter-assisted PEEMD |
对TNML站的原始GPS/PWV时间序列信号进行滤波辅助PEEMD分解。为了验证滤波辅助PEEMD的有效性,同时还对GPS/PWV时间序列采用Mallat快速算法、Danbechies4小波分解。图 4、5为长时间分解结果,其中图 4为滤波辅助的PEEMD结果,图 5为小波分解的结果。图 6、7为短时间分解结果,其中图 6为滤波辅助的PEEMD结果,图 7为小波分解的结果。

|
图 4 TNML站4 a滤波辅助PEEMD分解结果 Fig. 4 Filter-assisted PEEMD results of TNML PWV for 4 years |
|
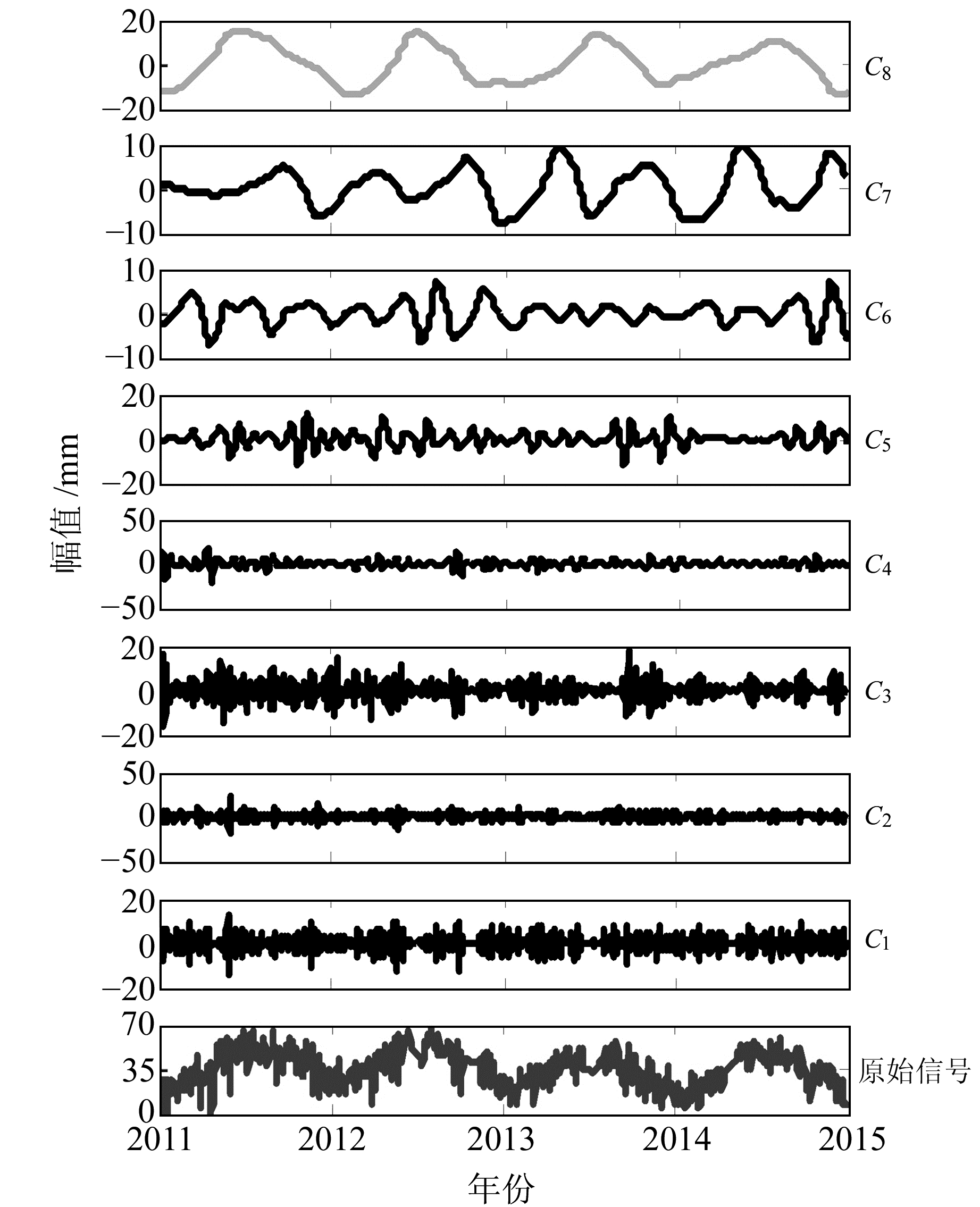
图 5 TNML站4 a小波分解结果 Fig. 5 Wavelet decomposition results of TNML PWV for 4 years |
|
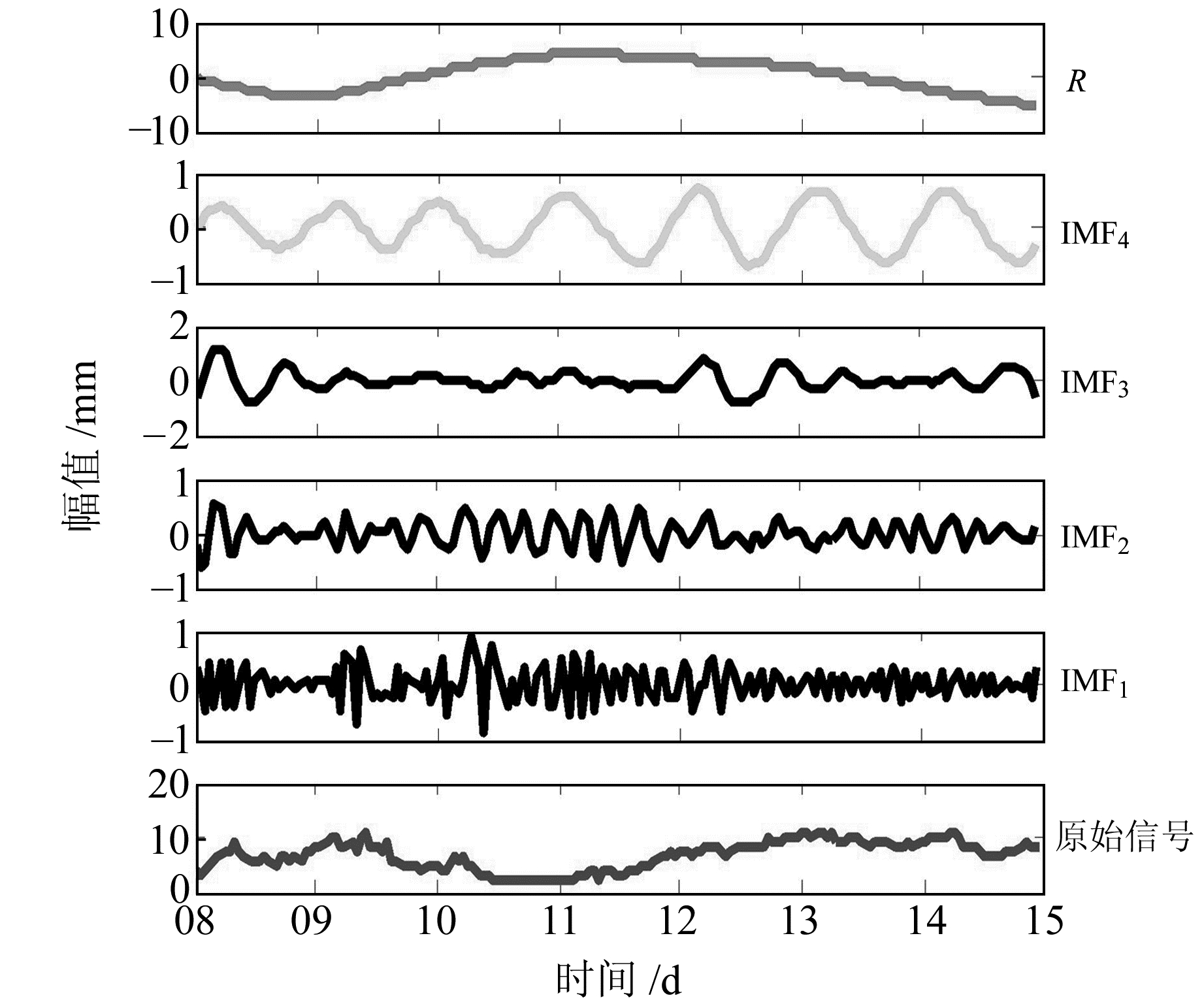
图 6 TNML站7 d滤波辅助PEEMD分解结果 Fig. 6 Filter-assisted PEEMD results of TNML PWV for 7 days |

|
图 7 TNML站7 d小波分解结果 Fig. 7 Wavelet decomposition results of TNML PWV for 7 days |
由图 4可以看出,滤波辅助PEEMD可以将GPS/PWV时间序列中的周年特征分量提取出来,即图中的IMF7分量,其中,TNML站的周年特征分量的振幅为20 mm。由图 5可以看出,小波分解也能将TNML站的GPS/PWV时间序列中的周年特征分量提取出来,即图中C8,周年特征分量的振幅与滤波辅助PEEMD结果一致。由图 6、7可以看出,GPS/PWV时间序列中还含有日特征分量,即图中IMF4和C4, TNML站的日特征分量的振幅均约为1 mm,滤波辅助PEEMD和小波分解的结果也基本一致,但前者特征分量的波形更加平滑均匀。在PEEMD的结果中可以看出,分解得到的趋势项R与原始时间序列的整体也基本一致,因此为了对比两者的差异,本文首先将原始GPS/PWV时间序列减去趋势项R,然后与滤波辅助PEEMD和小波分解的特征分量进行比较。图 8为TNML站的4 a时间序列对比结果,图 9为TNML站的7 d时间序列对比结果。
|
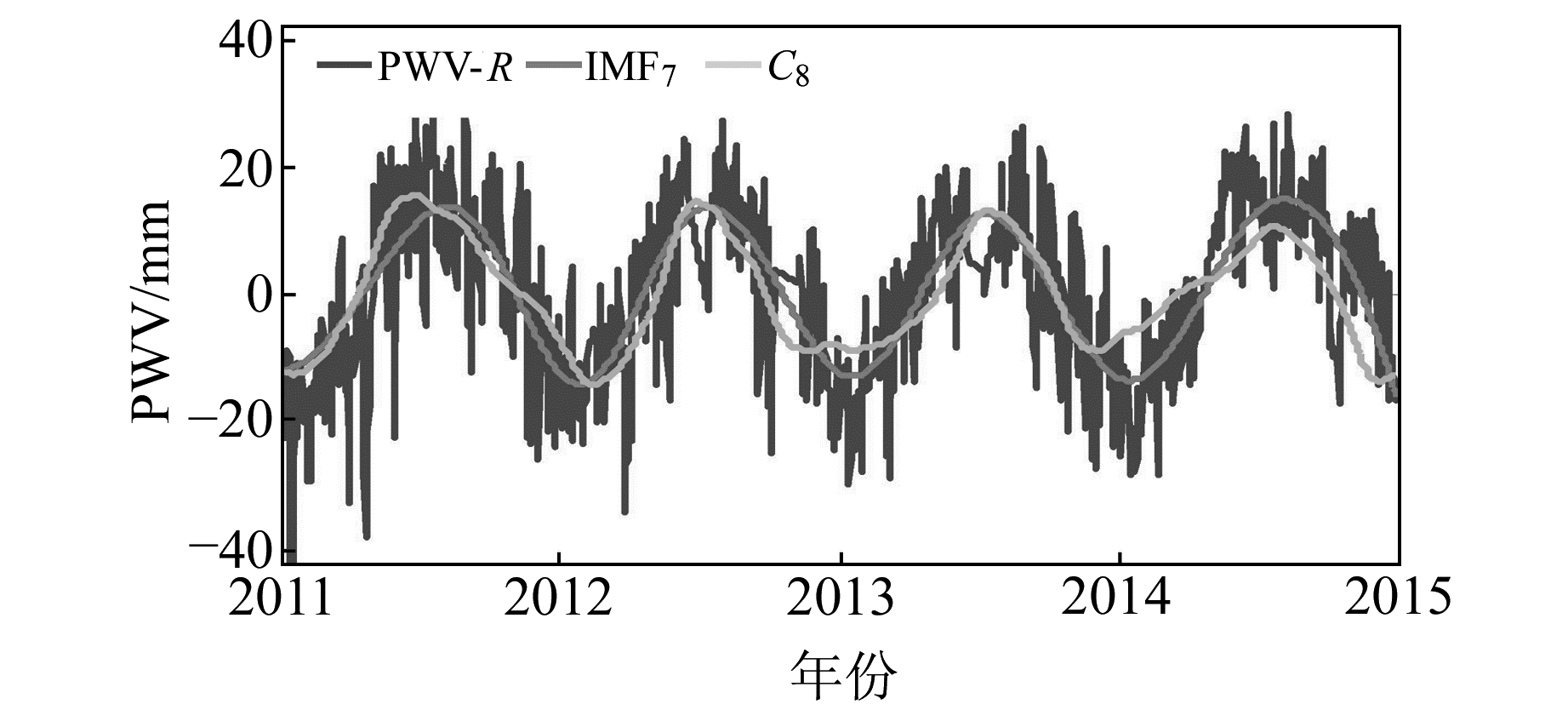
图 8 TNML站4 a滤波辅助PEEMD和小波分解的特征分量对比结果 Fig. 8 Feature component results between filter-assisted PEEMD and wavelet decomposition at TNML for 4 years |
|
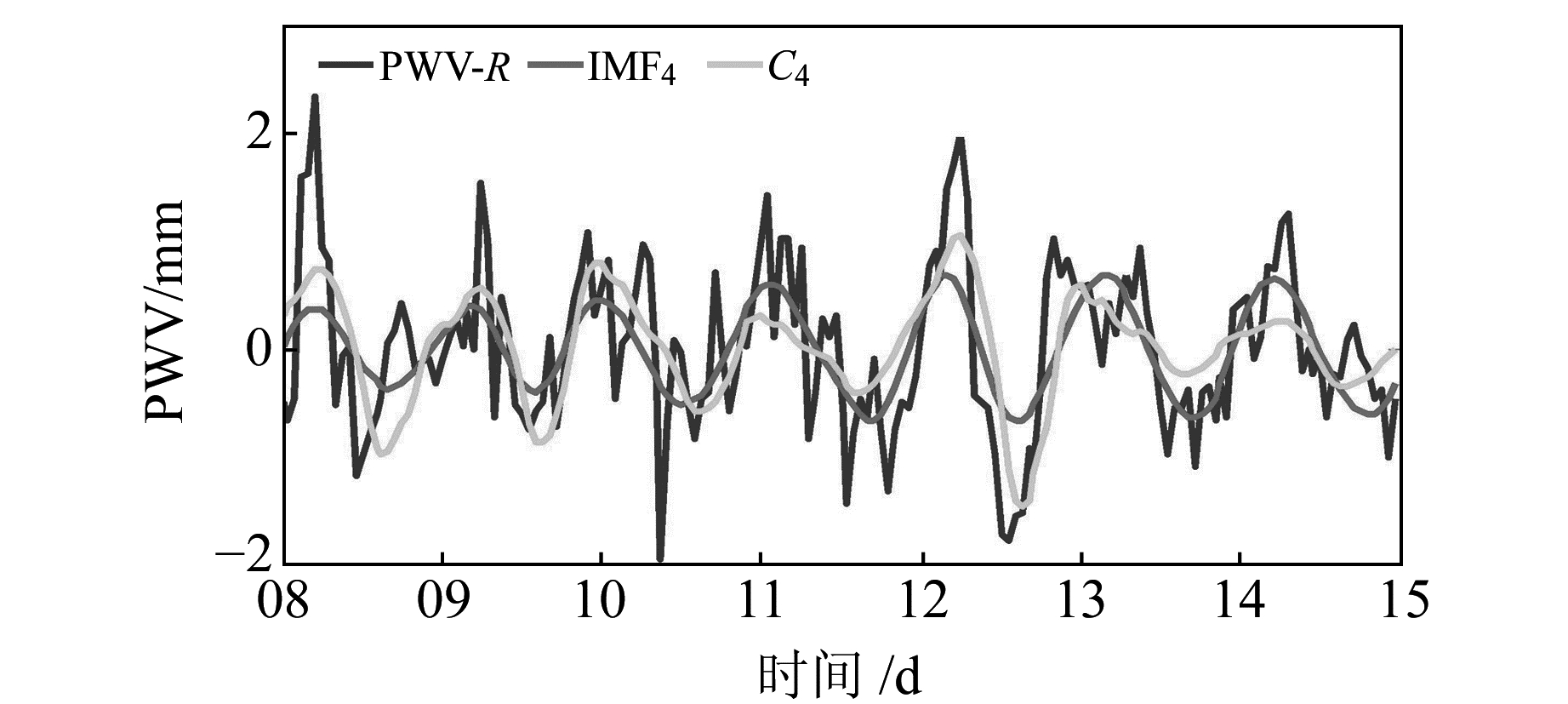
图 9 TNML站7 d滤波辅助PEEMD和小波分解的特征分量对比结果 Fig. 9 Feature component results between filter-assisted PEEMD and wavelet decomposition at TNML for 7 days |
由图 8可以看出,滤波辅助的PEEMD方法提取出的周年特征分量IMF7相比小波分解提取的周年特征分量C8而言,与原始GPS/PWV的时间序列更加吻合,波形更加均匀和光滑。由图 9可以看出,滤波辅助的PEEMD方法提取出的日特征分量IMF4相比小波分解提取的周年特征分量C4,波形也更加光滑。因此,滤波辅助的PEEMD在长时间和短时间的GPS/PWV时间序列分析中都是有效的。
为了更加准确地分析提取出的周年特征和日特征信息,对两者进行Hilbert包络谱分析。图 10为TNML站的周年特征分量Hilbert包络谱,图 11为TNML站的日特征分量Hilbert包络谱。
|
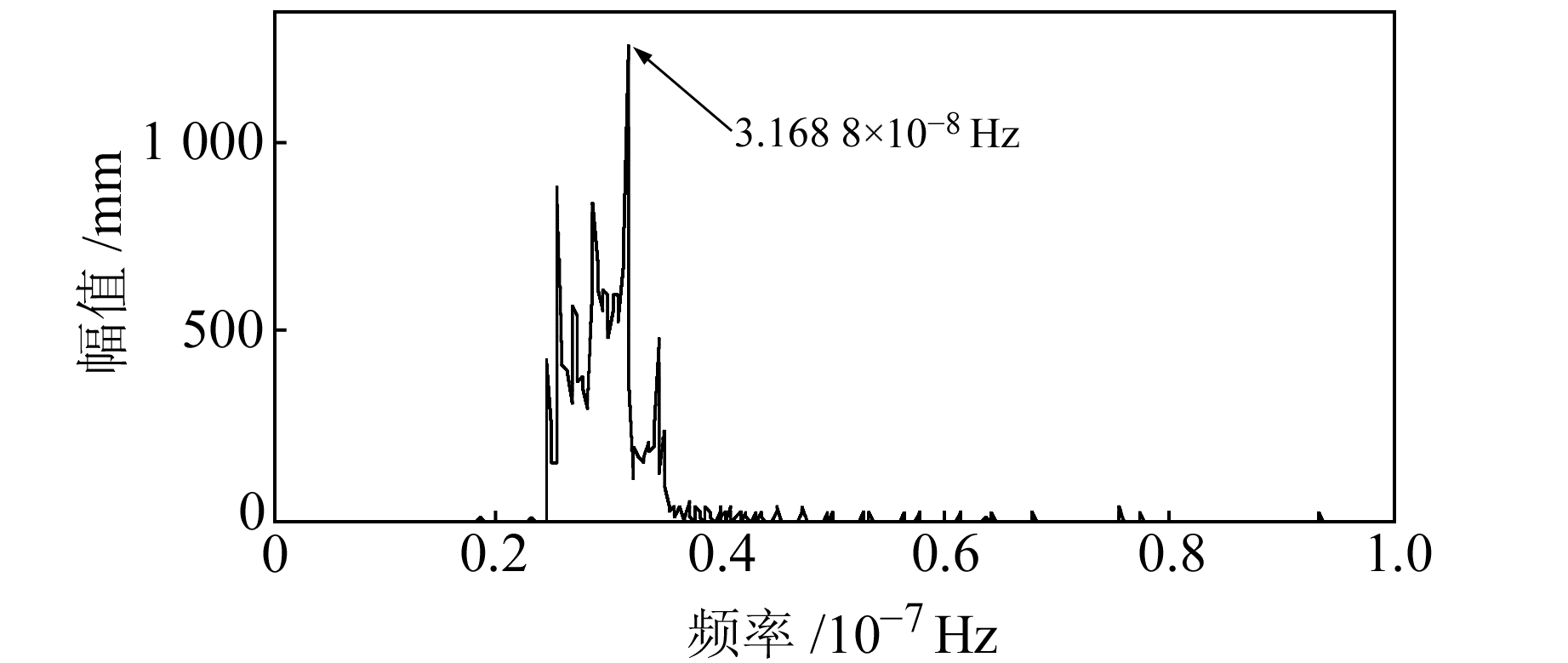
图 10 TNML站周年特征分量IMF7 Hilbert包络谱结果 Fig. 10 Hilbert envelope spectra of annual feature component IMF7 at TNML |
|
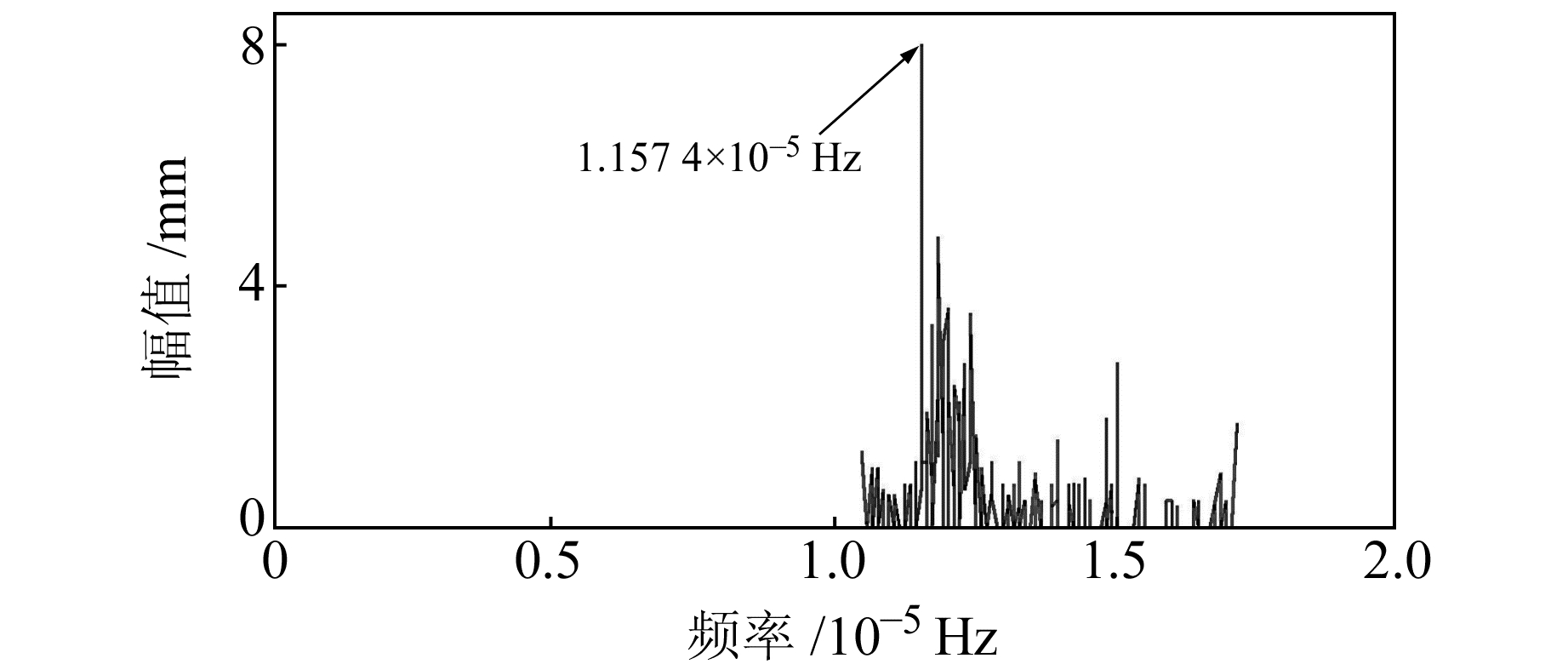
图 11 TNML站日特征分量IMF7 Hilbert包络谱结果 Fig. 11 Hilbert envelope spectra of daily feature component IMF7 at TNML |
由图 10可以看出,由滤波辅助PEEMD得到周年特征分量的Hilbert包络谱的特征频率为3.168 8×10-8 Hz(四舍五入前为3.168 800 87×10-8 Hz)。该特征频率转换成时间为365.25 d,这与本文使用的实验数据的平均年周期严格对应。由图 11可以看出,由滤波辅助PEEMD得到的日特征分量的Hilbert包络谱特征频率为3.157 4×10-5 Hz(四舍五入前为1.157 407 41×10-5Hz),对应的时间为24 h。因此使用滤波辅助PEEMD方法可以准确地提取水汽时间序列中的周年特征分量和日特征分量,这也进一步验证了滤波辅助PEEMD方法的有效性。
3 结语本文基于原始PEEMD方法,提出滤波辅助的PEEMD方法。在结合滤波辅助PEEMD方法和Hilbert谱分析方法的基础上,提出一种GPS/PWV时间序列特征提取方法,并应用于TNML站4 a长时间和7 d短时间的GPS/PWV时间序列中,得到以下结论:
1) 滤波辅助PEEMD方法能够有效地分解出GPS/PWV时间序列中的周年特征分量和日特征分量,与小波分解结果吻合一致,且波形更加光滑、均匀,验证了滤波辅助PEEMD方法的有效性。
2) 对应用滤波辅助PEEMD提取出来的GPS/PWV时间序列周年特征分量和日特征分量进行Hilbert包络谱分析,得到周期为365.25 d的周年特征频率和24 h的日特征频率,这在频率域上进一步验证了滤波辅助PEEMD方法的有效性。
应用有效的时间序列分析方法对GPS/PWV时间序列进行分析,能够挖掘出其中蕴含的特征信息,这些特征信息可以用来帮助寻找GPS/PWV的变化规律以及背后的机理。因此,本文将利用更长时间、更多GPS站点以及更高分辨率的GPS观测资料获得GPS/PWV时间序列资料,结合气象资料等,挖掘出水汽中更多时间尺度的周期振荡信息。
| [1] |
Ohtani R, Naito I. Comparisons of GPS-Derived Precipitable Water Vapors with Radiosonde Observations in Japan[J]. Journal of Geophysical Research Atmospheres, 2000, 105(D22): 26917-26929 DOI:10.1029/2000JD900362
(  0) 0) |
| [2] |
Suparta W, Rashid Z A A, Ali M A M, et al. Observations of Antarctic Precipitable Water Vapor and Its Response to the Solar Activity Based on GPS Sensing[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2008, 70(11-12): 1419-1447 DOI:10.1016/j.jastp.2008.04.006
(  0) 0) |
| [3] |
Jin S, Luo O F. Variability and Climatology of PWV from Global 13-Year GPS Observations[J]. IEEE Transactions on Geoscience & Remote Sensing, 2009, 47(7): 1918-1924
(  0) 0) |
| [4] |
毕研盟, 毛节泰, 刘晓阳, 等. 应用地基GPS遥感倾斜路径方向大气水汽总量[J]. 地球物理学报, 2006, 49(2): 335-342 (Bi Yanmeng, Mao Jietai, Liu Xiaoyang, et al. Remote Sensing of the Amount of Water Vapor along the Slant Path Using the Ground-Base GPS[J]. Chinese Journal of Geophysics, 2006, 49(2): 335-342 DOI:10.3321/j.issn:0001-5733.2006.02.005)
(  0) 0) |
| [5] |
Huang N E, Shen Z, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Proceedings Mathematical Physical & Engineering Sciences, 1998, 454(1971): 903-995
(  0) 0) |
| [6] |
郑祖光. 经验模态分析与小波分析及其应用[M]. 北京: 气象出版社, 2010 (Zheng Zuguang. Empirical Model Analysis and Wavelet Analysis and Their Application[M]. Beijing: China Meteorological Press, 2010)
(  0) 0) |
| [7] |
Wu Z, Huang N E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2011, 1(1): 1-41
(  0) 0) |
| [8] |
Yeh J R, Shieh J S, Huang N E. Complementary Ensemble Empirical Mode Decomposition: A Novel Noise Enhanced Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2010, 2(2): 135-156 DOI:10.1142/S1793536910000422
(  0) 0) |
| [9] |
Zheng J D, Cheng J S, Yang Y. Partly Ensemble Empirical Mode Decomposition: An Improved Noise-Assisted Method for Eliminating Mode Mixing[J]. Signal Processing, 2014, 96: 362-374 DOI:10.1016/j.sigpro.2013.09.013
(  0) 0) |
| [10] |
Veltcheva A, Soares C G. Analysis of Wave Groups by Wave Envelope-Phase and the Hilbert Huang Transform Methods[J]. Applied Ocean Research, 2016, 60: 176-184 DOI:10.1016/j.apor.2016.09.006
(  0) 0) |
| [11] |
Chen L, Zi Y Y, He Z J, et al. Rotating Machinery Fault Detection Based on Improved Ensemble Empirical Mode Decomposition[J]. Advances in Adaptive Data Analysis, 2014, 6(2-3)
(  0) 0) |
| [12] |
陈略, 訾艳阳, 何正嘉, 等. 体平均经验模式分解与1.5维谱方法的研究[J]. 西安交通大学学报, 2009, 43(5): 94-98 (Chen Lüe, Zi Yanyang, He Zhengjia, et al. Research and Application of Ensemble Empirical Mode Decomposition Principle and 1.5 Dimension Spectrum Method[J]. Journal of Xi'an Jiaotong University, 2009, 43(5): 94-98 DOI:10.3321/j.issn:0253-987X.2009.05.020)
(  0) 0) |
2. Dongguan Institute of Surveying and Mapping, 268 Dongcheng Road, Dongguan 523660, China
 2019, Vol. 39
2019, Vol. 39

