2. 广西空间信息与测绘重点实验室,桂林市雁山街319号,541006;
3. 青海省生态环境遥感监测中心,西宁市南山东路116号,810007
随着GPS技术在测绘领域的发展和完善,采用部分GPS水准重合点实现高程拟合越来越受到测绘工作者的青睐[1]。获取高精度的高程异常是高程拟合的核心内容[2]。对于地势起伏平缓的研究区域,常规高程拟合方法能够满足实际拟合精度的要求。但当地势起伏较大、地形结构较复杂时,拟合结果与实际高程异常往往存在较大的偏差。多面函数拟合法能以任意精度逼近复杂曲面,但中心节点的选取较为繁琐。本文提出将蚁群算法引入多面函数建模,并考虑粗差的影响,对中心节点的数量和点位分布进行合理的选取,采用稳健估计剔除粗差对拟合模型的影响,保证所选取数据可靠的情况下提高拟合模型精度。
1 多面函数 1.1 多面函数基本原理多面函数是一种将若干简单曲面叠加形成复杂连续曲面的方法[3]。任何一个圆滑曲面都可以通过多面函数法以任意精度逼近,该方法非常适合于在地势起伏较大且地形条件复杂区域的GPS高程拟合。该方法在每个已知的数据点建立曲面,在方向上将各旋转曲面按照一定比例叠加成连续曲面,使其严格过各数据点,从而达到逼近圆滑曲面的效果[4]。
设已知曲面函数为f(x, y),若函数φ(x, y)满足方程:
| $ \sum {{{\left( {f\left( {{x_i},{y_i}} \right) - \varphi \left( {{x_i},{y_i}} \right)} \right)}^2}} = \min $ | (1) |
则称φ(x, y)为曲面函数f(x, y)的逼近函数。将逼近函数φ(x, y)表示为:
| $ \varphi \left( {x,y} \right) = \sum\limits_{j = 1}^u {{\beta _j}{Q_j}\left( {\left( {x,y} \right),\left( {{x_j},{y_j}} \right)} \right)} $ | (2) |
式中,β为待定系数,Q为核函数,u为核函数的数量,(xj, yj)为选取的中心节点坐标。
核函数Q可选择任意的简单函数,为了计算方便通常选取为对称型或距离型核函数。有3种常用核函数:
倒双曲函数
| $ Q = {\left( {{{\left( {x - {x_j}} \right)}^2} + {{\left( {y - {y_j}} \right)}^2} + \delta } \right)^{ - 1/2}} $ | (3) |
正双曲函数
| $ Q = {\left( {{{\left( {x - {x_j}} \right)}^2} + {{\left( {y - {y_j}} \right)}^2} + \delta } \right)^{1/2}} $ | (4) |
三次曲面型函数
| $ Q = {\left( {{{\left( {x - {x_j}} \right)}^2} + {{\left( {y - {y_j}} \right)}^2}} \right)^{3/2}} + \delta $ | (5) |
式中,δ为核函数平滑因子,可调节核函数的形状,是影响函数模型精度的因素之一。
设有n组观测值(xi, yi, ζi),i=1,2,…,n,建立误差方程:
| $ \begin{array}{l} {v_1} = \sum\limits_{j = 1}^u {{{\hat \beta }_j}{Q_j}\left( {\left( {{x_1},{y_1}} \right),\left( {{x_{0j}},{y_{0j}}} \right)} \right)} - {\zeta _1}\\ {v_2} = \sum\limits_{j = 1}^u {{{\hat \beta }_j}{Q_j}\left( {\left( {{x_2},{y_2}} \right),\left( {{x_{0j}},{y_{0j}}} \right)} \right)} - {\zeta _2}\\ \;\;\;\;\;\; \cdots \\ {v_n} = \sum\limits_{j = 1}^u {{{\hat \beta }_j}{Q_j}\left( {\left( {{x_n},{y_n}} \right),\left( {{x_{0j}},{y_{0j}}} \right)} \right)} - {\zeta _n} \end{array} $ | (6) |
式中,(x0j, y0j)为中心节点的坐标,ζ为坐标对应的观测值。用矩阵表示为:
| $ \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{A\hat \beta }} - \mathit{\boldsymbol{\zeta }} $ | (7) |
式中,
| $ \begin{array}{*{20}{c}} {\mathop {\mathit{\boldsymbol{A}}}\limits_{n \times u} = }\\ {\left[ \begin{array}{l} {Q_1}\left( {\left( {{x_1},{y_1}} \right),\left( {{x_{01}},{y_{01}}} \right)} \right), \cdots ,{Q_u}\left( {\left( {{x_1},{y_1}} \right),\left( {{x_{0u}},{y_{0u}}} \right)} \right)\\ {Q_1}\left( {\left( {{x_2},{y_2}} \right),\left( {{x_{01}},{y_{01}}} \right)} \right), \cdots ,{Q_u}\left( {\left( {{x_2},{y_2}} \right),\left( {{x_{0u}},{y_{0u}}} \right)} \right)\\ \;\;\;\;\;\; \cdots \\ {Q_1}\left( {\left( {{x_n},{y_n}} \right),\left( {{x_{01}},{y_{01}}} \right)} \right), \cdots ,{Q_u}\left( {\left( {{x_n},{y_n}} \right),\left( {{x_{0u}},{y_{0u}}} \right)} \right) \end{array} \right]} \end{array} $ | (8) |
利用最小二乘原理求得系数项:
| $ \mathit{\boldsymbol{\hat \beta }} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{\zeta }} $ | (9) |
将
稳健估计是在数据存在粗差时,选用某种适合的估计方法使参数的估计值尽可能少受粗差的影响,得出最佳估计值[5]。本文将稳健估计中的选权迭代法与多面函数结合,用于数据中含有粗差时,求解多面函数拟合参数的最佳估值,从而有效提高拟合模型的精度。
选权迭代法的关键是选择ρ函数或者φ函数,然后利用wi=φi/vi和Pi=piwi关系式构造权因子w和等价权P,最后根据等价权进行迭代求解[6]。构造稳健估计的权函数,ρ函数表示为:
| $ \rho \left( v \right) = \left\{ \begin{array}{l} {v^2}/2,\left| v \right| < 1.5\sigma \\ \left| v \right|,1.5\sigma < \left| v \right| < 2.5\sigma \\ d,\left| v \right| > 2.5\sigma \end{array} \right. $ | (10) |
式中,v为残差值,d为任意常数,σ为单位权中误差,权函数ρ对应的权因子可表示为:
| $ w\left( v \right) = \left\{ \begin{array}{l} 1,\left| v \right| < 1.5\sigma \\ 1/\left( {\left| v \right| + {k_0}} \right),1.5\sigma < \left| v \right| < 2.5\sigma \\ 0,\left| v \right| > 2.5\sigma \end{array} \right. $ | (11) |
式中,w(v)为取任意v时的权值大小,k0通常取较小值。
在计算过程中,初始权矩阵设为单位权,再根据多面函数模型的误差方程式(7),按照最小二乘法求解参数估值及其残差表达式:
| $ {{\mathit{\boldsymbol{\hat \beta }}}^{\left( 1 \right)}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{P\zeta }} $ | (12) |
| $ {\mathit{\boldsymbol{V}}^{\left( 1 \right)}} = \mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{\hat \beta }}}^{\left( 1 \right)}} - \mathit{\boldsymbol{\zeta }} $ | (13) |
根据式(13)并结合式(10)和式(11),可求得等价权矩阵P。利用式(12)进行迭代计算,选定某一微小量ε,当第k次与第k-1次迭代所得的参数估值之差的绝对值小于给定的阈值ε时,结束迭代,即
| $ \left| {{{\mathit{\boldsymbol{\hat \beta }}}^{\left( k \right)}} - {{\mathit{\boldsymbol{\hat \beta }}}^{\left( {k - 1} \right)}}} \right| \le \varepsilon $ | (14) |
满足条件后停止迭代,得出最后的估值结果:
| $ {{\mathit{\boldsymbol{\hat \beta }}}^{\left( k \right)}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}{{\mathit{\boldsymbol{\bar P}}}^{\left( {k - 1} \right)}}\mathit{\boldsymbol{A}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}{{\mathit{\boldsymbol{\bar P}}}^{\left( {k - 1} \right)}}\mathit{\boldsymbol{\zeta }} $ | (15) |
| $ {\mathit{\boldsymbol{V}}^{\left( k \right)}} = \mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{\hat \beta }}}^{\left( k \right)}} - \mathit{\boldsymbol{\zeta }} $ | (16) |
通过式(15)的估值结果可知,迭代后的参数估值剔除了粗差对模型的影响。多面函数法的模型求解过程中,核函数的选择直接关系到拟合的效果,通常根据观测数据自身较强的相关性来选择核函数[7]。平滑因子取不同的值会影响核函数的细节变化。徐南等[8]将核函数加权系数和光滑因子共同参与遗传算法搜索,对光滑因子进行合理选取。中心节点位置及数量的选择是多面函数中的关键影响因素,点位选取的质量决定模型的精度。针对多面函数的特征点位选取比较繁琐和人工选取存在的缺陷,本文提出基于蚁群算法寻找多面函数中心节点的方法。
2 基于蚁群算法的多面函数蚁群算法是通过模拟蚂蚁在寻找食物源过程中的正反馈原理寻找最短路径的仿生算法[9]。蚂蚁寻找食物时,在经过的路径上释放易挥发的物质信息素(pheromone),蚂蚁之间通过信息素进行相互通信[10]。蚁群算法寻优过程分为3步:找出初始路径,构成完整规则;对构造的规则进行剪枝,去掉与实际条件不相关的节点;更新信息素浓度,为后续蚂蚁选择路径提供依据。蚁群算法寻优原理是蚂蚁在寻找完整路径时通过重复选择属性节点来实现的,属性节点的选取可以用随机方式进行。具体算法见文献[9-10]。
蚁群多面函数法是将蚁群算法用于多面函数建模时中心节点的选取,使所选择的特征点能够充分反映实际地形地貌特征。该方法的基本思想是:在已知数据覆盖的研究区随机分配一定数量的蚂蚁,给定相同的初始信息素浓度,设置信息素浓度挥发系数;然后让每只蚂蚁根据数据情况分别寻找地形复杂的山脊线和山谷线附近区域,通过构造初始规则寻找最优路径向山脊线或山谷线处靠拢;再根据信息素挥发后的浓度更新路径,确定地形复杂的特征点位置;最后汇集特征点。为避免局部区域的过度拟合,通过设置局部范围筛选密集特征点,选定地形复杂区域内均匀分布的中心节点,选取中心节点后构建拟合模型,得出最优估值。
3 算例分析采用文献[2]中的算例数据构建模型,该地区观测数据覆盖面积约100 km2,研究区域地势起伏明显,海拔最高3 602 m、最低2 781 m。本文从收集的GPS水准重合数据中选择400个用于构建拟合模型,采用蚁群算法从建模数据中搜索最优中心节点,剩余部分数据用于检核。
3.1 蚁群多面函数法拟合GPS高程对于地形复杂、起伏比较明显的地区,利用多面函数法求解拟合模型前需要找出研究区内最佳特征点。根据已知拟合数据数量,随机分配200只蚂蚁,设置迭代次数为80次,分别寻找地势起伏较大的特征点。通过蚁群寻优路径原理,蚂蚁快速寻找具有代表性的山脊线或山谷线上的点,通过迭代循环找出适用于构建拟合模型的最佳特征点。蚂蚁寻找特征点的前后位置分布见图 1。

|
图 1 蚂蚁寻找最优路径对比 Fig. 1 Ant looking for optimal path comparison chart |
由图 1看出,首先随机分配蚂蚁的初始位置,通过算法迭代及正反馈原理寻找特征点位后,蚂蚁向山脊线或山谷线靠拢,进一步缩小特征点的分布范围。通过设置一定阈值控制特征点的密集程度,找出山脊线和山谷线附近的分布点。为了使拟合效果更好,需要合理选取少量非特征点,采用均匀格网法补充选取变化平缓区域的中心节点,共同作为中心节点参与建模。
利用蚁群算法结合均匀格网找到研究区内的最优中心节点,用于多面函数构建拟合模型。因数据的坐标单位和高程异常的单位不统一,在参与建模之前需要对数据进行规格化处理,即完成坐标数据的预处理后可提高计算效率,同时也避免系数矩阵数值因过大而超界,降低计算效率。给定初始计算的权阵为单位阵,采用最小二乘原理解出系数矩阵,利用稳健估计的多面函数拟合模型迭代最优参数估值
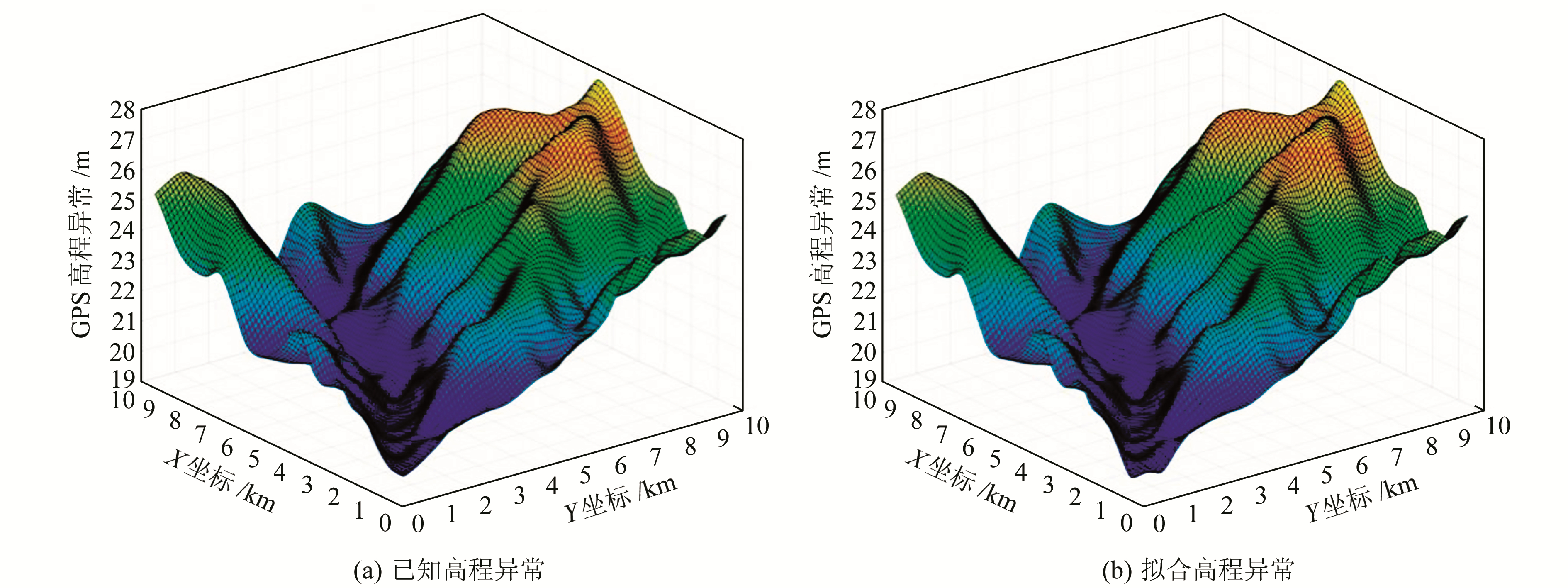
|
图 2 蚁群+稳健估计拟合模型三维效果 Fig. 2 Ant colony and robust estimation fitting model 3D effect |
蚁群算法结合稳健估计的多面函数拟合模型在剔除粗差影响情况下求得拟合模型的内符合精度σ0=±0.468 7 mm,从图 2也可直观地看出拟合模型精度较高。完成模型构建以后,用高精度拟合模型拟合其余80个检测点,并对拟合结果进行精度分析。
3.2 结果分析采用蚁群算法寻找多面函数拟合模型的中心节点,利用含稳健权的多面函数拟合模型求解系数矩阵
|
|
表 1 稳健估计加入前后模型精度比较 Tab. 1 Estimation of accuracy of model before and after accumulation |
由表 1可知,采用蚁群算法构建拟合模型所得结果精度高于均匀格网,加入稳健估计后所得拟合精度进一步提高。表明蚁群算法用于含稳健权的多面函数拟合模型有效可行,且模型精度高。
评定模型的内符合精度后,以80个已知点为检核数据,将该模型用于拟合检测点的GPS高程异常值,从检测点的拟合结果中随机抽取10组残差进行对比(表 2)。
|
|
表 2 不同方法拟合检测点残差结果 Tab. 2 Results of different methods fitting the detecting points residual |
由表 2可知,蚁群算法拟合结果波动较小,拟合精度趋于稳定;格网法拟合结果精度不太稳定,在选择多面函数中心节点的同时存在弊端,不能合理选取具有代表性的中心节点,从而很难提供稳定可靠的模型精度。
为合理评估蚁群算法结合稳健估计用于多面函数构建拟合模型的精度,求解80个检测点外符合精度,在大量实验的基础上,随机选取10次拟合计算结果与均匀格网结果进行对比(表 3)。
|
|
表 3 检测点拟合精度对比分析 Tab. 3 Comparison and analysis of accuracy of detecting points fitting |
由表 3可知,蚁群算法结合稳健估计拟合结果的精度为±7.1 mm,用均匀格网加入稳健估计拟合结果精度为±9.6 mm,采用蚁群算法的总体精度比格网法提高26%。对于已知数据中含有粗差的情况,在保证拟合数据可靠的同时,也提高了拟合模型的精度及可靠性。为了更加形象直观地体现蚁群算法的有效性及稳定性,分别绘制采用蚁群算法和格网法拟合检测点的残差对比图(图 3)。
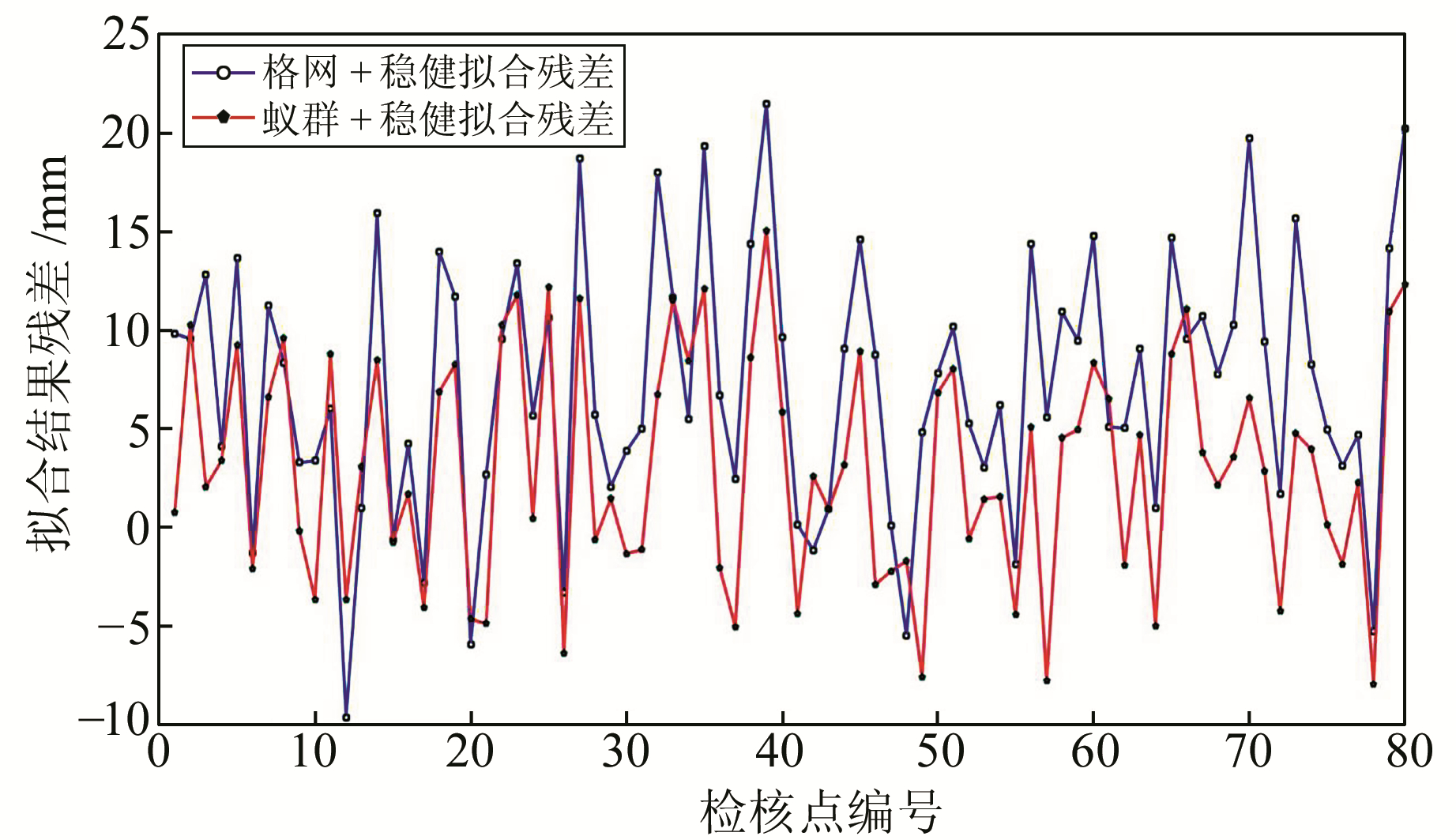
|
图 3 蚁群算法与均匀格网法拟合残差对比 Fig. 3 Comparison of ant colony algorithm and uniform grid method |
从图 3看出,格网法拟合结果残差波动性较大,稳定性较差;加入蚁群算法后拟合结果趋于稳定,且总体波动区间也有缩小,表明该方法对于精度的提高有效可行,并保证了拟合模型具有较好的稳定性。
4 结语考虑到多面函数法构建拟合模型参数难以选择以及剔除粗差的影响,本文将蚁群算法与稳健估计同时引入多面函数拟合法。该方法能够对地势起伏较大的区域合理选取特征点,结合格网选取少量非特征点作为中心节点参与多面函数模型构建。分别采用蚁群算法和格网法加入稳健估计前后对比分析,得到不同情况下的拟合模型结果。分析表明,将蚁群算法和稳健估计同时用于多面函数求解模型的参数更加合理,且拟合模型的精度得到很大提高,同时保证了拟合模型的稳定性。
| [1] |
刘亚彬, 郑南山, 张旭, 等. GPS高程拟合的加权总体最小二乘抗差估计[J]. 大地测量与地球动力学, 2016, 36(1): 30-34 (Liu Yabin, Zheng Nanshan, Zhang Xu, et al. Robust Weighted Total Least Squares Estimation for GPS Leveling Fitting[J]. Journal of Geodesy and Geodynamics, 2016, 36(1): 30-34)
(  0) 0) |
| [2] |
蒲伦, 唐诗华, 张紫萍, 等. 一种基于蚁群算法的山区GPS高程异常拟合方法[J]. 测绘通报, 2018(8): 26-31 (Pu Lun, Tang Shihua, Zhang Ziping, et al. A GPS Height Anomaly Fitting Method in Mountainous Area Based on Ant Colony Algorithm[J]. Bulletin of Surveying and Mapping, 2018(8): 26-31)
(  0) 0) |
| [3] |
孙佳龙, 焦明连, 梁青科. 基于聚类分析的多面函数拟合高程异常方法[J]. 测绘通报, 2013(2): 5-7 (Sun Jialong, Jiao Minglian, Liang Qingke. Fitting Method of Height Anomaly by Multi-Quadric Function Based on Cluster Analysis[J]. Bulletin of Surveying and Mapping, 2013(2): 5-7)
(  0) 0) |
| [4] |
田晓, 郑洪艳, 许明元, 等. 一种改进的适用于不同地形的GPS高程拟合模型[J]. 测绘通报, 2017(1): 35-38 (Tian Xiao, Zheng Hongyan, Xu Mingyuan, et al. An Improved GPS Elevation Fitting Model for Different Terrain[J]. Bulletin of Surveying and Mapping, 2017(1): 35-38)
(  0) 0) |
| [5] |
杨娟, 陶叶青. GPS高程异常拟合的稳健总体最小二乘算法[J]. 大地测量与地球动力学, 2014, 34(5): 130-133 (Yang Juan, Tao Yeqing. A Solution of GPS Elevation Anomaly Fitting Base on Robust Total Least Squares[J]. Journal of Geodesy and Geodynamics, 2014, 34(5): 130-133)
(  0) 0) |
| [6] |
王乐洋, 陈汉清. 多波束测深数据处理的抗差最小二乘配置迭代解法[J]. 测绘学报, 2017, 46(5): 658-665 (Wang Leyang, Chen Hanqing. Multi-Beam Bathymetry Data Processing Using Iterative Algorithm of Robust Least Squares Collocation[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(5): 658-665)
(  0) 0) |
| [7] |
李俊学.含稳健权的遗传神经网络在GPS高程拟合中的应用[D].南昌: 东华理工大学, 2015 (Li Junxue.With Robust Weight of Genetic Algorithmand Neural Network in Application of GPS Elevation Fitting[D]. Nanchang: East China University of Technology, 2015) http://cdmd.cnki.com.cn/Article/CDMD-10405-1015990528.htm
(  0) 0) |
| [8] |
徐南, 严朝霞, 马符讯. 基于遗传算法的多面函数GPS高程拟合模型[J]. 工程勘察, 2013, 41(11): 50-52 (Xu Nan, Yan Zhaoxia, Ma Fuxun. Multi-Surface Function Model of GPS Height Fitting Based on Genetic Algorithm[J]. Geotechnical Investigation & Surveying, 2013, 41(11): 50-52 DOI:10.3969/j.issn.1000-1433.2013.11.011)
(  0) 0) |
| [9] |
申铉京, 刘阳阳, 黄永平, 等. 求解TSP问题的快速蚁群算法[J]. 吉林大学学报:工学版, 2013, 43(1): 147-151 (Shen Xuanjing, Liu Yangyang, Huang Yongping, et al. Fast Ant Colony Algorithm for Solving TSP Problem[J]. Journal of Jilin University:Engineering and Technology Edition, 2013, 43(1): 147-151)
(  0) 0) |
| [10] |
赵开新, 孙新领, 王东署, 等. 基于改进蚁群算法的移动机器人路径规划研究[J]. 科技通报, 2017, 33(9): 76-79 (Zhao Kaixin, Sun Xinling, Wang Dongshu, et al. Mobile Robot Path Planning with Improved Ant Colony Algorithm[J]. Bulletin of Science and Technology, 2017, 33(9): 76-79)
(  0) 0) |
2. Guangxi Key Laboratory of Spatial Information and Geomatics, 319 Yanshan Street, Guilin 541006, China;
3. Qinghai Ecological Environment Remote Sensing Monitoring Center, 116 East-Nanshan Road, Xining 810007, China
 2019, Vol. 39
2019, Vol. 39


