2. 中国地震局地壳应力研究所武汉科技创新基地,武汉市洪山侧路40号,430071
北斗卫星导航系统(Beidou navigation satellite system,BDS)是中国自行研制的全球卫星导航系统。截至2018-01,北斗系统已发射27颗卫星,其中15颗在轨稳定运行。当前北斗系统的服务范围已覆盖亚太地区,能够为亚太地区用户提供稳定可靠的PNT服务。随着北斗系统星座的不断完善,其在动态变形监测中的应用越来越广泛。在实际GNSS变形监测中,所布设的基线一般较短,利用差分技术可以大幅削减有较强空间相关性的接收机钟差、卫星钟差、对流层延迟和电离层延迟等误差。但基线两端的多路径效应与站点环境有关,不具有空间相关性,利用差分技术无法消除其影响。
在一定条件下,多路径误差最大值为信号波长的1/4[1],在高精度的变形监测中必须消除其影响。削弱多路径误差除了选择测站环境较优的站址和提高接收机质量外,还可以从数据处理算法方面着手。Lau等[2-3]提出基于信噪比定权的SNR技术和射线追踪法;Ye等[4]提出基于观测值域双差残差的恒星日滤波算法;Ma等[5]分析北斗多路径误差的周期特性,提出基于北斗星座特性的坐标域恒星日滤波算法。奇异谱分析(singular spectrum analysis, SSA)发展于Karhumen-Loeve分解理论,是对一维时间序列进行分析的主成分分析方法,可以较好地提取时间序列中的信息[6]。卢辰龙等[7]利用SSA滤波法消除GPS多路径误差,并根据噪声与信号的Hurst指数的显著差异来确定SSA的嵌入维数和重构阶次,但此方法计算量较大,计算效率有待提高。本文采用相空间重构Cao算法确定奇异谱嵌入维度,并改进了Cao算法的参数选择准则,降低参数选择的主观性,提高SSA的计算效率。最后,利用实测北斗短基线数据验证基于SSA的北斗恒星日滤波算法的高效性。
1 SSA基本原理 1.1 SSA算法对于某一给定的一维时间序列x=(x1, x2, …, xN),其SSA实现过程等价于对其时滞矩阵作时间经验正交函数展开,主要分为以下4步。
1) 计算轨迹矩阵。
根据嵌入维数L计算时间序列的轨迹矩阵X:
| $ \begin{array}{l} \mathit{\boldsymbol{X}}{\rm{ = }}\left[{{X_1}, {X_2}, \cdots , {X_K}} \right] = \left( {{x_{ij}}} \right)_{i, j = 1}^{L, K} = \\ \;\;\;\;\left[\begin{array}{l} {x_1}\;\;\;\;{x_2}\;\;\; \cdots \;\;\;{x_{N - L + 1}}\\ {x_2}\;\;\;\;{x_3}\;\;\; \cdots \;\;\;{x_{N - L + 2}}\\ \; \vdots \;\;\;\;\;\; \vdots \;\;\;\;\; \ddots \;\;\;\;\;\;\; \vdots \\ {x_L}\;\;\;{x_{L + 1}}\;\; \cdots \;\;\;\;\;\;{x_N} \end{array} \right] \end{array} $ | (1) |
式中,轨迹矩阵X为L×K阶,其中K=N-L+1, 1<L≤
2) 奇异值分解。
定义矩阵CX=XXT,计算矩阵CX的特征值λi及特征向量Ui。将特征值降序排列,依次为λ1, …, λL且λ1≥…≥λL≥0,对应的特征向量为U1, …, UL。设d=L*, L*=min{L, K},Vi= XTUi/
3) 分组。
将初等矩阵Xi的下标{1, 2, …, d}分成p个不相交的子集I1, I2, …, Ip,设I={i1, i2, …, im},则合成矩阵XI=Xi1+Xi2+…+Xim,计算集合I=I1, I2, …, Ip的每个合成矩阵,则X=XI1+XI2+…+XIp,其中选择子集I1, I2, …, Ip的过程称为分组。
4) 重构。
将分组分解的每个矩阵XIj转换为长度为N的新序列。设Y是一个L×K的矩阵,其元素为yij,其中1≤i≤L, 1≤j≤K, K*=max{L, K},L*=min{L, K}且N=K+L-1,使用对角平均公式将矩阵Y转换成y1, …, yN的时间序列:
| $ {y_k} = \left\{ \begin{array}{l} \frac{1}{k}\sum\limits_{p = 1}^k {y_{p, k - p + 1}^*, 1 \le k \le {L^*}} \\ \frac{1}{{{L^*}}}\sum\limits_{p = 1}^{{L^*}} {y_{p, k - p + 1}^*, {L^*} \le k \le {K^*}} \\ \frac{1}{{N - k + 1}}\sum\limits_{p = k - {K^*} + 1}^{N - {K^*} + 1} {y_{p, k - p + 1}^*, {K^*} \le k \le N} \end{array} \right. $ | (2) |
将式(2)用在合成的矩阵XIk中,生成重构序列
| $ {x_n} = \sum\limits_{k = 1}^p {\tilde x_n^k, n = 1, 2, \cdots , N} $ | (3) |
嵌入维数L的选择直接影响信号分解的效果,若L较小,将导致信号分解不彻底,丢失部分信号;反之,则会导致奇异值分解得到的不同部分产生混叠。本文采用混沌时间序列分析中的相空间重构Cao算法来确定嵌入维数L。Cao算法是在伪最近邻点法(false nearest neighbors, FNN)的基础上发展起来的,通过计算与吸引子有关的几何不变量来确定嵌入维数L[8]。当嵌入维数增加到一定程度,吸引子的几何结构被完全打开,这些不变量将保持稳定状态,从而确定合适的嵌入维数。Cao算法具有对数据长度依赖不强、计算效率高等优良特性,具体由以下步骤实现。
首先,计算相空间中的点在各嵌入维数下的最近邻点的距离变化值:
| $ \begin{array}{l} d\left( {i, M} \right) = \frac{{\left\| {{\mathit{\boldsymbol{X}}_i}\left( {M + 1} \right) - {\mathit{\boldsymbol{X}}_{n\left( {i, M} \right)}}\left( {M + 1} \right)} \right\|}}{{\left\| {{\mathit{\boldsymbol{X}}_i}\left( M \right) - {\mathit{\boldsymbol{X}}_{n\left( {i, M} \right)}}\left( M \right)} \right\|}}, \\ \;\;\;\;\;\;\;\;i = 1, 2, \cdots , N - M \end{array} $ | (4) |
式中,‖·‖为向量的∞-范数,Xi(m+1)为第i个重构相空间向量,嵌入维数为m+1,Xn(i, M)为按上述范数定义下离Xi(m+1)最近的向量,其中n(i, m)为≥1且≤(N-M)的整数。
然后,计算相同维数下距离变化量的均值:
| $ E\left( M \right) = \frac{1}{{N - M}}\sum\limits_{i = 1}^{N - M} {d\left( {i, M} \right)} $ | (5) |
式中,E(M)为所有d(i, M)的均值。
最后,监测E(M)的变化:
| $ {E_1}\left( M \right) = \frac{{E\left( {M + 1} \right)}}{{E\left( M \right)}} $ | (6) |
当M>M0时,E1(M)停止变化或者波动较小,则最小嵌入维数为M0+1。
1.3 改进Cao算法Cao算法确定嵌入维数L是以E1(M)停止变化为标准。然而对于实际时间序列来说,E1(M)起伏不定,很难达到严格的稳定状态,因此实际中通过主观判断确定最佳嵌入维数L有一定的困难。针对此问题,本文提出一种嵌入维数的稳定性判定准则用于最佳嵌入维数的确定,计算过程如下:
1) 定义Δi=
2) 根据E1序列的波动设定阈值ε1,遍历E1序列得到第一个Δi<ε1对应的下标j;
3) 令ε2=
4) 若Δi+2<Δi+1<Δi<ε2, j≤i≤N-2,记录此时Δi的值,并找到最小Δi对应的下标k,则嵌入维数L=k+1。
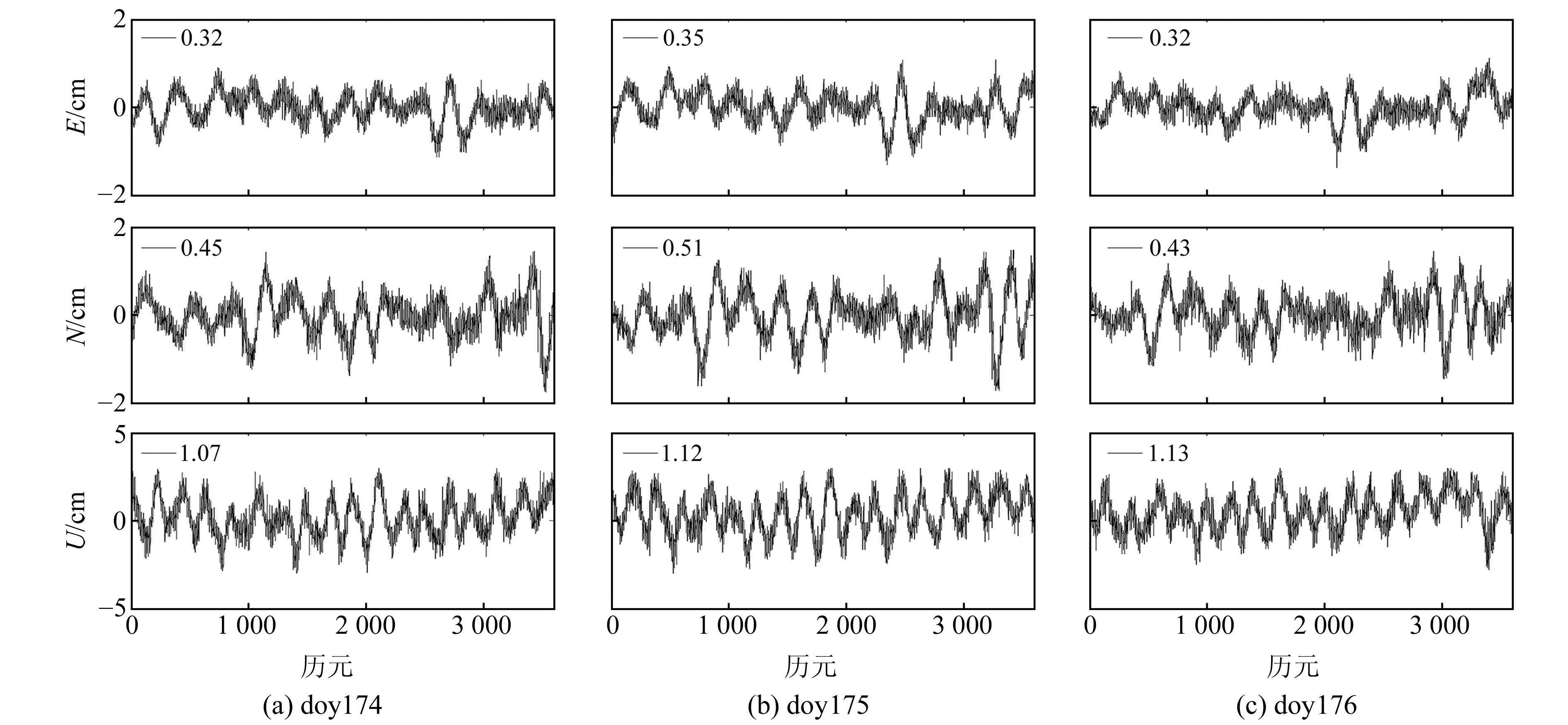
2 算例分析在某科研楼楼顶架设2台Topcon NET-G5双频接收机TP13、TP14进行同步观测,其中TP14测站旁有多处金属反射面。观测期间采样率设置为1 s,卫星截止高度角设置为10°,观测时间为2017年doy174 ~176。由于2台接收机间距离非常短,通过差分处理可以消除接收机钟差、卫星钟差、电离层延迟和对流层延迟等误差。因此,基线解算得到的坐标序列中主要包含随机噪声和多路径误差。连续3 d的坐标残差序列如图 1所示。
|
图 1 连续3 d坐标残差序列 Fig. 1 Residual sequence for three consecutive days |
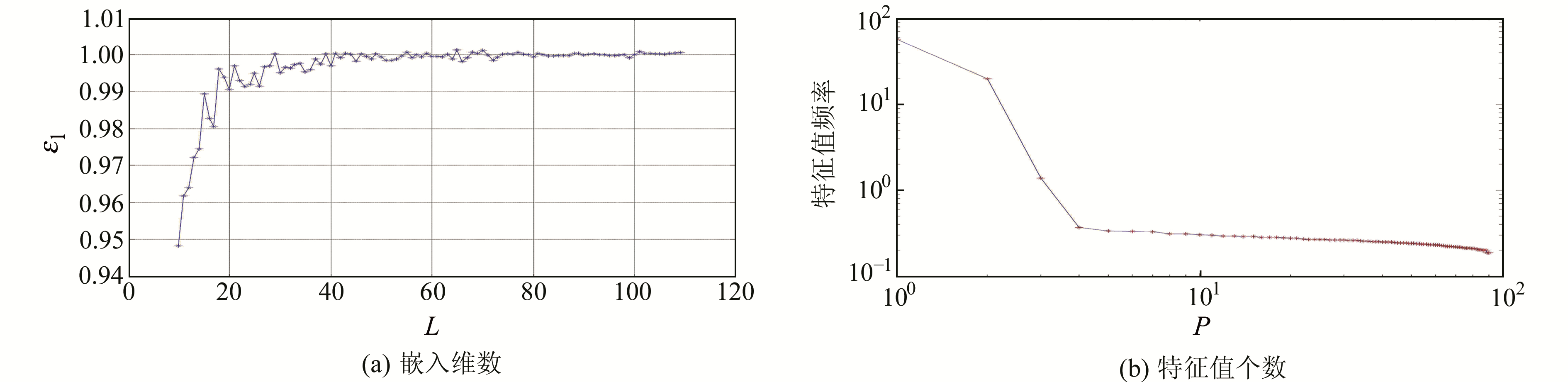
由图 1可知, 3 d解中各分量上的RMS值分别为3 mm、5 mm和11 mm左右,同时连续3 d坐标残差序列表现出明显的相似性,对3 d的坐标残差序列进行滤波处理,提取多路径误差序列。以第1天基线解算结果E方向坐标残差序列为例,利用db10小波和SSA对其进行滤波处理,奇异谱分析过程中,嵌入维数L和重构阶次P的选取如图 2所示。图 2(a)为利用Cao算法计算得到的嵌入维数L的变化趋势图。可以看出,当L=40时,E1开始趋于稳定。利用本文提出的稳定性判定准则,同时令阈值ε1=0.000 1,通过计算得到L=83。由Cao算法原理可知,当关联维数趋于稳定达到饱和值时,吸引子的几何结构完全打开,此时对应的嵌入维数L即为SSA算法的最佳嵌入维数。图 2(b)为E方向残差序列奇异谱对数图。可以看出,在P=4时,奇异谱的变化速率突降,出现明显的拐点,且前4个主分量的贡献率达到99%以上,因此选择将前4个主分量进行重构。将2种滤波方法得到的结果同原始坐标残差序列作比较,结果如图 3所示。
|
图 2 嵌入维度L和重构阶次P的选取 Fig. 2 The selection of embedded dimension and reconstitution order |
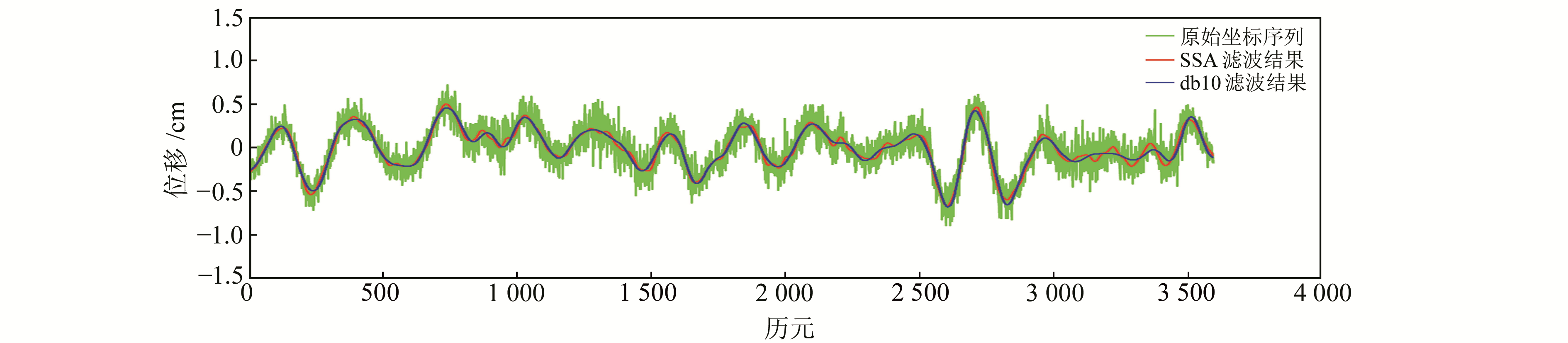
|
图 3 SSA、db10小波重构多路径误差序列 Fig. 3 The sequence of multipath error reconstituted by SSA and db10 wavelet |
由图 3可知,SSA、db10小波2种方法去噪后的序列都比较平滑,均能有效剔除序列中的高频噪声。同时还能看出,2种滤波结果中SSA滤波结果与原始信号符合度更好。对N和U方向坐标残差序列作相同处理,并计算SSA、db10小波去噪后的信号与原始信号的互相关系数,结果如表 1所示。可以看出,3个方向上SSA去噪后的信号与原始信号的相关性均高于db10小波去噪结果与原始信号的相关性,说明SSA去噪后的信号与原始信号更接近,获得的多路径改正模型更精确。
|
|
表 1 去噪后信号与原始信号的互相关系数 Tab. 1 The correlation coefficient between the original signal and the signal after filtering |
利用恒星日滤波算法消除多路径误差依据的是多路径误差的周期特性,而多路径误差的周期特性与卫星轨道的周期性关系密切。为了探讨北斗系统多路径误差周期特性,分别对基线解算结果的相关性和北斗卫星轨道重复周期进行计算与分析。
3.1 多路径误差时间序列相关性计算对3 d的坐标序列进行SSA滤波处理后得到多路径误差序列并计算其相关延迟(表 2)。由表 2可知,相邻2 d多路径误差的相关性最强,且相关延迟在240 s附近达到最大,同时间隔天数越久,最大相关系数越小。
|
|
表 2 TP14测站多路径误差相关延迟 Tab. 2 The correlation delay of TP14 multipath error |
利用广播星历计算北斗系统不同类型卫星的轨道重复周期。根据广播星历提供的长半轴的平方根和平均角速度摄动参数,由开普勒第三定律可得[9]:
| $ \left\{ \begin{array}{l} n = \sqrt {GM} /{a^{\frac{3}{2}}} + \Delta n\\ {T_0} = 2\pi /n\\ {T_R} = 2{T_0} \end{array} \right. $ | (9) |
式中,a为卫星轨道椭圆长半轴,GM为万有引力常数G与地球质量M的积,GM=3.986 004 418×1014 m3/s2,Δn为平均角速度的改正量,T0为卫星运行1周的时间,TR为轨道重复周期。本文计算2015-04-01~05-20北斗卫星的轨道重复周期,结果如图 4所示。图 4中包含3类卫星的轨道重复周期,1~5号为GEO卫星,6~10号为IGSO卫星,11、12、14号为MEO卫星。可以看到,3类不同类型的卫星轨道重复周期变化趋势明显不同,GEO卫星轨道重复周期在86 160 s附近波动,且变化幅度最大;IGSO卫星次之,同类型卫星之间的轨道重复周期变化较为平缓,且不都集中于某一常数;MEO卫星轨道重复周期的变化幅度最小,基本在1 s以内,并集中在46 392 s附近波动。GEO、IGSO和MEO卫星的平均轨道重复周期分别为86 163 s、86 165 s、46 392 s,即3类卫星每天提前时间分别为237 s、235 s、245 s。其中,北斗MEO卫星不同于GEO和IGSO卫星,MEO卫星7 d绕地球运行13圈,7 d累计比上一周提前1 715 s,平均每天提前245 s[10]。

|
图 4 广播星历计算得到的北斗卫星轨道重复周期 Fig. 4 Beidou satellite orbital repetition periods from broadcast ephemeris |
根据上文对多路径误差相关延迟和北斗卫星星座轨道重复周期的计算发现,两者延迟时间大体一致,略大于GPS系统的236 s,验证了多路径误差与卫星周日视运动的关系。结合上文计算的多路径误差相关延迟和卫星轨道重复周期,北斗卫星的提前时间约为240 s。
根据上述重复时间与SSA、db10小波滤波得到的多路径误差模型,分别对doy175、176的基线解算结果进行恒星日滤波处理。图 5、6分别为doy175、176使用SSA、db10小波滤波前后的坐标残差序列,通过对原坐标残差序列进行恒星日滤波处理,原始坐标残差序列的多路径误差基本消除,坐标序列的精度明显提升。
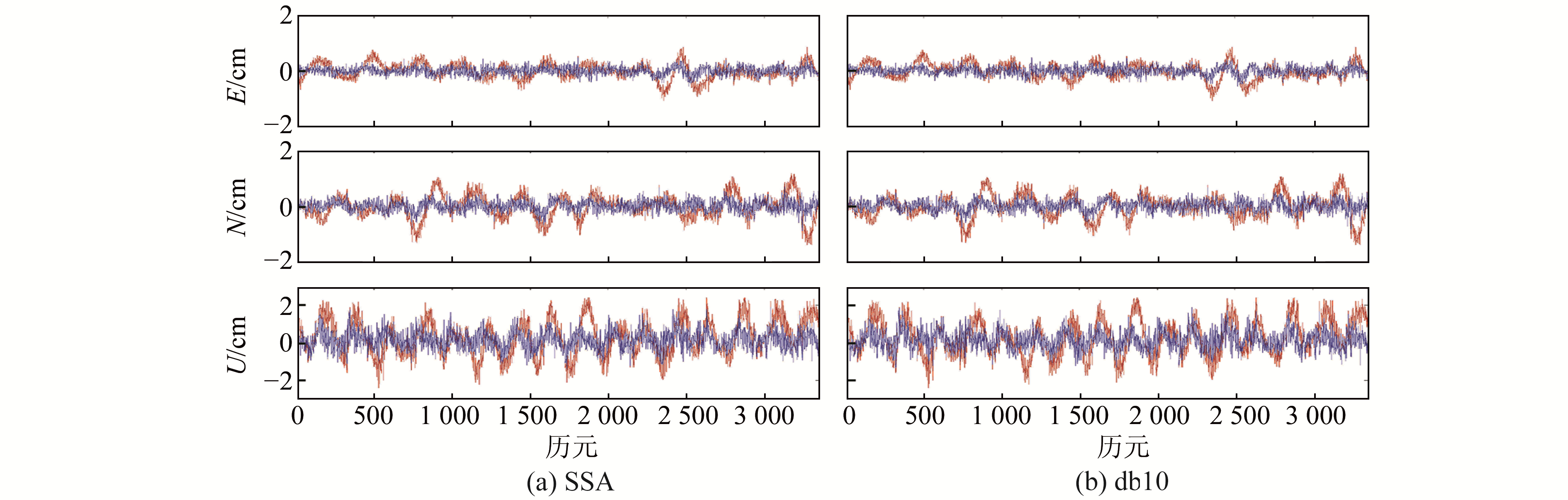
|
图 5 doy175多路径误差改正后坐标序列 Fig. 5 The coordinate series of doy 175 after multipath error correction was applied |
|
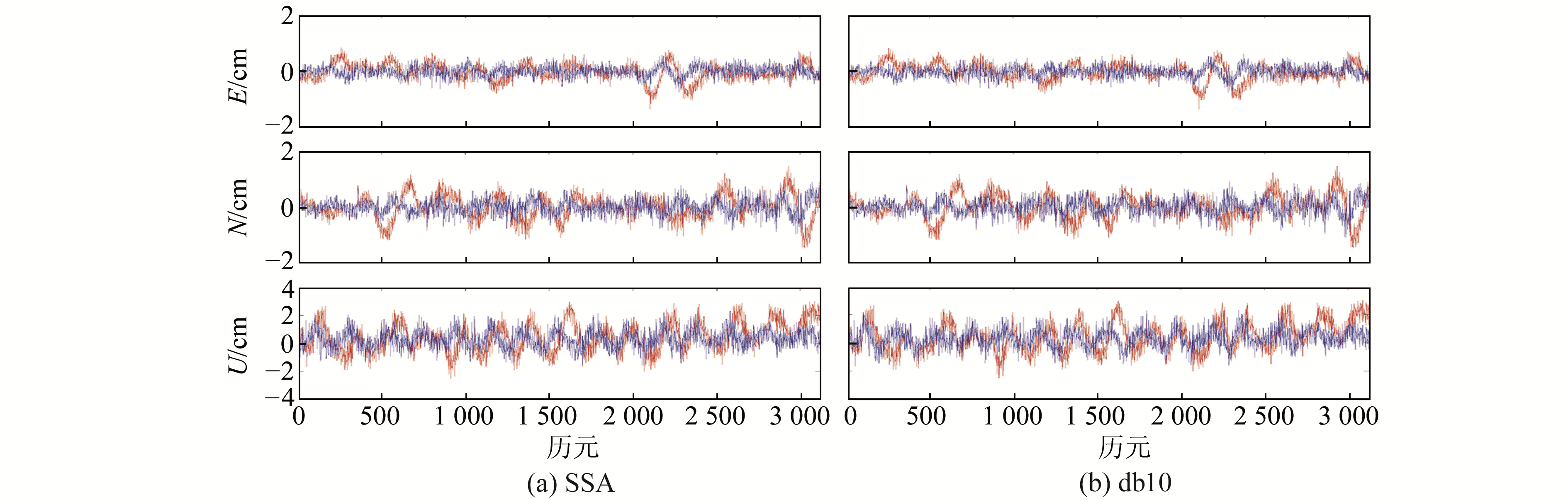
图 6 doy176多路径误差改正后坐标序列 Fig. 6 The coordinate series of doy 176 after multipath error correction was applied |
表 3给出了2种滤波方法滤波后的2 d坐标序列的RMS值。可以看出,2种滤波方式均能有效消除多路径误差的影响,同时基于SSA的恒星日滤波后的坐标序列的RMS值更小,坐标精度改善程度也高于db10小波滤波结果,进一步表明使用SSA方法能够更准确地消除多路径误差。
|
|
表 3 多路径误差统计分析 Tab. 3 Correlation statistic of multipath error |
本文利用改进相空间重构Cao算法确定嵌入维数L,并将其运用到SSA算法中,同时分析计算北斗系统不同星座卫星的轨道重复周期,最后将SSA算法用于北斗短基线恒星日滤波,并与传统小波去噪方法进行比较,得到以下结论:
1) 本文提出的嵌入维数的稳定性判定准则大大降低了Cao算法的主观性,将其运用到SSA中能显著提高SSA算法的准确性和计算效率。
2) 北斗系统3类卫星有着不同的轨道运动特性,不同类型的卫星轨道重复周期变化趋势不同,其中GEO卫星轨道重复周期变化幅度最大,IGSO卫星次之,MEO卫星轨道重复周期的变化幅度最小。北斗系统多路径误差周期约为86 160 s。
3) 基于SSA的北斗恒星日滤波算法相比基于小波的恒星日滤波算法能更有效地消除多路径误差的影响,经SSA方法滤波后的坐标序列精度优于小波滤波结果,利用该滤波方法可显著提高北斗动态变形监测的精度。
| [1] |
黄声享, 李沛鸿, 杨保岑, 等. GPS动态监测中多路径效应的规律性研究[J]. 武汉大学学报:信息科学版, 2005, 30(10): 877-880 (Huang Shengxiang, Li Peihong, Yang Baocen, et al. Study on the Characteristics of Multipath Effects in GPS Dynamic Deformation Monitoring[J]. Geomatics and Information Science of Wuhan University, 2005, 30(10): 877-880)
(  0) 0) |
| [2] |
Lau L, Mok E. Improvement of GPS Relative Positioning Accuracy by Using SNR[J]. Journal of Surveying Engineering, 1999, 125(4): 185-202 DOI:10.1061/(ASCE)0733-9453(1999)125:4(185)
(  0) 0) |
| [3] |
Lau L, Cross P. Development and Testing of a New Ray-Tracing Approach to GNSS Carrier-Phase Multipath Modeling[J]. Journal of Geodesy, 2007, 81(11): 713-732 DOI:10.1007/s00190-007-0139-z
(  0) 0) |
| [4] |
Ye S R, Chen D Z, Liu Y Y, et al. Carrier Phase Multipath Mitigation for Beidou Navigation Satellite System[J]. GPS Solutions, 2015, 19(4): 545-557 DOI:10.1007/s10291-014-0409-1
(  0) 0) |
| [5] |
Ma X Y, Shen Y Z. Multipath Error Analysis of COMPASS Triple Frequency Observations[J]. Positioning, 2014, 5(1): 12-21 DOI:10.4236/pos.2014.51002
(  0) 0) |
| [6] |
徐克红, 程鹏飞, 文汉江. 太阳黑子数时间序列的奇异谱分析和小波分析[J]. 测绘科学, 2007, 32(6): 35-38 (Xu Kehong, Cheng Pengfei, Wen Hanjiang. Singular Spectrum Analysis and Wavelet Analysis on the Series of Sunspot[J]. Science of Surveying and Mapping, 2007, 32(6): 35-38 DOI:10.3771/j.issn.1009-2307.2007.06.011)
(  0) 0) |
| [7] |
卢辰龙.奇异谱分析在大地测量时间序列分析中的应用研究[D].长沙: 中南大学, 2014 (Lu Chenlong. Research on Application of Singular Spectrum Analysis in Geodetic Survey Time Series[D]. Changsha: Central South University, 2014) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2687635
(  0) 0) |
| [8] |
Cao L Y. Practical Method for Determining the Minimum Embedding Dimension of a Scalar Time Series[J]. Physica D: Nonlinear Phenomena, 1997, 110(1-2): 43-50 DOI:10.1016/S0167-2789(97)00118-8
(  0) 0) |
| [9] |
Agnew D C, Larson K M. Finding the Repeat Times of the GPS Constellation[J]. GPS Solution, 2007, 11(1): 71-76
(  0) 0) |
| [10] |
韩晓飞, 马绪瀛, 丁晓光, 等. 北斗单历元基线解算与恒星日滤波算法[J]. 测绘通报, 2015(4): 5-9 (Han Xiaofei, Ma Xuying, Ding Xiaoguang, et al. Single Epoch Baseline Solution and Sidereal Filtering of Beidou[J]. Bulletin of Surveying and Mapping, 2015(4): 5-9)
(  0) 0) |
2. Wuhan Base of Institute of Crustal Dynamics, CEA, 40 Hongshance Road, Wuhan 430071, China
 2019, Vol. 39
2019, Vol. 39


