卫星精密定轨(precision orbit determination, POD)是低轨卫星顺利执行任务的关键。相比于DORIS、SLR和PRAPRE卫星定轨技术,星载GPS技术具有成本低、精度高、受天气影响小等优点,越来越广泛应用于对地观测的低轨卫星,例如GRACE、CHAMP、GOCE等[1-3],其定轨精度可达到cm级别。相比于几何法和动力学法,简化动力学定轨方法可以更好地调节低轨卫星的几何信息和动力信息,精度也较高,因此被更多地用于卫星定轨中[4]。并且GPS载波相位的测量精度远高于GPS伪距,利用高质量的载波相位观测值进行卫星定轨能有效提高精度。GPS天线相位中心误差是GPS载波相位观测值中的一个重要误差源,不同于测地型天线,星载GPS天线一般难以获取天线相位中心变化(phase center variations, PCV)信息,即使通过微波暗室检校或者地面机器人检校方法获取了先验PCV信息,但卫星入轨后,受到太空环境变化的影响,也会发生巨大变化。
本文重点研究星载GPS天线的PCV模型对卫星精密定轨的影响,以GRACE低轨卫星为例,采取简化动力学定轨方法,分别使用地面获取的先验PCV模型及利用残差法估计的在轨PCV模型对GRACE卫星进行精密定轨实验,并利用GFZ精密轨道对比和SLR检核等手段进行评估,验证该模型对提高低轨卫星定轨精度的有效性。
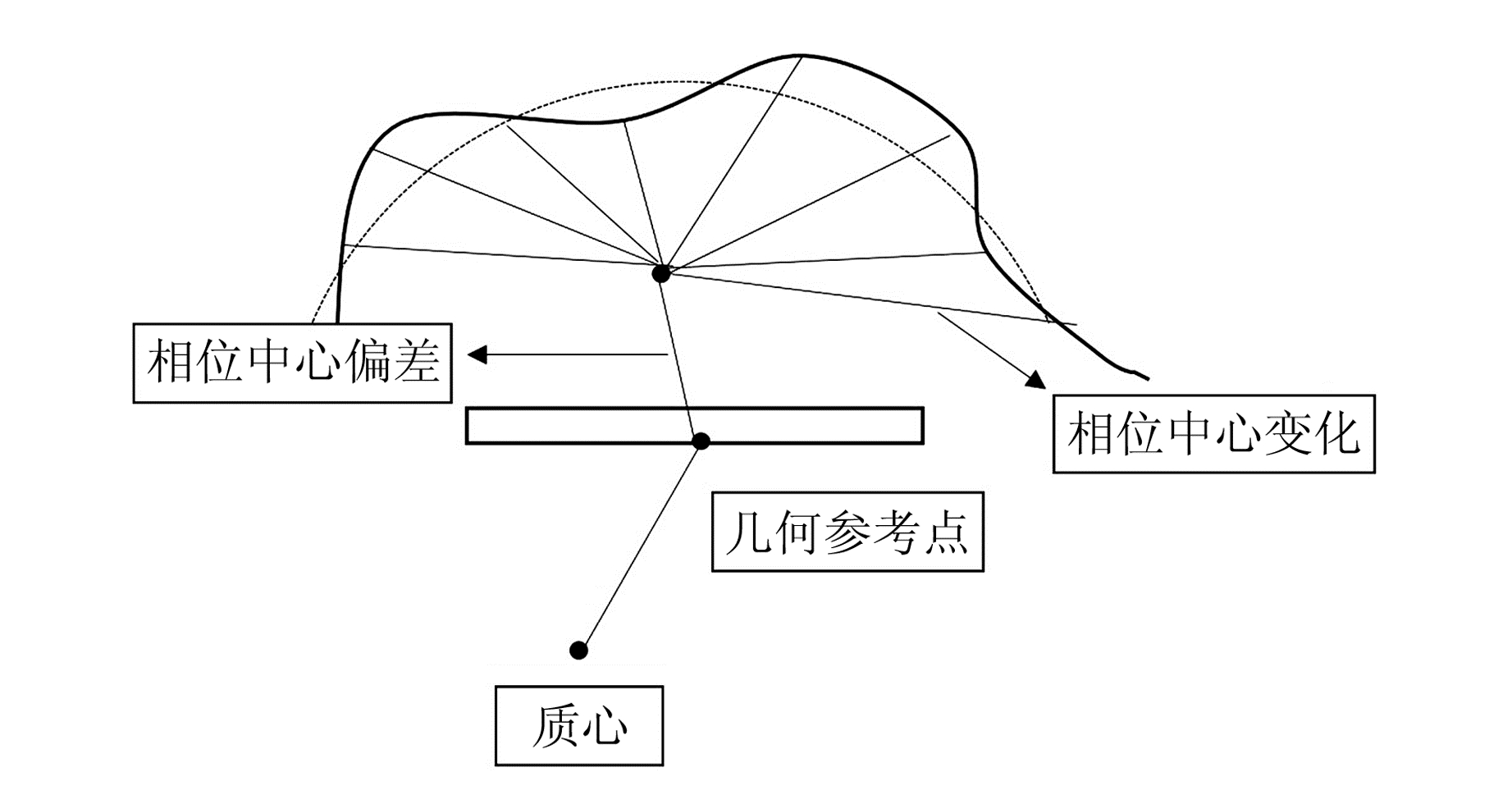
1 GPS接收机天线相位中心模型低轨卫星的轨道坐标是以质心为参考点,而GPS测量值实际是天线接收GPS信号的瞬时相位中心,两者并不重合,因此需要将瞬时相位中心改正到卫星质心。首先,卫星质心与天线几何参考点(antenna reference point, ARP)的改正值一般为固定值,由卫星制造商给出。几何参考点与平均相位中心的改正值为相位中心偏差(phase center offset, PCO)。由于天线制造工艺等因素,相位中心并不是稳定的点,而是会发生波动,瞬时相位中心和平均相位中心的偏差即为PCV[5]。因此,当有了PCV、PCO以及质心与ARP改正值后,就可以将瞬时相位中心改正到质心上,天线相位中心改正见图 1。
|
图 1 GPS接收机天线相位中心改正 Fig. 1 The antenna phase center variationsof GPS receiver |
GRACE卫星上装有质心调节设备,可使质心位置处于相对稳定状态,PCO相对变化也不大[6]。因此,本文采取地面获取的PCO信息为固定值,重点研究PCV模型对精密定轨的影响。PCO、PCV均定义在天线固定参考坐标系(antenna fixed system, AFS)下,AFS原点为ARP,z轴正方向与机械系统轴相连,指向视准轴方向;y轴和x轴与卫星本体坐标系(satellite body system, SBS)相关,指向因具体天线安装情况而异,如GRACE卫星x轴和SBS的X轴向指向一致,但y轴正好相反。为和地面天线描述标准一致,AFS中的x-y-z也可描述为North-East-Up,其中,N方向与+y方向一致,E方向与+x方向一致,U方向与+z方向一致,仅表述不同。方位角定义为一矢量在xoy平面内+y轴旋转至+x轴的角度,高度角定义为该矢量和xoy平面的夹角。
GRACE卫星搭载多种科学设备,如GPS接收机系统、SLR反射器系统、质心调节装置、加速度计等[7]。表 1(单位mm)列出了与定轨相关的GPS天线和SLR反射器在SBS下的坐标。
|
|
表 1 GRACE卫星GPS天线及SLR反射器在SBS下的位置 Tab. 1 The positions of GPS receiver antenna phase and SLR reflector of GRACE satellites in SBS |
GRACE卫星搭载Blackjack接收机,上面装有多副天线,用于定轨、大气探测、GPS信号测高实验等,其中,用于精密定轨的双频GPS天线是由GFZ制造的带有扼流圈的S67-1575-14+CRG双频天线,以更好地减小多路径等因素的影响,L1、L2频率的测量噪声仅为1 mm,L3频率则为2~3 mm[8]。GPS天线在地面通过自动机器人测量系统对PCO进行绝对校正,该校正方法可达到使用微波暗室校正的1 mm精度。通过机器人校正,S67-1575-14+CRG天线的各频率相应方向的PCO见表 2(单位mm)。
|
|
表 2 GPS天线地面标定PCO Tab. 2 The PCO by ground calibration of GPS receiver antenna |
设PCO矢量形式为Δr,PCV为与高度角α、方位角z有关的函数,则由PCO及PCV导致的距离误差为:
| $ \Delta \varphi \left( {\alpha , z} \right) = \mathit{\boldsymbol{re}} + {\rm{PCV}}\left( {\alpha , z} \right) $ | (1) |
式中,e为卫星信号入射方向的单位矢量。
PCV模型表示方法主要有球谐函数法和分段线性函数法。球谐函数法物理意义明确,但计算量大。而分段线性函数法计算量小,实现容易,效果与球谐函数法差异很小,所以本文采用分段线性函数模型表示PCV模型。该方法中,设PCV模型由高度角和方位角组成的网格图(图 2)中的不同格网点组成,利用双线性插值公式即可得到所求对应方位角和高度角的PCV值。

|
图 2 GPS接收机天线PCV格网点示意图 Fig. 2 The PCV grid point diagram ofGPS receiver antenna |
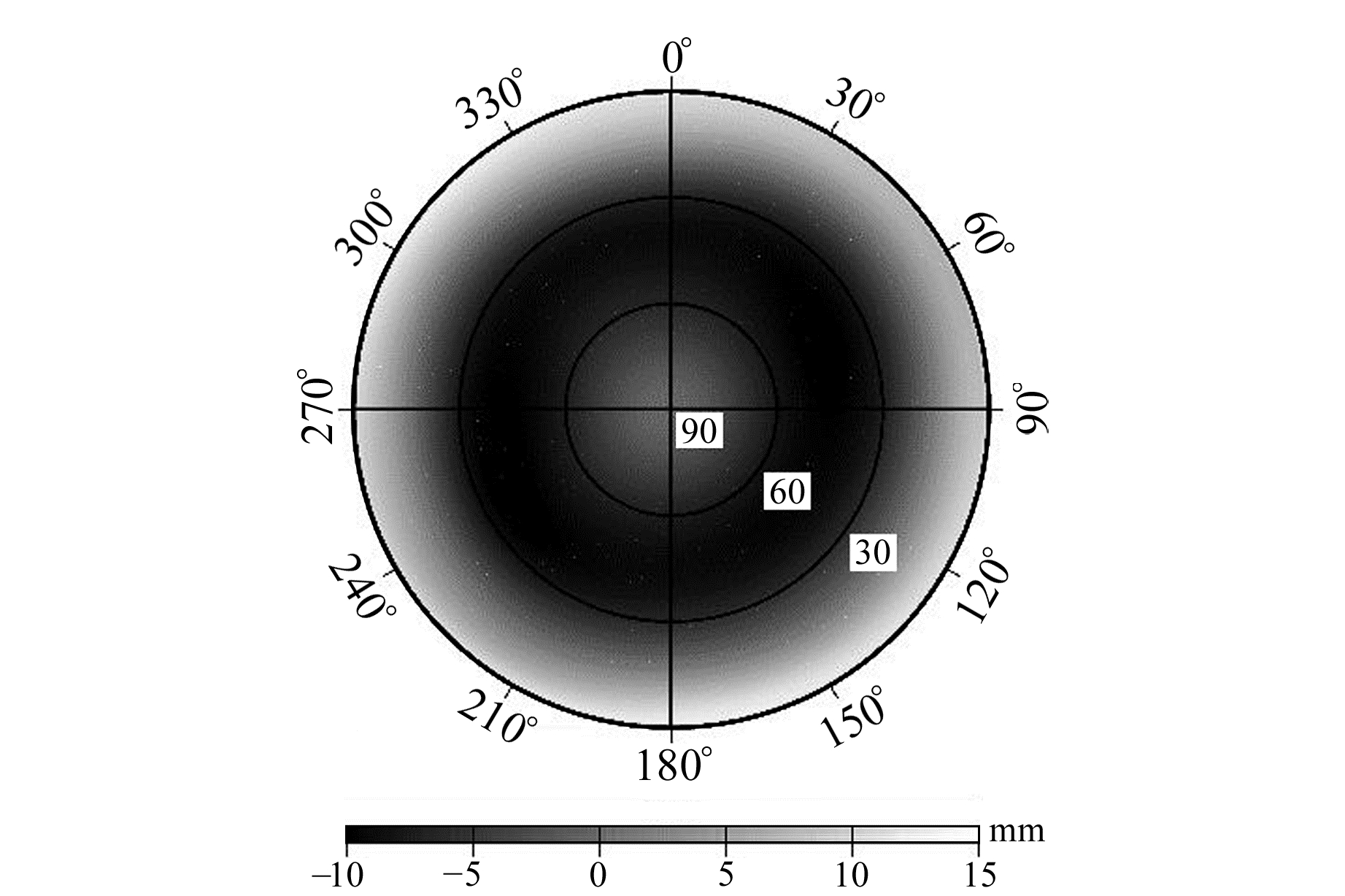
同PCO地面估计策略相同,该天线在地面使用自动机器人测量系统获取先验PCV模型,图 3展示了天线坐标系下无电离层组合观测值L3上的PCV模型。
|
图 3 GRACE卫星地面校正的PCV模型 Fig. 3 The PCV model by ground calibration ofGRACE satellites |
分析可知,先验PCV模型量级为[-10.43,14.31] mm,而且通过人工设计,先验PCV模型几乎是严格按照高度角分布的,随着高度角的增大呈现近似线性减小的分布特征。
为了更清楚地分析先验PCV模型对精密定轨的影响,设计2种定轨方案:方案一,不使用PCV模型,用“-PCV”表示;方案二,采用图 3所示的地面获取的先验PCV模型,用“+PCV”表示,其他定轨策略完全相同。选取的星载GPS数据为2016-02-01~02-29,定轨平台为Bernese5.2,采用简化动力学方法,利用统计定轨原理和最小二乘批处理算法进行定轨[9]。定轨中选取的力学模型和估计参数等见表 3。
|
|
表 3 GRACE卫星简化动力学定轨方案 Tab. 3 The reduced-dynamic orbit determination method of GRACE satellites |
本文使用多种方法评价PCV模型对精密定轨的影响。内符合精度采用观测值残差评估,残差RMS值在一定程度上体现了选用力学模型以及数据预处理情况,因此,在观测值充足时,可以选用该方法评定定轨内符合精度[10-11]。外符合精度采用外部精密轨道对比和SLR检核2种手段评估[12]。GFZ发布的最终精密轨道(precise science orbit, PSO)是公认的高精度轨道,与其对比可以直接反映定轨精度,而SLR检核更是一种高精度评估手段,其测距精度可达到1 cm。该方法实际就是比较SLR直接测得的站星距离和星载GPS定轨结果反算的站星距,SLR残差即为两者站星距之差。为保证SLR检核的可靠性,必须考虑SLR质心改正等各项改正。
由表 4(单位mm)可知,当未使用PCV模型时,2颗卫星已经可以达到较高定轨精度,残差水平在6 mm左右,SLR检核结果RMS值优于4 cm,与外部精密轨道相比,R、T、N 3个方向精度均在3 cm左右,三维位置精度在5 cm左右。当使用地面检校提供的先验PCV模型时,定轨精度反而开始下降,2颗卫星轨道残差分别上升0.15 mm、0.12 mm。SLR检核精度更是明显下降,平均值由原来的2 mm左右上升到10 mm左右,RMS值也均有所增大。与PSO轨道对比,R、T、N 3个方向精度均有所下降,三维位置精度更是增大了7.20 mm、7.01 mm。这说明PCV模型相比地面检测时已经发生变化,再使用先验PCV模型会降低定轨精度,也反映了在轨估计PCV模型的重要性。
|
|
表 4 先验PCV模型对GRACE卫星精密定轨的影响 Tab. 4 The impact on precise orbits determination based on the priori PCV model |
星载GPS天线PCV在轨估计主要有直接法和残差法[13-14]。直接法是将PCV值视为未知参数,将其保存在定轨方程中,与其他轨道参数一同求解,该方法不易受接收机钟差、模糊度参数等影响,但计算量大,对计算机运算和存储能力要求较高。而残差法则是利用简化动力学轨道的载波相位残差进行分析建模,计算简单、容易实现:
| $ {\rm{\Delta PCV}}\left( e \right) = {\rm{PC}}{{\rm{V}}_{{\rm{true}}}}\left( e \right) - {\rm{PC}}{{\rm{V}}_{{\rm{model}}}}\left( e \right) $ | (2) |
式中,PCVtrue(e)为真实的PCV模型,PCVmodel(e)为使用的PCV模型,其差值即为未被模型化的PCV误差。若定轨中不考虑PCV误差,则该误差在简化动力学轨道残差中分布极为明显,因此,未被模型化的PCV误差将会残留在定轨后的载波相位残差中:
| $ {\rm{\Delta PCV}}\left( e \right) \approx \Delta \left( {{L_{{\rm{IF}}}} - {Z_{{\rm{IF}}}}} \right) $ | (3) |
式中,LIF为GPS观测值,ZIF为改正其余误差(不考虑PCV)后的模型值。该方法容易受到其他轨道参数的影响,故采取多次迭代处理,迭代策略如式(4)所示:
| $ \begin{array}{l} {\rm{\Delta PCV}}\left( e \right) \approx \Delta \left( {{L_{{\rm{IF}}}} - {Z_{{\rm{IF}}}}} \right)\\ {\rm{PCV}}\left( {k + 1} \right) = {\rm{PCV}}\left( {k + 1} \right) + \Delta {\rm{PCV}}\left( k \right) \end{array} $ | (4) |
当定轨精度不再提升时迭代即可停止[7],一般选取3~5次迭代PCV就能达到足够收敛。2种方法实现的效果基本相同,而残差法更容易编程实现,因此本文选择残差法估计在轨PCV模型,迭代次数为3次。
同样,选取GRACE A与GRACE B 2颗卫星2016-02-01~02-29的星载GPS观测数据,利用残差法对这2颗低轨卫星的在轨PCV模型进行估计,定轨策略同表 3一致。
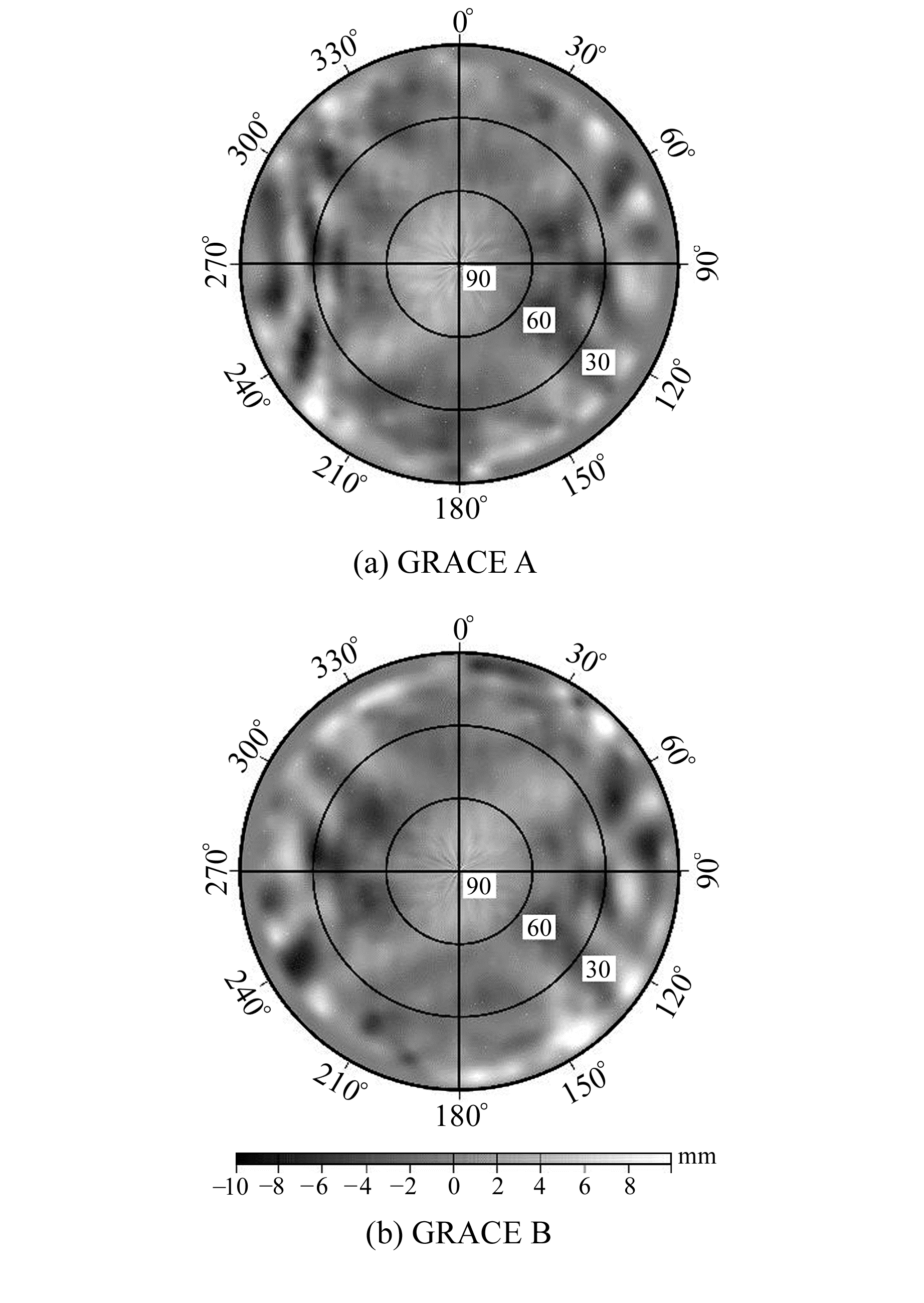
图 4展示了GRACE A和GRACE B在轨后的PCV模型。相比于地面PCV模型,在轨PCV模型发生了较大的变化,2颗卫星的PCV模型极为相似,这与2颗卫星的接收机及GPS天线相同、所处太空环境基本一致有关。不同于地面PCV模型几乎完全对称的特性,在轨估计的PCV模型更多地呈现条带分布,同时,较大的PCV值更多地分布在低高度角,这主要是因为高度角较低时,观测值精度较低。
|
图 4 GRACE A与GRACE B在轨估计PCV模型 Fig. 4 The in-flight PCV model of GRACE Aand GRACE B satellites |
为了更清楚地分析在轨PCV模型对精密定轨的影响,本文设计2种定轨方案:方案一,不使用PCV模型,用“-PCV”表示,方案二,采用图 4所示的在轨估计的PCV模型,用“+PCV”表示,其他定轨策略完全相同。
由表 5(单位mm)可见,当使用在轨估计的PCV模型时,无论是内符合精度指标,还是外符合精度指标,定轨精度相比不使用PCV模型均有所提高,相位观测值残差由6 mm降为5 mm左右,2颗卫星的SLR检核结果RMS值分别提高1.79 mm、3.61 mm。与PSO轨道对比,R,T,N 3个方向的精度均有所提高,2颗卫星在三维方向上的精度也分别提高5.32 mm、2.94 mm。可见,考虑星载GPS天线PCV模型对精密定轨精度的提高起到重要作用。因此,在定轨过程中,必须对PCV建立在轨模型并予以修正。
|
|
表 5 在轨PCV模型对GRACE卫星精密定轨的影响 Tab. 5 The impact on precise orbits determination based on the in-flight PCV model |
本文以GRACE A及GRACE B卫星为例,阐述了LEO卫星GPS接收机天线相位中心校正模型及其改正方法,介绍了残差法在轨估计PCV模型的基本原理。使用先验PCV模型不仅未提高定轨精度,反而使得定轨精度进一步下降,说明在轨PCV模型相比地面模型发生较大变化。通过使用残差法估计在轨模型,使用PSO对比和SLR检核等手段分析评估在轨PCV模型对精密定轨的影响,发现使用在轨PCV模型,2颗卫星SLR检核RMS值分别提高1.79 mm、3.61 mm;与PSO轨道对比,2颗卫星在三维方向上精度分别提高5.32 mm、2.94 mm,说明PCV误差是影响精密定轨的重要误差源。在卫星精密定轨中,应充分考虑星载GPS天线PCV信息,对其进行在轨估计能有效提高精密定轨的精度,这对我国的国产卫星或者其他低轨卫星的精密定轨有借鉴意义。
| [1] |
Tapley B D, Bettadpur S, Watkins M, et al. The Gravity Recovery and Climate Experiment: Mission Overview and Early Results[J]. Geophysical Research Letters, 2004, 31(9)
(  0) 0) |
| [2] |
Reigber C, Lühr H, Schwintzer P. CHAMP Mission Status[J]. Advances in Space Research, 2002, 30(2): 129-134 DOI:10.1016/S0273-1177(02)00276-4
(  0) 0) |
| [3] |
Bock H, Jäggi A, Švehla D, et al. Precise Orbit Determination for the GOCE Satellite Using GPS[J]. Advances in Space Research, 2007, 39(10): 1638-1647 DOI:10.1016/j.asr.2007.02.053
(  0) 0) |
| [4] |
赵春梅, 程鹏飞, 益鹏举. 基于伪随机脉冲估计的简化动力学卫星定轨方法[J]. 宇航学报, 2011, 32(4): 762-766 (Zhao Chunmei, Cheng Pengfei, Yi Pengju. Reduced-Dynamics Satellite Orbit Determination Based on Pseudo-Stochastic Pulse Estimation[J]. Journal of Astronautics, 2011, 32(4): 762-766 DOI:10.3873/j.issn.1000-1328.2011.04.009)
(  0) 0) |
| [5] |
田英国, 郝金明. Swarm卫星天线相位中心校正及其对精密定轨的影响[J]. 测绘学报, 2016, 45(12): 1406-1412 (Tian Yingguo, Hao Jinming. Swarm Satellite Antenna Phase Center Correction and Its Influence on the Precision Orbit Determination[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(12): 1406-1412 DOI:10.11947/j.AGCS.2016.20160132)
(  0) 0) |
| [6] |
Montenbruck O, Garcia-Fernandez M, Yoon Y, et al. Antenna Phase Center Calibration for Precise Positioning of LEO Satellites[J]. GPS Solutions, 2009, 13(1): 23-34 DOI:10.1007/s10291-008-0094-z
(  0) 0) |
| [7] |
Mao X, Visser P N A M, Ijssel J V D. Impact of GPS Antenna Phase Center and Code Residual Variation Maps on Orbit and Baseline Determination of GRACE[J]. Advances in Space Research, 2017, 59(12): 2987-3002 DOI:10.1016/j.asr.2017.03.019
(  0) 0) |
| [8] |
Jäggi A, Dach R, Montenbruck O, et al. Phase Center Modeling for LEO GPS Receiver Antennas and Its Impact on Precise Orbit Determination[J]. Journal of Geodesy, 2009, 83(12): 1145-1162 DOI:10.1007/s00190-009-0333-2
(  0) 0) |
| [9] |
赵春梅, 唐新明. 基于星载GPS的资源三号卫星精密定轨[J]. 宇航学报, 2013, 34(9): 1202-1206 (Zhao Chunmei, Tang Xinming. Precise Orbit Determination for ZY-3 Satellite Mission Using GPS Receiver[J]. Journal of Astronautics, 2013, 34(9): 1202-1206 DOI:10.3873/j.issn.1000-1328.2013.09.004)
(  0) 0) |
| [10] |
周晓青, 胡志刚, 张新远. 低轨卫星星载GNSS精密定轨的精度检核方法[J]. 武汉大学学报:信息科学版, 2010, 35(11): 1342-1345 (Zhou Xiaoqing, Hu Zhigang, Zhang Xinyuan. Discussion on POD Accuracy Evaluations for Satellite-Bone LEO Satellites[J]. Geomatics and Information Science of Wuhan University, 2010, 35(11): 1342-1345)
(  0) 0) |
| [11] |
赵齐乐, 刘经南, 葛茂荣, 等. CHAMP卫星cm级精密定轨[J]. 武汉大学学报:信息科学版, 2006, 31(10): 879-882 (Zhao Qile, Liu Jingnan, Ge Maorong, et al. Precision Orbit Determination of CHAMP Satellite with cm-Level Accuracy[J]. Geomatics and Information Science of Wuhan University, 2006, 31(10): 879-882)
(  0) 0) |
| [12] |
秦显平, 焦文海, 程芦颖, 等. 利用SLR检核CHAMP卫星轨道[J]. 武汉大学学报:信息科学版, 2005, 30(1): 38-41 (Qin Xianping, Jiao Wenhai, Cheng Luying, et al. Evaluation of CHAMP Satellite Orbit with SLR Measurements[J]. Geomatics and Information Science of Wuhan University, 2005, 30(1): 38-41)
(  0) 0) |
| [13] |
Haines B, Bar-Sever Y, Bertiger W, et al. One-Centimeter Orbit Determination for Jason-1: New GPS-Based Strategies[J]. Marine Geodesy, 2004, 27(1-2): 299-318 DOI:10.1080/01490410490465300
(  0) 0) |
| [14] |
Bock H, Jäggi A, Meyer U, et al. Impact of GPS Antenna Phase Center Variations on Precise Orbits of the GOCE Satellite[J]. Advances in Space Research, 2011, 47(11): 1885-1893 DOI:10.1016/j.asr.2011.01.017
(  0) 0) |
 2019, Vol. 39
2019, Vol. 39


