2. 地理信息工程国家重点实验室,西安市雁塔中路1号,710054;
3. 西安测绘研究所,西安市雁塔中路1号,710054
IGS从2011年起开展多GNSS实验(the multi-GNSS experiment,MGEX),其主要目的是跟踪、收集和分析所有可用的GNSS信号,进而提供多GNSS的精密轨道和钟差等产品,促进多GNSS技术的推广和应用。为了对GNSS的运行状态和主要性能指标进行监测和评估,促进多GNSS的兼容与互操作,中国率先发起国际GNSS监测评估系统(international GNSS monitoring and assessment system,iGMAS)。
统一时空基准下的精密轨道和钟差产品是多GNSS高精度应用的前提,因此多GNSS轨道和钟差产品的生成一直是国际导航领域的研究热点。Montenbruck等[1]、Hackel等[2]、Steigenberger等[3]先后对MGEX提供的Galileo轨道和钟差产品进行评估,发现其轨道和钟差产品中存在与太阳高度角相关的系统性误差。Prange等[4]公布了CODE分析中心的多GNSS产品解算策略,并分析其Galileo产品的精度,发现存在同样的系统性误差。随后各分析中心陆续对各自的解算策略和产品进行说明和评估[4-5]。Guo等[6]对MGEX提供的Galileo、BDS和QZSS产品进行评估和分析。对Galileo精密产品的评估直接促进了多GNSS解算策略的优化和产品精度的提高,例如Montenbruck等[7]首先提出Cuboid Box-Wing先验模型,将Galileo卫星在非地影期的轨道精度从20 cm提高至5 cm左右。同时也推动了动力学模型的革新,例如Arnold等[8]论证了ECOM模型对GLONASS、Galileo等长方体型卫星的不适用性,并提出对ECOM2经验模型进行补偿;Prange等[9]进一步将ECOM2模型应用于CODE的多GNSS产品解算,使Galileo产品的精度显著提高。
虽然上述研究已对MGEX提供的多GNSS产品作了初步分析,但大多局限于Galileo和BDS系统,未对GPS/GLONASS/Galileo/BDS 4大核心系统的精密产品作出综合分析。此外,中国发起的iGMAS尚处于初始阶段,其综合产品的精度和可靠性还有待进一步论证。因此,本文对MGEX和iGMAS提供的多GNSS轨道和钟差产品进行评估,以期为多GNSS产品的解算策略优化提供一定的借鉴和参考。
1 评估方法采用不同机构间互差以及SLR残差进行轨道精度评估。GPS和GLONASS系统的评估以IGS最终产品为基准,IGS通过将各分析中心的产品进行加权综合处理得到事后精密产品,其GPS的最终轨道精度在2.5 cm左右,最终钟差的标准差在20 ps左右;GLONASS的最终轨道精度优于3.0 cm。考虑到各分析中心的参考基准和数据处理策略的差异,本文在轨道比较时进行Helmert旋转[10]。在评估Galileo/BDS系统的轨道时,首先采用不同产品互比的方式来给出轨道一致性,然后利用SLR残差检核轨道的径向绝对精度。
同轨道评估类似,Galileo/BDS系统的卫星钟差评估也主要采用不同产品互比的方式。卫星钟差比较一般需要采用二次差法消除钟差基准不一致,但由于卫星钟差与轨道径向分量的强相关性,在钟差比较时还需要考虑轨道径向误差的影响,在实际应用时可以根据公式(1)计算轨道径向对钟差的误差改正[11]:
| $ \Delta {\rm{clk}}_i^s = \left( {\left( {\overrightarrow {{\rm{ord}}} _{1,i}^s - \overrightarrow {{\rm{ord}}} _{2,i}^s - \overrightarrow {{\rm{cen}}} _{1,2}^s} \right) \cdot \overrightarrow {{\rm{ord}}} _{1,i}^s} \right){\rm{/}}R_{1,i}^s/c $ | (1) |
式中,i为历元数,s为卫星数,
此外,Galileo卫星的被动型氢原子钟具有极高的短期稳定性,可将钟差拟合残差作为评定Galileo钟差产品优劣的指标。而BDS系统仅搭载有铷原子钟,在性能上与GPS铷钟和Galileo氢钟仍有较大差距,因此本文将能反映卫星钟稳定性的阿伦方差作为钟差产品质量的评定指标。
2 评估结果与分析 2.1 GPS/GLONASS轨道精度分析图 1给出了CODE、GFZ、WHU和iGMAS(产品分别为COM、GBM、ISC和WUM)的GPS/GLONASS轨道的一维RMS时间序列,其平均精度如表 1(单位cm)所示。从图 1和表 1可以看出:1)iGMAS提供的GPS和GLONASS卫星的轨道产品精度最优,GPS轨道精度优于1.0 cm,GLONASS轨道精度优于2.1 cm;2)GFZ与WHU的轨道精度较为接近,其GPS轨道精度优于1.3 cm,GLONASS轨道精度优于3.0 cm,但是iGMAS和WHU而言,其在个别天数出现异常;3)CODE的轨道产品精度略低于其他分析中心,其GPS轨道精度在1.4 cm左右,GLONASS轨道精度在3.7 cm左右,在个别天数也出现精度异常,其稳定性和可靠性仍有待提高。
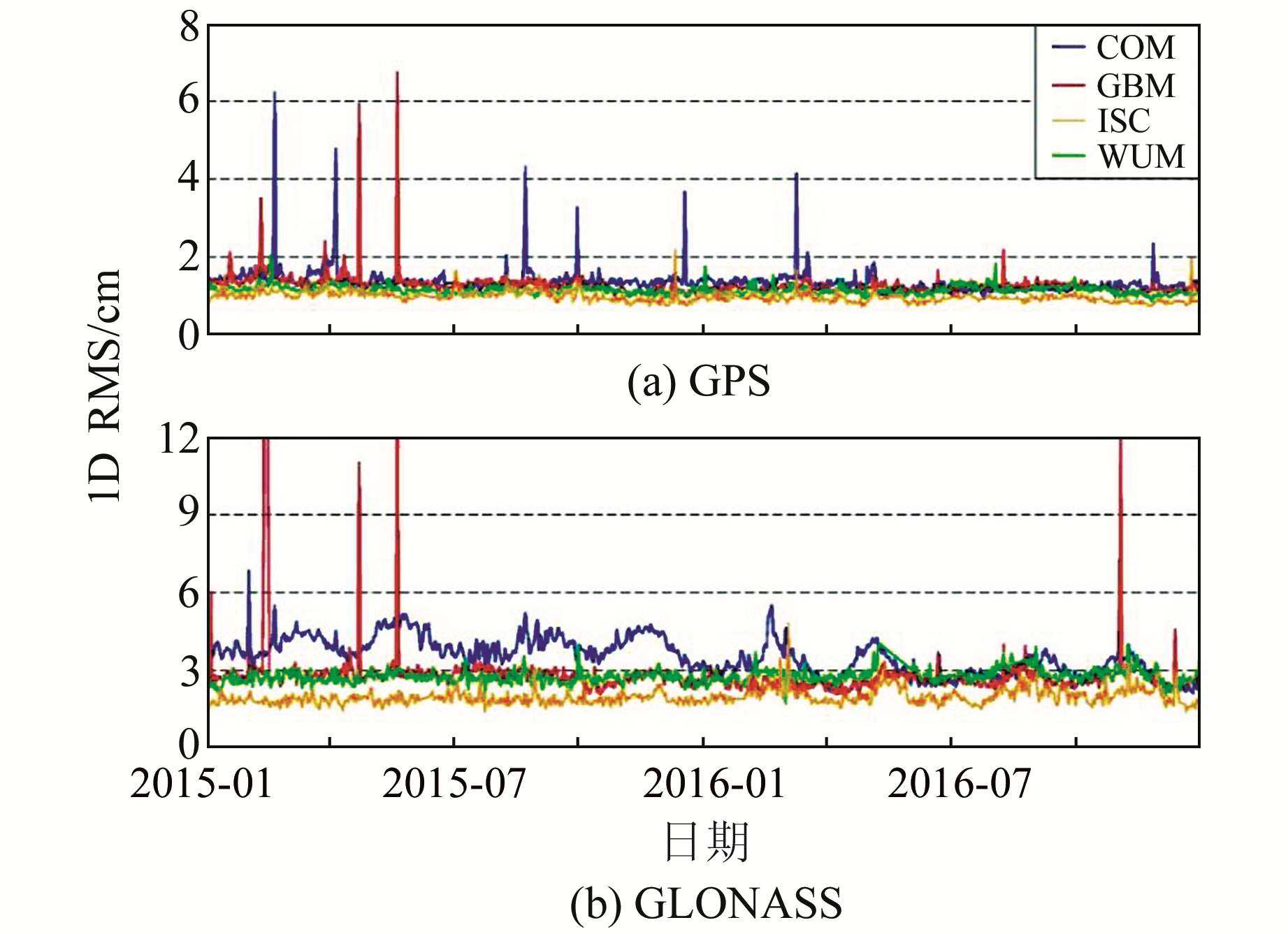
|
图 1 各分析中心的GPS/GLONASS轨道产品的一维RMS Fig. 1 The daily 1D RMS of the GPS and GLONASS orbit products from different ACs |
|
|
表 1 各分析中心的GPS/GLONASS轨道产品的一维平均RMS Tab. 1 The average 1D RMS of GPS and GLONASS orbit products from different ACs compared with the IGS final products |
图 2给出了GFZ、WHU和iGMAS相对于CODE的Galileo轨道产品在切向、法向和径向上的时间序列,表 2(单位cm)统计了各分析中心的轨道产品互差结果。从图 2、表 2可以看出,Galileo轨道的三维一致性在11~17 cm。随着卫星和地面测站数量的增多,各分析中心的Galileo轨道的精度逐渐提高。CODE与WHU的轨道一致性较好,与GFZ和iGMAS的轨道差距较大。
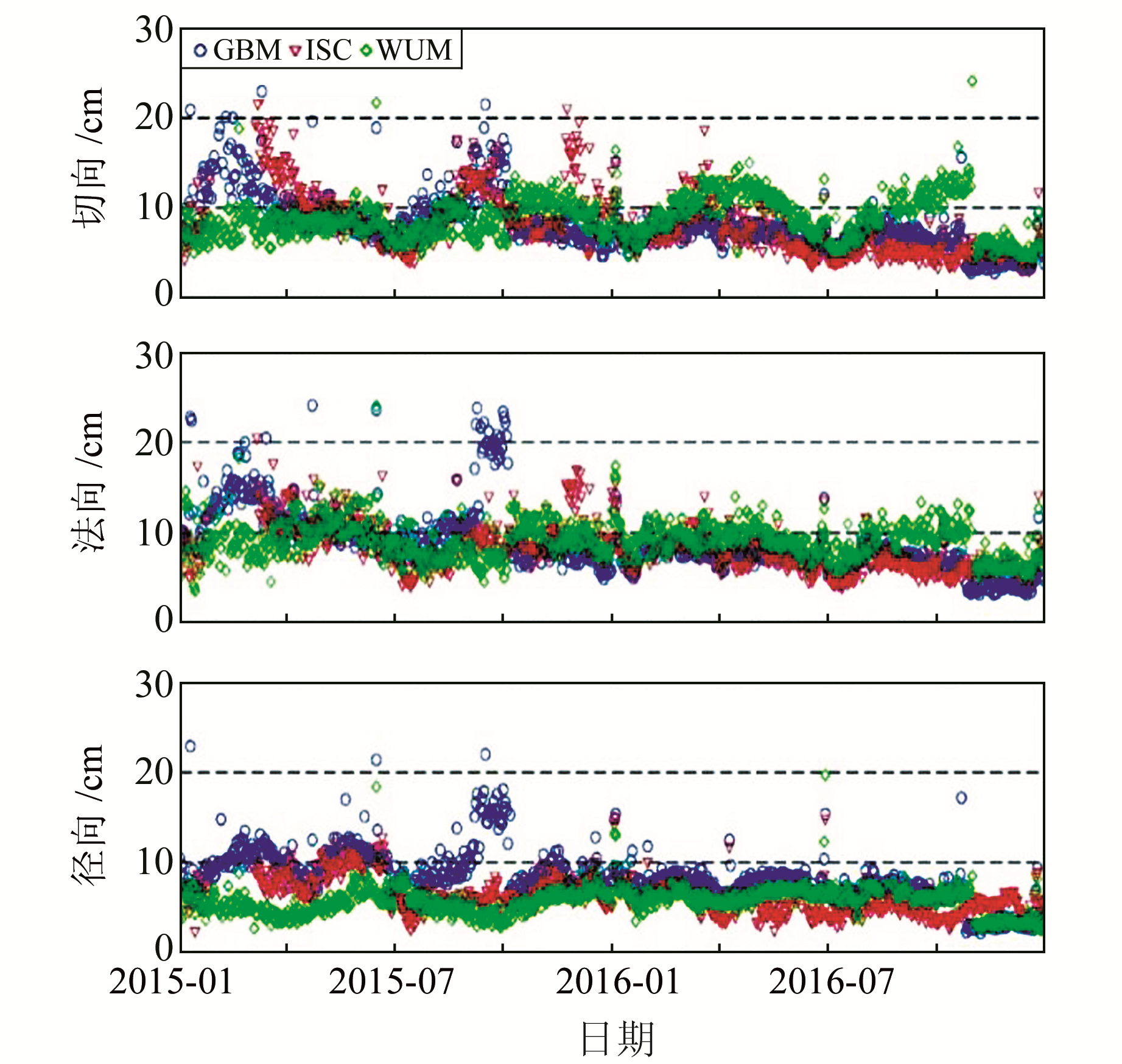
|
图 2 不同分析中心的Galileo轨道比较 Fig. 2 Galileo orbit comparisons (以CODE产品为基准) (with respect to the CODE orbit products) |
|
|
表 2 Galileo系统的三维轨道比较 Tab. 2 The average 3D RMS of Galileo orbit comparisons among different ACs |
对Galileo卫星的轨道径向精度进行SLR残差检核,结果如表 3所示,其中括号内的数据表示数据处理策略调整后的值。为进一步反映各分析中心的轨道产品特性,本文将SLR残差序列投影到卫星-地球-太阳平面,结果如图 3所示。图 3 (a)~(d)和(e)~(h)分别为Galileo-IOV卫星和Galileo-FOC卫星的SLR残差序列与γ角(太阳-卫星-地球的夹角)之间的关系,“□”表示数据处理策略调整后的SLR残差。从图 3、表 3(单位cm)可以看出:1) CODE的Galileo轨道径向精度在4 cm以内,采用ECOM2模型使得SLR残差与γ角仅存在较弱的线性关系;2)iGMAS的SLR残差的振幅在20 cm左右,与γ角存在明显的线性关系,这是由于目前多数iGMAS分析中心采用5参数ECOM模型造成的;3)GFZ在附加了Cuboid Box-Wing先验模型后的轨道精度有明显提高,SLR残差的标准差从8 cm降低至4 cm左右;4)WHU的Galileo-IOV的轨道精度与CODE相当,但Galileo-FOC的轨道表现出不同的特点,Galileo-FOC卫星的的轨道精度在数据处理策略调整后有明显提高。
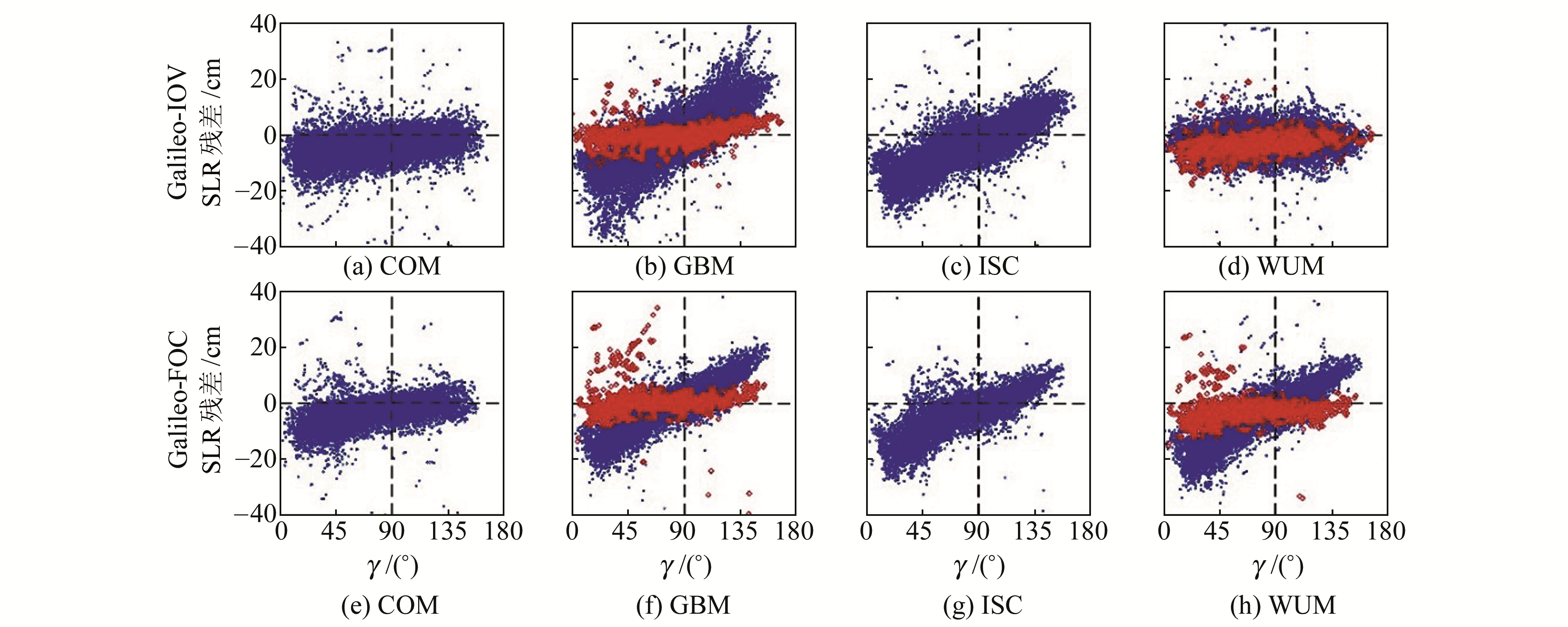
|
图 3 Galileo-IOV和Galileo-FOC的SLR残差与γ角的关系 Fig. 3 SLR residuals of Galileo-IOV and Galileo-FOC versus the γ angle |
|
|
表 3 Galileo-IOV和Galileo-FOC卫星的SLR残差统计 Tab. 3 Statistics of SLR residuals of Galileo-IOV and Galileo-FOC orbits |
BDS系统由GEO、IGSO和MEO 3类卫星组成,按卫星类型统计各分析中心轨道产品互比结果(表 4,单位cm)。以WHU的产品为基准,图 4给出了各分析中心各类卫星在切向、法向和径向上的轨道一致性结果。从图 4、表 4可以看出:1)BDS各类卫星的轨道精度差异较大,MEO卫星最优,IGSO卫星次之,GEO卫星最差,GEO卫星的一致性达到数m级,IGSO和MEO卫星的一致性分别在21~40 cm和11~18 cm;2)GEO卫星在切向和法向上的差异较大,但是径向上差异均在20 cm以内,IGSO卫星在切向、法向上的精度稳定在20 cm以内,径向精度能达到10 cm,MEO卫星的轨道切向和法向精度在10 cm以内,径向精度在3~5 cm。

|
图 4 BDS系统的轨道比较(以WHU产品为基准) Fig. 4 BDS orbit comparisons (with respect to WHU products) |
|
|
表 4 BDS系统的三维轨道比较 Tab. 4 3D RMS of BDS orbit comparisons among different ACs |
BDS系统的SLR残差检验结果如表 5所示。图 5描述了SLR残差与β角的时间序列,图中红色部分表示卫星处于零偏模式。从图 5、表 5(单位cm)可以看出:1)GEO卫星存在约-45 cm的平均偏差,STD值在24~30 cm;2)IGSO卫星的STD值在5~7 cm,其中WHU的STD值略大;3)MEO卫星的STD值在4 cm左右,其中WHU的结果最优, SLR残差检验与各分析中心产品互比的结果基本一致;4)IGSO和MEO卫星受地影期的影响较大,其中CODE的轨道精度下降最为明显。
|
|
表 5 BDS系统的SLR残差统计 Tab. 5 Statistics of SLR residuals of BDS orbits |
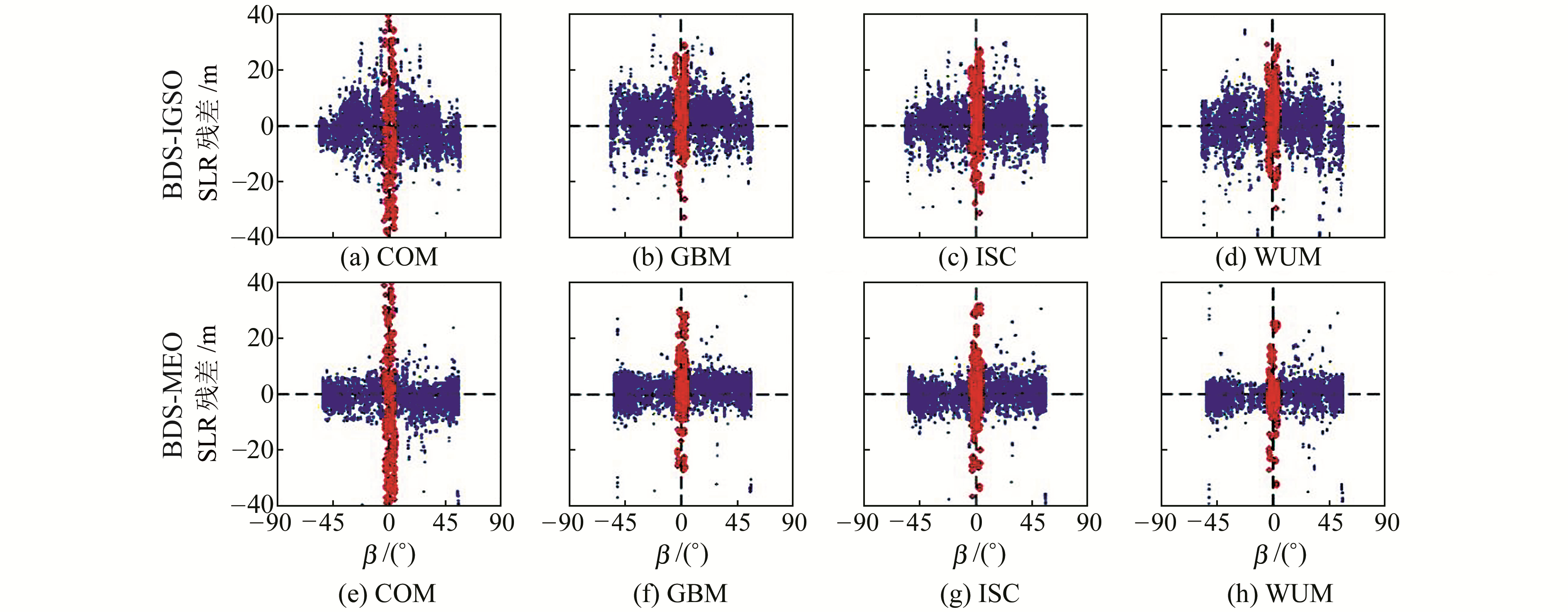
|
图 5 BDS卫星轨道SLR残差与β角的时间序列 Fig. 5 SLR residuals of BDS orbits versus the β angle |
图 6给出了GPS卫星钟差的一维STD和RMS时间序列以及GLONASS卫星钟差的一维STD时间序列。表 6(单位ps)统计了GPS/GLONASS系统的卫星钟差精度。由于IGS还没有提供GLONASS的精密钟差,但在IGS最终产品中GFZ与ESA产品所占权重较大,为了避免GFZ的IGS产品与MGEX产品之间的相关性,所以将ESA的事后精密钟差作为参考基准,ESA的钟差精度在120 ps左右[6]。由于GLONASS系统的信号采用频分多址体制,这将给双差解算的卫星钟差带来额外的偏差[4],因此本文仅统计STD值。从图 6、表 6可以看出:1)WHU的STD和RMS优于其他各分析中心;2)GFZ的STD值次于WHU,但是RMS值偏大,这可能是由于GPS的P1C1码偏差改正值未改正而被卫星钟差吸收所致;3)iGMAS的STD值和RMS值在评估时间段内出现较多的异常跳变,表明其钟差产品的精度和稳定性尚不如其轨道产品;4)WHU的GLONASS卫星钟差的STD值最小,GFZ次之,CODE最大,iGMAS的GLONASS卫星钟差产品不如轨道产品稳定。

|
图 6 GPS和GLONASS系统的单天STD与RMS时间序列 Fig. 6 The daily STD and RMS of GPS/GLONASS clock products |
|
|
表 6 GPS/GLONASS系统的卫星钟差精度统计 Tab. 6 The average STD and RMS of GPS/GLONASS clock products |
综上所述,WHU的GPS/GLONASS卫星钟差产品最优,这可能跟WHU的数据处理策略有关。iGMAS的钟差产品在精度和鲁棒性上不如轨道产品,其他分析中心的产品精度也有待进一步提高。
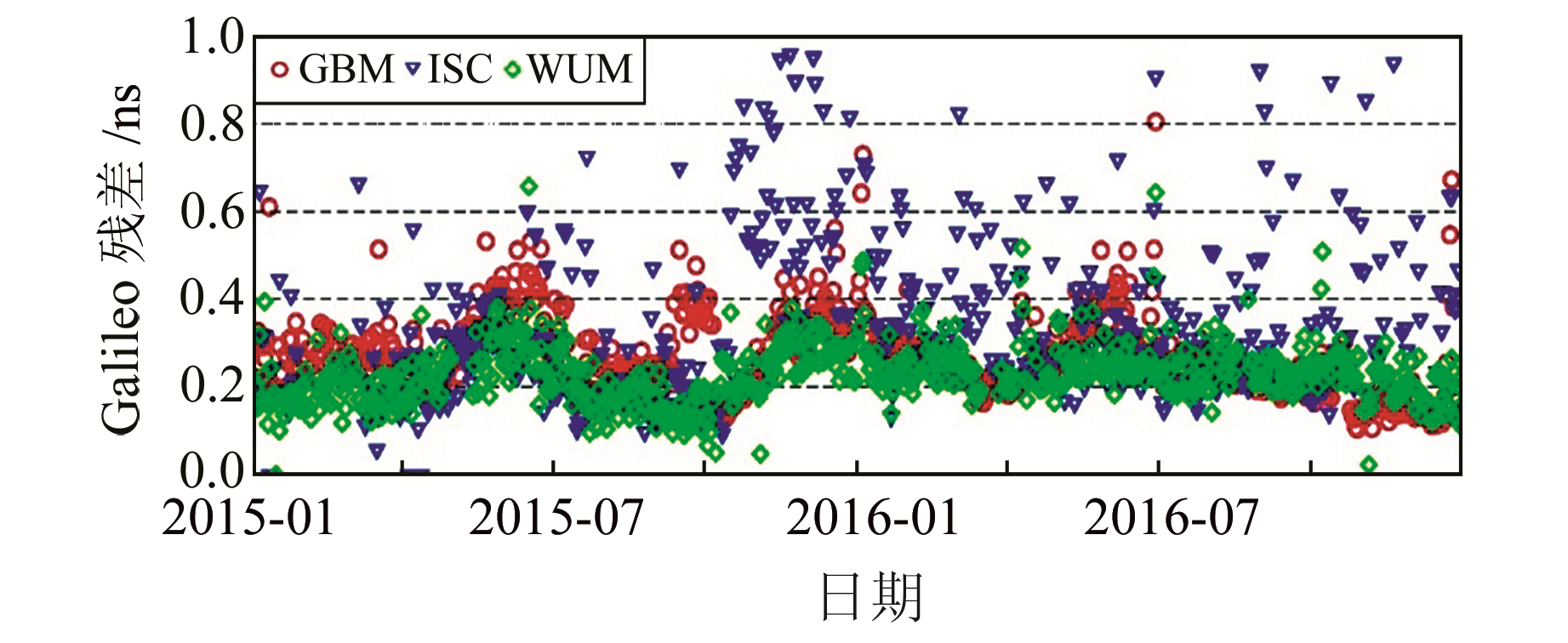
2.4 Galileo/BDS钟差精度分析Galileo系统的卫星钟差评估采用各分析中心互比的方式,结果如表 7(单位ps)所示。以CODE的卫星钟差为基准,图 7给出了各分析中心钟差产品的一致性。从图 7、表 7可以看出,Galileo的卫星钟差产品一致性在0.3 ns左右,其中CODE和WHU的钟差产品比较接近,iGMAS和其他分析中心的一致性较差。
|
|
表 7 不同分析中心Galileo卫星钟差的比较 Tab. 7 RMS of Galileo clock comparisons among different ACs |
|
图 7 Galileo系统的卫星钟差比较(以CODE为基准) Fig. 7 Galileo clocks comparisons (with respect to CODE products) |
Galileo卫星搭载的被动型氢原子钟具有极高的稳定性,本文筛选E11、E12和E19卫星的氢钟时段进行一维钟差拟合,将每天的RMS值绘制于图 8。图 8(a)~(d)分别为CODE、GFZ、iGMAS以及WHU的钟差单天RMS时间序列,图中红色虚线和红色阴影区域表示E19卫星的太阳高度角绝对值和星蚀期,黑色虚线和灰色阴影区域表示E11、E12卫星的太阳高度角绝对值和星蚀期。从图 8可以看出:1)CODE的E11、E12卫星的钟差精度较好,除在星蚀期的拟合精度有所下降外,其余时间段基本在0.2 ns以内;2)由于轨道径向与卫星钟差存在强相关性,轨道中与太阳高度角相关的系统性误差被卫星钟差吸收,所以GFZ和iGMAS的钟差产品中存在明显的周期项,当GFZ附加Cuboid Box-Wing先验模型后,钟差拟合精度基本稳定在0.2 ns左右;3)WHU的钟差拟合精度基本都在0.2 ns以内,未见明显的系统性误差,这与SLR检验结果表现一致。

|
图 8 Galileo星载氢钟的单天拟合残差 Fig. 8 RMS of daily linear fit for Galileo PHM clock-offsets |
BDS系统的卫星钟差按卫星类型进行评估,表 8 (单位ps)统计了各分析中心钟差产品的一致性结果。以WHU的钟差产品为基准,图 9给出了BDS各类型卫星的钟差互比时间序列。从表 8和图 9可知:1)GEO、IGSO和MEO卫星的钟差一致性分别在0.35~0.46 ns、0.25~0.33 ns和0.11~0.21 ns左右,CODE的IGSO和MEO卫星的一致性差距较大;2)CODE在处理北斗姿态转换问题的策略与其他分析中心不同,导致IGSO和MEO的卫星钟差在每年的春分、夏至、秋分以及冬至前后会有较大的跳动。
|
|
表 8 BDS系统的卫星钟差一致性 Tab. 8 RMS of BDS clock comparisons among different ACs |

|
图 9 BDS各类型卫星的钟差钟差互比时间序列(以WHU为基准) Fig. 9 BDS clock comparisons (with respect to WHU products) |
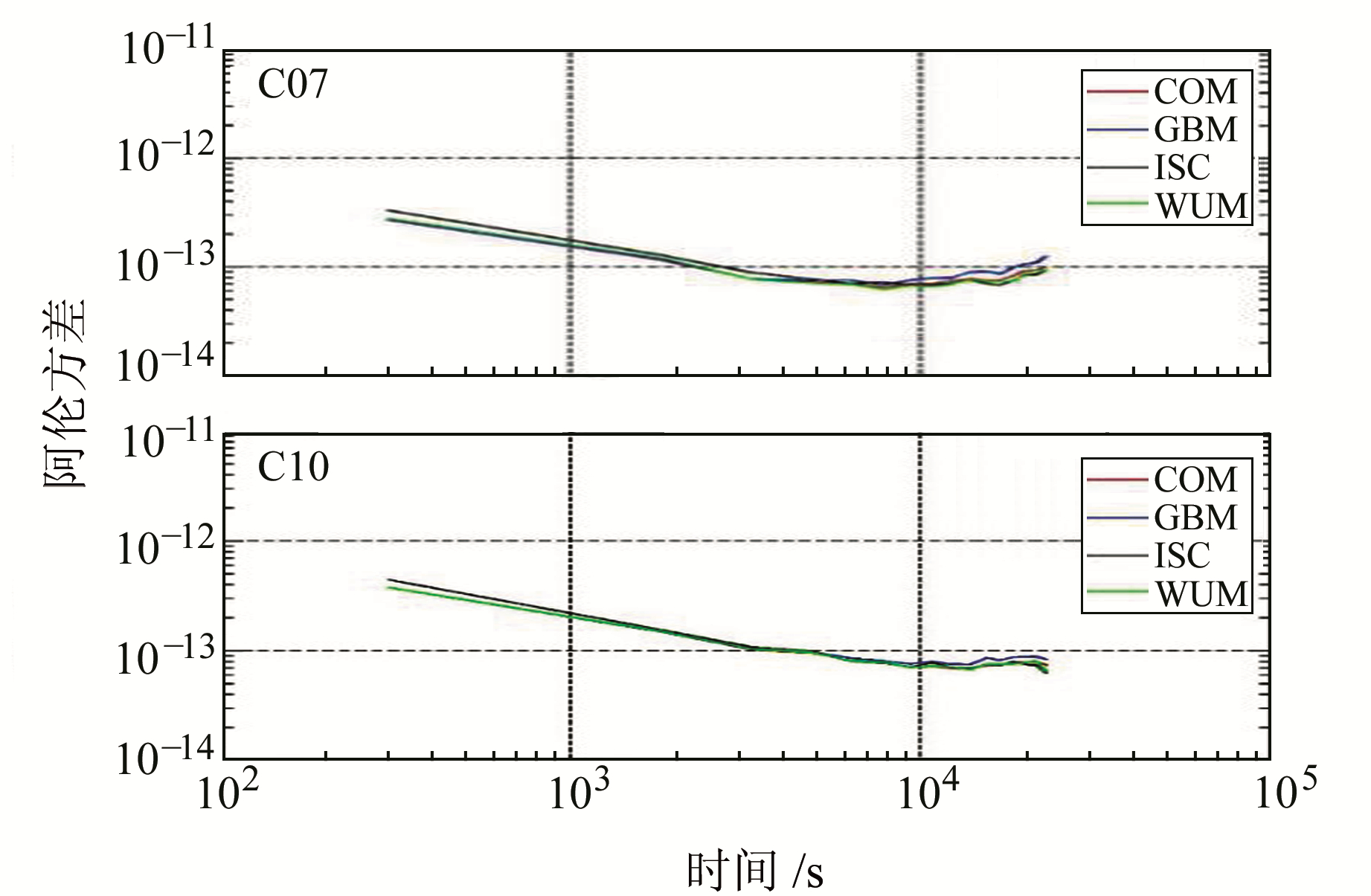
为了进一步分析姿态模式对钟差精度的影响,选取C07和C10卫星分别处于动偏模式和零偏模式下的2段数据计算平均阿伦方差。2016年第150~163天(时段A)卫星处于动偏模式,结果如图 10所示;2016年第192~205天(时段B)卫星处于零偏模式,结果如图 11所示。对比图 10和图 11可知,在动偏阶段,各分析中心的结果基本一致,但是受零偏模式处理策略的影响,CODE在时段B的万秒稳定度明显低于其他3个分析中心的结果。
|
图 10 BDS C07和C10钟差产品的平均阿伦方差对比(时段A) Fig. 10 Median Allan deviations of BDS C07 and C10 clock products from different ACs (period A) |

|
图 11 BDS C07和C10钟差产品的平均阿伦方差对比(时段B) Fig. 11 Median Allan deviations of BDS C07 and C10 clock products from different ACs (period B) |
本文主要采用各分析中心间互比、SLR残差检验、星载氢钟拟合残差及阿伦方差等方法对MGEX和iGMAS提供的GPS/GLONASS/Galileo/BDS系统的精密轨道和钟差产品进行精度分析,得到如下几点结论:
1) MGEX和iGMAS提供的GPS/GLONASS系统的轨道精度分别在1.0~1.3 cm和2.0~3.6 cm,钟差的STD分别在43~77 ps和120~180 ps。iGMAS的轨道产品最优,但是钟差产品在稳定性和可靠性上有待进一步提高。
2) Galileo的轨道相对精度在10~17 cm,采用ECOM2模型或者先验光压模型的轨道精度较高;Galileo的钟差相对精度在0.2~0.4 ns,星载氢钟分析结果与轨道分析结果一致。
3) BDS的IGSO和MEO卫星的轨道相对精度分别在21~40 cm和11~18 cm,轨道径向精度分别优于10 cm和5 cm;但GEO卫星的轨道精度在25 cm左右且伴随约-45 cm的系统性偏差。BDS的GEO、IGSO和MEO卫星的钟差一致性分别在0.35~0.46 ns、0.25~0.33 ns和0.11~0.21 ns。SLR残差检验和阿伦方差分析结果表明,CODE的轨道和钟差产品受卫星偏航姿态模式影响较大。
| [1] |
Montenbruck O, Steigenberger P, Khachikyan R, et al. IGS-MGEX: Preparing the Ground for Multi-Constellation GNSS Science[J]. Inside GNSS, 2014, 9(1): 42-49
(  0) 0) |
| [2] |
Hackel S, Steigenberger P, Hugentobler U, et al. Galileo Orbit Determination Using Combined GNSS and SLR Observations[J]. GPS Solutions, 2015, 19(1): 15-25 DOI:10.1007/s10291-013-0361-5
(  0) 0) |
| [3] |
Steigenberger P, Hugentobler U, Loyer S, et al. Galileo Orbit and Clock Quality of the IGS Multi-GNSS Experiment[J]. Advances in Space Research, 2015, 55(1): 269-281 DOI:10.1016/j.asr.2014.06.030
(  0) 0) |
| [4] |
Prange L, Dach R, Lutz S, et al. The CODE MGEX Orbit and Clock Solution[C]. IAG Scientific Assembly, Berlin, 2015 https://link.springer.com/chapter/10.1007%2F1345_2015_161
(  0) 0) |
| [5] |
Uhlemann M, Gendt G, Ramatschi M, et al. GFZ Global Multi-GNSS Network and Data Processing Results[M]. Berlin Heidelberg: Springer, 2015
(  0) 0) |
| [6] |
Guo J, Xu X L, Zhao Q L, et al. Precise Orbit Determination for Quad-Constellation Satellites at Wuhan University: Strategy, Result Validation, and Comparison[J]. Journal of Geodesy, 2016, 90(2): 1-17
(  0) 0) |
| [7] |
Montenbruck O, Steigenberger P, Hugentobler U. Enhanced Solar Radiation Pressure Modeling for Galileo Satellites[J]. Journal of Geodesy, 2015, 89(3): 283-297 DOI:10.1007/s00190-014-0774-0
(  0) 0) |
| [8] |
Arnold D, Meindl M, Beutler G, et al. CODE's New Solar Radiation Pressure Model for GNSS Orbit Determination[J]. Journal of Geodesy, 2015, 89(8): 775-791 DOI:10.1007/s00190-015-0814-4
(  0) 0) |
| [9] |
Prange L, Orliac E, Dach R, et al. CODE's Five-System Orbit and Clock Solution——The Challenges of Multi-GNSS Data Analysis[J]. Journal of Geodesy, 2016, 91(4): 1-16
(  0) 0) |
| [10] |
耿涛, 徐夏炎. IGS分析中心轨道综合算法实现及精度分析[J]. 大地测量与地球动力学, 2017, 37(4): 369-373 (Geng Tao, Xu Xiayan. Orbit Combination Algorithm and Accuracy Analysis of IGS Analysis Center[J]. Journal Geodesy and Geodynamics, 2017, 37(4): 369-373)
(  0) 0) |
| [11] |
Chen Y C, Yuan Y B, Ding W W, et al. GLONASS Pseudorange Inter-Channel Biases Considerations When Jointly Estimating GPS and GLONASS Clock Offset[J]. GPS Solutions, 2017, 21(4): 1-9
(  0) 0) |
2. State Key Laboratory of Geo-Information Engineering, 1 Mid-Yanta Road, Xi'an 710054, China;
3. Xi'an Research Institute of Surveying and Mapping, 1 Mid-Yanta Road, Xi'an 710054, China
 2019, Vol. 39
2019, Vol. 39


