2. 中国科学院大学,北京市玉泉路19号甲,100049
速度作为运动载体的重要参数之一,在车辆导航定位、无人机自动驾驶、惯性导航系统(inertial navigation system,INS)校准、精细农业播种与施肥、卫星轨道对接以及航空重力测量等领域都有重要应用[1],因此对高精度测速方法的研究尤为重要。
基于卫星导航系统的测速是一种常用的测速手段。载波相位历元差分(time differenced carrier phase,TDCP)测速是一种比较新颖的单点测速方法。其通过对相同卫星的载波相位在历元间进行差分,根据卫星与接收机的几何位置关系精确估计接收机的位移量,进而求解速度[2]。国内外学者已经对GPS的TDCP测速进行了大量研究,Freda[3]提出用连续的广播星历进行TDCP速度估计,实现了静态定位中mm/s级的测速精度;Grass等[4]用低动态飞行数据测试TDCP算法,与Ashtech后处理软件位置差分得到的结果在平面方向符合度为2~4 mm/s,在高程方向符合度为9.7 mm/s;Soon等[5]将TDCP技术与INS进行组合,有效抑制了INS位置误差的发散。
BDS作为中国自主研发的卫星导航系统,已于2012年底开始向亚太地区提供区域导航定位服务,并将在2020年实现全球服务。但针对北斗单点测速分析的文献相对较少。基于此,本文在分析现有TDCP方法的基础上,提出基于历元差分原理的BDS测速模型,并用实测的数据进行测速性能分析。
1 历元差分模型 1.1 TDCP测速算法载波相位的观测方程为:
| $ \begin{array}{*{20}{c}} {\lambda \mathit{\Phi }_{r\left( {ti} \right)}^s = \rho _{r\left( {ti} \right)}^s - {{\left( {\delta {t_r} - \delta {t_s}} \right)}_{\left( {ti} \right)}}c - }\\ {\lambda N_{\left( {ti} \right)}^s - {\delta _{{\rm{ion}}\left( {ti} \right)}} + {\delta _{{\rm{trop}}\left( {ti} \right)}}} \end{array} $ | (1) |
式中,Φ表示载波相位观测值,λ表示波长,ρ表示接收机到卫星的近似几何距离,c表示光速,δtr、δts分别表示接收机钟差和卫星钟差,N表示整周模糊度,δion、δtrop分别表示电离层延迟和对流层延迟,其他误差忽略不计。假设相邻历元没有周跳,将载波相位观测方程在历元间进行差分得到[6]:
| $ \begin{array}{*{20}{c}} {\Delta \lambda \mathit{\Phi }_{r\left( {t1,2} \right)}^s = \Delta \rho _{r\left( {t1,2} \right)}^s - \Delta \delta {t_{r\left( {t1,2} \right)}}c + }\\ {\Delta \delta {t_{s\left( {t1,2} \right)}}c - \Delta {\delta _{{\rm{ion}}\left( {t1,2} \right)}} + {\delta _{{\rm{trop}}\left( {t1,2} \right)}}} \end{array} $ | (2) |
式中,Δ表示历元间单差算子,历元差分后消弱了电离层、对流层误差,在连续无周跳条件下消除了载波相位的整周模糊度。
接收机到卫星近似几何距离ρ的矢量形式为:
| $ \rho _{r\left( {ti} \right)}^s = \left( {\mathit{\boldsymbol{e}}_{\left( {ti} \right)}^{\left( {ti} \right)},{\mathit{\boldsymbol{R}}_{sr\left( {ti} \right)}} - {\mathit{\boldsymbol{r}}_{\left( {ti} \right)}}} \right) $ | (3) |
故Δρr(t1, 2)s可表示为:
| $ \begin{array}{l} \Delta \rho _{r\left( {t1,2} \right)}^s = \left( {\mathit{\boldsymbol{e}}_{t2}^{t2},{\mathit{\boldsymbol{R}}_{sr\left( {t2} \right)}} - {\mathit{\boldsymbol{r}}_{\left( {t2} \right)}}} \right) - \left( {\mathit{\boldsymbol{e}}_{t1}^{t1},{\mathit{\boldsymbol{R}}_{sr\left( {t1} \right)}} - {\mathit{\boldsymbol{r}}_{\left( {t1} \right)}}} \right) = \\ \left( {\mathit{\boldsymbol{e}}_{t2}^{t2},{\mathit{\boldsymbol{R}}_{sr\left( {t2} \right)}}} \right) - \left( {\mathit{\boldsymbol{e}}_{t1}^{t1},{\mathit{\boldsymbol{R}}_{sr\left( {t1} \right)}}} \right) - \left( {\mathit{\boldsymbol{e}}_{t2}^{t2},{\mathit{\boldsymbol{r}}_{\left( {t2} \right)}}} \right) + \left( {\mathit{\boldsymbol{e}}_{t1}^{t1},{\mathit{\boldsymbol{r}}_{\left( {t1} \right)}}} \right) \end{array} $ | (4) |
式中,Rsr(tj)表示tj历元的卫星坐标矢量,r(ti)表示ti历元的接收机坐标矢量,e(ti)(tj)=
| $ \begin{array}{l} \Delta \rho _{r\left( {t1,2} \right)}^s = - \left( {\mathit{\boldsymbol{e}}_{t2}^{t2},\Delta \mathit{\boldsymbol{r}}} \right) + \left( {{\mathit{\boldsymbol{e}}_{\left( {t2} \right)}},{\mathit{\boldsymbol{R}}_{sr\left( {t2} \right)}}} \right) - \\ \left( {\mathit{\boldsymbol{e}}_{t1}^{t1},{\mathit{\boldsymbol{R}}_{sr\left( {t1} \right)}}} \right) - \left( {\mathit{\boldsymbol{e}}_{t2}^{t2},{\mathit{\boldsymbol{r}}_{\left( {t1} \right)}}} \right) + \left( {\mathit{\boldsymbol{e}}_{t1}^{t1},{\mathit{\boldsymbol{r}}_{\left( {t1} \right)}}} \right) = - \left( {\mathit{\boldsymbol{e}}_{t2}^{t2},} \right.\\ \left. {\Delta \mathit{\boldsymbol{r}}} \right) + \left( {\mathit{\boldsymbol{e}}_{t2}^{t2},{\mathit{\boldsymbol{R}}_{sr\left( {t2} \right)}} - {\mathit{\boldsymbol{r}}_{\left( {t1} \right)}}} \right) - \left( {\mathit{\boldsymbol{e}}_{t1}^{t1},{\mathit{\boldsymbol{R}}_{sr\left( {t1} \right)}} - {\mathit{\boldsymbol{r}}_{\left( {t1} \right)}}} \right) \end{array} $ | (5) |
联合式(2)和式(5),即可以实现TDCP测速求解。
1.2 改进的历元差分测速算法基于前文分析可以看出,在TDCP方法中,要解算相邻历元的位移向量需要前后2个历元的接收机坐标和卫星坐标,其中当前历元的接收机坐标需要通过伪距单点定位来提供,增加了解算工作量。本文对TDCP测速算法进行改进,同时增加伪距历元差分观测值,具体实现如下。
设r(ti)=r0(ti)+Δri,其中r0(ti)表示ti历元接收机的近似坐标,Δri表示ti历元接收机近似坐标的误差,则式(4)可以表示为:
| $ \begin{array}{*{20}{c}} {\Delta \rho _{r\left( {t1,2} \right)}^s = - \left( {\mathit{\boldsymbol{e}}_{t2}^{t2},\Delta \mathit{\boldsymbol{r}}} \right) + \left( {\mathit{\boldsymbol{e}}_{t2}^{t2},{\mathit{\boldsymbol{R}}_{sr\left( {t2} \right)}} - {\mathit{\boldsymbol{r}}_{0\left( {t1} \right)}} - \Delta {\mathit{\boldsymbol{r}}_1}} \right) - }\\ {\left( {\mathit{\boldsymbol{e}}_{t1}^{t1},{\mathit{\boldsymbol{R}}_{sr\left( {t1} \right)}} - {\mathit{\boldsymbol{r}}_{0\left( {t1} \right)}} - \Delta {\mathit{\boldsymbol{r}}_1}} \right) = - \left( {\mathit{\boldsymbol{e}}_{t2}^{t2},\Delta \mathit{\boldsymbol{r}}} \right) + }\\ {\left( {\mathit{\boldsymbol{e}}_{t2}^{t2},{\mathit{\boldsymbol{R}}_{sr\left( {t2} \right)}} - {\mathit{\boldsymbol{r}}_{0\left( {t1} \right)}}} \right) - \left( {\mathit{\boldsymbol{e}}_{t1}^{t1},{\mathit{\boldsymbol{R}}_{sr\left( {t1} \right)}} - {\mathit{\boldsymbol{r}}_{0\left( {t1} \right)}}} \right) + }\\ {\left( {\mathit{\boldsymbol{e}}_{t1}^{t1} - \mathit{\boldsymbol{e}}_{t2}^{t2},\Delta {\mathit{\boldsymbol{r}}_1}} \right)} \end{array} $ | (6) |
令r0(t2)=r0(t1),即用上一历元的接收机坐标作为这一历元的接收机坐标近似值[7],则式(6)表示为:
| $ \begin{array}{*{20}{c}} {\Delta \rho _{r\left( {t1,2} \right)}^s = - \left( {\mathit{\boldsymbol{e}}_{t1}^{t2},\Delta \mathit{\boldsymbol{r}}} \right) + \left( {\mathit{\boldsymbol{e}}_{t2}^{t2},{\mathit{\boldsymbol{R}}_{sr\left( {t2} \right)}} - {\mathit{\boldsymbol{r}}_{0\left( {t2} \right)}}} \right) - }\\ {\left( {\mathit{\boldsymbol{e}}_{t1}^{t1},{\mathit{\boldsymbol{R}}_{sr\left( {t1} \right)}} - {\mathit{\boldsymbol{r}}_{0\left( {t1} \right)}}} \right) + \left( {\mathit{\boldsymbol{e}}_{t1}^{t1} - \mathit{\boldsymbol{e}}_{t2}^{t2},\Delta {\mathit{\boldsymbol{r}}_1}} \right)} \end{array} $ | (7) |
式中,接收机的坐标向量误差与接收机和卫星的距离相比可以忽略不计,即(et1t1-et2t2, Δr1)可以忽略,式(7)化简为:
| $ \begin{array}{*{20}{c}} {\Delta \rho _{r\left( {t1,2} \right)}^s = - \left( {\mathit{\boldsymbol{e}}_{t1}^{t2},\Delta \mathit{\boldsymbol{r}}} \right) + \left( {\mathit{\boldsymbol{e}}_{t2}^{t2},{\mathit{\boldsymbol{R}}_{sr\left( {t2} \right)}} - {\mathit{\boldsymbol{r}}_{0\left( {t2} \right)}}} \right) - }\\ {\left( {\mathit{\boldsymbol{e}}_{t1}^{t1},{\mathit{\boldsymbol{R}}_{sr\left( {t1} \right)}} - {\mathit{\boldsymbol{r}}_{0\left( {t1} \right)}}} \right) = - \left( {\mathit{\boldsymbol{e}}_{t1}^{t2},\Delta \mathit{\boldsymbol{r}}} \right) + \rho _{r0\left( {t2} \right)}^s - \rho _{r\left( {t1} \right)}^s} \end{array} $ | (8) |
将式(8)代入式(2)得:
| $ \begin{array}{*{20}{c}} {\Delta \lambda \mathit{\Phi }_{r\left( {t1,2} \right)}^s = - \left( {\mathit{\boldsymbol{e}}_{t1}^{t2},\Delta \mathit{\boldsymbol{r}}} \right) - \Delta \delta {t_{r\left( {t1,2} \right)}}c + \Delta {\delta _{{\rm{trop}}\left( {t1,2} \right)}} + }\\ {\rho _{r\left( {t2} \right)}^s - \rho _{r\left( {t1} \right)}^s + \Delta \delta {t_{s\left( {t1,2} \right)}}c - \Delta {\delta _{{\rm{ion}}\left( {t1,2} \right)}}} \end{array} $ | (9) |
改进后的模型将上一历元的接收机坐标作为当前历元接收机坐标的近似值,不再需要通过伪距单点定位解算,上一历元接收机坐标加上解算得到的精确的位移向量即可得到当前历元的接收机坐标,为下一历元的速度解算提供坐标初值。
当载体处于高动态条件时,载波相位会频繁发生周跳,使可用卫星数减少。为了充分利用观测信息,增加方程个数,使周跳卫星数较多时方程仍能解算,本文增加了伪距历元差分模型。伪距历元差分的观测方程为:
| $ \begin{array}{*{20}{c}} {\Delta R_{r\left( {t1,2} \right)}^s = - \left( {\mathit{\boldsymbol{e}}_{t1}^{t2},\Delta \mathit{\boldsymbol{r}}} \right) - \Delta \delta {t_{r\left( {t1,2} \right)}}c + \Delta {\delta _{{\rm{trop}}\left( {t1,2} \right)}} + }\\ {\rho _{r\left( {t2} \right)}^s - \rho _{r\left( {t1} \right)}^s + \Delta \delta {t_{s\left( {t1,2} \right)}}c - \Delta {\delta _{{\rm{ion}}\left( {t1,2} \right)}}} \end{array} $ | (10) |
式(9)和式(10)构成新的历元差分测速的观测模型。
2 数据处理 2.1 数据预处理数据预处理阶段主要进行数据剔除,剔除如下卫星数据:1)双频伪距和载波观测值不完整的卫星数据;2)高度角不满足要求的卫星数据;3)周跳卫星的载波相位观测值。
若使用精密产品,还需剔除缺少轨道数据及钟差数据的卫星数据。
2.2 误差修正误差修正包括:1)通过双频无电离层组合修正电离层残差[8-9];2)通过UNB3模型修正对流层残差[10];3)将历元间的接收机钟差变化量作为参数进行估计。
2.3 参数估计采用卫星高度角定权,通过最小二乘算法进行参数估计。待估参数为:X=[Δx, Δy, Δz, Δδtr(t1, 2)]T,其中Δx、Δy、Δz为接收机位移向量在3个坐标轴方向的分量,Δδtr(t1, 2)为历元间接收机的钟差变化量,当卫星数大于4颗时进行参数求解。
3 数据测试 3.1 静态数据静态数据采用多模GNSS实验跟踪网(multi-GNSS experiment, MGEX) BRUN站2016-06-14~06-16连续3 d的BDS数据,采样间隔为30 s。测站速度真值视为0, 分别采用广播星历和精密星历对改进的历元差分测速方法进行验证。
3.1.1 精密星历解算图 1为使用精密星历测得测站在站心坐标系下E、N、U 3个方向的速度。可以看出,测站的速度时间序列呈现高斯白噪声分布,平面结果在0~2 mm/s,高程结果在0~5 mm/s,证明算法模型正确。作为对比,本文同时用GPS数据进行历元差分测速,2个系统测速精度的统计结果见表 1(单位mm/s)。

|
图 1 BRUN站精密星历BDS历元差分测速结果 Fig. 1 BDS time-differenced velocity estimation results of BRUN station using precise ephemeris |
|
|
表 1 BRUN站精密星历历元差分测速统计结果 Tab. 1 BDS and GPS time-differenced velocity estimation statistic results of BRUN station using precise ephemeris |
从表 1可以看出,使用静态数据模拟动态解算,BDS历元差分测速精度为mm/s量级,平面方向优于高程方向,测速性能与GPS相当。
3.1.2 广播星历解算图 2为使用广播星历测得测站在站心坐标系下E、N、U 3个方向的速度。可以看出,广播星历历元差分测速结果时间序列呈现高斯白噪声分布,精度达到mm/s, 平面方向优于高程方向,与精密星历测速结果相当。说明在静态条件下,广播星历的轨道误差对历元差分测速的影响很小,可以忽略。

|
图 2 BRUN站广播星历BDS历元差分测速结果 Fig. 2 BDS time-differenced velocity estimation results of BRUN station using broadcast ephemeris |
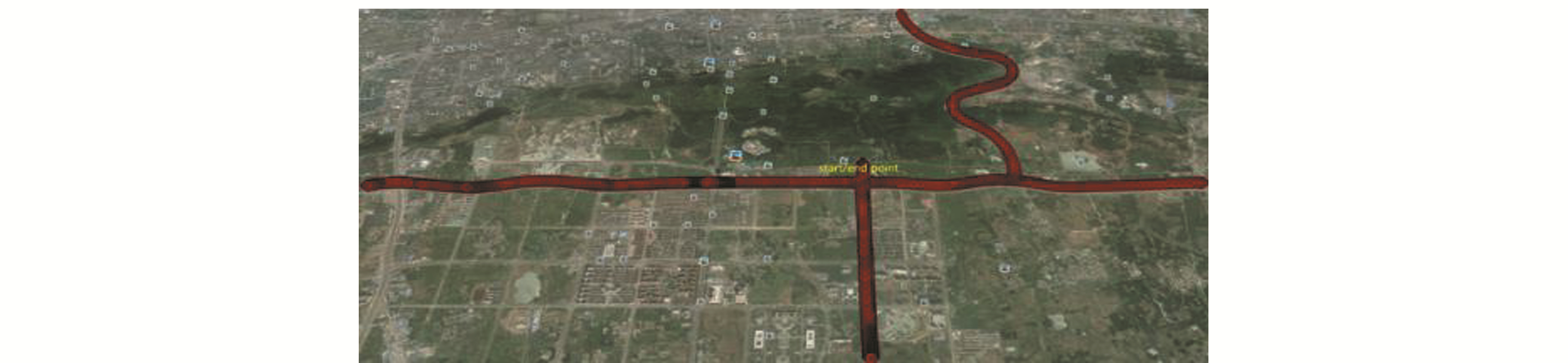
动态数据采用2015-01-18的车载数据,时段为06:54~08:59, 采样间隔为1 s。车上配有中海达接收机(TRM59800.00 NONE),可以接收GPS+BDS+GLONASS数据。路段周围环境遮挡较少,天气状况良好,适于观测。图 3为载体的运动轨迹图。
|
图 3 载体运动轨迹 Fig. 3 Movement track |
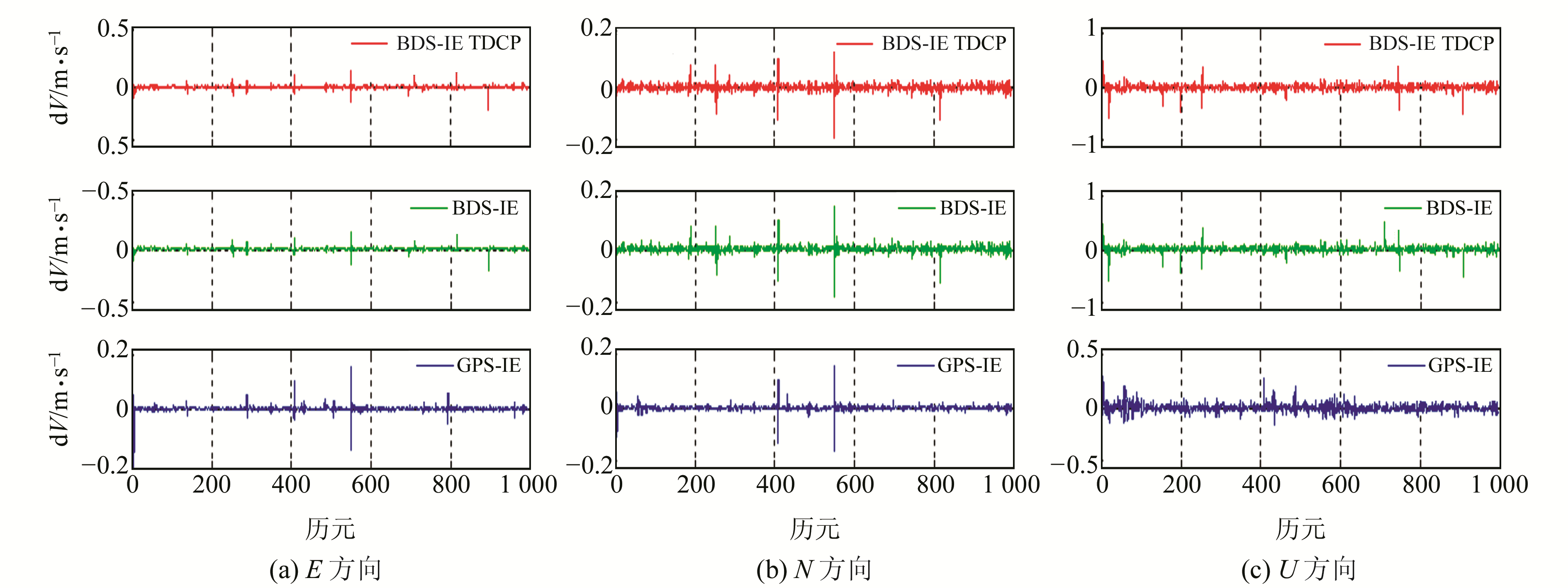
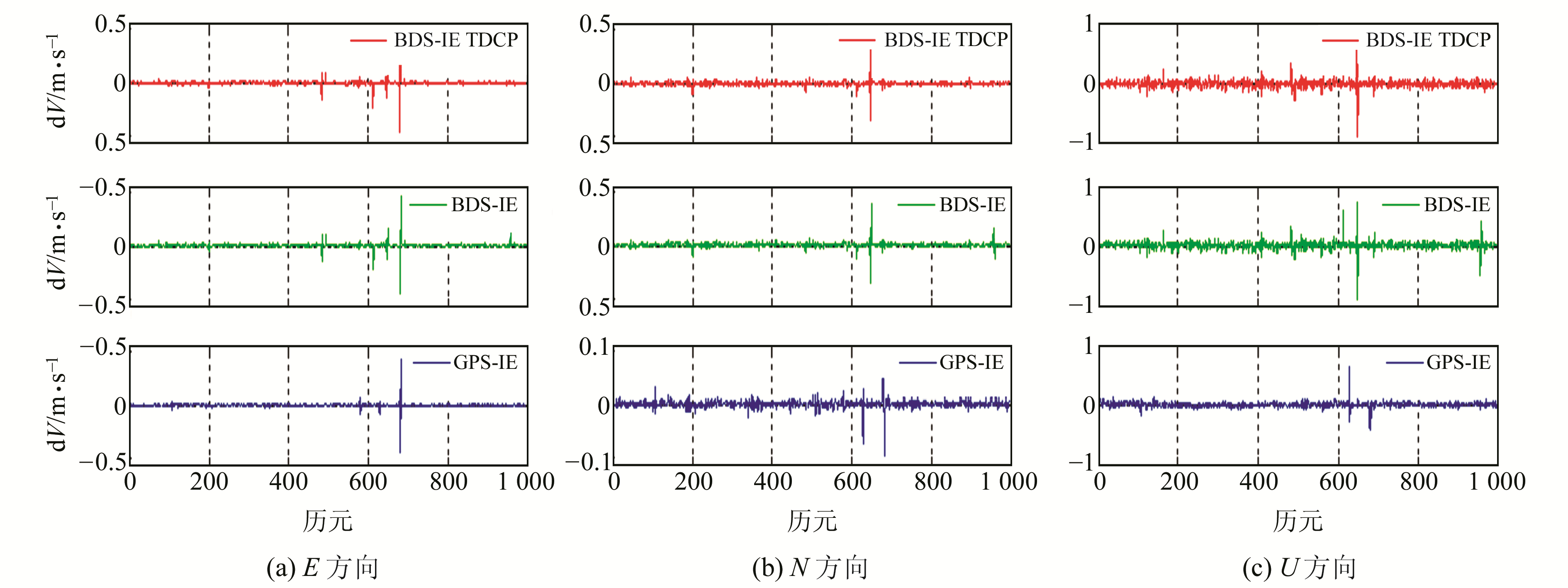
采用BDS历元差分测速算法测得载体在站心坐标系下E、N、U 3个方向的速度(图 4)。可以看出,所用动态数据为部分动态、部分静态。选取其中2个时段进行分析,第1时段选取第2 000~3 000历元,第2时段选取第6 000~7 000历元。图 5和图 6分别给出2个时段BDS TDCP-IE速度差值、BDS-IE速度差值以及GPS -IE速度差值。图 7给出2个时段BDS-IE速度差值与PDOP值和卫星数目的关系。表 2(单位mm/s)为2个时段的测速精度统计结果。

|
图 4 动态数据BDS历元差分测速结果 Fig. 4 BDS time-differenced velocity estimation results of dynamic data |
|
图 5 第1时段BDS TDCP-IE速度差值、BDS-IE速度差值以及GPS-IE速度差值 Fig. 5 BDS-IE TDCP velocity difference and BDS-IE velocity difference and GPS-IE velocity difference of first period |
|
图 6 第2时段BDS TDCP-IE速度差值、BDS-IE速度差值以及GPS-IE速度差值 Fig. 6 BDS-IE TDCP velocity difference and BDS-IE velocity difference and GPS-IE velocity difference of second period |

|
图 7 2个时段BDS-IE速度差值与PDOP值以及卫星数目的关系 Fig. 7 Relation between BDS-IE velocity difference and PDOP values and satellite numbers of two periods |
|
|
表 2 动态测速统计结果 Tab. 2 BDS and GPS time-differenced velocity estimation statistic results of dynamic data |
从图 5和图 6可以看出,BDS-IE速度差值结果的时间序列大致呈现白噪声,但也有一些跳变点。从图 7可以看出,卫星数目越少,PDOP值越大,测速精度越低,即测速结果受到卫星数目和卫星空间几何分布条件的影响。进一步比较发现, BDS-IE速度差值结果与GPS-IE速度差值结果的跳变点位置有多处重合,这是因为历元差分速度与IE位置差分速度均为载体的平均速度,测速精度受载体的动态条件变化影响较大,由于路面情况复杂,当载体处于高动态运动状态时,载体的瞬时速度和平均速度差异较大,历元差分测速精度降低。为提高精度,可进一步将历元差分测速技术与INS技术进行组合。
从表 2可以看出,改进后的BDS历元差分测速精度与BDS TDCP测速精度相当,证明算法模型正确。在平面方向,BDS历元差分速度与IE位置差分速度的外符合精度为1~3 cm/s,GPS历元差分速度与IE位置差分速度的外符合精度为1~2 cm/s,BDS历元差分测速的性能与GPS相当。在高程方向,BDS历元差分测速精度为6~7 cm/s,GPS历元差分测速精度为3~5 cm/s,GPS历元差分测速的性能更好。
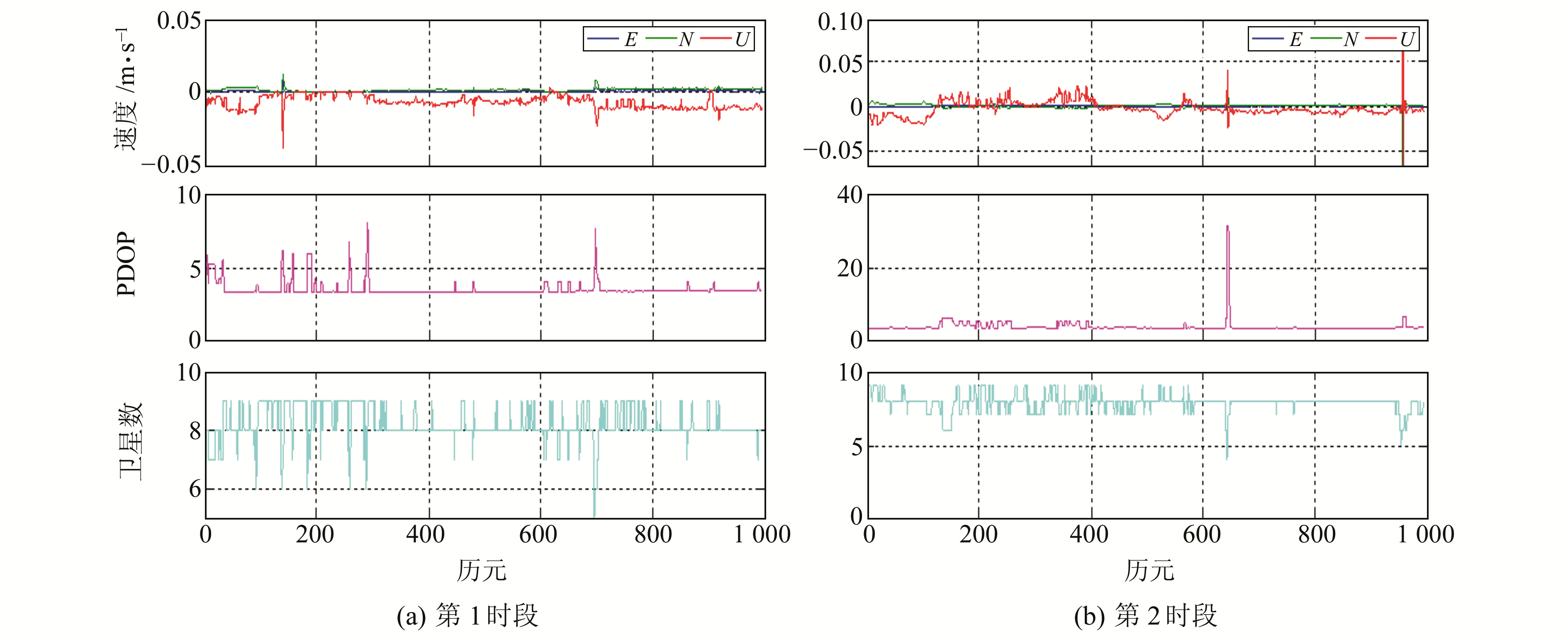
3.2.2 广播星历解算图 8为2个时段BDS广播星历和精密星历历元差分测速差值与PDOP值以及卫星数目的关系,表 3(单位mm/s)为测速差值的统计结果。
|
图 8 2个时段BDS广播星历和精密星历测速差值与PDOP值以及卫星数目的关系 Fig. 8 Relation between BDS broadcast-precise ephemeris velocity difference and PDOP values and satellite numbers of two periods |
|
|
表 3 2个时段BDS广播星历和精密星历测速差值统计结果 Tab. 3 BDS broadcast-precise ephemeris velocity difference estimation statistic results of two periods |
从表 3可以看出,在平面方向,BDS广播星历和精密星历历元差分测速符合度为mm/s,高程方向达到cm/s,平面方向优于高程方向。从图 8可以看出,卫星数目越少,PDOP值越大,广播星历测速精度越低,说明广播星历测速精度除星历本身误差外,还受到卫星数目和卫星空间几何分布条件的影响。
4 结语本文首先分析现有的TDCP测速算法,然后对其进行改进,增加伪距历元差分观测值,建立新的历元差分测速模型,并采用BDS静态数据和动态数据对算法进行验证。结果表明,静态条件下,BDS历元差分测速精度为mm/s级,与GPS测速精度相当;动态条件下,BDS历元差分测速结果与IE位置差分测速结果的外符合精度为cm/s级,平面方向优于高程方向,同时历元差分测速结果受到卫星数目和卫星空间几何分布条件以及载体动态条件变化的影响。
| [1] |
闫勇伟, 叶世榕, 夏敬潮. BDS载波相位历元间差分测速方法研究[J]. 测绘科学, 2016, 41(7): 193-196 (Yan Yongwei, Ye Shirong, Xia Jingchao. Research of BDS Velocity Estimation with Time Differenced Carrier Phase Method[J]. Science of Surveying and Mapping, 2016, 41(7): 193-196)
(  0) 0) |
| [2] |
刘洋.基于载波相位时间差分测速的GPS/INS组合导航研究[D].北京: 中国矿业大学, 2016 (Liu Yang. Research on GPS/INS Integrated Navigation Based on the Time Differenced Carrier Phase Velocity Estimation Approach[D]. Beijing: China University of Mining and Technology, 2016)
(  0) 0) |
| [3] |
Freda P, Angrisano A, Gaglione S, et al. Time-Differenced Carrier Phases Technique for Precise GNSS Velocity Estimation[J]. GPS Solutions, 2015, 19(2): 335-341 DOI:10.1007/s10291-014-0425-1
(  0) 0) |
| [4] |
Graas F V, Soloviev A. Precise Velocity Estimation Using a Stand-alone GPS Receiver[J]. Navigation, 2004, 51(4): 283-292 DOI:10.1002/navi.2004.51.issue-4
(  0) 0) |
| [5] |
Soon B K H, Scheding S, Lee H K, et al. An Approach to Aid INS Using Time-Differenced GPS Carrier Phase (TDCP) Measurements[J]. GPS Solutions, 2008, 12(4): 261-271 DOI:10.1007/s10291-007-0083-7
(  0) 0) |
| [6] |
刘志强, 王解先, 王虎. 基于相位单差精密测速的动态精密单点定位算法[J]. 宇航学报, 2012, 33(3): 405-410 (Liu Zhiqiang, Wang Jiexian, Wang Hu. An Approach for Kinematic Precise Point Positioning Based on Precise Velocity Estimation[J]. Journal of Astronautics, 2012, 33(3): 405-410 DOI:10.3873/j.issn.1000-1328.2012.03.019)
(  0) 0) |
| [7] |
Ding W D, Wang J L. Precise Velocity Estimation with a Stand-Alone GPS Receiver[J]. Journal of Navigation, 2011, 64(2): 311-325 DOI:10.1017/S0373463310000482
(  0) 0) |
| [8] |
范士杰, 牟春霖, 刘焱雄, 等. 历元间差分精密单点定位的精度分析[J]. 测绘科学, 2016, 41(1): 122-126 (Fan Shijie, Mu Chunlin, Liu Yanxiong, et al. Precision Analysis of Precise Point Positioning Based on the Epoch-Difference Model[J]. Science of Surveying and Mapping, 2016, 41(1): 122-126)
(  0) 0) |
| [9] |
李浩军, 王解先, 胡丛玮, 等. 基于历元间差分技术的精密单点定位研究[J]. 宇航学报, 2010, 31(3): 748-752 (Li Haojun, Wang Jiexian, Hu Congwei, et al. The Research on Precise Point Positioning Based on the Epoch-Difference[J]. Journal of Astronautics, 2010, 31(3): 748-752 DOI:10.3873/j.issn.1000-1328.2010.03.020)
(  0) 0) |
| [10] |
周命端, 郭际明, 孟祥广. GPS对流层延迟改正UNB3模型及其精度分析[J]. 测绘信息与工程, 2008, 33(4): 3-5 (Zhou Mingduan, Guo Jiming, Meng Xiangguang. GPS Tropspheric Delay Model UNB3 and Its Accuracy Analysis[J]. Journal of Geomatics, 2008, 33(4): 3-5 DOI:10.3969/j.issn.1007-3817.2008.04.002)
(  0) 0) |
2. University of Chinese Academy of Sciences, A19 Yuquan Road, Beijing 100049, China
 2019, Vol. 39
2019, Vol. 39

