2. 武汉大学地球空间信息技术协同创新中心,武汉市珞喻路129号,430079
BDS/GPS紧组合相比松组合能够提高导航定位的可用性、可靠性和精度,但在使用紧组合模型时必须考虑接收机端差分系统间偏差(DISB)的影响[1]。Paziewski等[2]、Odijk等[3-4]研究了GPS L1/Galileo E1紧组合模型;张小红等[1]、Wu等[5]、周英东等[6]研究了BDS B2/Galileo E5b紧组合模型,利用最小二乘估计紧组合中的DISB参数,并分析DISB的特性。此外,Odolinski等[7]研究了BDS、Galileo、QZSS和GPS 4系统紧组合单频RTK,但由于BDS B1与其他系统的频率不一致,文中并未详细给出BDS与其他系统的紧组合算法以及DISB的估计结果。
相比GPS L1/Galileo E1和BDS B2/Galileo E5b的紧组合来说,BDS B1/GPS L1紧组合由于存在频率不一致问题,估计的载波DISB小数部分易受到参考卫星站间单差模糊度的影响。楼益栋等[8]在研究BDS B1/GPS L1紧组合时,利用伪距计算的站间单差模糊度经多历元平滑后,改正由频率不一致引入的参考卫星站间单差模糊度,然后再由最小二乘估计DISB参数;隋心等[9]提出利用卡尔曼滤波算法,同时估计站间单差模糊度和DISB参数。但这2种算法都只估计了载波DISB小数部分,没有考虑载波DISB整数部分。然而由于BDS和GPS的信号频率不一致,在估计载波DISB小数部分时,其整数部分会影响参考卫星站间单差模糊度的精度。另外,Tian等[10]针对GPS L1/Galileo E1紧组合中载波DISB的估计问题,提出一种粒子滤波估计算法。本文针对BDS B1/GPS L1紧组合推导了其相对定位模型,考虑到BDS B1/GPS L1紧组合中频率不一致的问题,提出联合卡尔曼滤波与粒子滤波算法估计BDS B1/GPS L1紧组合中的DISB,并通过实验对比分析卡尔曼滤波算法和本文算法的效果。
1 BDS/GPS紧组合相对定位模型在相对定位时,假设接收机r(=1, 2)能同时接收到BDS和GPS卫星的伪距和载波,则对于任意卫星p和接收机r,可得非差观测方程:
| $ \begin{array}{*{20}{c}} {P_r^p = \rho _r^p + c\left( {{\rm{d}}{T_r} - {\rm{d}}{t^p}} \right) + }\\ {{\rm{d}}{r_r} - {\rm{d}}{s^p} + I_r^p + T_r^p + {\varepsilon _p}} \end{array} $ | (1) |
| $ \begin{array}{*{20}{c}} {{\lambda ^p}\varphi _r^p = \rho _r^p + c\left( {{\rm{d}}{T_r} - {\rm{d}}{t^p}} \right) + }\\ {{\rm{b}}{{\rm{r}}_r} - {\rm{b}}{{\rm{s}}^p} + {\lambda ^p}N_r^p - I_r^p + T_r^p + {\varepsilon _\varphi }} \end{array} $ | (2) |
式中,P为伪距观测值,ρ为卫星到接收机的几何距离,c为光在真空中的传播速度,dT为接收机钟差,dt为卫星钟差,dr为接收机对伪距的硬件延迟,ds为卫星对伪距的硬件延迟,I为电离层延迟,T为对流层延迟,εp为伪距测量噪声,λ为载波波长,φ为载波观测值,br为接收机对载波的硬件延迟,bs为卫星对载波的硬件延迟,N为整周模糊度,εφ为载波观测噪声。
在接收机间求差可得站间单差观测方程:
| $ \Delta P_{12}^p = \Delta \rho _{12}^p + c\Delta {\rm{d}}{T_{12}} + \Delta {\rm{d}}r_{12}^p + \Delta \varepsilon _p^p $ | (3) |
| $ \begin{array}{*{20}{c}} {{\lambda ^p}\Delta \varphi _{12}^p = \Delta \rho _{12}^p + c\Delta {\rm{d}}{T_{12}} + }\\ {\Delta {\rm{br}}_{12}^p + {\lambda ^p}\Delta N_{12}^p + \Delta \varepsilon _\varphi ^p} \end{array} $ | (4) |
式中,Δ(·)12p为站间单差运算符号,上标p=G、B分别为GPS和BDS卫星。站间单差可以消除与卫星相关的卫星钟差和卫星端硬件延迟等,削弱电离层延迟和对流层延迟误差等大气延迟;对于短基线,残留的大气延迟可以忽略不计。另外还需指出,当基线两端接收机类型不同时,BDS的GEO卫星与IGSO/MEO卫星之间还可能存在ISTB(inter-satellite type bias)的影响,在数据处理时需提前改正[11-12]。
与常规的BDS/GPS松组合相对定位模型不同,紧组合模型在2个系统中只选取了1颗参考卫星。假设选取GPS中的G1卫星作为参考卫星,则可组成站星双差观测方程:
| $ \Delta \nabla P_{12}^{{G_1}{G_i}} = \Delta \nabla \rho _{12}^{{G_1}{G_i}} + \Delta \nabla \varepsilon _p^{GG} $ | (5) |
| $ \begin{array}{*{20}{c}} {{\lambda ^G}\Delta \nabla \varphi _{12}^{{G_1}{G_i}} = }\\ {\Delta \nabla \rho _{12}^{{G_1}{G_i}} + {\lambda ^G}\Delta \nabla N_{12}^{{G_1}{G_i}} + \Delta \nabla \varepsilon _p^{GG}} \end{array} $ | (6) |
| $ \Delta \nabla P_{12}^{{G_1}{B_j}} = \Delta \nabla \rho _{12}^{{G_1}{B_j}} + \Delta {\rm{d}}r_{12}^{GB} + \Delta \nabla \varepsilon _p^{GB} $ | (7) |
| $ \begin{array}{*{20}{c}} {{\lambda ^B}\Delta \varphi _{12}^{{B_j}} - {\lambda ^G}\Delta \varphi _{12}^{{G_1}} = \Delta \nabla \rho _{12}^{{G_1}{B_j}} + }\\ {\Delta \nabla {\rm{br}}_{12}^{GB} + \left( {{\lambda ^B}\Delta N_{12}^{{B_j}} - {\lambda ^G}\Delta N_{12}^{{G_1}}} \right) + \Delta \nabla \varepsilon _\varphi ^{GB}} \end{array} $ | (8) |
式中,Δ∇(·)12pq为卫星p、q和接收机1、2间的双差运算符号,Gi=G1, G2…Gn为GPS观测卫星,Bj=B1, B2…Bm为BDS观测卫星,Δdr12GB为伪距DISB,Δ∇br12GB为载波DISB。DISB是在系统间双差观测方程中,由于2颗卫星所属的系统不同而在接收机端引起的系统间偏差。
在估计出DISB小数部分后,可用估计的DISB改正紧组合,当采用卡尔曼滤波估计站间单差模糊度的方式处理改正DISB后的紧组合相对定位模型时,方程可表示为:
| $ \begin{array}{*{20}{c}} {{\lambda ^B}\Delta \varphi _{12}^{{B_j}} - {\lambda ^G}\Delta \varphi _{12}^{{G_1}} - {\lambda ^B}{F_{{\rm{br}}}} = }\\ {\Delta \nabla \rho _{12}^{{G_1}{B_j}} + {\lambda ^B}{N_{{\rm{br}}}} + {\lambda ^B}\nabla N_{12}^{{B_j}} - {\lambda ^G}\Delta N_{12}^{{G_1}} + }\\ {\Delta \nabla \varepsilon _p^{GB} = \Delta \nabla \rho _{12}^{{G_1}{B_j}} + {\lambda ^B}\left( {\nabla N_{12}^{{B_j}} + N_{{\rm{br}}}^B} \right) - }\\ {{\lambda ^G}\left( {\nabla N_{12}^{{G_1}} - N_{{\rm{br}}}^G} \right) + \Delta \nabla \varepsilon _p^{GB} = \Delta \nabla \rho _{12}^{{G_1}{B_j}} + {\lambda ^B} \cdot }\\ {\left( {\Delta \nabla N_{12}^{{G_1}{B_j}} + {N_{{\rm{br}}}}} \right) + \left( {{\lambda ^B} - {\lambda ^G}} \right) \cdot }\\ {\left( {\nabla N_{12}^{{G_1}} - N_{{\rm{br}}}^G} \right) + \Delta \nabla \varepsilon _p^{GB}} \end{array} $ | (9) |
式中,Fbr为已知的载波DISB小数部分,Nbr为载波DISB整数部分,NbrB和NbrG为载波DISB整数部分对站间单差模糊度的影响,且λBNbr=λBNbrB+λGNbrG。式(9)中,最后一个等号表示由模糊度浮点解到固定双差模糊度,由于双差模糊度被固定为整数,则等号右边会多出载波DISB整数部分对参考卫星站间单差模糊度的影响,故方程中还会残留其整数部分与频率不一致引起的小数偏差,因此在估计载波DISB小数部分时还需提前考虑该偏差。
2 DISB估计算法 2.1 卡尔曼滤波估计算法载波DISB和频率不一致参数的存在,导致方程秩亏,并且载波DISB与模糊度参数紧密联系在一起,很难分离。因此,利用卡尔曼滤波算法估计DISB参数时,首先要对方程进行参数重整:
| $ \begin{array}{*{20}{c}} {{\lambda ^B}\Delta \varphi _{12}^{{B_j}} - {\lambda ^G}\Delta \varphi _{12}^{{G_1}} = \Delta \nabla \rho _{12}^{{G_1}{B_j}} + }\\ {\left( {\Delta \nabla {\rm{br}}_{12}^{GB} + {\lambda ^B}\Delta \nabla N_{12}^{{G_1}{B_1}}} \right) + {\lambda ^B} \cdot }\\ {\Delta \nabla N_{12}^{{B_1}{B_j}} + \left( {{\lambda ^B} - {\lambda ^G}} \right)\Delta N_{12}^{{G_1}} + \Delta \nabla \varepsilon _p^{GB}} \end{array} $ | (10) |
考虑到存在频率不一致引起的ΔN12G1参数,故将Δ∇N12G1Gi和Δ∇N12B1Bj均以站间单差模糊度的方式进行估计,且在方程中将Δ∇br12GB+λB·Δ∇N12G1B1当作一个λBΔ∇
本文联合算法的基本思想是:首先基于卡尔曼滤波和粒子滤波算法估计出载波DISB的小数部分,然后再采用卡尔曼滤波算法一同估计坐标参数、伪距DISB参数以及模糊度参数。由于粒子滤波只需估计载波DISB不足1周的部分,故载波DISB的取值范围可假设为[-0.5, 0.5]周,约为[-0.1, 0.1] m。给定采样间隔为1 mm,可以得到N=200个粒子x0i,给定每个粒子的初始权重为w0i=1/N,其中i=1, 2, …, N。
当载波DISB小数部分已知时,粒子滤波的观测方程为:
| $ \mathit{\boldsymbol{Z}} = \mathit{\boldsymbol{HX}} + \mathit{\boldsymbol{v}} $ | (11) |
式中,Z为观测值减去计算值残差,H为设计矩阵,X为状态向量,v为测量噪声,且有X=[x y z Δ∇dr ΔN12G1 … ΔN12Gn ΔN12B1 … ΔN12Bm]T。
参考文献[10, 15]中的粒子滤波算法,先根据概率函数更新每个粒子的权重。对于概率函数的选取,文献[10, 15]通过实验证明,当一个越接近正确值的DISB值代入紧组合模型中时,通过LAMBDA算法固定双差模糊度时的Ratio值越大,因此可根据Ratio值的大小来判断DISB的正确性,故本文采用双差模糊度固定时的Ratio值来构造观测值的概率函数。将每个粒子代入方程中,由卡尔曼滤波计算出站间单差模糊度浮点解,并将站间单差模糊度投影变换为双差模糊度,再用LAMBDA算法固定双差模糊度,计算出对应的Ratio值。于是可得每个粒子的概率函数:
| $ p\left( {{b_k}\left| {\mathit{\boldsymbol{x}}_k^i} \right.} \right) = \frac{{{\rm{Rati}}{{\rm{o}}^i}}}{{\sum\limits_{j = 1}^N {{\rm{Rati}}{{\rm{o}}^j}} }} $ | (12) |
需要注意的是,每个粒子代入卡尔曼滤波计算出对应的Ratio值即可,此时状态参数不需要更新。根据概率函数更新每个粒子的权重并归一化:
| $ \hat w_k^i = \frac{{w_{k - 1}^ip\left( {{b_k}\left| {\mathit{\boldsymbol{x}}_k^i} \right.} \right)}}{{\sum\limits_{j = 1}^N {w_{k - 1}^jp\left( {{b_k}\left| {\mathit{\boldsymbol{x}}_k^j} \right.} \right)} }} $ | (13) |
更新状态参数及其方差:
| $ {{\mathit{\boldsymbol{\hat x}}}_k} \approx \sum\limits_{i = 1}^N {\hat w_k^i\mathit{\boldsymbol{x}}_k^i} $ | (14) |
| $ {{\hat p}_k} \approx \sum\limits_{i = 1}^N {\left( {\mathit{\boldsymbol{x}}_k^i - {{\mathit{\boldsymbol{\hat x}}}_k}} \right){{\left( {\mathit{\boldsymbol{x}}_k^i - {{\mathit{\boldsymbol{\hat x}}}_k}} \right)}^{\rm{T}}}\hat w_k^i} $ | (15) |
每个历元计算出载波DISB后,将载波DISB估值
| $ {\mathit{\boldsymbol{X}}_k} = {\mathit{\boldsymbol{F}}_{k\left| {k - 1} \right.}}{\mathit{\boldsymbol{X}}_{k - 1}} + \mathit{\boldsymbol{w}} $ | (16) |
式中,Xk和Xk-1为k和k-1时刻的状态向量,Fk|k-1为状态转移矩阵,w为预测噪声。
一次粒子滤波计算完成后,每个粒子的验后权不再是相等的,靠近正确值附近的粒子权重较大,远离正确值的粒子权重较小。经多次计算后,权重较大的有效粒子数越来越少,因此,需要对粒子进行重采样[10, 15]。计算过程如下:
构造一个随机序列:
| $ \left\{ {{u_i} = \frac{{\left( {i - 1} \right) + {{\tilde u}_i}}}{N}} \right\}_{i = 1}^N $ | (17) |
式中,
计算累积权序列:
| $ \left\{ {\tilde w_k^j = \sum\limits_{h = 1}^j {\hat w_k^h} } \right\}_{j = 1}^N $ | (18) |
比较
需要说明的是,文献[10, 15]提出的重采样步骤计算量较大,当所有粒子的权重满足
由于紧组合中的DISB参数在短期内是稳定不变的,因此粒子滤波的预测方程可表示为:
| $ {\mathit{\boldsymbol{x}}_k} = {\mathit{\boldsymbol{x}}_{k - 1}} + \mathit{\boldsymbol{w}} $ | (19) |
式中,x为载波DISB粒子,w为预测噪声。下一个历元的粒子即可通过方程进行预测。
3 实验分析选取2016年年积日001天澳大利亚科廷大学的4条短基线数据进行实验,观测时长为24 h,采样间隔为30 s,详细信息见表 1。
|
|
表 1 基线信息 Tab. 1 Baseline information |
实验中选取高度角最高的GPS卫星作为参考卫星,并设置卫星截止高度角为10°,然后利用2种算法估计BDS/GPS紧组合中的DISB。图 1给出了基线两端接收机类型和固件版本都相同的基线1和2由2种算法估计的DISB结果;图 2给出了基线两端接收机类型不同的基线3和4的DISB结果。由上节的估计算法可知,2种算法估计伪距DISB都是采用卡尔曼滤波,故其估计的伪距DISB基本一致,因此图 1和图 2中仅给出了卡尔曼滤波算法估计的伪距DISB结果。

|
图 1 基线1和基线2的DISB估计结果 Fig. 1 The estimated DISB results of baseline 1 and 2 |

|
图 2 基线3和4的DISB估计结果 Fig. 2 The estimated DISB results of baseline 3 and 4 |
2种算法的估计结果表明,BDS和GPS之间的DISB是稳定的,因此在BDS/GPS紧组合时可以提前校正DISB参数。此外,在卡尔曼滤波估计算法中,载波DISB是由估计的Δ∇
另一方面,比较图 1和图 2中2种算法的DISB可以发现,无论基线两端接收机类型是否相同,2种算法估计的载波DISB小数部分都可能会存在一定偏差。从上节的理论分析可以看到,这一偏差主要是由载波DISB整数部分与频率差异引起的小数偏差。在卡尔曼滤波估计载波DISB小数部分时,其整数部分可被Δ∇N12G1Bj直接吸收,此时,
| $ \begin{array}{*{20}{c}} {{\lambda ^B}\Delta \varphi _{12}^{{B_j}} - {\lambda ^G}\Delta \varphi _{12}^{{G_1}} = \Delta \nabla \rho _{12}^{{G_1}{B_j}} + {\lambda ^B} \cdot }\\ {{{\tilde F}_{{\rm{br}}}} + {\lambda ^B}\left( {\Delta \nabla N_{12}^{{G_1}{B_1}} + {N_{{\rm{br}}}}} \right) + {\lambda ^B} \cdot }\\ {\Delta \nabla N_{12}^{{B_1}{B_j}} + \left( {{\lambda ^B} - {\lambda ^G}} \right)\Delta N_{12}^{{G_1}} + \Delta \nabla \varepsilon _\varphi ^{GB}} \end{array} $ | (20) |
而联合算法在估计DISB小数部分时,其整数部分最后虽然可被Δ∇N12G1Bj吸收,但是在估计过程中,其整数部分会影响到参考卫星站间单差模糊度。比较式(20)和式(9)可得:
| $ {{\tilde F}_{{\rm{br}}}} = {F_{{\rm{br}}}} - \left( {{\lambda ^B} - {\lambda ^G}} \right)N_{{\rm{br}}}^G $ | (21) |
式中,
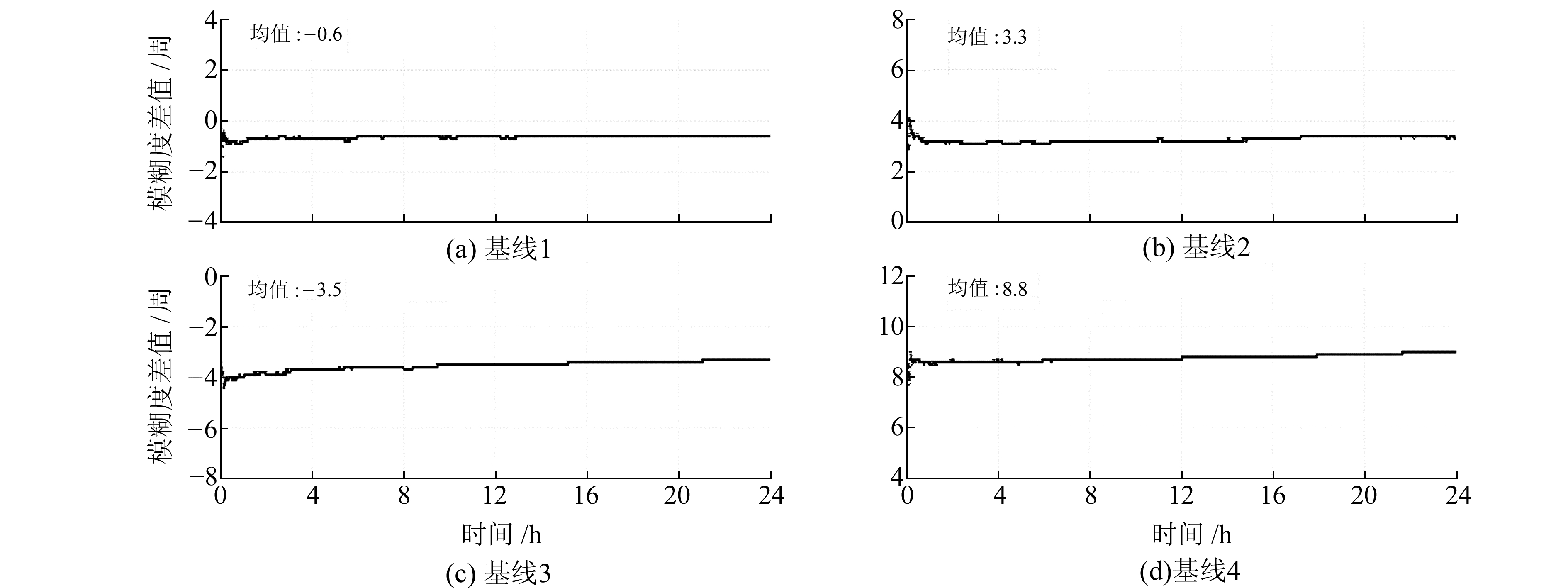
|
图 3 2种算法估计的参考卫星站间单差模糊度之差 Fig. 3 The difference series of reference satellite single-differenced ambiguity between stations estimated by two algorithms |
为进一步验证2种算法估计结果的准确性和可靠性,将2种算法估计的DISB均值代入BDS/GPS紧组合相对定位模型中,分别设置卫星截止高度角为10°和30°,然后采用动态单历元模式解算这4条基线数据,并设定Ratio值阈值为3,统计固定解的RMS、平均Ratio值以及模糊度固定率,详细情况如表 2和表 3所示。
|
|
表 2 截止高度角10°时用卡尔曼滤波/本文算法估计结果改正DISB后紧组合的定位结果统计 Tab. 2 Positioning results of tight combination using Kalman filter/proposed algorithm estimations to correct DISB with 10° cut-off elevation angle |
|
|
表 3 截止高度角30°时用卡尔曼滤波/本文算法估计结果改正DISB后紧组合的定位结果统计 Tab. 3 Positioning results of tight combination using Kalman filter/proposed algorithm estimations to correct DISB with 30° cut-off elevation angle |
由表 2可知,在卫星截止高度角为10°时,由于观测卫星数较多,2种算法估计的DISB差异对紧组合定位结果影响不明显。由表 3可知,在卫星截止高度角为30°时,2种算法估计的载波DISB小数部分的差异对定位结果有比较明显的影响,且用本文算法估计的载波DISB小数部分改正紧组合后的定位精度,其模糊度固定率和可靠性均优于卡尔曼滤波。其中,对于差异最大的基线4来说,用本文算法估计的结果改正紧组合后的固定解RMS提高了10%~20%。
4 结语本文推导了BDS B1/GPS L1紧组合相对定位模型,详细研究了BDS B1/GPS L1紧组合中DISB参数估计问题。考虑到BDS B1/GPS L1紧组合中存在频率不一致的问题,在估计载波DISB小数部分时还需考虑其整数部分与频率差异产生的小数偏差,本文提出联合卡尔曼滤波与粒子滤波算法估计BDS B1/GPS L1紧组合中的DISB,并利用4条实测短基线数据对比分析本文算法和卡尔曼滤波算法估计DISB的性能。结果表明,载波DISB的整数部分会影响参考卫星站间单差模糊度的估计,从而影响DISB小数部分的估计结果。将2种算法估计的DISB代入紧组合模型中进行单历元相对定位表明,相比用卡尔曼滤波估计结果改正DISB,用本文算法估计结果改正DISB后的紧组合在模糊度固定率、模糊度固定可靠性以及固定解RMS方面均有一定提高,尤其是当载波DISB整数部分较大时,固定解精度可提高10%~20%。
致谢: 感谢科廷大学GNSS中心(Curtin GNSS Research Centre)提供的短基线数据。
| [1] |
张小红, 吴明魁, 刘万科. Beidou B2/Galileo E5b短基线紧组合相对定位模型及性能评估[J]. 测绘学报, 2016, 45(增2): 1-11 (Zhang Xiaohong, Wu Mingkui, Liu Wanke. Model and Performance Analysis of Tight Combined Beidou B2 and Galileo E5b Relative Positioning for Short Baseline[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S2): 1-11)
(  0) 0) |
| [2] |
Paziewski J, Wielgosz P. Accounting for Galileo-GPS Inter-System Biases in Precise Satellite Positioning[J]. Journal of Geodesy, 2015, 89(1): 81-93 DOI:10.1007/s00190-014-0763-3
(  0) 0) |
| [3] |
Odijk D, Teunissen P J G, Huisman L. First Results of Mixed GPS+GIOVE Single-Frequency RTK in Australia[J]. Journal of Spatial Science, 2012, 57(1): 3-18
(  0) 0) |
| [4] |
Odijk D, Teunissen P J G. Characterization of between-Receiver GPS-Galileo Inter-System Biases and Their Effect on Mixed Ambiguity Resolution[J]. GPS Solutions, 2013, 17(4): 521-533 DOI:10.1007/s10291-012-0298-0
(  0) 0) |
| [5] |
Wu M K, Zhang X H, Liu W K, et al. Tightly Combined Beidou B2 and Galileo E5b Signals for Precise Relative Positioning[J]. Journal of Navigation, 2017, 70(6): 1-14
(  0) 0) |
| [6] |
周英东, 柴洪洲, 王敏, 等. BDS/Galileo紧组合系统间偏差估计与模糊度固定效果分析[J]. 测绘科学技术学报, 2017, 34(2): 141-146 (Zhou Yingdong, Chai Hongzhou, Wang Min, et al. Assessment of BDS/Galileo Inter-System Biases and Their Effect on Ambiguity Resolution[J]. Journal of Geomatics Science and Technology, 2017, 34(2): 141-146)
(  0) 0) |
| [7] |
Odolinski R, Teunissen P J G, Odijk D. Combined BDS, Galileo, QZSS and GPS Single-Frequency RTK[J]. GPS Solutions, 2014, 19(1): 151-163
(  0) 0) |
| [8] |
楼益栋, 龚晓鹏, 辜声峰, 等. BDS/GPS混合双差分RTK定位方法及结果分析[J]. 大地测量与地球动力学, 2016, 36(1): 1-5 (Lou Yidong, Gong Xiaopeng, Gu Shengfeng, et al. An Algorithm and Results Analysis for GPS+BDS Inter-System Mix Double-Difference RTK[J]. Journal of Geodesy and Geodynamic, 2016, 36(1): 1-5)
(  0) 0) |
| [9] |
隋心, 邹鑫慈, 徐爱功, 等. BDS/GPS接收机端系统偏差实时估计方法[J]. 测绘科学, 2016, 41(12): 106-109 (Sui Xin, Zou Xinci, Xu Aigong, et al. A Real-Time Estimation Algorithm for the BDS/GPS Inter-System Biases at the Receiver End[J]. Science of Surveying and Mapping, 2016, 41(12): 106-109)
(  0) 0) |
| [10] |
Tian Y M, Ge M R, Neitzel F, et al. Particle Filter-Based Estimation of Inter-System Phase Bias for Real-Time Integer Ambiguity Resolution[J]. GPS Solutions, 2017, 21(3): 949-961 DOI:10.1007/s10291-016-0584-3
(  0) 0) |
| [11] |
Nadarajah N, Teunissen P J G, Raziq N. Beidou Inter-Satellite-Type Bias Evaluation and Calibration for Mixed Receiver Attitude Determination[J]. Sensors, 2013, 13(7): 9435-9463 DOI:10.3390/s130709435
(  0) 0) |
| [12] |
Nadarajah N, Teunissen P J G, Sleewaegen J M, et al. The Mixed-Receiver Beidou Inter-Satellite-Type Bias and Its Impact on RTK Positioning[J]. GPS Solutions, 2015, 19(3): 357-368 DOI:10.1007/s10291-014-0392-6
(  0) 0) |
| [13] |
Takasu T, Yasuda A. Development of the Low-Cost RTK-GPS Receiver with an Open Source Program Package RTK LIB[C]. International Symposium on GPS/GNSS, Jeju, 2009 https://www.researchgate.net/publication/228811569_Development_of_the_low-cost_RTK-GPS_receiver_with_an_open_source_program_package_RTKLIB
(  0) 0) |
| [14] |
Teunissen P J G. The Least-Squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70(1-2): 65-82 DOI:10.1007/BF00863419
(  0) 0) |
| [15] |
Tian Y M, Ge M R, Neitzel F. Particle Filter-Based Estimation of Inter-Frequency Phase Bias for Real-Time GLONASS Integer Ambiguity Resolution[J]. Journal of Geodesy, 2015, 89(11): 1145-1158 DOI:10.1007/s00190-015-0841-1
(  0) 0) |
2. Collaborative Innovation Center of Geospatial Technology, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2019, Vol. 39
2019, Vol. 39

