2. 云南省地震局,昆明市北辰大道148号,650224;
3. 中国地震局地震研究所地震大地测量重点实验室,武汉市洪山侧路40号,430071
震害分析表明,框架结构的扭转振动是结构地震破坏的重要原因之一[1],结构强震观测是了解结构在地震作用下响应特征和破坏机理的重要途径[2]。基于云南省防灾减灾综合楼结构强震观测台阵,分别选取2009年姚安MS6.0、2014年鲁甸MS6.5地震的结构强震记录,对比两次地震作用下强震记录的差异并分析其原因。利用SAP2000有限元软件,建立大楼的有限元模型,分别选取场地强震观测记录作为输入地震动,通过模态分析、动力时程分析计算两次地震作用下结构动力响应状况,并结合强震记录进一步讨论两者差异的主要原因。
1 结构及其强震观测云南省防灾减灾综合楼为框架剪力墙结构,长46.8 m,宽15.6 m,总高度39.3 m。主楼共10层(包含地下室),标准层层高3.9 m,底层层高4.5 m。作为结构强震观测台阵,该楼地下室、2层、4层、6层、8层、9层平面分别安装K2型内置摆式数字强震记录仪(图 1)。
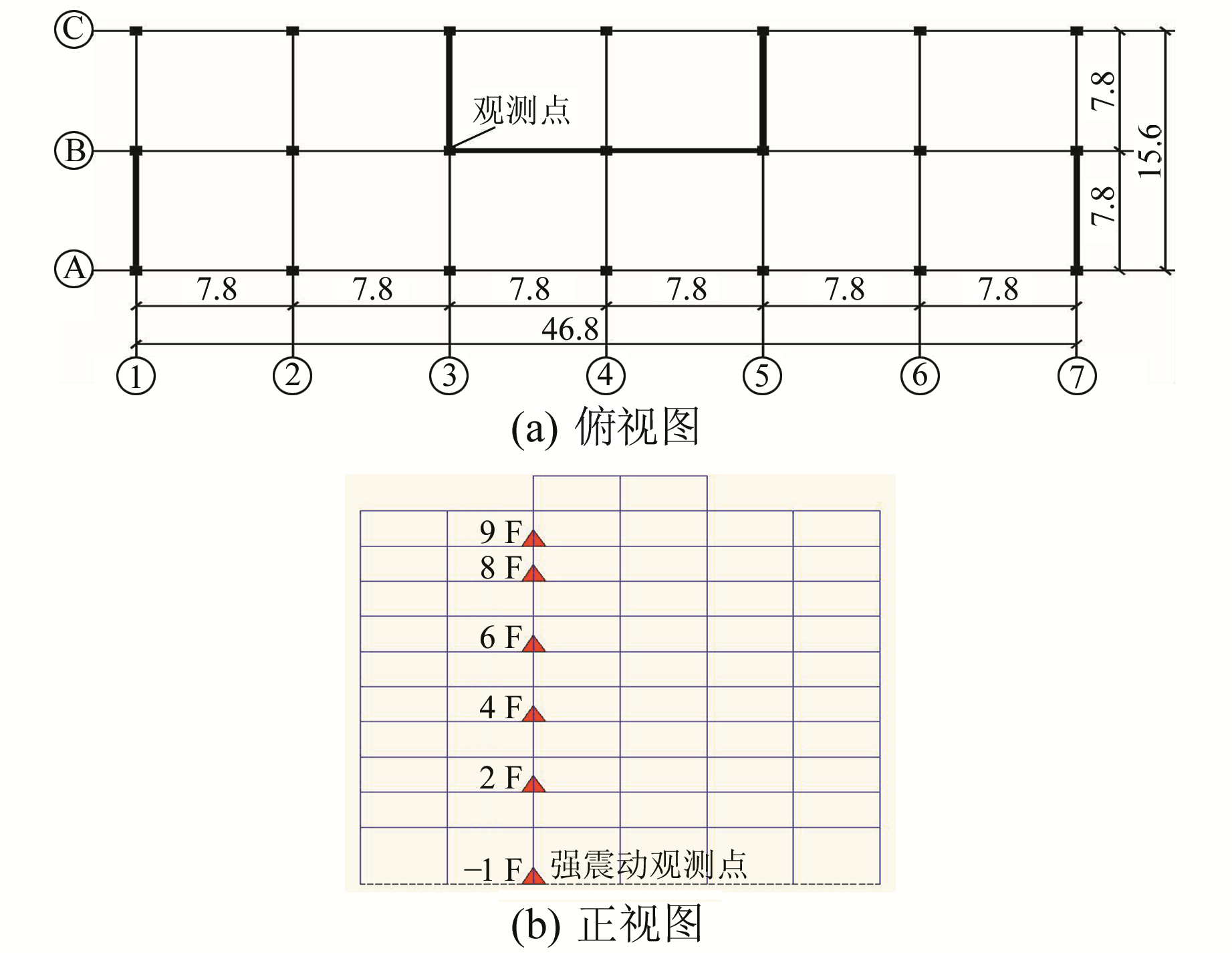
|
图 1 结构强震观测系统布设示意图 Fig. 1 Lay out of the strong motion observation equipment |
大楼与两次地震的位置如图 2。若以震源和建筑长轴向夹角为地震动输入方向,则姚安MS6.0地震动入射角约20°,鲁甸MS6.5地震动约83°。强震观测设备架设于S点,其水平观测分量分别沿结构的长轴、短轴。姚安MS6.0地震时,该台阵的6台强震观测设备都有相应记录,将地下室的观测记录作为输入地震动(图 3)。鲁甸MS6.5地震时,除地下室外,其余各层都有相应记录,故选择距该建筑约2 km的云南财贸学院场地观测记录作为输入地震动(图 4)。
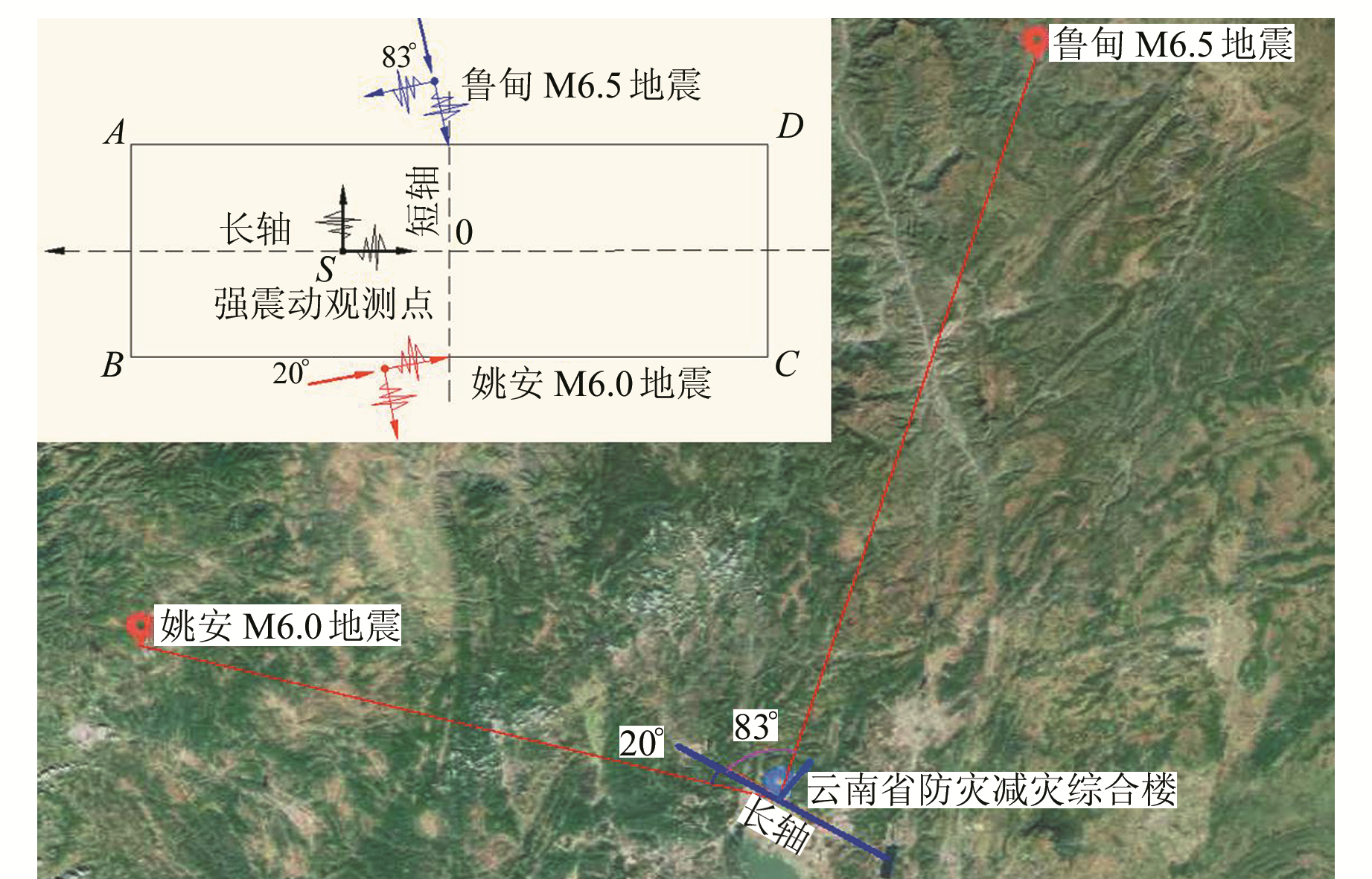
|
图 2 地震动入射角度示意图(姚安约20°、鲁甸约83°) Fig. 2 Angle of input ground motion |
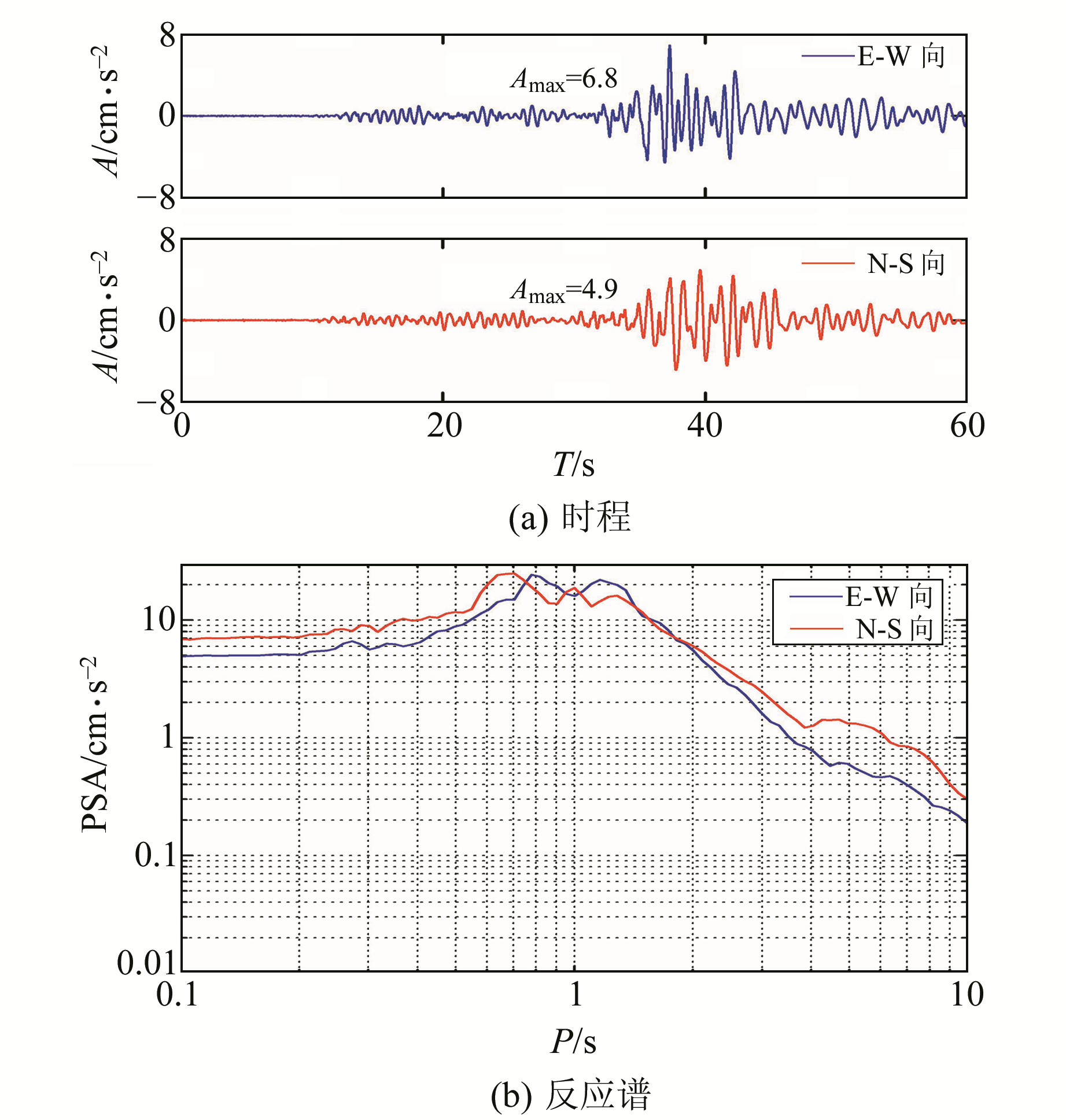
|
图 3 姚安地震输入地震动 Fig. 3 Input ground motion of Yaoan earthquake |

|
图 4 鲁甸地震输入地震动 Fig. 4 Input ground motion of Ludian earthquake |
采用频域分析法分析频谱特征,有效识别结构的振型模态[3-4]。平面扭转振型如图 5所示。假定楼层平面为绝对刚性的矩形(ABCD),长2L,宽2B,本文中L=3B。强震观测点为S1,水平观测分量分别沿X、Y轴向。
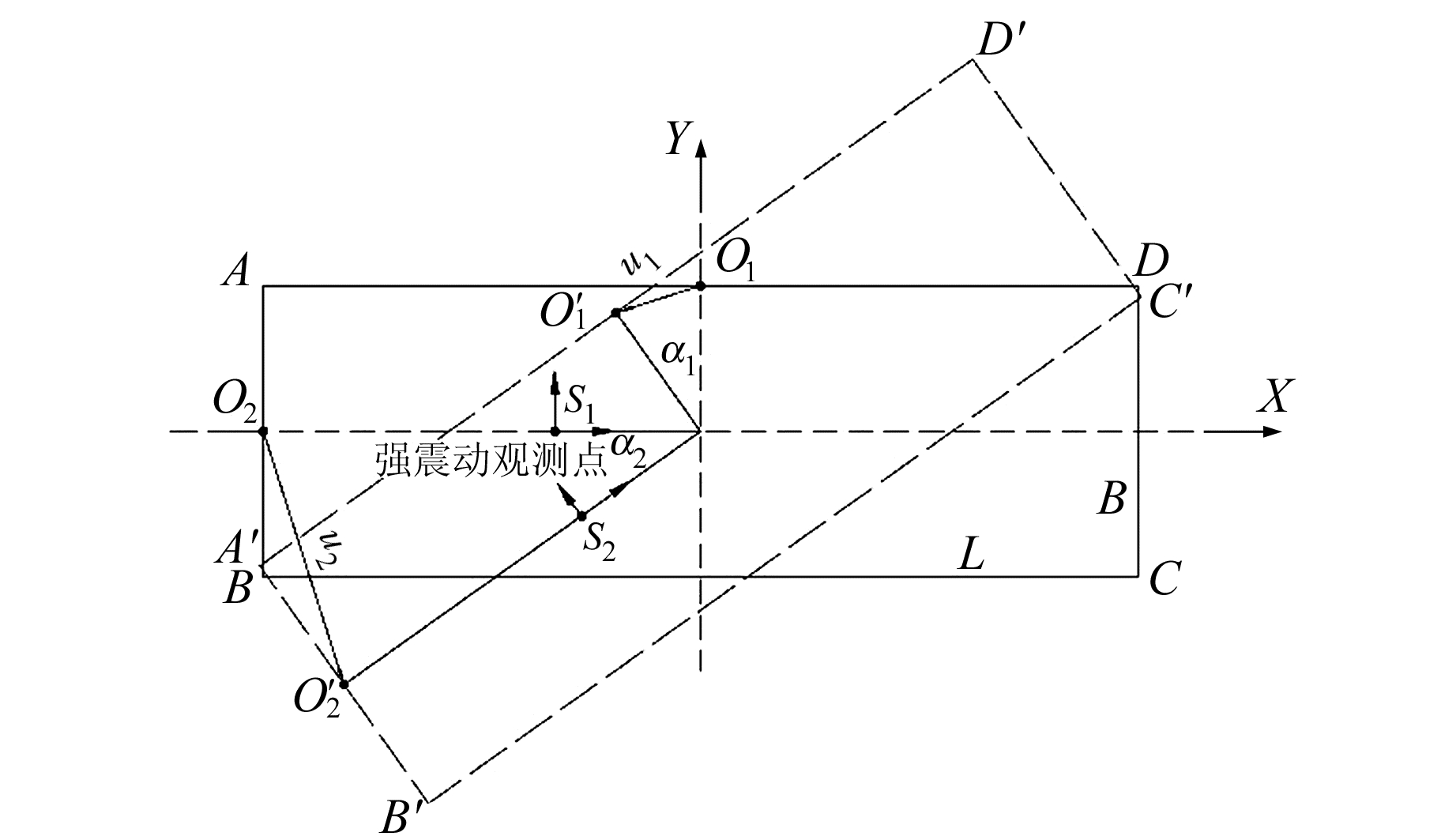
|
图 5 楼层平面扭转示意图 Fig. 5 Sketch map of floor torsion |
AD、AB边中点O1、O2的振动分别与强震观测X、Y分量的方向一致。当该楼层发生平面扭转变形后(A'B'C'D'),强震观测点运动至S2,此时O1、O2点的位移分别为u1、u2,其中,
| $ {u_1}(t) = {\alpha _1}(t)B, \;\;{u_2}(t) = {\alpha _2}(t)L $ | (1) |
经微分变换得到加速度:
| $ {a_1}(t) = {u''_1}(t) = {\alpha ''_1}(t)B $ | (2) |
| $ {a_2}(t) = {u''_2}(t) = {\alpha ''_2}(t)L $ | (3) |
由于楼层平面为绝对刚性,未发生变形,因此各轴向的转角相等,即
| $ {\alpha _1}(t) = {\alpha _2}(t) = \alpha (t) $ | (4) |
由式(2)、式(3)知,当结构发生平面扭转振动时,O1、O2点的水平X、Y分量同时发生振动。将O1、O2点的水平加速度转换至强震观测点S,得到观测点沿X、Y轴的水平加速度分量:
| $ {a_1}(t) = \alpha ''(t)B $ | (5) |
| $ {a_2}(t) = \alpha ''(t)L = 3\alpha ''(t)B/3 = \alpha ''(t)B $ | (6) |
由上式可知,强震观测点X、Y向水平加速度相等,将时程转换为频谱时其值亦相等。因此,当该观测点的X、Y向傅里叶谱达到峰值点且幅值相等时,可认为此建筑产生了平面扭转振动。
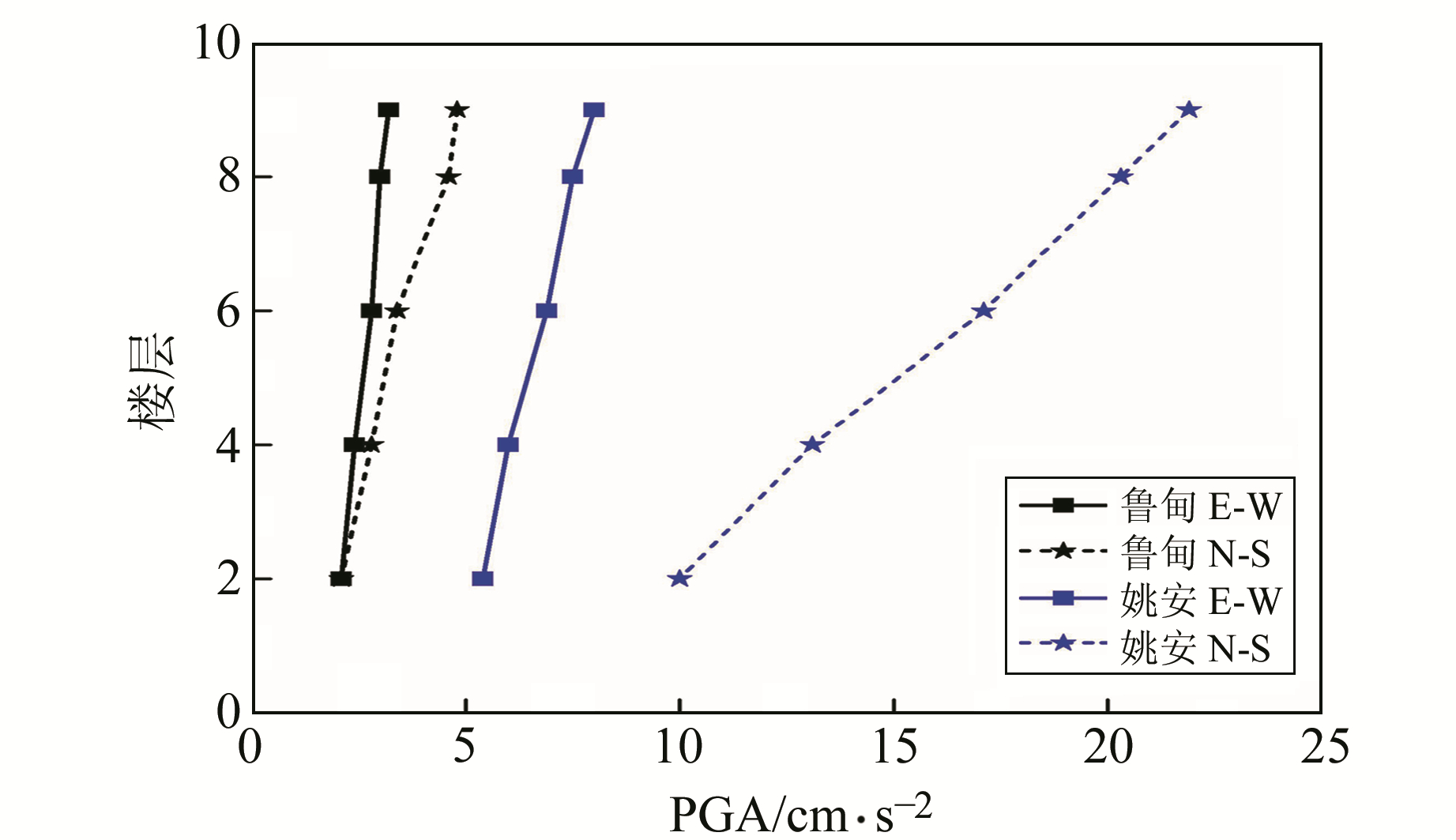
2.2 扭转振型识别与对比对比各楼层强震记录最大加速度峰值(图 6)可知,随着楼层升高,最大加速度峰值近似呈线性增加,且短轴向峰值明显高于长轴向,说明该结构在两次地震作用下均处于弹性变形状态[2-4]。
|
图 6 各楼层最大加速度峰值 Fig. 6 The maximum acceleration of each floor |
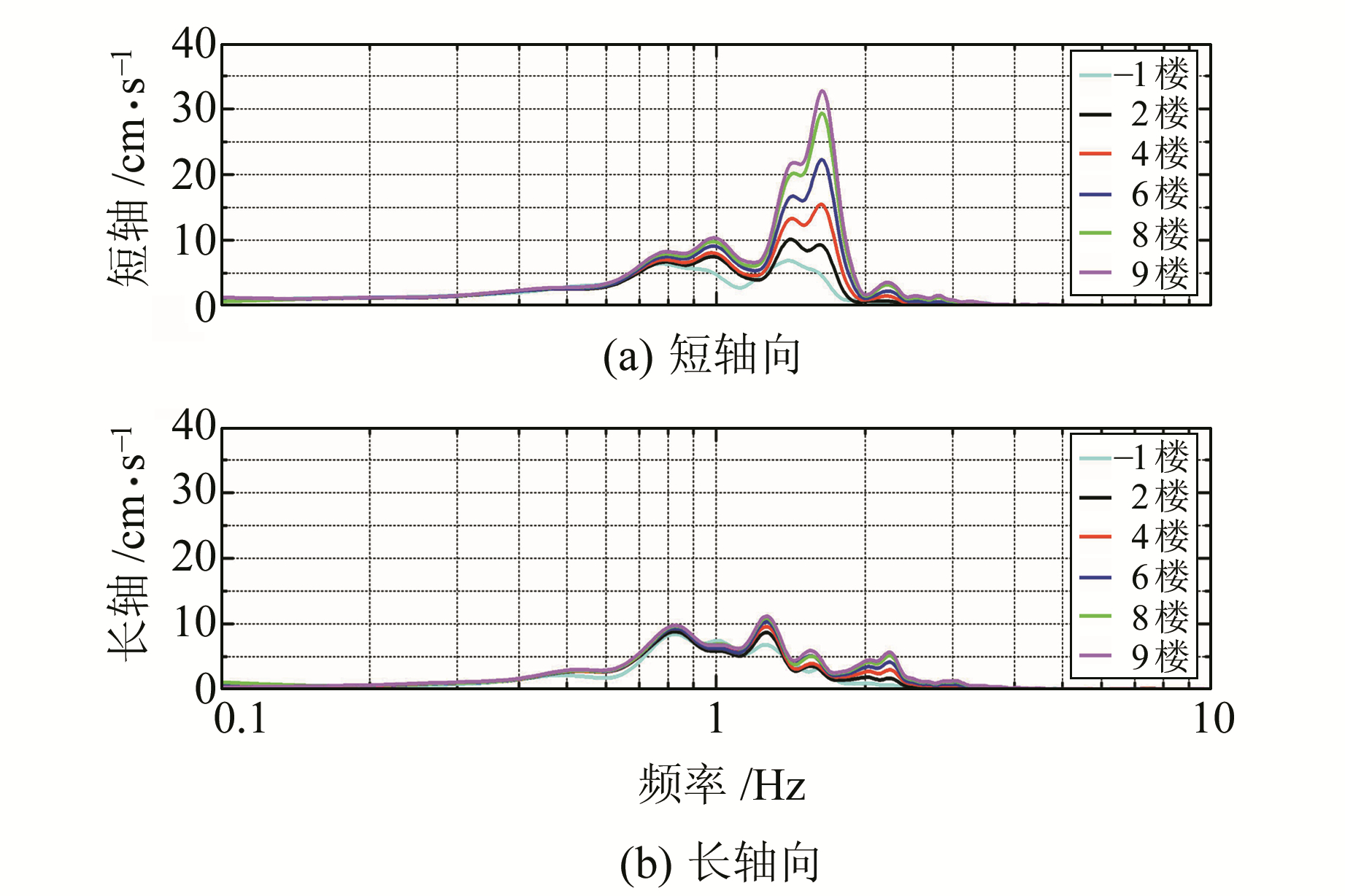
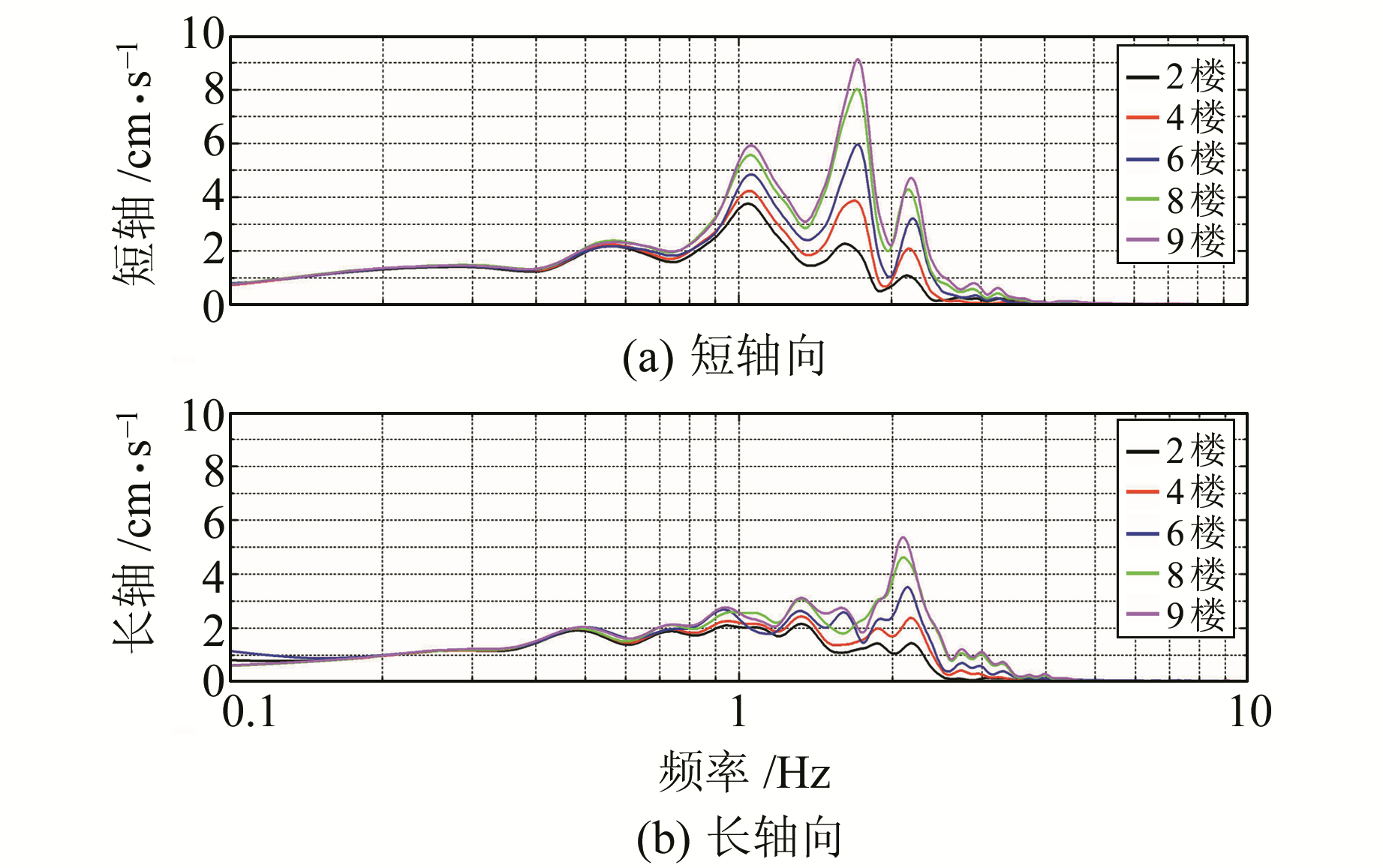
经傅里叶变换后,得到两次地震时各楼层强震傅里叶谱(图 7、图 8)。经对比得到以下结论:
|
图 7 姚安MS6.0地震各楼层强震傅里叶谱 Fig. 7 The Fourier spectrum of each floor in Yaoan MS6.0 earthquanke |
|
图 8 鲁甸MS6.5地震各楼层强震傅里叶谱 Fig. 8 The Fourier spectrum of each floor in Ludian MS6.06.5 earthquanke |
1) 短轴向的傅里叶谱在1.0 Hz、1.7 Hz、2.1 Hz处出现明显峰值。1.7 Hz为最高值,由于结构第一振型所需能量最低,振动最强烈,因此该频率对应结构的第一振型。
2) 长轴向的傅里叶谱在1.3 Hz、2.1 Hz处出现明显峰值。结构的平动振型只会沿一个轴向振动,而扭转振型沿两个轴向振动。当结构长、短轴向的强震记录傅里叶谱在同一频率处同时出现峰值时,结构产生了扭转振动,该频率对应扭转振动频率。因此,2.1 Hz对应该结构的扭转频率。
3) 鲁甸MS6.5地震对应的结构扭转振动显著强于姚安MS6.0地震(2.1 Hz对应峰值显著高于其他频率对应值)。因两次地震结构的输入地震动相近(峰值、频谱),振型模态一致,因此地震动输入方向是影响结构扭转振动差异的主要原因。
3 有限元建模分析 3.1 模型建立采用SAP2000结构分析软件,建立该结构的有限元模型。其中主梁、框架柱采用梁单元模拟,梁柱节点采用固接形式,楼板、剪力墙、填充墙采用壳单元模拟,其自身平面内的刚度无限大。由于填充墙质量、刚度对结构的整体刚度、振型特征有较强影响,能显著提升结构的抗震性能,提高结构的自振频率[5-6],采用自定义的混凝土材料作为填充墙,墙厚度统一取120 mm,弹性模量EC为1.85×104 N/mm2,泊松比取0.2,密度取0,轴心标准抗压强度取4.8 MPa[6-7]。填充墙与梁、柱相接处添加法向束缚,同时将填充墙的质量简化为等效线性荷载P=8.7 kN/m,均布于框架梁。由于该建筑前墙、后墙均为填充墙,且开有较大的门窗洞口,对于整体刚度影响较小,为了简化计算,建模中不考虑这部分墙体对整体刚度的影响。其建模参数如表 1、模型如图 9所示。
|
|
表 1 模型参数 Tab. 1 The parameters in finite element model |
|
图 9 云南省防灾减灾综合楼有限元模型 Fig. 9 Finite element model of comprehensive building in Yunnan province |
模态分析结果显示,该结构的第一振型为短轴向的平动,自振频率为1.64 Hz;第二振型为平面的扭转振动,频率为1.98 Hz,模拟值与傅里叶谱分析结果相近。
|
|
表 2 振型模态对比 Tab. 2 The parameters comparison of mode shape |
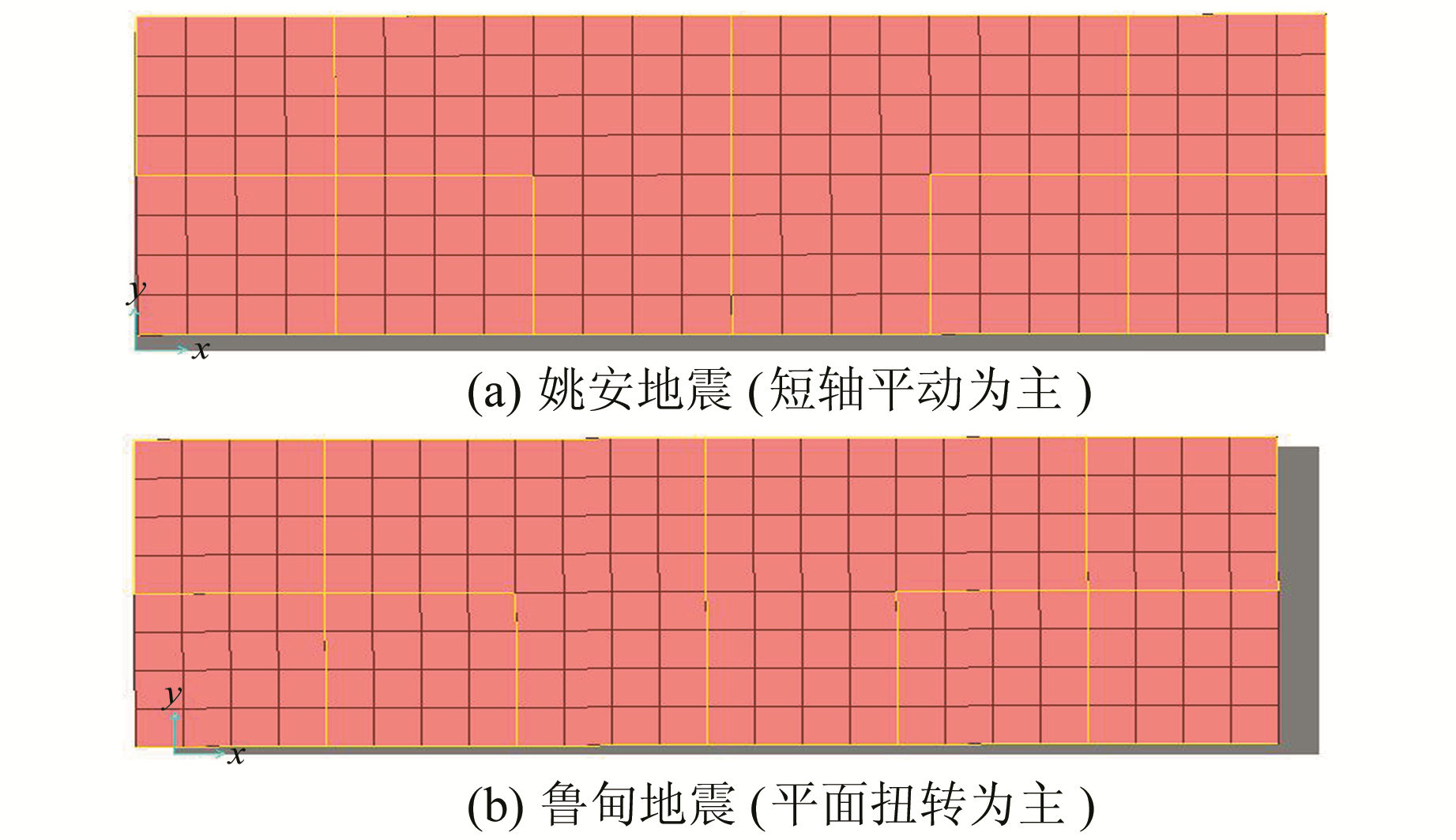
采用双向输入法,将场地东西、南北向强震记录分别以一定角度输入(图 2),其中鲁甸夹角约83°,姚安约20°。时程分析得到结构平面的主要振动形式,其中鲁甸MS6.5地震动作用下该结构平面运动主要以短轴向平动、水平向扭转振动为主,而姚安MS6.0地震主要以短轴向水平振动为主,如图 10所示。
|
图 10 不同地震动作用下代表楼层平面运动特征 Fig. 10 Plane motion features of representative floors under different ground motions |
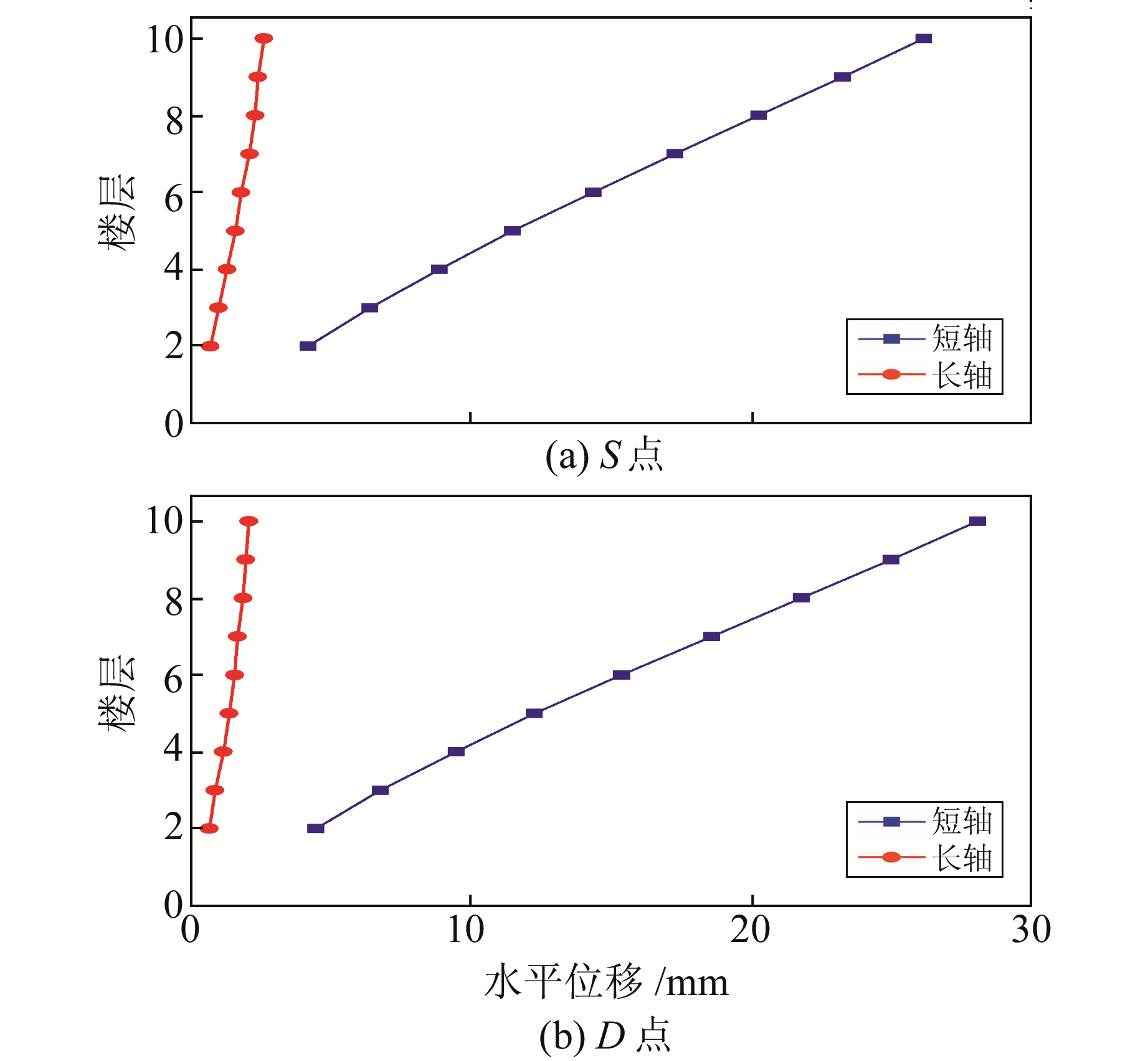
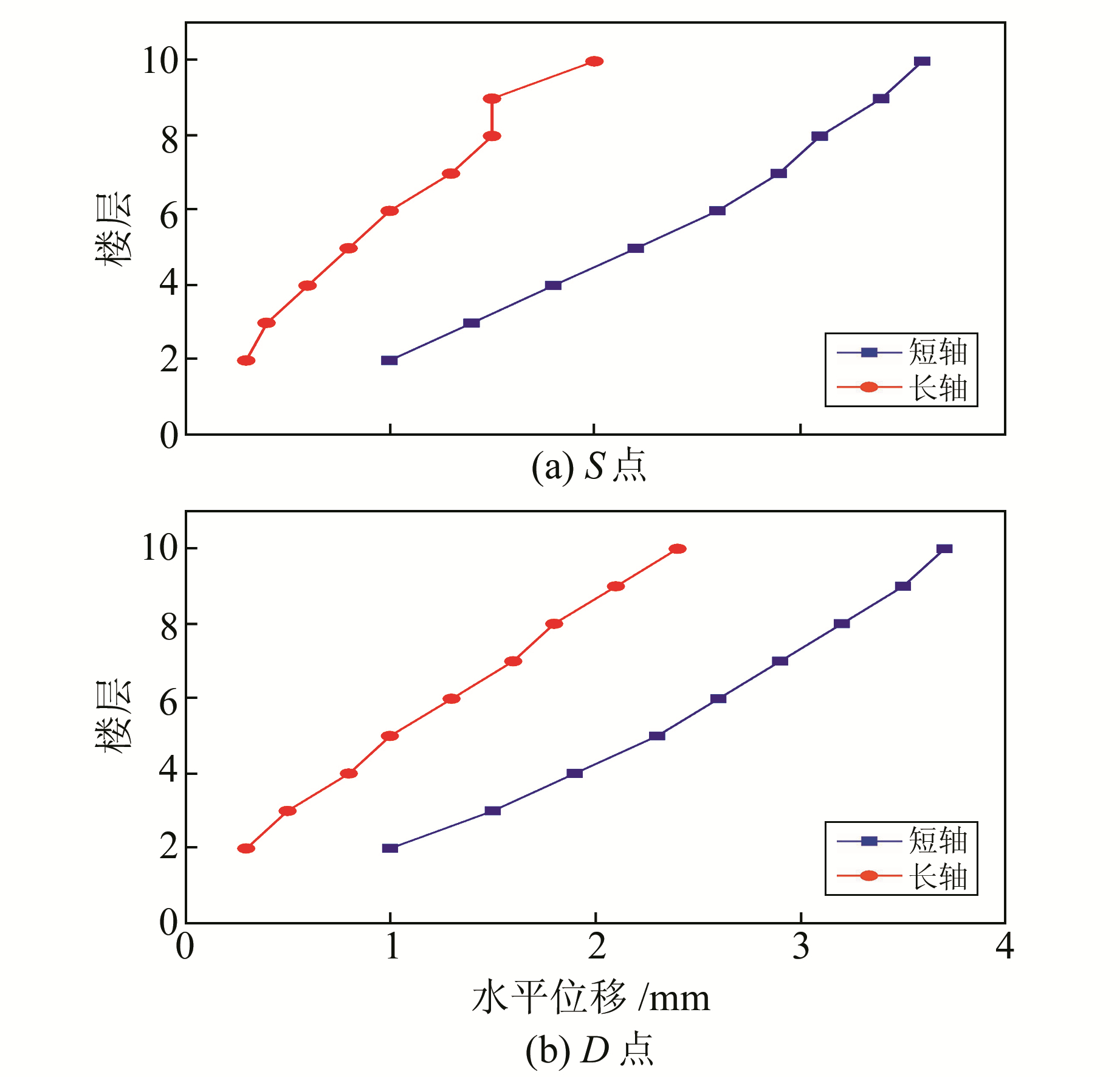
分别选取强震观测点S、右角柱D点为监测点,分析上述监测点沿长轴、短轴的最大水平位移(图 11~12)。
|
图 11 姚安MS6.0地震各楼层水平位移 Fig. 11 The horizontal displacement of each floor under the Yaoan MS6.0 earthquake |
|
图 12 鲁甸MS6.5地震各楼层位移 Fig. 12 The horizontal displacement of each floor under the Ludian MS6.5 earthquake |
1) 两次地震作用下,各楼层的水平位移(长、短轴)随楼层的增高近似呈线性增加,说明该结构始终处于弹性反应阶段,未出现结构非线性效应。
2) 姚安MS6.0地震动作用下,各楼层S和D点的短轴向水平位移量、水平位移增长率都远高于长轴向,说明该结构主要以短轴向水平运动为主,其水平向的扭转运动不明显。
3) 鲁甸MS6.5地震动作用下,各楼层S和D点的短轴向水平位移量、水平位移增长率相近,说明该结构沿上述两个方向发生明显运动,该运动为楼层平面的扭转运动。
综上所述,结合傅里叶谱分析结论,说明地震动的输入方向是引起上述差异的主要原因,是影响结构地震动扭转振动的重要因素。
4 结语本文基于云南省防灾减灾综合楼强震观测记录,对比分析姚安MS6.0、鲁甸MS6.5地震动作用下结构扭转振动差异。利用SAP2000建立有限元模型,将场地强震观测记录作为输入地震动,分别以实际角度输入并进行动力时程分析,主要结论如下。
1) 短轴向傅里叶谱在1.0 Hz、1.7 Hz、2.1 Hz处出现明显峰值。1.7 Hz对应最大值,由于结构第一振型所需能量最低,振动最强烈,该频率对应结构第一振型(短轴平动)。2.1 Hz处长短轴都出现明显峰值,因此该频率对应该结构的第二振型,为平面扭转振型。
2) 鲁甸MS6.5地震作用下结构的扭转振动强于姚安MS6.0地震,由于两次地震的场地强震记录相近(峰值、频谱),地震动输入方向不同造成了结构扭转振动的差异。
3) 有限元模拟结果显示,姚安MS6.0地震作用下,各楼层短轴向水平位移量、水平位移增长率都远高于长轴向,结构主要以短轴向的水平运动为主,扭转振动不显著;而鲁甸MS6.5地震作用下,各楼层短轴向水平位移量、水平位移增长率相近,结构沿上述两个方向发生明显运动,为平面的扭转运动。上述现象均与强震观测记录吻合。
4) 地震动入射方向是影响结构平面扭转振动的重要原因,结构抗震设计中应验算最不利地震动入射方向。
| [1] |
徐培福, 黄吉锋, 韦承基. 高层建筑结构的扭转反应控制[J]. 土木工程学报, 2006, 39(7): 1-8 (Xu Peifu, Huang Jifeng, Wei Chengji. Control of Torsional Response of Tall Building Structures[J]. China Civil Engineering Journal, 2006, 39(7): 1-8 DOI:10.3321/j.issn:1000-131X.2006.07.001)
(  0) 0) |
| [2] |
庞骢骢, 丁海平. 基于结构台阵记录的地震响应分析[J]. 华南地震, 2013, 33(4): 11-19 (Pang Congcong, Ding Haiping. Seismic Response Analysis of a High-rise Building Structure Based on Seismic Observation Data[J]. South China Journal of Seismology, 2013, 33(4): 11-19)
(  0) 0) |
| [3] |
公茂盛, 谢礼立, 欧进萍. 基于结构强震记录框剪结构自振周期经验公式[J]. 土木工程学报, 2010, 43(12): 35-40 (Gong Maosheng, Xie Lili, Ou Jinping. Empirical Formula for Fundamental Period of Frame-Shear Wall Structures Based on Structural Strong Motion Records[J]. China Civil Engineering Journal, 2010, 43(12): 35-40)
(  0) 0) |
| [4] |
公茂盛, 鹿嶋俊英, 谢礼立, 等. 基于结构强震记录的结构时变模态参数识别[J]. 振动与冲击, 2010, 29(5): 171-175 (Gong Maosheng, Toshihide K, Xie Lili, et al. Structural Time-Varying Modal Parameter Identification Based on Its Strong Motion Records[J]. Journal of Vibration & Shock, 2010, 29(5): 171-175 DOI:10.3969/j.issn.1000-3835.2010.05.037)
(  0) 0) |
| [5] |
黄思凝, 郭迅, 孙得璋, 等. 轻质填充墙框架结构抗震性能的振动台试验研究[J]. 工程力学, 2014, 31(9): 182-189 (Huang Sining, Guo Xun, Sun Dezhang, et al. Shaking Table Seismic Teston Performance of Frame-Structure with Light-Weight Infilled Walls[J]. Engineering Mechanics, 2014, 31(9): 182-189)
(  0) 0) |
| [6] |
魏勇, 崔建文, 王秋良, 等. 填充墙对于框架结构抗震性能影响分析[J]. 建筑结构, 2017, 47(S2): 351-355 (Wei Yong, Cui Jianwen, Wang Qiuliang, et al. Analysis of Seismic Performance of Infilled Walls to Frames[J]. Building Structure, 2017, 47(S2): 351-355)
(  0) 0) |
| [7] |
谭德先, 周云, 米斯特, 等. 环境激励下高层建筑结构模态测试与有限元建模分析[J]. 土木工程学报, 2015, 48(9): 41-50 (Tan Dexian, Zhou Yun, Mi Site, et al. Ambient Vibration Dynamic Test and Finite Element Analysis for High-Rise Buildings[J]. China Civil Engineering Journal, 2015, 48(9): 41-50)
(  0) 0) |
2. Yunnan Earthquake Agency, 148 Beichen Road, Kunming 650224, China;
3. Key Laboratory of Earthquake Geodesy, Institute of Seismology, CEA, 40 Hongshance Road, Wuhan 430071, China
 2018, Vol. 38
2018, Vol. 38


