2. 地理信息工程国家重点实验室,西安市雁塔路中段1号,710054;
3. 地理国情监测国家测绘地理信息局工程技术研究中心,西安市雁塔路中段1号,710054;
4. 西安测绘研究所,西安市雁塔路中段1号,710054
在航空重力测量中,测线往往布设成纵横交错的网状,根据测线交叉点的符合程度来评估测区的测量精度。交叉点不符值是进行航空重力测量精度评估的依据[1-6]。航空重力测量资料后处理的核心就是搜索测线交叉点位置,对重力值进行补偿。由于航空重力测量采样率较高、测点数目众多,用传统的逐一比对搜索法求取测线交叉点不仅耗时长、效率低,而且不准确。因此,需要对搜索算法进行优化,使交叉点搜索的范围尽可能小,从而减少搜索时间、提高效率。常用的交叉点搜索方法有跳跃搜索法[6]、主副测线斜率法[7]、坐标平均法[8]以及多项式拟合法[9],但这些方法都是将交叉点附近相距最近的两个测点作为交叉点来处理,在理论上不够严密,且搜索的正确率较低,适用性较差。本文提出一种快速精确求定交叉点的搜索方法——基于滑动窗口的交叉点搜索法,能适用于大多数测线情况。
1 滑动窗口交叉点搜索方法本文以主测线点为中心,采用一定宽度的搜索框对主副测线点进行搜索,将搜索到的相邻测点组成线段,运用行列式方法精确求出交叉点及不符值,称为滑动窗口交叉点搜索方法。
1.1 测线交叉点计算如图 1,设p为主副测线交叉点,p1和p2是主测线上相邻的两个测点,对应的重力值为ga1和ga2,p3和p4是副测线上位于交叉点两侧的相邻测点,对应的重力值为ga3和ga4。
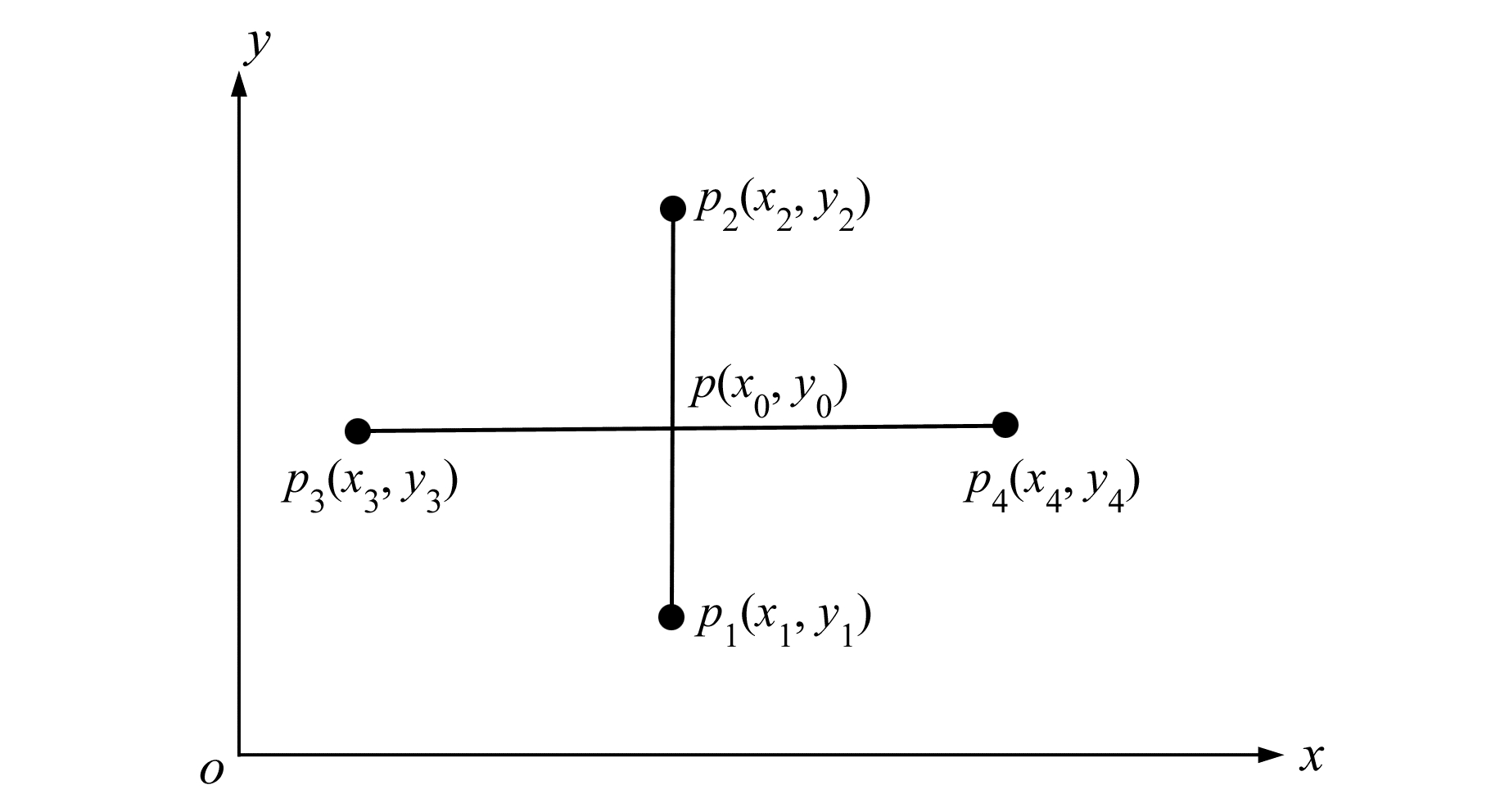
|
图 1 交叉点示意图 Fig. 1 Line intersection schematic |
将p1、p2和p3、p4连接起来,组成线段p1p2和p3p4,它们所在直线的参数方程分别为:
| $ \left\{ \begin{array}{l} x = {x_1} + \lambda ({x_2} - {x_1})\\ y = {y_1} + \lambda ({y_2} - {y_1}) \end{array} \right.\left\{ \begin{array}{l} x = {x_3} + \mu ({x_4} - {x_3})\\ y = {y_3} + \mu ({y_4} - {y_3}) \end{array} \right. $ | (1) |
若两线段相交,则交点p的参数值应满足:
| $ \left\{ \begin{array}{l} {x_0} = {x_1} + \lambda ({x_2} - {x_1}) = {x_3} + \mu ({x_4} - {x_3})\\ {y_0} = {y_1} + \lambda ({y_2} - {y_1}) = {y_3} + \mu ({y_4} - {y_3}) \end{array} \right. $ | (2) |
将式(2)变形,得:
| $ \left\{ \begin{array}{l} ({x_2} - {x_1})\lambda - ({x_4} - {x_3})\mu = {x_3} - {x_1}\\ ({y_2} - {y_1})\lambda - ({y_4} - {y_3})\mu = {y_3} - {y_1} \end{array} \right. $ | (3) |
若
| $ \Delta = \left| \begin{array}{l} {x_2} - {x_1}\;\;\;\; - ({x_4} - {x_3})\\ {y_2} - {y_1}\;\;\; - ({y_4} - {y_3}) \end{array} \right| = 0 $ | (4) |
则表示两线段p1p2和p3p4重合或平行,一般将它们视为不相交来处理;若Δ≠0,则可求出交点对应的两个参数值:
| $ \left\{ \begin{array}{l} \lambda = \frac{1}{\Delta }\left| \begin{array}{l} {x_3} - {x_1}\;\;\;\; - ({x_4} - {x_3})\\ {y_3} - {y_1}\;\;\;\; - ({y_4} - {y_3}) \end{array} \right|\\ \mu = \frac{1}{\Delta }\left| \begin{array}{l} {x_2} - {x_1}\;\;\;\; - ({x_3} - {x_1})\\ {y_2} - {y_1}\;\;\;\; - ({y_3} - {y_1}) \end{array} \right| \end{array} \right. $ | (5) |
需要注意的是,只有当0≤λ≤1, 0≤μ≤1同时满足时,两线段才真正相交。否则,交点在两线段或其中一条线段的延长线上,这时仍然认为两线段是不相交的。
设主副测线在交叉点p的重力值为ga主和ga副,利用主副测线上位于交叉点两侧的相邻测点重力值通过线性内插得到交叉点处的重力值:
| $ \left\{ \begin{array}{l} {g_{{a_{主}}}} = {g_{{a_1}}} + \lambda \left( {{g_{{a_2}}} - {g_{{a_1}}}} \right)\\ {g_{{a_{副}}}} = {g_{{a_3}}} + \mu \left( {{g_{{a_4}}} - {g_{{a_2}}}} \right) \end{array} \right. $ | (6) |
则主副测线在交叉点的重力不符值为:
| $ {g_{{a_p}}} = {g_{{a_{主}}}} - {g_{{a_{副}}}} $ | (7) |
由以上讨论可知,当确定了p1、p2和p3、p4四点后,计算交叉点及其不符值非常容易,但问题的关键是如何确定主副测线上位于交叉点两侧的两个相邻测点。
1.2 测线交叉点搜索在航空重力测量作业中,飞机难免受到气流、离心力等干扰,测线在局部往往是波动的。因此,如果直接用主副测线的端点按照§1.1中的交叉点求交公式求得的交叉点p'势必不是真正的交叉点p。如图 2所示,图中黑点、红点分别表示主副测线上的观测点,以主测线点为中心点,采用一定宽度的矩形框为搜索窗口,然后遍历整条主副测线,判断落入搜索窗口的测线点。接着依照§1.1对落入搜索窗口的主副测线上相邻测点组成的线段进行相交判断,如果相交就求出交叉点位置及不符值,若没有就继续循环判断,直到找到交叉点为止。若测量航线如图 2(a)所示,即近似为南北航线时,可对搜索条件进行优化,此时将主测线点的平均经度、副测线点的平均纬度作为近似交叉点,以其为搜索中心采用一定大小的搜索框对落入交叉点附近的主副测线点进行搜索,然后依据§1.1的交叉点理论进行求解。具体的判断过程如下所述。

|
图 2 主副测线点示意图 Fig. 2 The main and sub line points schematic |
pi(xi, yi)和pj(xj, yj)(i=1, 2, …, n; j=1, 2, …, m)表示主副测线上的观测点,以pi为搜索窗口的中心,然后遍历整条副测线,判断pj是否落在窗口内。为了减小交叉点搜索范围,可依据测量时的飞行速度v来确定搜索窗口的大小。比如航向近似为南北向时,搜索窗口的大小可取1.5v或更大一些。副测线点落入窗口的判断准则为:
| $ \left\{ \begin{array}{l} {x_i} - \Delta x \le {x_j} \le {x_i} + \Delta x\\ {y_i} - \Delta y \le {y_j} \le {y_i} + \Delta y \end{array} \right. $ | (8) |
当把落入搜索窗口内的副测线点pj找到后,搜索窗口的中心I0就确定了,这时可依据式(9)确定主测线上落入搜索窗口内的点:
| $ \left\{ \begin{array}{l} {x_{{I_0}}} - \Delta x \le {x_i} \le {x_{{I_0}}} + \Delta x\\ {y_{{I_0}}} - \Delta y \le {y_i} \le {y_{{I_0}}} + \Delta y \end{array} \right. $ | (9) |
交叉点附近主副测线点都确定下来了,就可按照§1.1的交叉点理论对pi(xi, yi)、pi+1(xi+1, yi+1)和pj(xj, yj)、pj+1(xj+1, yj+1)4点进行判断,如果满足0≤λ≤1, 0≤μ≤1,就可求出交叉点及交叉点不符值。
2 测线交叉点计算程序实现 2.1 测线交叉点计算流程测线交叉点计算的具体流程如图 3所示。
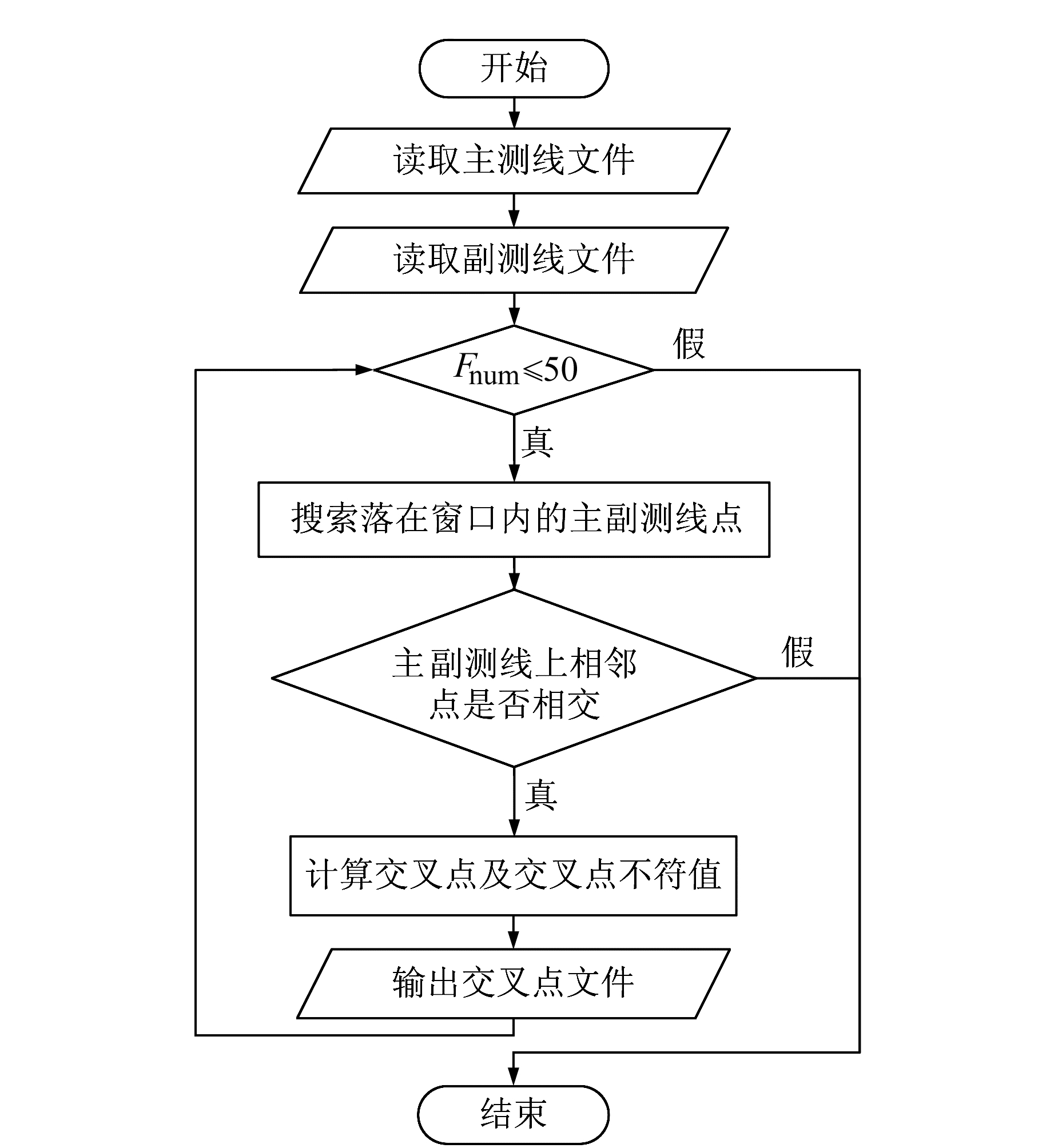
|
图 3 交叉点计算流程 Fig. 3 Intersection calculation process |
某航空重力测区如图 4所示,以南北方向为主测线、东西方向为副测线,主副测线各5条,共有5 500个测点,合计有19对交叉点。
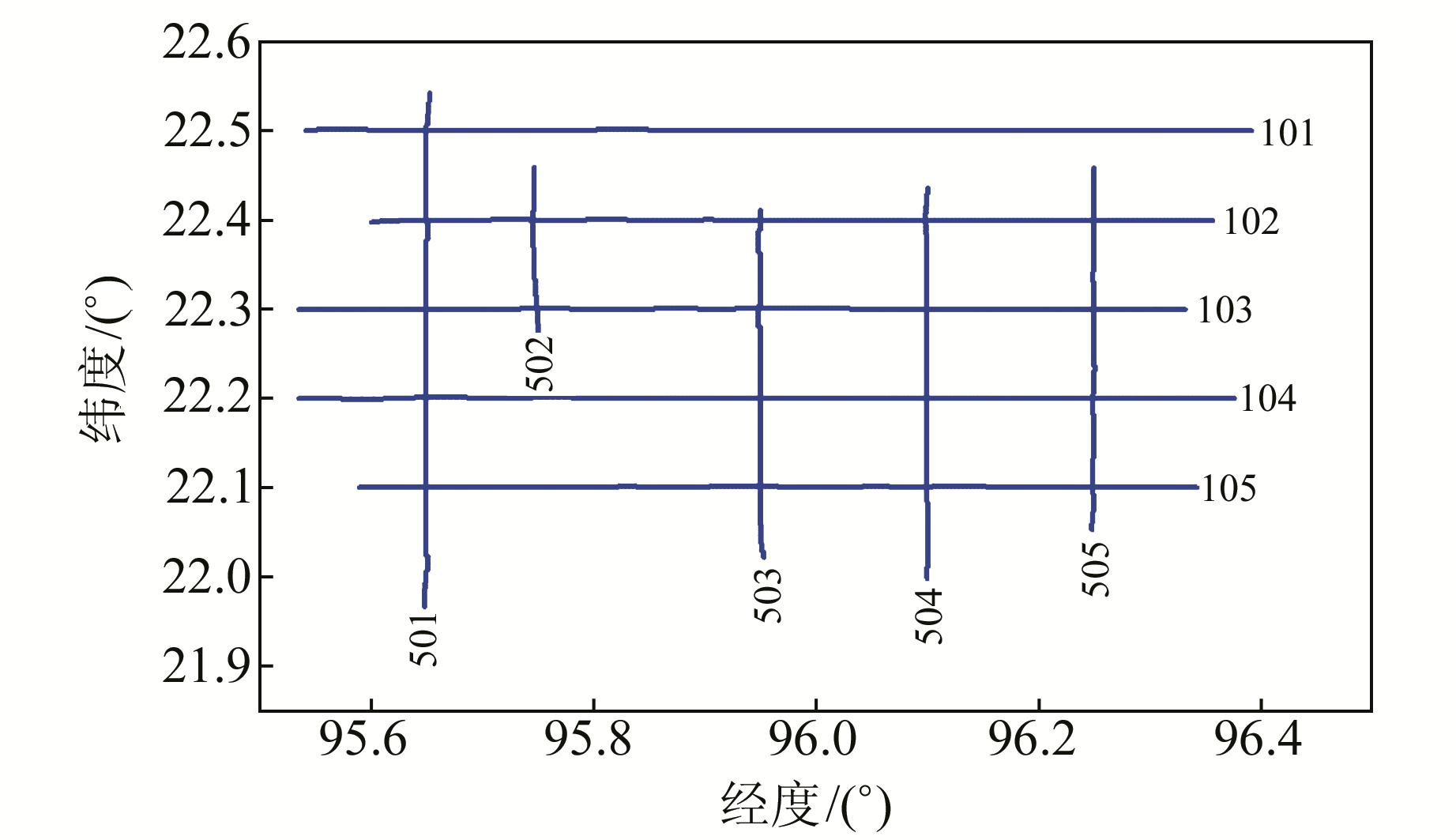
|
图 4 测区概况 Fig. 4 Measuring area introduction |
对该测区实测数据用坐标平均法、主副测线斜率法及滑动窗口算法分别进行搜索,从搜索时间和正确率两方面进行对比,见表 1。
|
|
表 1 3种搜索方法的相关统计信息 Tab. 1 Statistics of three search methods |
算例中,主副测线斜率法和滑动窗口法的搜索半径均设为0.003°;坐标平均法计算的近似交叉点误差较大,将搜索半径扩大到0.08°。
从表 1可以看出,坐标平均法和主副测线斜率法的搜索正确率相当,都在65%左右。主副测线斜率法比坐标平均法搜索速度快,这是因为其搜索半径远小于坐标平均法。同时,这两种方法在测线端点处会出现错误搜索的情况,后期还需经过判断处理,当测线数较多时既繁琐又耗时。滑动窗口法能够快速准确地确定交叉点,正确率达100%,在测线端点处不会出现误搜的情况。滑动窗口法最终搜索结果如图 5所示,图中红色三角表示计算的交叉点。
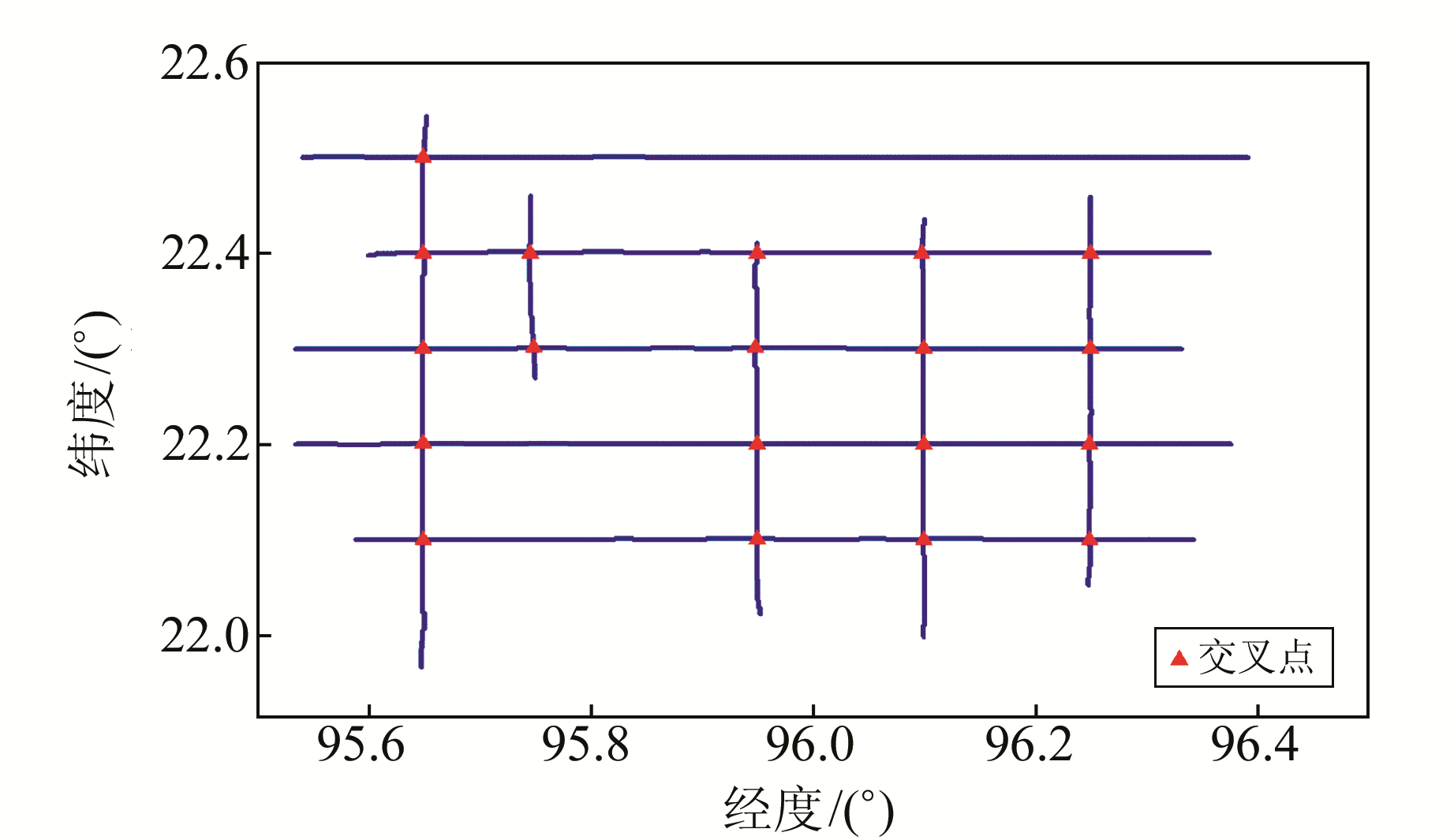
|
图 5 交叉点搜索结果 Fig. 5 Intersection search results |
航空重力测量中求取测线交叉点的常规搜索方法都有其适用范围。基于滑动窗口的搜索方法简单有效,较好地弥补了常规搜索方法的不足,可快速精确求出交叉点位置及其不符值,提高交叉点计算效率。值得注意的是,本文仅对单一航次数据进行了分析,后续还需要对其他实测数据进行再检验。
| [1] |
黄谟涛. 海洋重力场测定及其应用[M]. 北京: 测绘出版社, 2005 (Huang Motao. Determination of Ocean Gravitational Field and Its Application[M]. Beijing: Surveying and Mapping Press, 2005)
(  0) 0) |
| [2] |
孙中苗, 石磐, 夏哲仁, 等. 航空重力仪的动态检测[J]. 测绘通报, 2001(10): 42-44 (Sun Zhongmiao, Shi Pan, Xia Zheren, et al. Dynamic Detection of Airborne Gravimeter[J]. Bulletin of Surveying and Mapping, 2001(10): 42-44 DOI:10.3969/j.issn.0494-0911.2001.10.019)
(  0) 0) |
| [3] |
欧阳永忠. 海空重力测量数据处理关键技术研究[J]. 测绘学报, 2014, 43(4): 435-435 (Ouyang Yongzhong. On Key Technologies of Data Processing for Air-Sea Gravity Surveys[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 435-435)
(  0) 0) |
| [4] |
王丽红, 张传定, 王俊勤, 等. 航空重力测量数学模型及其测量精度分析[J]. 测绘科学技术学报, 2008, 25(1): 68-71 (Wang Lihong, Zhang Chuanding, Wang Junqin, et al. Mathematical Model and Accuracy Analysis of Airborne Gravimetry[J]. Journal of Geomatics Science and Technology, 2008, 25(1): 68-71)
(  0) 0) |
| [5] |
孙中苗, 翟振和, 李迎春. 航空重力测量的分辨率和精度分析[J]. 地球物理学进展, 2010, 25(3): 795-798 (Sun Zhongmiao, Zhai Zhenhe, Li Yingchun. Analysis on the Resolution and Accuracy of Airborne Gravity Survey[J]. Progress in Geophysics, 2010, 25(3): 795-798 DOI:10.3969/j.issn.1004-2903.2010.03.008)
(  0) 0) |
| [6] |
李海.航空重力测量测线网平差的理论与方法[D].郑州: 信息工程大学, 2002 (Li Hai. Theory and Methods of Network Adjustment of Airborne Gravimetry[D]. Zhengzhou: Information Engineering University, 2002)
(  0) 0) |
| [7] |
孙中苗.航空重力测量理论、方法及应用研究[D].郑州: 信息工程大学, 2004 (Sun Zhongmiao. Theory, Methods and Applications of Airborne Gravimetry[D]. Zhengzhou: Information Engineering University, 2004)
(  0) 0) |
| [8] |
蔡劭琨.航空重力测量网络平差方法研究[D].长沙: 国防科学技术大学, 2009 (Cai Shaokun. Research on the Network Adjustment of Airborne Gravimetry[D]. Changsha: National University of Defense Technology, 2009)
(  0) 0) |
| [9] |
戢锐, 康双双, 李川, 等. 基于Matlab的航空重力交叉点搜索[J]. 工程地球物理学报, 2011, 8(5): 551-555 (Qi Rui, Kang Shuangshuang, Li Chuan, et al. Intersection Search of Airborne Gravity Based on Matlab[J]. Journal of Engineering Geophysics, 2011, 8(5): 551-555 DOI:10.3969/j.issn.1672-7940.2011.05.008)
(  0) 0) |
2. State Key Laboratory of Geographic Information Engineering, 1 Mid-Yanta Road, Xi'an 710054, China;
3. Engineering Research Center of Geographic National Conditions Monitoring, NASMG, 1 Mid-Yanta Road, Xi'an 710054, China;
4. Xi'an Research Institute of Surveying and Mapping, 1 Mid-Yanta Road, Xi'an 710054, China
 2018, Vol. 38
2018, Vol. 38

