2. 微波成像技术重点实验室,北京市北四环西路19号, 100190;
3. 中国科学院大学,北京市玉泉路19号甲,100049
研究表明,在中高轨SAR成像[1]、地质研究[2-3]等领域,都需要对电离层电子密度进行准确反演,其中一个重要分支就是利用GPS卫星进行电离层层析成像。1988年,Austen[4]借鉴CT成像技术提出电离层层析(CIT),从此开辟了人们探究电离层的新方法[5-11]。以代数重构算法为代表的电离层层析方法是研究电离层层析反演的主流方法之一,其原理是将初始值向各观测方程进行投影,投影过程中将残差分配到各个网格的电子密度中,通过不断迭代修正得到更接近于真实值的电子密度。Pryse等[12]提出的MART(multiplicative algebraic reconstruction technique)算法则是每次迭代时将STEC实测值与STEC反演值的比值作为电子密度的缩放因子分配到有信号穿过的电离层网格内,通过乘法和乘方运算进行电子密度的修正。在后续的发展过程中, 霍星亮等[13]通过在不同电子密度的网格中重新分配STEC实测值与STEC反演值的残差改进了代数重构方法,但依然只有被信号穿过的网格才会逐渐逼近真值。本文借鉴代数重构算法和乘法代数重构算法,将STEC实测值与STEC反演值的比值(基准尺度因子)分配到反演空间内的所有网格上。对于有信号穿过的网格,其缩放尺度即为基准尺度因子;由于电子密度在空间中具有相关性,距离较近的网格内电子密度一般差别较小,距离较远的网格可能差别较大,所以对于没有信号穿过的网格,通过计算其网格中心与观测射线的距离,结合基准尺度因子确定其对应的尺度因子,在每次迭代过程中利用尺度因子带动电子密度逐渐向真值“靠近”。
1 代数重构方法电离层层析常用的一种方法是根据GPS卫星的观测延迟计算斜向电子总量(slant total electron content,STEC),进行一定区域内的电子密度重构。STEC可以表示为GPS卫星到接收机之间的斜向路径电子密度积分值:
| $ {\rm{STEC}} = \int_l {{N_e}(s){\rm{d}}s} $ | (1) |
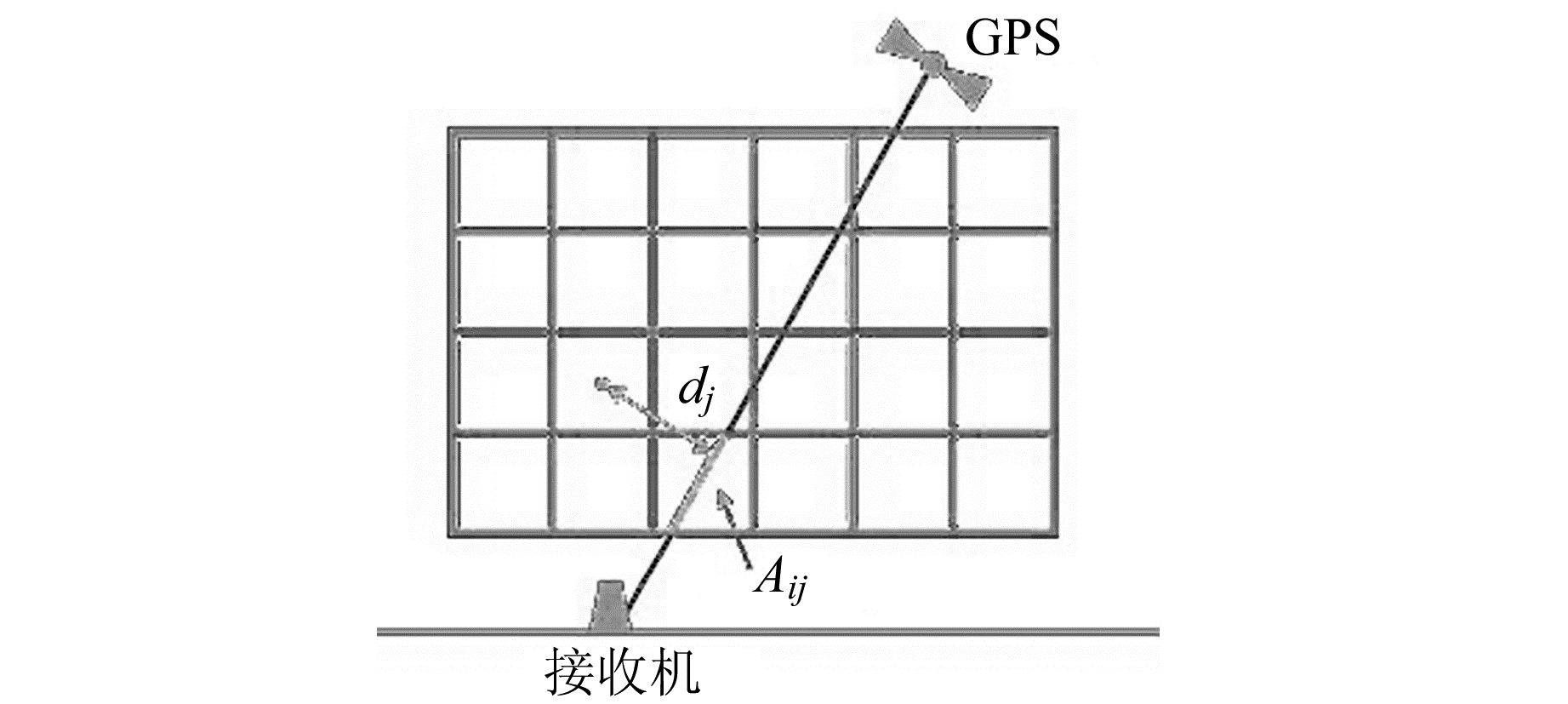
式中,l表示观测射线,在反演中当观测仰角足够大时将观测射线假设为直线;Ne(s)表示空间某处的电子密度,ds表示GPS卫星到接收机的斜向距离元的长度。为了便于计算和进行重构,通常将电离层按照经纬度划分为均匀网格。图 1为电离层像素模型和观测几何示意图,图中dj表示第j个网格中心到测量射线的距离。
|
图 1 GPS测量层析成像原理示意图 Fig. 1 Principle of GPS-based tomography in pixel model |
将式(1)改写成离散形式:
| $ {\rm{STE}}{{\rm{C}}_i} = \sum\limits_{j = 1}^n {{A_{ij}}{x_j} + {e_i}, i = 1, 2, ..., m} $ | (2) |
式中,xj表示第j个网格的电子密度。写成矩阵形式为:
| $ {\mathit{\boldsymbol{y}}_{m \times 1}} = {\mathit{\boldsymbol{A}}_{m \times n}}{\mathit{\boldsymbol{x}}_{n \times 1}} + {\mathit{\boldsymbol{e}}_{m \times 1}} $ | (3) |
式中,y表示m次测量得到的STEC排列成的列向量,xn×1表示将n个三维空间网格按照特定顺序展开成的列向量,Aij表示第i次测量在第j个网格上的截距长度。通常,由于地面接收机数量、卫星轨道以及观测仰角的限制,可利用的观测量很少,因此需要对上式病态方程进行优化求解。
Pryse等[12]提出代数重构(ART)算法:
| $ x_j^{k + 1} = x_j^k + {\lambda _k}\frac{{{y_i} - \sum\limits_{j = 1}^n {{A_{ij}}x_j^k} }}{{{{\left\| {{A_i}} \right\|}^2}}}{A_i} $ | (4) |
式中,i=kmodm+1,k为迭代次数,每m次迭代称为一轮迭代, Ai表示截距矩阵的第i行。1990年,Raymund等[14]改进ART得到新算法——MART算法并运用于电离层层析中。乘法代数重构迭代式如下:
| $ x_j^{k + 1} = x_j^k{\left( {{y_i}/\sum\limits_{j = 1}^n {{A_{ij}}x_j^k} } \right)^{\frac{{{\lambda _k}{A_{ij}}}}{{{\rm{max}}{A_{ij}}}}}} $ | (5) |
本文提出附加尺度因子的代数重构算法(Scaling-ART)。在每次迭代完成之前计算每个网格对应的尺度因子,距离观测射线越远的网格受到尺度缩放的影响越小,通过迭代计算尺度因子、不断修正电子密度值,使其逼近真值,得到更为准确的反演结果。具体表达式如下:
| $ x_j^{k + 1} = \left\{ \begin{array}{l} {s_{ij}}^kx_j^k, {A_{ij}} = 0\\ x_j^k + {\lambda _k}\frac{{{y_i} - \sum\limits_{j = 1}^n {{A_{ij}}x_j^k} }}{{{{\left\| {{A_i}} \right\|}^2}}}{A_i}, {A_{ij}} \ne 0 \end{array} \right. $ | (6) |
假设第k次迭代时电子密度反演值为xk,通过对应的截距向量Ai 得到观测射线上的基本尺度因子值si0k,形如MART算法中的底数部分:
| $ s_{i0}^k = \frac{{{y_i}}}{{\sum\limits_{j = 1}^n {{A_{ij}}x_j^k} }} $ | (7) |
将此尺度作为尺度基准,未被信号穿过的网格的尺度因子通过计算网格中心与该观测射线的距离确定:
| $ s_{ij}^k = f({d_{ij}}) $ | (8) |
式中,sijk表示第k次迭代时j号网格对应第i条观测射线的尺度因子,dij表示第j号网格到观测射线的距离,f(dij)表示dij的单调函数。将[mindj, maxdj]映射到[si0, 1], si0<1或[1, si0], si0>1范围内,对于未被观测射线穿过的网格,尺度因子若为1表示本次迭代不发生变化,从而有效防止STEC测量误差在整个反演区域的传播。本文所用的单调函数如下:
| $ f({d_{ij}}) = {\rm{exp}}(a{d_{ij}} + b) $ | (9) |
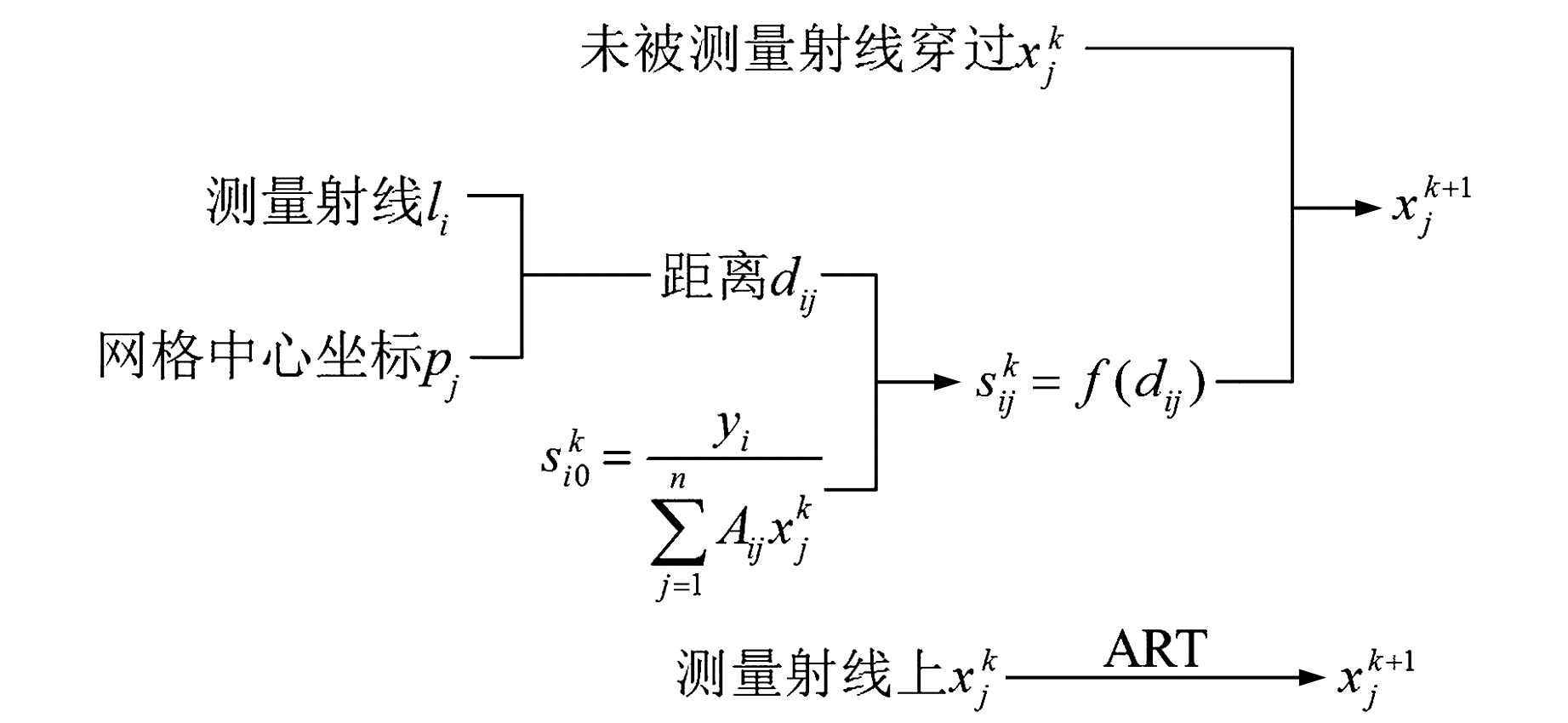
在迭代时,根据上述映射区间和网格中心到观测射线的距离得到一组参数ak和bk,之后即可计算出所有网格的尺度因子。算法流程见图 2。
|
图 2 Scaling-ART算法流程 Fig. 2 Flowchart of Scaling-ART algorithm |
为了分析本文算法在电离层电子密度反演中的重构精度,进行模拟实验和真实数据验证。两个实验选取的区域为95°~120°E、27°~42°N,反演高度为100~1 000 km。进行网格划分时,经度和纬度向间隔分别为1°,高度间隔为50 km。
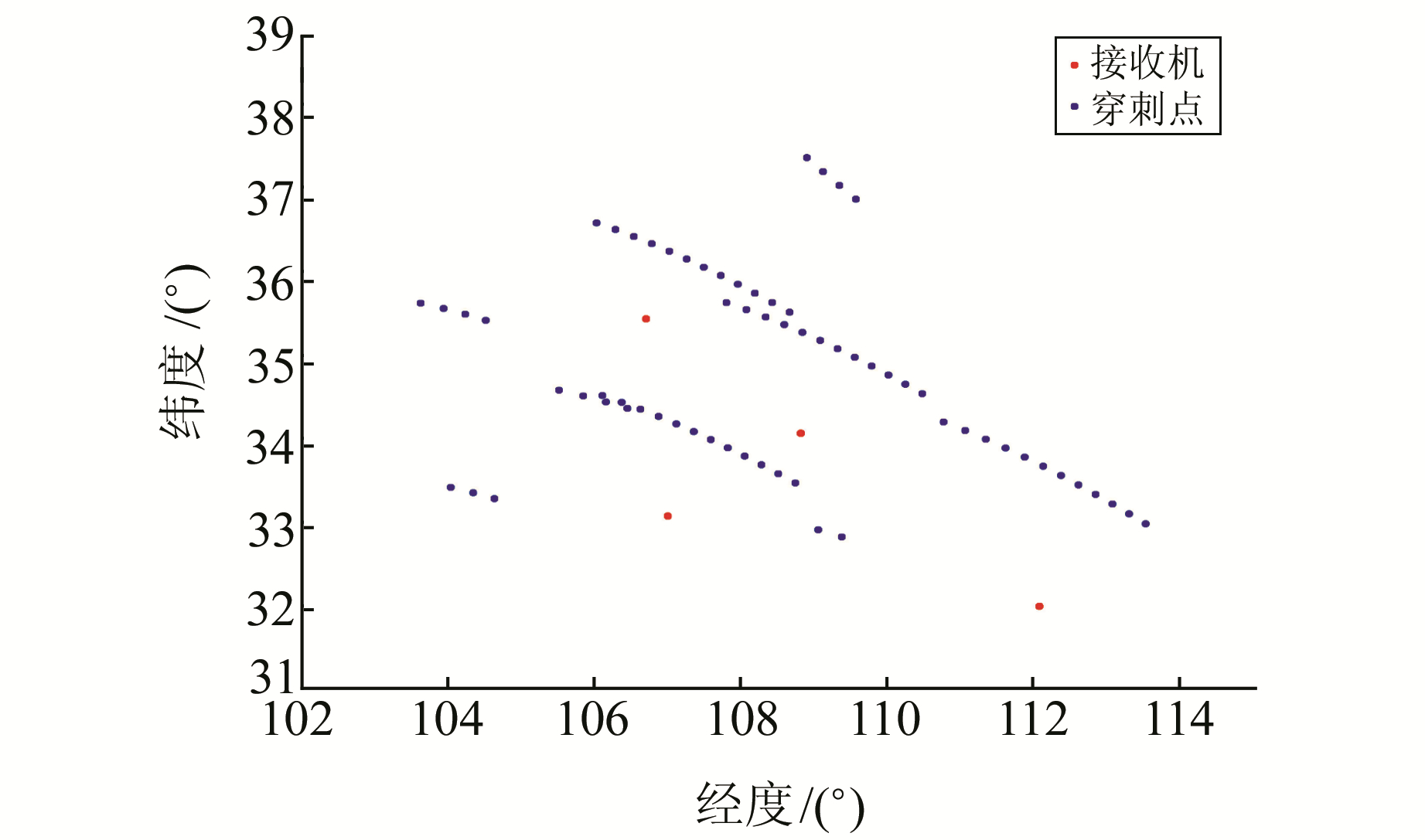
3.1 数值模拟实验在模拟实验中将IRI模型值作为电子密度“真值”进行实验。选取若干接收机和GPS卫星坐标进行截距矩阵的计算,此过程中需要避免截止高度角过大,以保证测量射线能够被假设为直线。接收机和电离层顶部穿刺点分布如图 3。
|
图 3 接收机以及穿刺点坐标 Fig. 3 Position of receiver and ionospheric pierce points |
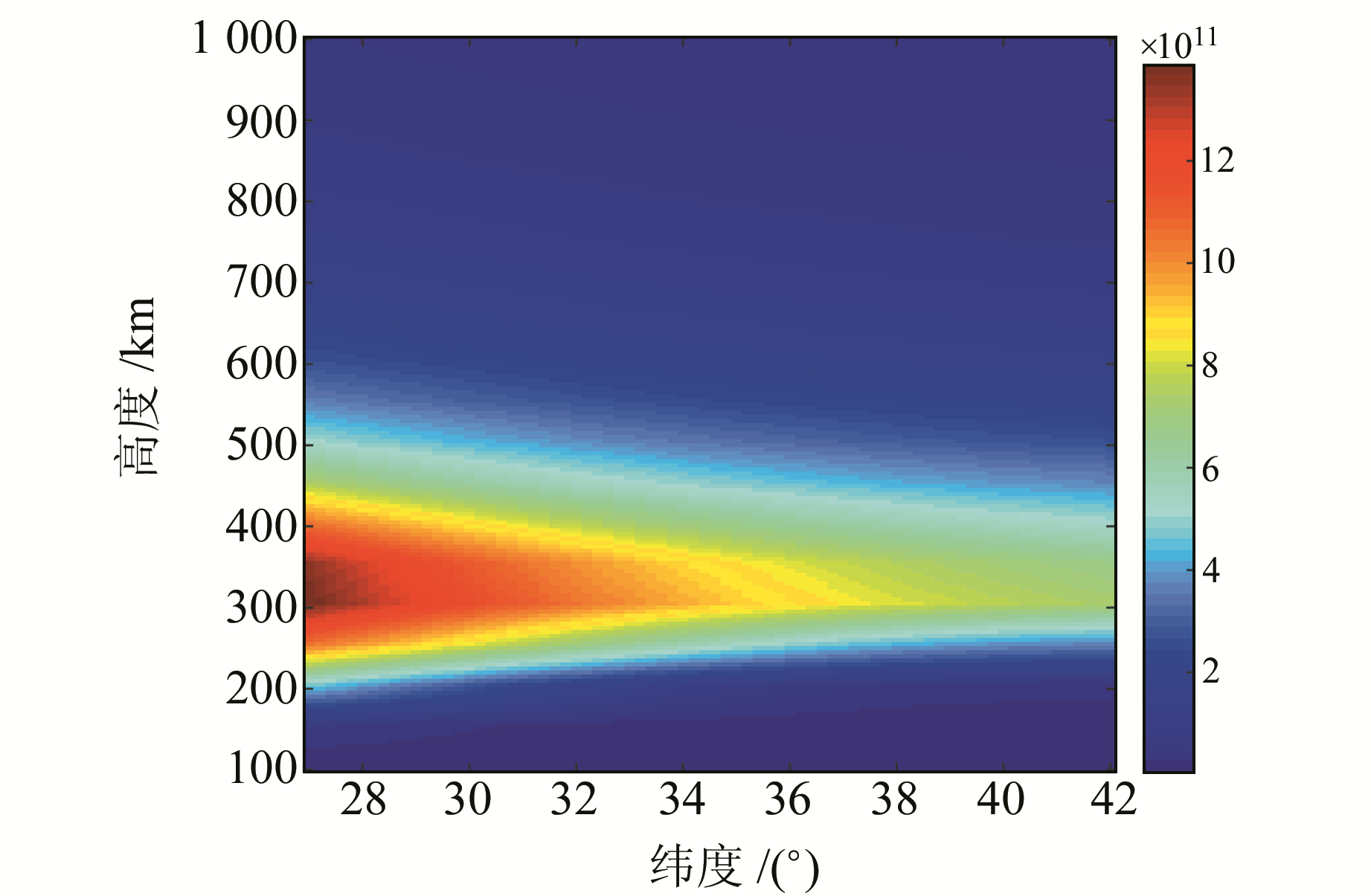
STEC通过“真值”数据和截距矩阵得到。考虑到STEC测量时存在误差,生成STEC时加入一定量的随机噪声,噪声在[-10%, 10%]内均匀分布。图 4是IRI模型在100°E子午面的电子密度分布情况,电子密度峰值在300~350 km高度,随纬度增加电子密度呈现减小的趋势。
|
图 4 IRI模型电子密度剖面分布 Fig. 4 IED image of IRI model |
尺度因子空间分布状况如图 5,红色线段表示观测射线,观测射线穿过的电离层底部和顶部两个网格对应的高度、纬度和经度分别为6 470 km、26°N、112°E及7 370 km、30°N、118°E。不同颜色的点表示对应位置网格的尺度因子,距离观测射线越远的网格其尺度因子呈现蓝色,其值越接近于1;距离越近的尺度因子在图中呈现黄色。根据上述公式,尺度因子为1,意味着此次迭代完成时该网格的电子密度值不会发生变化。

|
图 5 尺度因子空间分布 Fig. 5 Image of spatial distribution of scaling factor |
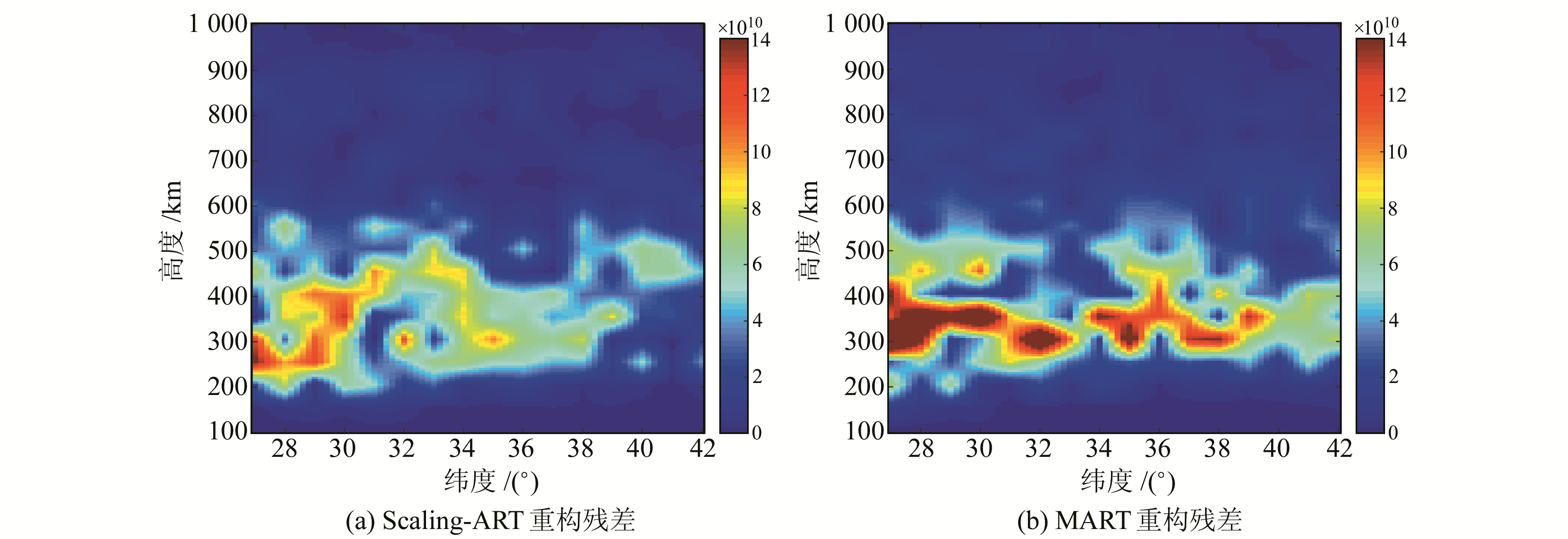
图 6所示的是在98°E处的子午面反演得到的绝对残差图,残差定义为真值与反演结果的差值。图 6(a)表示使用本文Scaling-ART方法进行反演的残差绝对值,图 6(b)表示利用MART算法进行电子密度重构得到的残差绝对值。图中显示,27°~34°N范围内,图 6(b)比图 6(a)红色区域更大,即表明使用MART反演得到的残差比Scaling-ART的残差更大,说明Scaling-ART算法所得结果优于MART算法。根据所选取的接收机位置和GPS测量时的坐标,由于电离层穿刺点主要集中在34°~36°N附近,而穿刺点一般在电子密度最大的高层,因此在此范围内反演的效果相对较好,在残差图中表现为该区域主要呈浅色;而此图中穿刺点分布很少的低纬度地区会存在较大误差,呈现偏红的状态,最大误差接近1.4×1010 el/m3。
|
图 6 2种算法同一经度反演残差对比 Fig. 6 Comparison of IED residual by MART and Scaling-ART vertical across along longitude |
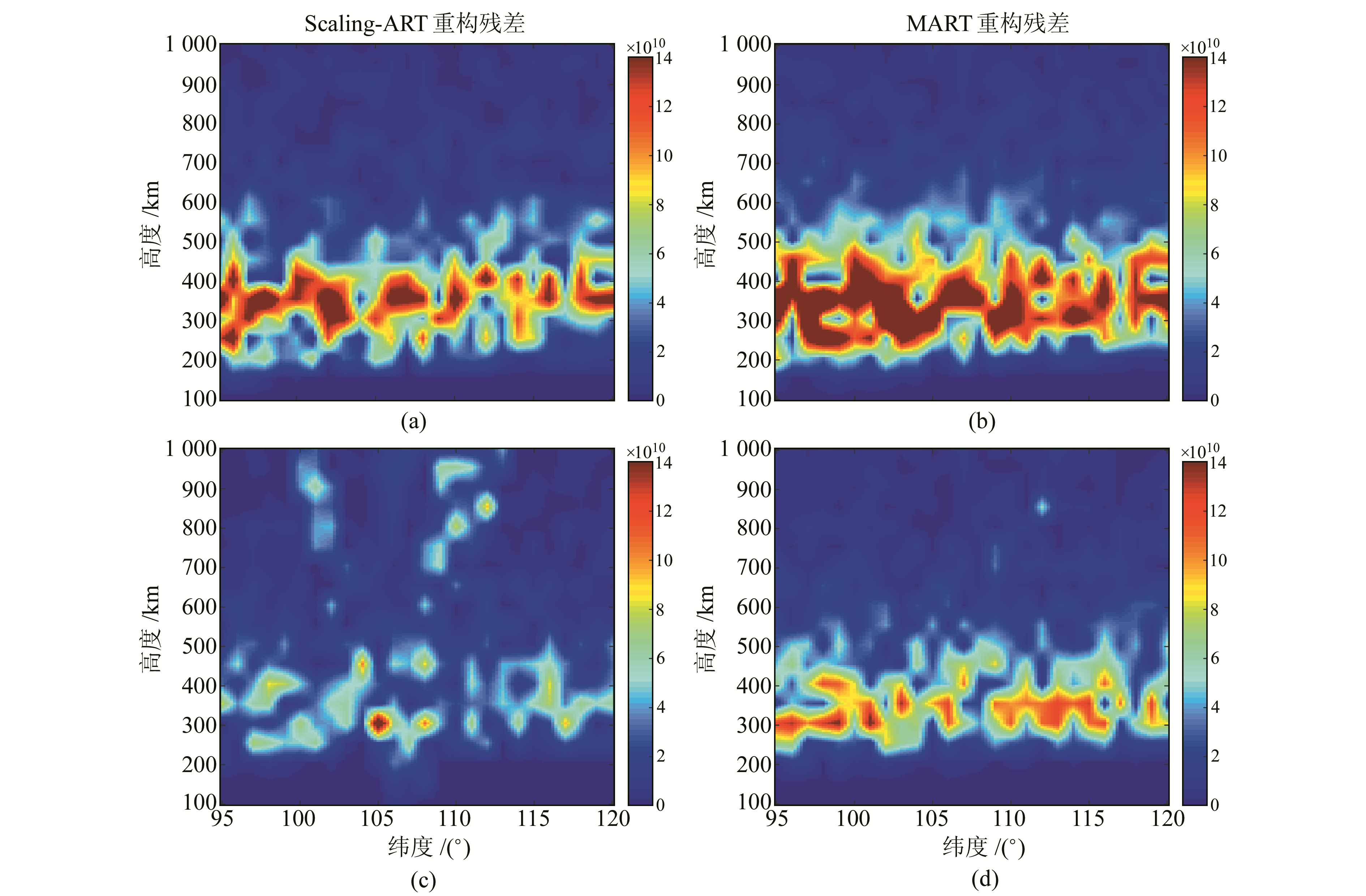
图 7分别是在27°N和36°N两个纬度面上的反演结果,其中图 7(a)、图 7(b)和图 7(c)、图 7(d)分别表示在27°N和36°N纬度面用Scaling-ART算法和MART算法得到的残差。可以看出,在同一纬度下,使用两种算法得到的残差最大值为1.4×1010 el/m3。使用Scaling-ART算法得到的残差红色区域面积更小,表示残差更小,反演效果优于MART算法。从图 7(a)与图 7(c)对比来看,27°N处的反演残差明显大于36°N处,与图 6结论一致,在测量信号分布较少的空间内,反演精度相对较低。
|
图 7 2种算法不同纬度反演残差比较 Fig. 7 Comparison of IED residual by MART and Scaling-ART vertical across along different latitude |
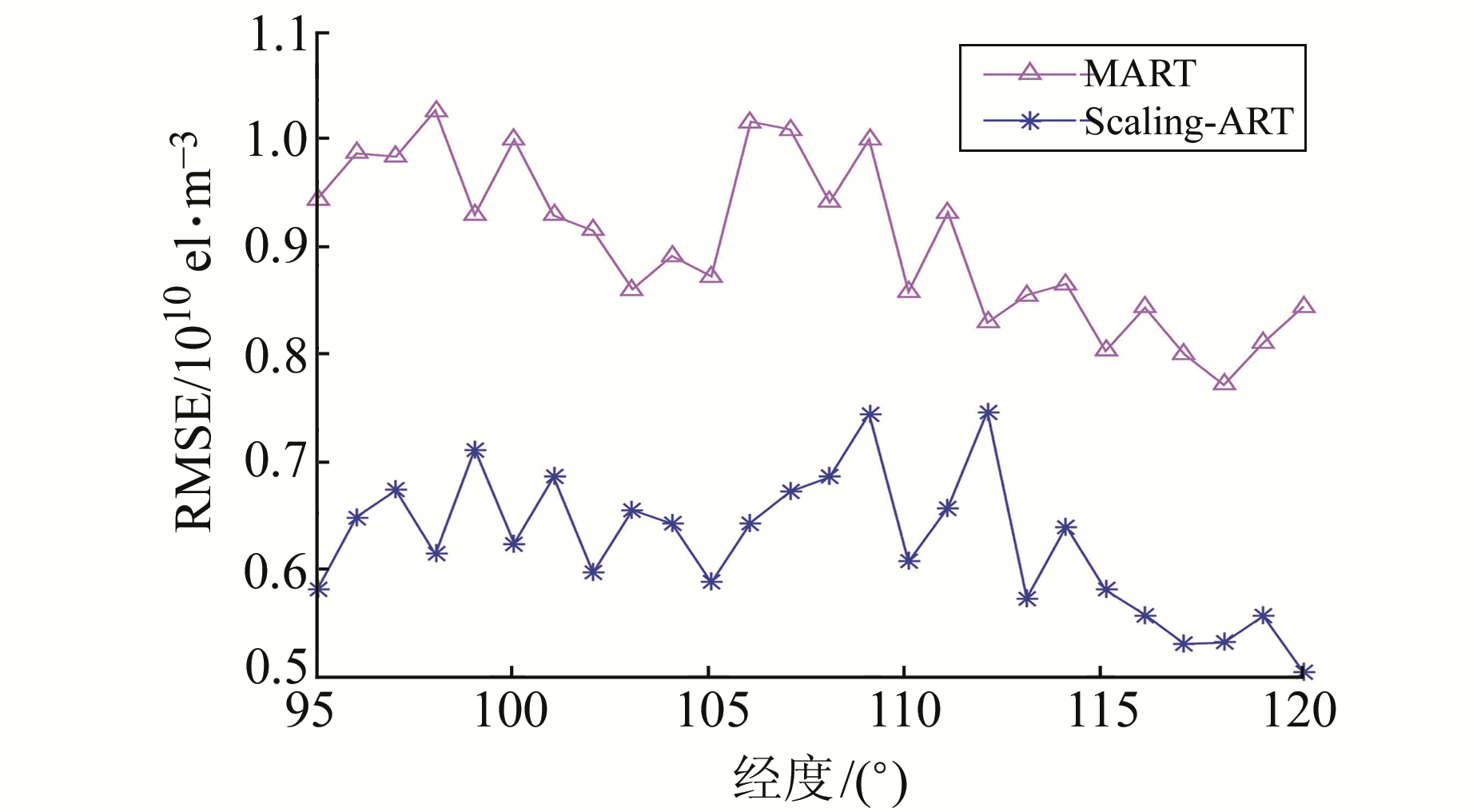
图 8表示反演区域内各经度分别用上述两种算法反演得到的电子密度与真值之间的均方根误差。误差定义如下:
| $ {\rm{RMSE}} = \sqrt {\frac{{\sum\limits_{j = 1}^n {({x_{r, j}} - {x_{e, j}})} }}{n}} $ | (10) |
|
图 8 各个经度反演RMSE Fig. 8 RMSE of IED at various longitude |
式中,xr表示电子密度真值,在本实验中为IRI模型值; xe表示使用重构方法得到的电子密度重构值(或称为估计值)。
可以看出,在反演区域的各个经度上,本文Scaling-ART算法反演得到的电子密度均方根误差相比于MART算法更小,说明改进算法的有效性和优越性。图中所示的均方根误差对于两种反演算法而言,都有随经度增加而逐渐减小的趋势,主要是实验所选取的观测射线在不同经度上分布不均匀导致。具体而言,在95°~105°E范围内,二者反演结果相差较大,而在110°E附近,反演误差差别较小。从图 3接收机和穿刺点分布来看,95°~105°E范围内穿刺点数量很少,本文算法能够通过尺度因子在整个反演区域的作用使各个网格的电子密度逐渐接近于真值;而在穿刺点分布较为均匀且密集的区域,很多网格都被信号穿过,使用原有MART算法也能达到较好的效果。在GPS获取STEC精度较高、测量射线分布稀疏的情况下,可以考虑利用本算法进行电离层电子密度的重构。
3.2 实测数据验证实验选区与上述模拟实验相同,在118°E、34°N附近共有4台GPS接收机分别位于汉中、平凉、西安、襄阳。实验起始时间为2014-08-25 18:00,选取的时段长度为1 h,采样间隔为30 s,截止高度角为30°。根据GPS卫星坐标和地面布设的接收机经纬度计算出真实截距矩阵,STEC亦通过GPS数据处理得到。实验中在所有符合条件的测量射线中随机选取一部分和其对应的STEC进行电离层电子密度的反演,剩余测量射线和STEC用于验证反演效果。对用于测试的测量射线,计算两种算法重构之后的STEC,求出其与实测STEC的差的绝对值,err=|STECr-STECe|,之后将两种算法得到的STEC绝对误差进行比较:
| $ {\rm{dif}} = {\rm{er}}{{\rm{r}}_{{\rm{MART}}}} - {\rm{er}}{{\rm{r}}_{{\rm{Scaling - ART}}}} $ | (11) |
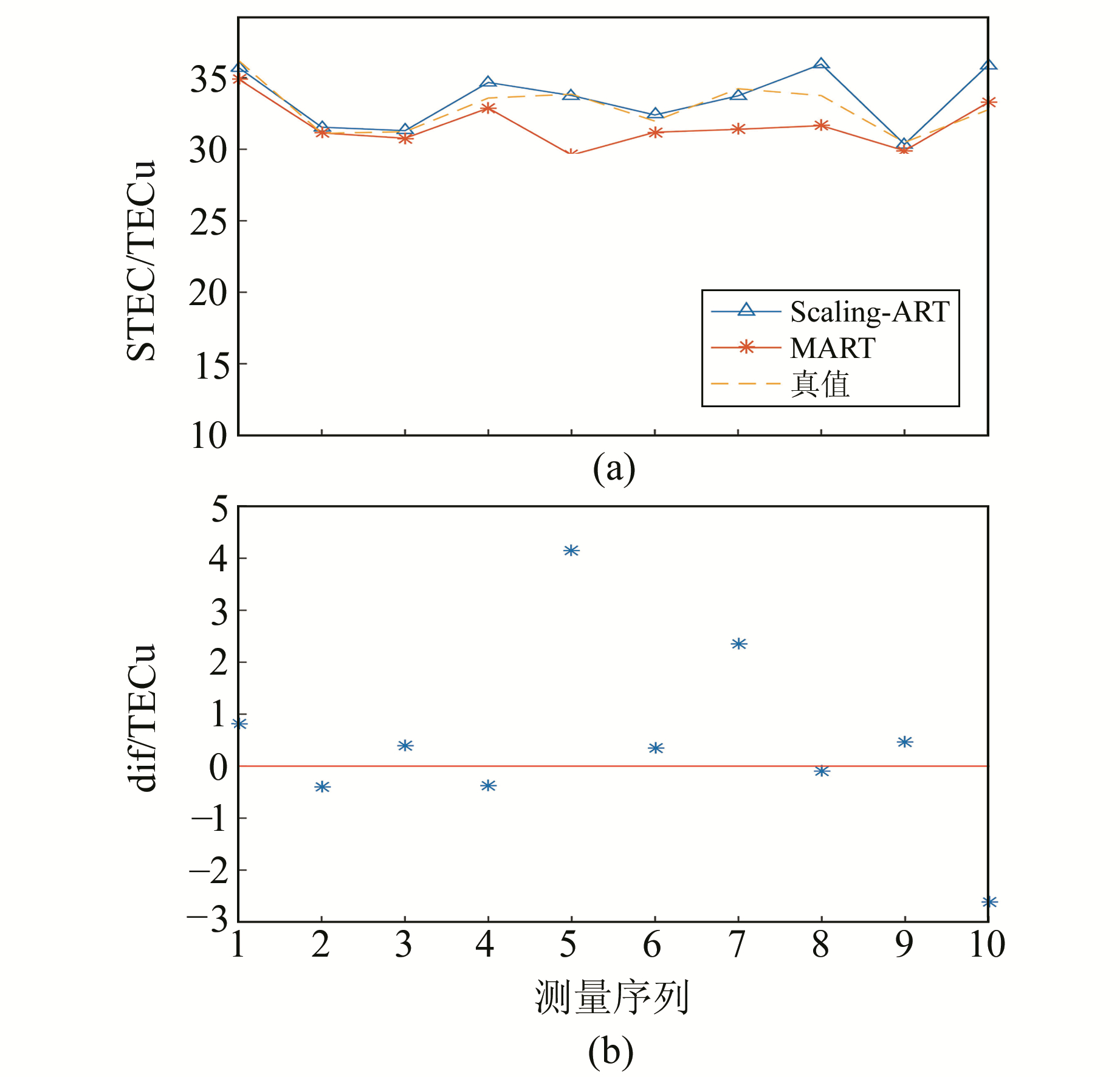
图 9(a)表示两种算法得到的重构STEC与实测STEC的比较,红色星标实线表示使用MART算法的绝对误差,橙色虚线表示真值,蓝色表示本文算法重构得到的STEC。本文算法得到的STEC误差大约在0~3TECu,说明该算法能够达到较好的重构效果。图 9(b)表示式(11)所定义的dif值,dif>0表示使用MART方法的绝对误差更大,反之使用本文算法误差更大,落在红线上的点表示两种算法得到的反演精度相当。从图 9可以看出,在用于验证的10组观测射线中,使用本文算法进行反演之后,多数情况下绝对误差小于原有的MART算法,说明本文改进算法相比原始算法具有优越性。
|
图 9 MART算法与Scaling-ART算法STEC绝对误差比较 Fig. 9 Comparison of absolute STEC error of two algorithms |
本文提出在代数重构中对每个网格加入不同尺度因子的算法。数值模拟实验中,首先计算STEC“实测”值,每次迭代中结合当前电子密度重构值得到STEC重构值,将二者的比例作为测量射线穿过网格的缩放因子;再根据其他网格中心到观测射线的距离计算每个网格对应的尺度因子,通过不断的迭代修正电子密度重构值。本算法解决了原有算法中没有测量射线穿过的网格电子密度重构结果严重依赖于初始化值的问题。在实测数据验证中,使用部分实测STEC作为已知观测值,其余实测STEC用于验证,分别利用两种方法进行电子密度重构。通过比较两种方法在测试集上的STEC绝对误差,证明了本文方法的有效性以及优越性。未来将针对电离层的各向异性进一步考虑尺度因子的选取方案,以达到更好的重构效果。
| [1] |
李亮, 洪峻, 明峰. 电离层对中高轨SAR影响机理研究[J]. 雷达学报, 2017, 6(6): 619-629 (Li Liang, Hong Jun, Ming Feng. Mechanism Study of Ionospheric Effects on Medium-Earth-Orbit SAR[J]. Journal of Radars, 2017, 6(6): 619-629)
(  0) 0) |
| [2] |
聂兆生, 祝芙英, 付宁波, 等. Kalman滤波在地震电离层TEC异常探测中的应用[J]. 大地测量与地球动力学, 2011, 31(3): 47-50 (Nie Zhaosheng, Zhu Fuying, Fu Ningbo. Application of Kalman Filtering in Detecting Ionospheric TEC Anomaly Prior to Earthquake[J]. Jouranl of Geodesy and Geodynamics, 2011, 31(3): 47-50)
(  0) 0) |
| [3] |
姚宜斌, 翟长治, 孔建, 等. 2015年尼泊尔地震的震前电离层异常探测[J]. 测绘学报, 2016, 45(4): 385-395 (Yao Yibin, Zhai Changzhi, Kong Jian, et al. The Pre-Earthquake Ionosphere Anomaly of the 2015 Nepal Earthquake[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 385-395)
(  0) 0) |
| [4] |
Austen J R, Franke S J, Liu C H. Ionospheric Imaging Using Computerized Tomography[J]. Radio Science, 1988, 23(3): 299-307 DOI:10.1029/RS023i003p00299
(  0) 0) |
| [5] |
徐继生, 邹玉华, 马淑英. GPS地面台网和掩星观测结合的时变三维电离层层析[J]. 地球物理学报, 2005, 48(4): 759-767 (Xu Jisheng, Zou Yuhua, Ma Shuying. Time Dependent 3D Computerized Ionospheric Tomography with Ground Based GPS Network and Occultation Observations[J]. Chinese Journal of Geophysics, 2005, 48(4): 759-767 DOI:10.3321/j.issn:0001-5733.2005.04.005)
(  0) 0) |
| [6] |
Garcia R, Crespon F. Radio Tomography of the Ionosphere: Analysis of an Underdetermined, Ill‐Posed Inverse Problem, and Regional Application[J]. Radio Science, 2008, 43(2): 661-668
(  0) 0) |
| [7] |
Lee J K, Kamalabadi F. GPS-Based Radio Tomography With Edge-Preserving Regularization[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(1): 312-324 DOI:10.1109/TGRS.2008.2001637
(  0) 0) |
| [8] |
Yao Y, Chen P, Zhang S, et al. A New Ionospheric Tomography Model Combining Pixel-Based and Function-Based Models[J]. Advances in Space Research, 2013, 52(4): 614-621 DOI:10.1016/j.asr.2013.05.003
(  0) 0) |
| [9] |
Wen D, Zhang X, Tong Y J, et al. GPS-Based Ionospheric Tomography with a Constrained Adaptive Simultaneous Algebraic Reconstruction Technique[J]. Journal of Earth System Science, 2015, 124(2): 283-289 DOI:10.1007/s12040-015-0542-4
(  0) 0) |
| [10] |
Yao Y B, Kong J, Tang J. A New Ionosphere Tomography Algorithm with Two-Grid Virtual Observations Constraints and Three-Dimensional Velocity Profile[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(5): 2 373-2 383 DOI:10.1109/TGRS.2014.2359762
(  0) 0) |
| [11] |
Ghaffari M R, Voosoghi B. Ionosphere Tomography Using Wavelet Neural Network and Particle Swarm Optimization Training Algorithm in Iranian Case Study[J]. GPS Solutions, 2017, 21(3): 1 301-1 314 DOI:10.1007/s10291-017-0614-9
(  0) 0) |
| [12] |
Pryse S, Kersley L, Mitchell C, et al. A Comparison of Reconstruction Techniques Used in Ionospheric Tomography[J]. Radio Science, 1998, 33(6): 1 767-1 779 DOI:10.1029/98RS01613
(  0) 0) |
| [13] |
霍星亮, 袁运斌, 欧吉坤, 等. 顾及电离层变化的层析反演新算法[J]. 地球物理学报, 2016, 59(7): 2 393-2 401 (Huo Xingliang, Yuan Yunbin, Ou Jikun, et al. A New Ionospheric Tomographic Algorithm Taking into Account the Variation of the Ionosphere[J]. Chinese J Geophs, 2016, 59(7): 2 393-2 401)
(  0) 0) |
| [14] |
Raymund T D, Austen J R, Franke S, et al. Application of Computerized Tomography to the Investigation of Ionospheric Structures[J]. Radio Science, 1990, 25(5): 771-789 DOI:10.1029/RS025i005p00771
(  0) 0) |
2. Science and Technology on Microwave Imaging Laboratory, 19 West-Beisihuan Road, Beijing 100190, China;
3. University of Chinese Academy of Sciences, 19 A Yuquan Road, Beijing 100049, China
 2018, Vol. 38
2018, Vol. 38

