基于载波相位的RTK、PPP技术可以获得cm级定位结果[1-2]。然而,GPS信号受到干扰、遮挡等影响时极易导致载波相位发生不连续[3-4],需要RTK、PPP重新固定模糊度,严重影响高精度定位的连续性,尤其是PPP [5-6]。学者们分别从观测值和信号处理层面采用不同的方法应对载波相位周跳的影响。文献[7-8]分别提出相位减伪距与电离层残差组合方法和基于贝叶斯概率统计的周跳探测与修复方法,能对双频系统中小采样间隔数据的周跳作出准确探测并修复,但对于采样间隔大的数据不能准确探测,且在单频系统中无法使用。文献[9]提出基于小波变换的周跳探测方法,并建立基于经验模式分解与径向神经网络的组合预测模型对周跳进行修复,解决了单频载波相位数据1周以上周跳的准确探测和修复,但对于更小的周跳则无能为力。Peng等[10]提出在卫星信号遭遇短暂失锁时利用载波相位预测来保证载波相位连续性,能实现在卫星失锁的5~8 s内,失锁通道仍保持对载波相位的开环跟踪,使载波相位误差不至于影响周整模糊度的固定。然而,该方法仅基于卫星与接收机的动态来预测多普勒,没有充分考虑接收机晶振钟漂对多普勒的影响。
相位预测方法可从根源上解决卫星失锁对载波相位连续性的影响,如果进一步延长载波相位预测时间,对复杂环境下的GPS精密定位具有重要意义。针对现有相位预测方法存在的不足,本文重点对晶振钟漂引起的多普勒作更为精确的预测,并基于软件接收机平台测试改进后的相位预测性能。
1 载波相位预测方法 1.1 载波相位预测原理GPS接收机对观测量信息的获取完全依赖于跟踪环对卫星信号的紧密跟踪,当卫星信号受到一段时间的环境遮挡时,锁相环经历失锁和重捕后,输出的载波相位在失锁前后不再连续,精密定位需要重新固定周整模糊度。真实环境中GPS信号短时间(10 s以内)遮挡最为频繁,因此可以在信号遮挡时对通道卫星的多普勒进行估计,并由式(1)对多普勒积分得到载波相位预测值:
| $ {\varphi _{k + 1}} = {\varphi _k} + \int_{{t_k}}^{{t_{k + 1}}} f {\rm{d}}t + \Delta \varphi $ | (1) |
式中,φk+1、φk分别为历元k和k+1对应的载波相位,f为通道卫星的预测多普勒,Δφ为载波相位的估计误差。
多普勒测量值主要由4部分组成[11]:1)卫星与接收机之间的相对运动;2)卫星和接收机的晶振钟漂;3)传播路径延迟变化率;4)噪声。传播路径延迟变化率和噪声引起的多普勒误差在载波相位预测时引起的误差较小且很难预测,可以忽略。因此,估计多普勒的表达式为:
| $ {f_d} = \frac{{({v^i} - v)({p^i} - p)}}{{\lambda \left\| {{p^i} - p} \right\|}} + \frac{{cd}}{\lambda } $ | (2) |
式中,p、v分别为接收机的位置(m)和速度(m/s); pi、vi分别为第i颗卫星的位置(m)和速度(m/s); λ为卫星信号载波波长(m); d为晶振钟漂(s/s); c为光速(m/s)。
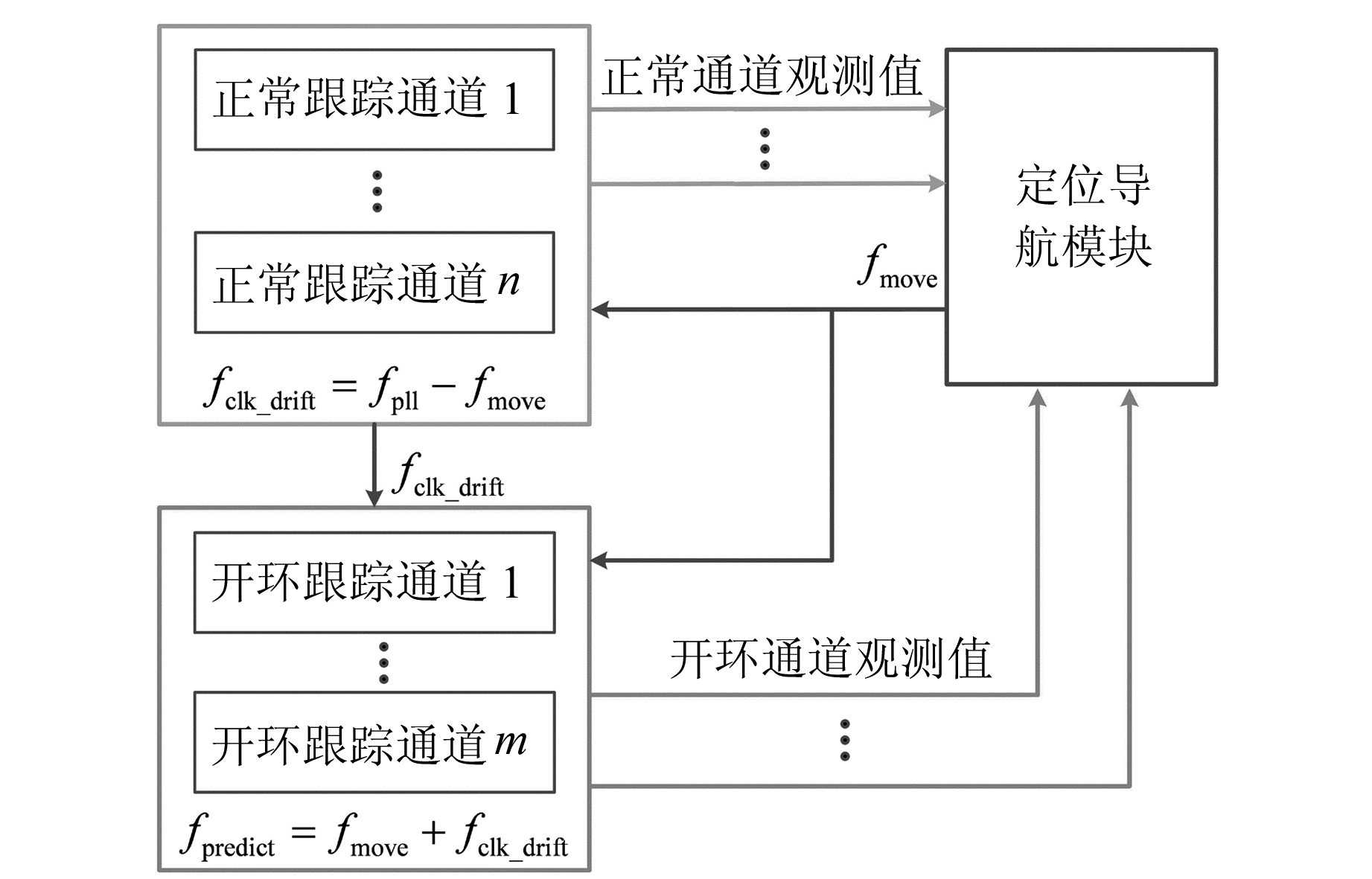
载波相位预测原理如图 1所示。根据接收机和卫星的位置速度信息计算相对运动引起的多普勒fmove。在无外部辅助时,需要至少4颗可见卫星计算接收机位置和速度。晶振钟漂引起的多普勒由卫星和接收机的晶振钟漂两部分组成。卫星晶振钟漂很小,短时间内可以忽略。由于接收机的晶振钟漂对每个卫星信号通道的多普勒影响理论上是一致的,可以从正常跟踪的信号通道中分离出晶振钟漂引起的多普勒fclk_drift,进而辅助到需要进行开环跟踪的信号通道。图中,fpll表示由各载波环通道得到的多普勒测量值,fpredict表示开环跟踪通道得到的多普勒预测值。在卫星短暂失锁期间,开环跟踪通道将使用fpredict更新载波环的NCO,从而输出连续的载波相位观测值。
|
图 1 相位预测原理示意图 Fig. 1 Schematic diagram of phase prediction principle |
为了得到开环跟踪通道的多普勒预测值,需要精确求解fmove和fclk_drift。fmove由接收机运动导致的多普勒fuser_move和卫星运动引起的多普勒fsat_move两部分组成,可表示为:
| $ {f_{{\rm{move}}}} = {f_{{\rm{sat\_move}}}} + {f_{{\rm{user\_move}}}} $ | (3) |
接收机计算卫星和用户的位置和速度的更新率通常为1 Hz,而基带载波环的更新率一般较高,因此将fmove反馈到载波环时需要考虑更新速率匹配的问题。由于卫星与用户的距离非常远,则1 s内卫星与接收机的视线角度变化可以忽略不计,因此主要是要得到高速率的卫星和接收机的速度。通过提高接收机测速更新率或者外部辅助(例如惯导)来得到高速率的fuser_move,而高速率的fsat_move可以对整秒的卫星运动多普勒进行等加速度外推得到:
| $ {f_{{\rm{sat\_move}}}} = {f_{{\rm{sat\_move1}}}} + \Delta {f_{{\rm{sat\_move}}}}/{R_{{\rm{loop\_update}}}} $ | (4) |
式中, fsat_move1为整秒时更新的卫星运动多普勒频率,Δfsat_move为1 s内前后两次历元卫星运动多普勒的变化量,Rloop_update为环路的更新率。
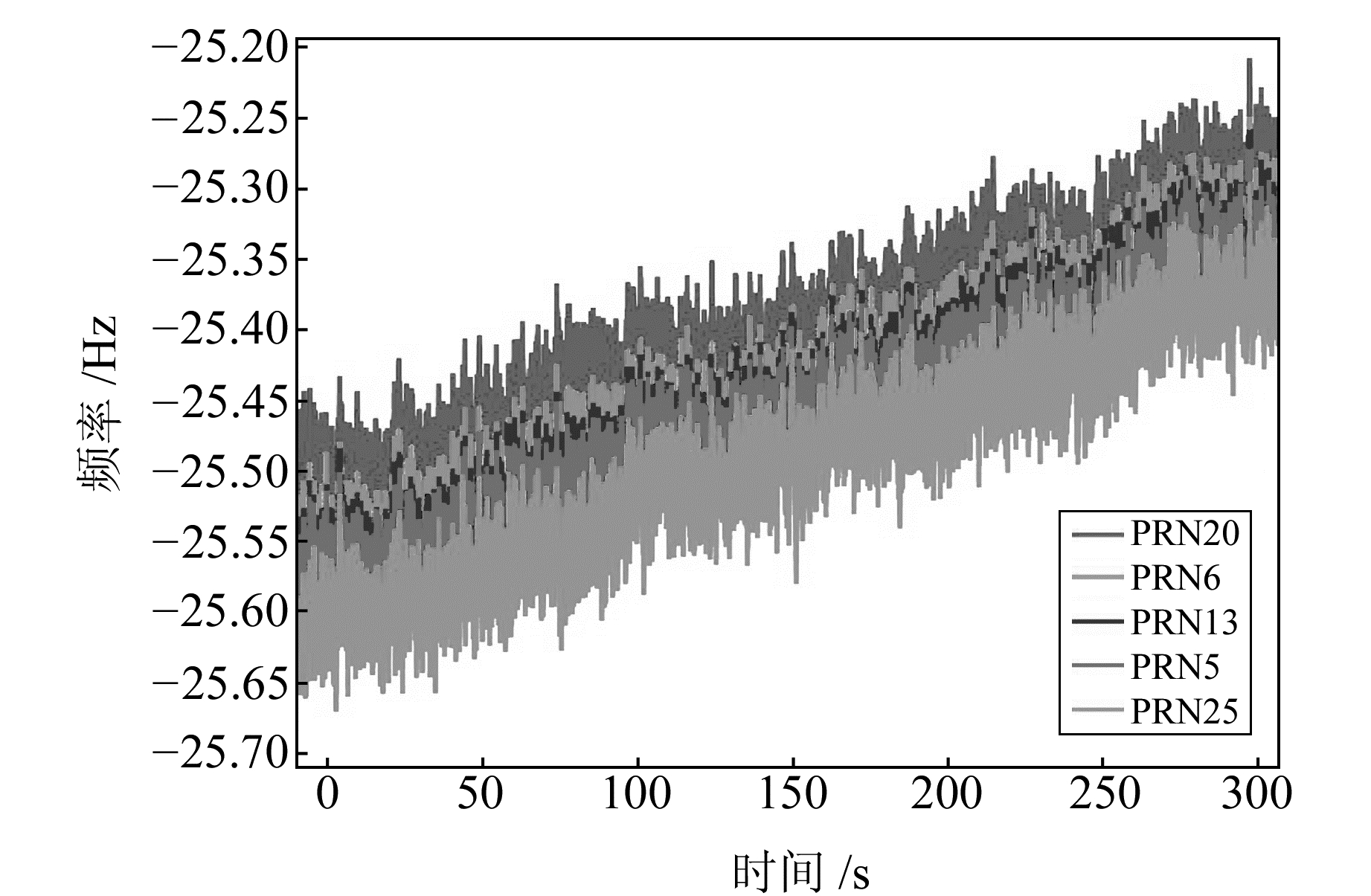
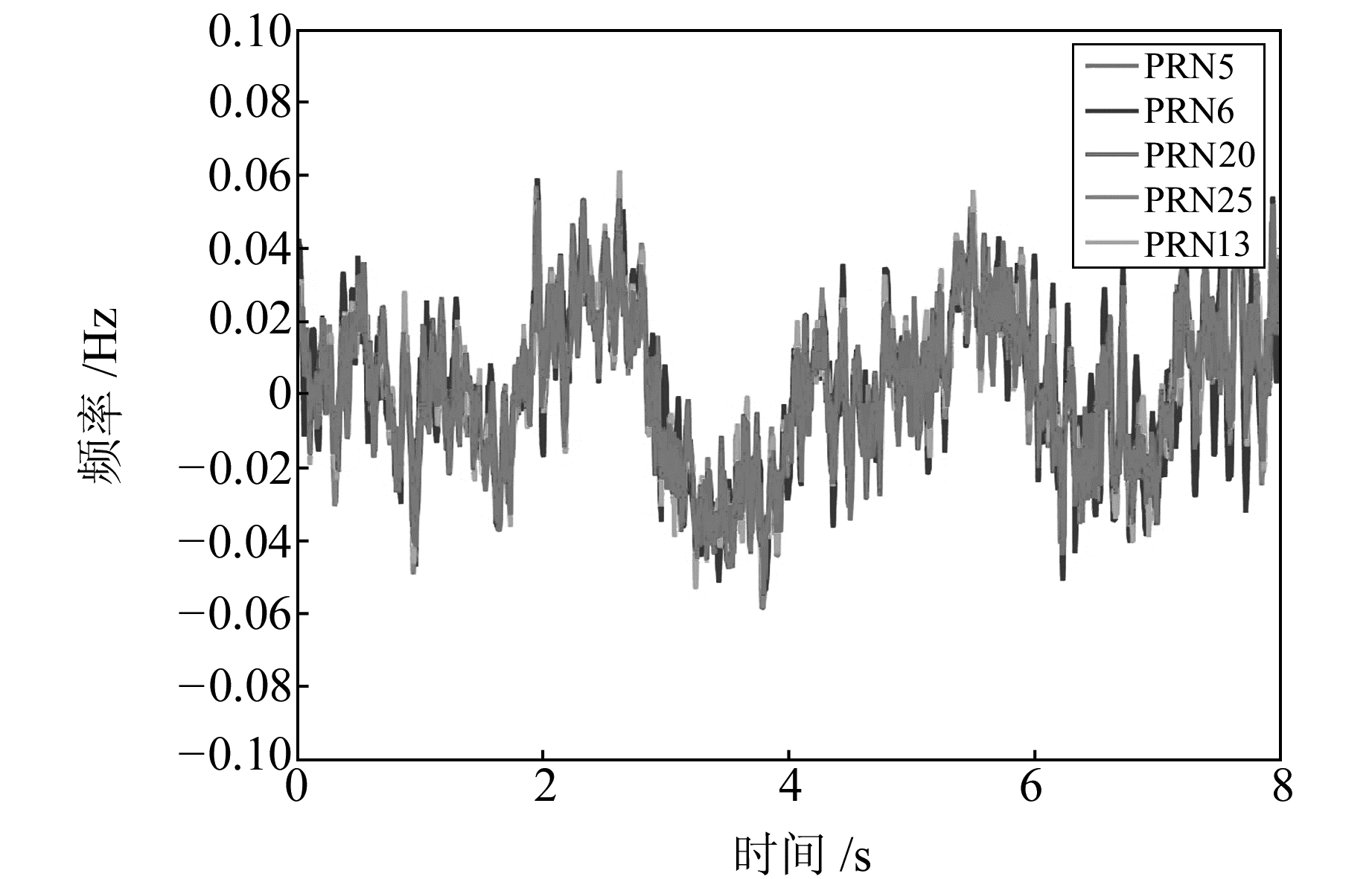
跟踪环多普勒测量值fpll减去fmove可以得到各可见卫星通道估计的晶振钟漂引起的多普勒fclk_drift,如图 2。一个通道fclk_drift与其他通道作差可以得到通道间晶振钟漂估计的差异,如图 3。各通道的fclk_drift估计差异在±0.1 Hz左右,这种差异性一方面是由各卫星的运动速度计算误差引起,另一方面是各卫星信号在不同的传播路径上受到电离层和对流层影响导致。将这种存在通道间差异性的fclk_drift直接辅助到开环跟踪通道,将导致载波相位误差在短时间内快速发散,因此需要对各通道的fclk_drift作进一步处理。
|
图 2 各通道fclk_drift随时间变化 Fig. 2 fclk_drift of each channel changes with time |

|
图 3 各通道间晶振引起的多普勒差异 Fig. 3 Doppler difference caused by crystal oscillator between channels |
从图 2可见,虽然各通道的fclk_drift在直流偏置上具有一定差异,但在随时间变化的波动趋势上具有很强的一致性。为此,可以从各通道的原始fclk_drift中分离出变化缓慢的偏置项和快速变化的抖动项,分别记为fclk_bias和fclk_jitter。其中fclk_bias是对原始fclk_drift进行200个历元(历元间隔为10 ms)滑动平均得到,则:
| $ {f_{{\rm{clk\_jitter}}}} = {f_{{\rm{clk\_drift}}}} - {f_{{\rm{clk\_bias}}}} $ | (5) |
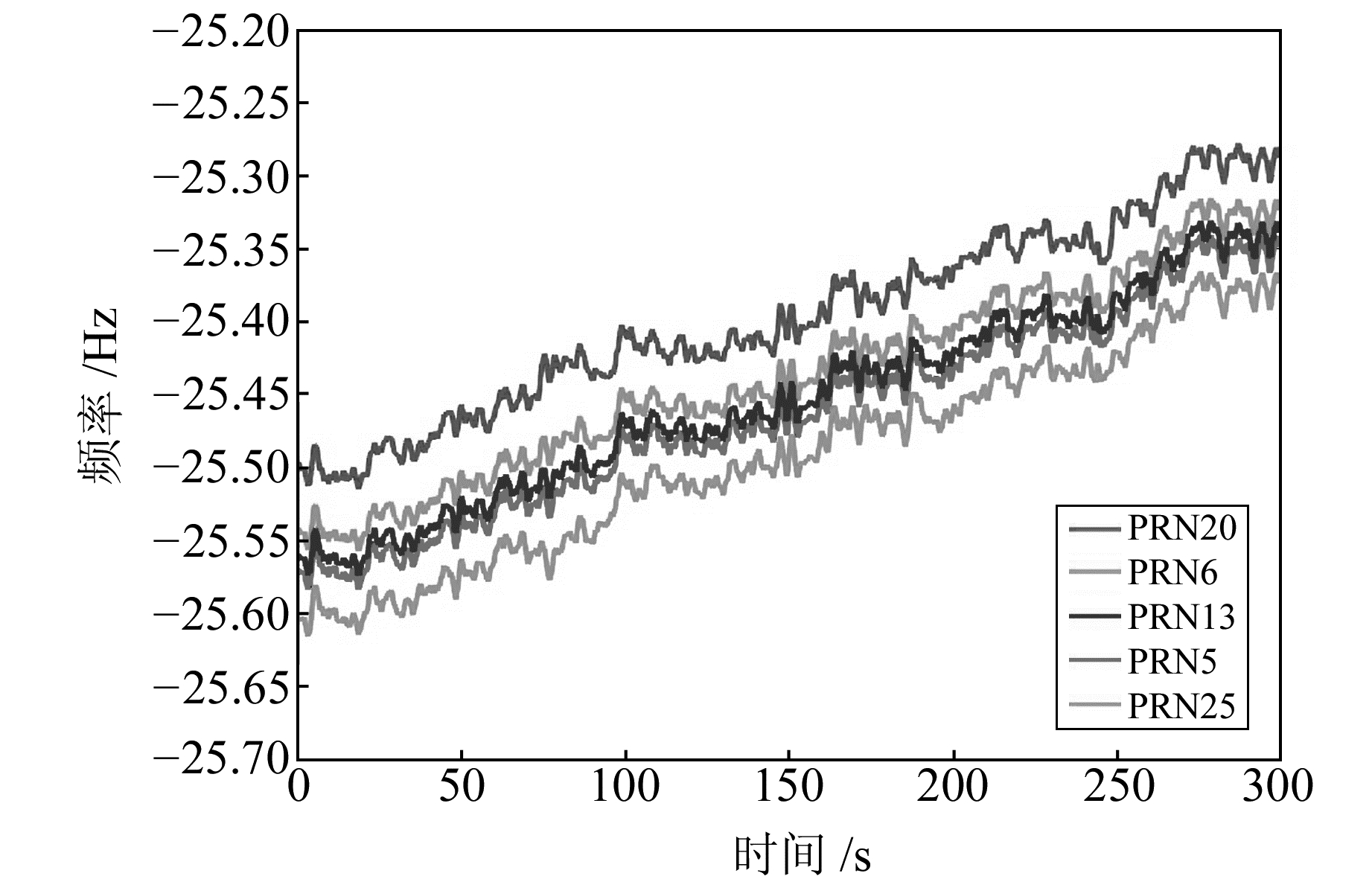
如图 4和图 5所示,各通道fclk_bias具有较大差异性,但变化较为平缓;而各通道fclk_jitter具有极好的变化一致性,但变化快速且无规律。基于两者的这些特性,开环跟踪通道在对fclk_drift进行开环估计时,fclk_bias部分可以使用通道开环之前保存的结果,记为fclk_bias_init,而fclk_jitter部分由其余正常跟踪通道取平均值进行实时辅助,记为
| $ {f_{{\rm{clk\_drift}}}} = {f_{{\rm{clk\_bias\_init}}}} + \Delta {\overline f _{{\rm{clk\_bias}}}} + {\overline f _{{\rm{clk\_jitter}}}} $ | (6) |
|
图 4 各通道钟漂估计多普勒的偏置项 Fig. 4 Bias term of each channel's Doppler estimated by clock drift |
|
图 5 各通道钟漂估计多普勒的抖动项 Fig. 5 Jitter term of each channel's Doppler estimated by clock drift |
采用Spirent记录回放仪GSS6425采集实验室楼顶静态天线GPS L1频点数据,然后在软件接收机平台验证相位预测方法。为了验证GPS信号失锁时相位预测效果,人为设定卫星通道的开环。一方面,采用人为设定卫星通道开环方式,可以以输入信号的真实相位为参考评估开环预测载波相位的误差。人为设定开环方式时,卫星信号仍然可以进入跟踪环,并与本地NCO输出信号一起送入鉴相器,检测NCO输出信号的相位误差,但不会用相位误差反馈修正NCO。另一方面,采用人为设定卫星通道开环可以方便灵活地设定开环的卫星通道、开环的时刻、每次开环的时长、开环的次数,为定量验证相位预测精度随时间发散程度创造了条件,也便于增加样本数量、减小实验结果的随机影响。载波相位误差不超过1/4周时,不需要对整周模糊度进行重新固定[12],因此,1/4周误差被作为评估载波相位误差发散水平的重要指标。在测试中,对全程能正常跟踪的6颗卫星中的其中1颗进行开环测试,其余5颗用于开环通道的相位预测,测试通道在开环与闭环之间循环切换,共设置了100个开环过程。
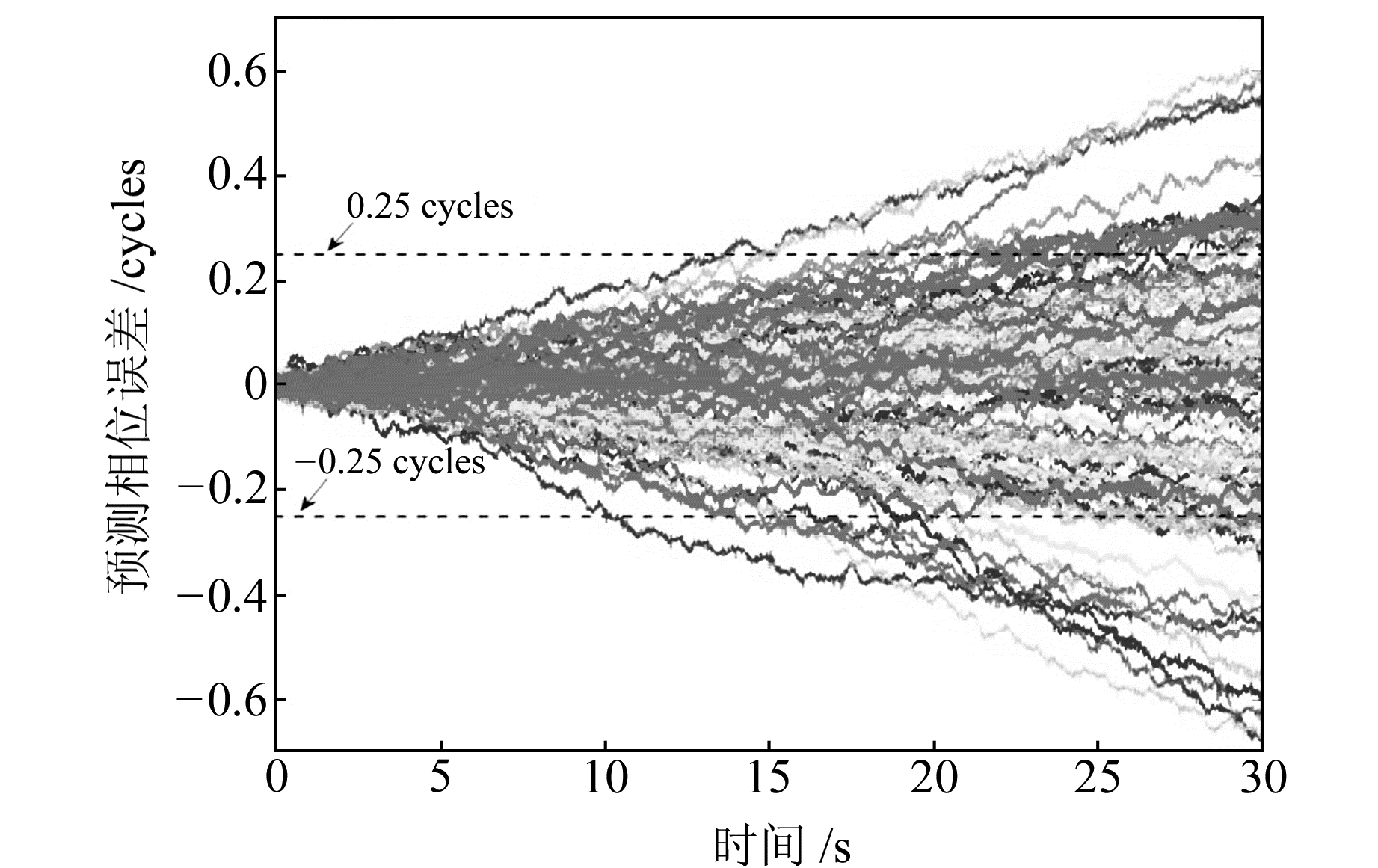
图 6给出开环测试通道在每次开环过程载波相位误差随开环时间的变化情况。可以看出,在开环跟踪过程中,载波相位误差随时间发散,发散的速度取决于相位预测的精确度。结果表明,多数开环过程都能在15 s内保证相位误差不超过1/4周,这对于部分卫星遮挡情形下,接收机在环路失锁过程中保持载波相位连续具有重要意义。
|
图 6 载波相位误差随时间发散 Fig. 6 Carrier phase error diverges with time |
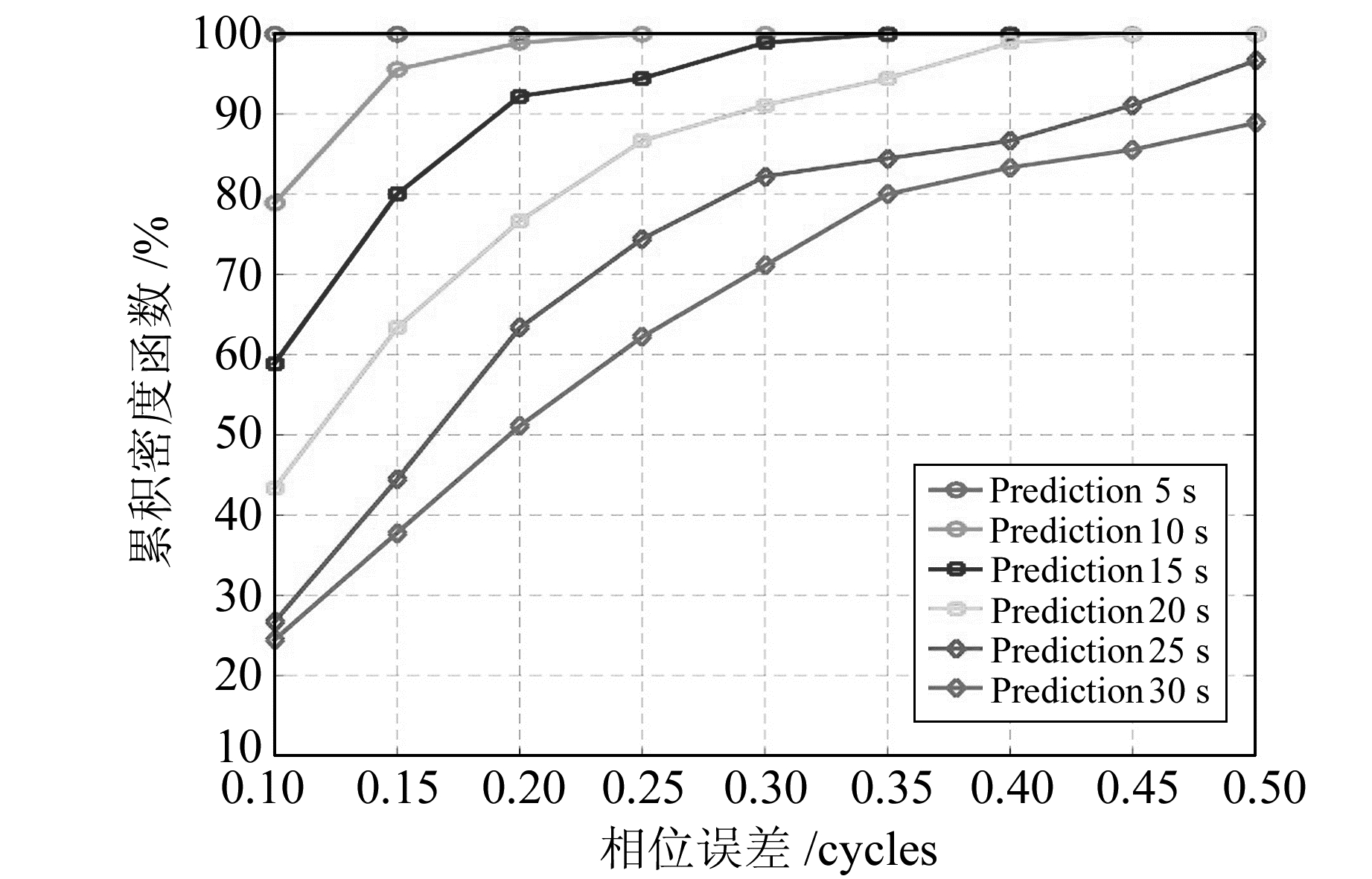
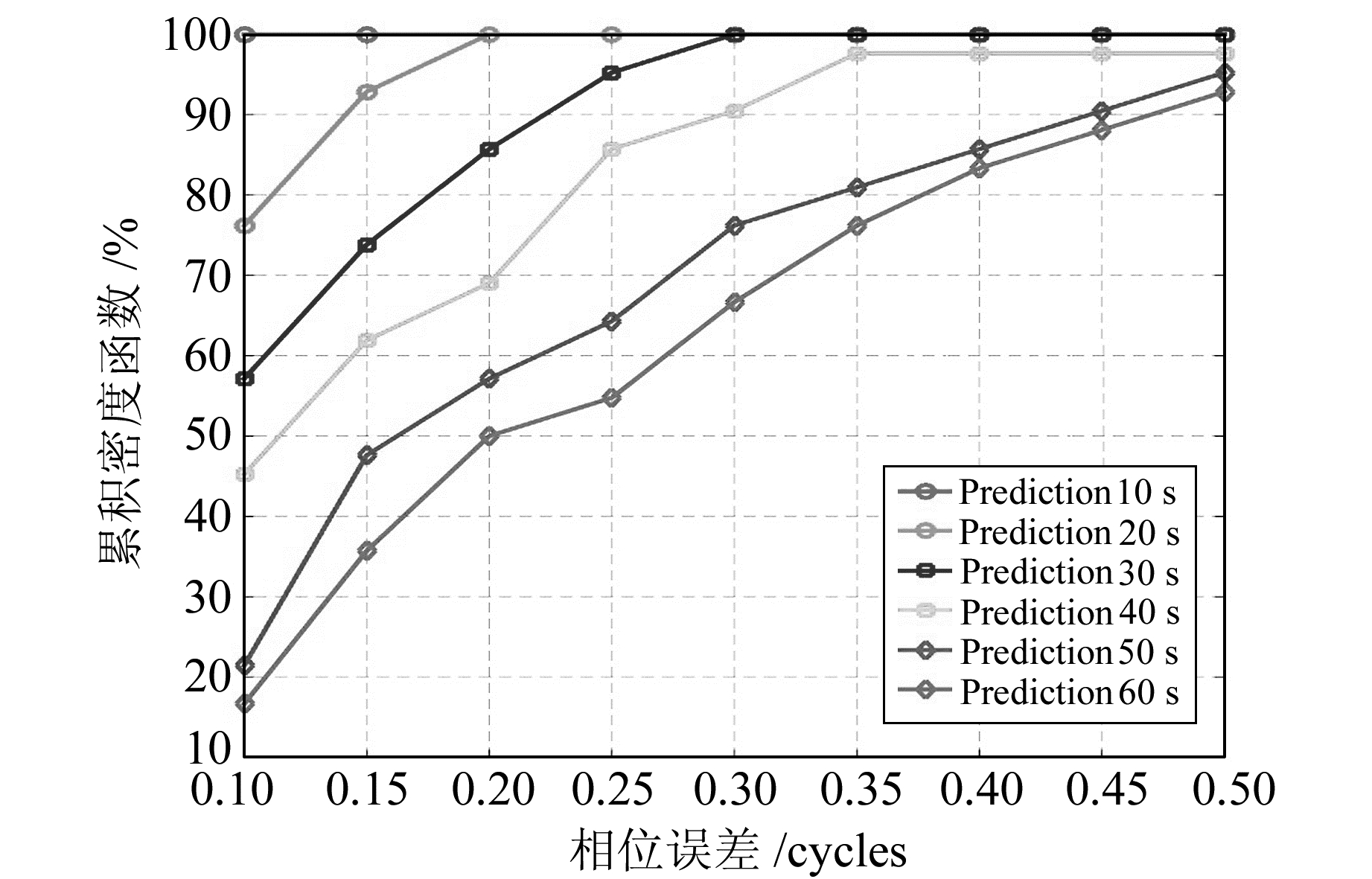
为了充分评估相位预测性能,图 7和图 8给出不同开环跟踪时间下载波相位误差的累积密度函数(CDFs)。图 7是没有外部辅助信息情况下的测试结果,图 8是在外部信息辅助下的测试结果。两者的区别在于,当有外部辅助条件时,例如基于IMU的惯导辅助,接收机可以从辅助条件中判断用户是否处于静止状态,而当确定接收机处于静止状态时,式(3)中的fuser_move等于0,进而消除了定位与测速误差对相位预测精度的影响;反之,当无外部辅助时,接收机需要对本地接收机的速度和位置进行估计,其估计误差必将影响相位预测的效果。图中每条曲线表示不同的开环时间,横轴表示在开环时间内的最大相位误差,纵轴表示开环相位误差不超过横轴坐标的比例。从图中可以看到,当无外部辅助时,90%以上的测试结果在15 s内能保证相位误差不超过1/4周;有外部辅助时,90%以上的测试结果在30 s内能保证相位误差不超过1/4周,外部辅助的引入将相位预测效果提升了近1倍。文献[12]中的相位预测方法,同样在静态测试条件下,40%的测试结果在8 s的开环时间内相位误差不大于1/4周。相比之下,本文提出的载波相位预测方法在开环跟踪效果上有了大幅提升。
|
图 7 相位误差的累积密度函数(无外部辅助) Fig. 7 Cumulative density function of carrier phase error(without external assistance) |
|
图 8 相位误差的累积密度函数(有外部辅助) Fig. 8 Cumulative density function of carrier phase error(with external assistance) |
针对遮挡导致接收机载波相位不连续问题,本文提出一种基带信号处理层面的载波相位预测方法,并在软件接收机平台进行实现和评估。测试结果表明,利用这种方法,能保证在15 s的开环跟踪时间内,90%以上的测试结果都能使载波相位的开环跟踪误差不大于1/4周,可以解决接收机在部分卫星短时间遮挡情况下的载波相位不连续问题,对精密定位具有重要的实用价值。
| [1] |
Driscoll C, Lachapelle G. Comparison of Traditional and Kalman Filter Based Tracking Architectures[C]. Proceedings of European Navigation Conference, Naples, Italy, 2009
(  0) 0) |
| [2] |
Soloviev A, Gunawardena S, Graas F. Deeply Integrated GPS/Low-Cost IMU for Low CNR Signal Processing: Flight Test Results and Real Time Implementation[C]. International Technical Meeting of the Satellite Division of the Institute of Navigation, 2004
(  0) 0) |
| [3] |
Groves P D, Long D C. Inertially Aided GPS Signal Reacquisition in Poor Signal to Noise Environments and Tracking Maintenance through Short Signal Outages[C]. The 18th International Technical Meeting of the Satellite Division of the Institute of Navigation, 2005
(  0) 0) |
| [4] |
Xie P, Petovello M G. Improving Carrier Phase Reacquisition Using Advanced Receiver Architectures[C].Position Location and Navigation Symposium, IEEE, 2010
(  0) 0) |
| [5] |
张顺, 姚宜斌, 陈鹏, 等. GPS非差数据周跳探测方法研究[J]. 大地测量与地球动力学, 2012, 32(1): 101-104 (Zhang Shun, Yao Yibin, Chen Peng, et al. Research on Cycle Slip Detection Methods for Un-Differenced GPS Data[J]. Journal of Geodesy and Geodynamics, 2012, 32(1): 101-104)
(  0) 0) |
| [6] |
李峰, 张建军, 李健, 等. 载波相位约束整周模糊度在短基线RTK中的应用[J]. 测绘工程, 2016, 25(5): 64-68 (Li Feng, Zhang Jianjun, Li Jian, et al. A Method of Using Carrier Phase to Constrain Integer Ambiguity and Application to Short Baseline RTK[J]. Engineering of Surveying and Mapping, 2016, 25(5): 64-68 DOI:10.3969/j.issn.1006-7949.2016.05.014)
(  0) 0) |
| [7] |
陈品馨, 章传银, 黄昆学. 用相位减伪距法和电离层残差法探测和修复周跳[J]. 大地测量与地球动力学, 2010, 30(2): 120-124 (Chen Pinxin, Zhang Chuanyin, Huang Kunxue. Cycle Slips Detecting and Repairing by Use of Phase Reduce Pseudorange Law and Ionized Layer Remnant Method of Difference[J]. Journal of Geodesy and Geodynamics, 2010, 30(2): 120-124)
(  0) 0) |
| [8] |
王甫红, 韩秀飞, 龚学文, 等. 基于贝叶斯概率统计的GPS载波相位周跳探测与修复方法[J]. 测绘地理信息, 2017(6): 11-15 (Wang Fuhong, Han Xiufei, Gong Xuewen, et al. A Method of Cycle-slip Detection and Repair for GPS Carrier Phase Based on Bayesian Probability Statistics[J]. Journal of Geomatics, 2017(6): 11-15)
(  0) 0) |
| [9] |
滕云龙, 师奕兵, 郑植. 单频载波相位的周跳探测与修复算法研究[J]. 仪器仪表学报, 2010, 31(8): 1 700-1 705 (Teng Yunlong, Shi Yibing, Zheng Zhi. Algorithm of Cycle-Slip Detection and Correction in Single-Frequency Carrier Phase[J]. Chinese Journal of Scientific Instrument, 2010, 31(8): 1 700-1 705)
(  0) 0) |
| [10] |
Peng X, Mark G P. Phase Prediction Method in GNSS Receivers with Application to Phase Reacquisition[J]. Journal of Institute of Navigation, 2012, 59(2): 107-118 DOI:10.1002/navi.9
(  0) 0) |
| [11] |
张骞丹, 田红心. GPS系统多普勒频移估算的研究[J]. 无线电工程, 2007, 37(4): 21-23 (Zhang Qiandan, Tian Hongxin. Research on Doppler Frequency-Shift Estimation of GPS[J]. Radio Engineering, 2007, 37(4): 21-23 DOI:10.3969/j.issn.1003-3106.2007.04.008)
(  0) 0) |
| [12] |
Wang B X. Carrier Phase Prediction of Weak Signal for High-Accuracy Navigation[D]. Calgary: University of Calgary, 2015
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38

