2. 中国科学院上海天文台,上海市南丹路80号,200030;
3. 北京卫星导航中心,北京市北清路22号,100094;
4. 大地测量与地球动力学国家重点实验室,武汉市徐东大街340号,430077
北斗系统于2015~2016年发射的5颗新一代导航试验卫星搭载了Ka频段星间链路验证平台。星间链路(inter-satellite link, ISL)技术可以在一定程度上维持导航星座的自主运行,自主解算高精度星历和钟差参数,也可用于自主导航模式下地面锚固站与卫星间的测距和通信,进行星地联合定轨和时间同步,从而解决单纯依靠星间测距的星座自主导航存在的空间基准和时间基准漂移问题[1-2]。
北斗区域系统卫星采用L波段星地双向时间同步体制。针对该体制,文献[3]提出星地双向时间同步的数学模型,试验精度达到0.34 ns;文献[4]利用北斗二号卫星试验数据获得1.0 ns的星地时间同步精度。国内针对ISL体制的双向钟差观测和时间同步亦有研究。文献[5]分析了ISL测距数据特性认为,ISL体制和L波段体制钟差观测一致性较好,但L波段1 d弧段拟合结果存在系统偏差;文献[6]讨论ISL体制下星地双向时间同步的数学模型,利用I1S星试验数据分析钟差观测精度,得到10 000 s频率稳定度优于8×10-4;文献[7]对北斗试验星ISL星地设备时延进行标定,提高了Ka频段星地钟差观测与L波段的一致性。以上文献仅对个别试验星数据的固定弧段钟差观测精度进行讨论,而针对所有试验星不同弧长ISL时间同步精度的探讨尚不充足。本文利用星地ISL设备的观测数据和L波段观测数据进行对比检验(2016-07北京站),同时采集星间观测数据进行星地星间联合钟差观测的验证。
1 星地双向时间同步数学模型北斗卫星的星间链路测距体制是一种时分体制,在一个固定周期内依次完成所有可见链路的双向测量。这种双向测量虽然在时间上十分相近,但存在测量时间差。观测方程表示为[5]:
| $ \begin{array}{l} {\rho _{{\rm{AB}}}}({t_1}) = \left| {\overrightarrow {{r_{\rm{B}}}} ({t_1}) - \overrightarrow {{r_{\rm{A}}}} ({t_1} - \Delta {t_1})} \right| + \\ \;\;\;\;\;\;c\left( {{\tau _{\rm{B}}}({t_1}) - {\tau _{\rm{A}}}({t_1})} \right) + {\delta _{{\rm{AB}}}}\\ {\rho _{{\rm{BA}}}}({t_2}) = \left| {\overrightarrow {{r_{\rm{A}}}} ({t_2}) - \overrightarrow {{r_{\rm{B}}}} ({t_2} - \Delta {t_2})} \right| + \\ \;\;\;\;\;\;c\left( {{\tau _{\rm{A}}}({t_2}) - {\tau _{\rm{B}}}({t_2})} \right) + {\delta _{{\rm{BA}}}} \end{array} $ | (1) |
式中,ρAB(t1)、ρBA(t2)为A星到B星和B星到A星在相应时刻的单程伪距观测量,
| $ \begin{array}{l} {\delta _{{\rm{AB}}}} = c \cdot \\ \left( {\tau _{\rm{A}}^{{\rm{Send}}} + \tau _{\rm{B}}^{{\rm{Rcv}}} + \tau _{\rm{B}}^{{\rm{ant}}} + {\tau _{{\rm{rel}}}} + {\tau _{{\rm{ion}}}} + {\tau _{{\rm{trop}}}} + \tau _{{\rm{sagnac}}}^{{\rm{AB}}}} \right)\\ {\delta _{{\rm{BA}}}} = c \cdot \\ \left( {\tau _{\rm{B}}^{{\rm{Send}}} + \tau _{\rm{A}}^{{\rm{Rcv}}} + \tau _{\rm{A}}^{{\rm{ant}}} + {\tau _{{\rm{rel}}}} + {\tau _{{\rm{ion}}}} + {\tau _{{\rm{trop}}}} + \tau _{{\rm{sagnac}}}^{{\rm{BA}}}} \right) \end{array} $ | (2) |
其中包括设备的信号发射和接收时延偏差τASend、τARcv、τBSend和τBRcv、天线相位中心偏差τAant和τBant、相对论效应τrel、对流层延迟τtrop、电离层延迟τion以及Sagnac效应延迟τsagnacAB和τsagnacBA[6]。以上偏差中设备时延可以精确标定,其他均可精确建模。需指出,由于钟速的存在,信号的光行时之内两星的钟差都会产生变化。但对于5颗新一代试验星,信号光行时均小于0.12 s,期间的钟差漂变可以忽略不计,故式(1)中将其忽略。对于星地ISL双向观测,只需把B星换为S站,由于地面站时钟保持与BDT同步,可认为星地相对钟差即为卫星钟差[6],对钟差时间序列进行拟合可得到钟速模型。
BD-2应用L波段星地双向时频传递技术(TWSTFT)获取卫星钟相对于BDT的偏差,该体制中卫星和地面站在同一钟面时发射、接收伪距信号[3, 8],则式(1)中t1=t2。而ISL时分体制双向伪距观测量需要归算到同一钟面才能进行钟差解算,设定将两个观测量归算到t0时刻:
| $ \begin{array}{l} {\rho _{{\rm{AB}}}}({t_0}) = {\rho _{{\rm{AB}}}}({t_1}) + {\rm{d}}{\rho _{{\rm{AB}}}} = \\ \left| {\overrightarrow {{r_{\rm{B}}}} ({t_0}) - \overrightarrow {{r_{\rm{A}}}} ({t_0})} \right| + c\left( {{\tau _{\rm{B}}}({t_0}) - {\tau _{\rm{A}}}({t_0})} \right) + {\delta _{{\rm{AB}}}}\\ {\rho _{{\rm{BA}}}}({t_0}) = {\rho _{{\rm{BA}}}}({t_2}) + {\rm{d}}{\rho _{{\rm{BA}}}} = \\ \left| {\overrightarrow {{r_{\rm{A}}}} ({t_0}) - \overrightarrow {{r_{\rm{B}}}} ({t_0})} \right| + c\left( {{\tau _{\rm{A}}}({t_0}) - {\tau _{\rm{B}}}({t_0})} \right) + {\delta _{{\rm{BA}}}} \end{array} $ | (3) |
式中,ρAB(t0)和ρBA(t0)表示归算到t0时刻后的双向伪距观测量;dρAB和dρBA为从测量时刻(t1和t2)到目标时刻(t0)的观测量改正量,包括两颗卫星(或地面站)的位置变化和钟差变化引起的改正量,由卫星预报星历和预报钟差信息解算,一般采用拉格朗日多项式插值的方法[9]。
将ρAB(t0)和ρSA(t0)作差,可将观测量的测距信息和钟差信息解耦,获得相对钟差信息:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;{\tau _{\rm{A}}}({t_0}) - {\tau _{\rm{B}}}({t_0}) = \\ \frac{{{\rho _{{\rm{AB}}}}({t_0}) - {\rho _{{\rm{BA}}}}({t_0})}}{{2c}} - \frac{{{\delta _{{\rm{AB}}}} - {\delta _{{\rm{BA}}}}}}{{2c}} \end{array} $ | (4) |
在残余误差中,设备时延可以作为待估参数在后期精确标定[7]。对于星间观测,存在相对论效应和卫星天线相位中心修正,可精确建模;对于星地观测,还包括电离层延迟、对流层延迟和固体潮效应,其中,由于ISL体制Ka频段频率很高,残余电离层误差约3 cm,可以忽略不计,对流层延迟采用Saastamonien模型进行改正,误差约10 cm,固体潮效应可精确建模[5]。由于历元归化后双向观测量的信号传播路径近似对称(不论L波段体制还是ISL体制),解耦后大部分误差均可消除,最终仅包含测量噪声,这是双向时间对比策略的重要优势[6]。
2 星地钟差观测量分析采集5颗新一代试验星2016-07对地ISL体制和L波段体制的双向伪距数据进行钟差计算和对比。由于M3S卫星处于调试阶段,故将其剔除。由于钟差拟合精度与观测时长有关,且由于观测弧段不连续,卫星每次重入境时存在钟差跳变,故选取7 d、1 d和1 h观测时长的拟合结果进行分析。
2.1 7 d拟合结果分析选取观测数据较充分的连续7 d数据,时段为2016-07-05 00:00~07-12 00:00,即北斗时548周172 800 s~549周172 800 s,将各星数据进行二阶拟合。对比两种观测体制的拟合参数进行一致性检验,见表 1,各卫星两种体制下的钟速拟合结果偏差Δa1均在10-14 s/s以下,表明ISL体制钟速拟合结果可靠。但ISL体制星地钟差参数a0较L波段相差数十ns,这与ISL星地设备时延有关,可通过后期精确标定解决[7]。
|
|
表 1 星地钟差7 d拟合参数比较 Tab. 1 Comparison of 7 days' fitting parameters of satellite-ground clock offset |
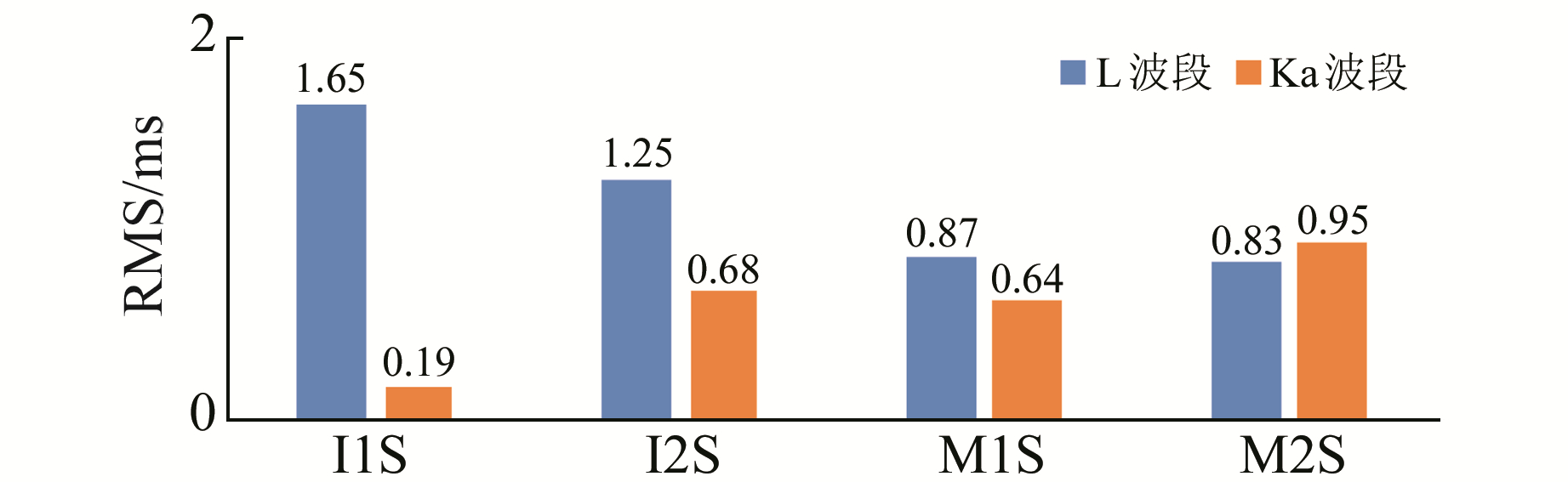
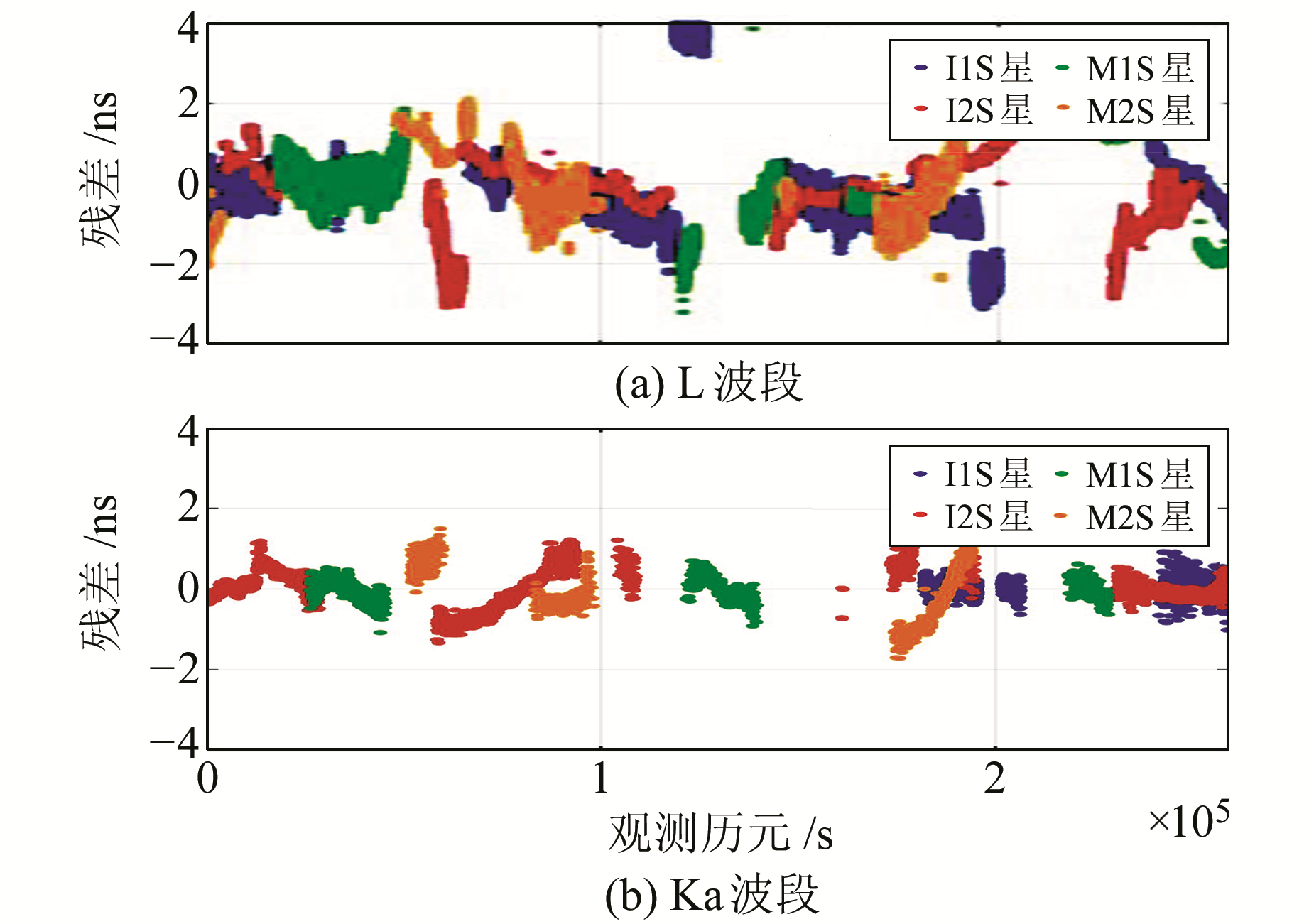
拟合残差如图 1(观测历元秒数以北斗时548周0 s起始),L波段星地钟差拟合残差在±4 ns之间波动,且受卫星再入境偏差的影响较大,ISL体制拟合残差在±2 ns之间波动。残差的RMS如图 2,虽然存在M2S星Ka拟合精度略差于L波段(如受降雨影响等),但ISL体制的拟合残差的RMS都在1 ns以内,而L波段在2 ns以内。

|
图 1 星地钟差7 d拟合残差 Fig. 1 7 days' fitting residuals of satellite-ground clock offset |
|
图 2 星地钟差7天拟合残差RMS比较 Fig. 2 RMS comparison of 7 days' fitting residuals of satellite-ground clock offset |
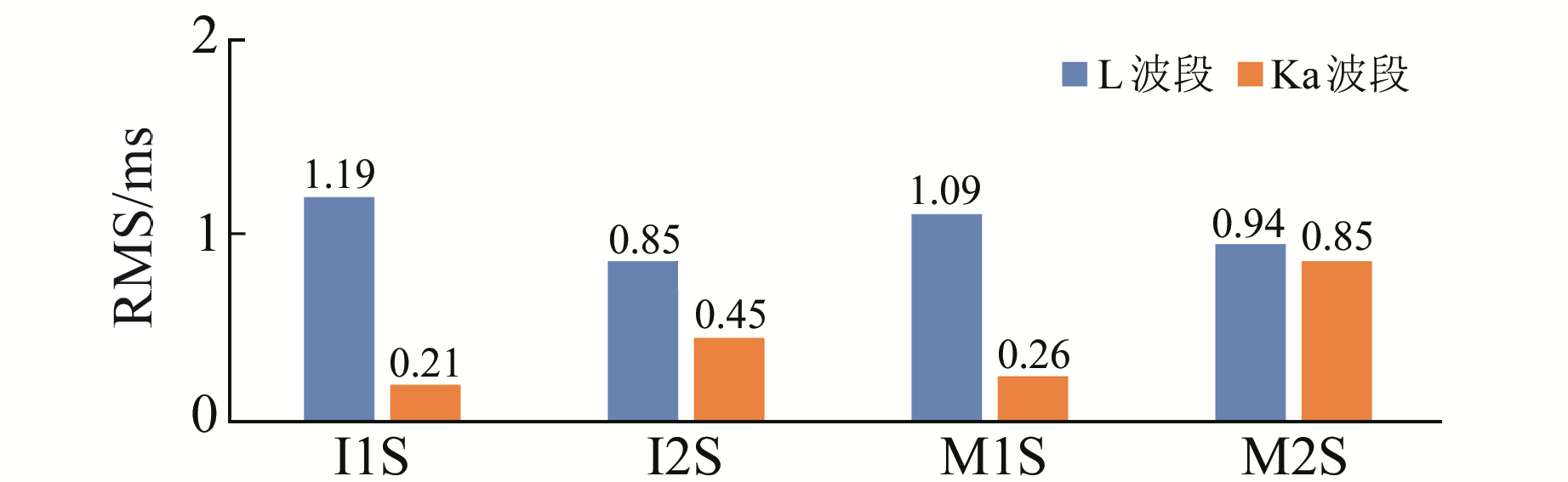
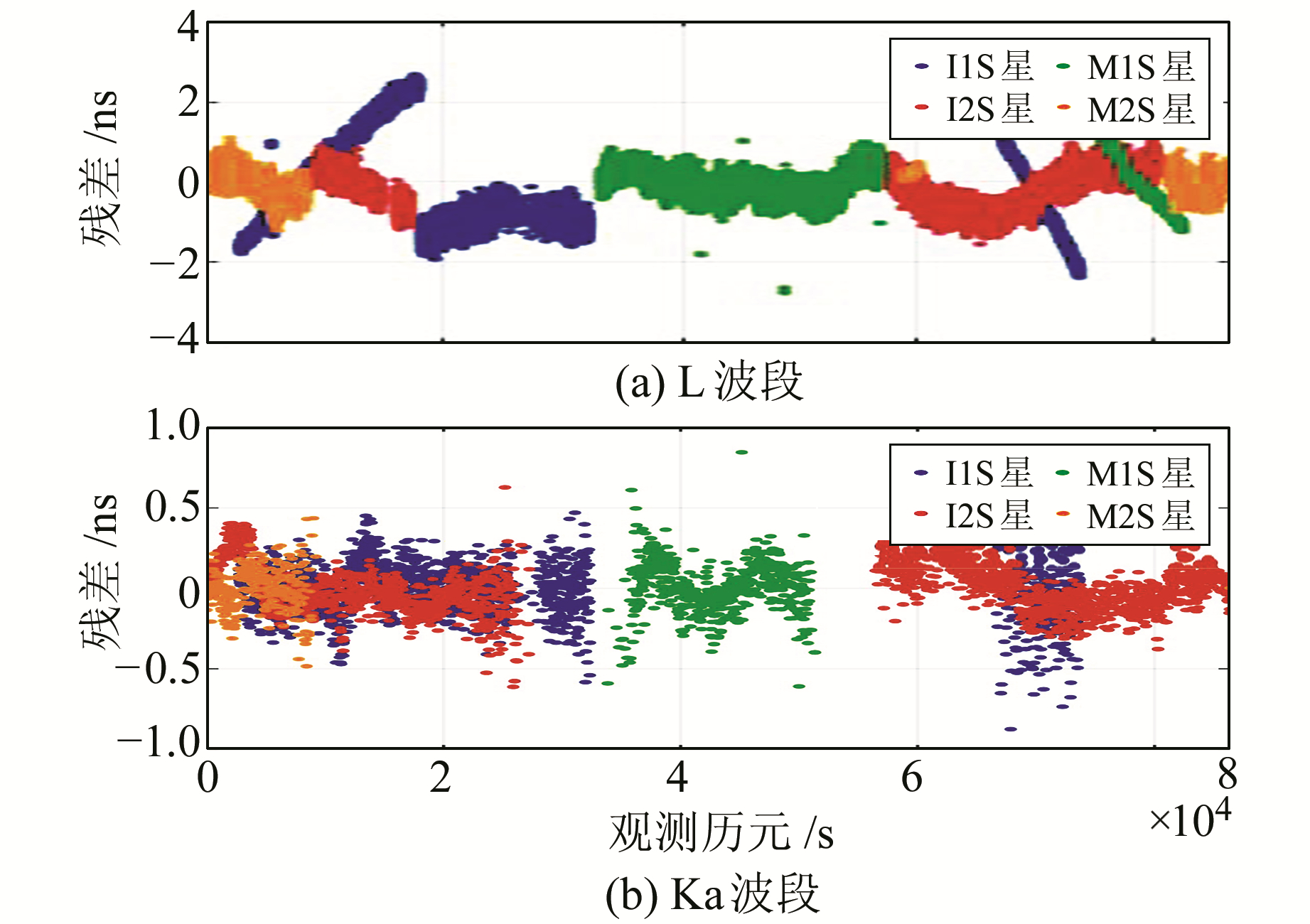
拟合弧长缩短为3 d,取2016-07-09 00:00~07-12 00:00数据,如图 3和图 4。与7 d弧段拟合结果相比,再入境偏差对L波段时间同步的影响仍然较大,故L波段拟合精度整体变化不大,但Ka波段拟合误差除I1S星外都有所降低,幅度在0.2 ns左右。
|
图 3 星地钟差3 d拟合残差 Fig. 3 3 days' fitting residuals of satellite-ground clock offset |
|
图 4 星地钟差3 d拟合残差RMS比较 Fig. 4 RMS comparison of 3 days' fitting residuals of satellite-ground clock offset |
选取1 d内较充足的数据,时段为2016-07-17 00:00~07-18 00:00。如图 5,L波段星地钟差拟合残差在±3 ns之间波动,而ISL体制拟合残差在±1 ns之间波动。由图 6可见,相比7 d的拟合结果,两种体制在1 d时长的拟合精度均有提高,而ISL星地钟差拟合残差的RMS均在0.2 ns以下,显著优于L波段。
|
图 5 星地钟差1 d拟合残差 Fig. 5 1 day's fitting residuals of satellite-ground clock offset |

|
图 6 星地钟差1 d拟合残差RMS比较 Fig. 6 RMS comparison of 1 day's fitting residuals of satellite-ground clock offset |
由于存在卫星轨道相位差,地面单站不能在1 h内同时观测所有试验星,分别取各星不同时段1 h连续观测数据并将钟差拟合残差结果展示在同一图中(图 7),两个波段均为07-05数据。两种体制拟合残差大小基本一致(主要在0.6 ns内波动,见图 7),二者RMS均在0.2 ns左右(图 8)。总体来看,ISL体制星地钟差观测1 h弧段拟合较1 d弧段拟合精度提升不明显,表明其1 d弧段拟合结果中已不存在明显的系统偏差。
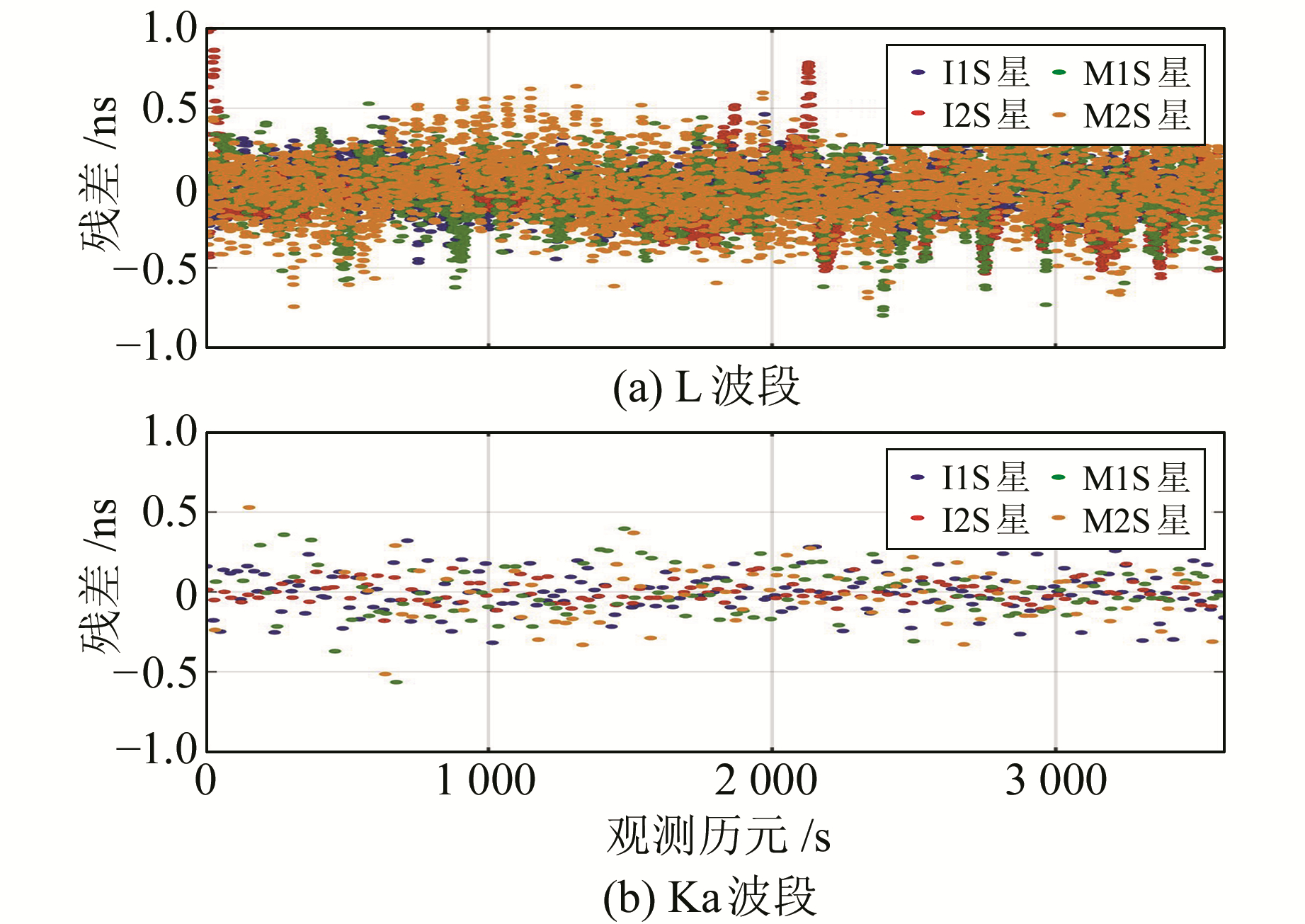
|
图 7 星地钟差1 h拟合残差 Fig. 7 1 hour's fitting residuals of satellite-ground clock offset |
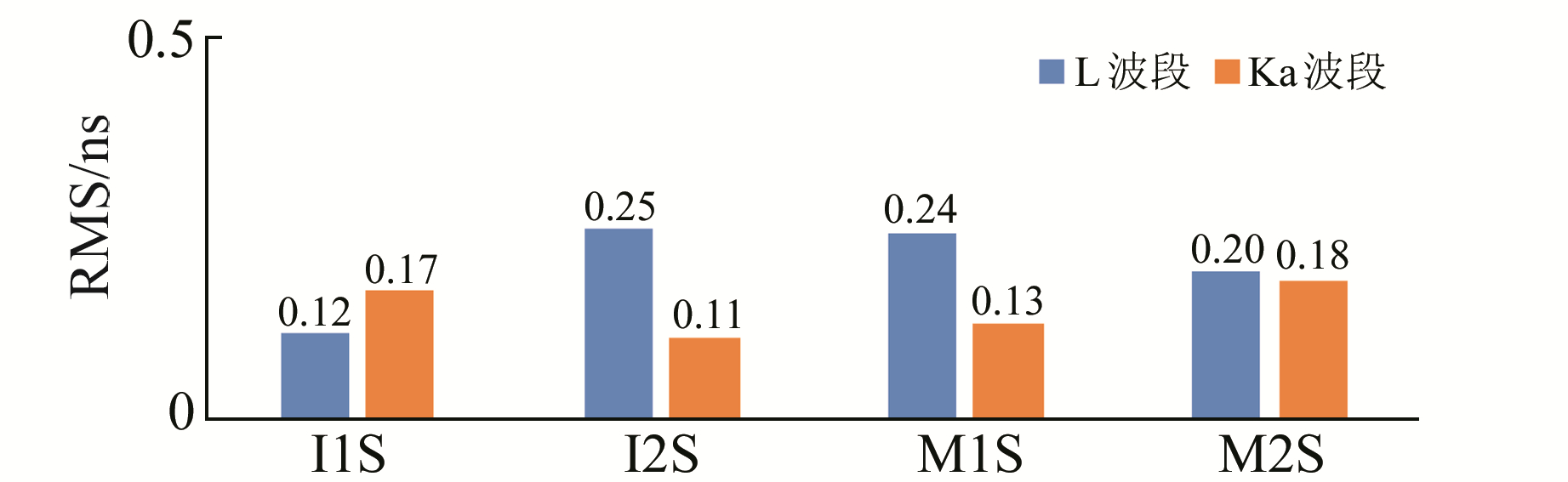
|
图 8 星地钟差1 h拟合残差RMS比较 Fig. 8 RMS comparison of 1 hour's fitting residuals of satellite-ground clock offset |
为进一步分析ISL体制星地时间同步的可行性,分别采集两种体制2016-07-10 00:00~07-17 00:00(即北斗时549周0~604 800 s)的星地钟差观测数据对未来1 d钟差进行预报,并与实际观测值相减求预报误差(图 9)。

|
图 9 星地钟差预报误差 Fig. 9 Prediction errors of satellite-ground clock offset |
由图 9可见,ISL体制的预报误差在1 d内小于2 ns,预报误差呈现轻微的系统性偏差,是由于钟速a1的预报不准确和观测量的局部波动导致;L波段在4 ns以内,较前者稍差。这表明,ISL体制星地钟差观测和时间同步的稳健性较好,减小了卫星再入境时的钟差偏差。
4 星地星间联合钟差观测为进一步验证星间观测量的可靠性,采用星地星间联合观测的方法检验星间ISL体制时间同步的可行性。
如图 10,由于IGSO轨道卫星可用弧段较长,取I1S星为中继星,间接观测M1S星的钟差。其原理为,若同一时段内存在I1S与地面站的星地双向ISL观测钟差ΔtI1S-BDT和I1S、M1S两星的星间双向ISL观测量ΔtI1S-M1S,则M1S星的钟差(间接)为:
| $ \Delta {t'_{{\rm{M1S - BDT}}}} = \Delta {t_{{\rm{M1S - I1S}}}} + \Delta {t_{{\rm{I1S - BDT}}}} $ | (5) |
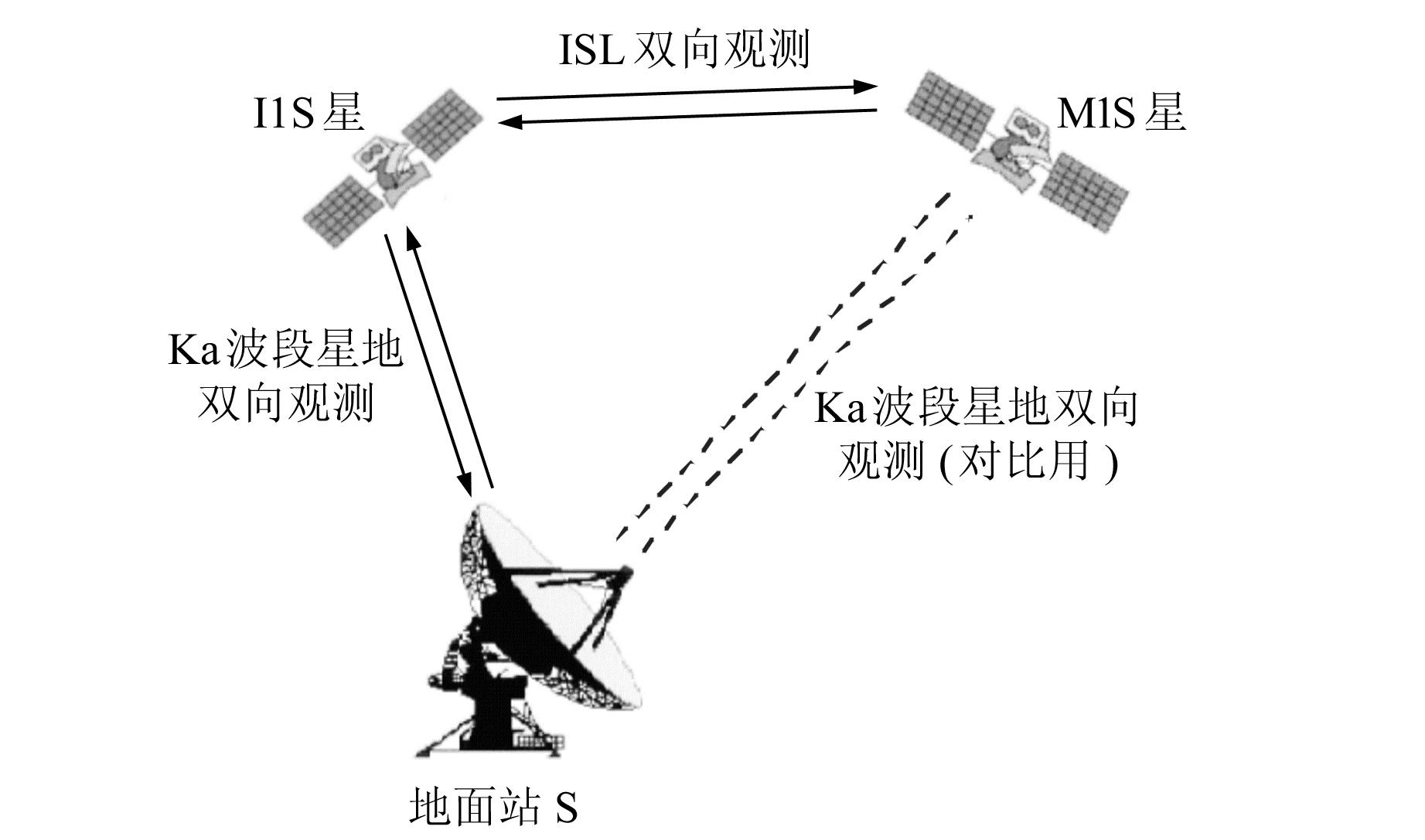
|
图 10 星地星间测量示意图 Fig. 10 A schematic diagram of inter-satellite and satellite-ground measurement |
将ΔtM1S-BDT'与M1S星地直接双向观测量ΔtI1S-BDT作差,可得到间接钟差的残差。由于实际观测中很难找到ΔtI1S-BDT、ΔtI1S-M1S和ΔtM1S-BDT的同时段观测量,故取2016-07-14~07-16数据,分别对ΔtI1S-BDT和ΔtI1S-M1S进行拟合,由式(5)得到ΔtM1S-BDT'间接拟合参数,在ΔtM1S-BDT直接观测时段求其间接拟合残差,如图 11所示。

|
图 11 星地联合钟差解算及拟合残差 Fig. 11 Fitting residuals of satellite-ground joint clock calculation |
可以看出,通过星地星间联合观测,M1S星的间接钟差观测量与直接观测量十分吻合,间接拟合残差在1 ns以内,RMS为0.52 ns,表明ISL星间钟差观测的准确性和可靠性较好。
5 结语本文推导了ISL体制双向时间同步的数学模型,并采集全部试验星ISL实测数据进行分析,与L波段结果进行对比,检验了7 d、1 d和1 h弧段内ISL体制星地钟差观测精度,进行钟差预报精度分析,并进行ISL星地星间联合钟差计算,得到如下结论:
1) ISL体制钟差拟合参数与L波段一致性较好,其7 d、3 d、1 d和1 h弧段的星地时间同步误差分别为1 ns、0.85 ns、0.2 ns和0.2 ns。其中,1 d弧段拟合精度比L波段有明显提高,且在1 d弧段上ISL体制的观测量已经不存在明显的系统差,再缩小拟合时长对精度提高不明显,故1 d为最优拟合时长。
2) ISL钟差1 d预报精度为2 ns,略好于L波段,钟差预报较为可靠。
3) ISL星间观测可靠,2 d间接钟差观测拟合残差为0.52 ns。
| [1] |
Ananda M P, Bernstein H, Cunningham K E, et al. Global Positioning System(GPS) Autonomous Navigation[J]. IEEE Position Location & Navigation Symposium, 2002, 27(1): 497-508
(  0) 0) |
| [2] |
Rajan J A, Brodie P, Rawicz H. Modernizing GPS Autonomous Navigation with Anchor Capability[C]. International Technical Meeting of the Satellite Division of the Institute of Navigation, 2003
(  0) 0) |
| [3] |
Liu L, Zhu L F, Han C H, et al. The Model of Radio Two-Way Time Comparison between Satellite and Station and Experimental Analysis[J]. Chinese Astronomy & Astrophysics, 2009, 33(4): 431-439
(  0) 0) |
| [4] |
李瑞锋, 王元明. 星地双向时间同步技术在COMPASS中的应用[J]. 武汉大学学报:信息科学版, 2013, 38(7): 842-844 (Li Ruifeng, Wang Yuanming. Application of Two-Way Satellite-Ground Time Synchronization in COMPASS[J]. Geomatics and Information Science of Wuhan University, 2013, 38(7): 842-844)
(  0) 0) |
| [5] |
唐成盼, 胡小工, 周善石, 等. 利用星间双向测距数据进行北斗卫星集中式自主定轨的初步结果分析[J]. 中国科学:物理学力学天文学, 2017, 47(2): 95-105 (Tang Chengpan, Hu Xiaogong, Zhou Shanshi, et al. Centralized Autonomous Orbit Determination of Beidou Navigation Satellites with Inter-Satellite Link Measurements: Preliminary Results[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2017, 47(2): 95-105)
(  0) 0) |
| [6] |
吕宏春, 卢晓春, 武建锋. 星间链路体制下的星地双向时间同步方法[J]. 宇航学报, 2017, 38(7): 728-734 (Lǖ Hongchun, Lu Xiaochun, Wu Jianfeng. A Method of Two Way Satellite Ground Time Synchronization Under Inter Satellite Links System[J]. Journal of Astronautics, 2017, 38(7): 728-734)
(  0) 0) |
| [7] |
潘军洋, 胡小工, 唐成盼, 等. 北斗新一代卫星时分体制星间链路测量的系统误差标定[J]. 科学通报, 2017, 62(23): 2 671-2 679 (Pan Junyang, Hu Xiaogong, Tang Chengpan, et al. System Error Calibration for Time Division Multiple Address Inter-Satellite Equipment of Next-Generation Beidou Satellites[J]. Chinese Science Bulletin, 2017, 62(23): 2 671-2 679)
(  0) 0) |
| [8] |
Han C, Cai Z, Lin Y, et al. Time Synchronization and Performance of Beidou Satellite Clocks in Orbit[J]. International Journal of Navigation and Observation, 2013, Article ID: 371450
(  0) 0) |
| [9] |
方琳.基于双向星间链路的自主时间同步仿真分析[D].北京: 中国科学院研究生院(国家授时中心), 2013 (Fang Lin. Simulation and Analysis of Autonomous Time Synchronization Based on Two-Way Inter-Satellite Link[D]. Beijing: University of Chinese Academy of Science(National Time Service Center), 2013)
(  0) 0) |
2. Shanghai Astronomical Observatory, CAS, 80 Nandan Road, Shanghai 200030, China;
3. Beijing Satellite Navigation Center, 22 Beiqing Road, Beijing 100094, China;
4. State Key Laboratory of Geodesy and Earth's Dynamics, 340 Xudong Street, Wuhan 430077, China
 2018, Vol. 38
2018, Vol. 38

