2. 西安测绘研究所地理信息工程国家重点实验室,西安市雁塔路中段1号,710054;
3. 北京卫星导航中心,北京市北清路22号,100094;
4. 中国地震台网中心,北京市三里河南横街5号,100045
GPS/BDS联合定轨方式通常分两种:1)“两步法”,首先利用GPS精密轨道和钟差确定多模跟踪站坐标、接收机钟差以及天顶对流层延迟,然后固定这些系统间公共参数进行BDS的精密定轨[1-8];2)“一步法”,即统一处理GPS/BDS双系统观测数据,直接联合平差求解双系统的轨道和钟差[9-10]。刘伟平等[6]讨论了模糊度固定对多系统联合定轨中北斗卫星轨道精度的提高。文献[7]从参数估值、轨道精度及卫星钟差精度等方面比较了GPS/BDS联合定轨的“两步法”和“一步法”。文献[8]利用全球分布的28个跟踪站的观测数据,对比3 d弧长解算时BDS独立定轨与GPS/BDS联合定轨两种方法得到的北斗卫星轨道精度。文献[11]基于IGS和MGEX全球网比较GPS/GLONASS/BDS/Galileo 4个系统联合定轨与各单系统独立定轨的精度,文献[12]则分析了联合定轨对系统间公共参数求解的贡献。本文首先给出采用“一步法”进行GPS/BDS联合定轨的观测方程,然后分别在区域网和全球网条件下采用不同定轨弧长进行GPS/BDS联合定轨与BDS独立定轨实验,从不同方面比较两种定轨结果,分析联合定轨对北斗卫星轨道精度的影响。
1 联合定轨观测方程动力学定轨中,各卫星的动力学模型相互独立,而观测模型通过公共参数产生联系。本文采用双频非差消电离层组合(LC)观测值进行GPS/BDS联合定轨。对于GPS卫星(G),地面站r对卫星s的观测方程为:
| $ \begin{array}{l} {\rm P}_{{\rm{LC}}, r}^{{\rm{G}}, s} = \rho _r^{{\rm{G}}, s} + m_r^{{\rm{G}}, s}{T_r} + (c\delta t_r^{\rm{G}} + d_{{P_{{\rm{LC}}}}, r}^{\rm{G}}) - \\ \;\;\;\;\;\;\;\;\;\;\;\;(c\delta {t^{{\rm{G}}, s}} + d_{{P_{{\rm{LC}}}}}^{{\rm{G}}, s}) + \varepsilon _{{{\rm P}_{{\rm{LC}}}}}^{\rm{G}} \end{array} $ | (1) |
| $ \begin{array}{l} \mathit{\Phi }_{{\rm{LC}}, r}^{{\rm{G}}, s} = \rho _r^{{\rm{G}}, s} + m_r^{{\rm{G}}, s}{T_r} + (c\delta t_r^{\rm{G}} + d_{{P_{{\rm{LC}}}}, r}^{\rm{G}}) - \\ \;\;\;\;\;\;\;\;(c\delta {t^{{\rm{G}}, s}} + d_{{P_{{\rm{LC}}}}}^{{\rm{G}}, s}) + [\lambda _{{\rm{LC}}}^{\rm{G}}N_{{\rm{LC}}, r}^{{\rm{G}}, s} + (d_{{P_{LC}}}^{G, s} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;d_{{\mathit{\Phi }_{LC}}}^{{\rm{G}}, s} - d_{{P_{{\rm{LC}}}}, r}^{\rm{G}} + d_{{\mathit{\Phi }_{{\rm{LC}}}}, r}^{\rm{G}})] + \varepsilon _{{\mathit{\Phi }_{{\rm{LC}}}}}^{\rm{G}} \end{array} $ | (2) |
对于BDS卫星(C),观测方程为:
| $ \begin{array}{l} \;\;\;\;P_{{\rm{LC}}, r}^{{\rm{C}}, s} = \rho _r^{{\rm{C}}, s} + m_r^{{\rm{C}}, s}{T_r} + (c\delta t_r^{\rm{G}} + d_{{P_{{\rm{LC}}}}, r}^{\rm{G}}) - \\ (c\delta {t^{{\rm{C}}, s}} + d_{{P_{{\rm{LC}}}}}^{{\rm{C}}, s}) - ({\delta _{{\rm{GC}}}} + d_{{P_{{\rm{LC}}}}, r}^{\rm{G}} - d_{{P_{{\rm{LC}}}}, r}^{\rm{C}}) + \varepsilon _{{P_{{\rm{LC}}}}}^{\rm{C}} \end{array} $ | (3) |
| $ \begin{array}{l} \;\;\;\;\mathit{\Phi }_{{\rm{LC}}, r}^{{\rm{C}}, s} = \rho _r^{{\rm{C}}, s} + m_r^{{\rm{C}}, s}{T_r} + (c\delta t_r^{\rm{G}} + d_{{P_{{\rm{LC}}}}, r}^{\rm{G}}) - \\ \;\;\;\;(c\delta {t^{{\rm{C}}, s}} + d_{{P_{{\rm{LC}}}}}^{{\rm{C}}, s}) - ({\delta _{{\rm{GC}}}} + d_{{P_{{\rm{LC}}}}, r}^{\rm{G}} - d_{{P_{{\rm{LC}}}}, r}^{\rm{C}}) + \\ {\rm{[}}\lambda _{{\rm{LC}}}^{\rm{C}}N_{{\rm{LC}}, r}^{{\rm{C}}, s} + (d_{{P_{{\rm{LC}}}}}^{{\rm{C}}, s} - d_{{\mathit{\Phi }_{{\rm{LC}}}}}^{{\rm{C}}, s} - d_{{P_{{\rm{LC}}}}, r}^{\rm{C}} + d_{{\mathit{\Phi }_{{\rm{LC}}}}, r}^{\rm{C}}){\rm{]}} + \varepsilon _{{\mathit{\Phi }_{{\rm{LC}}}}}^{\rm{C}} \end{array} $ | (4) |
式中,PLC和ΦLC分别表示相应卫星的码伪距与载波相位伪距组合观测值,ρ为站星几何距离,Tr为测站天顶方向对流层延迟,mrs为测站天顶至站星方向的对流层延迟映射函数,δtr和δts分别为测站接收机钟与卫星钟钟差,δGC表示GPS与BDS之间的系统时偏差,dPLC, r和dΦLC, r分别表示接收机端信号的码伪距和载波相位伪距的组合延迟,dPLCs和dΦLCs分别为卫星端信号的码伪距和载波相位伪距的组合延迟,λLC和NLC分别为组合相位的波长与模糊度,εPLC和εΦLC分别表示码伪距和载波相位伪距组合观测值中的其他误差(包含多路径误差与随机噪声等)。
对比式(1)~(4)可知,测站坐标、接收机钟差以及天顶对流层延迟均为系统间公共参数,可以通过星座完整、模型精确的GPS加强约束,从而提高非公共参数(即北斗卫星轨道和卫星钟差)的解算精度[12]。
在不同测站分布和不同定轨弧长条件下比较GPS/BDS联合定轨与BDS独立定轨的结果,以分析不同条件下联合定轨对BDS卫星轨道精度的影响。实验数据来自2015-09-01~09-07中国地壳运动观测网(CMONOC)和国际GNSS服务中心的多模实验跟踪网(MGEX),数据处理策略见文献[13]。
2 区域网定轨定轨区域网由分布于中国及周边地区20个能同时接收GPS和BDS信号的多模跟踪站构成,其中包括18个CMONOC站和2个MGEX站。利用区域网的观测数据分别进行1 d与3 d弧长的BDS独立定轨与GPS/BDS联合定轨,从轨道重叠弧段不符值、与MGEX分析中心产品比较以及卫星激光测距(SLR)检核残差3个方面对两种方法的定轨结果进行分析。
2.1 轨道重叠弧段不符值采用3 d弧长定轨时,连续解算弧段之间存在2 d的重叠,其差值即为轨道重叠弧段不符值。1 d弧长定轨解得的连续轨道的结束历元与下一天的零点相差一个积分输出步长,通过轨道积分将当天的轨道外推一个输出步长至下一天的零点,并与下一天解得的零点轨道作差,其差值通常称作轨道天边界不符值,可视作1 d弧长定轨时的重叠弧段不符值。由于比较双方均为解算值,重叠弧段不符值反映轨道的内符合精度[14-15]。图 1和图 2分别给出区域网1 d和3 d弧长定轨时,BDS独立定轨与GPS/BDS联合定轨解得的BDS卫星轨道重叠弧段不符值的平均RMS。
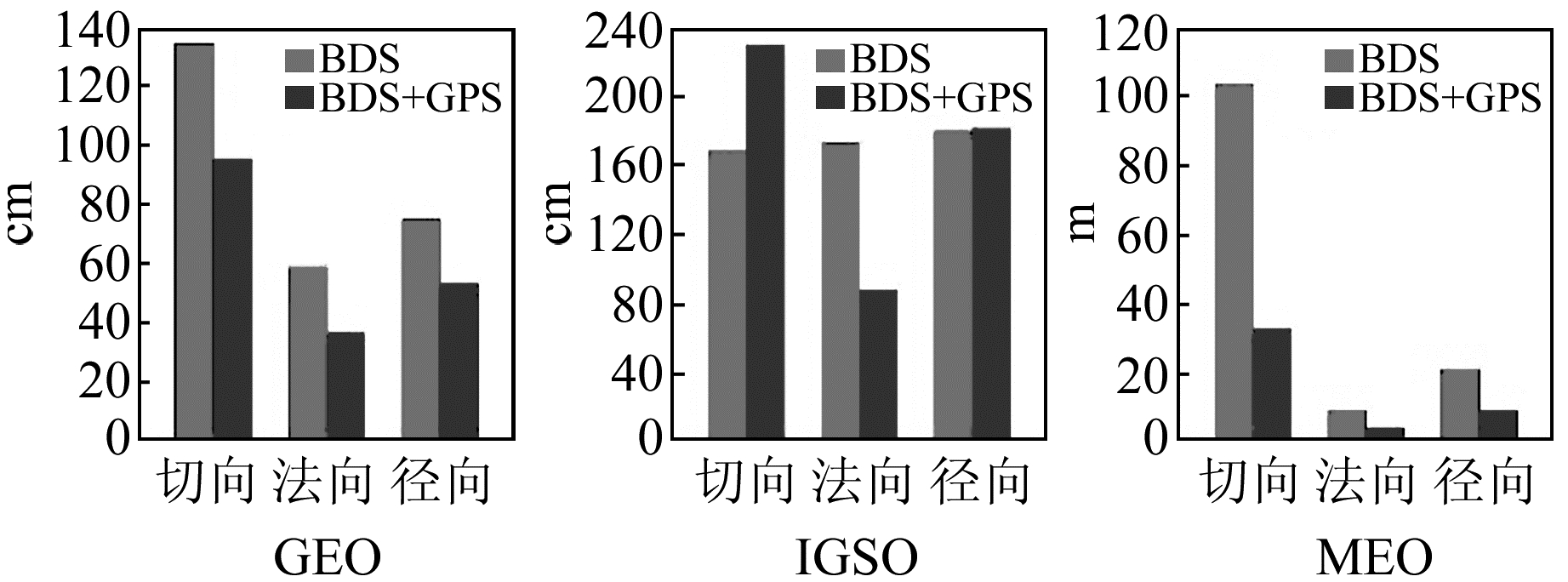
|
图 1 区域网1 d解轨道天边界不符值平均RMS Fig. 1 Mean RMS of orbit day boundary discrepancy of 1 d solution with the regional tracking network |
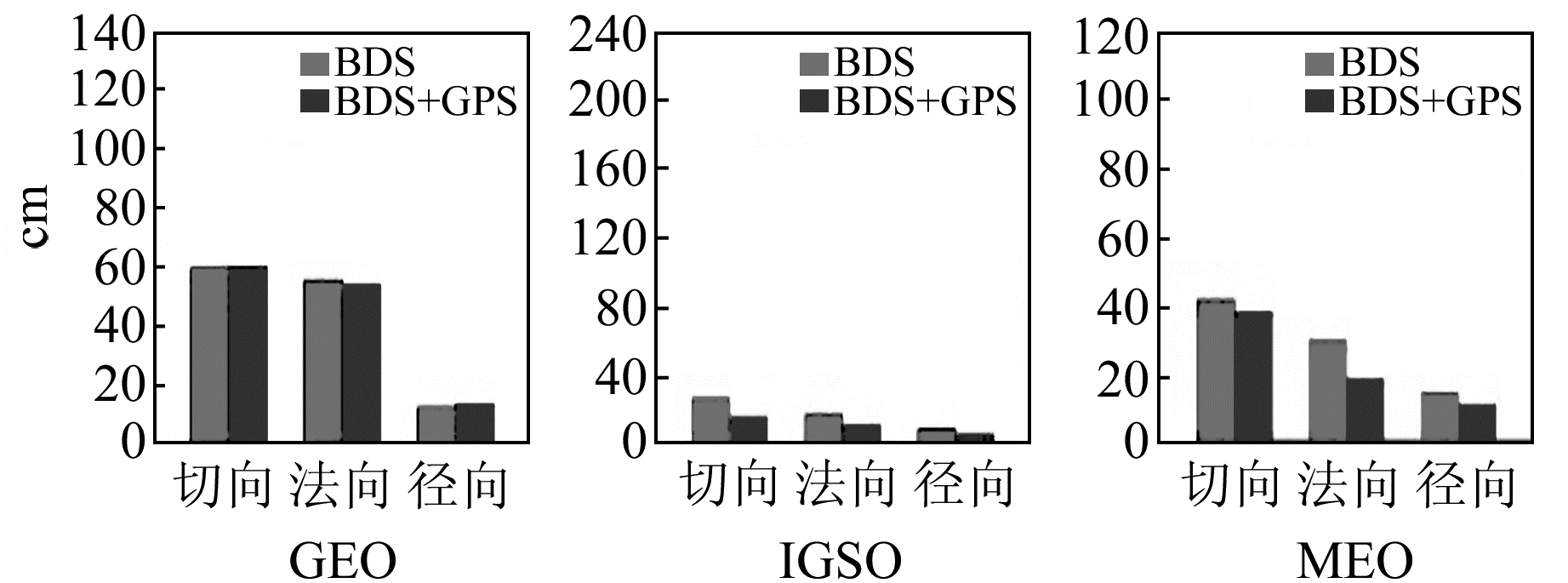
|
图 2 区域网3 d解轨道重叠弧段不符值平均RMS Fig. 2 Mean RMS of orbit overlapping arc difference of 3 d solution with the regional tracking network |
由图 1可知,仅有地面区域跟踪网的条件下,GPS/BDS联合定轨能明显提升1 d解BDS卫星定轨的内符合精度,尤其是北斗MEO卫星,其沿迹方向天边界不符值由超过100 m降至30 m左右。IGSO卫星轨道径向不符值反而明显变大,主要是由C07和C09两颗卫星引起的,具体原因有待进一步研究。图 2显示,区域网条件下延长定轨弧段有助于提升所有北斗卫星的定轨精度(尤其是MEO卫星),但相比于1 d定轨弧长,采用3 d定轨弧长时联合定轨对于BDS卫星定轨精度的改善幅度明显较小。
2.2 与MGEX分析中心产品比较将不同条件下的定轨结果与GFZ发布的轨道和钟差产品进行比较。图 3和图 4分别给出了区域网条件下1 d解与3 d解的BDS轨道与GFZ轨道产品的差异,表 1(单位ns)和表 2(单位ns)分别统计了1 d解与3 d解的卫星钟差与GFZ卫星钟差产品的差异。
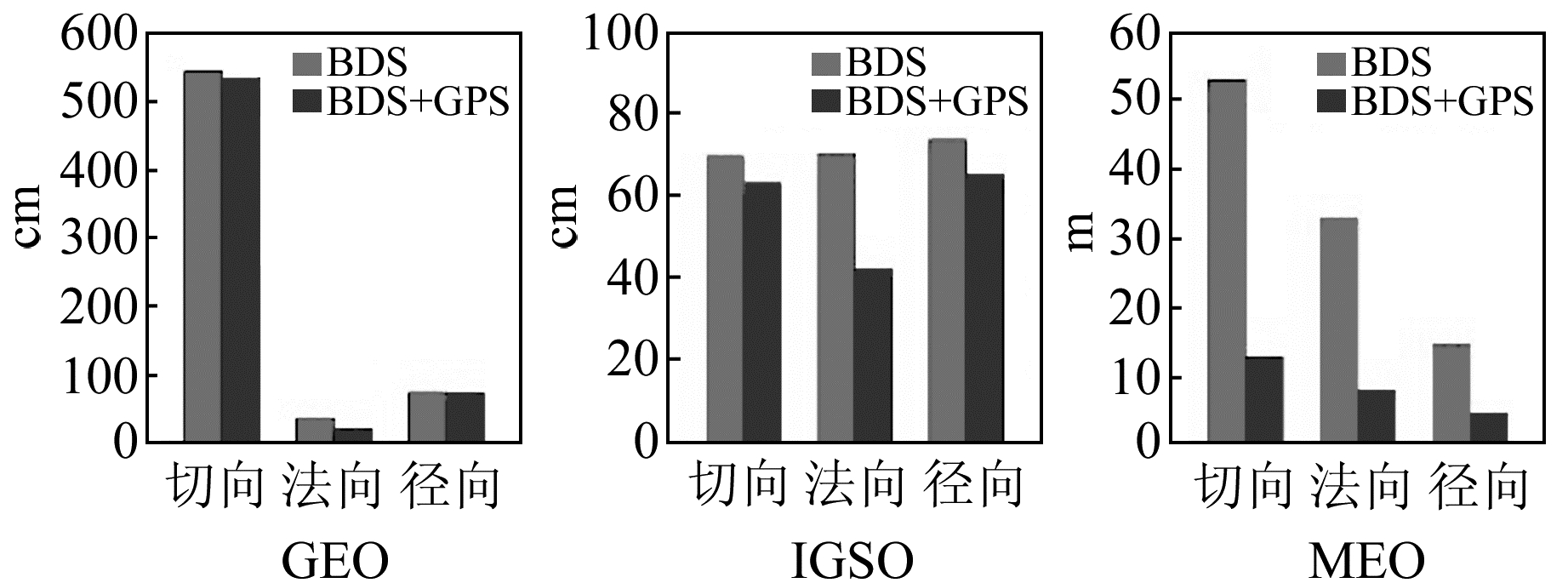
|
图 3 区域网1 d解轨道与GFZ轨道差值平均RMS Fig. 3 Mean RMS of orbit difference with GFZ orbit of 1 d solution with the regional tracking network |
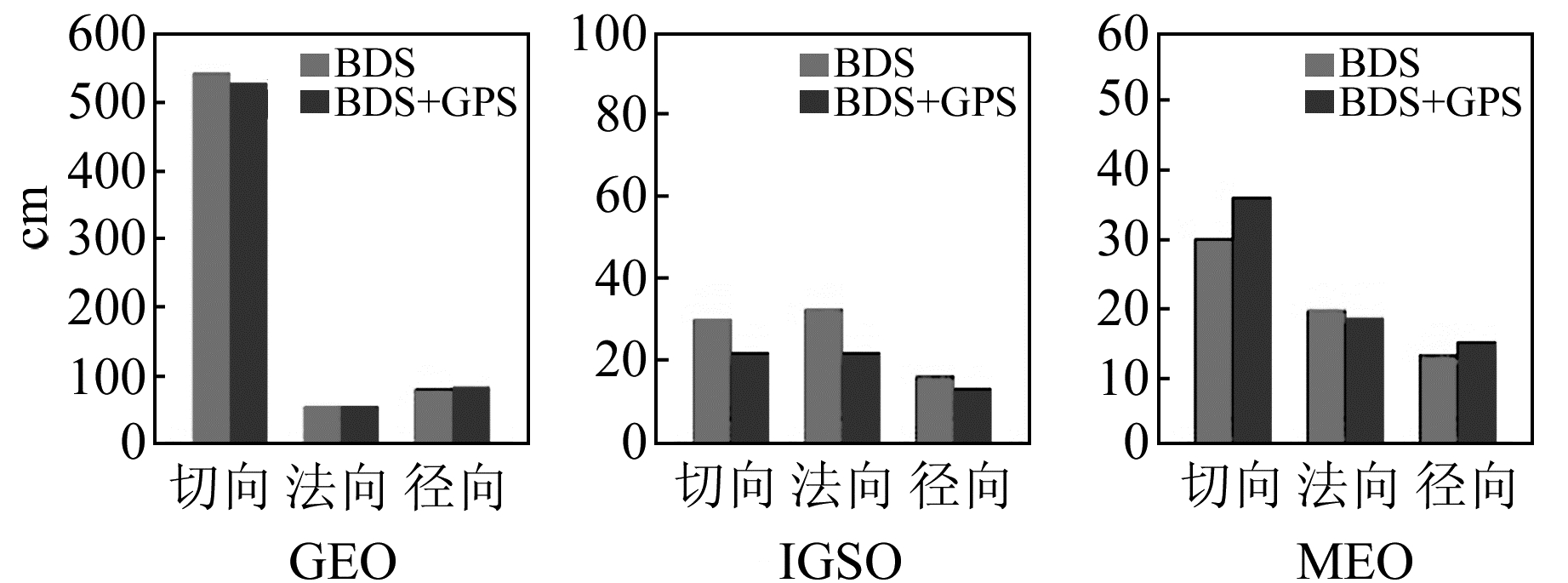
|
图 4 区域网3 d解轨道与GFZ轨道差值平均RMS Fig. 4 Mean RMS of orbit difference with GFZ orbit of 3 d solution with the regional tracking network |
|
|
表 1 区域网1 d解卫星钟差与GFZ钟差差异 Tab. 1 Satellite clock difference with GFZ clock of 1 d solution with the regional tracking network |
|
|
表 2 区域网3 d解卫星钟差与GFZ钟差差异 Tab. 2 Satellite clock difference with GFZ clock of 3 d solution with the regional tracking network |
由图 3和图 4可以看出,区域网条件下1 d解的联合定轨对北斗MEO卫星的轨道外符合精度改善最为显著,而对GEO卫星影响较小;3 d解的联合定轨仅对IGSO卫星的轨道外符合精度有略微改善,考虑到实际的定轨精度,可以认为两种方法解得的GEO/MEO卫星轨道外符合精度基本一致。由于观测几何结构较差,区域网条件下的卫星轨道误差与卫星钟差之间存在较强的相关性。表 1和表 2显示,采用1 d定轨弧长时联合定轨解得的卫星钟差精度明显优于独立定轨,而采用3 d定轨弧长时两种方法解得的卫星钟差精度基本相当,这与图 3和图 4的轨道比较结果相符。
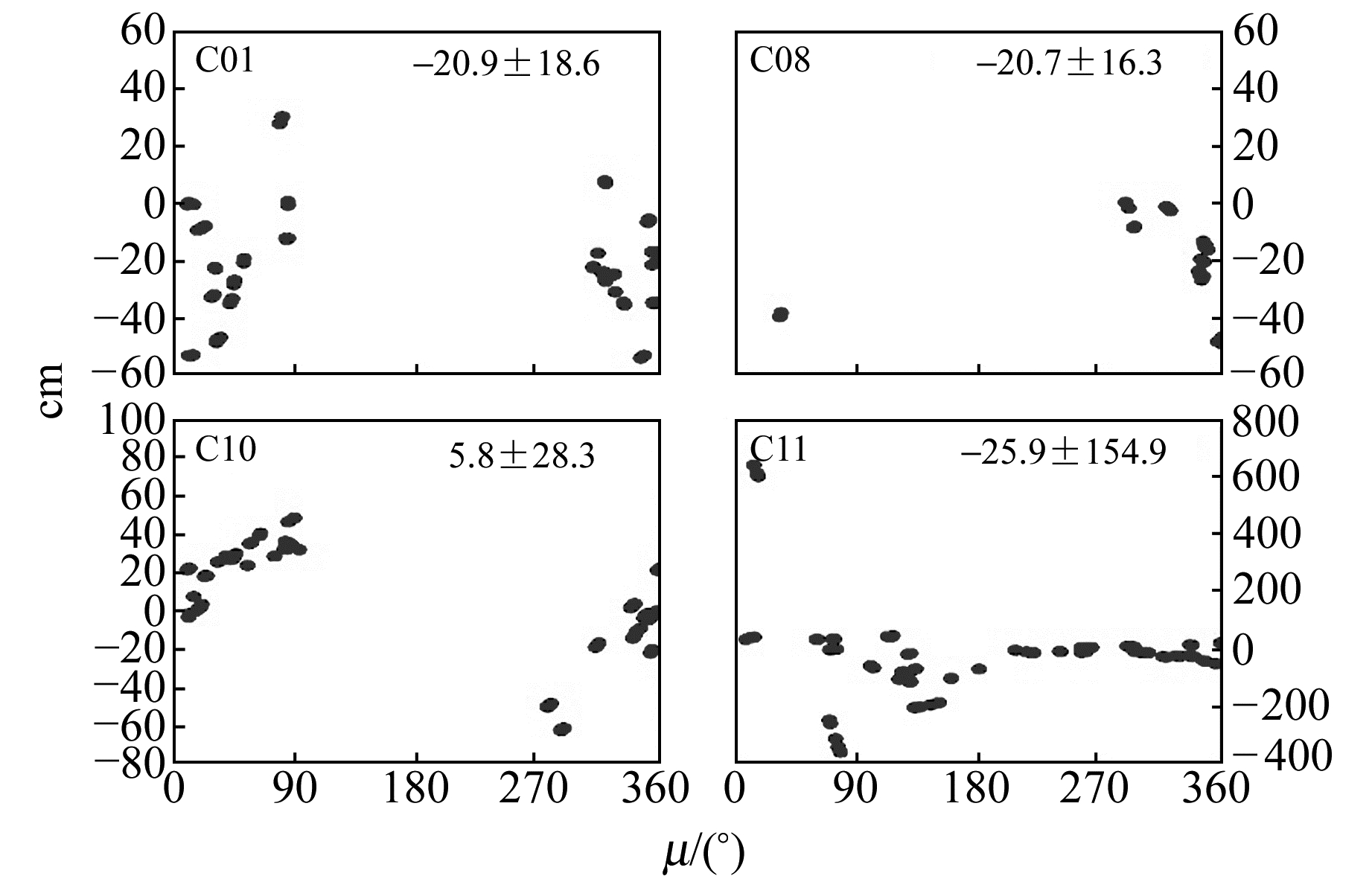
2.3 SLR检核残差图 5~图 8依次给出区域网条件下采用1 d和3 d弧长解算时BDS独立定轨与GPS/BDS联合定轨解得的北斗C01、C08、C10、C11卫星轨道的SLR检核残差相对卫星轨道角μ(即地心-卫星向量和卫星轨道面内离太阳最远的点与地心连线向量之间的夹角)的变化,并在各图右上角给出相应残差序列的均值和标准差。表 3 (单位cm)则统计了相应定轨结果的SLR残差RMS。

|
图 5 区域网1 d解BDS独立定轨的SLR残差 Fig. 5 SLR residuals of 1 d BDS-only solution with the regional tracking network |
|
图 6 区域网1 d解GPS/BDS联合定轨的SLR残差 Fig. 6 SLR residuals of 1 d GPS/BDS combined solution with the regional tracking network |
|
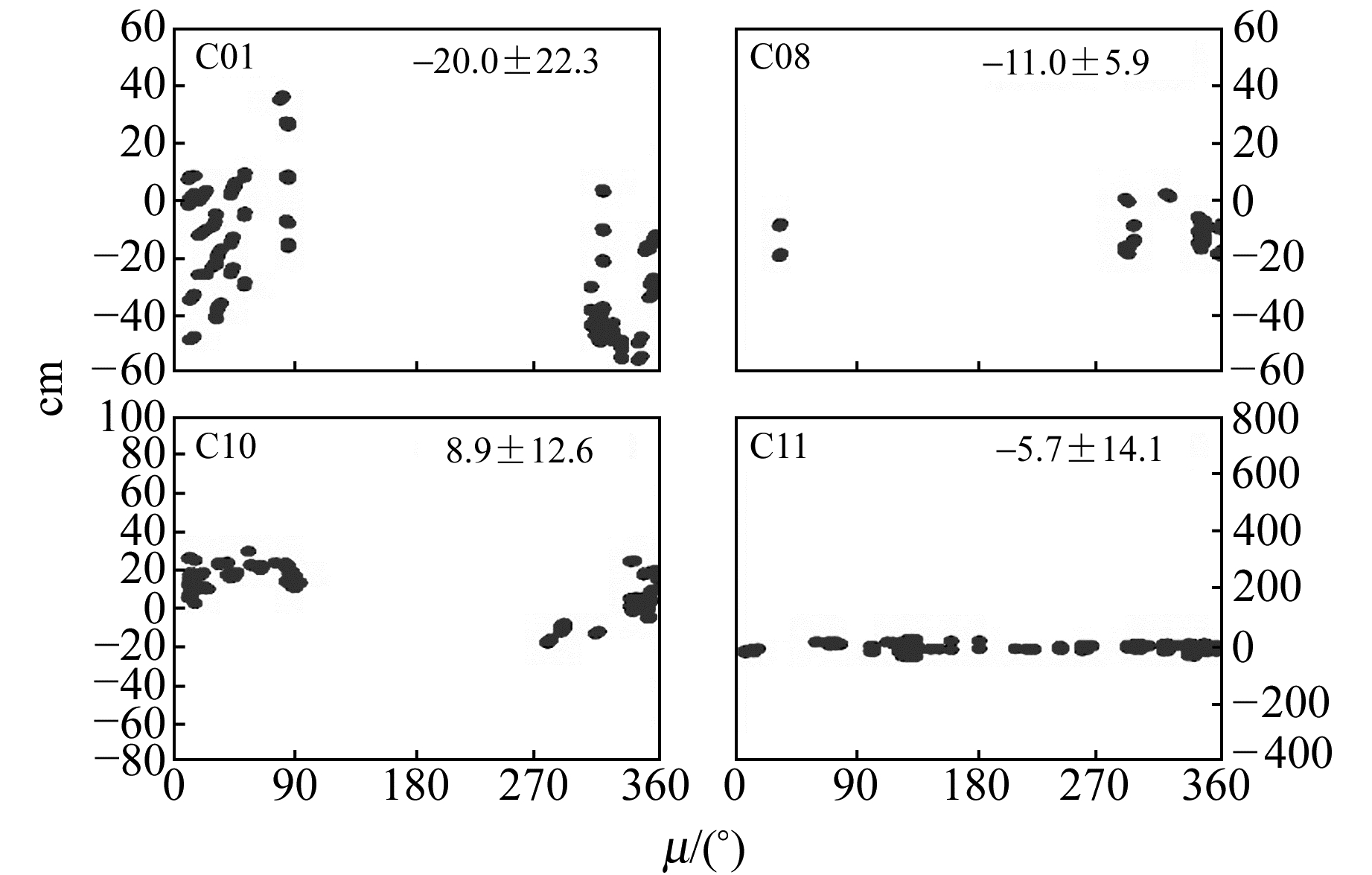
图 7 区域网3 d解BDS独立定轨的SLR残差 Fig. 7 SLR residuals of 3 d BDS-only solution with the regional tracking network |
|
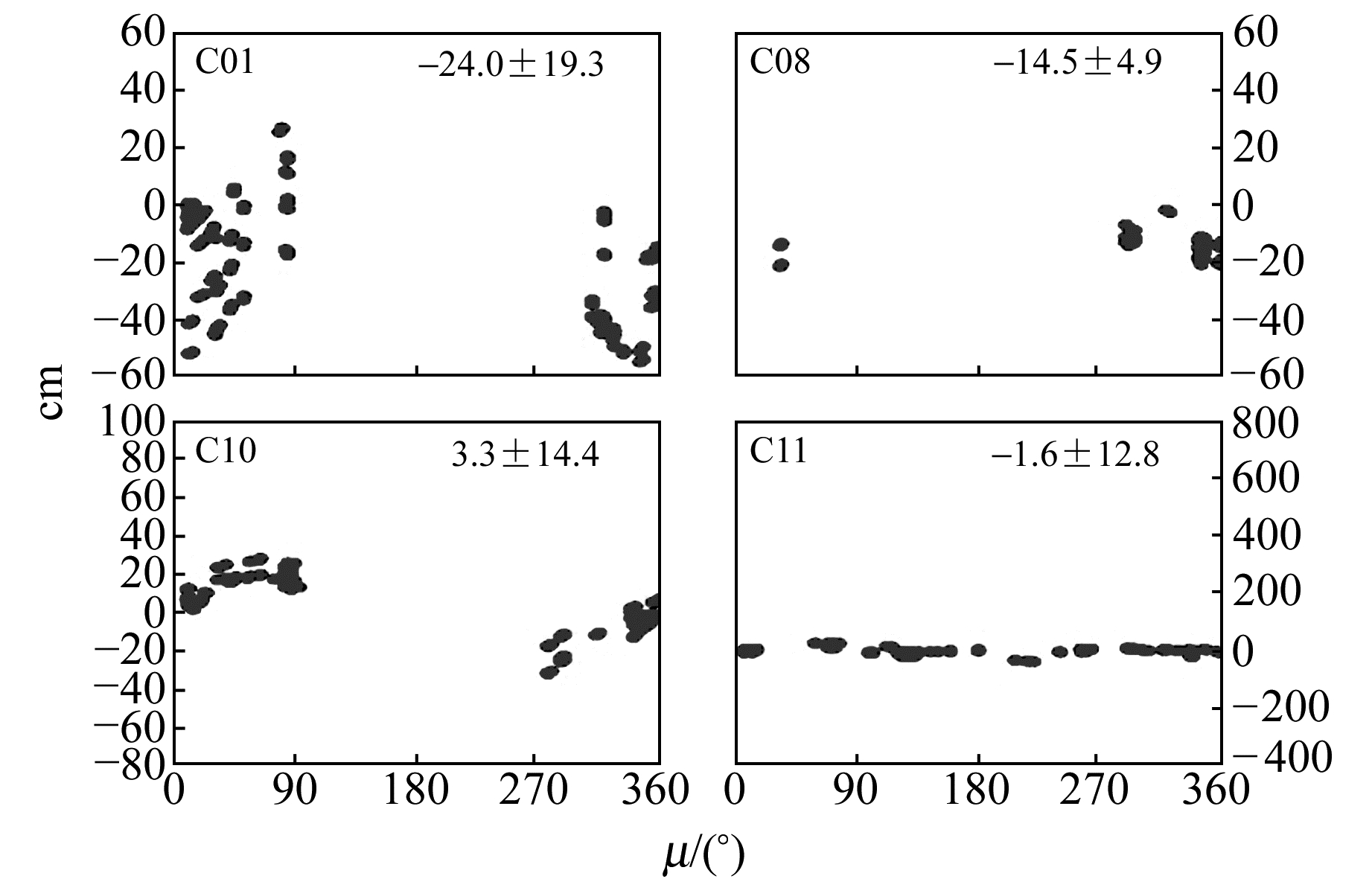
图 8 区域网3 d解GPS/BDS联合定轨的SLR残差 Fig. 8 SLR residuals of 3 d GPS/BDS combined solution with the regional tracking network |
|
|
表 3 区域网定轨结果的SLR残差RMS Tab. 3 RMS of SLR residuals of orbits with the regional tracking network |
由图 5~图 8及表 3可以看出,区域网条件下,采用3 d定轨弧长能够显著提升北斗IGSO/MEO轨道的径向绝对精度并削弱其轨道径向残差与轨道角之间存在的相关性,尤其是MEO卫星(因为相比而言MEO卫星定轨精度受跟踪弧段的影响更大)。采用1 d解时,联合定轨能够略微提升IGSO轨道的径向绝对精度,但MEO卫星轨道径向精度反而明显变差。这一方面是因为1 d解联合定轨对MEO卫星轨道精度的改善主要体现在沿迹方向,另一方面可能是由于采用1 d弧长解算时MEO卫星的跟踪弧段较短且观测值较少,导致实际定轨精度较低且不稳定。采用3 d解时,联合定轨与独立定轨得到的轨道径向绝对精度相当,这也与前面轨道重叠弧段不符值以及与MGEX分析中心产品的比较结果较为一致。
3 全球网定轨在区域网基础上增加51个全球分布的能同时跟踪GPS和BDS卫星的MGEX测站,构成本文定轨的全球网。与区域网定轨类似,利用全球网观测数据分别进行1 d弧长与3 d弧长的BDS独立定轨与GPS/BDS联合定轨,并从轨道重叠弧段不符值、与MGEX分析中心产品比较以及SLR检核残差3个方面对全球网条件下两种定轨方法的结果进行比较分析。
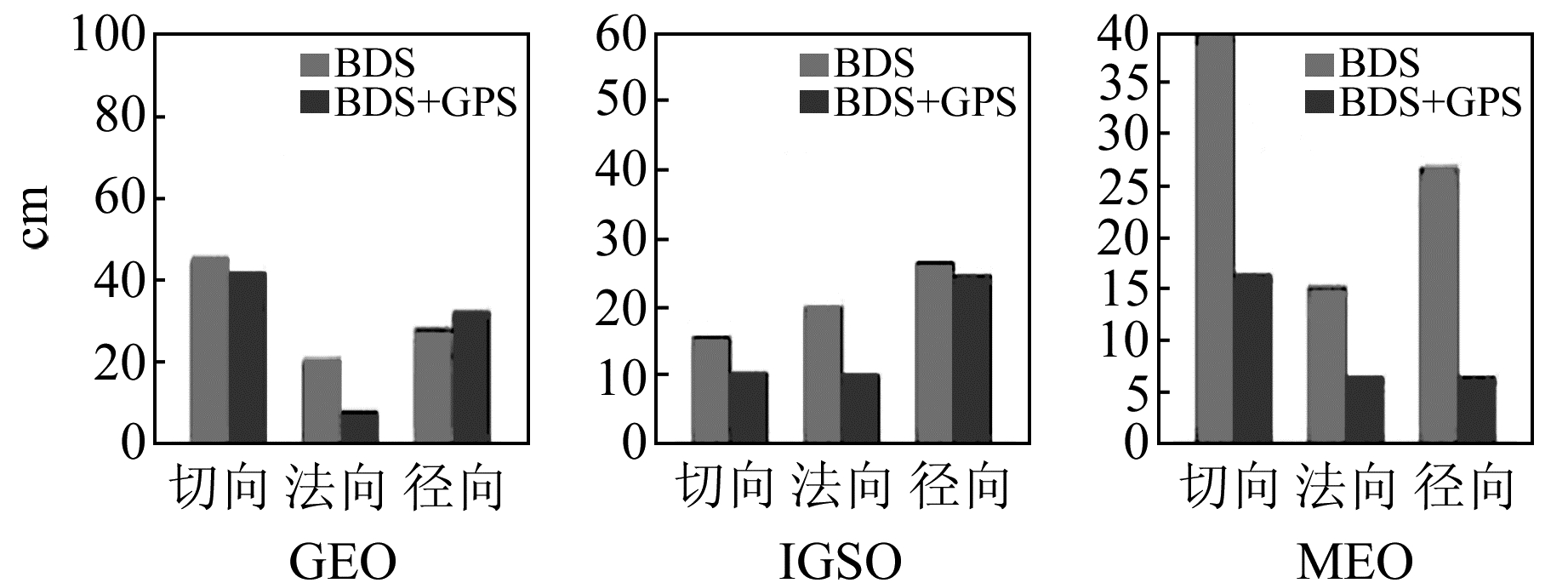
3.1 轨道重叠弧段不符值图 9和图 10分别给出全球网条件下采用1 d和3 d弧长解算时独立与联合定轨得到的BDS卫星轨道的重叠弧段不符值的平均RMS。
|
图 9 全球网1 d解轨道天边界不符值平均RMS Fig. 9 Mean RMS of orbit day boundary discrepancy of 1 d solution with the global tracking network |
|
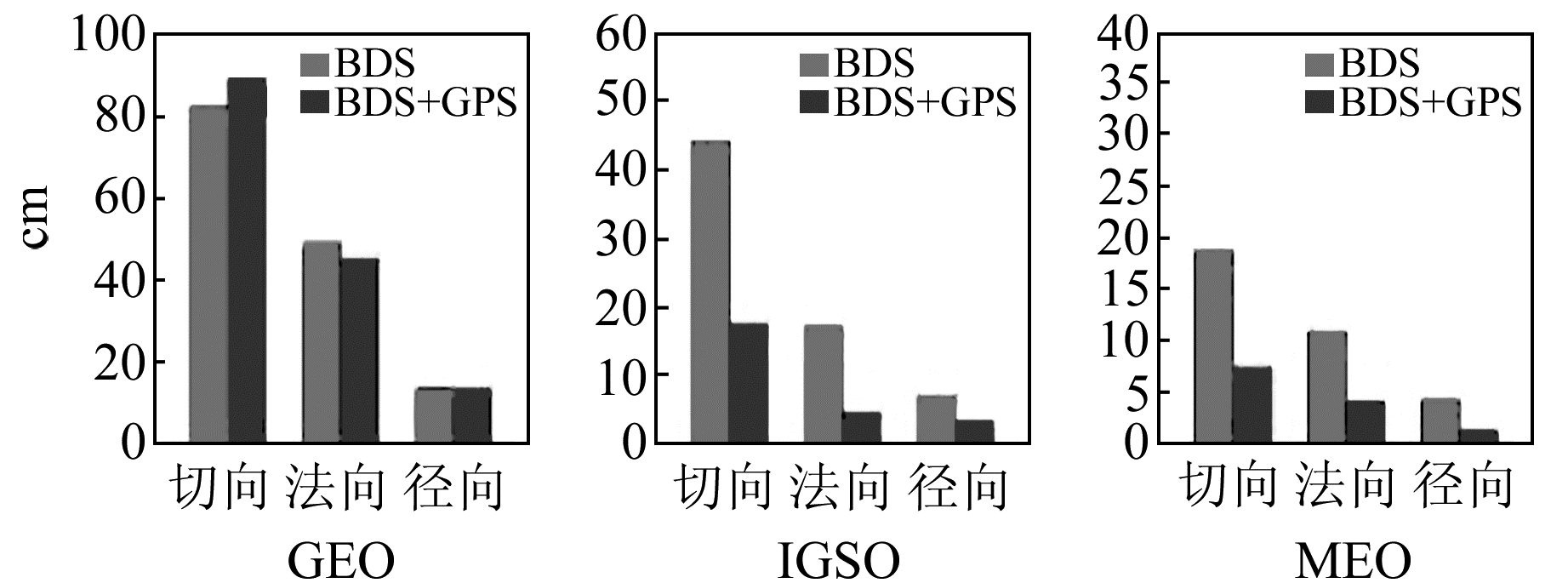
图 10 全球网3 d解轨道重叠弧段不符值平均RMS Fig. 10 Mean RMS of orbit overlapping arc difference of 3 d solution with the global tracking network |
由图 9和图 10看出,在全球网支持下,无论采用1 d弧长还是3 d弧长,GPS/BDS联合定轨对北斗IGSO/MEO卫星轨道的内符合精度仍有明显提升,尤其是在轨道沿迹方向。而对于北斗GEO卫星,联合定轨对1 d解和3 d解定轨结果的影响均较小。与文献[6]的全球网3 d解重叠弧段精度相比,本文GEO卫星轨道的切向精度更高而法向精度较差,MEO卫星的法向精度更优,这应该与跟踪站的数量与分布有关。
3.2 MGEX分析中心产品比较图 11和图 12分别给出全球网条件下1 d解与3 d解的BDS卫星轨道与GFZ轨道产品的差异,表 4和表 5(单位ns)则分别统计了1 d解与3 d解的卫星钟差与GFZ卫星钟差产品的差异。
|
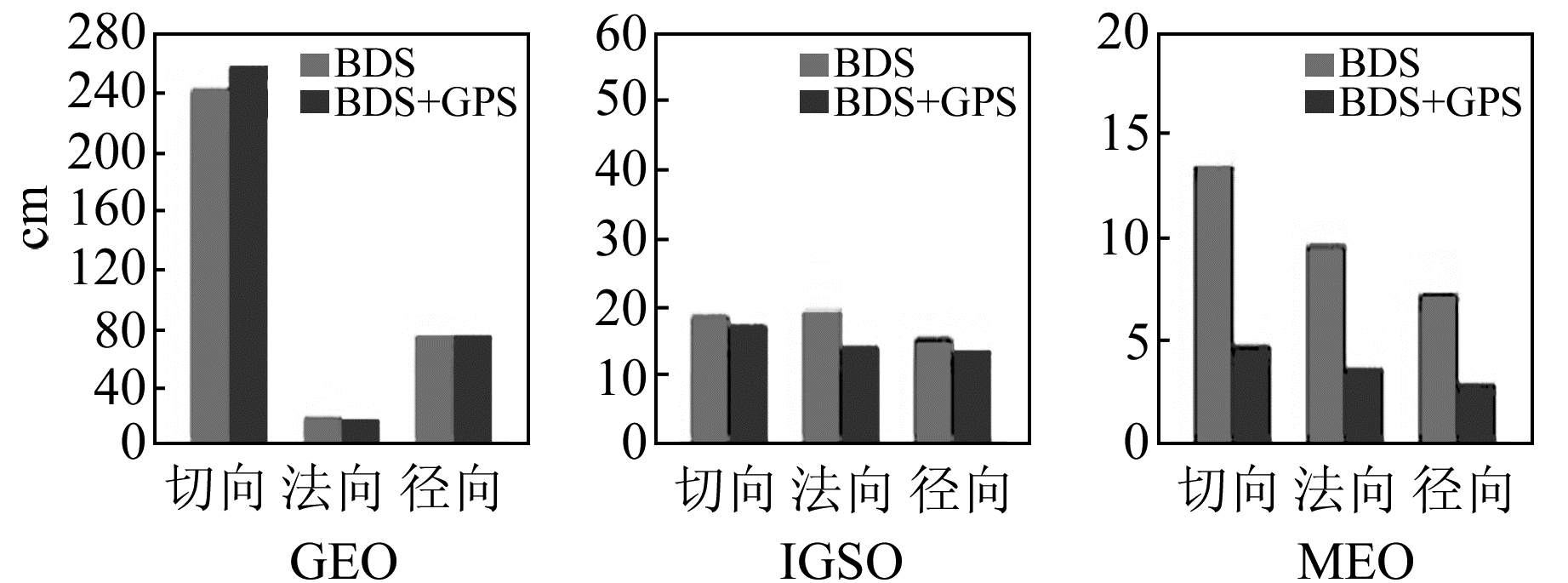
图 11 全球网1 d解轨道与GFZ轨道差值平均RMS Fig. 11 Mean RMS of orbit difference with GFZ orbit of 1 d solution with the global tracking network |
|
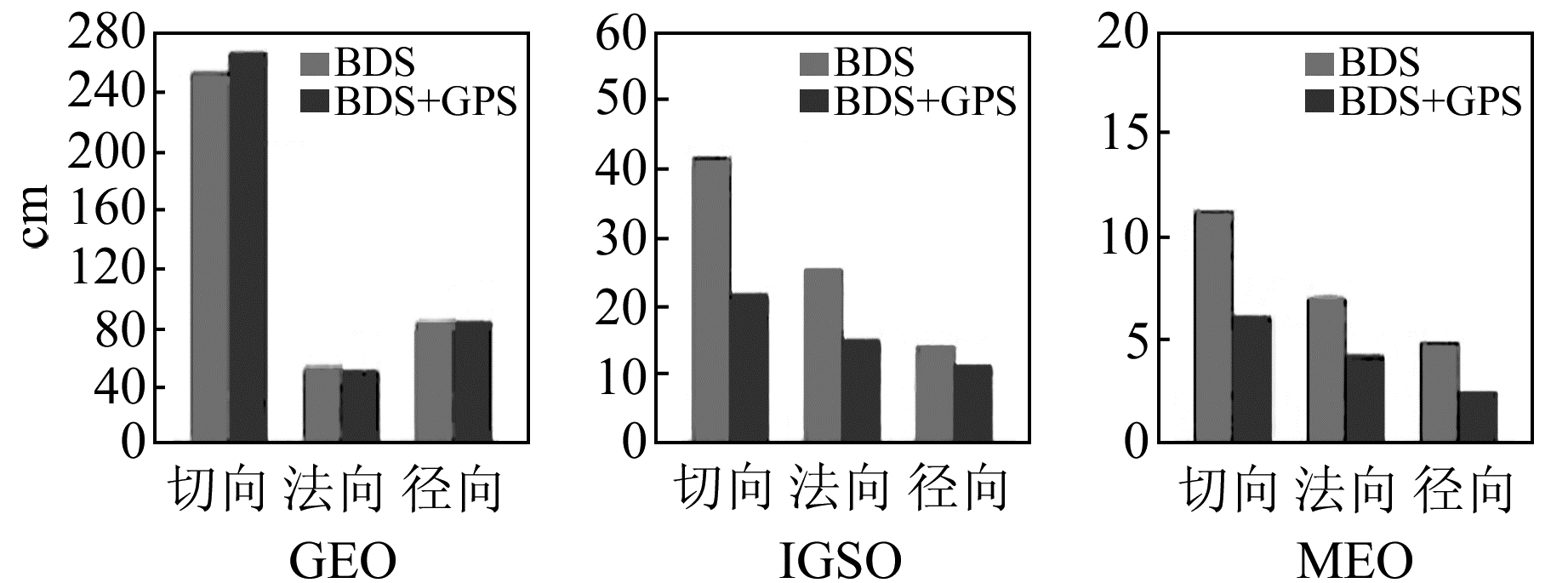
图 12 全球网3 d解轨道与GFZ轨道差值平均RMS Fig. 12 Mean RMS of orbit difference with GFZ orbit of 3 d solution with the global tracking network |
|
|
表 4 全球网1 d解卫星钟差与GFZ钟差差异 Tab. 4 Satellite clock difference with GFZ clock of 1 d solution with the global tracking network |
|
|
表 5 全球网3 d解卫星钟差与GFZ钟差差异 Tab. 5 Satellite clock difference with GFZ clock of 3 d solution with the global tracking network |
由图 11和图 12可知,全球网条件下的联合定轨对1 d解和3 d解的北斗IGSO/MEO卫星轨道的外符合精度也均有一定的改善,但对GEO卫星影响较小。从表 4和表 5的卫星钟差比较结果中也可以得出同样的结论。
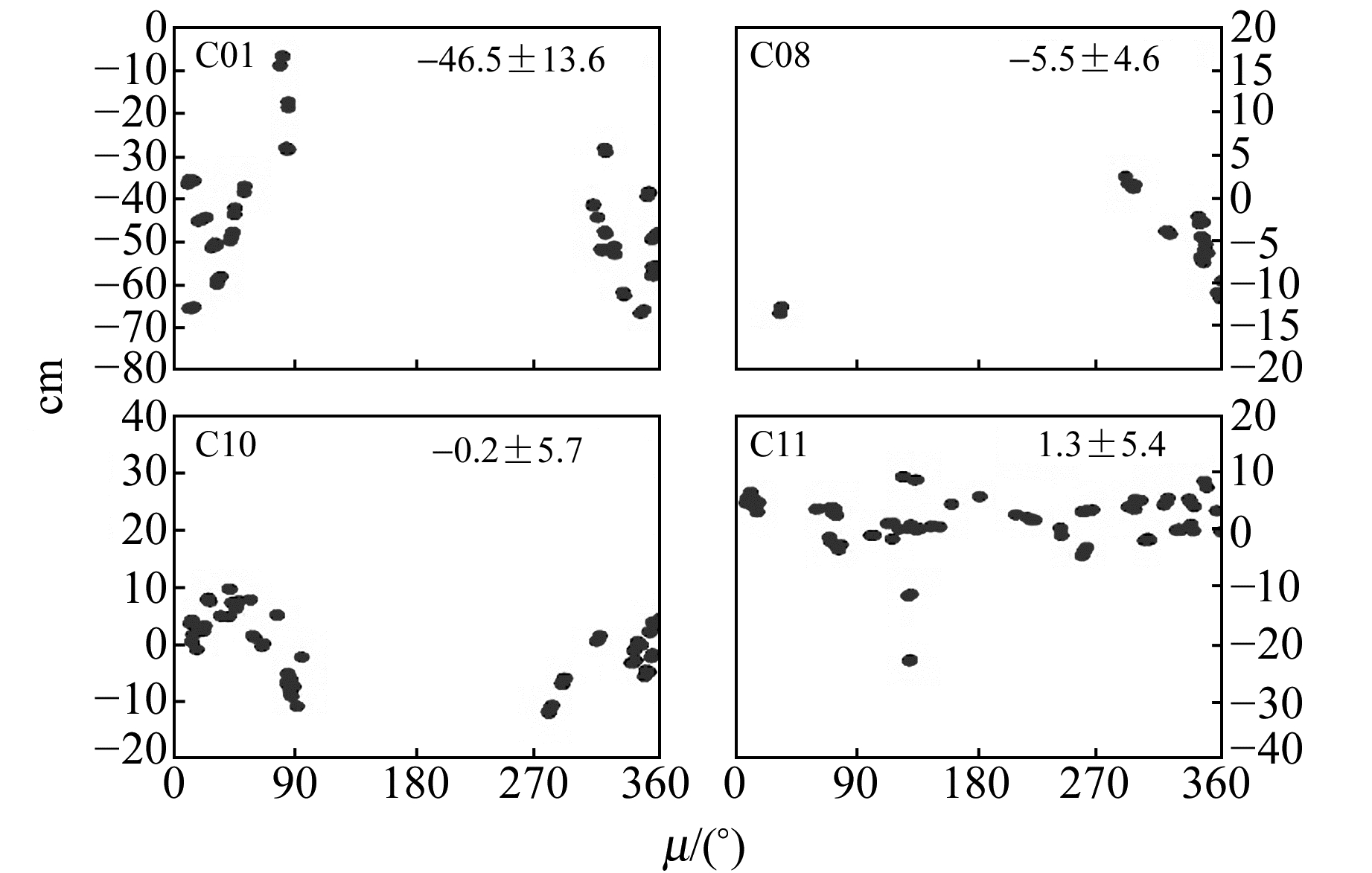
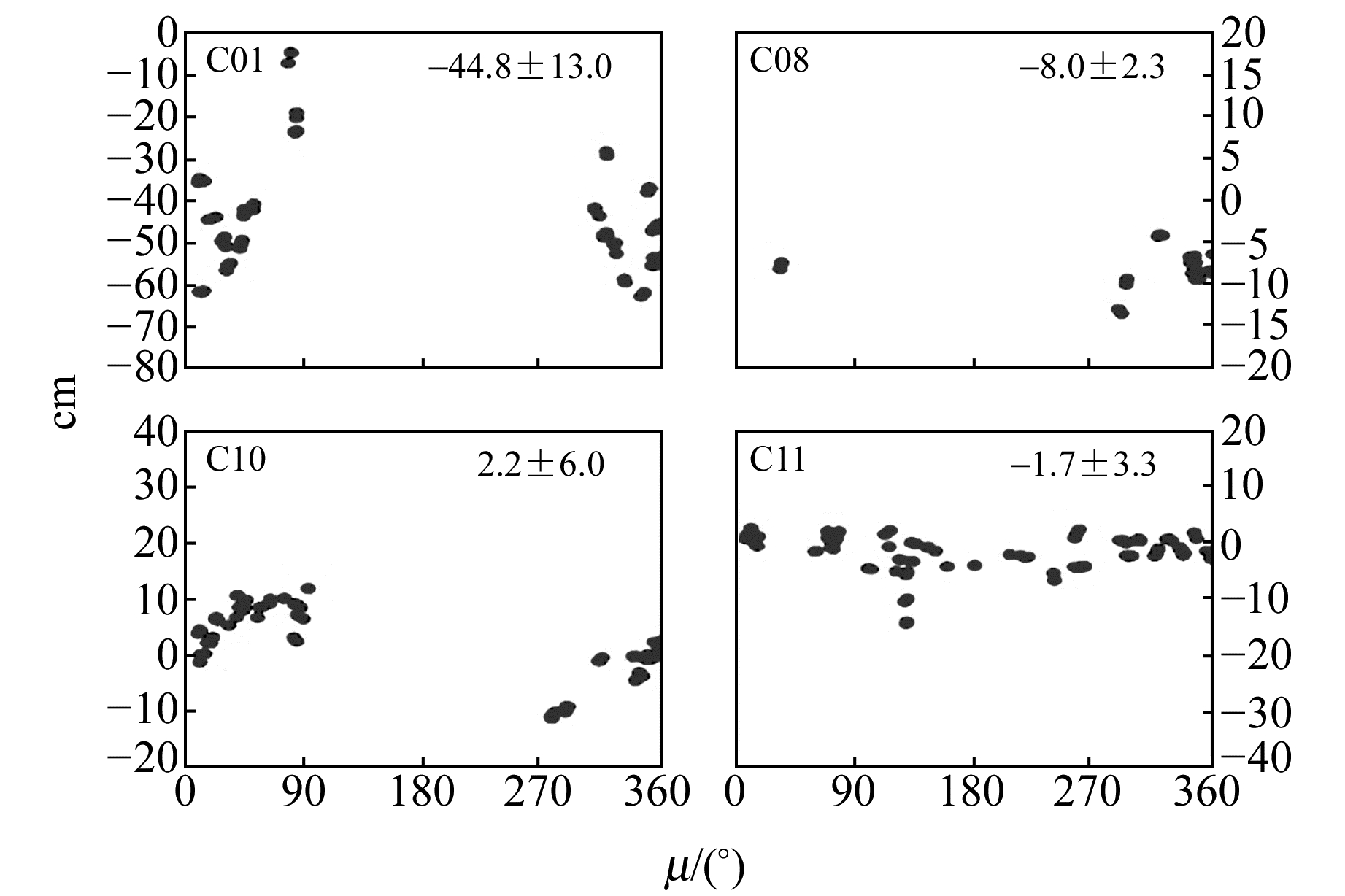
3.3 SLR检核残差图 13~图 16给出全球网条件下采用1 d和3 d弧长解算时BDS独立定轨与GPS/BDS联合定轨解得的北斗4颗卫星轨道的SLR检核残差相对卫星轨道角μ的变化,并于各图右上角给出相应残差序列的均值和标准差。表 6(单位cm)则统计了相应定轨结果的SLR残差RMS。
|
图 13 全球网1 d解BDS独立定轨的SLR残差 Fig. 13 SLR residuals of 1 d BDS-only solution with the global tracking network |
|
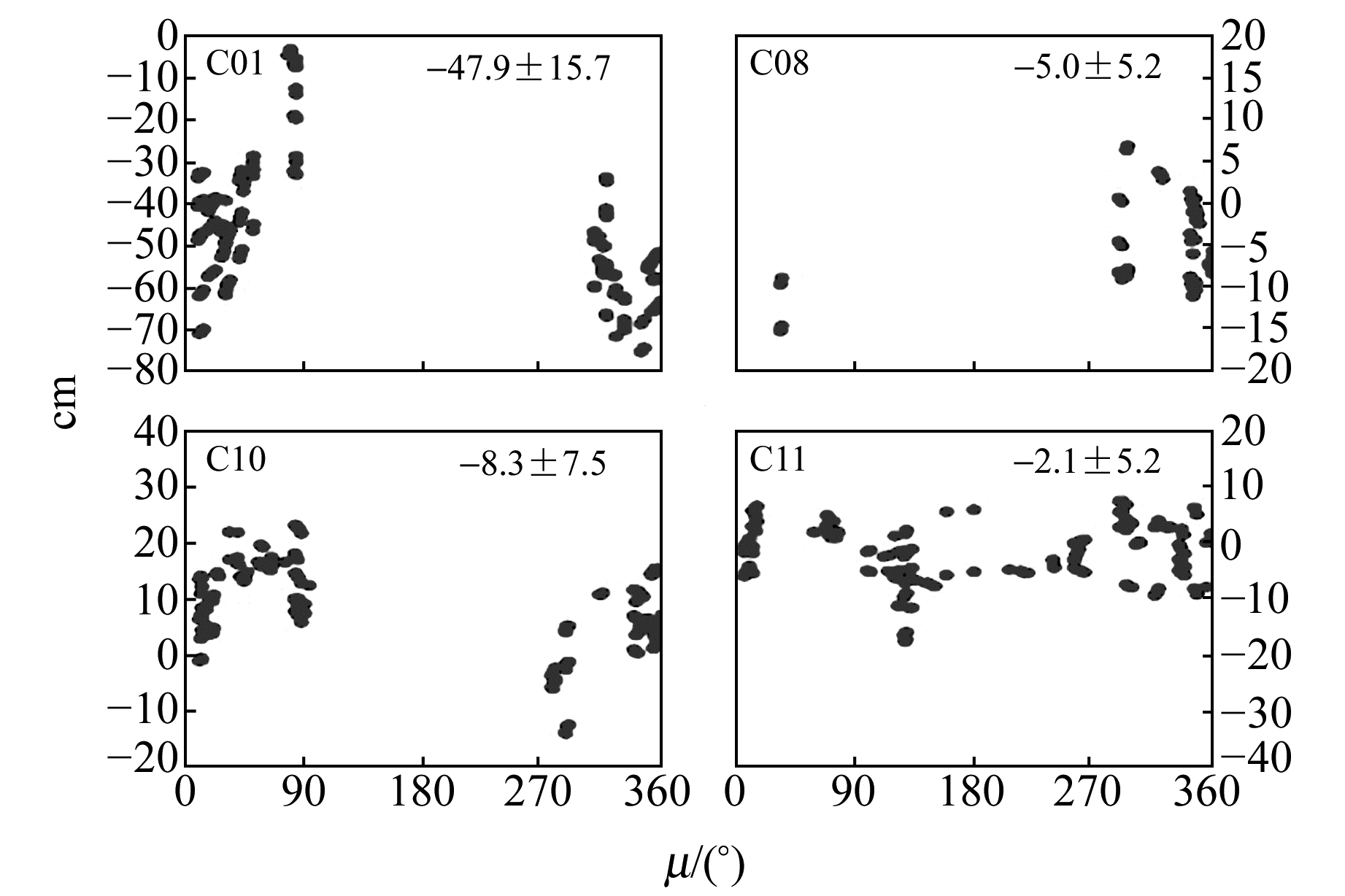
图 14 全球网1 d解GPS/BDS联合定轨的SLR残差 Fig. 14 SLR residuals of 1 d GPS/BDS combined solution with the global tracking network |
|
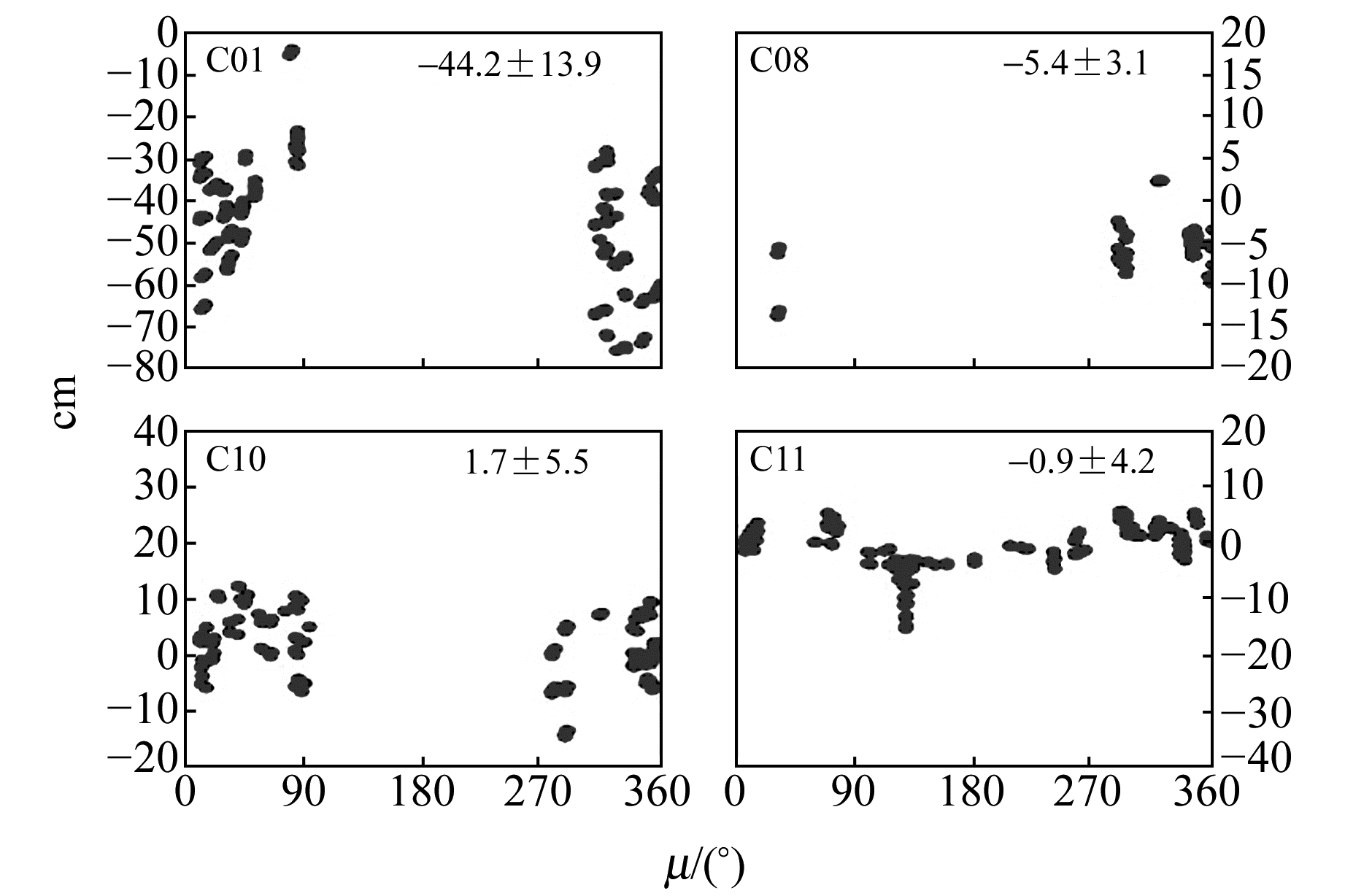
图 15 全球网3 d解BDS独立定轨的SLR残差 Fig. 15 SLR residuals of 3 d BDS-only solution with the global tracking network |
|
图 16 全球网3 d解GPS/BDS联合定轨的SLR残差 Fig. 16 SLR residuals of 3 d GPS/BDS combined solution with the global tracking network |
|
|
表 6 全球网定轨结果的SLR残差RMS Tab. 6 RMS of SLR residuals of orbits with the global tracking network |
由图 13~图 16以及表 6可以看出,全球网条件下,就轨道径向绝对精度而言,采用1 d定轨弧长的BDS独立定轨已能够达到相当的水平[16],即GEO卫星在50 cm左右(径向存在超过40 cm的系统性偏差),IGSO/MEO卫星优于10 cm,这也与文献[7]的结果基本一致。延长定轨解算弧长以及采用联合定轨,对于BDS卫星轨道的径向绝对精度均无显著提升。
4 结语本文通过实测数据详细分析不同跟踪站分布和定轨弧长条件下联合定轨对于BDS卫星定轨精度的改善,主要结论如下:
1) 区域网条件下,采用1 d定轨弧长时,联合定轨能够显著提升北斗IGSO/MEO卫星的轨道精度,尤其是MEO卫星的沿迹方向;而采用3 d定轨弧长时,联合定轨对BDS各类卫星定轨精度的改善作用均较小。
2) 全球网条件下,无论是1 d还是3 d定轨弧长,联合定轨均能够在一定程度上改善北斗IGSO/MEO卫星轨道沿迹方向和法向的精度,但对径向绝对精度的改善较小。而对于北斗GEO卫星,全球网条件下的联合定轨对其轨道各方向的精度影响均较小。
| [1] |
施闯, 赵齐乐, 李敏, 等. 北斗卫星导航系统的精密定轨与定位研究[J]. 中国科学:地球科学, 2012, 42(6): 854-861 (Shi Chuang, Zhao Qile, Li Min, et al. Precise Orbit Determination of Beidou Satellites with Precise Positioning[J]. Science in China: Earth Science, 2012, 42(6): 854-861)
(  0) 0) |
| [2] |
刘伟平, 郝金明, 李建文, 等. 一种北斗卫星精密定轨方法[J]. 测绘科学技术学报, 2013, 30(3): 247-250 (Liu Weiping, Hao Jinming, Li Jianwen, et al. A Method of Precise Orbit Determination of Beidou Navigation Satellite[J]. Journal of Geomatics Science and Technology, 2013, 30(3): 247-250 DOI:10.3969/j.issn.1673-6338.2013.03.007)
(  0) 0) |
| [3] |
Montenbruck O, Hauschild A, Steigenberger P, et al. Initial Assessment of the COMPASS/Beidou-2 Regional Navigation Satellite System[J]. GPS Solutions, 2013, 17(2): 211-222 DOI:10.1007/s10291-012-0272-x
(  0) 0) |
| [4] |
Steigenberger P, Hugentobler U, Hauschild A, et al. Orbit and Clock Analysis of Compass GEO and IGSO Satellites[J]. Journal of Geodesy, 2013, 87(6): 515-525 DOI:10.1007/s00190-013-0625-4
(  0) 0) |
| [5] |
Lou Y, Liu Y, Shi C, et al. Precise Orbit Determination of Beidou Constellation Based on BETS and MGEX Network[J]. Scientific Reports, 2014, 4(8): 1 255-1 264
(  0) 0) |
| [6] |
刘伟平, 郝金明, 李建文, 等. 多GNSS融合的北斗卫星精密定轨[J]. 测绘学报, 2014, 43(11): 1 132-1 138 (Liu Weiping, Hao Jinming, Li Jianwen, et al. Multi-GNSS Joint Precise Orbit Determination of Beidou Navigation Satellite System[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1 132-1 138)
(  0) 0) |
| [7] |
Lou Y, Liu Y, Shi C, et al. Precise Orbit Determination of Beidou Constellation: Method Comparison[J]. GPS Solutions, 2016, 20(2): 259-268 DOI:10.1007/s10291-014-0436-y
(  0) 0) |
| [8] |
刘伟平, 郝金明, 魏伟, 等. 两种北斗卫星精密定轨方法的对比[J]. 大地测量与地球动力学, 2016, 36(3): 211-215 (Liu Weiping, Hao Jinming, Wei Wei, et al. Comparison of Two Methods of Precise Orbit Determination of Beidou Satellites[J]. Journal of Geodesy and Geodynamics, 2016, 36(3): 211-215)
(  0) 0) |
| [9] |
Tegedor J, Øvstedal O, Vigen E. Precise Orbit Determination and Point Positioning Using GPS, GLONASS, Galileo and Beidou[J]. Journal of Geodetic Science, 2014, 4(1): 65-73
(  0) 0) |
| [10] |
Dai X, Ge M, Lou Y, et al. Estimating the Yaw-Attitude of BDS IGSO and MEO Satellites[J]. Journal of Geodesy, 2015, 89(10): 1 005-1 018 DOI:10.1007/s00190-015-0829-x
(  0) 0) |
| [11] |
戴小蕾, 施闯, 楼益栋. 多GNSS融合精密轨道确定与精度分析[J]. 测绘通报, 2016(2): 12-16 (Dai Xiaolei, Shi Chuang, Lou Yidong. Multi-GNSS Precise Orbit Determination and Its Precision Analysis[J]. Bulletin of Surveying and Mapping, 2016(2): 12-16)
(  0) 0) |
| [12] |
张睿, 杨元喜, 张勤, 等. BDS/GPS联合定轨的贡献分析[J]. 武汉大学学报:信息科学版, 2017, 42(5): 600-608 (Zhang Rui, Yang Yuanxi, Zhang Qin, et al. Contribution Analysis of BDS/GPS Combined Orbit Determination[J]. Geomatics and Information Science of Wuhan University, 2017, 42(5): 600-608)
(  0) 0) |
| [13] |
彭汉兵.北斗导航卫星定轨方法及星蚀期定轨问题研究[D].郑州: 信息工程大学, 2016 (Peng Hanbing. Research on Orbit Determination Method and Problem Related to Eclipsing Seasons for BDS[D]. Zhengzhou: Information Engineering University, 2016)
(  0) 0) |
| [14] |
Arnold D, Meindl M, Beutler G, et al. CODE's New Solar Radiation Pressure Model for GNSS Orbit Determination[J]. Journal of Geodesy, 2015, 89(8): 775-791 DOI:10.1007/s00190-015-0814-4
(  0) 0) |
| [15] |
杨元喜. 卫星导航的不确定性、不确定度与精度若干注记[J]. 测绘学报, 2012, 41(5): 646-650 (Yang Yuanxi. Some Notes on Uncertainty, Uncertainty Measure and Accuracy in Satellite Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 646-650)
(  0) 0) |
| [16] |
彭汉兵, 杨元喜, 王刚, 等. 星蚀期北斗卫星轨道性能分析——SLR检核结果[J]. 测绘学报, 2016, 45(6): 639-645 (Peng Hanbing, Yang Yuanxi, Wang Gang, et al. Performance Analysis of BDS Satellite Orbits during Eclipse Periods: Results of Satellite Laser Ranging Validation[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(6): 639-645)
(  0) 0) |
2. State Key Laboratory of Geo-Information Engineering, 1 Mid-Yanta Road, Xi'an 710054, China;
3. Beijing Satellite Navigation Center, 22 Beiqing Road, Beijing 100094, China;
4. China Earthquake Networks Center, 5 Sanlihenanheng Street, Beijing 100045, China
 2018, Vol. 38
2018, Vol. 38

