在地震同震滑动分布反演中，地表形变位移值与滑动参数之间为线性关系。滑动分布参数与地表形变位移的线性模型依赖于系数格林矩阵的构造。系数格林矩阵元素通常是在确定断层的几何参数后，将断层破裂面进一步离散成若干断层子块，继而由每个子块的单位滑动量引起的地表形变位移构成^[1]。通常系数格林矩阵在地震滑动分布反演过程中是病态的，一般采用Tikhonov正则化方法解决系数格林矩阵的病态问题^[2]。

在Tikhonov正则化过程中，正则化参数的选取尤为重要，不同的正则化参数会使反演结果大不相同。目前常用的方法有广义交叉核实法(generalized cross validation, GCV)^[3]、岭迹法^[4]、L曲线法^[5-6]。GCV法理论上能获得较优的正则化参数，但有时GCV方法函数绘制的曲线过于平缓，很难定位到最优正则化参数^[7]；岭迹法计算简单，但在确定正则化参数时存在主观性。在地震同震滑动分布反演中，一般采用数据拟合残差和模型粗糙度之间的折中曲线来确定(由于其形似“L”，故称其为L曲线法)，但L曲线法在确定正则化参数过程中具有以下缺点：无法从L曲线图中根据横坐标轴直观读取正则化参数的大小；L曲线法过于依赖数据拟合精度^[8]，求解过程可能不收敛^[9]。

针对以上问题，本文提出利用U曲线法确定地震滑动分布反演的正则化参数，通过模拟实验以及芦山实际震例反演，验证U曲线法确定地震滑动分布反演正则化参数的可行性与优势。

1 U曲线法确定正则化参数 1.1 地震滑动分布反演基本方程

地震滑动分布反演中，地震滑动分布位移与地震滑动参数之间关系可表达为：

$ \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{Gm}} + \mathit{\boldsymbol{\varepsilon }} $

(1)

式中，d表示用InSAR观测到的LOS向形变量或GPS观测到的3个方向的形变量；G为系数格林矩阵；m为地震滑动参数；ε 为InSAR数据或GPS数据观测误差。

在地震滑动分布反演中，为避免系数格林矩阵的秩亏性同时保证断层面各断层块间的平滑度，本文采用Tikhonov正则化解法求解滑动分布，并引入目前较为成功的用于断层面平滑约束的二阶拉普拉斯平滑算子进行约束，使得：

$ \mathit{\boldsymbol{Hm}} = {\bf{0}} $

(2)

式中，0 视为虚拟观测矩阵，H为拉普拉斯平滑矩阵，R=H^TH视为正则化矩阵。

根据Tikhonov提出的正则化理论，得到估计准则为:

$ \begin{array}{l} \;\;{\left\| {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Gm}}} \right\|^2} + \alpha \Omega \left( \mathit{\boldsymbol{m}} \right) = \\ {\left\| {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Gm}}} \right\|^2} + \alpha {\mathit{\boldsymbol{m}}^{\rm{T}}}\mathit{\boldsymbol{Rm}} = {\rm{min}} \end{array} $

(3)

式中，Ω(m)为稳定泛函；‖·‖为·的二范数；α为地震滑动分布反演时的正则化参数，在本文中采用U曲线法确定正则化参数α。

1.2 U曲线法基本原理

由式(1)、(2)可得地震滑动参数解为：

$\mathit{\boldsymbol{m}} = {({\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{pG}} + \alpha \mathit{\boldsymbol{R}})^{-1}}{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{pd}} $

(4)

式(4)表明，地震滑动参数解的大小随正则化参数α的变化而变化，因此选择一个合理的正则化参数在地震滑动分布反演中尤为重要。

U曲线法确定正则化参数与L曲线法类似。L曲线法是根据不同的α值分别得到一组‖ d-Gm‖²、‖Hm‖²值，以‖ d-Gm‖²为横坐标、‖Hm‖²为纵坐标拟合成一条类似“L”形状的曲线，取L曲线上拐点附近对应的α值作为最优正则化参数^[10]。可以看出，L曲线法的精度依赖于‖d-Gm‖²与‖Hm‖²数据之间的拟合程度。U曲线法则是通过定义U(α)函数，根据α的取值得到U(α)-α曲线，曲线左侧近似垂直部分曲率最大点所确定的α值即为最优正则化参数^[11-12]。U曲线法定义如下：

$ U\left( \alpha \right) = \frac{1}{{{{\left\| {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Gm}}} \right\|}^2}}} + \frac{1}{{{{\left\| {\mathit{\boldsymbol{Hm}}} \right\|}^2}}} $

(5)

式中，${{{{\left\| {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Gm}}} \right\|}^2}}} = \sum\limits_{i = 1}^r {\frac{{{\alpha ^4}\beta _i^4\theta _i^2}}{{{{(\sigma _i^2 + \alpha \beta _i^2)}^2}}}} $，$ {\left\| {\mathit{\boldsymbol{Hm}}} \right\|^2} = \sum\limits_{i = 1}^r {\frac{{\alpha _i^2\beta _i^2\theta _i^2}}{{{{(\sigma _i^2 + \alpha \beta _i^2)}^2}}}} $，θ=u^Td，其中 u为系数格林矩阵 G经过奇异值分解后的左侧奇异值矩阵，σ₁≥σ₂…≥σ_r＞0为系数格林矩阵 G经过奇异值分解后r个从大到小排列的奇异值，β₁≥β₂…≥β_r＞0为拉普拉斯二阶平滑矩阵经过奇异值分解后r个从大到小排列的奇异值。

1.3 两种方法比较

由L曲线定义可以得出，L曲线在确定正则化参数的过程中需要依赖于数据拟合残差‖d-Gm‖²以及模型粗糙度‖Hm‖²之间的数据拟合程度，且从L曲线图上无法直观地从横坐标获得最优正则化参数的大小。由文献[11]及U曲线定义可以得出以下结论：U曲线在区间$\alpha \in \left( {0, \sigma _r^{\frac{2}{3}}} \right)$内严格递减，在区间$\alpha \in \left( { \sigma _1^{\frac{2}{3}}} , + \infty \right)$严格递增，此处σ₁≥σ₂…≥σ_r＞0为系数格林矩阵 G经过奇异值分解后r个从大到小排列的奇异值；U曲线在区间$\alpha \in \left( {\sigma _r^{\frac{2}{3}}, \sigma _1^{\frac{2}{3}}} \right)$存在局部最小值，并且当系数格林矩阵 G只含一个非零奇异值时，U(α)函数只含有一个极小值；$\mathop {\lim }\limits_{\alpha \to {0^ + }} U\left( \alpha \right) = + \infty, \mathop {\lim }\limits_{\alpha \to + \infty } U\left( \alpha \right) = + \infty $。

综合以上分析可以看出，利用U曲线法确定正则化参数较L曲线法具有无需依赖数据拟合度，不会出现因曲线发散而无法确定正则化参数的情况^[7]，可以从U曲线图中直观读取正则化参数大小等优势。另外，在同震滑动分布反演中，观测值与位错模型反演值之间的均方根误差(RMS)大小常常用作评判滑动分布反演精度，其可表达为：

$ {\rm{RMS}} = \sqrt {\frac{{\sum\limits_{i = 1}^n {{P_i}{{({d_i} - {c_i})}^2}} }}{n}} $

(6)

式中，n表示观测值个数，d和c分别表示观测值和模型反演值所构成的矩阵，P表示观测值权阵。

2 模拟实验

在模拟实验中，断层面几何参数如下：断层面几何中心位置X=0 km，Y=0 km，断层中心深度Depth=10 km，长度L=42 km，宽度W=42 km，走向角strike=55°，倾角dip=40°，滑动角φ=60°。根据点位与震中距离设置形变点密度模拟InSAR数据592个如图 1所示，并给InSAR形变点施加观测误差N(0, 3²mm²)。为了使观测数据更贴近实际，本文采取拉奎拉实际地震^[13]InSAR观测时的升轨和降轨迹线的方位角以及雷达波入射角，确定InSAR数据LOS向形变观测值与地表形变分量的转换系数。

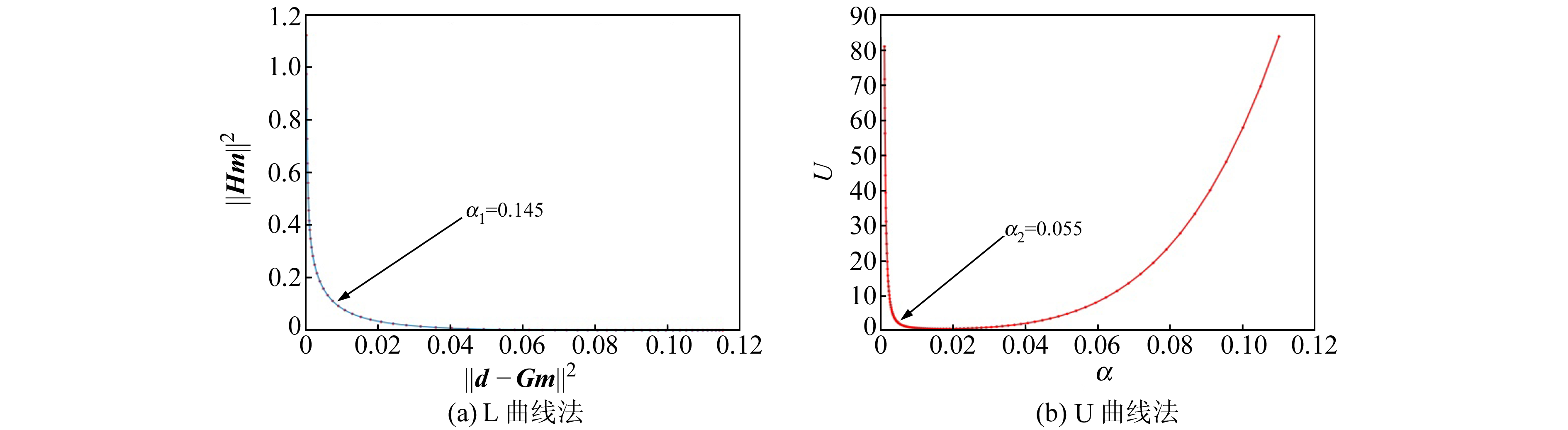
在模拟实验中，本文分别采用L曲线法、U曲线法确定反演过程中的正则化参数(见图 2)，其中，L曲线法得到的正则化参数为α₁=0.145，U曲线法确定的正则化参数为α₂=0.055。两种方法反演地震滑动分布结果及残差分布如图 3所示，其中，图 3(a)、(b)分别为利用L曲线法、U曲线法反演的滑动分布结果；图 3(c)、(d)为两种方法反演的滑动分布结果与真值的差值分布。

在模拟实验中，利用L曲线法、U曲线法反演地震滑动分布各参数结果见表 1；部分参数与真值的差值以及U曲线法反演结果较L曲线法改进程度见表 2。

从表 1、表 2可以看出，用U曲线法确定正则化参数反演模拟实验各参数结果较L曲线法反演结果更接近预设参数(真值)，在最大滑动量、平均滑动量上U曲线法反演结果优势更明显。另外，在地震滑动分布反演中均方根误差常常作为评判反演精度的指标，均方根误差越小，说明反演参数大小与真值越接近，反演精度越高。两种方法反演结果的均方根误差大小可以进一步说明U曲线法反演地震滑动分布精度要优于L曲线法。

3 芦山实际震例反演

2013-04-20 08：02四川芦山发生M7.0地震，震源深度13 km。地震发生后，不同研究机构对此次地震进行快速反演分析，研究地震震源机制和反演地震震源参数，但基于不同的手段所反演出的震源参数结果具有一定的差异。本文采用文献[14]获取的GPS三维形变数据来约束地表形变场，利用文献[1]通过多峰值颗粒群算法获得的芦山地震断层参数作为反演芦山地震的断层参数。在此基础上将断层破裂面沿断层走向、倾向把断层长度、宽度均扩展至51 km，并将破裂面延伸至地表，将断层面均匀剖分成1.5 km×1.5 km大小的矩形单元，共得到了1 156个矩形断层单元。

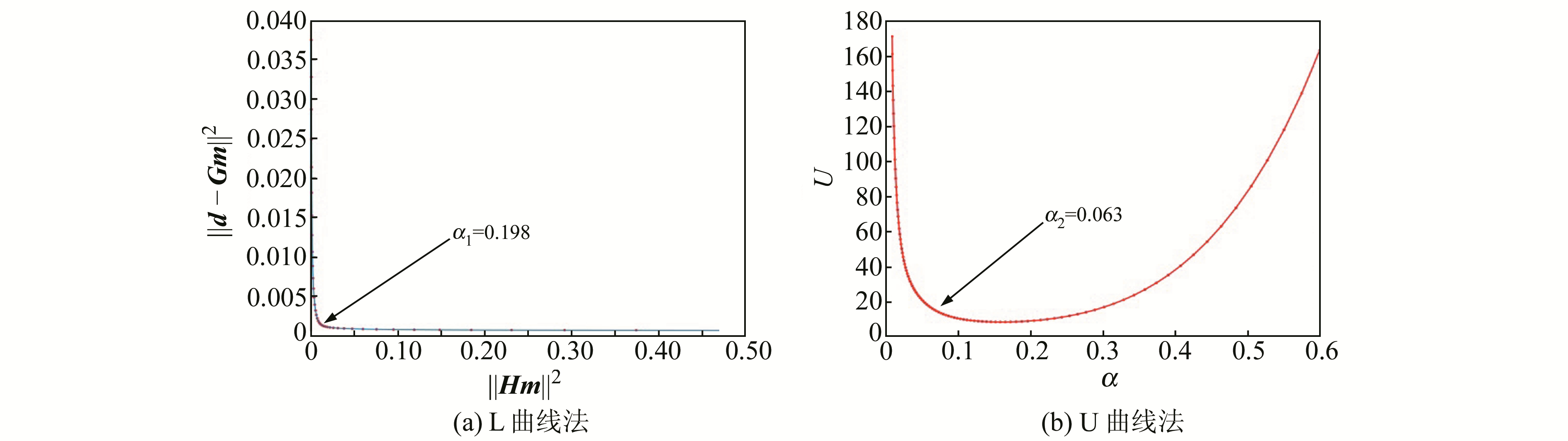
分别采用L曲线法、U曲线法确定反演的正则化参数(见图 4)，其大小分别为α₁=0.198，α₂=0.063。

两种方法反演的地震滑动分布结果及残差分布如图 5所示，其中，图 5(a)、(b)分别为利用L曲线法、U曲线法反演的滑动分布结果；图 5(c)为两种方法反演的滑动分布结果差值分布。

两种方法反演芦山地震滑动分布各参数结果见表 3；近年来部分学者研究芦山地震各参数结果见表 4。

由图 5(a)、(b)可以看出，本文两种方法反演的芦山地震结果均显示芦山地震主震区分布在地下4~20 km深度范围内。由表 3可以看出，由于正则化参数选取方法不同，使反演芦山地震震源各参数结果具有一定的差异。表 4给出了近年来多位学者基于不同数据、不同方法反演的芦山地震各震源参数结果。综合表 3、表 4可以看出，本文确定的断层位置与文献[14]确定的位置以及CENC、USGS机构利用地震波确定的结果较一致；对于最大滑动量，本文两种方法反演结果分别为0.54 m、0.68 m，略小于文献[1]、文献[15]反演的结果。对于最大滑动量，文献[16]综合地震震源机制及断层的地质构造资料确定出断层的位置、走向、倾角等参数，反演出最大滑动量为1.59 m；文献[14]反演得到的最大滑动量为0.61 m，结果也小于其通过格网搜索法均匀反演得到的0.70 m。最大滑动量差别比较明显，主要的原因可能与约束的地震数据有关。对于矩震级参数，本文两种方法反演的矩震级分别为M_W6.65、M_W6.69，对应的矩张量分别为1.06×10¹⁹ N·m、1.24×10¹⁹ N·m，这两种方法反演结果均在其他学者研究范围内。均匀滑动反演的矩震级和矩张量分别为M_W6.54和0.72×10¹⁹ N·m。均匀滑动将断层面看作均匀整体，所以可能遗漏了细节滑动，导致整体矩张量偏小。文献[16]反演的矩震级和矩张量分别为M_W6.7和1.54×10¹⁹ N·m，相对其他几位学者反演结果更大；对于均方根误差，U曲线法反演结果要小于L曲线法。由以上分析可以看出，本文两种方法反演的芦山地震滑动分布结果均在其他学者研究范围内；由于原始数据来源、研究方法以及预设的断层参数的不同，导致最后反演得出的各断层参数具有一定的差异。综上，利用U曲线法确定实际地震正则化参数具有一定的可行性与优势。

对于本文所做的模拟实验以及芦山实际地震实验，可以看出U曲线法确定正则化参数较L曲线法的优势为：1)对于反演精度，从模拟实验中可以看出，利用U曲线法确定正则化参数反演的滑动分布各参数结果与真值的差值均小于L曲线法，即在模拟实验中U曲线法确定的正则化参数反演精度要高于L曲线法；从模拟实验以及芦山实际震例反演的均方根误差参数可以看出，利用U曲线法反演结果的均方根误差均小于L曲线法，其原因是利用U曲线法确定的正则化参数要小于L曲线法，由图 2(b)、图 4(b)及式(6)可知，正则化参数越小，对应的拟合残差越小，使反演的均方根误差也相对变小。但正则化参数α的大小也不能无限变小，只能在一定的范围内，否则无法起到正则化的作用，不能削弱系数格林矩阵病态问题，从而使反演结果不稳定。从本文模拟实验以及实际震例实验可以看出，U曲线法确定的平滑因子能很好地控制在α的合适范围内，使反演结果平滑度相当，从而进一步表明在地震滑动分布反演中利用U曲线法确定正则化参数较L曲线法更为合适。2)从绘制的L曲线图与U曲线图可以看出，由于U曲线图横坐标即为平滑因子α的大小，故从U曲线图上可以直观地读取平滑因子的大小，而从L曲线图中却不能直观读取α大小；L曲线图绘制的时候需要依赖‖d-Gm‖²和‖Hm‖²之间的数据拟合精度，U曲线法则不需要。

4 结语

本文提出的U曲线法为地震滑动分布反演中正则化参数的确定增加了一条新的途径。本文通过模拟实验以及芦山实际地震反演表明，U曲线法较L曲线法确定正则化参数具有反演精度高、U曲线图横坐标直观反映正则化参数大小、无需依赖于数据拟合度等优势。另外，对于U曲线法确定的正则化参数要小于L曲线法，这可能与L曲线法过度依赖于‖d-Gm‖²与‖Hm‖²之间的数据拟合程度，使绘制的L曲线有时收敛性差有关，至于具体原因有待于进一步探讨与研究。