2. 海岛(礁)测绘技术国家测绘地理信息局重点实验室, 青岛市前湾港路579号, 266590
机载LiDAR系统集激光扫描仪、GNSS和INS、航空数码相机等传感器于一体,以飞机为载体,获得被测物体反射激光到达激光器的时间差,加以各项改正(系统校准、姿态改正、航带拼接等)后即可计算出点位坐标。该系统可快速获取高密度的三维地形信息,地形特征提取自动化程度高,是地形特征提取的重要手段之一[1-2]。在激光点云基础上,地形特征信息(曲率、粗糙度、坡度等)的提取能够为地图制图、地震地质、地形分类及DEM生产等应用研究领域提供丰富、高价值的数据支撑。因此,如何快速有效地利用机载LiDAR系统获取地形特征信息已成为重要的研究课题。
目前,国内外相继开展了基于机载LiDAR的地形特征信息的提取研究。对于提取整体地形特征参数,Lohmann等[3]基于统计理论的线性预估方法过滤点云,实现了地形特征参数的提取,该方法的局限性是必须进行迭代,否则中等地势以上点的精度会受到很大影响;Susaki[4]针对预先估计DTM的初始值,斜率参数随DTM的值变化而变化的特点,利用平面特征和斜率参数实现了地形特征的提取;Park等[5]将接触式传感器用于地形特征提取中,并将该方法与基于快速傅里叶变换的地形特征提取方法作比较进行了验证。对于地形粗糙度和坡度的提取,Matthies等[6]提出一种基于纹理信息提取地形粗糙度和基于像差原理提取坡度的算法,该方法采用灰度分布标准差拟合地形信息,因坡度估计对误差过于敏感,在一定程度上影响了提取精度;王强锋等[7]采用双线性插值重采样法对地形高程数据进行预处理,并利用拟合的中值平面进行粗糙度和坡度的提取,该方法的重采样过程破坏了数据的原始分布,且平面拟合相对曲面拟合精度较低;Hollaus等[8]利用地形点的平面拟合残差的标准偏差来计算地表粗糙度,该算法不能有效地表达地形复杂程度。对于曲率和坡度的提取,Klingseisen等[9]利用规则格网实现了地形坡度与平面曲率、剖面曲率的计算,即先将原始激光点规则格网化,该方法虽然提取速度快,但由此得到的曲率和坡度精度会随之降低;张蓉[10]提出一种基于稳健统计的移动最小二乘曲面计算曲率的方法,该方法通过变窗宽最大核密度估计得到最佳子点集,并以该点集拟合出最优移动最小二乘曲面,从而计算曲面的曲率,该算法相对传统的曲率计算较复杂,提取曲率的时间较长。
针对目前地形特征提取方法中的提取精度低、提取时间较长等问题,本文在现有地形特征提取研究的基础上,提出了一种机载LiDAR地形特征信息的快速提取算法,并验证了该方法的有效性。
1 地形特征信息提取地形特征的提取是地形研究的重要环节,机载LiDAR地形特征信息快速提取算法是机载LiDAR数据处理、构建DEM模型的关键环节之一。提取步骤为:首先,建立二次曲面拟合模型,构建实测LiDAR地形数据与拟合曲面的几何规则;然后,采用LM算法迭代参数寻优,获得最优化结果下的地形拟合参数;最后,以地形拟合模型为基础,进行地形特征信息的快速提取,并结合机载LiDAR实测数据进行精度分析。
地形特征参数通常包括地形点的高程、坡度、曲率和粗糙度等,本文根据地形分类工作需求,确定了需要提取的地形特征信息参数,如表 1所示。
|
|
表 1 地形特征参数描述 Tab. 1 Description of the terrain feature variables |
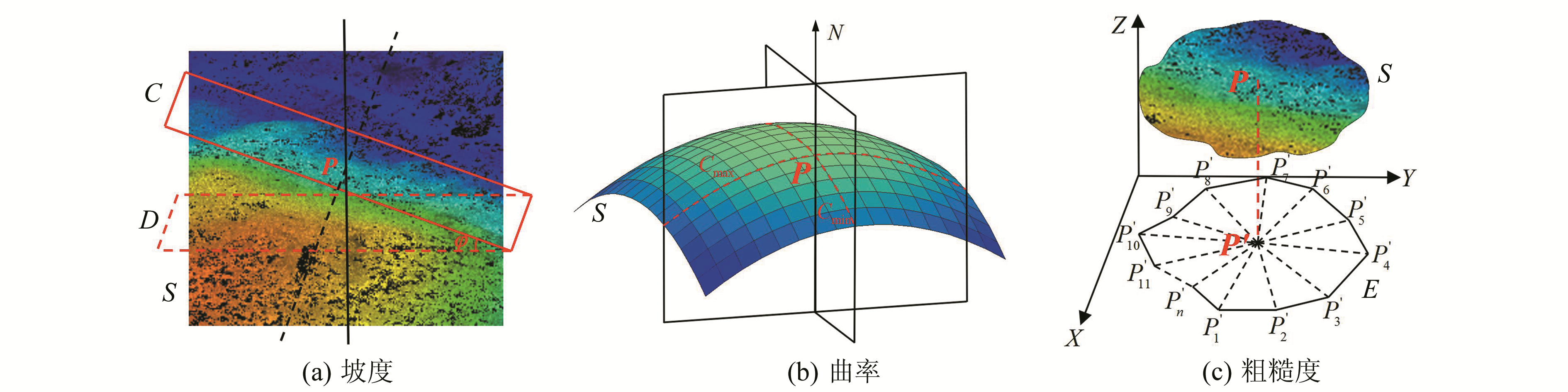
表 1描述了6类地形特征参数,其中局部点密度是统计该点在局部范围内的点位密度;高程标准差是计算该点在局部范围内点的高程标准偏差,二者较易计算。然而,坡度、曲率(高斯曲率、平均曲率)和粗糙度表征的地形意义相对复杂,为便于理解,给出示意图如图 1所示。
|
图 1 部分地形特征示意图 Fig. 1 Schematic illustration of the part of terrain feature variables |
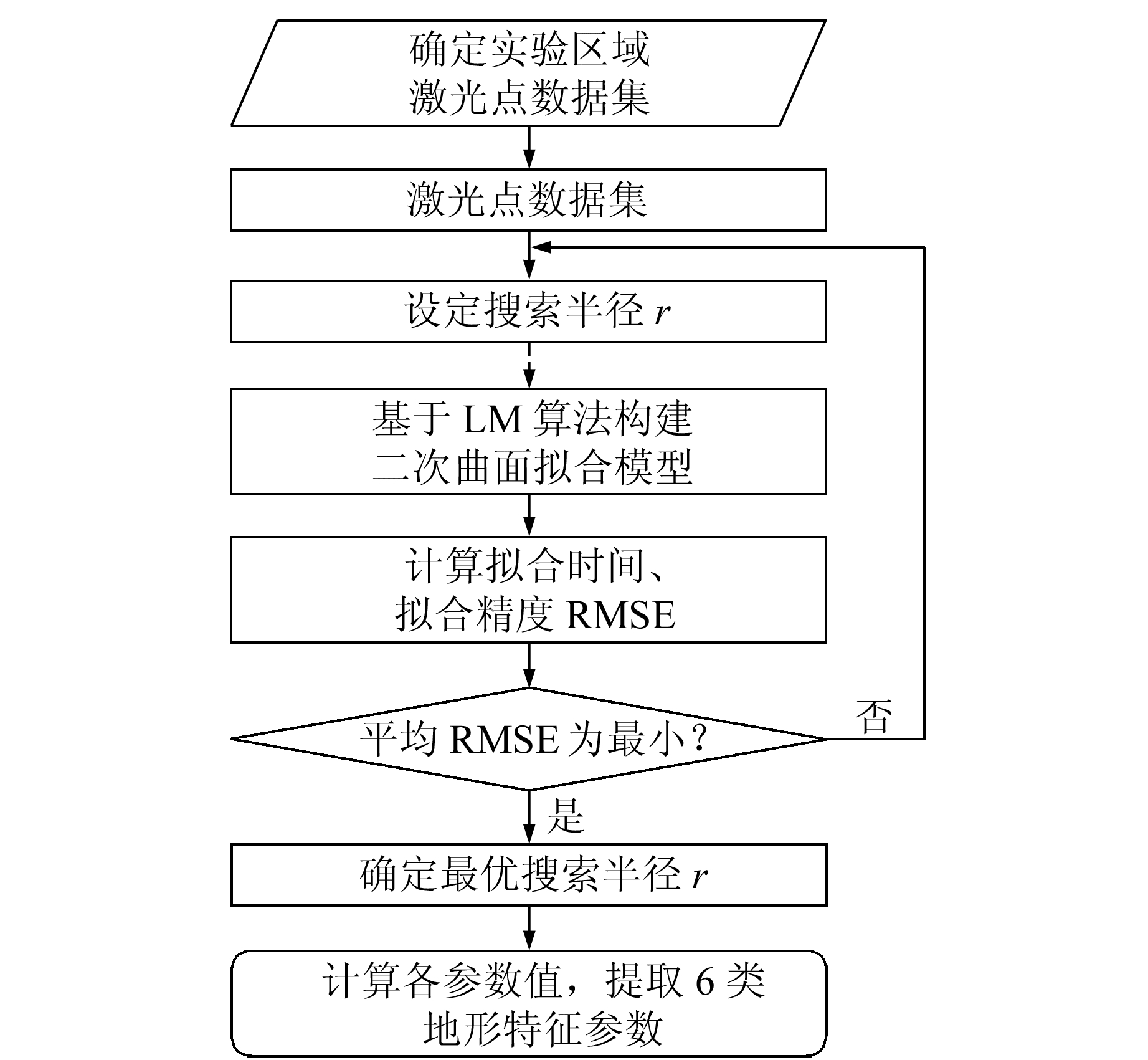
地形特征参数提取的具体步骤如图 2所示。
|
图 2 地形特征参数提取流程 Fig. 2 Flowchart of the terrain features extraction |
6类地形特征参数中,局部点密度和高程标准差不再详细叙述,坡度、曲率(高斯曲率、平均曲率)和粗糙度的提取过程如下。
1.1 二次曲面拟合二次曲面函数能较好地表达曲面的连续性和真实性,故采用LM算法建立地形点的二次曲面拟合模型。以r为搜索半径遍历整个数据集,获得采样点P的采样点集、空间区域大小和曲面特征等信息,统计采样点密度及高程标准差,并根据采样信息进行局部的二次曲面拟合。
设二次曲面拟合模型的表达式为:
| $ z = f\left( {x,y} \right) = a{x^2} + b{y^2} + cxy + dx + ey + f $ | (1) |
式中,(x, y, z)为地形点在局部坐标系中的地理坐标,a、b、c、d、e、f为二次曲面拟合参数。故二次曲面拟合的目标函数为:
| $ \begin{array}{l} {Q^2} = \min \sum\limits_{j = 1}^k {\left[ {{z_j} - \left( {ax_j^2 + by_j^2 + } \right.} \right.} \\ \;\;\;\;{\left. {\left. {c{x_j}{y_j} + d{x_j} + e{y_j} + f} \right)} \right]^2} \end{array} $ | (2) |
其中,(xj, yj, zj)为采样点P的邻域点集N(Pj)内的点, j=1, 2, …, k。
利用奇异值分解法获得二次曲面拟合的最小二乘解,则:
| $ \left\{ \begin{array}{l} \frac{{\partial {Q^2}}}{{\partial a}} = 0,\frac{{\partial {Q^2}}}{{\partial b}} = 0\\ \frac{{\partial {Q^2}}}{{\partial c}} = 0,\frac{{\partial {Q^2}}}{{\partial d}} = 0\\ \frac{{\partial {Q^2}}}{{\partial e}} = 0,\frac{{\partial {Q^2}}}{{\partial f}} = 0 \end{array} \right. $ | (3) |
式(3)可简化为:
| $ \mathit{\boldsymbol{AX}} = \mathit{\boldsymbol{B}} $ | (4) |
其中 A、B为含有(xj, yj, zj)表达式的矩阵,X =(a, b, c, d, e, f)T。假定系数矩阵 A可逆,则:
| $ \mathit{\boldsymbol{X}} = {\mathit{\boldsymbol{A}}^{ - 1}}\mathit{\boldsymbol{B}} $ | (5) |
将(xj, yj, zj)的值代入式(5),求得拟合参数a、b、c、d、e、f的值,即可得到二次曲面拟合的方程式。
1.2 坡度计算坡度反映了地形的倾斜程度,即地形曲面在该点处的切平面与水平面的夹角。图 1(a)中,S为仿真的地形曲面,C为采样点P的切平面,D为水平面。将坡度φ分为x和y方向[11],则有:
| $ \varphi \mathit{\boldsymbol{ = }}{\rm{arctan}}\sqrt {{{\tan }^2}{\varphi _x} + {{\tan }^2}{\varphi _y}} $ | (6) |
其中,
| $ \left[ {\begin{array}{*{20}{c}} {\tan {\varphi _x}}\\ {\tan {\varphi _y}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} p\\ q \end{array}} \right],\left\{ \begin{array}{l} p = \frac{{\partial z}}{{\partial x}} = 2ax + cy + d\\ q = \frac{{\partial z}}{{\partial y}} = 2by + cx + e \end{array} \right. $ |
地形曲率是地形曲面在各个截面方向上的形状和凹凸变化的表达,反映了地形的结构和形态,是地形特征表达的重要因素[12]。已知采样点P具有最大曲率Cmax和最小曲率Cmin,对应的曲率半径分别为Rmax和Rmin,Rmax和Rmin分别是式(7)关于曲率半径R的两个根[13]:
| $ \begin{array}{*{20}{c}} {\left( {rt - {s^2}} \right){R^2} + h\left[ {2pqs - \left( {1 + {p^2}} \right)t - } \right.}\\ {\left. {\left( {1 + {q^2}} \right)r} \right]R + {h^4} = 0} \end{array} $ | (7) |
其中,
通过解方程式(7)可得到Rmax和Rmin,所以最大曲率与最小曲率[14]分别为:
| $ \left. \begin{array}{l} {C_{\max }} = \frac{1}{{{R_{\max }}}}\\ {C_{\min }} = \frac{1}{{{R_{\min }}}} \end{array} \right\} $ | (8) |
根据微分几何原理,高斯曲率CG为最大曲率Cmax和最小曲率Cmin的乘积,即
| $ {C_{\rm{G}}} = {C_{\max }}{C_{\min }} = \frac{{rt - {s^2}}}{{{{\left( {1 + {p^2} + {q^2}} \right)}^2}}} $ | (9) |
平均曲率Cm为最大曲率Cmax和最小曲率Cmin的算术平均值,即
| $ \begin{array}{*{20}{c}} {{C_{\rm{m}}} = \frac{1}{2}\left( {{C_{\max }} + {C_{\min }}} \right) = }\\ { - \frac{{\left( {1 + {q^2}} \right)r - 2pqs + \left( {1 + {p^2}} \right)t}}{{2{{\left( {1 + {p^2} + {q^2}} \right)}^{\frac{3}{2}}}}}} \end{array} $ | (10) |
地形粗糙度常用来表达地表单元地势起伏的复杂程度。地形粗糙度由地表的实际面积与投影面积之间的比值表示[15]。由于地表的实际面积难以求出,故用采样点P及其邻域内的点集拟合成的曲面面积代替实际面积进行计算。图 1(c)中,S为二次拟合曲面,E为曲面的投影平面。设采样点P最外部的邻域点集按逆时针排序为P′1, P′2, …, P′n,投影平面E则可看作是由多边形{(x1, y1), (x2, y2), …, (xn, yn), (x1, y1)}构成的空间封闭区域,故地形粗糙度Kr可由式(11)、(12)计算:
| $ \begin{array}{*{20}{c}} {{K_{\text{r}}} = \frac{{{S_S}}}{{{S_E}}} = \frac{{\iint\limits_E {\sqrt {\left( {1 + {p^2} + {q^2}} \right)} {\text{d}}x{\text{d}}y}}}{{{S_E}}} = } \\ {\frac{{\int_{{x_{\min }}}^{{x_{\max }}} {\int_{{y_{\min }}}^{{y_{\max }}} {\sqrt {\left( {1 + {p^2} + {q^2}} \right)} {\text{d}}x{\text{d}}y} } }}{{{S_E}}}} \end{array} $ | (11) |
| $ {S_E} = \frac{1}{2}\left( {\left| {\begin{array}{*{20}{c}} {{x_1}}&{{y_1}}\\ {{x_2}}&{{y_2}} \end{array}} \right| + \left| {\begin{array}{*{20}{c}} {{x_2}}&{{y_2}}\\ {{x_3}}&{{y_3}} \end{array}} \right| + \cdots + \left| {\begin{array}{*{20}{c}} {{x_n}}&{{y_n}}\\ {{x_1}}&{{y_1}} \end{array}} \right|} \right) $ | (12) |
式中,SS表示采样点P的二次拟合曲面面积,SE表示采样点P的二次拟合曲面相对应的平面投影面积。
2 实验与分析 2.1 研究数据研究数据来自于美国林务局2014年Tahoe国家森林机载LiDAR数据,该机载LiDAR数据是由美国林业第五区域实验室采用全波形LiDAR采集,可由Open Topography开源数据网站下载(http://opentopo.sdsc.edu)。该研究区域约为4.62 km2,东西长约2 403 m,南北宽约1 923 m,共包括3.9×107个激光点的LAS格式数据,地形点密度约为8点/m2,研究数据的影像如图 3(a)所示。研究数据包括地面点数据及非地面点数据,由于地形特征信息的提取主要针对地面点,故需要进行滤波去除非地面点。经TerraScan滤波后,地面点云如图 3(b)所示。滤波后的点云总数约为1.9×107个,点密度约为4点/m2。由于研究区域较大,故选取地形较为复杂(高程变化约为50 m)的300 m×300 m区域作为研究对象、激光点作为样本数据进行地形特征信息的快速提取实验,样本数据如图 3(c)所示。

|
图 3 研究数据 Fig. 3 Study data |
本文采用LM算法进行采样点的局部二次曲面拟合模型构建,采样点的搜索半径r决定了曲面拟合的空间采样点集、空间区域大小和曲面特征等信息。为了选取最优的搜索半径,拟采用不同的搜索半径r分别进行曲面拟合并进行精度的分析。当r=1 m时,用以拟合曲面的激光点数过少,拟合存在较大的不确定性,因此未采取该半径进行实验,实际选取r=2、3、5、10 m。以样本数据为例,采用拟合时间、均方根误差(RMSE)、平均误差作为拟合质量衡量指标,具体结果见表 2和图 4。
|
|
表 2 不同搜索半径的曲面拟合结果 Tab. 2 The surface fitting results of different search radius |
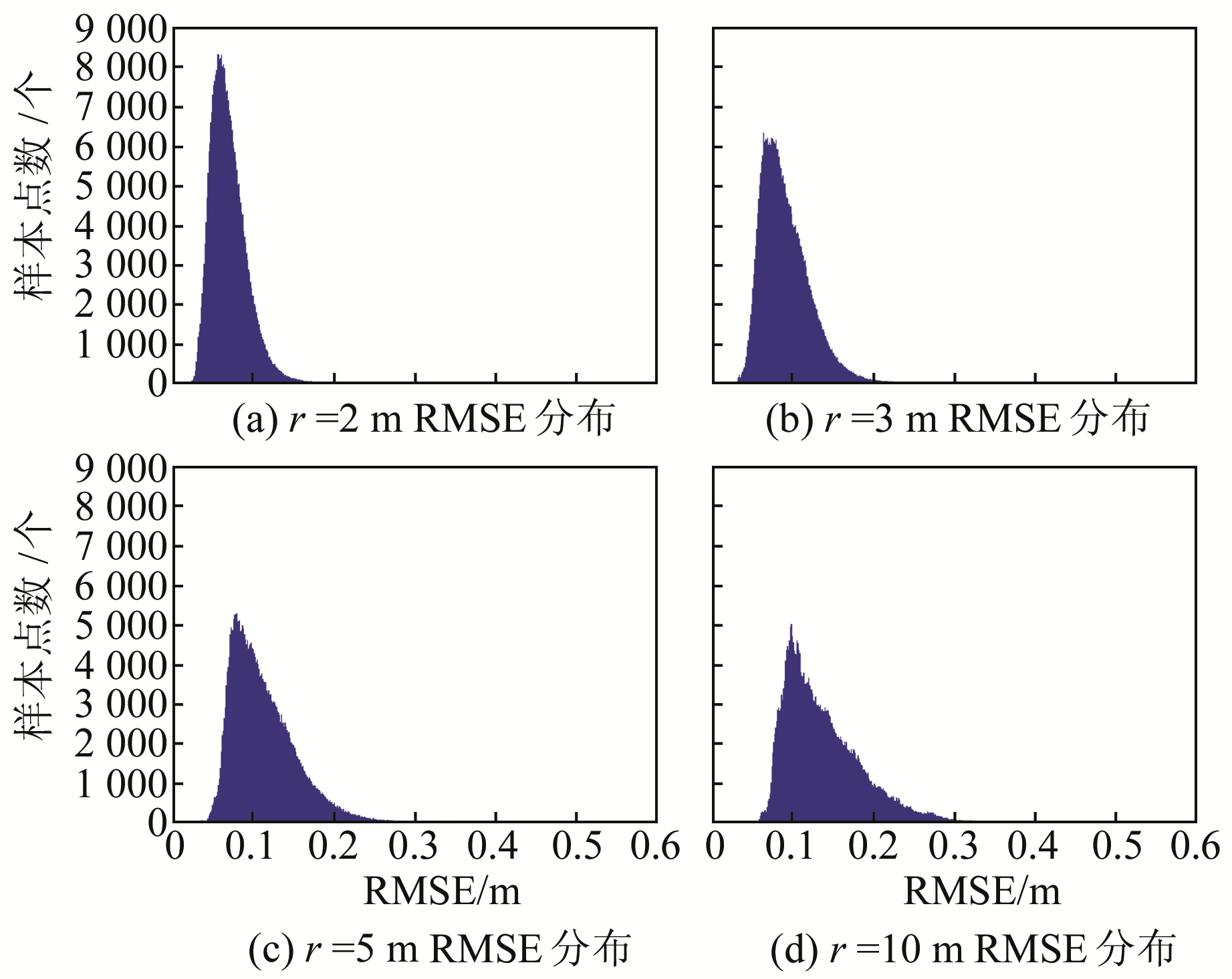
|
图 4 不同搜索半径r的RMSE分布直方图 Fig. 4 RMSE distribution histograms of different r |
由表 2可知,当搜索半径r=2 m时,曲面拟合效果最为理想,其拟合时间和RMSE在所有曲面拟合结果中均最小,分别为0.02 s和5.09 cm,保证了地形特征信息提取的效率和精度。曲面拟合的实质为迭代寻优,是地形特征信息提取过程中最为耗时的步骤。确定拟合曲面后,其后续计算时间在μs级,因此本文仅统计了曲面拟合时间,并以此作为衡量地形特征信息提取效率的标准。同时,拟合结果中的平均误差均小于1 mm,说明拟合的精度较高,采用LM进行二次曲面拟合是可行的。为了更直观地表达不同搜索半径r的RMSE分布状态,将每组实验的激光点误差作如下统计,见图 4。
由图 4可知,当r=2 m时,其拟合精度最高,稳定性最强,其RMSE主要分布在0.03~0.1 m之间;比较其他r的RMSE分布,r=2 m的直方图分布更集中,拟合效果最理想。故选用r=2 m作为最优搜索半径,以此进行LM拟合获得地形拟合参数。
2.3 地形特征提取结果分析为了保证地形特征提取的有效精度,以最优地形拟合模型为基础,进行地形特征信息的快速提取,共提取局部点密度、高程标准差、坡度、高斯曲率、平均曲率、粗糙度等6类地形信息,得到的地形特征向量统计情况如图 5所示。

|
图 5 地形特征向量提取结果 Fig. 5 Results of terrain features vector extraction |
由图 5可知,6类地形特征向量均能很好地突出地形特征点,特征点的表达一致性也很高。由于该样本数据的最大高程差可达51 m,地势起伏较大,地形特征较为明显,图 5中提取的地形特征参数均能很好地表达地形特征信息,突出地势变化的一致性,由此说明了本文提出的机载LiDAR地形特征信息的快速提取算法其精度和可信度较高,提取效果较为理想。
3 结语本文提出一种机载LiDAR地形特征信息快速提取算法。针对机载LiDAR数据,采用LM算法迭代计算获得最优地形拟合参数,并以地形拟合模型为基础,实现地形信息的快速提取。针对本文提出的算法,结合相应的机载LiDAR实测数据进行验证,结果表明,当最优搜索半径为2 m时,其拟合时间仅为0.02 s,RMSE仅为5.09 cm,拟合精度最高;基于地形拟合模型提取的地形特征向量结果完整性和一致性较好,提取效果较为理想。因此,该地形信息快速提取算法应用到科学研究和工程领域是切实可行的。
| [1] |
刘经南, 张小红. 激光扫描测高技术的发展与现状[J]. 武汉大学学报:信息科学版, 2003, 28(2): 132-137 (Liu Jingnan, Zhang Xiaohong. Progress of Airborne Laser Scanning Altimetry[J]. Geomatics and Information Science of Wuhan University, 2003, 28(2): 132-137)
(  0) 0) |
| [2] |
Zhang J, Zhang L, Zeng F, et al. Development Status of Airborne 3D Imaging LiDAR System[J]. Chinese Journal of Optics and Applied Optics, 2011, 4(3): 213-232
(  0) 0) |
| [3] |
Lohmann P, Koch A. Quality Assessment of Laser-scanner-data[C].The International Society of Photogrammetry and Remote Sensing (ISPRS), Hannover, Germany, 1999
(  0) 0) |
| [4] |
Susaki J. Adaptive Slope Filtering of Airborne LiDAR Data in Urban Areas for Digital Terrain Model (DTM) Generation[J]. Remote Sensing, 2012(4): 1 804-1 819
(  0) 0) |
| [5] |
Park B, Kim J, Lee J. Terrain Feature Extraction and Classification for Mobile Robots Utilizing Contact Sensors on Rough Terrain[J]. Procedia Engineering, 2012, 41: 846-853 DOI:10.1016/j.proeng.2012.07.253
(  0) 0) |
| [6] |
Matthies L, Huertas A, Yang C, et al.Landing Hazard Detection with Stereo Vision and Shadow Analysis[R]. AIAA-2007-2835, 2007 http://www.mendeley.com/research/stereo-vision-shadow-analysis-landing-hazard-detection/
(  0) 0) |
| [7] |
王强锋, 李建军, 张公平. 从随机非概率数据中提取粗糙度及其可靠度[J]. 计算机工程与应用, 2012, 48(29): 168-171 (Wang Qiangfeng, Li Jianjun, Zhang Gongping. Research of Extraction of Target Roughness and Its Reliability from Randomly Non-probabilistic Data[J]. Computer Engineering and Applications, 2012, 48(29): 168-171 DOI:10.3778/j.issn.1002-8331.2012.29.034)
(  0) 0) |
| [8] |
Hollaus M, Aubrecht C, Höfle B, et al. Roughness Mapping on Various Vertical Scales Based on Full-Waveform Airborne Laser Scanning Data[J]. Remote Sensing, 2011, 3(3): 503-523 DOI:10.3390/rs3030503
(  0) 0) |
| [9] |
Klingseisen B, Metternicht G, Paulus G. GeomorphometricLandscape Analysis Using a Semi-Automated GIS-Approach[J]. Environmental Modeling & Software, 2008, 23(1): 109-121
(  0) 0) |
| [10] |
张蓉.散乱点云的数据分割与特征提取技术研究[D].南昌: 南昌大学, 2016 (Zhang Rong. Research on Data Segmentation and Feature Extraction Techniques of Scattered[D]. Nanchang: Nanchang University, 2016) http://cdmd.cnki.com.cn/Article/CDMD-10403-1016256520.htm
(  0) 0) |
| [11] |
Yi D, Zwally H J, Sun X. ICESat Measurement of Greenland Ice Sheet Surface Slope and Roughness[J]. Annals of Glaciology, 2005, 42(1): 86-89
(  0) 0) |
| [12] |
杨荣华, 花向红, 游扬声. 基于散乱点的局部n次曲面拟合及其曲率计算[J]. 大地测量与地球动力学, 2013, 33(3): 141-144 (Yang Ronghua, Hua Xianghong, You Yangsheng. Local N-th Order Surface Fitting and Curvature Estimation Based on Scattered-Point Cloud Data[J]. Journal of Geodesy and Geodynamics, 2013, 33(3): 141-144)
(  0) 0) |
| [13] |
Shary P A. Land Surface in Gravity Points Classification by a Complete System of Curvatures[J]. Mathematical Geology, 1995, 27(3): 373-390 DOI:10.1007/BF02084608
(  0) 0) |
| [14] |
Shary P A, Sharaya L S, Mitusov A V. Fundamental Quantitative Methods of Land Surface Analysis[J]. Geoderma, 2002, 107(1-2): 1-32 DOI:10.1016/S0016-7061(01)00136-7
(  0) 0) |
| [15] |
Mukherjee S, Mukherjee S, Garg R D, et al. Evaluation of Topographic Index in Relation to Terrain Roughness and DEM Grid Spacing[J]. Journal of Earth System Science, 2013, 122(3): 869-886 DOI:10.1007/s12040-013-0292-0
(  0) 0) |
2. Key Laboratory of Surveying and Mapping Technology on Island and Reef, NASMG, 579 Qianwangang Road, Qingdao 266590, China
 2018, Vol. 38
2018, Vol. 38

