2. 海岛(礁)测绘技术国家测绘地理信息局重点实验室,青岛市前湾港路579号,266590;
3. 中国海监北海航空支队,青岛市云岭路27号,266061
机载测深LiDAR系统在浅水区域具有很好的优势,特别是在分布有岛礁、暗礁等船只无法安全到达的水域,近年来被逐渐应用到解决浅水区域的测深问题,为海底地形探测提供了一种高效的方法[1-2]。波形参数提取是机载测深LiDAR数据处理的首要工作,如何采用合适的波形数据分析方法,以便于精确提取如振幅、波宽、面积、峭度及斜度等波形参数,从而进行水深计算、底质类型反演和水体浑浊度分析等应用,成为机载测深LiDAR的重要研究方向之一。
常见的机载LiDAR波形数据分析方法包括脉冲阈值检测方法、反卷积方法和波形拟合/分解方法[3-6]。其中,高斯分解法以其易于实现的性能成为目前机载测深LiDAR波形提取中广泛运用的方法之一。高斯分解法的核心为高斯分量个数及初始参数的估计以及参数的优化,因此,如何更好地估计高斯分量个数及初始参数十分重要。Hofton等[7]将回波脉冲信号的波形分解为一个或多个高斯函数,高斯函数的个数通过拐点数来确定,并将每个高斯函数按“重要性”分类,选择“重要性”高的以达到减少冗余的目的;Wagner等[8]对高斯分解法进行了理论阐述与分析,并使用重心法和一阶导数零交叉法估计高斯分量个数。以上方法受噪声影响较大,且难以分解复杂叠加及微弱回波信号。
针对机载LiDAR在水体测深方面的应用,Wong等[9]提出将机载测深LiDAR回波波形分为海面和海底两个反射信号分量,并将海面反射信号表示为高斯函数与指数衰减函数的卷积,该方法(简称WH算法)初始参数确定较复杂;姚春华等[10]提出一种双高斯脉冲拟合方法,对叠加信号中的海面和海底反射信号进行波形分解,该方法虽易于确定初始参数,但仅适用于极浅水深水域,忽略了水体散射信号影响。上述两种方法虽能简单、高效地对机载测深LiDAR的波形数据进行拟合,但其受噪声影响较大,并且其自身性能存在缺陷。
为便于理解,对上述两种传统机载测深LiDAR波形拟合算法进行说明。
去噪后波形信号为海面反射信号、水体散射信号和海底反射信号3部分的叠加。文献[11]假设海水是均匀的,则水体散射信号可用一个指数衰减函数来表示。Wong等[9]提出将水体散射信号视为海面反射信号的一部分,则海面反射信号Psc为高斯函数和指数衰减函数的卷积:
| $ {P_{{\rm{sc}}}}\left( t \right) = {f_1}\left( t \right) * {f_2}\left( t \right) $ | (1) |
式中,f1(t)=Asexp[-(t-ts)2/2σs2]为高斯函数,ts为峰值位置,As为峰值,σs为标准偏差;f2(t)=(1/τ)exp(-t/τ)U(t)为指数衰减函数,τ为衰减因子,与海水浑浊度有关,U(t)为阶跃函数。
对于海底反射信号,假设激光脉冲的弥散和入射角度对深度偏差的综合影响很小,则海底反射信号Pb可用一个高斯函数表示:
| $ {P_{\rm{b}}}\left( t \right) = {A_{\rm{b}}}{\rm{exp}}[-{(t-{t_{\rm{b}}})^2}/2\sigma _{\rm{b}}^2] $ | (2) |
式中,Ab为海底反射信号的峰值,tb为峰值位置,σb为标准偏差。WH算法的表达式为:
| $ {P_{\rm{T}}}\left( t \right) = {P_{{\rm{sc}}}}\left( t \right) + {P_{\rm{b}}}\left( t \right) $ | (3) |
文献[10]提出,在水深极浅的水域,其水体散射分量的影响很小,可以忽略不计,因此,式(3)可近似表示为两个高斯函数的叠加:
| $ {P_{\rm{d}}}\left( t \right) = \sum\limits_{i = 1}^2 {{A_i}{\rm{exp}}[-{{(t-{\mu _i})}^2}/2\sigma _i^2]} $ | (4) |
此即双高斯拟合算法表达式。式中,Ai、μi、σi分别为第i个高斯分量所对应的峰值、位置以及半峰波宽。
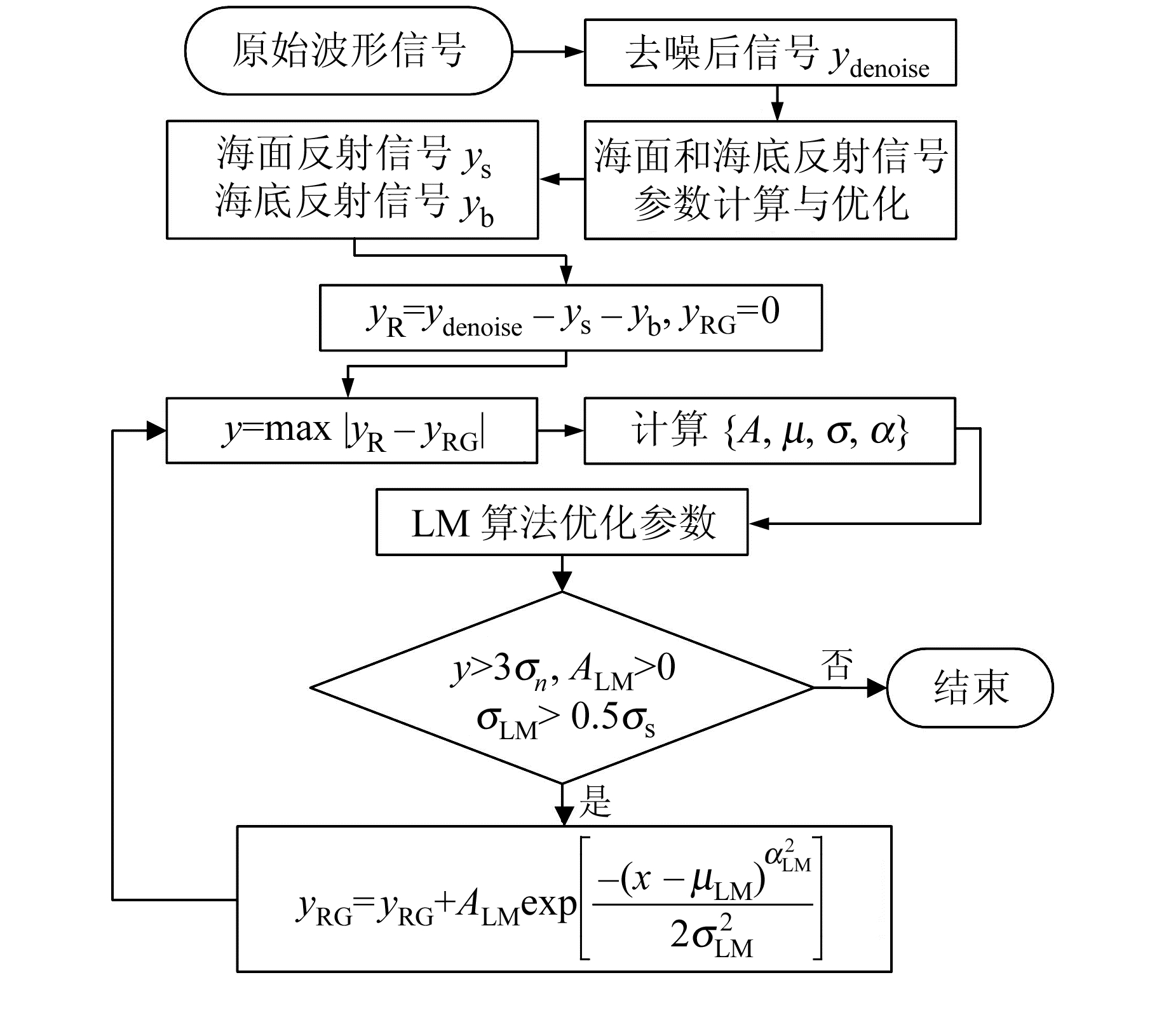
针对传统算法受噪声干扰严重、对微弱回波信号及复杂波形形状拟合不准确的问题,本文提出一种基于广义高斯模型的波形拟合算法。原始信号经滤波后,将滤波前后尾段波形差值的平均值作为噪声,引入广义高斯模型,首先提取海面与海底反射信号分量,若拟合效果不理想则对剩余信号进行迭代拟合,直到小于一定阈值条件;然后利用LM算法对参数进行优化,得到拟合效果优良的波形,从而满足后续应用需求;最后通过南海实验数据对其拟合效果进行验证。
1 波形去噪 1.1 机载测深LiDAR波形信号特征机载测深LiDAR系统接收的回波波形可以表示为海面反射信号、水体散射信号、海底反射信号以及噪声4部分信号(图 1)在时域上的能量叠加[11]:
| ${P_{\rm{T}}}\left( t \right) = {P_{\rm{s}}}\left( t \right) + {P_{\rm{c}}}\left( t \right) + {P_{\rm{b}}}\left( t \right) + {P_{\rm{N}}}\left( t \right) $ | (5) |

|
图 1 机载测深LiDAR波形信号 Fig. 1 Waveform signal of airborne LiDAR bathymetry |
式中,PT(t)为机载测深LiDAR系统接收的总回波信号,Ps(t)为海面反射信号,Pc(t)为水体散射信号,Pb(t)为海底反射信号,PN(t)为噪声。其中,噪声包括背景噪声和传感器内部噪声,其存在可能对高斯分量个数及初始参数的估计造成一定影响,从而阻碍后续的工作。因此,波形分解之前需要进行去噪处理。
1.2 原始波形去噪为获得高质量的波形信号,采用一种改进的高斯滤波算法,该算法通过比例因子λ对波形信号进行一次高斯滤波后,利用一个与λ异号的比例因子μ(0<λ<-μ<1)进行二次高斯滤波,对以上两步进行迭代计算,直到滤波结果达到最优为止。该算法克服了高斯滤波算法迭代耗时长及边缘收缩的缺陷,其本质为一个低通滤波器[12]。具体表达为:
| $ {\mathit{\boldsymbol{X}}^T} = {\left[{\left( {\mathit{\boldsymbol{I}}-\mu \mathit{\boldsymbol{K}}} \right)\left( {\mathit{\boldsymbol{I}}-\lambda \mathit{\boldsymbol{K}}} \right)} \right]^T}\mathit{\boldsymbol{X}} $ | (6) |
式中,T为迭代次数;X为n×1原始波形信号采样值矩阵,n为采样点个数;XT为迭代T次后波形信号采样值矩阵;λ和μ为比例因子,且满足
通过式(6)对原始波形信号进行滤波后,本文将滤波前后波形信号最后若干采样点之差Δsi的平均值Nmean作为噪声PN(t)的估计值,消除后即认为得到去噪后信号ydenoise。本文选择尾段的15个采样点(此处15个采样点的选择是为了避免海底反射信号影响,经测试后得出的结果),其标准偏差
本文提出一种基于广义高斯模型的拟合算法,旨在结合双高斯拟合算法参数易于确定与WH算法考虑水体散射信号影响的优点;同时,对浅水或深水区的叠加、微弱及复杂波形形状的LiDAR测深回波信号,也有较好的拟合效果。
2.1 广义高斯模型文献[8]指出,RIEGL系统获取的波形数据中,超过98%的数据可以用高斯函数叠加拟合。但是,不同的机载LiDAR系统所获得的波形数据并不总是高斯型的,有时会表现出非对称性、展宽和尖峰的特性。因此,Chauve等[1]提出一种广义高斯模型,通过引入形状参数以调节高斯模型的特征,从而提高了复杂波形形状拟合时的适应性。式(7)为广义高斯模型函数表达:
| ${f_{{\rm{GG}}}}\left( t \right) = A{\rm{exp}}[-{\left( {t-\mu } \right)^{{\alpha ^2}}}/2{\sigma ^2}] $ | (7) |
式中,α为形状参数。当

|
图 2 高斯、尖峰及展宽波形 Fig. 2 Gaussian, peaked and broadening waveform |
本文算法的重点是确定合适的分量个数N以及每个广义高斯分量对应的4个初始参数{Ai, μi, σi, αi}i=1N。海面反射信号和海底反射信号通过拐点对计算峰值A,通过峰值一半处对应的两点计算μ和σ;对于剩余部分信号,其峰值A为信号最大值,μ为峰值位置,σ为系统半峰波宽,初始形状参数
根据机载测深LiDAR波形的特性,首先可以确定波形数据中包含海面反射信号和海底反射信号两个分量。
计算回波波形中拐点值大于3倍噪声标准偏差σn的拐点。假设第k个采样点为拐点,若其与第k+1个采样点的连线斜率为正,则该拐点是左拐点;若斜率为负,则该拐点为右拐点。由于一个高斯函数可由连续的一左一右两个拐点唯一确定,因此可以得到海面反射信号和海底反射信号所对应的两对连续且采样值较大的左、右拐点[13]。海面反射信号所对应分量的左、右拐点所夹波峰值即为A1,计算峰值一半处所对应的两点x1和x2,且x1<x2,根据式(8)得到位置参数μ1和半峰波宽σ1,初始形状参数α1=
| $ \left\{ \begin{array}{l} {\sigma _1} = {x_2} - {x_1}\\ {\mu _1} = ({x_1} + {x_2})/2 \end{array} \right. $ | (8) |
同理,可得海底反射信号所对应分量的4个初始参数{A2, μ2, σ2, α2}。
对海面反射信号和海底反射信号的初始参数{Ai, μi, σi, αi}i=12进行初次优化(见§2.3),并分别代入式(7)得到其对应的广义高斯函数ys、yb,将这两部分从去噪后信号ydenoise中消去得到剩余部分信号yR。判断yR是否满足增加高斯分量的要求(判定方法见§2.3),若满足,则增加一个分量(A=max|yR-yRG|,μ=μA,σ=σs,
特别地,当水深较浅时,海面反射信号和海底反射信号会发生叠加,使海底反射信号无法辨认。对于海底反射信号的初始参数,传统算法通常选择上一个波形的参数作为本次拟合的参数,若是第一个波形,则选取一定范围内任意数字作为参数。对于本文算法,将海面反射信号进行优化拟合并从去噪信号中消除后,容易判断海底反射信号并得到其参数。
2.3 参数优化本文采用LM算法对广义高斯函数的初始参数进行优化,以求解参数的精确值。计算得到海面反射信号和海底反射信号所对应分量的初始参数后,对其进行一次优化,然后将优化后参数代入式(7),得到精确的海面反射信号ys与海底反射信号yb拟合波形。在浅水信号叠加区,通常仅对海面和海底反射信号进行优化拟合即可满足精度要求。
对于剩余部分波形的迭代优化拟合,为避免冗余分量,当且仅当剩余部分波形yR与优化拟合后波形yRG(初始值为0)满足max|yR-yRG|>3σn且优化后的峰值ALM>0且半峰波宽σLM>0.5σs时,增加一个分量。
本文算法流程如图 3所示。
|
图 3 算法流程 Fig. 3 Flowchart of algorithm |
为了分析本文算法的效果,选取了5个评价指标,具体定义如下。
1) RMSE,指原始信号与处理后信号之间差值的平方和与信号采样数之比值的平方根。RMSE越接近0,说明拟合效果越好:
| $ {\rm{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{({{s'}_i} - {s_i})}^2}} } $ | (9) |
式中,si为回波信号,s′i为处理后的回波信号。
2) R-square,也称为拟合优度、决定系数,用R2表示。R2的值越接近1,说明处理效果越好:
| $ {R^2} = 1-\frac{{\sum\limits_{i = 1}^N {{{({{s'}_i} - {s_i})}^2}} }}{{\sum\limits_{i = 1}^N {{{({s_i} - \bar s)}^2}} }} $ | (10) |
式中,s为回波信号的均值。
3) C,指回波信号si与拟合信号s′i的相关系数,用于衡量算法精度。C越接近1,说明拟合结果与原始回波信号之间的相关性越好,拟合效果也越好:
| $ C = \frac{{\sum\limits_{i = 1}^N {({{s'}_i} - \bar s'){{({s_i} - \bar s)}}} }}{{\sqrt {\sum\limits_{i = 1}^N {{{({{s'}_i} - {{\bar s'}_i})}^2}} \sum\limits_{i = 1}^N {{{({s_i} - \bar s)}^2}} } }} $ | (11) |
式中,s′为拟合信号的均值。
4) M-diff,指最大偏差,用以表示回波信号与拟合信号同一位置差值绝对值的最大值,反映了拟合结果与原始回波信号之间的局部差异。
5) T,指处理每一波形所需时间,反映算法的运算效率。
需要注意的是,RMSE等指标在此仅用于比较算法性能,其值受多种因素的影响,并不代表实际精度。
3 实验与分析为了检验本文算法的效果,对2012-12三亚蜈支洲岛海域的机载测深LiDAR实验波形数据进行处理分析。实验采用Optech Aquarius机载测深系统,该系统是一款全波形LiDAR (full waveform LiDAR, FWL),激光脉冲频率为70 kHz,能够以1~2 GHz的高采样率来记录全数字化散射激光脉冲信号。所用波形数据以1 ns的时间间隔、288个连续采样点进行采样并记录。
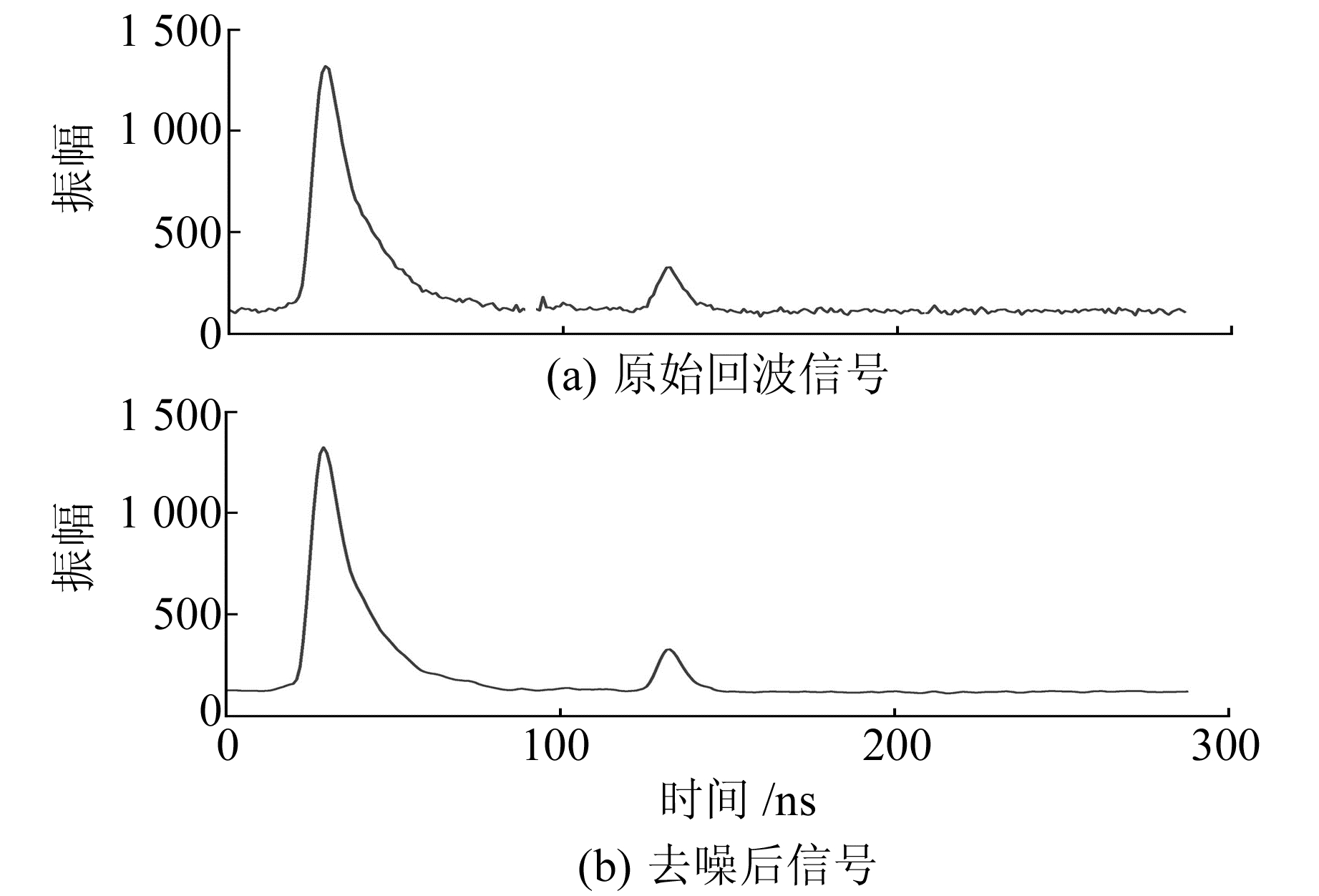
3.1 波形去噪结果利用§1.2给出的算法对原始回波信号进行滤波去噪处理,kPB取0.16,λ取0.630 7,则μ为-0.637 2,迭代次数为4。由图 4可以看出,噪声信号得到明显的滤除,去噪效果理想。
|
图 4 去噪效果 Fig. 4 The results of denoising |
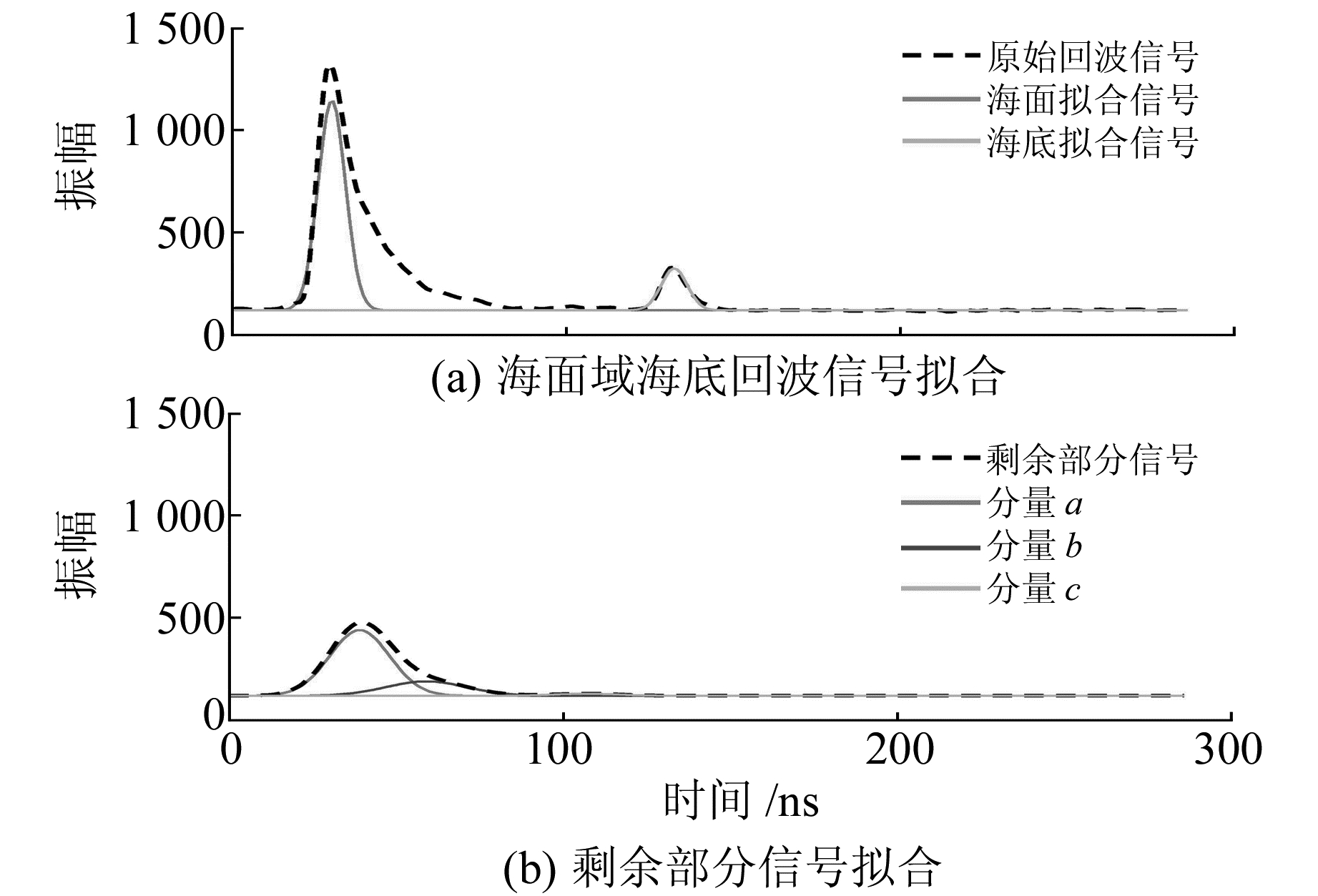
通过本文算法对去噪后波形数据进行拟合,结果如图 5所示。图 5(a)中虚线表示去噪后信号,实线为拟合信号。可以看出,海面和海底反射信号得到较好的拟合,而中间水体散射信号部分还未得到分解。图 5(b)为去掉海面和海底拟合信号后的剩余部分信号拟合,将两部分拟合结果之和与去噪后信号进行比较,其RMSE为4.725 2,R2为0.998 3,拟合效果较好。
|
图 5 本文算法处理结果 Fig. 5 The result of algorithm |
为分析本文算法的性能,利用双高斯拟合算法和WH算法与本文算法拟合同一波形信号,比较结果见表 1。由于双高斯拟合算法仅针对海面和海底反射信号叠加的水深极浅水域,忽略了水体散射的影响,该算法的拟合精度不理想,所以对非浅水波形信号,本文算法只与WH算法进行比较。由表 1可以看出,两种传统算法在拟合浅水区波形时精度较高,而对于深水区,由于WH算法对复杂波形形状及微弱回波的探测能力较弱,所以拟合效果一般。不论是浅水还是较深水域,本文算法的拟合效果皆表现更好,但由于增加了分量个数,处理每一波形信号所需时间较长。在实际应用时,通常将剩余部分信号分解所需的分量个数限制在3个以内,在保证拟合精度的同时,能较好地克服该问题。
|
|
表 1 算法性能 Tab. 1 The performance of algrithms |
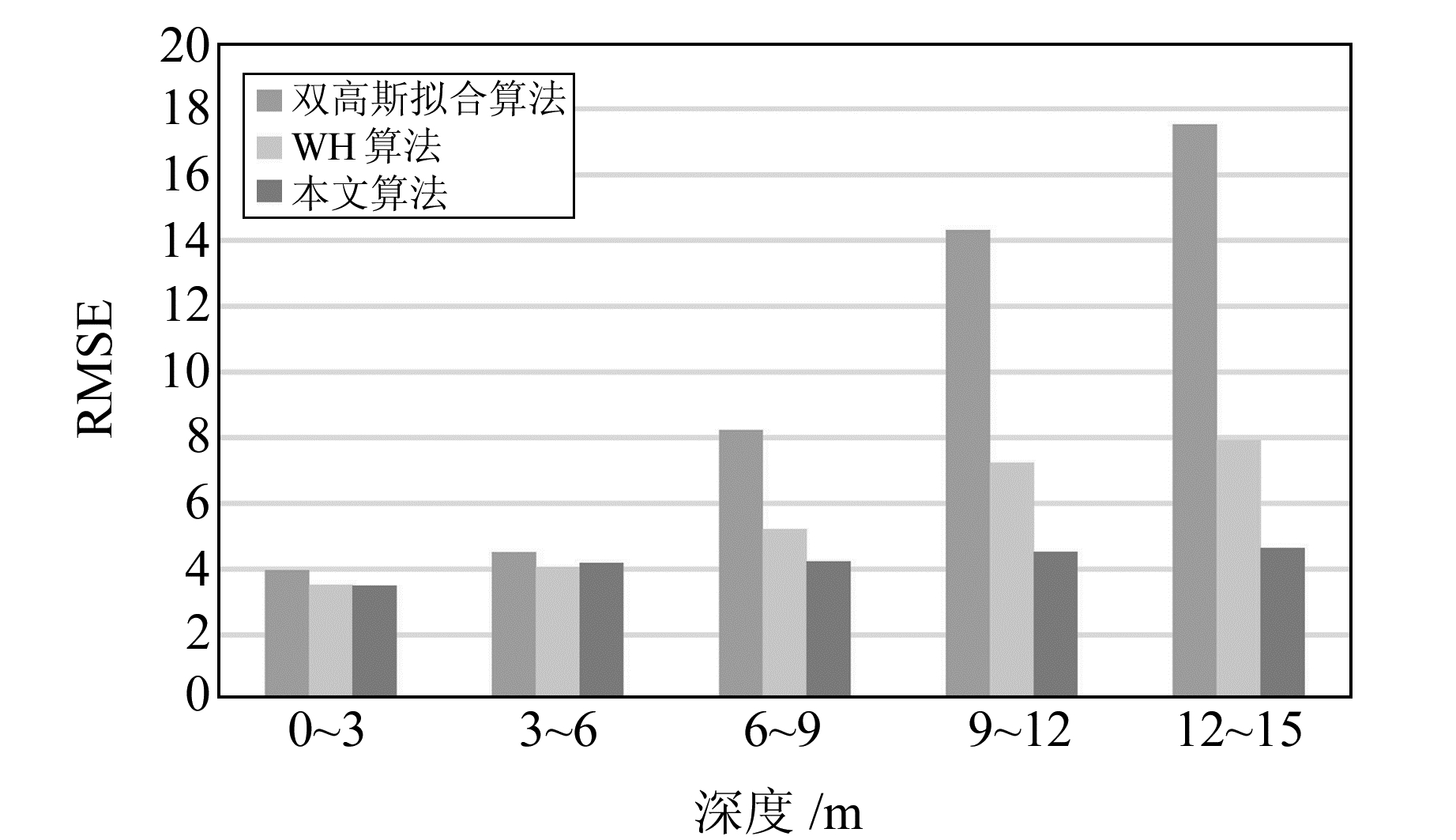
通过3种算法分别对不同水深区域的500个波形信号进行拟合,其RMSE的平均值如图 6所示。可以看出,双高斯拟合算法和WH算法的RMSE随深度的增加逐渐增大,而本文算法在不同水深处的拟合效果较稳定。
|
图 6 不同深度的RMSE Fig. 6 The RMSE of different depth |
波形分解法在机载LiDAR陆地地形测绘的数据处理中已得到广泛应用,但在测深中应用较少。本文提出的方法针对机载测深LiDAR数据,利用滤波前后波形尾段数据的平均差值作为任意波形的噪声,减小了噪声对算法的影响;引入广义高斯模型,提出海面反射信号、海底反射信号与剩余部分信号的两步优化拟合策略,克服了传统算法对复杂波形形状和微弱回波拟合能力不足的问题,并给出了避免冗余分量的应对策略;最后利用南海实测回波信号数据对算法进行验证,结果表明,该算法初始参数易于确定,对微弱回波信号及复杂波形拟合能力强,其拟合精度优于两种传统算法,从而保证了后续波形参数提取的可靠性。
| [1] |
Chauve A, Mallet C, Bretar F, et al. Processing Full-Waveform LiDAR Data: Modeling Raw Signals[J]. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2007, 36(Part 3/W52): 102-107
(  0) 0) |
| [2] |
Fernandez-Diaz J C, Glennie C L, Carter W E, et al. Early Results of Simultaneous Terrain and Shallow Water Bathymetry Mapping Using a Single-Wavelength Airborne LiDAR Sensor[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2014, 7(2): 623-635
(  0) 0) |
| [3] |
Wang C, Li Q, Liu Y, et al. A Comparison of Waveform Processing Algorithms for Single-Wavelength LiDAR Bathymetry[J]. ISPRS Journal of Photogrammetry & Remote Sensing, 2015, 101: 22-35
(  0) 0) |
| [4] |
Wagner W, Roncat A, Melzer T, et al. Waveform Analysis Techniques in Airborne Laser Scanning[J]. Swiss Federal Institute of Technology Zürich, 2007, 3(1): 602-605
(  0) 0) |
| [5] |
Lucy L B. An Iterative Technique for the Rectification of Observed Distributions[J]. Astronomical Journal, 1974, 79(6): 745-754
(  0) 0) |
| [6] |
Wu J, Aardt J A N V, Asner G P. A Comparison of Signal Deconvolution Algorithms Based on Small-Footprint LiDAR Waveform Simulation[J]. IEEE Transactions on Geoscience & Remote Sensing, 2011, 49(6): 2 402-2 414
(  0) 0) |
| [7] |
Hofton M, Minster J B, Blair J B. Decomposition of Laser Altimeter Waveforms[J]. IEEE Transactions on Geoscience & Remote Sensing, 2000, 38(4): 1 989-1 996
(  0) 0) |
| [8] |
Wagner W, Ullrich A, Duclc V, et al. Gaussian Decomposition and Calibration of a Novel Small-footprint Full-Waveform Digitising Airborne Laser Scanner[J]. ISPRS Journal of Photogrammetry & Remote Sensing, 2006, 60(2): 100-112
(  0) 0) |
| [9] |
Wong H, Antoniou A. Characterization and Decomposition of Waveforms for Larsen 500 Airborne System[J]. IEEE Transactions on Geoscience & Remote Sensing, 1991, 29(6): 912-921
(  0) 0) |
| [10] |
姚春华, 陈卫标, 臧华国, 等. 机载激光测深系统的最小可探测深度研究[J]. 光学学报, 2004, 24(10): 1 406-1 410 (Yao Chunhua, Chen Weibiao, Zang Huaguo, et al. Study of the Capability of Minimum Depth Using an Airborne Laser Bathymetry[J]. Acta Optica Sinica, 2004, 24(10): 1 406-1 410)
(  0) 0) |
| [11] |
Abdallah H, Baghdadi N, Bailly J S, et al. Wa-LiD: A New LiDAR Simulator for Waters[J]. IEEE Geoscience & Remote Sensing Letters, 2012, 9(4): 744-748
(  0) 0) |
| [12] |
Taubin G.Curve and Surface Smoothing Without Shrinkage[C].International Conference on Computer Vision, 1995 http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=466848
(  0) 0) |
| [13] |
段乙好, 张爱武, 刘诏, 等. 一种用于机载LiDAR波形数据高斯分解的高斯拐点匹配法[J]. 激光与光电子学进展, 2014, 51(10): 189-197 (Duan Yihao, Zhang Aiwu, Liu Zhao, et al. A Gaussian Inflexion Points Matching Method for Gaussian Decomposition of Airborne LiDAR Waveform Data[J]. Laser & Optoelectronics Progress, 2014, 51(10): 189-197)
(  0) 0) |
2. Key Laboratory of Surveying and Mapping Technology on Island and Reef, NASMG, 579 Qianwangang Road, Qingdao 266590, China;
3. Northern Sea Airborne Detachment, China Marine Surveillance, 27 Yunling Road, Qingdao 266061, China
 2018, Vol. 38
2018, Vol. 38


