2. 武汉大学测绘学院,武汉市珞喻路129号,430079
随着陆地资源的日益枯竭,世界各国已将资源开发和利用的重点由陆地转向海洋,我国为此制定了“海洋强国”、“一带一路”等战略。在这些大趋势和大战略的指引下,针对海洋的勘察活动也日益增多,了解海底表层及浅表层结构对海洋科学研究意义重大。侧扫声呐(side scan sonar,SSS)作为高分辨率海底地貌图像的获取设备,目前应用日益广泛[1-4]。但受复杂海洋环境噪声及作业模式影响,SSS回波强度数据易受海底底质和地形、TVG(time vary gain)增益及拖鱼高度变化等因素影响,导致其形成的图像存在辐射畸变,图像的获取质量难以满足后续更深层次的应用需要。国内外学者针对辐射畸变产生的原因,提出了许多改正方法。王爱学等[5-6]研究了灰度增益的补偿并给出了统计改正方法,该方法适合于条带图像,但复杂底质下改正效果不佳;Anstee[7]、Capus等[8]将辐射畸变分为两个部分,给出分步骤改正方法,作为标准算法应用于Triton软件[9];Zhao等[10]给出一种顾及底质变化的SSS图像辐射畸变改正新方法,有效改善了复杂底质下SSS图像的辐射畸变改正效果。上述研究均没有考虑人工增益量的影响。阳凡林等[11]对SSS图像增益方法开展相关研究,取得较好的增益补偿效果;程彬彬等[12]提出一种基于局部信息的图像增强方法。上述两种方法仅对截取图像进行处理,应用于实时条带图像效率不高、效果不佳。
为此,本研究通过分析SSS图像辐射畸变诱因,有针对性地给出不同影响下的辐射畸变改正算法,并形成一种综合改正方法,实现了图像的高质量获取。
1 SSS辐射畸变诱因分析作业过程中,受海底地形、拖鱼高度变化及SSS作业模式的影响,图像存在辐射畸变。主要诱因有:作业时人为设置不同增益参数;海底线附近区域由于波束模式引起的高亮区;声波随时间传播损失,造成图像远端目标不清晰。
上述辐射畸变的存在严重影响SSS图像质量,需要后期进行各种改正以改善成图效果。从理论上说,处理后的图像应与仪器、入射角、波束角大小和水深等因素无关,即代表真实的海底反向散射强度系数[11]。
2 传统辐射畸变改正方法SSS图像辐射畸变具体表现为图像沿纵向及横向灰度变化不均衡。传统的辐射畸变改正方法主要有时变增益法和统计法。
2.1 SSS增益的理论基础SSS换能器的整体电能响应为PT=ηPA+NE,PT为系统接收的总电能,η为换能器和增益装置的声学效率,NE为系统的噪声水平,PA为声信号能量(PAS)和噪声能量(PAN)之和:
| $ P_A^S = {P_0}\frac{{\exp \left( { - 2\alpha r} \right)}}{{{r^4}}}{b^2}\left( \theta \right){S_b}\left( \gamma \right) $ | (1) |
式中,P0为换能器发射时的脉冲能量;α为声波在水中的吸收系数;b为换能器的波束模式;Sb为海底的后向散射强度;r=r(t)为斜距随时间的变化量;θ=θ(t)为波束角与换能器表面法向量的夹角;γ=γ(t)为波束与海底表面的掠射角。
经过增益处理后,系统整体能量变为:
| $ {{P'}_T} \cong g\left( t \right){P_A} + {10^{\frac{{{N_F}}}{{10}}}}g\left( t \right){N_E} $ | (2) |
式中,g(t)为随时间变化的增益量,NF为噪声系数,当g(t)不能很好地与真实测量环境相匹配时,会出现错误的增益现象。
2.2 时变增益改正时变增益主要用于图像的实时辐射畸变改正,其利用经验公式来补偿回波随传播距离增大而产生的各种损失[5]。
2.3 统计法沿航迹向一定窗口内,假设地形及底质引起的回波强度变化一致,且横向上声波各种损失表现一致。在这个窗口内,计算各列信号的均值,认为可得到声波在横向上的能量变化曲线。设置合理的改正基值,利用该曲线可求取图像各列的改正系数[5]:
| $ {\partial _j} = \frac{{\frac{1}{{dl}}\sum\limits_i^d {\sum\limits_k^l {{E_{i,k}}} } }}{{\frac{1}{d}\sum\limits_i^d {{E_{i,j}}} }}\\ {{E'}_{i,j}} = {E_{i,j}} \times {\partial _j} $ | (3) |
式中,d为窗口高度,l为图像宽度,i表示行号,j表示列号,∂为改正系数,E为原始图像回波强度,E′为辐射畸变改正后的强度值。当外部测量环境较好、海底地形地貌特征简单、作业规范时,统计改正法可取得比较好的改正效果。但上述假设往往不成立,导致在海底地形、底质变化复杂区域,图像的统计法辐射畸变改正效果不佳。
3 辐射畸变综合改正针对SSS辐射畸变诱因,给出相应改正算法,并形成辐射畸变综合改正法。
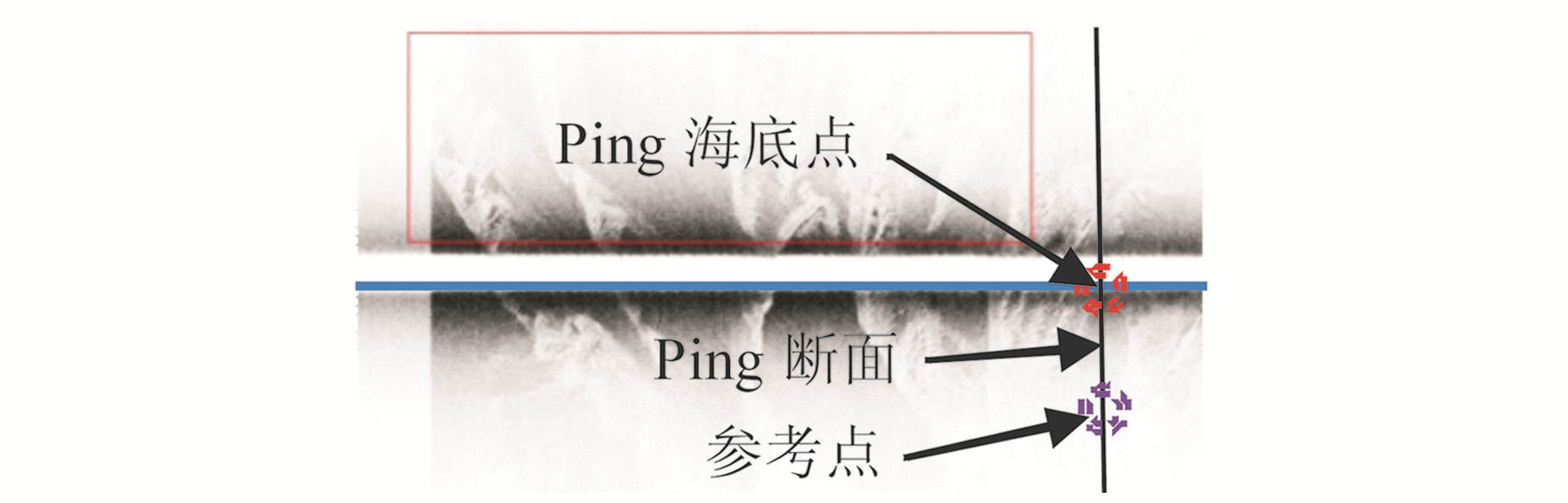
3.1 人工增益量消除TVG增益一般固定在仪器硬件中,在数据采集过程中操作人员会实时调整增益曲线以便更好地发现海底目标,但影响了整个条带图像的视觉效果(图 1,蓝色线表征海底线,黑色虚线为某Ping断面位置,两线交点为当前Ping海底点位置)。在红色方框标注的区域,进行过增益参数调整,导致局部区域与条带图像灰度不均衡。
|
图 1 受人为增益影响的SSS图像 Fig. 1 SSS image influenced by human TVG |
假设在海底局部区域内海底地形遵循渐进性变化的规律。
步骤1 统计各个Ping断面灰度均值,根据相邻Ping灰度变化判断是否出现灰度突变,并将灰度突变的Ping进行标注。可将各Ping取均值,根据3倍中误差原则判断是否为进行过人工增益的Ping。
步骤2 将人工增益区域附近若干Ping按列取平均(Ping数选择基准可根据拖鱼高度变化序列取地形变化平坦区域),得到正常Ping断面的灰度变化曲线,并应用小波变换提取其低频趋势项。
步骤3 将人工增益区域内若干Ping按列取均值与步骤2中低频趋势项相减,得到人工增益量,依然将此曲线通过小波变换提取其低频趋势项。
步骤4 将人工增益区域内Ping断面灰度曲线减去步骤3中得到的低频趋势,据此将人工增益量消除。
3.2 与距离有关的辐射畸变改正以右舷为例,设在某一Ping(n)中的数据采样序列为Ns,且该Ping灰度值序列为S(n, i),i=1, 2, …, Ns-1。设海底跟踪得到海底线位置为b(n),Nmin为条带内b(n)最大时对应的图像区宽度,可按下式计算:
| $ {N_{\min }} = \min \left( {{N_s} - b\left( n \right)} \right),n = 1,2, \cdots {N_p} $ | (4) |
再由下式计算Ping断面位置的改正数δ:
| $\delta \left( i \right) = \frac{1}{{{N_p}}}\sum\limits_{n = 0}^{{N_p} - 1} {S\left( {n,i - b\left( n \right)} \right)} \\ \ \ \ \ \ \ \ b\left( n \right) \le i \le {N_{\min }} $ | (5) |
式中,Np为沿航迹向Ping平滑数量。由式(5)得到的δ(i)是一个不够平滑的序列,一般采用下述移动平滑方法来处理δ(i):
| $ \delta '\left( i \right) = \frac{1}{{q\left( i \right) - p\left( i \right) + 1}}\sum\limits_{j = p\left( i \right)}^{q\left( i \right)} {\delta \left( j \right)} $ | (6) |
式中,p(i)=max(0, i-l);q(i)=min(Nmin-1, i+l);l=Nmin/50。由此计算改正因子:
| $ C\left( i \right) = A/\max \left( {1,\delta '\left( i \right)} \right)\\ A = \frac{1}{{{N_{\min }}}}\sum\limits_{i = 0}^{{N_{\min }} - 1} {\delta '\left( i \right)} $ | (7) |
综上,可得Ping断面各位置回波数据的改正公式:
| $ {S_C}\left( {n,i} \right) = C\left( i \right)S\left( {n,i} \right) $ | (8) |
式中,SC(n, i)为改正后回波强度值。该步骤可消除图像远端灰度的强变化,但无法消除拖鱼正下方海底附近位置由波束模式引起的辐射畸变。
3.3 与波束模式有关的辐射畸变改正SSS图像拖鱼正下方海底位置处灰度强变化与波束指向性残差有关,其主要受拖鱼高度及波束角的影响。图 2给出了换能器距离海底的高度和波束在海底位置的比率关系,即每Ping回波的波束指向性。

|
图 2 拖鱼高度对波束角的影响 Fig. 2 Beam angle influenced by towfish altitude |
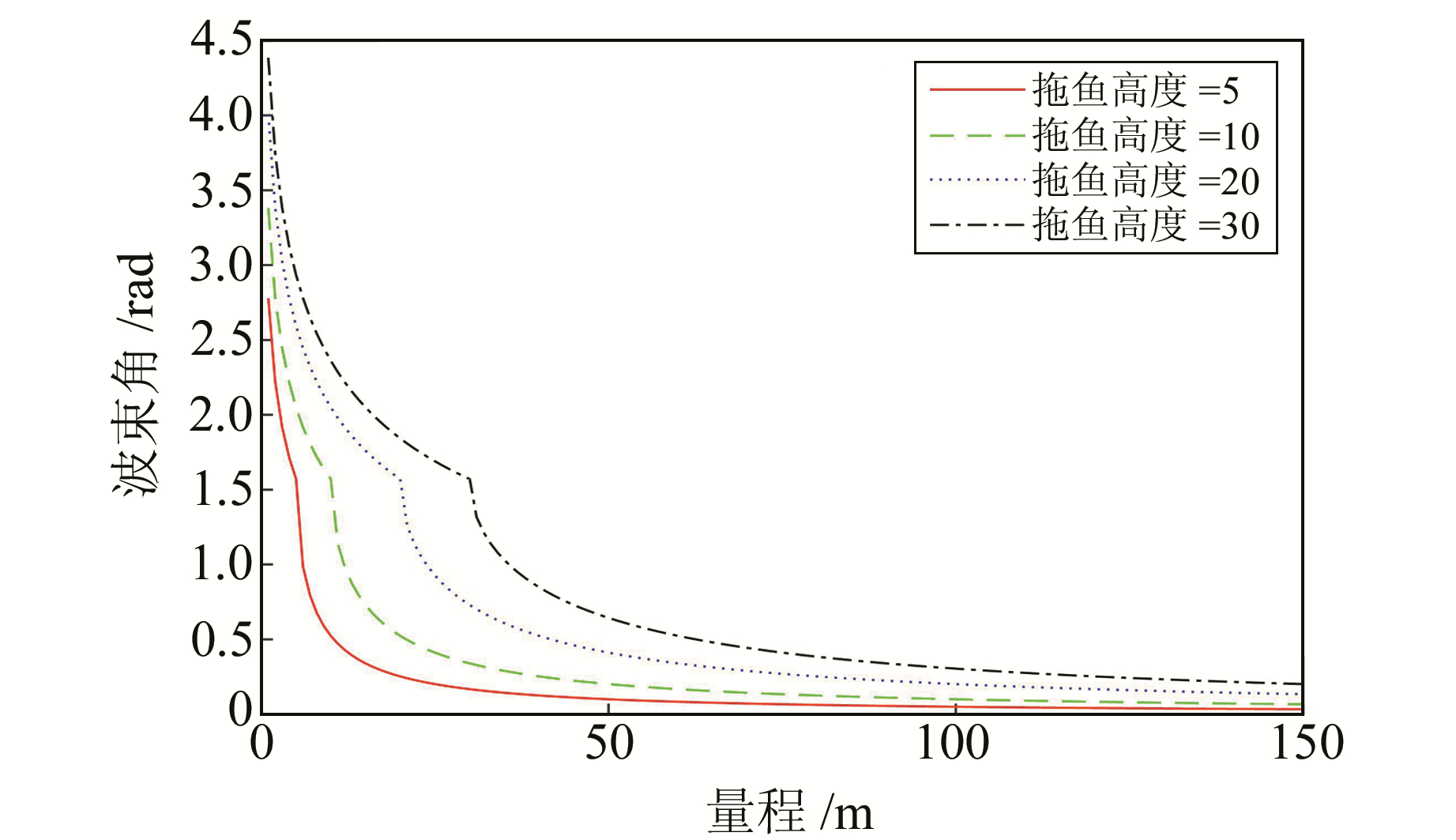
图 3给出了波束角随声传播距离和拖鱼高度的变化关系。拖鱼正下方海底一段距离内波束角快速变化,当传播距离大于拖鱼高度一定倍数后,传播距离对波束角的影响逐渐减弱,且波束角随拖鱼高度的增加而增大。
|
图 3 波束角随拖鱼高度和传播距离的变化关系 Fig. 3 Variation of beam angle with slant range and towfish altitude |
根据波束指向性残差的影响机理,可取Ping海底点及距其某一短距离处的海底图像点为参考点(图 1),通过式(9)重新计算拖鱼正下方海底的回波强度:
| $ v_n^ \pm = \frac{1}{L}\left[ {\left( {L - 1} \right){v_{n - 1}} + {S^ \pm }\left( {n,b\left( n \right) + \mathit{\Delta }} \right)} \right] $ | (9) |
式中,Δ为参考点到海底点的距离,可取1/10倍作业量程;L为Ping数;+和-分别代表左舷和右舷;b(n)为海底线位置;vn表示灰度值。Ping断面灰度改正值如下:
| $v_n^ \pm \left( i \right) = \frac{1}{L}\left[ {\left( {L - 1} \right){v_{n - 1}}\left( i \right) + {S^ \pm }\left( {n,b\left( n \right) + \mathit{i}} \right)} \right]\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ i = 0,1,2, \cdots ,\mathit{\Delta } $ | (10) |
通过式(11)计算Ping断面各点的改正系数:
| $\mathit{C}_n^ \pm \left( i \right) = \left[ {{u_n} + \left( {v_n^ \pm - {u_n}} \right)\frac{i}{\mathit{\Delta }}} \right]/v_n^ \pm \left( i \right),\\ \ \ \ \ \ \ \ \ \ \ \ i = 0,1,2, \cdots ,\mathit{\Delta }\\ {u_n} = \left( {v_n^ + + v_n^ - } \right)/2 $ | (11) |
基于式(12)进行拖鱼正下方海底附近图像强回波的改正:
| ${S'}_C^ \pm \left( {n,i} \right) = C_n^ \pm \left( {i + b\left( n \right)} \right)S\left( {n,i + b\left( n \right)} \right)\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ i = 0,1,2, \cdots ,\mathit{\Delta } $ | (12) |
联合人工增益量消除算法、分离距离相关和波束模式的辐射畸变改正算法,本文定义新方法为辐射畸变综合改正方法。
4 实验及分析为检验上述算法的正确性,对渤海湾某水域实测SSS图像开展辐射畸变改正处理。实验区共布设了3条测线,SSS仪器为Analog and Digital(DSSS),设置扫幅为150 m,频率为100 kHz,实验区水深变化范围为8~45 m,海底底质、地形变化明显,且作业过程中进行过增益参数调整,导致生成图像质量不佳。以第1条测线为例,获得图像如图 4所示,可见图像质量很差。

|
图 4 第1条测线对应的图像 Fig. 4 SSS image of the first strip line |
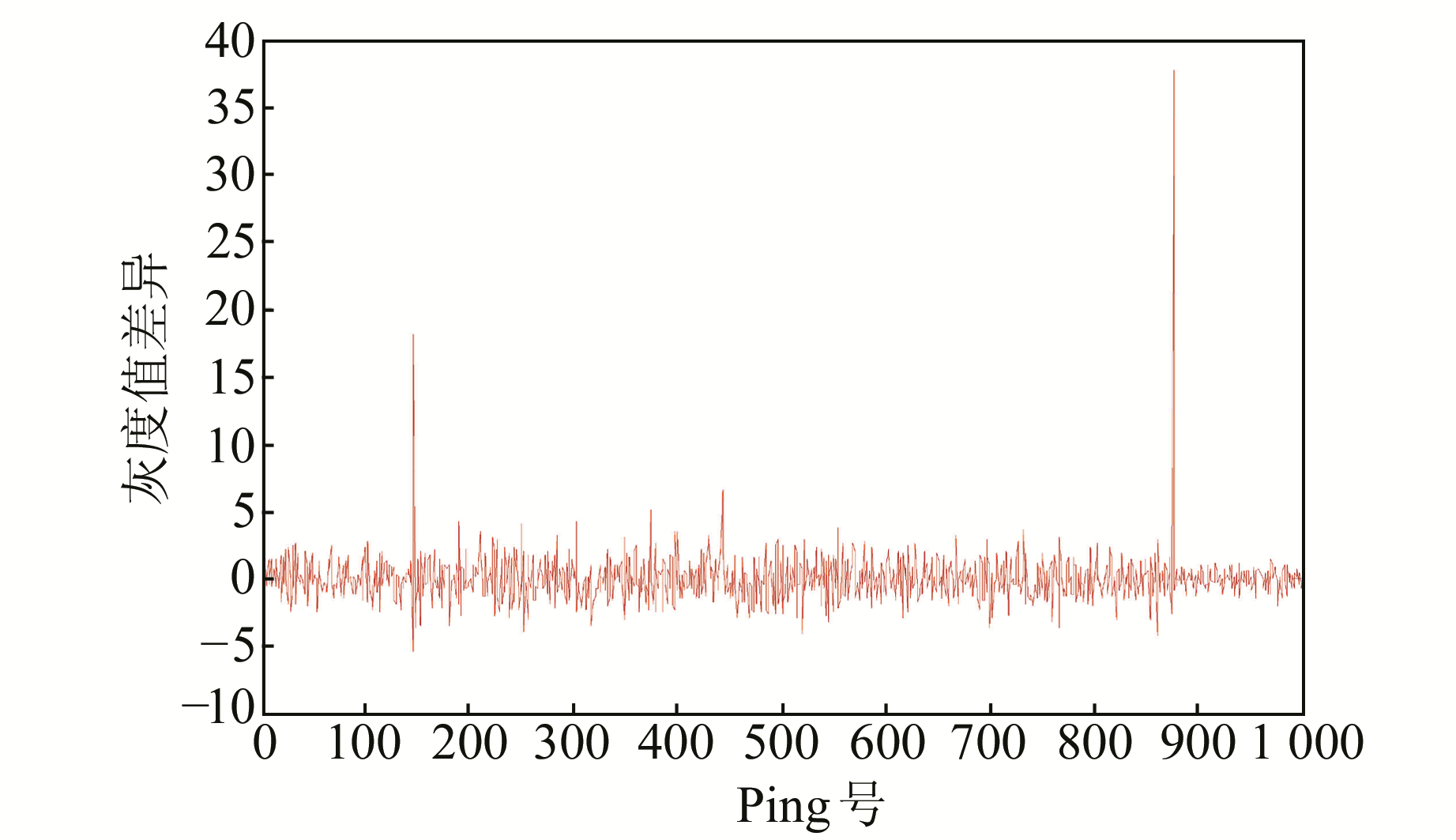
首先,为验证人工增益消除算法的有效性,对图 4中部分区域(图 1)进行处理,将各Ping取均值并相减得到Ping间差异曲线,如图 5所示。通过3倍中误差原则得到146~875 Ping为经过人工增益处理的Ping断面。
|
图 5 相邻Ping均值差值曲线 Fig. 5 Mean value difference curve of adjacent Ping |
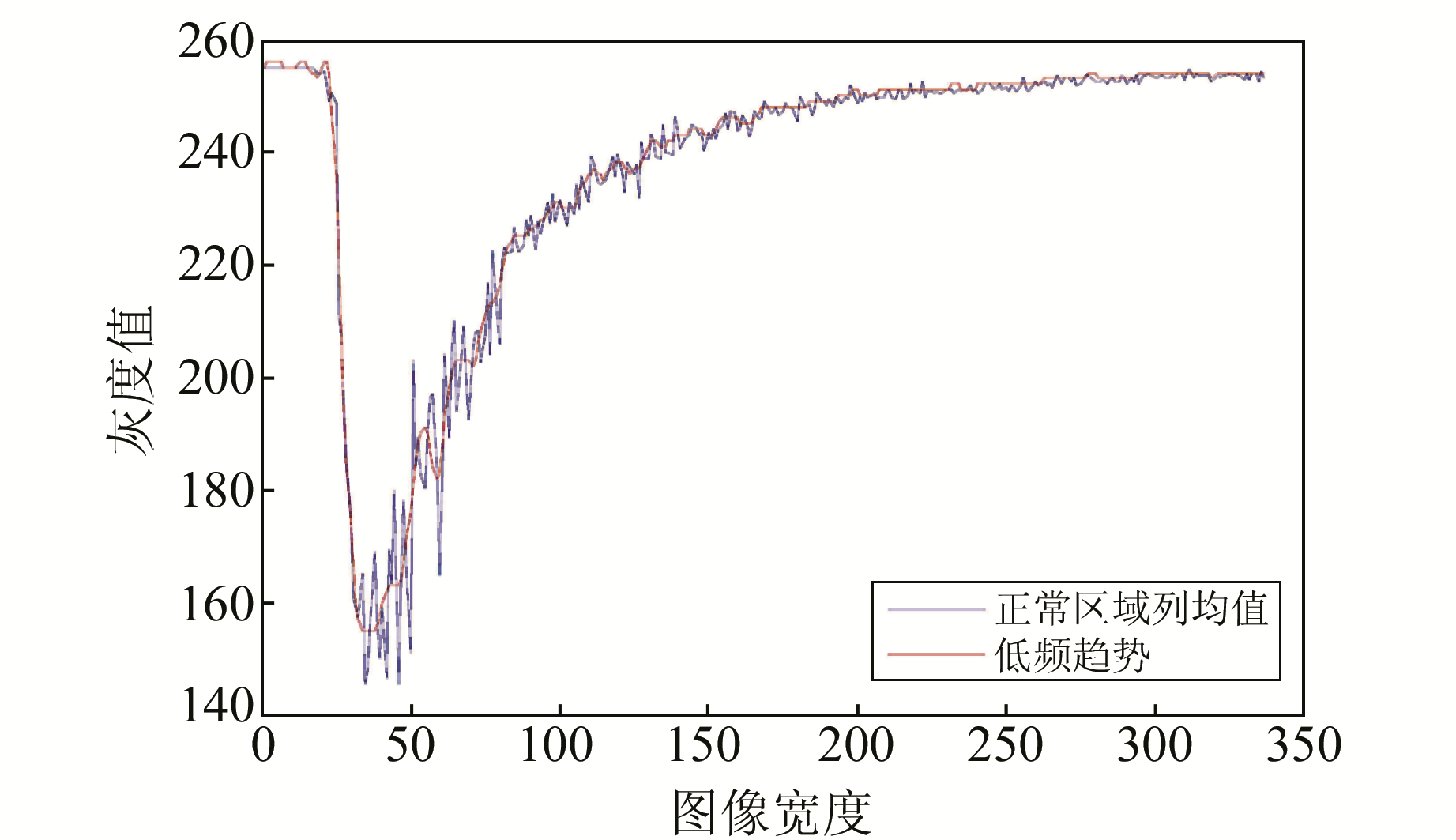
以右舷为例,统计第877~881 Ping均值。经过大量实验选取db7小波,分解7层,提取第2层的低频作为正常区域的趋势,如图 6所示。顾及人工增益区域地貌特征的存在,沿航迹向20 Ping取均值,减去正常区域的低频趋势项并提取小波低频,如图 7所示。此时得到的灰度统计曲线为增益量和特征信号,提取其低频趋势,便可得到增益量而保留特征信号。将原始图像减去此增益量得到去除人工增益的图像,如图 8所示。可以看出,消除人工增益量的图像灰度在纵向上实现了较好的均衡,且有效保持了图像的纹理特征。
|
图 6 非人工增益区域的列均值及其小波低频趋势 Fig. 6 The column mean of the region without human TVG and its wavelet low frequency trend |

|
图 7 增益和正常区域的差值及其小波低频趋势 Fig. 7 The difference of TVG and normal region and its wavelet low frequency trend |

|
图 8 消除人为TVG影响后的SSS图像 Fig. 8 SSS image eliminated by human TVG |
由图 4同时可看出,海底线附近存在异常高亮区,由于距离引起的增益补偿不恰当,图像远端目标不清晰。
以图 9(a)(图 4部分区域放大结果, 红色为海底线)为例,首先进行距离相关改正。根据前述方法改正后的图像如图 9(b)所示,实验时根据船速及海底地形的变化情况,Np取100。可见经过改正后的图像整体灰度变得均匀,图像远端改正效果较好,目标得到突出显示,靠近海底线附近仍存在明显亮度异常,即波束模式改正不彻底。

|
图 9 原始图像和距离相关辐射畸变改正后图像 Fig. 9 Raw SSS image and image removed by range-dependent effect (red line is sea-bottom line) |
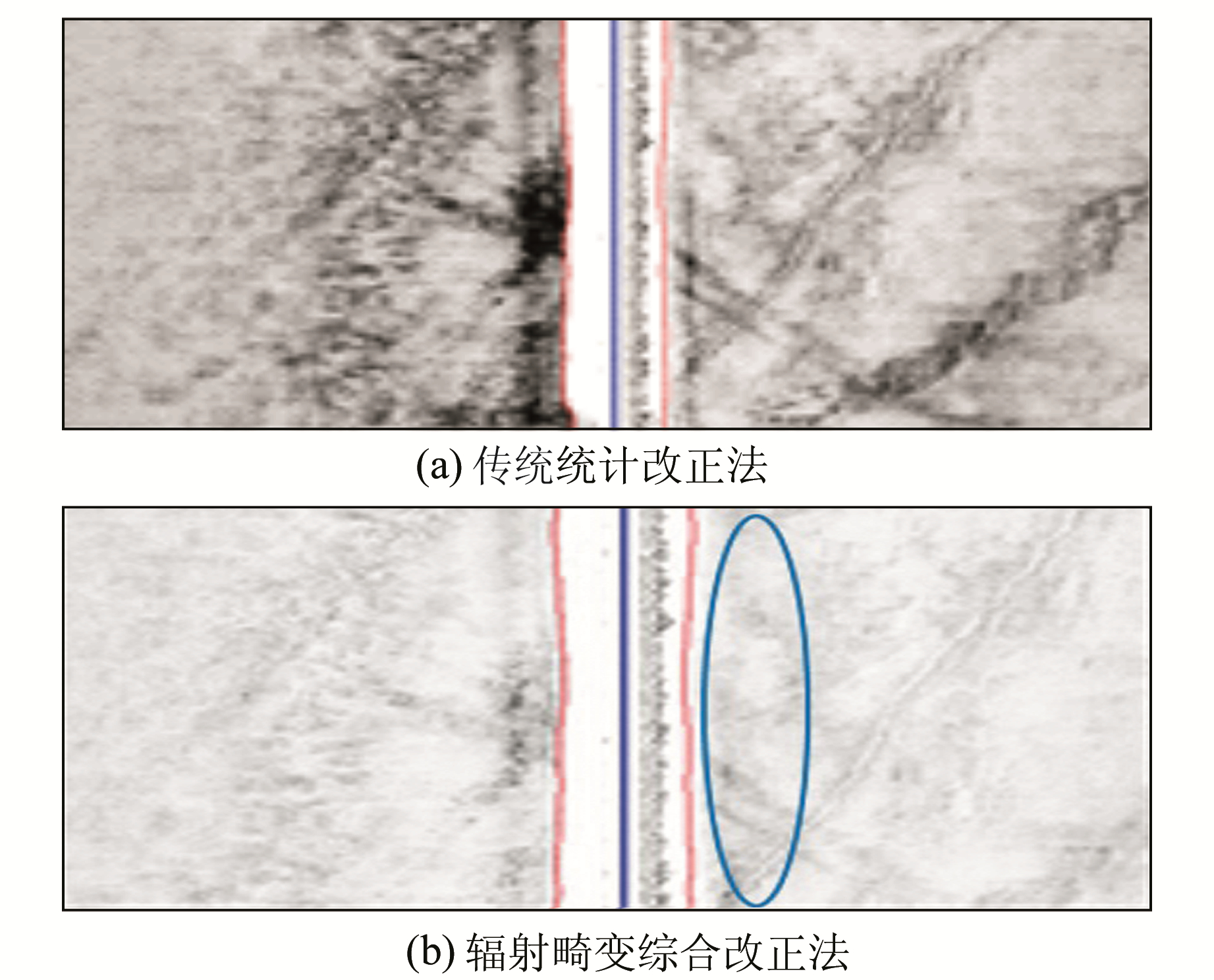
因此,对图 9(b)进一步依据与波束模式有关的方法进行改正,实验时L依然取100,Δ取1/10倍作业量程。传统统计改正法与综合改正法处理后的图像分别如图 10(a)、(b)所示。可见,经综合法改正后海底线附近高亮异常区域得到有效压制,且图像整体灰度变化均匀;传统方法改正后海底线附近亮区仍然存在,改正效果不佳。为定量分析传统统计改正法与综合改正法的优劣,采用熵值和峰值信噪比(peak signal to noise ratio, PSNR)来定量评价处理后图像质量,统计结果如表 1所示。一般熵值越小、PSNR越大,图像质量越高[14]。可见经综合法改正后,图像熵值小、PSNR大。究其原因,统计法对平滑窗口内图像整体进行统计分析,简单地得出了灰度沿横向的变化规律,进而进行增益处理,其未考虑人工增益、地形(海底跟踪)和波束指向性残差影响;综合法首先去除人工增益量影响,在平滑窗口内统计图像横向灰度变化趋势时,充分考虑了海底跟踪结果及波束模式影响,可实现灰度的整体均衡,减少了图像的混乱程度和失真现象。数值量化指标和理论分析均表明,综合法改正后图像质量优于传统方法。
|
图 10 辐射畸变改正 Fig. 10 Radiometric distortion correction |
|
|
表 1 传统统计改正法与综合改正法处理后图像熵值及PSNR数值比较 Tab. 1 Entropy and PSNR of SSS image corrected by traditional statistic and the comprehensive method |
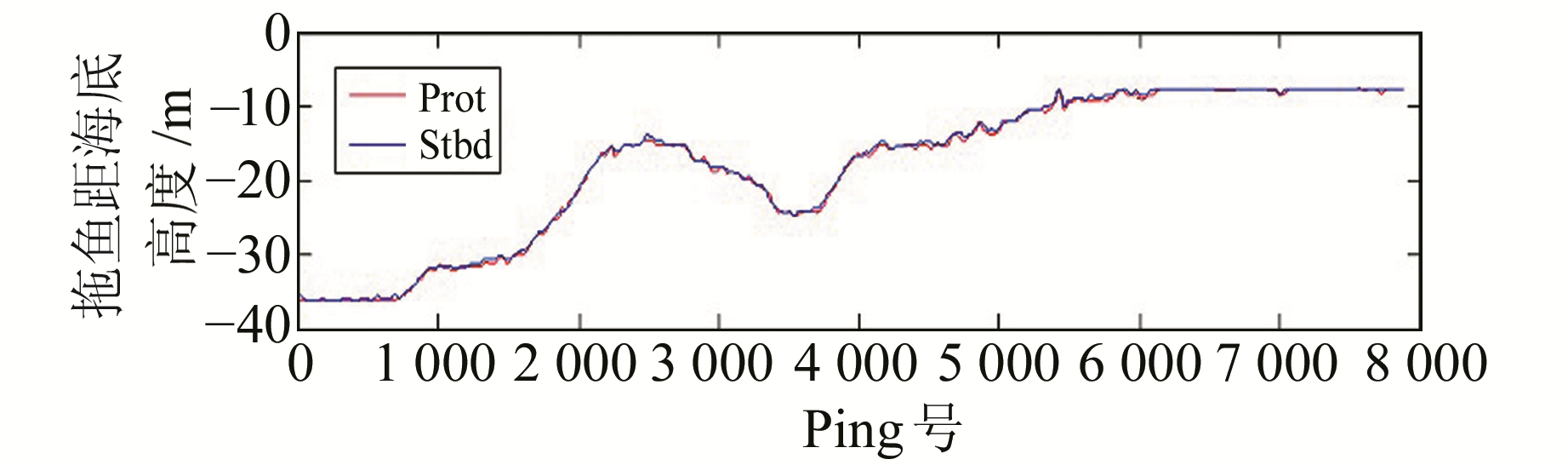
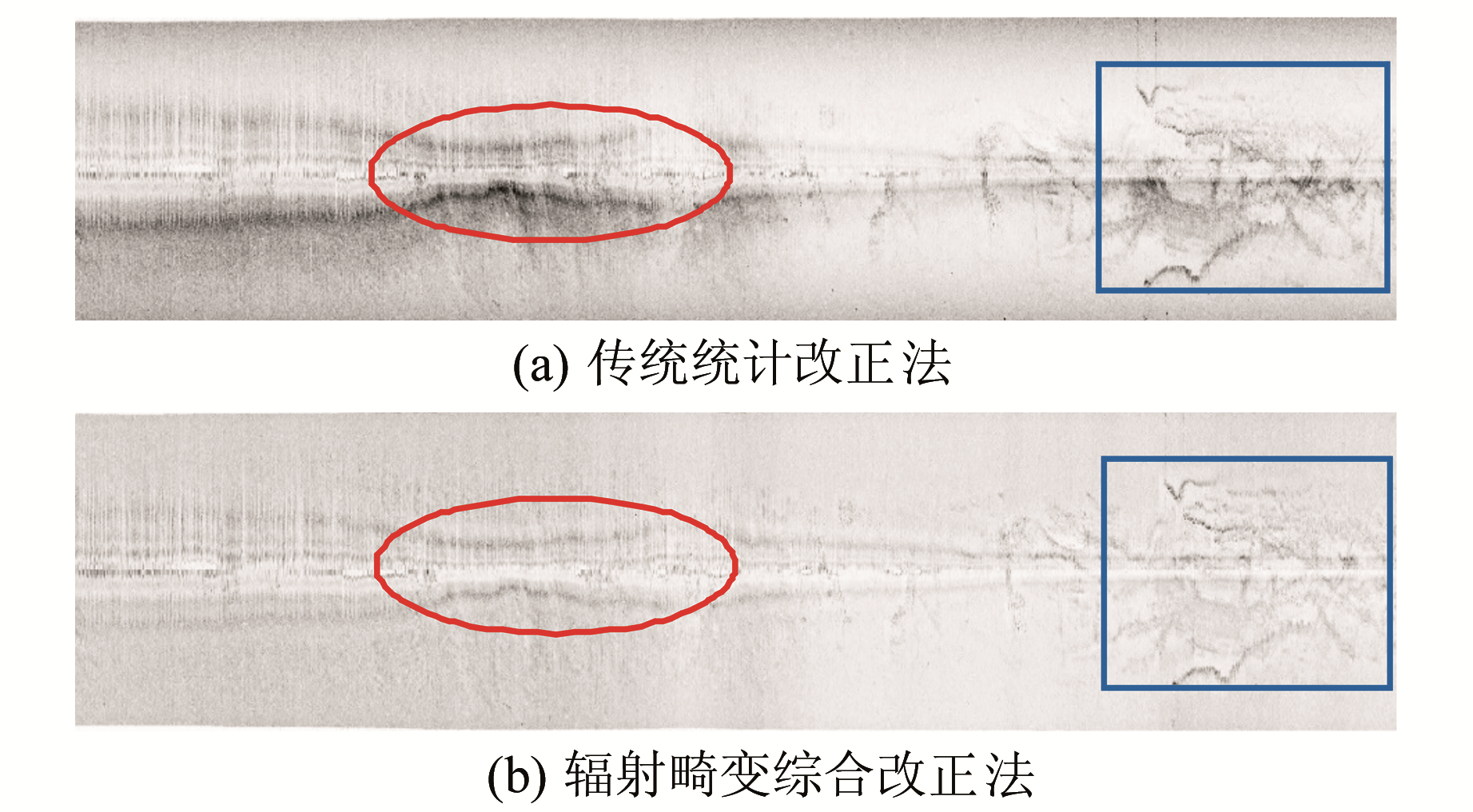
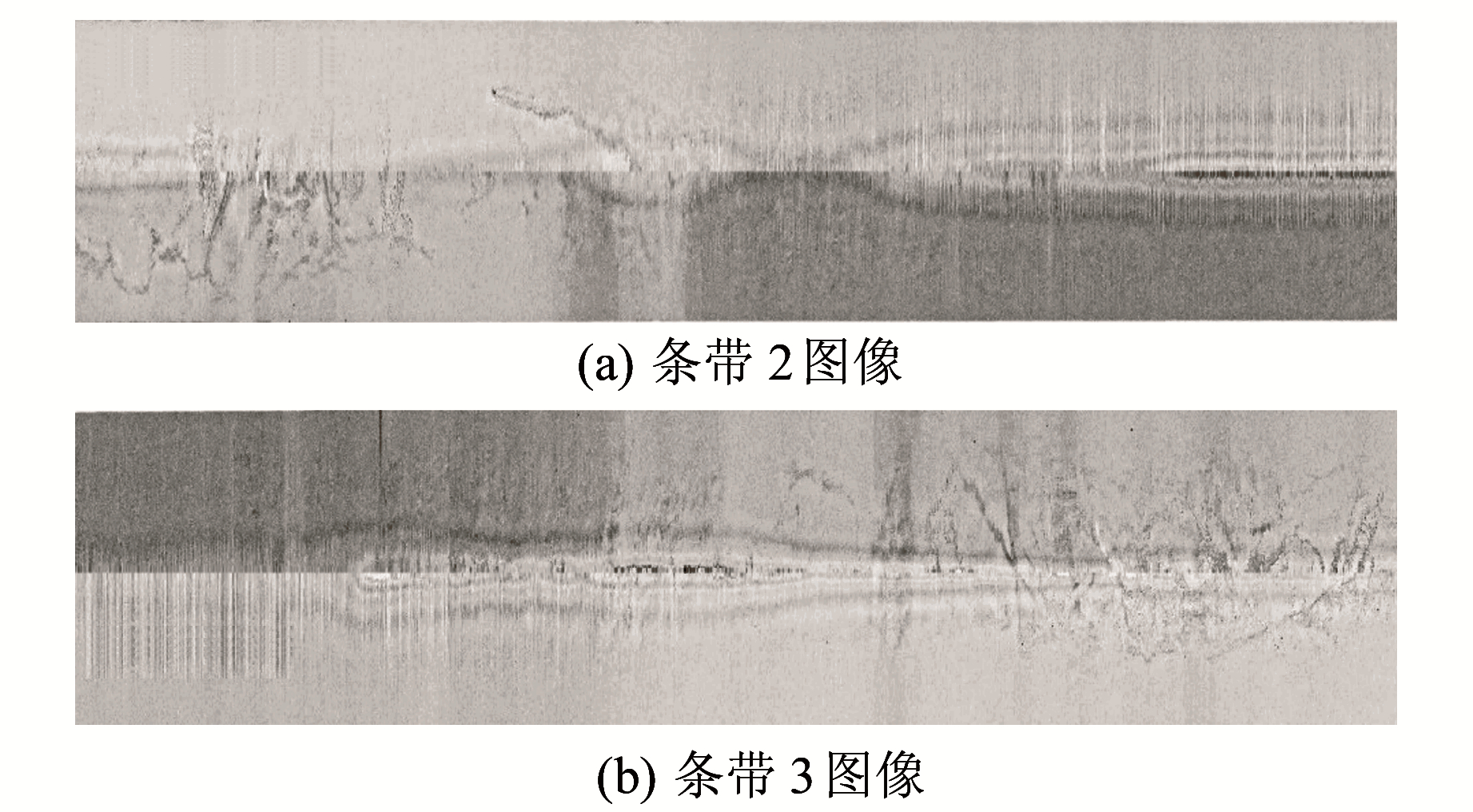
为验证辐射畸变综合改正法处理条带图像的有效性,对测区单个条带(图 4)依次进行辐射畸变综合改正及斜距改正[15]。左、右舷图像海底跟踪结果(文献[13]方法)如图 11所示,左、右舷拖鱼距海底高度保持了高度的一致性,表明左舷和右舷图像在换能器正下方具有一致性(反映的海底位置近似相同,底质和地形起伏变化相同)。基于传统统计法与综合法改正后图像分别如图 12(a)、(b)所示,从图中红框、蓝框区域可看出,传统方法未能实现海底线附近位置处灰度的均衡;综合改正法有效实现了其异常高亮区的压制,实现了条带图像灰度的整体均衡。同样对另外2条测线进行综合改正,处理后图像如图 13所示。可见经辐射畸变综合改正后,获得了高质量的单条带SSS图像,为后续图像拼接及目标探测、识别提供了前期高质量的条带图像。
|
图 11 左、右舷图像海底线跟踪结果 Fig. 11 Bottom tracking results of the port and stbd image |
|
图 12 条带辐射畸变和斜距改正后图像 Fig. 12 SSS image with radiometric distortion and slant range correction |
|
图 13 其余2条测线经综合改正后的图像 Fig. 13 The other two strip images corrected by the comprehensive method |
针对SSS图像存在严重的辐射畸变问题,研究了SSS图像辐射畸变改正算法。将影响SSS图像辐射畸变的因素分为人工增益、波束模式和距离相关3种,提出了一种辐射畸变综合改正方法。与传统辐射畸变统计改正方法比较,辐射畸变综合改正法处理后图像熵值减小、PSNR增大,数值结果表明图像质量提高,且视觉上图像质量得到明显改善,验证了辐射畸变综合改正方法的有效性。
考虑海底底质变化,给出的Ping均值平滑参数均为经验值。为彻底避免海底底质变化影响,后续需深入研究海底底质分类方法,依据条带分类图像进行区域定位,进而实施辐射畸变改正。
| [1] |
Bryant R. Side Scan Sonar for Hydrography-An Evaluation by the Canadian Hydrographic Service[J]. The International Hydrographic Review, 2015, 52(1): 43-55
(  0) 0) |
| [2] |
Davy C M, Fenton M B. Technical Note: Side-Scan Sonar Enables Rapid Detection of Aquatic Reptiles in Turbid Lotic Systems[J]. European Journal of Wildlife Research, 2013, 59(1): 123-127 DOI:10.1007/s10344-012-0680-9
(  0) 0) |
| [3] |
Nakamura K, Toki T, Mochizuki N, et al. Discovery of a New Hydrothermal Vent Based on an Underwater, High-Resolution Geophysical Survey: Deep Sea Research Part Ⅰ[R]. Oceanographic Research Papers, 2013 https://www.sciencedirect.com/science/article/pii/S0967063712002440
(  0) 0) |
| [4] |
Healy C A, Schultz J J, Parker K, et al. Detecting Submerged Bodies: Controlled Research Using Side-Scan Sonar to Detect Submerged Proxy Cadavers[J]. Journal of Forensic Sciences, 2015, 60(3): 743-752 DOI:10.1111/jfo.2015.60.issue-3
(  0) 0) |
| [5] |
王爱学, 赵建虎, 尚晓东, 等. 单波束水深约束的侧扫声呐图像三维地形反演[J]. 哈尔滨工程大学学报, 2017, 38(5): 739-745 (Wang Aixue, Zhao Jianhu, Shang Xiaodong, et al. Recovery of Seabed 3D Micro-Topography from Side-Scan Sonar Image Constrained by Single-Beam Soundings[J]. Journal of Harbin Engineering University, 2017, 38(5): 739-745)
(  0) 0) |
| [6] |
王爱学, 张红梅, 王晓, 等. 侧扫声呐条带数据处理及其无缝成图[J]. 测绘地理信息, 2017, 42(1): 26-29 (Wang Aixue, Zhang Hongmei, Wang Xiao, et al. Processing Principles of Side-Scan Sonar Data for Seamless Mosaic Image[J]. Journal of Geomatics, 2017, 42(1): 26-29)
(  0) 0) |
| [7] |
Anstee S. Removal of Range-Dependent Artifacts from Side Scan Sonar Imagery[R]. DSTO Aeronautical and Maritime Research Laboratory, DTIC Document, Australia, 2001
(  0) 0) |
| [8] |
Capus C, Ruiz I T, Petillot Y. Compensation for Changing Beam Pattern and Residual Tvg Effects with Sonar Altitude Variation for Side Scan Mosaicing and Classification[C]. 7th Eur Conf Underwater Acoustics, Delft, Netherlands, 2004
(  0) 0) |
| [9] |
Ramirez T M. Triton Perspective-SS Sidescan Processing Guide[Z]. 2014
(  0) 0) |
| [10] |
Zhao J, Yan J, Zhang H, et al. A New Radiometric Correction Method of Side Scan Sonar Images by Considering Seabed Sediment Variation[J]. Remote Sensing, 2017, 9(6): 1-18
(  0) 0) |
| [11] |
阳凡林, 刘经南, 赵建虎. 基于数据融合的侧扫声呐图像预处理[J]. 武汉大学学报:信息科学版, 2004, 29(5): 402-406 (Yang Fanlin, Liu Jingnan, Zhao Jianhu. Sidescan Sonar Image Preprocessing Techniques Based on Data Fusion[J]. Geomatics and Information of Wuhan University, 2004, 29(5): 402-406)
(  0) 0) |
| [12] |
程彬彬, 齐彦生, 查智. 声呐图像局部对比度增强方法[J]. 水雷战与舰船防护, 2008, 16(3): 6-9 (Cheng Binbin, Qi Yansheng, Zha Zhi. A Method of Enhancing the Local Contrast of Sonar Image[J]. Mine Warfare & Ship Self-Defence, 2008, 16(3): 6-9)
(  0) 0) |
| [13] |
Zhao J H, Wang X, Zhang H M. A Comprehensive Bottom-Tracking Method for Sidescan Sonar Image Influenced by Complicated Measuring Environment[J]. IEEE Journal of Oceanic Engineering, 2017, 42(3): 619-631 DOI:10.1109/JOE.2016.2602642
(  0) 0) |
| [14] |
赵春晖, 尚政国. 自适应单尺度Ridgelet声呐图像去噪方法[J]. 哈尔滨工程大学学报, 2007, 28(11): 1 263-1 267 (Zhao Chunhui, Shang Zhengguo. Adaptive Monoscale Ridgelet Denoising Method for Sonar Images[J]. Journal of Harbin Engineering University, 2007, 28(11): 1 263-1 267)
(  0) 0) |
| [15] |
邓雪清, 巩丹超, 罗瑞. 侧扫声呐图像地理编码技术研究[J]. 海洋测绘, 2002, 22(4): 14-17 (Deng Xueqing, Gong Danchao, Luo Rui. Research on the Geo-Coding Technique of Side Scan Sonar Image[J]. Hydrographic Surveying and Charting, 2002, 22(4): 14-17 DOI:10.3969/j.issn.1671-3044.2002.04.003)
(  0) 0) |
2. School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road, Wuhan 430079, China
 2018, Vol. 38
2018, Vol. 38


