2. 北京航天宏图信息技术股份有限公司, 北京市杏石口路65号, 100195;
3. 北京遥测技术研究所, 北京市丰滢东路1号, 100094;
4. 国网河北省电力有限公司建设公司, 石家庄市塔北路107号, 050021
截至2017-08,Galileo卫星导航系统在轨运行卫星达到18颗,其中4颗为在轨实验(IOV)卫星(E11、E12、E19、E20),14颗为全运行能力(FOC)卫星(E01、E02、E03、E04、E05、E07、E08、E09、E14、E18、E22、E24、E26、E30)。伽利略系统是全球导航系统的重要组成部分,对其广播星历精度进行系统的统计和分析十分必要。许多学者对北斗卫星、GPS卫星和GLONASS卫星广播星历的精度进行了详细的分析[1-4],但很少有人对Galileo卫星广播星历的精度进行全面评估。刘朝英等[5]2015年对IOV卫星的空间信号精度进行了分析,那时实验数据较早,卫星数少,精度较低,并不能体现现阶段Galileo卫星的精度,而且当时伽利略系统尚处于实验阶段。本文以精密星历为参考,对Galileo在轨的IOV和FOC卫星的广播星历精度进行简要分析,希望能为以后相关的研究与应用以及评估现阶段导航定位系统提供一定的参考。
1 广播星历精度计算与评估方法广播星历的评估方法一般有两种,一是利用事后精密星历进行评估,二是采用SLR技术进行激光检核[2]。本文采用第一种方法。
本文采用的精密星历是由GFZ发布的GBM数据,精度为cm级,比广播星历高出两个数量级[1]。因此可以把GBM的精密星历的数据当作真值,对Galileo广播星历进行评估。GBM精密星历提供等间隔的卫星钟差和位置,如果求任意时刻卫星的钟差和位置,需要对精密星历进行内插。本文利用拉格朗日内插的方法计算卫星在任意时刻的位置和速度,为了避免龙格震荡现象,在数据前后多添加2 h,并采用9阶插值。
在具体的实验中需要注意以下6个问题。
1) 数据质量的检查。在计算之前需要剔除无效卫星的数据,控制数据质量。具体包括:①广播星历中卫星标识不正常的予以剔除;②精密星历中卫星的坐标和钟差标记不正常的不予考虑;③数据缺失的历元不参与统计分析;④卫星没有标记错误,但计算结果中存在明显误差的历元予以剔除。
2) 时空基准的统一。Galileo卫星广播星历和GFZ发布的精密星历采用的时间系统和坐标参考框架不一致[6]。
3) 卫星天线相位中心改正。在比较广播星历与精密星历时需要进行相位中心偏移改正,本文利用IGS08.atx文件中的校正数据对Galileo卫星的PCOs(相位中心偏移)和PCVs(相位中心变化)进行校准。
4) 轨道误差表现形式。将卫星轨道误差从地心地固坐标系转到卫星轨道(RTN)坐标系,需从R(径向)、T(切向)、N(法向)3个方向考虑轨道误差,并加以分析[7]。
5) 钟差评估。广播星历和精密星历的参考时间基准不一样,为了避免由于基准的选取不同而引起卫星钟差的误差,在选择基准钟求差的基础上,分别再与国际上的精密星历中的值进行比较,即采用二次差法[3]。分别统计二次差的RMS(均方根误差)和STD(标准差)[3]。
6) 精度评定。采用RMS和SISRE(空间信号测距误差)对Galileo广播星历的精度进行统计分析[5]。
2 实验分析采用2016-11-25~12-24(年积日330~359 d)Galileo卫星广播星历计算的卫星在任意时刻的位置与GFZ发布的GBM精密数据进行对比分析,获得Galileo卫星广播星历精度变化情况。目前,在轨运行的18颗Galileo卫星中E03、E04、E05、E07为最新发射卫星,还没有正式工作,E14,E18卫星钟稳定性较差,E20卫星在2014年已经出现故障,因此不对这些卫星进行统计分析[8-9]。
2.1 广播星历轨道精度评估首先以年积日330~336 d计算结果为例,计算结果在3个方向的比较见表 1。
|
|
表 1 Galileo卫星广播星历轨道误差 Tab. 1 The Galileo satellite broadcast ephemeris orbit error |
图 1表示一周的广播星历轨道误差在径向、切向、法向3个方向的均值,其中横坐标表示卫星编号,纵坐标表示RMS值。从表 1和图 1可以看出,广播星历轨道误差在3个方向的分量均优于1.0 m;其中径向误差最小,精度最高,均值为0.51 m;法向次之,均值为0.67 m;切向误差最大,均值为0.89 m。因为地面跟踪站在跟踪Galileo卫星时,其观测值对Galileo卫星径向变化比切向和法向更加敏感;另一方面卫星在轨运行状态符合开普勒定律,卫星运行轨迹近似椭圆形,在卫星运行周期能够精确测定的前提下可以较高精度地估计出卫星运行轨迹的长半轴,也就是卫星的高度方向即径向。卫星在切向和法向的误差较大,这2个方向的力学模型有待进一步完善。Galileo卫星的一维RMS均值为0.72 m,各颗卫星的精度优于0.8 m。IOV卫星的平均RMS值为0.71 m,FOC卫星的平均RMS值为0.73 m。FOC卫星的轨道精度与IOV卫星的精度相当,所以轨道精度与卫星的类型无关。

|
图 1 广播星历轨道误差 Fig. 1 The broadcast ephemeris of orbit error |
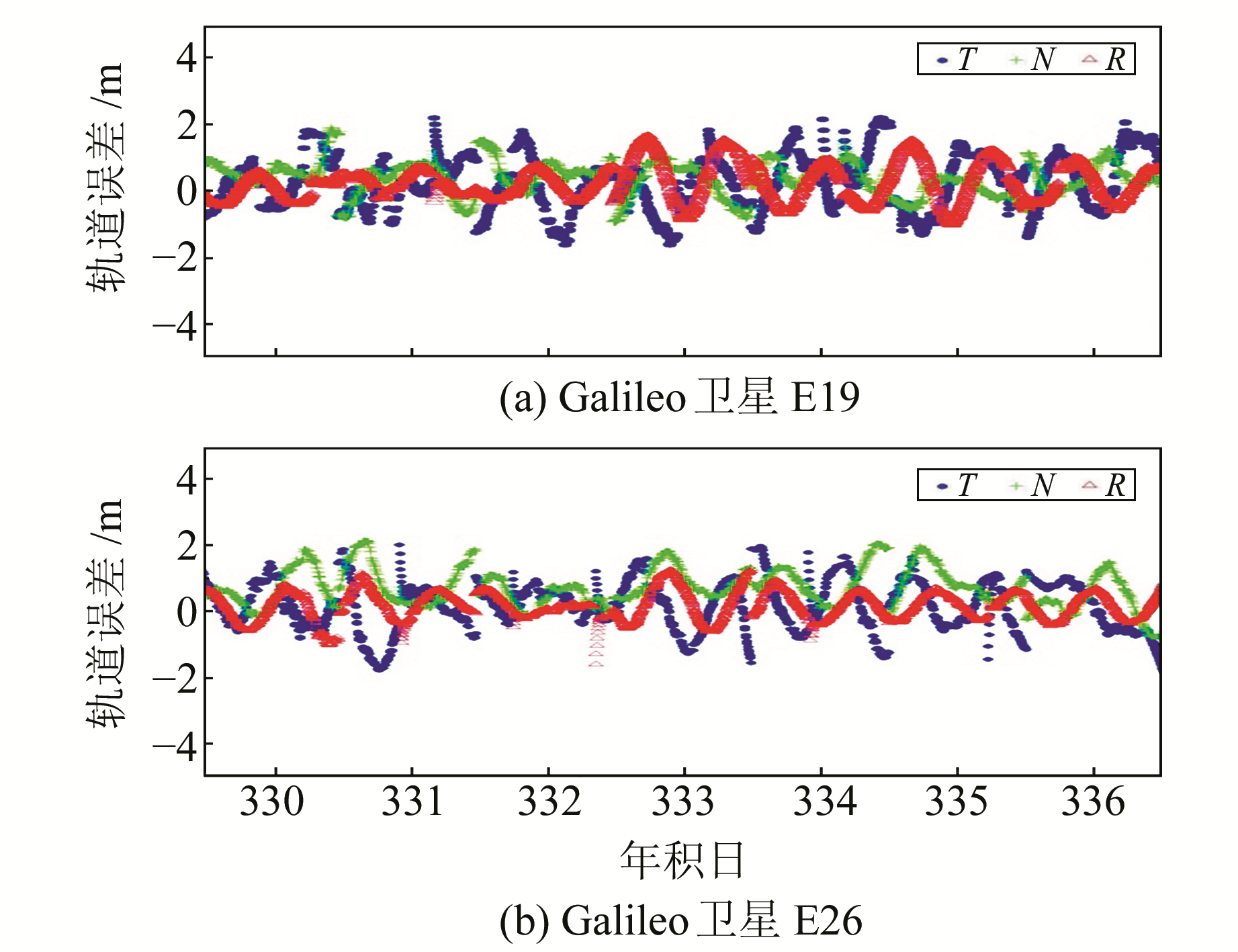
为了进一步分析Galileo卫星广播星历轨道误差的量级及其变化规律,限于篇幅,每种类型的卫星选取一颗(E19、E26),绘出一周内轨道误差在3个方向的误差曲线图(图 2)。
|
图 2 广播星历轨道误差变化曲线 Fig. 2 The curve of broadcast ephemeris orbit error |
从图 2可以看出,Galileo卫星在3个方向的轨道误差值在-2~2 m范围内波动,而且有一定的周期性。卫星运行周期大约为14 h,与图中卫星轨道误差表现的周期性基本一致,说明轨道误差与卫星在轨运行的特点有关。此外,卫星的径向误差曲线变化比较平缓,说明径向比较稳定,切向和法向误差波动大,误差较大。E26卫星在3个方向的变化趋势与E19卫星基本相同,说明FOC卫星与IOV卫星的轨道精度没有明显差异。另外,相邻2 d轨道误差在3个方向具有明显的跳跃现象,这与广播星历的更新周期和预报精度随时间变化有关,而且相邻2 d的精密星历的精度也存在跳跃现象[10]。
为了能完全反映Galileo卫星广播星历精度状况,统计所有卫星30 d平均RMS值(图 3)。

|
图 3 30 d的广播星历轨道误差均值 Fig. 3 The average of broadcast ephemeris orbit error for 30 days |
从图 3可以看出,Galileo各颗卫星轨道RMS均值为0.526 m。不同天的卫星广播星历轨道精度也有差别,整体上各颗卫星轨道误差的一维RMS优于0.8 m,有的单天轨道精度能达到0.3 m。从均值来看,IOV卫星30 d的轨道平均RMS值为0.526 m,FOC卫星30 d的平均RMS值为0.527 m,统计结果表明,FOC卫星广播星历轨道与IOV卫星轨道的精度相当。
2.2 广播星历钟差精度评估Galileo卫星上的卫星钟有两种类型,一种是铷钟,另一种是无源氢钟。氢钟为卫星的主钟,当它出现问题时,启用备用的铷钟作为时间基准。它们具有很高的稳定性,但是随着时间的推移,卫星钟会发生一定漂移。首先选择一周的广播星历为例,计算卫星的钟差误差,选择Galileo卫星中的E08号为参考卫星钟估算Galileo卫星钟差,再与GBM精密星历作二次差。计算误差结果见表 2和图 4(不包含E08号星)。
|
|
表 2 Galileo卫星钟差 Tab. 2 Galileo satellite clock difference |
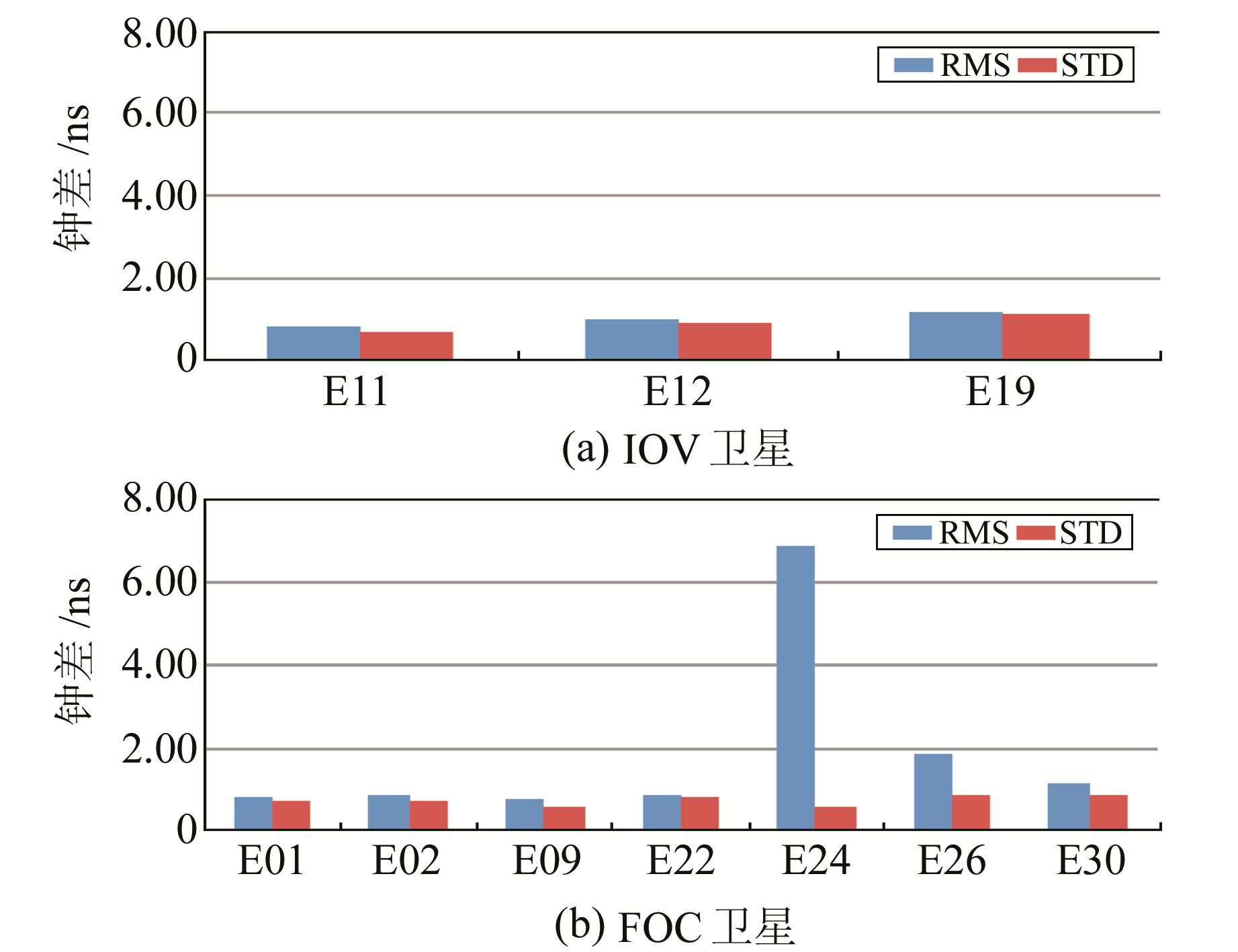
|
图 4 广播星历钟差误差 Fig. 4 Broadcast ephemeris clock error |
从表 2和图 4可以看出,卫星钟误差的RMS值基本在1.2 ns以内,但E24号卫星钟差误差比较大,可能由于Galileo卫星的氢钟出现问题,使用了铷钟,而参考星为氢钟;也可能是由于卫星钟的偏移比较大,所以不对E24卫星钟差统计分析。Galileo卫星平均RMS值为1.0 ns,平均标准差为0.8 ns。IOV卫星的平均标准差为0.92 ns,FOC卫星的平均标准差为0.79 ns,说明FOC卫星和IOV卫星的钟差精度相当。
为了具体分析Galileo卫星钟差的长时间变化趋势,同样选择E19、E26号卫星,给出其连续30 d的RMS值的变化曲线图(图 5)。

|
图 5 30 d的广播星历钟误差曲线 Fig. 5 Broadcast ephemeris clock error curve of 30 days |
从图 5可以看出,卫星钟的误差值基本在-3~3 ns范围内波动。在有些时间段会出现一些跳跃现象,原因是Galileo卫星广播星历的钟差与精密星历产生了粗差。E19卫星与E26卫星的钟差误差变化曲线基本一致。卫星钟的钟差像卫星轨道误差一样具有明显的周期性,这与卫星14 h的运行周期密切相关。
图 6为卫星在30 d的卫星钟差RMS的均值,大多数卫星钟的RMS在1 ns以内,平均误差值为0.98 ns。对Galileo两类卫星结果分别进行统计,IOV卫星的平均钟误差为0.97 ns,FOC卫星的平均钟差为0.99 ns,两种类型的卫星精度相当。Galileo广播星历钟差能够保证较高的精度,这与地面监测站的分布和数量有明显的关系[2]。
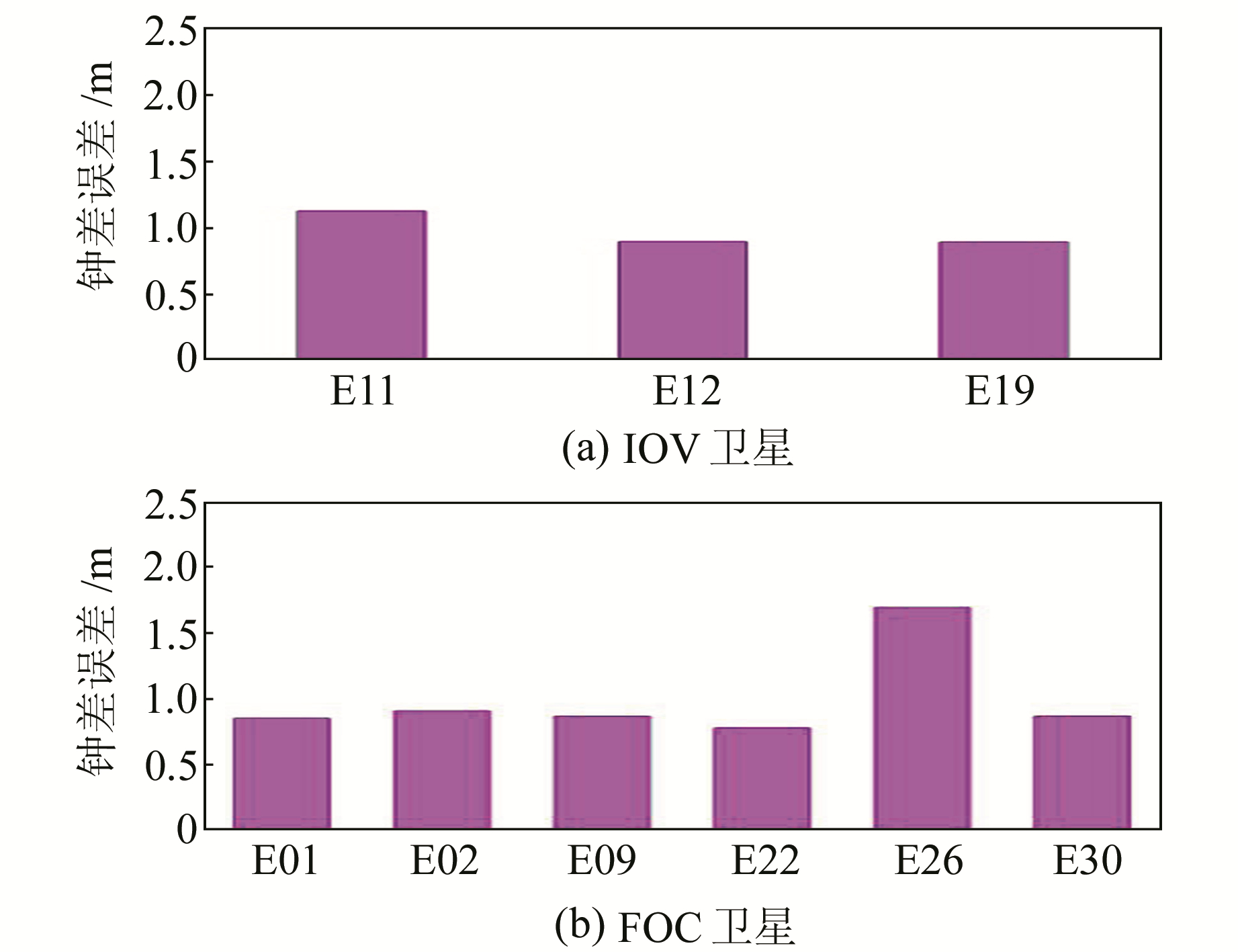
|
图 6 30 d的广播星历钟误差平均值 Fig. 6 The average value of the broadcast ephemeris clock error for 30 days |
以上分析了Galileo广播星历轨道和钟差两者的精度。目前,一般采用空间信号测距(SISRE)误差综合评价广播星历的精度[2]。空间信号测距误差的大小可以直接影响导航定位的精度,它反映卫星的轨道和钟差与卫星实际位置的差值在视线方向上的综合影响。图 7绘制了卫星E19和E26连续一周的空间用户测距误差的曲线。

|
图 7 一周广播星历SISRE误差 Fig. 7 Broadcast ephemeris SISRE error for a week |
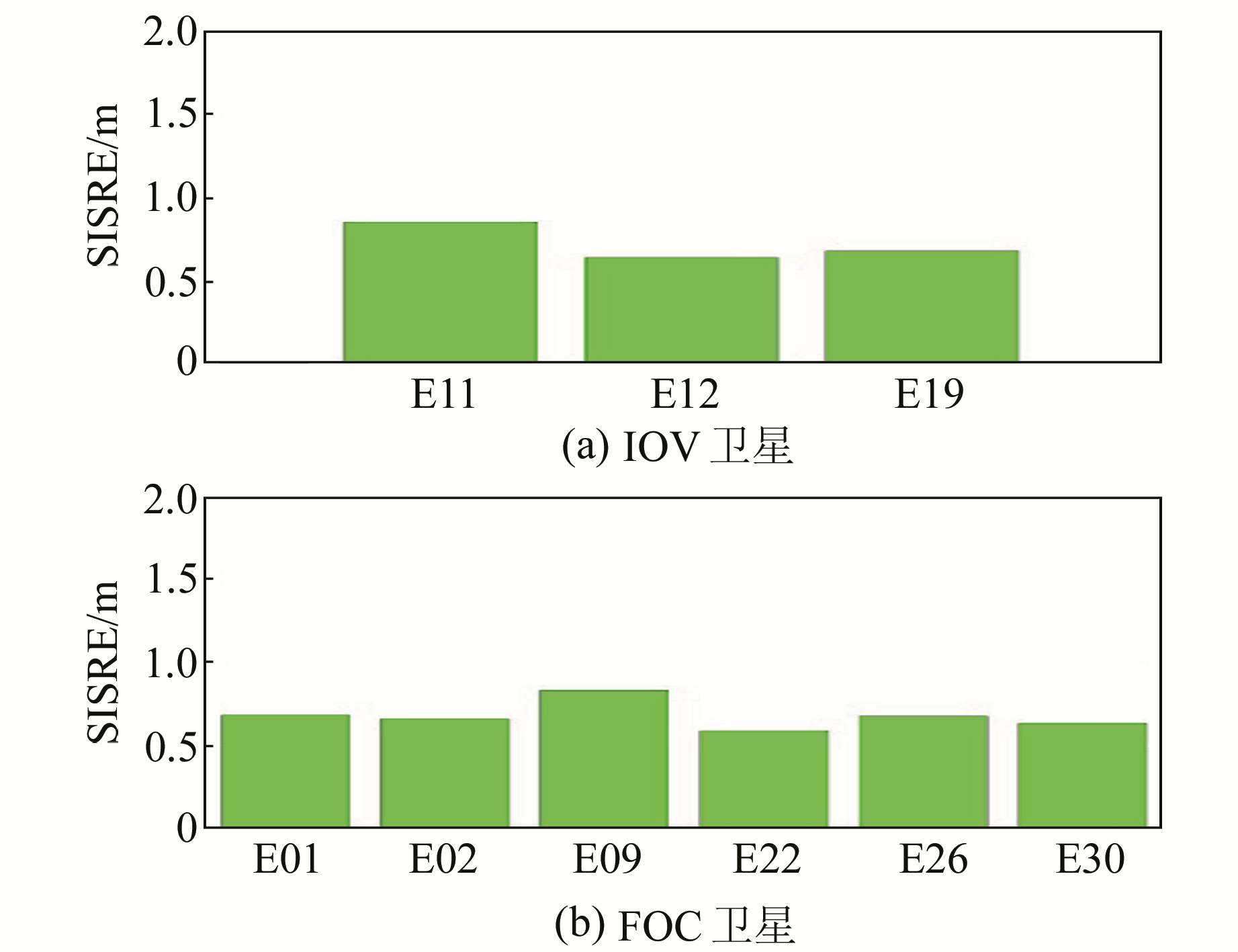
由图 7可知,卫星的SISRE误差比较稳定,基本都在2 m以内波动。Galileo卫星的SISRE误差的周期性不明显,这是卫星轨道和钟差误差共同作用的结果。E19卫星和E26卫星的SISRE精度相当。为了更加精确地分析测距误差的长期精度,图 8统计了SISRE在30 d的曲线图,可以看出与一周的曲线分析结果一致。图 9表示所有卫星30 d的SISRE平均值,可以发现各颗卫星的用户距离误差基本在1.0 m以下,FOC卫星的平均值为0.68 m,IOV卫星的平均值为0.72 m,说明两种类型卫星的SISRE精度相当,Galileo卫星的整体精度优于1 m。
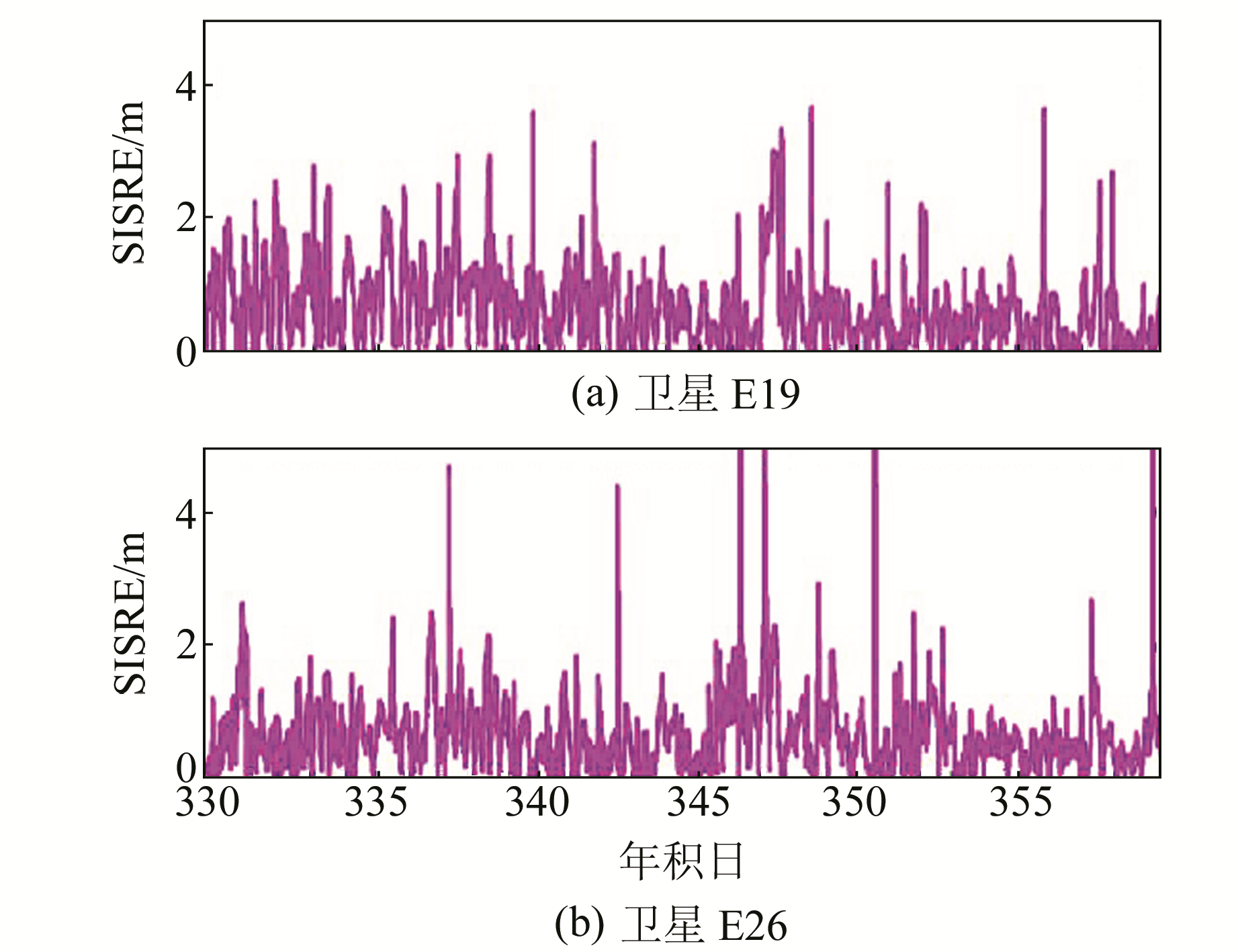
|
图 8 30 d广播星历SISRE误差 Fig. 8 Broadcast ephemeris SISRE error for 30 days |
|
图 9 广播星历SISRE误差均值 Fig. 9 The average of broadcast ephemeris SISRE error |
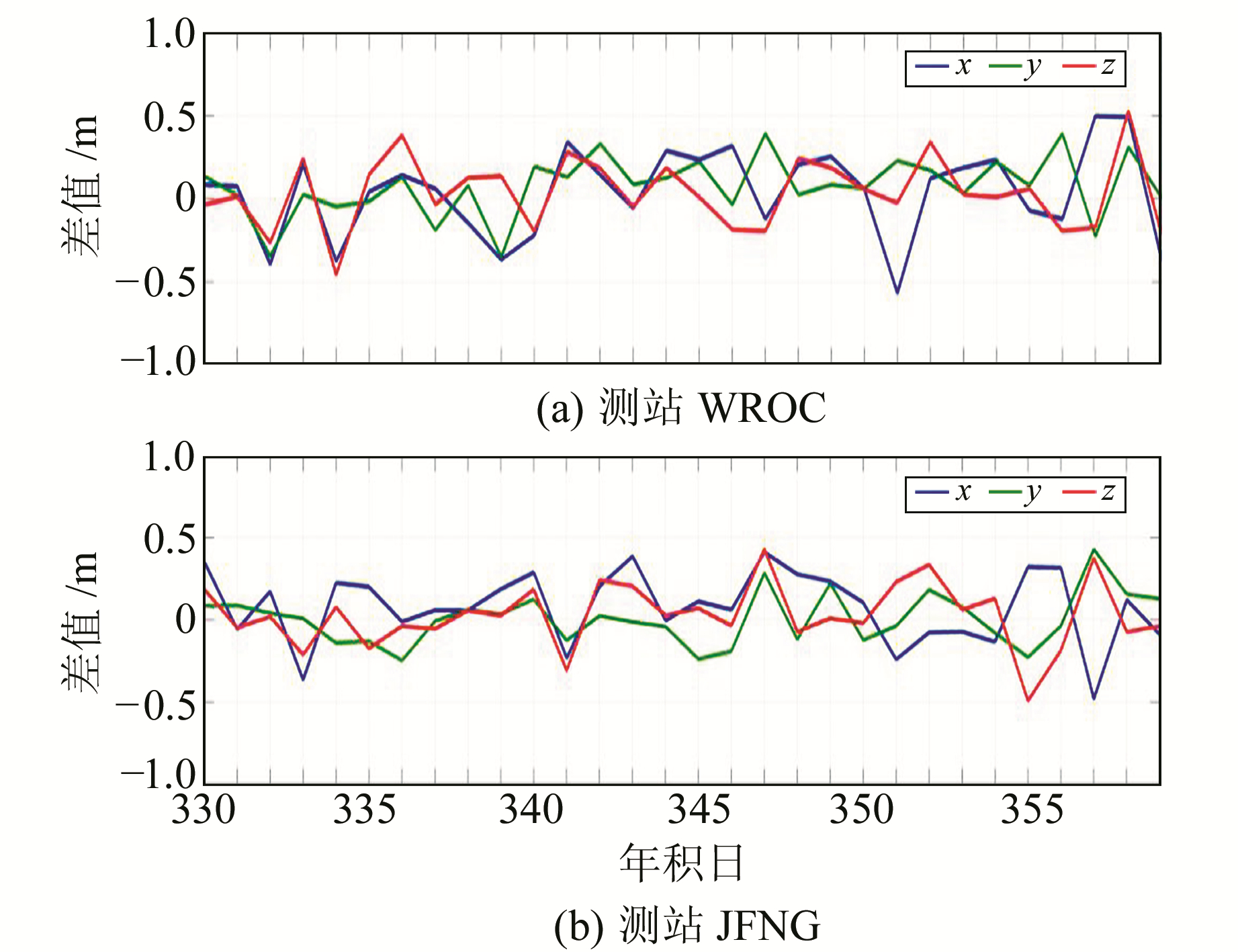
卫星轨道误差直接影响定位精度,本文用广播星历进行单点定位,计算中电离层延迟采用双频伪距改正,对流层延迟采用Saastamoinon模型估计,用最小二乘原理解算地面坐标,迭代计算得到精度较高的坐标值。将计算坐标结果与IGS官方网站公布的多天解的mm级精确坐标对比分析。选择国内JFNG和欧洲WROC 2个MGEX(multi-GNSS-experment)站,每天计算1个坐标值,30 d的单点定位结果见图 10。
|
图 10 单点定位结果比较 Fig. 10 The comparison of point positioning results |
从图 10可以看出,2个测站在3个方向的坐标差值在-0.5~0.5 m范围内波动,从30 d统计结果得出,大部分坐标差值在0.2 m以内,有的差值仅有几个cm,因此Galileo广播星历对单点定位的影响可以认为在dm级。当用户对单点定位的精度要求在dm级时,可以直接使用广播星历解算轨道参数。
5 结语1) Galileo卫星广播星历的轨道误差、卫星钟差和空间信号测距误差与卫星的类型无关。FOC卫星与IOV卫星在这3个方面的精度相当,并且轨道和钟差误差均存在一定的周期性,这与卫星运行的周期有关。
2) 广播星历的轨道误差表现出在径向方向误差最小,法向次之,切向误差最大的特点。其中,径向误差优于0.5 m,法向优于0.7 m,切向优于1.0 m,轨道一维RMS值优于0.8 m。
3) FOC和IOV卫星的轨道误差在-2~2 m内波动,钟差误差基本在-3~3 ns内波动,30 d钟差的平均RMS值达到1.0 ns。广播星历的空间信号测距误差在2 m以内,平均精度优于1.0 m。
4) Galileo广播星历对实时精密单点定位影响较大,且卫星星座不完善,在事后处理数据时建议采用精密星历进行精密单点定位。
| [1] |
孟祥广, 孙越强, 白伟华, 等. 北斗卫星广播星历精度分析[J]. 大地测量与地球动力学, 2016, 36(10): 870-873 (Meng Xiangguang, Sun Yueqiang, Bai Weihua, et al. The Beidou Satellite Broadcast Ephemeris Precision[J]. Journal of Geodesy and Geodynamics, 2016, 36(10): 870-873)
(  0) 0) |
| [2] |
曾琪, 吴多, 刘万科. 基于长期数据的北斗广播星历精度评估[J]. 大地测量与地球动力学, 2016, 36(11): 958-961 (Zeng Qi, Wu Duo, Liu Wanke. Long Term Data Accuracy Assessment Based on Beidou Broadcast Ephemeris[J]. Journal of Geodesy and Geodynamics, 2016, 36(11): 958-961)
(  0) 0) |
| [3] |
楼益栋, 施闯, 周小青, 等. GPS精密卫星钟差估计与分析[J]. 武汉大学学报:信息科学版, 2009, 34(1): 88-91 (Lou Yidong, Shi Chuang, Zhou Xiaoqing, et al. Estimation and Analysis of GPS Precise Satellite Clock Error[J]. Geomatics and Information Science of Wuhan University, 2009, 34(1): 88-91)
(  0) 0) |
| [4] |
Warren D L M, Raquet J F. Broadcast vs.Precise GPS Ephemerides:A Historical Perspective[J]. GPS Solutions, 2003, 7(3): 151-156 DOI:10.1007/s10291-003-0065-3
(  0) 0) |
| [5] |
刘朝英, 陈国, 胡志刚, 等. Galileo空间信号误差和标准定位性能初步分析[J]. 大地测量与地球动力学, 2016, 36(4): 308-312 (Liu Chaoying, Chen Guo, Hu Zhigang, et al. Preliminary Analysis of Galileo Spatial Signal Error and Standard Positioning Performance[J]. Journal of Geodesy and Geodynamics, 2016, 36(4): 308-312)
(  0) 0) |
| [6] |
邹蓉, 刘晖, 杨蜀江. 伽利略地球参考框架对建立我国自主的地球参考框架的启示[J]. 武汉大学学报:信息科学版, 2009, 34(11): 1266-1270 (Zou Rong, Liu Hui, Yang Shujiang. The Enlightenment of the Galileo Earth Reference Frame to the Establishment of the Autonomous Reference Frame of China[J]. Geomatics and Information Science of Wuhan University, 2009, 34(11): 1266-1270)
(  0) 0) |
| [7] |
韩德强, 党亚民, 王虎, 等. 引入国家基准站的北斗导航卫星精密定轨[J]. 测绘通报, 2017(8): 1-6 (Han Deqiang, Dang Yamin, Wang Hu, et al. Precise Orbit Determination of Beidou Navigation Satellite by Introducing National Base Station[J]. Bulletin of Surveying and Mapping, 2017(8): 1-6)
(  0) 0) |
| [8] |
Rodriguez R L.Galileo IOV Status and Results[C].ION GNSS, Nashville, 2013
(  0) 0) |
| [9] |
于碧云, 张慧君, 李孝辉. GPS/Galileo组合定位和Galileo卫星钟评估[J]. 时间频率学报, 2016, 39(2): 111-120 (Yu Biyun, Zhang Huijun, Li Xiaohui. GPS/Galileo Combination Positioning and Galileo Satellite Clock Evaluation[J]. Time Frequency Journal, 2016, 39(2): 111-120)
(  0) 0) |
| [10] |
陈明, 武军郦, 李志才. 北斗精密定轨及广播星历轨道精度评估[J]. 测绘工程, 2016, 25(11): 1-6 (Chen Ming, Wu Junli, Li Zhicai. Orbit Accuracy Evaluation of Beidou Precise Orbit Determination and Broadcast Ephemeris[J]. Engineering of Surveying and Mapping, 2016, 25(11): 1-6)
(  0) 0) |
2. Beijing Aerospace Hongtu Information Technology Co Ltd, 65 Xingshikou Road, Beijing 100195, China;
3. Beijing Research Institute of Telemetry, 1 East-Fengying Road, Beijing 100094, China;
4. Construction Company, State Grid Hebei Electric Power Co Ltd, 107 Tabei Road, Shijiazhuang 050021, China
 2018, Vol. 38
2018, Vol. 38


