2. 中国地震局地壳应力研究所武汉科技创新基地,武汉市洪山侧路40号,430071
中性大气掩星反演是通过在LEO (low earth orbit)卫星上安装GNSS接收机观测来自GNSS卫星的无线电信号,从信号中获取大气附加相位延迟来反演中性大气物理参量的技术。地球大气无线电掩星观测技术作为导航卫星应用的新手段,可以提供高精度、高分辨率、全球覆盖的中性大气剖面,是21世纪最先进的空间探测技术之一[1]。目前国际上先后发射了Orsted、SUNSAT、CHAMP、SAC-C、IOX、GRACE、COSMIC1和Metop-A等卫星或星座[2-4]。各国掩星卫星的发射为我们提供了大量的中性大气层及电离层的观测数据。
本文简要介绍了GPS-LEO掩星大气反演算法的基本原理,利用EGOPS软件,采用三维射线追踪法模拟仿真卫星的掩星过程,研究接收机钟误差、轨道误差、噪声误差及多路径效应等对反演结果造成的影响。
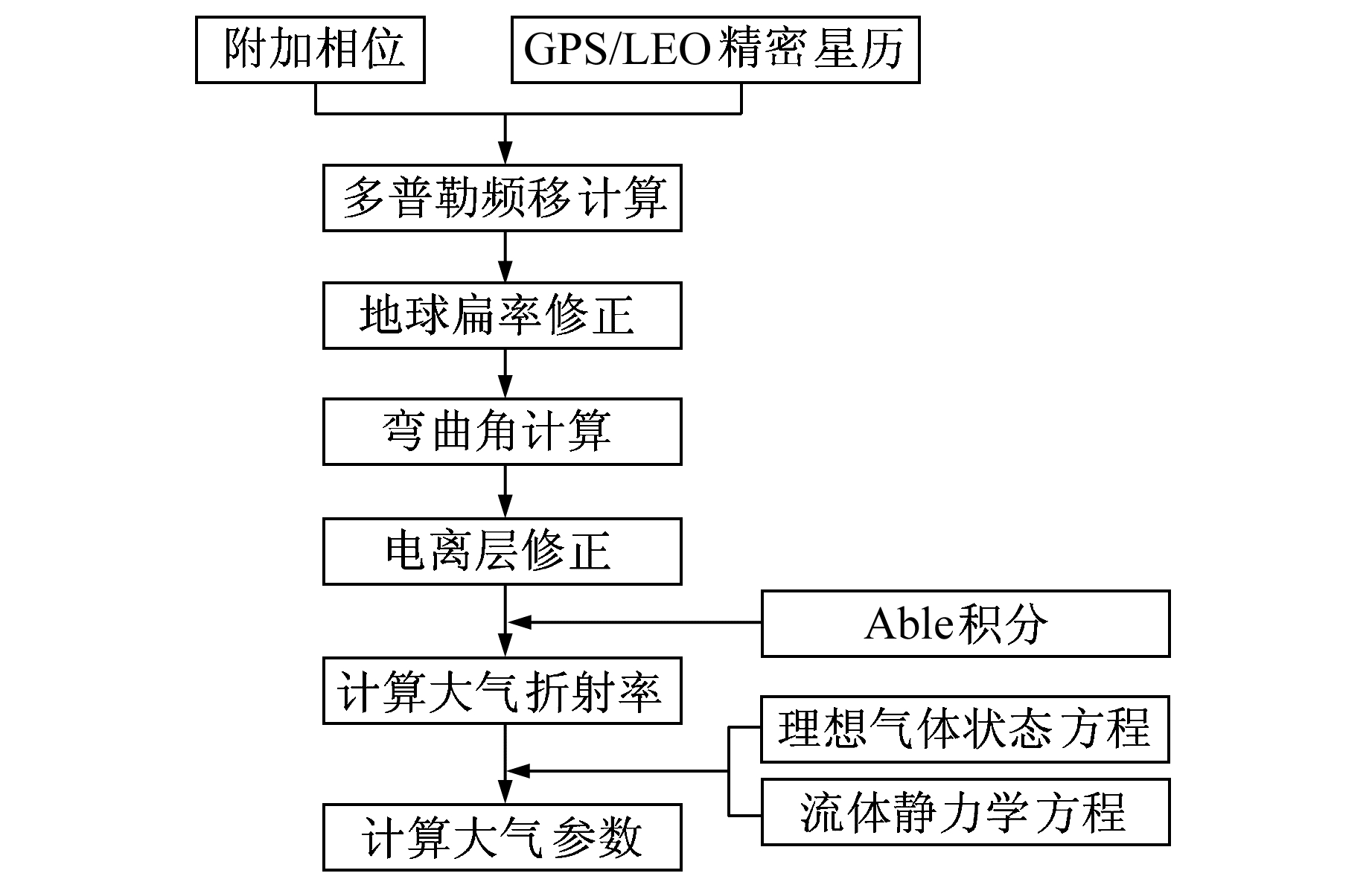
1 GPS-LEO掩星反演基本流程在LEO上搭载GPS接收机来接收GPS卫星发射的无线电波,通过GPS和LEO相对运动来测量GPS卫星信号的相位和振幅。由于电离层和大气层介质的垂直密度变化,GPS信号在通过该区域时射线路径会发生变化,其延迟和弯曲与大气的温度、压力以及水汽分布有密切关系,其基本流程如图 1所示[5]。
|
图 1 GPS-LEO掩星反演基本流程 Fig. 1 Retrieval processing for GPS-LEO radio occultaion |
第一步,利用卫星精密轨道数据,去除几何距离以及接收机钟差,获得大气掩星附加相位数据,计算得到多普勒频移:
| $ \frac{{\Delta {f_i}}}{{{f_i}}} = \frac{1}{c}\frac{{{\rm{d}}{\varphi _i}}}{{{\rm{d}}t}},i = 1,2 $ | (1) |
式中,c为真空中光速,φi和fi分别为信号的附加相位延迟和载波频率,Δfi为电波的附加多普勒频移,其包含了电离层和中性大气的贡献[6]。
第二步,对数据进行地球扁率修正,具体修正方法可参考文献[5]。之后进行弯曲角的计算,在局部球对称假设下,有多普勒观测方程[7]:
| $ \Delta {f_i} = \frac{{{f_i}}}{c}\left[ {{\mathit{\boldsymbol{v}}_{\rm{L}}}{{\mathit{\boldsymbol{\bar T}}}_{\rm{G}}} - {\mathit{\boldsymbol{v}}_{\rm{G}}}{{\mathit{\boldsymbol{\hat T}}}_{\rm{L}}} - \left( {{\mathit{\boldsymbol{v}}_{\rm{L}}}{{\mathit{\boldsymbol{\hat r}}}_{{\rm{LG}}}} - {\mathit{\boldsymbol{v}}_{\rm{G}}}{{\mathit{\boldsymbol{\hat r}}}_{{\rm{LG}}}}} \right)} \right] $ | (2) |
式中,射线路径由方向矢量
第三步,进行弯曲角的统计优化以及电离层的修正。大气折射弯曲角序列为αstat,可以由Abel积分变换来反演大气折射率剖面[5]:
| $ n\left( a \right) = \exp \left( {\frac{1}{\pi }\int_a^\infty {\frac{{{\alpha _{{\rm{stat}}}}\left( \xi \right)}}{{\sqrt {{\xi ^2} - {a^2}} }}{\rm{d}}\xi } } \right) $ | (3) |
最后,通过流体静力平衡方程和理想气体状态方程可以求得大气的气压、温度及水汽等参数。
2 仿真模拟本文利用EGOPS软件,选择CHAMP卫星2006-01-15的实测轨道数据和大气模型,在模拟背景数据中不考虑电离层影响以及其他各项误差源,采用CIRA86aQ_UoG(COSPAR International Reference Atmosphere,CIRA)大气模型[8],模拟了全天426个掩星事件作为标准的掩星观测数据,认为其不含任何测量及平台引起的误差,具体模拟仿真参数设置见表 1。
|
|
表 1 仿真数据设置 Tab. 1 Simulation data settings |
逐一向系统中加入各项误差源,将各种情况下的反演结果同标准情况进行统计分析。模拟获取的1 d内426个掩星事件作为统计结果显示,模拟的掩星事件全球分布均匀。
3 误差分析 3.1 接收机钟误差在掩星测量中,GPS掩星观测量是以精密测时为依据的,测量要求接收机钟和发射机保持严格同步,且保持频标稳定。但在实际观测中,接收机钟和发射机与GPS标准时之间都存在着钟差和漂移, 并且随着时间的推移, 这些量还会发生变化, 给伪距和载波相位测量带来误差[9]。
通常无法知道卫星钟具体的误差,需要采用随机性时间模型来描述卫星钟的频率特性。目前,钟的稳定度通常采用双取样方差(Allan方差)来衡量[10]。在给定Allan方差后,相位观测值的误差ΔL的计算公式为:
| $ {y_n} = \sqrt 6 \tau _s^{ - 0.5}{A_{1{\rm{sec}}}}{\rm{ran}}{{\rm{d}}_n} $ | (4) |
| $ \Delta {L_n} = c{\tau _s}{y_n} + \Delta {L_{n - 1}} $ | (5) |
式中,τs为采样间隔,A1sec为给定的1 s的Allan方差,randn为[-1, 1]区间内的随机数,c为真空中的光速,yn为采样间隔内的相对频率误差。
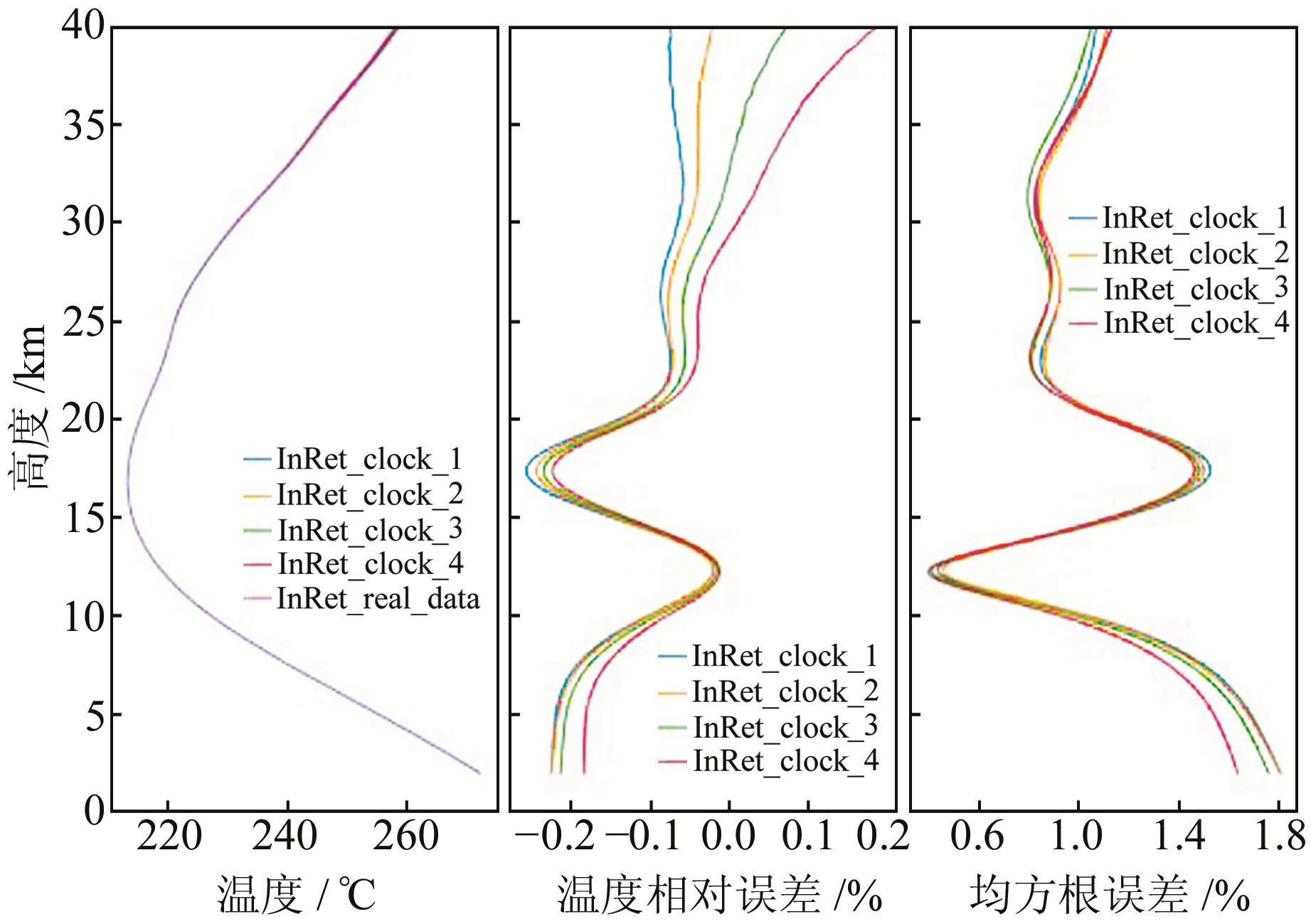
为探测钟误差对掩星反演结果的影响以及影响量级,分别设置了小量级钟稳定及较大量级钟稳定影响对比实验,表 2为小量级钟稳定影响设定及结果,图 2为小量级钟稳定影响的结果统计分析。
|
|
表 2 小量级钟稳定性影响设定及结果 Tab. 2 Minor level clock stability influence settings and results |
|
图 2 小量级钟稳定性影响统计分析 Fig. 2 Statistical analysis of minor level clock stability |
由图 2可以看出,钟稳定性在(0~8)×10-13secAllan之间时,温度平均偏差在±0.2%之间,温度的均方根误差不超过2%,完全符合掩星大气的反演精度要求。图 2中温度反演误差从20 km以上开始显著增大,说明钟误差主要作用于高层大气,且随着钟差的增大,反演误差逐渐增大,呈现明显的正相关特性。
为进一步探究钟稳定性的最低要求,设置了较大量级的钟稳定性实验,设置了4组较大量级的钟稳定参数。可以看出,钟参数大于40×10-13时,相对误差均值接近1%,具有较大的反演误差,具体参数见表 3。
|
|
表 3 较大量级钟稳定性影响设定及结果 Tab. 3 Larger level clock stability influence settings and results |
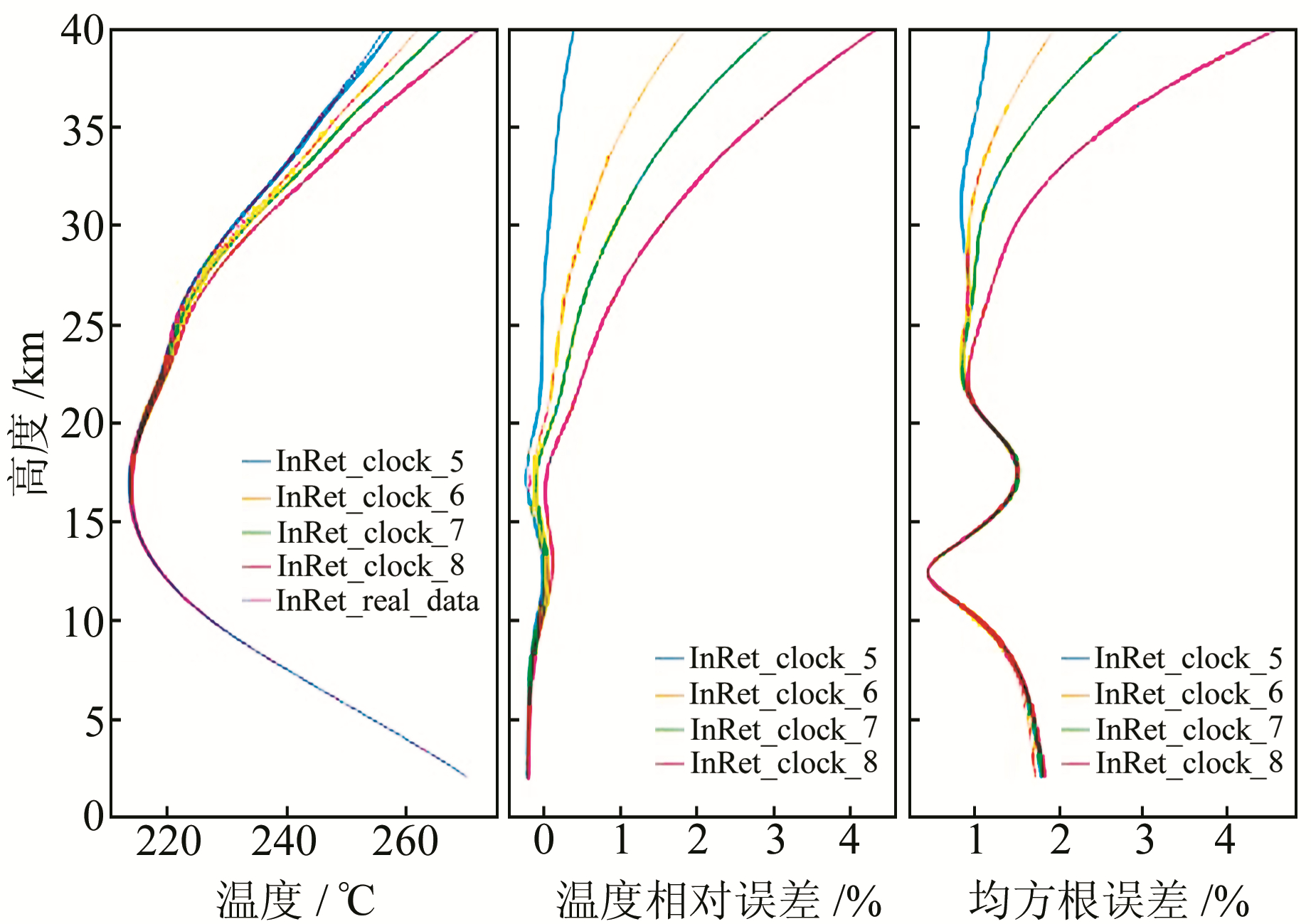
可以看出,钟稳定性在(10~40)×10-13secAllan时,反演温度的相对误差明显变大,温度均方根也明显增大。图 3表示了较大量级钟误差稳定性的温度、温度偏差以及温度均方根统计结果,在20 km以上温度偏差逐渐增大,且呈现明显的正相关特性。当钟稳定性在40×10-13secAllan时,温度偏差接近1%,均方根误差超过1.5%。但在实际掩星观测中,GPS钟稳定性完全可以满足现有的反演精度需求。
|
图 3 较大量级钟稳定性统计分析 Fig. 3 Statistical analysis of larger level clock stability |
卫星轨道误差分为位置误差和速度误差,这两种误差都会对反演造成影响。考虑径向方向,位置误差影响有两方面:一方面表现为位置误差引发星间距离偏差, 从而造成附加相位值的误差;另一方面, 位置误差使掩星的几何关系发生变化, 从而在弯曲角的计算中引入误差。卫星切线方向的速度误差也有着不可忽视的影响。假设未加入误差时,双频载波的附加相位为Lk1,k表示载波L1、L2,GPS和LEO卫星的几何距离为ρ1;加入误差后,双频载波的附加相位为Lk2,卫星间距为ρ2。设GPS卫星加入轨道前后的径向矢量分别为RG1(XG1, YG1, ZG1)、RG2(XG2, YG2, ZG2),LEO卫星的径向矢量为RL(XL, YL, ZL),则有:
| $ \begin{array}{*{20}{c}} {{\rho _1} = }\\ {\sqrt {{{\left( {{X_{{\rm{G1}}}} - {X_{\rm{L}}}} \right)}^2} + {{\left( {{Y_{{\rm{G1}}}} - {Y_{\rm{L}}}} \right)}^2} + {{\left( {{Z_{{\rm{G1}}}} - {Z_{\rm{L}}}} \right)}^2}} } \end{array} $ |
| $ \begin{array}{*{20}{c}} {{\rho _2} = }\\ {\sqrt {{{\left( {{X_{{\rm{G2}}}} - {X_{\rm{L}}}} \right)}^2} + {{\left( {{Y_{{\rm{G2}}}} - {Y_{\rm{L}}}} \right)}^2} + {{\left( {{Z_{{\rm{G2}}}} - {Z_{\rm{L}}}} \right)}^2}} } \end{array} $ | (6) |
可得到相位误差:
| $ \Delta {L_k} = {L_{k2}} - {L_{k1}} = {\rho _2} - {\rho _1} $ | (7) |
引入轨道误差后,只要代入有误差的位置坐标(XG2, YG2, ZG2)进行计算即可。LEO径向位置误差的加入方式与GPS卫星相同,可参考上述数学模型[11]。
为探究轨道位置误差及速度误差对反演造成的影响,分别考虑了径向方向的位置误差。表 4为轨道位置误差的参数设置。
|
|
表 4 轨道径向位置误差影响设定及结果 Tab. 4 Radial position errors influence settings and results |
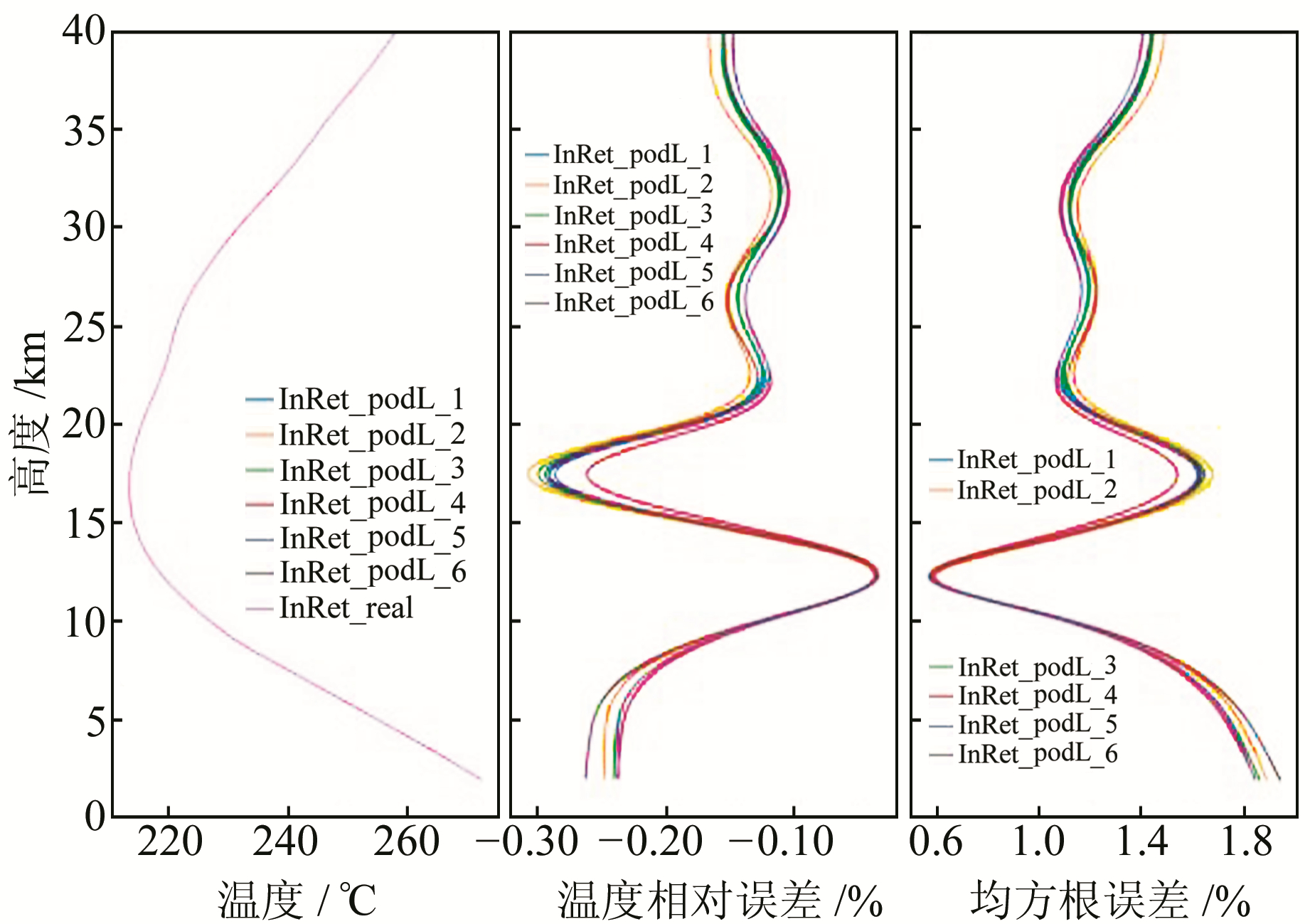
图 4表示轨道位置误差的温度反演结果统计。可以看出,轨道位置误差在现有的定轨精度范围内,相对偏差绝对值不足0.4%,均方根误差在1.3%左右。
|
图 4 轨道位置误差统计分析 Fig. 4 Statistical analysis of radial position errors |
为进一步探究轨道误差对反演结果的影响,下面对轨道的速度误差进行模拟反演,表 5为轨道的射线速度误差及射线加速度误差,图 5为反演的温度统计结果。
|
|
表 5 轨道射线误差影响设定及结果 Tab. 5 Along-ray errors influence settings and results |
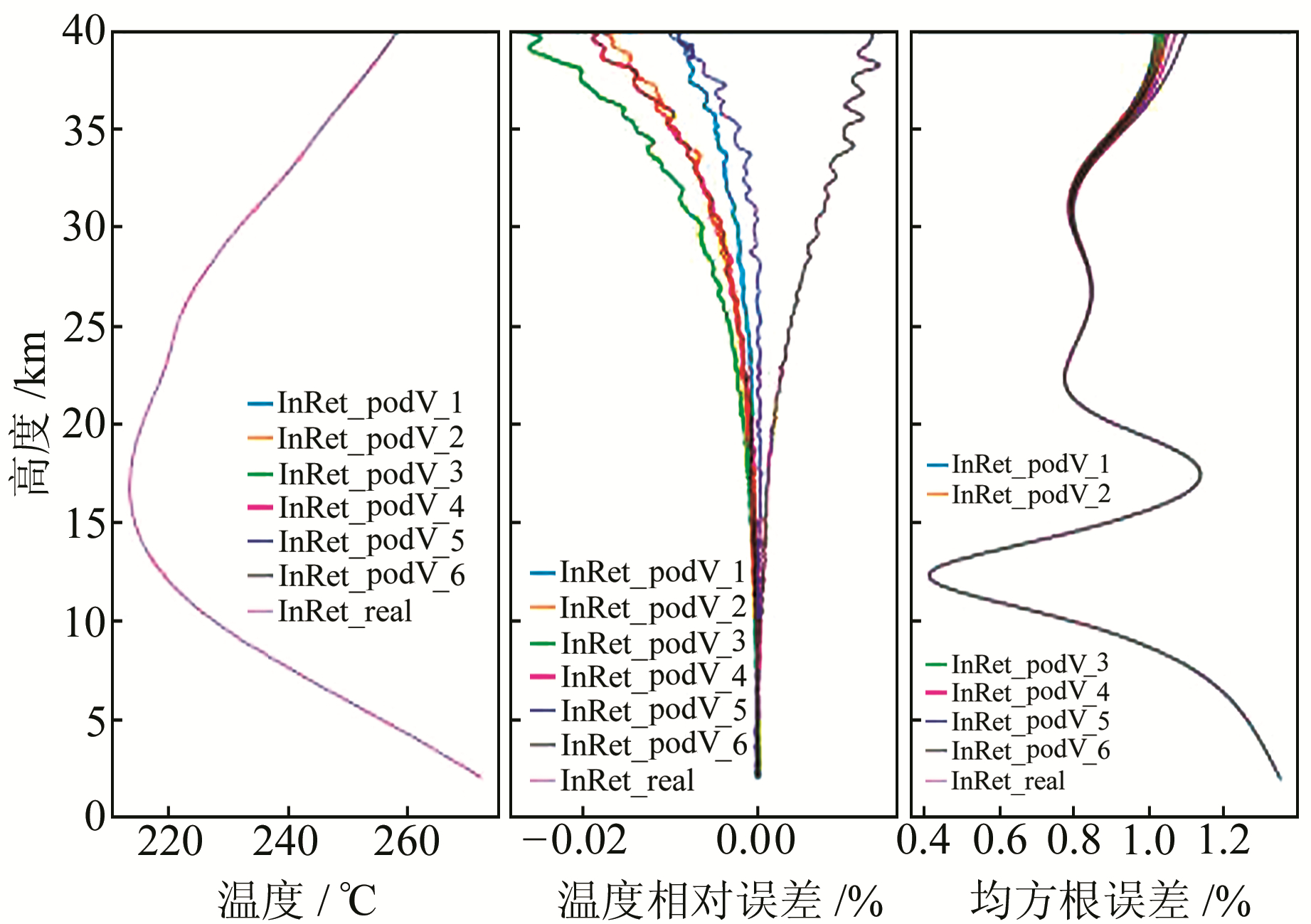
|
图 5 轨道射线误差统计分析 Fig. 5 Statistical analysis of along-ray errors |
由图 5可以看出,在20 km以上反演误差显著增大,且相对偏差随轨道速度误差的增大呈现明显的正相关特性。在该射线误差算例中,其相对温度偏差对反演结果的影响在±0.01%以内,温度均方根误差均值在1%以内。
通过该误差分析可以看出,轨道射线速度以及轨道位置误差其反演结果较真值相差较小,现有的轨道定位精度完全可以满足20 cm以内的定位需求,其轨道误差可忽略不计。
3.3 噪声误差随机噪声来自于LEO和地面接收机的热噪声、地面站观测中的中性大气折射噪声等。热噪声与信号的强度、背景辐射、接收机的硬件质量等因素有关。本文采用高斯相位噪声来模拟该随机误差,其数学模型为:
| $ {\left( {\delta {\varphi ^2}} \right)^{1/2}} = \frac{{\lambda {\sigma _n}\left( \tau \right)}}{{2\pi A}} = \frac{\lambda }{{2\pi }}{\left( {2{\rm{SN}}{{\rm{R}}_0}\tau } \right)^{ - 1/2}} $ | (8) |
式中,(δφ2)1/2为观测相位的均方根误差,以长度来衡量;τ为积分时间;λ为GPS信号的波长;A为信号的振幅;σn是热噪声的均方根误差;SNR0是1 s积分时间内的信噪比。式(8)表明,噪声误差与接收机的信噪比有直接关系[10]。在该模拟仿真中,通过直接输入不同的高斯噪声来进行设置(表 6),模拟了0~10 mm不同等级的高斯噪声及反演结果。可以看出,随着高斯噪声的不断增加,相对误差呈现明显的负偏差现象,其均方根误差也随噪声增加而增大。高斯噪声超过4 mm时,相对误差均值达到-1.7%,均方根误差超过1.3%,并且在较高对流层探测误差更为明显。
|
|
表 6 高斯噪声影响设定及结果 Tab. 6 Gaussian phase noise parameters settings and results |
图 6显示了不同高斯噪声的空间统计分布,在20 km以上高斯噪声造成的误差特性明显增加,在35 km处,高斯噪声为4.0 mm时最大相对偏差接近-6%,均方根误差超过2%。由该统计结果可以看出,高斯噪声必须控制在2 mm以内,否则对反演精度有极大的影响。
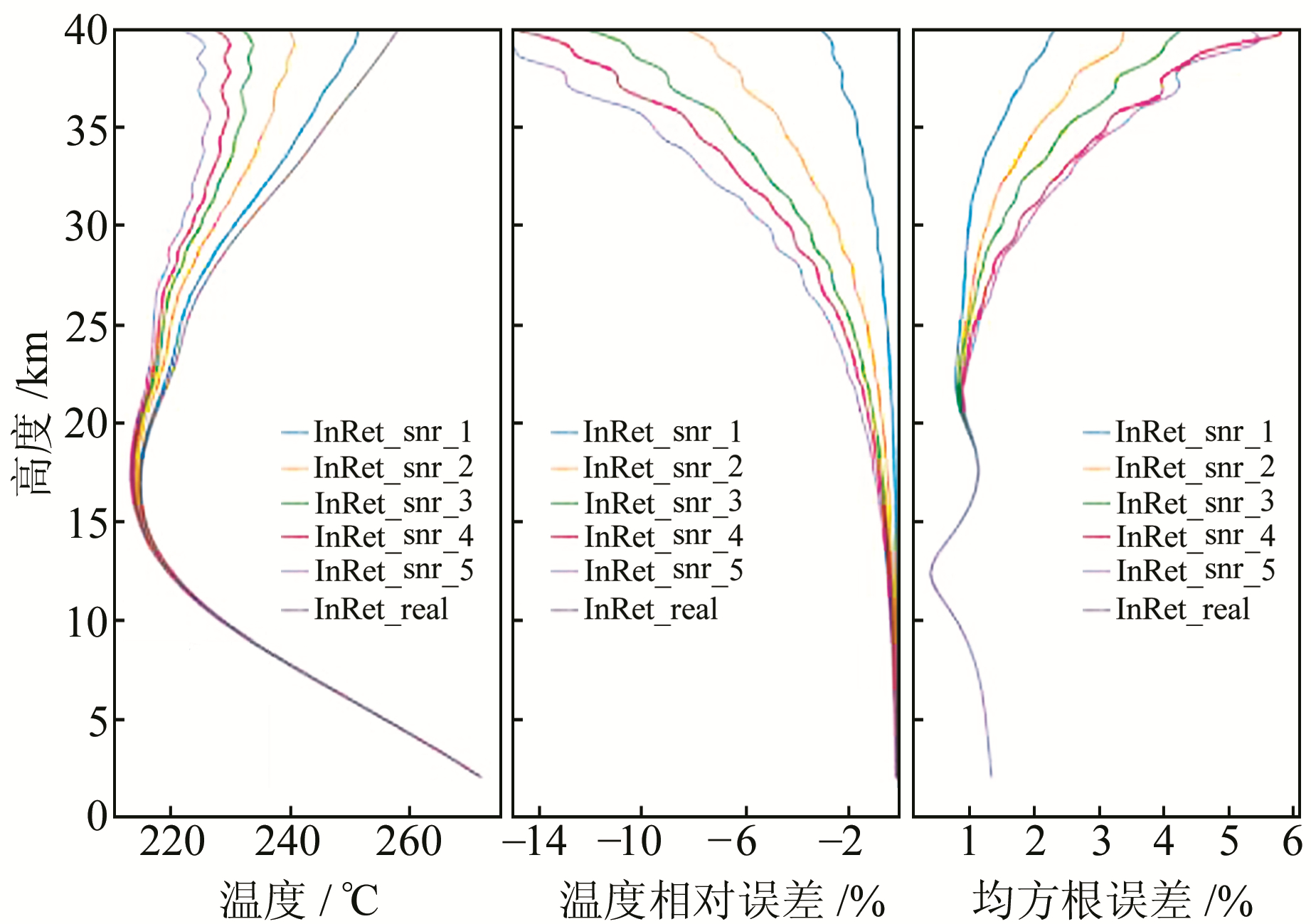
|
图 6 高斯噪声误差统计分析 Fig. 6 Statistical analysis of Gaussian phase noise errors |
掩星反演中的多路径误差是指从发射机发出的信号到达接收机时,受其周围散射结构的影响产生多值信号,而接收机只能进行单一的相位记录,不能区分信号的真伪,从而给掩星测量带来误差[12]。
将周围环境的多路径信号模拟为正弦波,其误差数学模型可表示为:
| $ {t_{\sin us}} = {t_{{\rm{begin}}}} - \frac{P}{{2\pi }}{\rm{arcsin}}\left( {\frac{{{A_{{\rm{start}}}}}}{A}} \right) $ | (9) |
| $ \Delta L = A\sin \left[ {\frac{{2\pi }}{P}\left( {{t_{{\rm{ra}}y}} - {t_{\sin us}}} \right)} \right] $ | (10) |
式中,A是多路径相位误差的振幅;Astart是顶部射线的多路径误差幅度;P是多路径相位误差的周期;tbegin是掩星第一条射线的接收时刻;tsinus是正弦波误差的起始时刻,默认在25 km以下的观测量中叠加误差;tray为该条掩星射线的接收时刻;ΔL是局部多路径的相位误差。当有多个正弦波叠加时,也可以把第一个正弦波设为随机数,则其他的正弦波的误差值就是相对于这个波计算的[10]。
将式(9)代入式(10),得到:
| $ L = A\sin \left[ {\frac{{2\pi }}{P}\left( {{t_{{\rm{ray}}}} - {t_{{\rm{begin}}}}} \right)} \right] $ | (11) |
可以看出,多路径相位误差的振幅A和周期P有决定性作用。具体影响性质笔者分别就振幅和周期进行两组实验,表 7为多路径效应中周期对反演结果的影响参数设定,表 8为探究多路径效应中振幅对反演结果的影响参数设定。
|
|
表 7 局部多路径误差周期影响设定及结果 Tab. 7 Local multipath error period influence settings and results |
|
|
表 8 多路径误差振幅影响设定及结果 Tab. 8 Multipath error amplitude influence settings and results |
由表 7可知,周期为100~2 000 s,温度均方根与周期P变化成反相关关系,但温度偏差关系不明显,且第二组数据周期与温度偏差成正相关,可能由周期和振幅综合影响导致。
由图 7可以看出,影响温度偏差及均方根的大气结构在25 km以上,反演误差逐渐增大,但反演温度的相对误差在±0.1%以内,可以满足现有的反演精度需求。
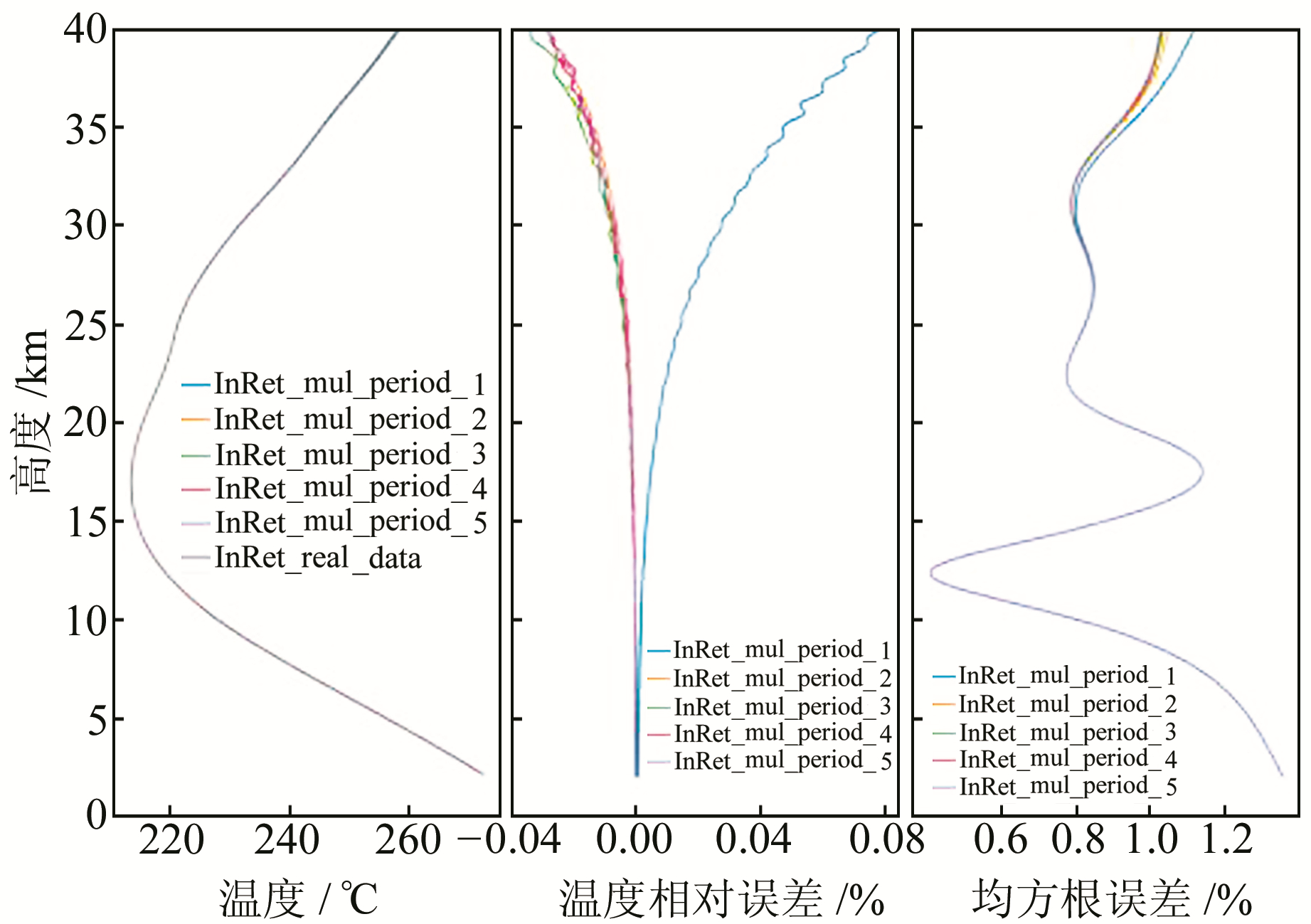
|
图 7 局部多路径误差周期影响统计分析 Fig. 7 Statistical analysis of local multipath error period influence |
由表 8可知,振幅在0~20 mm之间时,温度均方根与振幅A变化成正相关。温度偏差随着振幅增加而不断增大,具有明显的正相关特性。
由图 8可以看出,在空间分布上,25 km以上温度误差明显增大,温度均方根也在25 km以上有明显变化;温度相对偏差在40 km处最大超过2%。因此进行无线电掩星反演时,需要对信号进行一定的滤波处理,将振幅降低到一定水平,以减小观测误差。
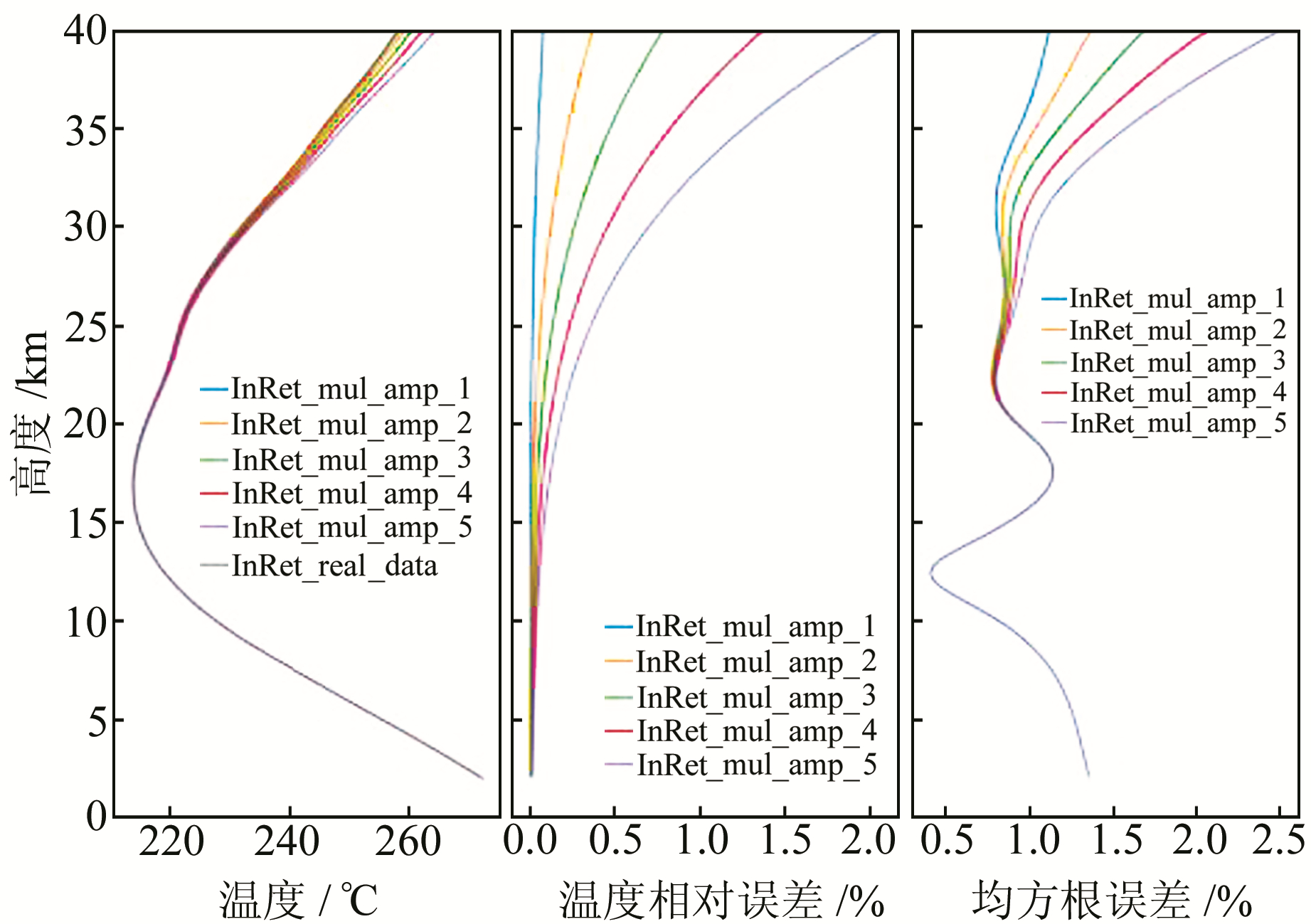
|
图 8 多路径误差振幅影响统计分析 Fig. 8 Statistical analysis of local amplitude error period influence |
本文简要介绍了GPS-LEO中性大气掩星技术的基本流程,同时对掩星反演的误差来源进行了模拟及分析,得到以下结论:
1) 钟的稳定度越高,其反演精度越高。为保证反演精度需求,需将钟稳定性控制在2×10-13以下。
2) 卫星轨道越精确,反演误差越小。现有的卫星cm级的径向位置误差及射线速度误差,可以满足反演需求。
3) 噪声误差对反演精度影响较大,高斯噪声误差在4 mm时,最大相对偏差接近-6%。应当采取其他手段来降低噪声影响,将误差控制在2 mm以内。
4) 多路径误差中,周期影响远小于振幅影响。在20 km以上振幅与温度均方根误差成正相关特性,振幅对中高层大气的反演精度影响较大。
| [1] |
宫晓艳, 胡雄, 吴小成, 等. 大气掩星反演误差特性初步分析[J]. 地球物理学报, 2007, 50(4): 1017-1029 (Gong Xiaoyan, Hu Xiong, Wu Xiaocheng, et al. Preliminary Analysis of Error Characteristics in Atmospheric Inversion of GPS Radio Occultation[J]. Chinese J Geophys, 2007, 50(4): 1017-1029 DOI:10.3321/j.issn:0001-5733.2007.04.009)
(  0) 0) |
| [2] |
徐晓华, 李征航. GPS气象学研究的最新进展[J]. 黑龙江工程学院学报, 2002, 16(1): 14-18 (Xu Xiaohua, Li Zhenghang. The Advanced Development on the Research of GPS Meteorology[J]. Journal of Heilongjiang Institute of Technology, 2002, 16(1): 14-18 DOI:10.3969/j.issn.1671-4679.2002.01.003)
(  0) 0) |
| [3] |
Beyerle G, Schmidt T, Michalak G, et al. GPS Radio Occultation with GRACE:Atmospheric Profiling Utilizing the Zero Difference Technique[J]. Geophysical Research Letters, 2005, 32(13): 313-320
(  0) 0) |
| [4] |
Schreiner W, Rocken C, Sokolovskiy S, et al. Estimates of the Precision of GPS Radio Occultations from the COSMIC/FORMOSAT-3 Mission[J]. Geophysical Research Letters, 2007, 34(4): 545-559
(  0) 0) |
| [5] |
Fjeldbo G, Kliore A J, Eshleman V R. The Neutral Atmosphere of Venus as Studied with the Mariner V Radio Occultation Experiments[J]. Astronomical Journal, 1971, 76: 123-140 DOI:10.1086/111096
(  0) 0) |
| [6] |
宫晓艳.大气无线电GNSS掩星探测技术研究[D].北京: 中国科学院空间科学与应用研究中心, 2009 (Gong Xiao-yan.Research on GNSS Atmospheric Radio Occultation Technique[D].Beijing: Center for Space Science and Applied Research, CAS, 2009)
(  0) 0) |
| [7] |
Syndergaard S. Retrieval Analysis and Methodologies in Atmospheric Limb Sounding Using the GNSS Radio Occultation Technique[M]. Danish: Danish Meteorological Institute, 1999
(  0) 0) |
| [8] |
Rees D, Barnett J J, Labitzke K. COSPAR International Reference Atmosphere:1986.Pt.2:Middle Atmosphere Models[J]. Advances in Space Research, 1990, 56(4): 538-539
(  0) 0) |
| [9] |
Fu N F, Guo P, Wu M J, et al. Retrieval Processing Technique for LEO-LEO Radio Occultation Atmospheric Data and Error Sources Analysis[J]. Remote Sensing Science, 2016, 4(2): 51-64
(  0) 0) |
| [10] |
Fritzer J, Kirchengast G, Pock M, et al.End-to-End Generic Occultation Performance Simulation and Processing System Version5.5(EGOPS 5.5) Software User Manual[Z].Univ of Graz, Austria, 2010
(  0) 0) |
| [11] |
Gorbunov M E, Kirchengast G, Lauritsen K B.Advanced Wave-Optics Forward Modeling and Bending Angle and Transmission Retrieval Including Turbulent Random Refractivity Field Modeling[R].Wegener Center, Univ of Graz, Austria, 2006
(  0) 0) |
| [12] |
Kursinski E R, Hajj G A. The GPS Radio Occulation Technique[J]. TAO, 2000, 11(1): 53-114
(  0) 0) |
2. Wuhan Base of Institute of Crustal Dynamics, CEA, 40 Hongshance Road, Wuhan 430071, China
 2018, Vol. 38
2018, Vol. 38


