随着各卫星导航系统相继建成和完善,多系统组合精密单点定位PPP(precise point positioning)成为可能。文献[1-2]分析了多系统状态下精密单点定位的定位性能,相对于单系统,多系统组合PPP能够明显增加可见卫星数、优化卫星几何构型,提高定位的收敛速度与精度。但由于各卫星系统、各类型观测值测距精度存在差异,在多系统组合PPP时,根据传统经验定权方法确定的观测值权阵不再可靠,这势必影响定位精度。因此,如何合理地确定各系统、各类型观测值的权成为研究多系统组合导航定位的重要方面。
Helmert方差分量估计是利用平差后观测值残差估计方差因子进行重定权,自适应地调整不同类或不等精度观测值之间权比的一种验后估计方法。在多系统伪距最小二乘定位中,高晓等[3]利用Helmert方差分量估计来确定GPS与BDS观测值的先验权比; 文献[4-6]分析了Helmert方差分量估计在GPS/BDS、GPS/GLONASS以及GPS/BDS /GLONASS组合伪距单点定位中的应用效果。在精密单点定位方面,蒋光伟等[7]在GPS单系统PPP中运用Helmert方差分量估计调整伪距观测值与载波观测值之间的权比。目前,针对多系统组合PPP中的Helmert方差分量估计应用方法研究相对较少。
考虑到GPS/BDS组合PPP中GPS观测值与BDS观测值、载波观测值与伪距观测值之间的权比不合理情况,本文在卡尔曼滤波参数估计过程中利用Helmert方差估计合理地确定GPS/BDS组合PPP的各类观测值权比。同时,进一步针对卡尔曼滤波过程中预报值权阵和观测值权阵的验前单位方差不一致情况,将卡尔曼滤波预报值作为伪观测值,与GPS/BDS组合PPP中当前历元各类观测值同时进行Helmert方差分量估计处理。实验结果证明,考虑卡尔曼滤波伪观测值的Helmert方法明显提高了GPS/BDS组合PPP的收敛速度与定位精度。
1 基于GPS/BDS组合PPP的Helmert方差分量估计本文采用双频无电离层组合模型来消除电离层的影响,采用高度角正弦函数作为权函数模型[8-9]。
1.1 基于卡尔曼滤波的Helmert方差因子计算卡尔曼滤波本质上是将滤波预报值Xk作为伪观测值参与平差的一种最小二乘算法[10]。在组合伪距定位中常按照卫星系统对观测值进行分类。同理,在GPS/BDS组合PPP中,可将观测值残差Vk分为GPS和BDS两类,从而k历元时刻的卡尔曼滤波可表示为如下误差方程形式:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{V}}_{{G_k}}} = {\mathit{\boldsymbol{H}}_{{G_k}}}{{\mathit{\boldsymbol{\hat X}}}_k} - {\mathit{\boldsymbol{L}}_{{G_k}}},\\ {\mathit{\boldsymbol{V}}_{{C_k}}} = {\mathit{\boldsymbol{H}}_{{C_k}}}{{\mathit{\boldsymbol{\hat X}}}_k} - {\mathit{\boldsymbol{L}}_{{C_k}}},\\ {\mathit{\boldsymbol{V}}_{{{\bar X}_k}}} = {{\mathit{\boldsymbol{\hat X}}}_k} - {{\bar X}_k}, \end{array} \right.\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{P}}_k} = {{\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{D}}_{{G_k}}}}&0\\ 0&{{\mathit{\boldsymbol{D}}_{{C_k}}}} \end{array}} \right]}^{ - 1}}}\\ {{{\mathit{\boldsymbol{\bar P}}}_{{{\bar X}_k}}} = \mathit{\boldsymbol{D}}_{{{\bar X}_k}}^{ - 1}} \end{array} $ | (1) |
式中,L、H分别为观测向量和观测向量系数阵,D为滤波值方差阵,各观测值数量分别为nGk、nCk、nXk。根据Helmert方差原理可得:
| $ \begin{array}{*{20}{c}} {E\left( {\mathit{\boldsymbol{V}}_i^{\rm{T}}{\mathit{\boldsymbol{P}}_i}{\mathit{\boldsymbol{V}}_i}} \right) = {\rm{tr}}\left( {{\mathit{\boldsymbol{P}}_i}{\mathit{\boldsymbol{D}}_i}} \right) = \left[ {{n_i} - 2{\rm{tr}}\left( {{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}_i}} \right) + } \right.}\\ {\left. {{\rm{tr}}{{\left( {{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}_i}} \right)}^2}} \right]\hat \sigma _{0i}^2 + \sum\limits_{m = \left( {{G_k},{C_k},{{\mathit{\boldsymbol{\bar X}}}_k}} \right)}^{m \ne i} {\left[ {{\rm{tr}}\left( {{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}_i}{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}_m}} \right)\hat \sigma _{0m}^2} \right],} }\\ {i = \left( {{G_k},{C_k},{{\mathit{\boldsymbol{\bar X}}}_k}} \right)} \end{array} $ | (2) |
式中,
| $ \hat \sigma _{0{G_k}}^2 = \frac{{\mathit{\boldsymbol{V}}_{{G_k}}^{\rm{T}}{\mathit{\boldsymbol{P}}_{{G_k}}}{\mathit{\boldsymbol{V}}_{{G_k}}}}}{{{n_{{G_k}}} - {\rm{tr}}\left( {{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}_{{G_k}}}} \right)}} $ |
| $ \hat \sigma _{0{C_k}}^2 = \frac{{\mathit{\boldsymbol{V}}_{{C_k}}^{\rm{T}}{\mathit{\boldsymbol{P}}_{{C_k}}}{\mathit{\boldsymbol{V}}_{{C_k}}}}}{{{n_{{C_k}}} - {\rm{tr}}\left( {{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{N}}_{{C_k}}}} \right)}} $ | (3) |
| $ \hat \sigma _{0{{\bar X}_k}}^2 = \frac{{\mathit{\boldsymbol{V}}_{{{\bar X}_k}}^{\rm{T}}{\mathit{\boldsymbol{P}}_{{{\bar X}_k}}}{\mathit{\boldsymbol{V}}_{{{\bar X}_k}}}}}{{{n_{{{\bar X}_k}}} - {\rm{tr}}\left( {{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{P}}_{{{\bar X}_k}}}} \right)}} $ |
在组合伪距定位中常按式(4)进行重定权,以调整BDS和GPS两系统间的权比:
| $ {\mathit{\boldsymbol{D}}_{{C_k}}} = \left( {\hat \sigma _{0{C_k}}^2/\hat \sigma _{0{G_k}}^2} \right){\mathit{\boldsymbol{D}}_{{C_k}}} $ | (4) |
在多系统组合PPP中,同一卫星系统的观测值有载波观测值和伪距观测值2类,若进一步考虑将载波精度固定为伪距精度的100倍并不合理,因此可将GPS/BDS组合PPP观测值分为GPS伪距、GPS载波、BDS伪距与BDS载波4类观测值,根据上述Helmert原理可计算得GPS伪距方差因子
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{D}}_{{\mathit{\boldsymbol{P}}_k}}^{\rm{G}} = \left( {\hat \sigma _{0\mathit{\boldsymbol{P}}_k^{\rm{G}}}^2/\hat \sigma _{0\mathit{\boldsymbol{L}}_k^{\rm{G}}}^2} \right)\mathit{\boldsymbol{D}}_{{\mathit{\boldsymbol{P}}_k}}^{\rm{G}}\\ \mathit{\boldsymbol{D}}_{{\mathit{\boldsymbol{L}}_k}}^{\rm{C}} = \left( {\hat \sigma _{0\mathit{\boldsymbol{L}}_k^{\rm{C}}}^2/\hat \sigma _{0\mathit{\boldsymbol{L}}_k^{\rm{G}}}^2} \right)\mathit{\boldsymbol{D}}_{{\mathit{\boldsymbol{L}}_k}}^{\rm{C}}\\ \mathit{\boldsymbol{D}}_{{\mathit{\boldsymbol{P}}_k}}^{\rm{C}} = \left( {\hat \sigma _{0\mathit{\boldsymbol{P}}_k^{\rm{C}}}^2/\hat \sigma _{0\mathit{\boldsymbol{L}}_k^{\rm{G}}}^2} \right)\mathit{\boldsymbol{D}}_{{\mathit{\boldsymbol{P}}_k}}^{\rm{C}} \end{array} \right. $ | (5) |
以上重定权公式仅利用Helmert方差分量估计对观测值内部的权比进行调整,而在卡尔曼滤波中,平差过程不仅仅有观测值参与,还有滤波预报值参与。同时,由于观测值方差阵Dk是由经验模型给出的,并不可靠,观测值权阵Pk与预报值权阵PXk的验前单位权方差并不一致,需要确定观测值和卡尔曼滤波预报值之间的合理权比。本文将卡尔曼滤波预报值Xk视为伪观测值,同时与各类观测值进行重定权,可得到:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{D}}_{{\mathit{\boldsymbol{L}}_k}}^{\rm{G}} = \left( {\hat \sigma _{0\mathit{\boldsymbol{L}}_k^{\rm{G}}}^2/\hat \sigma _{0{{\bar X}_k}}^2} \right)\mathit{\boldsymbol{D}}_{{\mathit{\boldsymbol{L}}_k}}^{\rm{G}}\\ \mathit{\boldsymbol{D}}_{{\mathit{\boldsymbol{P}}_k}}^{\rm{G}} = \left( {\hat \sigma _{0\mathit{\boldsymbol{P}}_k^{\rm{G}}}^2/\hat \sigma _{0{{\bar X}_k}}^2} \right)\mathit{\boldsymbol{D}}_{{\mathit{\boldsymbol{P}}_k}}^{\rm{G}}\\ \mathit{\boldsymbol{D}}_{{\mathit{\boldsymbol{L}}_k}}^{\rm{C}} = \left( {\hat \sigma _{0\mathit{\boldsymbol{L}}_k^{\rm{C}}}^2/\hat \sigma _{0{{\bar X}_k}}^2} \right)\mathit{\boldsymbol{D}}_{{\mathit{\boldsymbol{L}}_k}}^{\rm{C}}\\ \mathit{\boldsymbol{D}}_{{\mathit{\boldsymbol{P}}_k}}^{\rm{C}} = \left( {\hat \sigma _{0\mathit{\boldsymbol{P}}_k^{\rm{C}}}^2/\hat \sigma _{0{{\bar X}_k}}^2} \right)\mathit{\boldsymbol{D}}_{{\mathit{\boldsymbol{P}}_k}}^{\rm{C}} \end{array} \right. $ | (6) |
设k历元的卡尔曼滤波预报值Xk及其方差阵DXk已知,k历元时刻考虑卡尔曼滤波伪观测值的GPS/BDS组合PPP中Helmert算法流程如下:
1) 根据GPS/BDS组合PPP的函数模型与随机模型,组建观测值的系数阵Hk与方差阵Dk。
2) 利用卡尔曼滤波理论递推,获得k历元时刻各类观测值的残差信息。
3) 利用简化公式(3),计算得各类观测值方差因子
4) 重复步骤2)~3),直至
5) 利用一步预报方程估计k+1历元时刻的预报值Xk+1及其方差阵DXk+1。
2 实验分析为进行静态PPP实验,采用MGEX NNOR站2016-04-30的观测数据,采样间隔为30 s、卫星截止高度角为5°。精密钟差和星历分别采用武汉大学GNSS中心提供的5 min精密钟差和15 min的精密星历。GPS/BDS组合PPP误差处理策略如表 1所示,测站坐标参考真值为ITRF发布的该站当日坐标。
|
|
表 1 精密单点定位误差处理策略 Tab. 1 Processing strategy of precise point position |
图 1为NNOR站当天GPS、BDS以及GPS/BDS组合系统随历元的可用卫星数示意图。由图可知,GPS/BDS组合系统相对于单系统成倍增加了可用卫星数,可用卫星数一直保持在15颗以上。

|
图 1 GPS、BDS与GPS/BDS组合可用卫星数 Fig. 1 The number of available satellites of GPS, BDS and GPS/BDS system |
为了验证基于卡尔曼滤波的伪观测值的Helmert方差分量估计在GPS/BDS组合PPP中的应用效果,设计以下方案。
方案1:采用标准卡尔曼滤波解算,将GPS和BDS观测值在相同卫星高度角下视为等精度,同一卫星的载波与伪距观测值权比固定为10 000倍。
方案2:针对GPS和DBS观测精度的差异性,将GPS/BDS组合PPP观测值分为GPS和BDS 2类,利用Helmert方差分量估计确定GPS和BDS 2个系统的权比,载波与伪距观测值权比仍固定为10 000倍。
方案3:在方案2的基础上,进一步考虑载波与伪距定比不合理的问题,将观测值分为GPS伪距、GPS载波、BDS伪距、BDS载波4类,利用Helmert方差分量估计确定这4类观测值的权比。
方案4:在方案3的基础上,将卡尔曼滤波预报值视为伪观测值,利用Helmert方差分量估计确定GPS伪距、GPS载波、BDS伪距、BDS载波以及伪观测值的权比。
图 2是4种方案下GPS/BDS组合PPP定位结果与测站坐标参考真值3个方向上的偏差图,为了便于显示,图中只给出了前3 h的解算结果。可以看出,大部分历元4种实验方案的定位残差依次降低,其中方案4要明显优于其他方案;方案2利用Helmert方差分量估计对组合PPP中GPS和BDS观测值的权重进行了有效调整,定位效果优于将GPS和BDS视为等权的方案1;方案3在方案2的基础上利用Helmert方差分量估计合理确定了载波观测值和伪距观测值的权比,提高了PPP的定位精度;方案4在方案3的基础上利用Helmert方差分量估计有效平衡观测信息与预报信息对参数估计的贡献,进一步提高了定位精度。
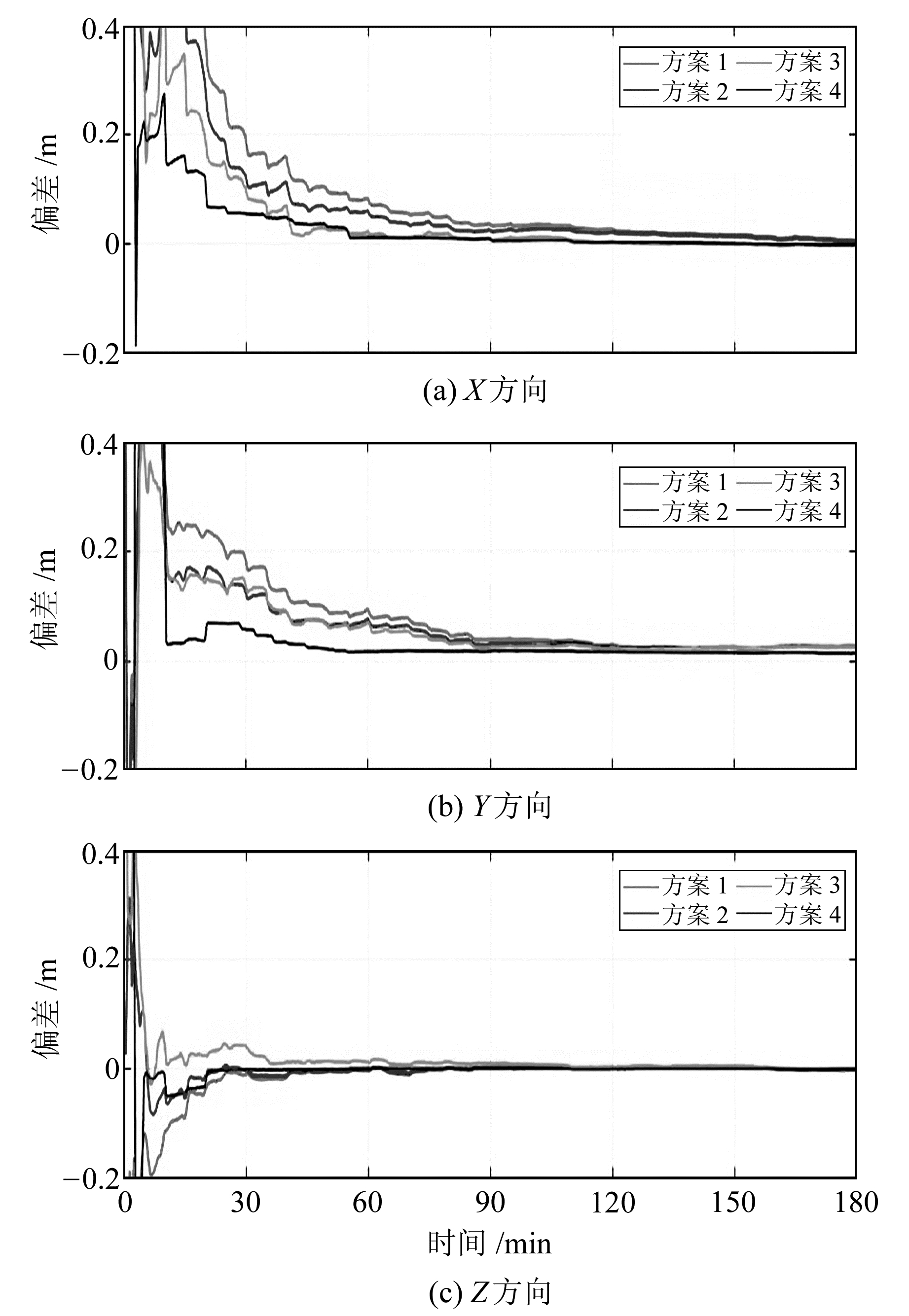
|
图 2 4种实验方案下的定位偏差 Fig. 2 Position bias under four kinds of experimental scheme |
图 3是4种方案下PPP收敛时间统计图,收敛时间计算根据文献[12]中的均值变换法,阈值选为2 cm,搜索窗口选为10个历元。从图中可知,4种方案下的PPP收敛时间依次递减,其中方案1在X、Y、Z方向上的收敛时间分别为90 min、90 min和27 min,而方案4将收敛时间减少至55 min、55 min和23 min,3个方向上分别优化了约39%、39%、15%。从点位收敛时间上看,方案4同比其他方案分别优化了35%、30%、26%。
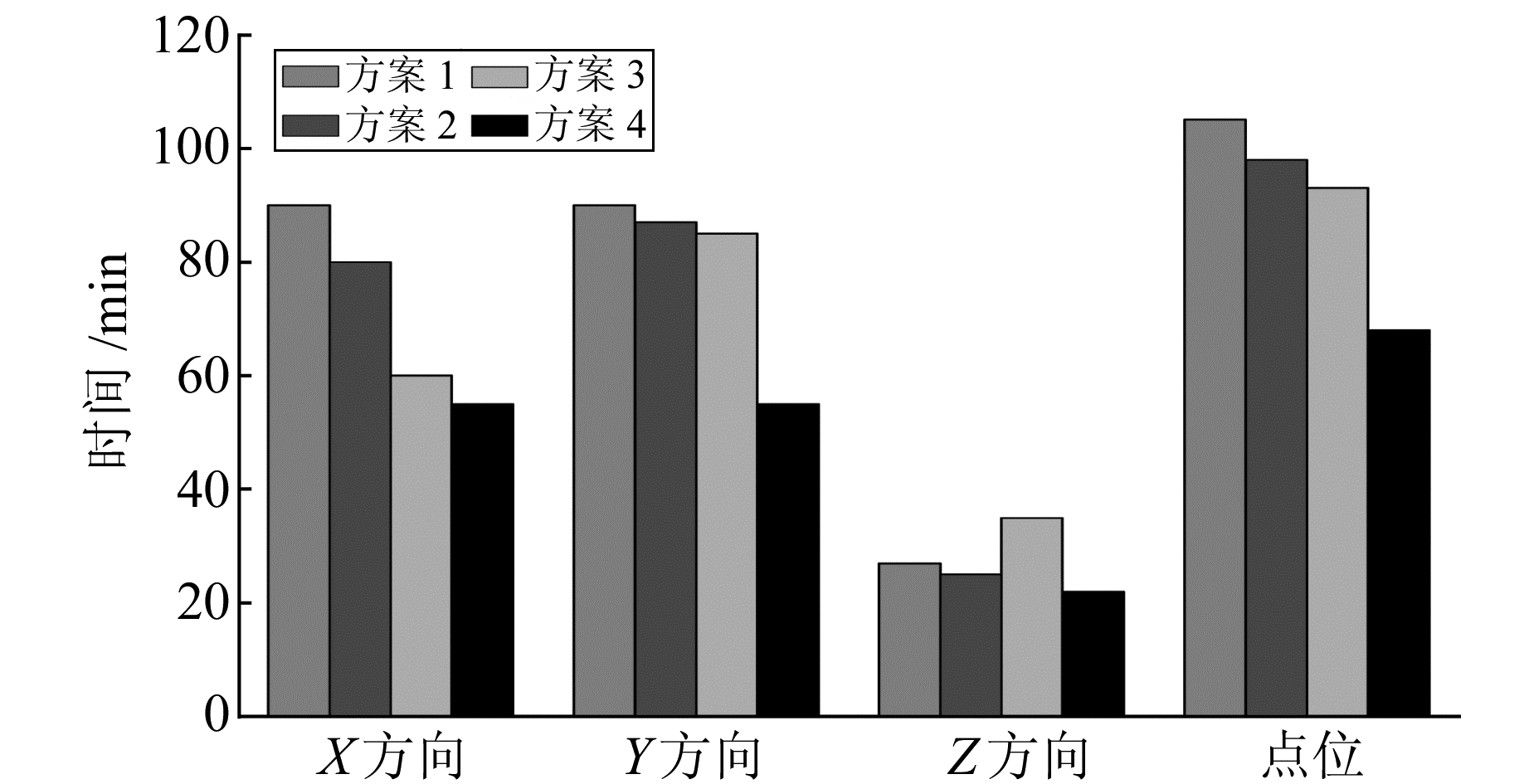
|
图 3 4种实验方案下的PPP收敛时间 Fig. 3 Convergence time of PPP under four kinds of experimental scheme |
|
|
表 2 4种实验方案下定位偏差的RMS统计 Tab. 2 RMS of position bias under four kinds of experimental scheme |
表 2统计了4种实验方案下各时段GPS/BDS组合PPP定位偏差的RMS值。可以看出,方案1到方案4的定位精度依次提高,在PPP解算5 h后,方案4相对于方案1在X、Y、Z方向上分别提高4 mm、12 mm、3 mm,点位RMS达到0.017 5 m,同比其他方案分别提高了43%、33%与30%。
3 结语基于卡尔曼滤波的Helmert方差分量估计可以在GPS/BDS组合PPP参数估计过程中合理地确定当前历元各类观测值权比,提高PPP定位精度。同时,将卡尔曼滤波预报值视为伪观测值与各类观测值同时进行Helmert方差分量估计,可在合理确定当前历元各类观测值权比的基础上,有效平衡当前历元观测信息与卡尔曼滤波预报信息对参数估计的贡献,能够明显加快PPP收敛速度,提高PPP的定位精度。
| [1] |
任晓东, 张柯柯, 李星星, 等. Beidou、Galileo、GLONASS、GPS多系统融合精密单点定位[J]. 测绘学报, 2015, 44(12): 1307-1313 (Ren Xiaodong, Zhang Keke, Li Xing-xing, et al. Precise Point Positioning with Multi-constellation Satellite Systems:Beidou、Galileo、GLONASS、GPS[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1307-1313)
(  0) 0) |
| [2] |
丁赫, 孙付平, 李亚萍, 等. BDS/GPS/GLONASS组合精密单点定位模型及性能分析[J]. 大地测量与地球动力学, 2016, 36(4): 303-307 (Ding He, Sun Fuping, Li Yaping, et al. Modeling and Performance Analysis of Combiner BDS/GPS/GLONASS Precise Point Positioning[J]. Journal of Geodesy and Geodynamics, 2016, 36(4): 303-307)
(  0) 0) |
| [3] |
高晓, 戴吾蛟. 基于方差分量估计确定GPS/BD2组合定位先验权比[J]. 大地测量与地球动力学, 2013, 33(2): 136-138 (Gao Xiao, Dai Wujiao. Determination of Prior Weight Ratio for Combined GPS-BD2 Positioning Based on Variance Component Estimation[J]. Journal of Geodesy and Geodynamics, 2013, 33(2): 136-138)
(  0) 0) |
| [4] |
高晓, 戴吾蛟. 抗差Helmert方差分量估计在GPS/BDS组合定位中的应用[J]. 大地测量与地球动力学, 2014, 34(1): 173-176 (Gao Xiao, Dai Wujiao. Application of Robust Helmert Variance Component Estimation to Position in Combination of GPS and BDS[J]. Journal of Geodesy and Geodynamics, 2014, 34(1): 173-176)
(  0) 0) |
| [5] |
段举举, 沈云中. 基于方差分量估计的GPS/GLONASS组合点定位[J]. 测绘通报, 2011(4): 4-6 (Duan Juju, Shen Yunzhong. GPS/GLONASS Combined Point Positioning Using Variance Component Estimation[J]. Bulletin of Surveying and Mapping, 2011(4): 4-6)
(  0) 0) |
| [6] |
冯彪, 柴洪洲, 王敏, 等. 基于方差分量估计的不同截止高度角下的组合单点定位[J]. 测绘工程, 2017, 26(4): 32-42 (Feng Biao, Chai Hongzhou, Wang Min, et al. Combined Single Point Positioning with Different Cut[J]. Engineering of Surveying and Mapping, 2017, 26(4): 32-42)
(  0) 0) |
| [7] |
蒋光伟, 涂锐. 抗差Helmert方差分量估计在精密单点定位中的应用[J]. 测绘科学, 2011, 36(6): 187-188 (Jiang Guang-wei, Tu Rui. Applications of Robust Helmert Variance Component Estimation to PPP[J]. Science of Surveying and Mapping, 2011, 36(6): 187-188)
(  0) 0) |
| [8] |
Gerdan G P. A Comparison of Four Methods of Weighting Double Difference Pseudorange Measurements[J]. The Australian Surveyor, 1995, 40(4): 60-66 DOI:10.1080/00050334.1995.10558564
(  0) 0) |
| [9] |
Han S. Quality Control Issues Relating to Instantaneous Ambiguity Resolution for Real-Time GPS Kinematic Positioning[J]. Journal of Geodesy, 1997, 71(6): 351-361 DOI:10.1007/s001900050103
(  0) 0) |
| [10] |
杨元喜, 张晓东. 基于严密Helmert方差分量估计的动态卡尔曼滤波[J]. 同济大学学报:自然科学版, 2009, 37(9): 1241-1245 (Yang Yuanxi, Zhang Xiaodong. Variance Component Estimation of Helmert Type Based Dynamic Kalman Filtering[J]. Journal of Tongji University:Natural Science, 2009, 37(9): 1241-1245)
(  0) 0) |
| [11] |
刘长建, 吴洪举, 明锋. Helmert方差分量估计严密公式与简化公式等价性的证明[J]. 测绘科学, 2006, 31(2): 66-67 (Liu Changjian, Wu Hongju, Ming Feng. Equivalence of Rigorous Formula to Simplified Formula of Helmert Variance Components Estimation[J]. Science of Surveying and Mapping, 2006, 31(2): 66-67 DOI:10.3771/j.issn.1009-2307.2006.02.021)
(  0) 0) |
| [12] |
周承松, 彭月, 张小红, 等. 精密单点定位收敛时间的确定方法研究[J]. 导航定位学报, 2016, 4(1): 80-87 (Zhou Chengsong, Peng Yue, Zhang Xiaohong, et al. A Study of Methods in Determining the Precise Point Position-ing Convergence Time[J]. Journal of Navigation and Position, 2016, 4(1): 80-87)
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38


