Kalman滤波在大地测量、卫星导航和卫星定轨等方面有着广泛应用[1-3]。离散动态系统中观测矩阵的病态性会对Kalman滤波状态估计产生很大影响,为了克服这种影响,提高参数估计的精度,许多学者提出改进算法[4-6]。目前,已有学者从有偏估计角度提出解决离散动态系统中病态性问题的一些方法。Tan等[5]将有偏估计与Kalman滤波相结合,提出Biased Kalman Filter;韩松辉[3]将岭回归与Kalman滤波相结合,通过对增益阵进行修正,克服观测矩阵病态性对滤波值的不良影响;李永明[7]将Stein压缩估计和岭回归与Kalman滤波相结合,提出相应的压缩型Kalman滤波和岭型Kalman滤波以及它们的算法,给出压缩系数和岭参数的选取方法。以上改进方法的一个共同不足是没有将离散动态系统病态性的诊断与处理相结合,没有考虑各个参数受到病态性影响大小的差异,而对所有参数进行完全一致的修正。实际上,观测矩阵的病态性对每个状态参数估计的危害大小是不同的,这种危害的大小既与参数本身数量级大小有关,也与参数所对应观测矩阵数据列参与复共线性的程度有关。本文将Kalman滤波病态性的危害度量与处理结合,利用信噪比统计量对参数估计受病态性影响的大小进行度量,根据度量结果对Kalman滤波递推过程采取针对性措施,改进岭型Kalman滤波算法,进一步降低病态性对参数估计的影响。
目前我国还没有在全球范围内布设地面观测站,所以BDS无法基于全球地面观测站进行有效定轨,导致观测几何结构差、观测矩阵病态,从而采用Kalman滤波进行定轨的精度不高甚至很差[6]。本文给出了完整的基于信噪比检验的双参数岭型Kalman滤波算法,应用于BDS定轨中并取得良好效果。
1 Kalman滤波算法及病态性分析 1.1 离散动态系统及Kalman滤波基本方程动力系统的状态空间模型为[1]:
| $ {\mathit{\boldsymbol{X}}_{k + 1}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k + 1/k}}{\mathit{\boldsymbol{X}}_k} + {\mathit{\boldsymbol{W}}_k} $ | (1) |
| $ {\mathit{\boldsymbol{Y}}_k} = {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{X}}_k} + {\mathit{\boldsymbol{V}}_k} $ | (2) |
式中,k为离散时间,系统在时刻k的状态为Xk∈Rt,Yk∈Rn为对应的观测信号;Φk+1/k为t×t非奇异矩阵,是tk时刻至tk+1时刻的一步状态转移矩阵;Hk为n×t观测矩阵;Wk∈Rt为输入白噪声;Vk∈Rn为观测噪声。式(1)为状态方程,式(2)为观测方程。
同时,Wk和Vk满足:
| $ E\left( {{\mathit{\boldsymbol{W}}_k}} \right) = 0,{\rm{cov}}\left( {{\mathit{\boldsymbol{W}}_k},{\mathit{\boldsymbol{W}}_j}} \right) = E\left( {{\mathit{\boldsymbol{W}}_k}\mathit{\boldsymbol{W}}_j^{\rm{T}}} \right) = {\mathit{\boldsymbol{Q}}_k}{\delta _{kj}} $ |
| $ E\left( {{\mathit{\boldsymbol{V}}_k}} \right) = 0,{\rm{cov}}\left( {{\mathit{\boldsymbol{V}}_k},{\mathit{\boldsymbol{V}}_j}} \right) = E\left( {{\mathit{\boldsymbol{V}}_k}\mathit{\boldsymbol{V}}_j^{\rm{T}}} \right) = {\mathit{\boldsymbol{R}}_k}{\delta _{kj}} $ |
| $ {\rm{cov}}\left( {{\mathit{\boldsymbol{W}}_k},{\mathit{\boldsymbol{V}}_j}} \right) = E\left( {{\mathit{\boldsymbol{W}}_k}\mathit{\boldsymbol{V}}_j^{\rm{T}}} \right) = 0 $ | (3) |
式中,Qk为输入噪声的方差阵,假设为非负定阵;Rk为观测噪声的方差阵,假设为正定阵;δkj为Kronecher-δ函数。由式(3)可以看出,Wk和Vk是均值为零、方差阵为Qk和Rk的不相关白噪声。
Kalman滤波基本方程如下:
状态一步预测
| $ {{\mathit{\boldsymbol{\hat X}}}_{k + 1/k}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k + 1/k}}{{\mathit{\boldsymbol{\hat X}}}_k} $ | (4) |
一步预测协方差阵
| $ {\mathit{\boldsymbol{P}}_{k + 1/k}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k + 1/k}}{\mathit{\boldsymbol{P}}_k}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k + 1/k}^{\rm{T}} + {\mathit{\boldsymbol{Q}}_k} $ | (5) |
滤波增益矩阵
| $ {\mathit{\boldsymbol{K}}_{k + 1}} = {\mathit{\boldsymbol{P}}_{k + 1/k}}\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}{\left( {{\mathit{\boldsymbol{H}}_{k + 1}}{\mathit{\boldsymbol{P}}_{k + 1/k}}\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}} + {\mathit{\boldsymbol{R}}_{k + 1}}} \right)^{ - 1}} $ | (6) |
状态更新
| $ {{\mathit{\boldsymbol{\hat X}}}_{k + 1}} = {{\mathit{\boldsymbol{\hat X}}}_{k + 1/k}} + {\mathit{\boldsymbol{K}}_{k + 1}}\left( {{\mathit{\boldsymbol{Y}}_{k + 1}} - {\mathit{\boldsymbol{H}}_{k + 1}}{{\mathit{\boldsymbol{\hat X}}}_{k + 1/k}}} \right) $ | (7) |
估计误差方差阵
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_{k + 1}} = \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_{k + 1}}{\mathit{\boldsymbol{H}}_{k + 1}}} \right){\mathit{\boldsymbol{P}}_{k + 1/k}}{{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_{k + 1}}{\mathit{\boldsymbol{H}}_{k + 1}}} \right)}^{\rm{T}}} + }\\ {{\mathit{\boldsymbol{K}}_{k + 1}}{\mathit{\boldsymbol{R}}_{k + 1}}\mathit{\boldsymbol{K}}_{k + 1}^{\rm{T}}} \end{array} $ | (8) |
式(4)~(8)是递推Kalman滤波的基本方程。给定初始值
由Kalman滤波基本方程可知[8],tk+1时刻的状态估计又可表示为:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat X}}}_{k + 1}} = {{\left( {\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{R}}_{k + 1}^{ - 1}{\mathit{\boldsymbol{H}}_{k + 1}} + \mathit{\boldsymbol{P}}_{k + 1/k}^{ - 1}} \right)}^{ - 1}} \cdot }\\ {\left( {\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{R}}_{k + 1}^{ - 1}{\mathit{\boldsymbol{Y}}_{k + 1}} + \mathit{\boldsymbol{P}}_{k + 1/k}^{ - 1}{{\mathit{\boldsymbol{\hat X}}}_{k + 1/k}}} \right)} \end{array} $ | (9) |
即
| $ \begin{array}{*{20}{c}} {\left( {\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{R}}_{k + 1}^{ - 1}{\mathit{\boldsymbol{H}}_{k + 1}} + \mathit{\boldsymbol{P}}_{k + 1/k}^{ - 1}} \right){{\mathit{\boldsymbol{\hat X}}}_{k + 1}} = }\\ {\left( {\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{R}}_{k + 1}^{ - 1}{\mathit{\boldsymbol{Y}}_{k + 1}} + \mathit{\boldsymbol{P}}_{k + 1/k}^{ - 1}{{\mathit{\boldsymbol{\hat X}}}_{k + 1/k}}} \right)} \end{array} $ | (10) |
这里,设Nk+1= Hk+1TRk+1-1Hk+1+Pk+1/k-1,Ik+1= Hk+1TRk+1-1Yk+1+Pk+1/k-1
| $ {\mathit{\boldsymbol{N}}_{k + 1}} = {\mathit{\boldsymbol{U}}_{k + 1}}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{k + 1}}\mathit{\boldsymbol{U}}_{k + 1}^{\rm{T}} $ | (11) |
则:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat X}}}_{k + 1}} = {{\left( {\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{R}}_{k + 1}^{ - 1}{\mathit{\boldsymbol{H}}_{k + 1}} + \mathit{\boldsymbol{P}}_{k + 1/k}^{ - 1}} \right)}^{ - 1}}\left( {\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{R}}_{k + 1}^{ - 1}{\mathit{\boldsymbol{Y}}_{k + 1}}} \right. + }\\ {\left. {\mathit{\boldsymbol{P}}_{k + 1/k}^{ - 1}{{\mathit{\boldsymbol{\hat X}}}_{k + 1/k}}} \right) = {\mathit{\boldsymbol{U}}_{k + 1}}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{k + 1}^{ - 1}\mathit{\boldsymbol{U}}_{k + 1}^{\rm{T}}\left( {\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{R}}_{k + 1}^{ - 1}{\mathit{\boldsymbol{Y}}_{k + 1}}} \right. + }\\ {\left. {\mathit{\boldsymbol{P}}_{k + 1/k}^{ - 1}{{\mathit{\boldsymbol{\hat X}}}_{k + 1/k}}} \right) = }\\ {\sum\limits_{i = 1}^t {\mathit{\boldsymbol{u}}_{k + 1}^i{{\left( {\mathit{\boldsymbol{u}}_{k + 1}^i} \right)}^{\rm{T}}}} \frac{1}{{\sigma _{k + 1}^i}}\left( {\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{R}}_{k + 1}^{ - 1}{\mathit{\boldsymbol{Y}}_{k + 1}} + \mathit{\boldsymbol{P}}_{k + 1/k}^{ - 1}{{\mathit{\boldsymbol{\hat X}}}_{k + 1/k}}} \right)} \end{array} $ | (12) |
式中,Uk+1=(uk+11, uk+12, …, uk+1t),Uk+1TUk+1= It,σk+11≥σk+12≥…≥σk+1t>0,Λk+1=diag(σk+11, σk+12, …, σk+1t)。
如果观测矩阵Hk+1存在病态性,则Hk+1和Pk+1/k-1的联合作用很可能使得Nk+1存在病态性。研究表明,Pk+1/k-1对观测矩阵病态性的控制作用是微弱的,并不能消除观测矩阵病态性对状态估计的不良影响[7],因此Nk+1存在一个或多个小特征值。若Yk+1和
文献[6]给出了岭型Kalman滤波(ridge-type Kalman filter, RTKF)的完整算法,tk+1时刻的岭型Kalman滤波状态估计可以表示为:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat X}}}_{k + 1}} = {{\left( {\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{R}}_{k + 1}^{ - 1}{\mathit{\boldsymbol{H}}_{k + 1}} + \mathit{\boldsymbol{P}}_{k + 1/k}^{ - 1}{\alpha _{k + 1}}\mathit{\boldsymbol{I}}} \right)}^{ - 1}} \cdot }\\ {\left( {\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{R}}_{k + 1}^{ - 1}{\mathit{\boldsymbol{Y}}_{k + 1}} + \mathit{\boldsymbol{P}}_{k + 1/k}^{ - 1}{{\mathit{\boldsymbol{\hat X}}}_{k + 1/k}}} \right) = }\\ {{{\left( {{\mathit{\boldsymbol{N}}_{k + 1}} + {\alpha _{k + 1}}\mathit{\boldsymbol{I}}} \right)}^{ - 1}}\left( {\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{R}}_{k + 1}^{ - 1}{\mathit{\boldsymbol{Y}}_{k + 1}} + \mathit{\boldsymbol{P}}_{k + 1/k}^{ - 1}{{\mathit{\boldsymbol{\hat X}}}_{k + 1/k}}} \right) = }\\ {\sum\limits_{i = 1}^t {\mathit{\boldsymbol{u}}_{k + 1}^i{{\left( {\mathit{\boldsymbol{u}}_{k + 1}^i} \right)}^{\rm{T}}}} \frac{1}{{\sigma _{k + 1}^i + {\sigma _{k + 1}}}}\left( {\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{R}}_{k + 1}^{ - 1}{\mathit{\boldsymbol{Y}}_{k + 1}}} \right. + }\\ {\left. {\mathit{\boldsymbol{P}}_{k + 1/k}^{ - 1}{{\mathit{\boldsymbol{\hat X}}}_{k + 1/k}}} \right)} \end{array} $ | (13) |
式中,αk+1为岭参数,岭型Kalman滤波就是利用岭参数对小特征值进行压制,降低估计的方差,从而减弱小特征值对观测误差的放大作用。
岭型Kalman滤波存在两个缺陷:一是没有利用病态信息,从而导致岭参数的修正具有盲目性,即对所有参数进行完全一致的修正;二是岭型Kalman滤波引入了偏差,此偏差在不断的递推过程中有可能被放大,进而影响估计精度。因此为了尽可能提高估计的精度,应该尽量减少偏差的引入。综合以上两方面,提出基于信噪比检验的双参数岭型Kalman滤波,其思想就是根据病态信息将状态参数分为两部分,并进行不同强度的修正,通过这种精细化的处理,在有效降低病态性影响的同时也减少了偏差的引入。
2.2 基于信噪比检验的双参数岭型Kalman滤波由以上分析可知,tk+1时刻的状态估计为式(10)的解,若法矩阵Nk+1存在病态性,则tk+1时刻的状态估计将变得极不稳定,这是观测矩阵的病态性对状态估计施加影响的地方。法矩阵Nk+1存在病态性的原因是数据列之间存在复共线性关系,从而导致tk+1时刻的状态估计效果不好,但并非所有状态估计的效果都不好。研究发现,法矩阵的病态性只对参与复共线性的数据列所对应状态参数的估计影响较大,而对未参与复共线性的数据列所对应状态参数的估计影响较小[9]。
通过计算各状态估计分量的信噪比统计量,可将每个待估参数的估计效果进行区分:
| $ F_{k + 1}^i = \frac{{{{\left( {\mathit{\boldsymbol{\hat X}}_{k + 1}^i} \right)}^2}}}{{{\mathop{\rm var}} \left( {\mathit{\boldsymbol{\hat X}}_{k + 1}^i} \right)}} $ | (14) |
式中,
式(14)称为第i个参数Xi的信噪比统计量。利用文献[9]的检验法则:当Fi≤χ1,τ2(ω)时,认为复共线性对相应参数估计
通过计算信噪比统计量,可将tk+1时刻的状态参数分为两部分,即X =(X1T, X2T)T,其中信噪比统计量较小的s个参数为X1,其受复共线性的危害较大,称为涉扰参数;信噪比统计量较大的t-s个参数为X2,其受复共线性的危害较小,称为非涉参数。对于X1,由于其估计较差,对这部分参数作较大的修正;对于X2,对其作较小的修正,据此构造修正矩阵:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Z}}_{k + 1}} = }\\ {\left[ {\begin{array}{*{20}{c}} {\alpha _{k + 1}^1}&0&{}& \cdots &0&0\\ 0& \ddots &{}&{}&{}&0\\ {}&{}&{\alpha _{k + 1}^1}&{}&{}&{}\\ \vdots &{}&{}&{\alpha _{k + 1}^2}&{}& \vdots \\ 0&{}&{}&{}& \ddots &0\\ 0&0&{}& \cdots &0&{\alpha _{k + 1}^2} \end{array}} \right]\begin{array}{*{20}{c}} {{\rm{第}}s{\rm{行}}}\\ {}\\ {}\\ {{\rm{第}}s + 1{\rm{行}}}\\ {}\\ {} \end{array}} \end{array} $ | (15) |
式中,αk+11、αk+22为两个岭参数,且αk+12>αk+22。基于信噪比检验的双参数岭型Kalman滤波(double parameters ridge-type Kalman filter based on signal-to-noise test, DPRTKF)为:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat X}}}_{k + 1}} = {{\left( {\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{R}}_{k + 1}^{ - 1}{\mathit{\boldsymbol{H}}_{k + 1}} + \mathit{\boldsymbol{P}}_{k + 1/k}^{ - 1} + {\mathit{\boldsymbol{Z}}_{k + 1}}} \right)}^{ - 1}} \cdot }\\ {\left( {\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{R}}_{k + 1}^{ - 1}{\mathit{\boldsymbol{Y}}_{k + 1}} + \mathit{\boldsymbol{P}}_{k + 1/k}^{ - 1}{{\mathit{\boldsymbol{\hat X}}}_{k + 1/k}}} \right)} \end{array} $ | (16) |
合理地确定tk+1时刻的岭参数αk+11和αk+12是一个应用上很重要的问题。注意到双参数岭估计是广义岭估计的一个特例,同时借鉴岭估计中确定岭参数的Hoerl-Kennard方法的思想,本文采用以下方法确定αk+11和αk+12[10-11]。
令θk+1=(θk+11, θk+12, …, θk+1t)T= Uk+1T Xk+1,称θk+1为典则参数[12],其最小二乘估计为:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\theta }}_{k + 1}} = {{\left( {\mathit{\boldsymbol{\theta }}_{k + 1}^1,\mathit{\boldsymbol{\theta }}_{k + 1}^2, \cdots ,\mathit{\boldsymbol{\theta }}_{k + 1}^t} \right)}^{\rm{T}}} = }\\ {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{k + 1}^{ - 1}\mathit{\boldsymbol{U}}_{k + 1}^{\rm{T}}\left( {\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{R}}_{k + 1}^{ - 1}{\mathit{\boldsymbol{Y}}_{k + 1}} + \mathit{\boldsymbol{P}}_{k + 1/k}^{ - 1}{{\mathit{\boldsymbol{\hat X}}}_{k + 1/k}}} \right)} \end{array} $ | (17) |
两个岭参数αk+11和αk+12分别取为:
| $ \alpha _{k + 1}^1 = \frac{1}{{\left( {\hat \theta _{k + 1}^i} \right)_{\max }^2}},\alpha _{k + 1}^2 = {c_{k + 1}}\alpha _{k + 1}^1, $ |
| $ 0 < {c_{k + 1}} < 1 $ | (18) |
实际应用中,参数ck+1应根据两部分参数X1T和X2T的估计受复共线性危害的大小灵活选取,本文算例中的ck+1按照式(19)确定。将所有信噪比统计量(Fk+11, Fk+12, …, Fk+1t)按从小到大顺序重新排列并编号为(Fk+1(1), Fk+1(2), …, Fk+1(t)),令
| $ {c_{k + 1}} = \frac{{\mathop {{\rm{mean}}}\limits_{i = s + 1, \cdots ,t} \left( {1/F_{k + 1}^{\left( i \right)}} \right)}}{{\mathop {{\rm{mean}}}\limits_{i = 1, \cdots ,\mathit{s}} \left( {1/F_{k + 1}^{\left( i \right)}} \right)}} $ | (19) |
式中,Fk+1(i)为信号噪声比,则其倒数1/Fk+1(i)为噪声信号比,噪声信号比越大,则对应的参数估计受复共线性危害程度就越大。用X1T和X2T噪声信号比均值的比值来定量地反映X1T和X2T参数估计受复共线性危害程度之间的比例关系,从而确定ck+1。
综上所述,完整的基于信噪比度量的双参数岭型Kalman滤波算法如下。
1) 初始化:给定状态参数的初始值
2) 时间更新:
| $ {{\mathit{\boldsymbol{\hat X}}}_{k + 1/k}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k + 1/k}}{{\mathit{\boldsymbol{\hat X}}}_{k/k}} $ | (20) |
| $ {\mathit{\boldsymbol{P}}_{k + 1/k}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k + 1/k}}{\mathit{\boldsymbol{P}}_{k/k}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k + 1/k}^{\rm{T}} + {\mathit{\boldsymbol{Q}}_k} $ | (21) |
3) 状态更新:
| $ {{\mathit{\boldsymbol{\hat X}}}_{k + 1}} = {{\mathit{\boldsymbol{\hat X}}}_{k + 1/k}} + {\mathit{\boldsymbol{K}}_{k + 1}}\left( {{\mathit{\boldsymbol{Y}}_{k + 1}} - {\mathit{\boldsymbol{H}}_{k + 1}}{{\mathit{\boldsymbol{\hat X}}}_{k + 1/k}}} \right) $ | (22) |
| $ {\mathit{\boldsymbol{K}}_{k + 1}} = {\mathit{\boldsymbol{P}}_{k + 1/k}}\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}{\left[ {{\mathit{\boldsymbol{H}}_{k + 1}}{\mathit{\boldsymbol{P}}_{k + 1/k}}\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}} + {\mathit{\boldsymbol{R}}_{k + 1}}} \right]^{ - 1}} $ | (23) |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_{k + 1}} = \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_{k + 1}}{\mathit{\boldsymbol{H}}_{k + 1}}} \right){\mathit{\boldsymbol{P}}_{k + 1/k}}{{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_{k + 1}}{\mathit{\boldsymbol{H}}_{k + 1}}} \right)}^{\rm{T}}} + }\\ {{\mathit{\boldsymbol{H}}_{k + 1}}{\mathit{\boldsymbol{R}}_{k + 1}}\mathit{\boldsymbol{K}}_{k + 1}^{\rm{T}}} \end{array} $ | (24) |
4) 判断法矩阵中Nk+1= Hk+1 Rk+1-1Hk+1T+ Pk+1/k-1的条件数是否大于500,若大于500,则进行下一步,否则返回2)。
5) 进行信噪比检验,确定涉扰参数和非涉参数。
6) 确定两个岭参数αk+11、αk+22。
7) 利用双参数岭型Kalman滤波对状态估计进行修正,并计算均方误差:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat X}}_{k + 1}^{{\rm{DPRTKF}}} = {{\left( {\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{R}}_{k + 1}^{ - 1}{\mathit{\boldsymbol{H}}_{k + 1}} + \mathit{\boldsymbol{P}}_{k + 1/k}^{ - 1} + {\mathit{\boldsymbol{Z}}_{k + 1}}} \right)}^{ - 1}} \cdot }\\ {\left( {\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{R}}_{k + 1}^{ - 1}{\mathit{\boldsymbol{Y}}_{k + 1}} + \mathit{\boldsymbol{P}}_{k + 1/k}^{ - 1}{{\mathit{\boldsymbol{\hat X}}}_{k + 1/k}}} \right)} \end{array} $ | (25) |
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat P}}_{k + 1}^{{\rm{DPRTKF}}} = \mathit{\boldsymbol{M}}_{k + 1}^{ - 1}\left( {{\mathit{\boldsymbol{N}}_{k + 1}}{\mathit{\boldsymbol{X}}_{k + 1}}\mathit{\boldsymbol{X}}_{k + 1}^{ - 1} + \mathit{\boldsymbol{I}}} \right){\mathit{\boldsymbol{N}}_{k + 1}}\mathit{\boldsymbol{M}}_{k + 1}^{ - 1} - }\\ {\mathit{\boldsymbol{M}}_{k + 1}^{ - 1}{\mathit{\boldsymbol{N}}_{k + 1}}{\mathit{\boldsymbol{X}}_{k + 1}}\mathit{\boldsymbol{X}}_{k + 1}^{\rm{T}} - {\mathit{\boldsymbol{X}}_{k + 1}}\mathit{\boldsymbol{X}}_{k + 1}^{\rm{T}}{\mathit{\boldsymbol{N}}_{k + 1}}\mathit{\boldsymbol{M}}_{k + 1}^{ - 1} + {\mathit{\boldsymbol{X}}_{k + 1}}\mathit{\boldsymbol{X}}_{k + 1}^{\rm{T}}} \end{array} $ | (26) |
其中,
| $ {\mathit{\boldsymbol{M}}_{k + 1}} = \mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}\mathit{\boldsymbol{R}}_{k + 1}^{ - 1}{\mathit{\boldsymbol{H}}_{k + 1}} + \mathit{\boldsymbol{P}}_{k + 1/k}^{ - 1} + {\mathit{\boldsymbol{Z}}_{k + 1}} $ | (27) |
8) 令
本文采用STK模拟5颗GEO卫星(地球静止轨道)+24颗MEO卫星(中圆地球轨道)+3颗IGSO卫星(倾斜地球同步轨道)的北斗卫星星座。其中,5颗GEO卫星分别处于59°E、89.5°E、110.5°E、142°E和163°E;3颗IGSO卫星均匀分布在3个倾斜同步轨道面上,轨道倾角为55°,星下点轨迹重合,交叉点在东经118°, 相位差120°;24颗MEO卫星组成Walker24/3/1星座。采用J2000地心赤道惯性坐标系仿真各卫星的真实轨道,星间观测采用双向测距方式,观测噪声均方差取0.75 m。为简单起见,只考虑J2项,不考虑钟差及大气延迟等,滤波采样周期为15 min,仿真时间为5 d。各卫星轨道根数先验均方差的先验值设置为δa=100 m, δe=1.0×10-5, δθ=1.0×10-5,δΩ=1.0×10-10,δω=1.0×10-10, δM=1.0×10-5,其中a、e、θ、Ω、ω、Μ分别为轨道长半轴、偏心率、轨道倾角、升交点赤经、近地点角距和平近点角。采用卫星轨道根数与卫星速度位置关系,把轨道根数先验均方差转化为卫星位置速度先验均方差,进而对Ω、ω进行限制。
增加西安、上海、昆明、广州、海南和喀什6个地面观测站,为星座提供地面基准,结合星间观测实现星地联合定轨。评价自主定轨精度的指标采用星座的用户测距误差(URE)和均方根误差(RMS)[7],计算方法为:
| $ {\rm{URE = }}\sqrt {\frac{1}{{{N_{{\rm{Sat}}}}}}\sum\limits_{i = 1}^{{N_{{\rm{Sat}}}}} {S\left( i \right)} } $ | (28) |
| $ \begin{array}{*{20}{c}} {S\left( i \right) = }\\ {\sqrt {R_{{\rm{ERR}}}^2\left( i \right) + 0.019\;2 \times \left( {T_{{\rm{ERR}}}^2\left( i \right) + N_{{\rm{ERR}}}^2\left( i \right)} \right)} } \end{array} $ | (29) |
式中,NSat为星座中卫星总数,RERR(i)为第i颗卫星的径向误差,TERR(i)为第i颗卫星的沿迹误差,NERR(i)为第i颗卫星的法向误差。
径向误差、沿迹误差、法向误差的均方根误差(RMS)计算公式分别为:
| $ {\rm{RM}}{{\rm{S}}_R} = \sqrt {\frac{1}{{{N_{{\rm{Sat}}}}}}\sum\limits_{i = 1}^{{N_{{\rm{Sat}}}}} {R_{{\rm{ERR}}}^2\left( i \right)} } $ | (30) |
| $ {\rm{RM}}{{\rm{S}}_T} = \sqrt {\frac{1}{{{N_{{\rm{Sat}}}}}}\sum\limits_{i = 1}^{{N_{{\rm{Sat}}}}} {T_{{\rm{ERR}}}^2\left( i \right)} } $ | (31) |
| $ {\rm{RM}}{{\rm{S}}_N} = \sqrt {\frac{1}{{{N_{{\rm{Sat}}}}}}\sum\limits_{i = 1}^{{N_{{\rm{Sat}}}}} {N_{{\rm{ERR}}}^2\left( i \right)} } $ | (32) |
运用本文提出的DPRTKF算法和KF算法及RTKF算法进行计算并比较,结果如图 1~6所示。
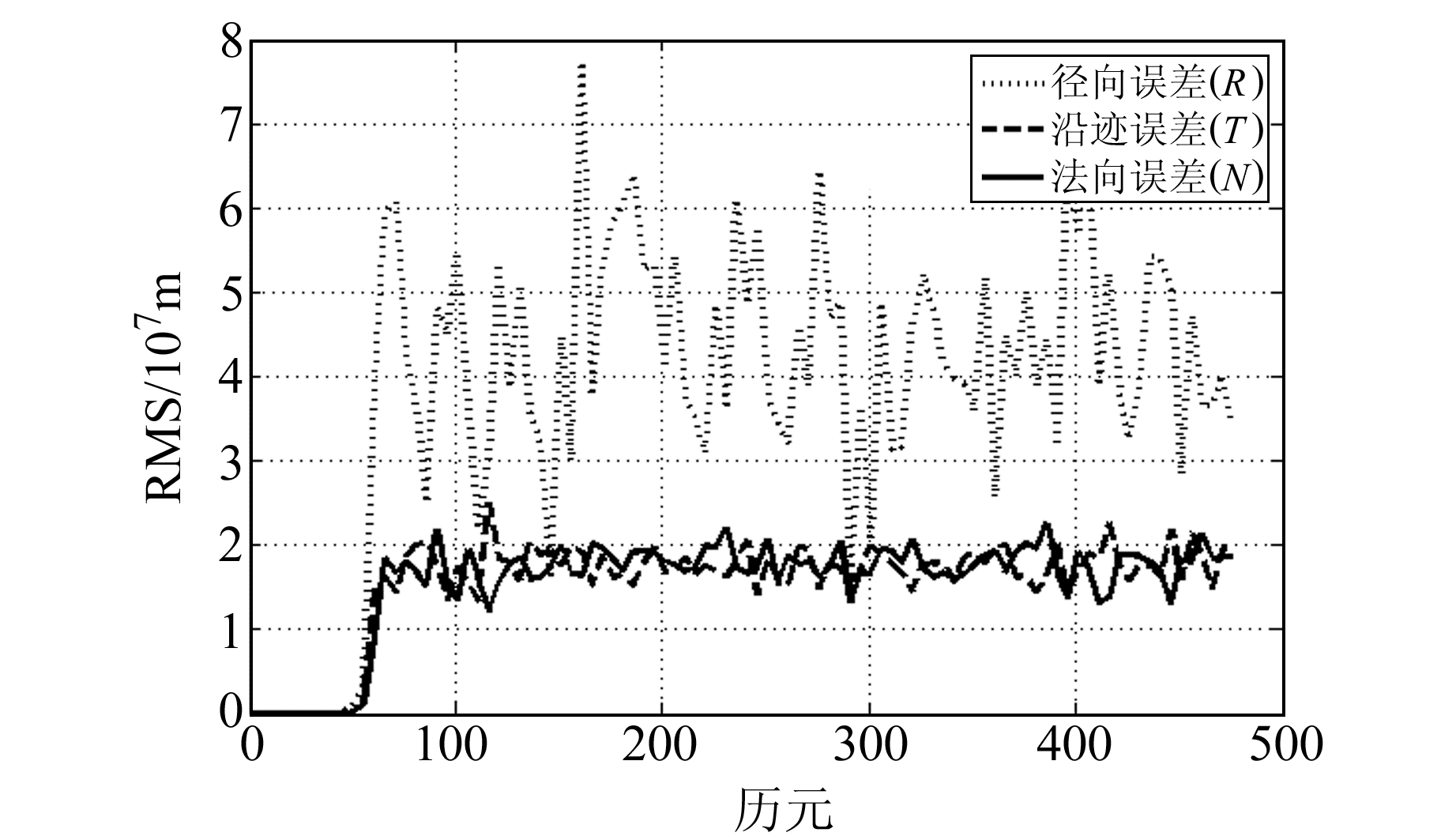
|
图 1 KF算法的径向、沿迹和法向误差 Fig. 1 KF algorithm radial error, trace error and normal error |
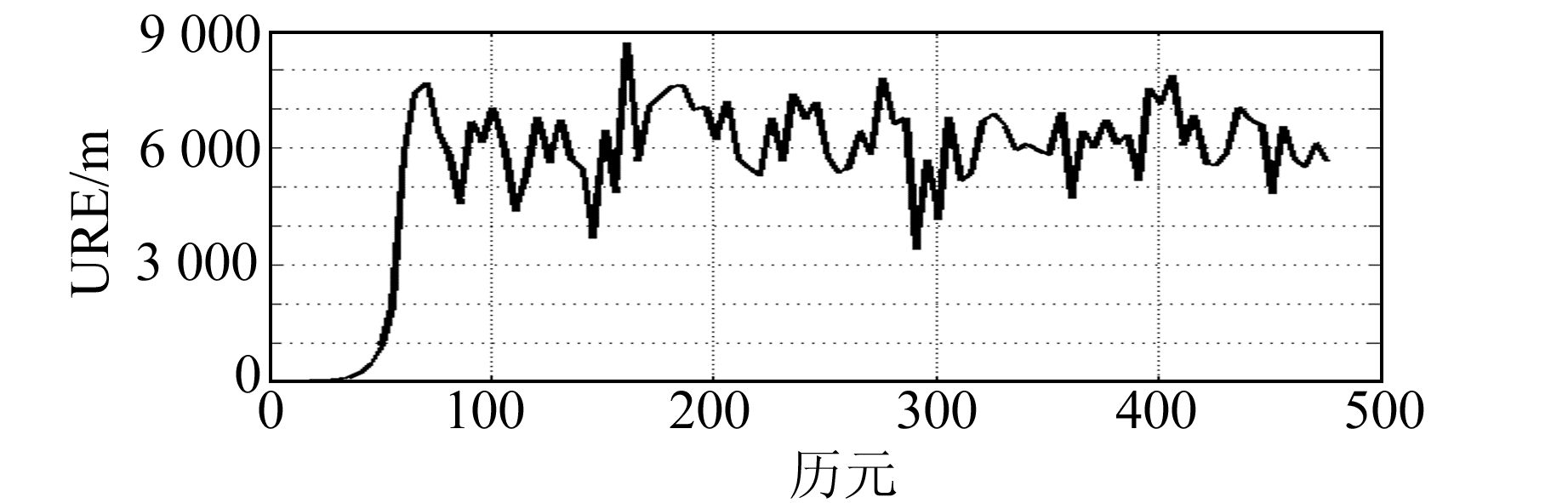
|
图 2 KF算法的星座URE Fig. 2 KF algorithm constellation URE |
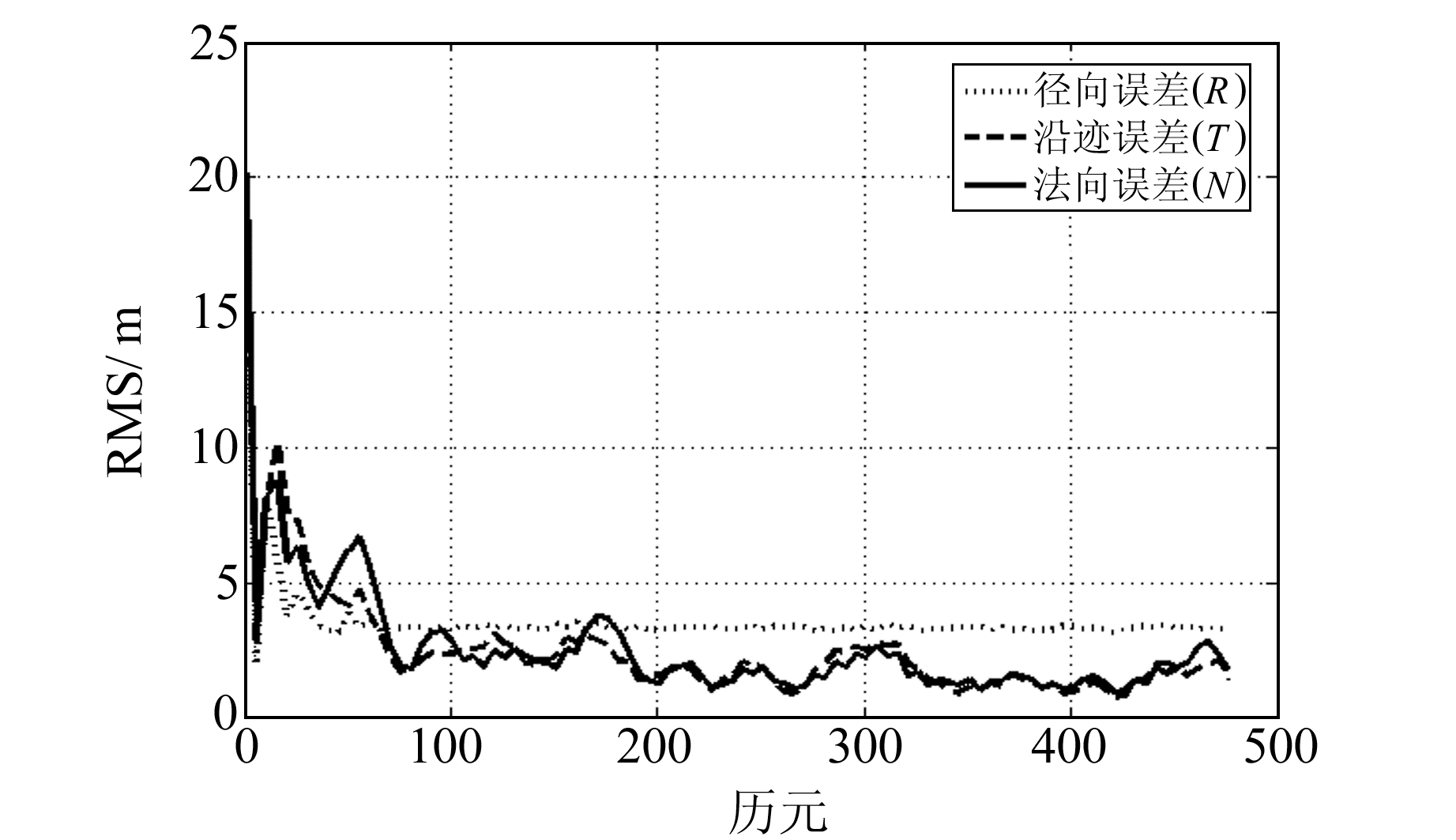
|
图 3 RTKF算法的径向、沿迹和法向误差 Fig. 3 RTKF algorithm radial error, trace error and normal error |
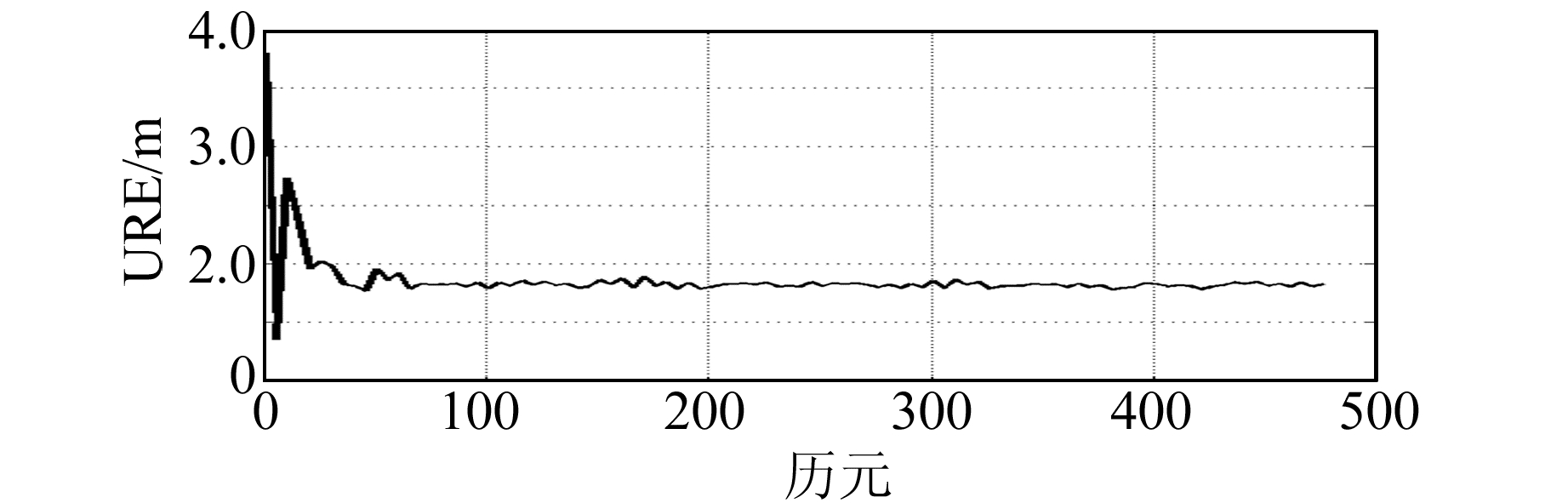
|
图 4 RTKF算法的星座URE Fig. 4 RTKF algorithm constellation URE |
|
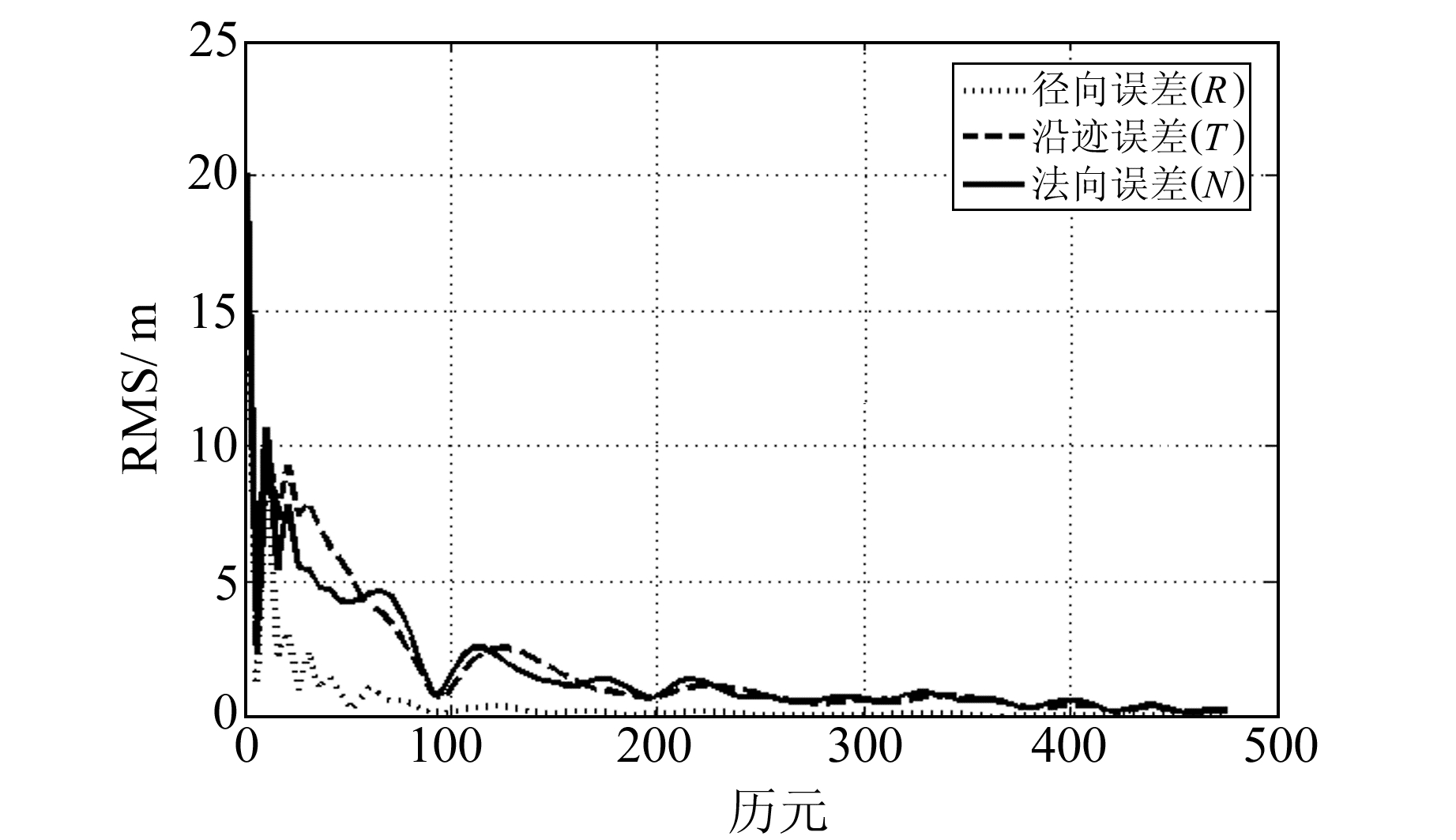
图 5 DPRTKF算法的径向、沿迹和法向误差 Fig. 5 DPRTKF algorithm radial error, trace error and normal error |
|
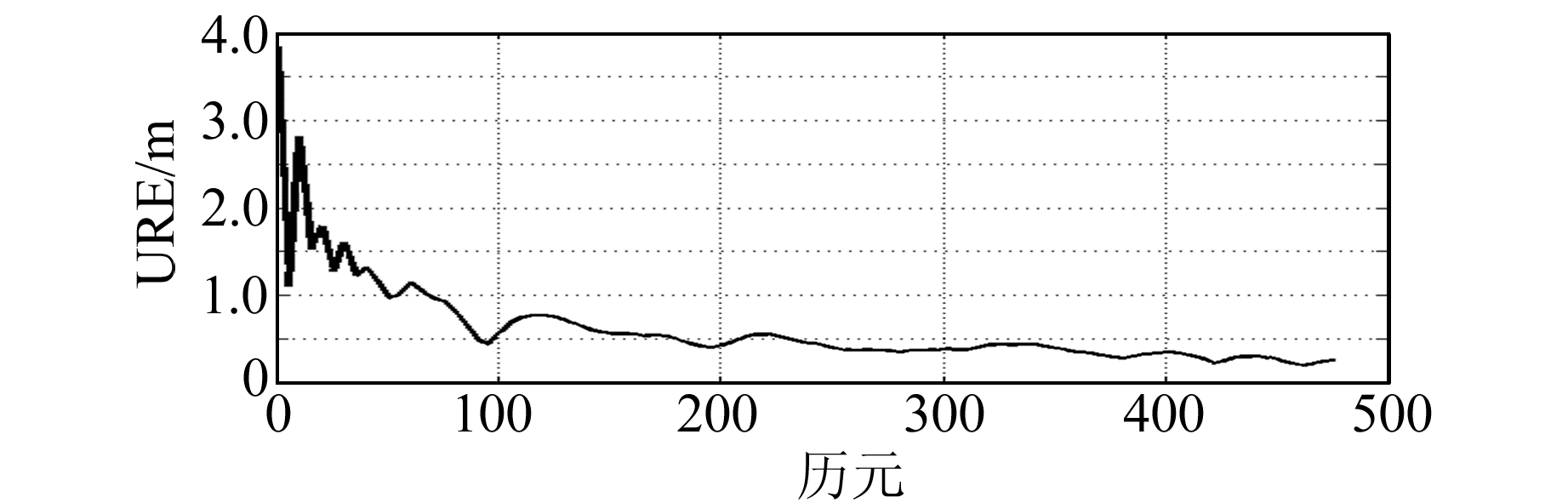
图 6 DPRTKF算法的星座URE Fig. 6 DPRTKF algorithm constellation URE |
1) 由于BDS地面观测的局限性,导致观测的几何结构较差,进而导致离散动态系统中的观测矩阵呈现严重病态性,KF算法计算结果迅速发散,无法进行星地联合定轨。
2) RTKF算法利用岭参数对法矩阵的小特征值进行压制,降低了估计的方差,减弱了小特征值对观测误差的放大作用,可以有效地进行星地联合定轨。
3) DPRTKF算法不但可以抑制观测矩阵病态性的影响,而且可以有效减少RTKF算法中岭参数引入的偏差对滤波值造成的影响,在星地联合定轨中具有比RTKF算法精度更高的定轨结果。
4 结语本文提出的DPRTKF算法将复共线性对参数估计危害的度量结果与岭型Kalman滤波相结合,根据每个参数估计信噪比统计量的大小将待估状态参数分为涉扰参数和非涉参数两部分,并对这两部分参数的状态估计进行不同强度的岭型修正。对于涉扰参数,使其修正岭参数相对较大;对于非涉参数,使其修正岭参数相对较小,精细化的处理在降低状态参数估计方差的同时有效减少了岭型Kalman滤波中偏差的引入,使得状态参数估计结果在均方误差意义下更优。数字实验结果表明,该方法可以得到比一般方法精度更高的参数估计结果。
| [1] |
秦永元, 张洪钺, 汪叔华. Kalman滤波与组合导航原理[M]. 西安: 西北工业大学出版社, 2012 (Qin Yongyuan, Zhang Hongyue, Wang Shuhua. Theory of Kalman Filter and Integrated Navigation Principles[M]. Xi'an: Northwestern Polytechnical University Press, 2012)
(  0) 0) |
| [2] |
曾旭平.导航卫星自主定轨研究及模拟结果[D].武汉: 武汉大学, 2004 (Zeng Xuping.Research and Simulation on Autonomous Orbit Determination for Navigation Satellites[D].Wuhan: Wuhan University, 2004)
(  0) 0) |
| [3] |
韩松辉.混合导航星座星间链路设计及自主定轨算法研究[D].郑州: 信息工程大学, 2014 (Han Songhui.Research on Inter-Satellite Link Design and Autonomous Orbit Determination Algorithm in Mixed Navigation Constellation[D].Zhengzhou: Information Engineering University, 2014)
(  0) 0) |
| [4] |
Kaipio J, Somersalo E. Nonstationary Inverse Problems and State Estimation[J]. Journal of Inverse Ill-Posed Problems, 1998, 7(3): 273-282
(  0) 0) |
| [5] |
Tan J J, Li D, Zhang J Q, et al.Biased Kalman Filter[C].International Conference on Sensing Technology, Palmerson North, 2011
(  0) 0) |
| [6] |
Li Y M, Gui Q M, Gu Y W, et al. Ridge-Type Kalman Filter and Its Algorithm[J]. WSEAS Transactions on Mathematics, 2014, 13: 852-862
(  0) 0) |
| [7] |
李永明.正则化Kalman滤波算法及其在卫星定轨中的应用[D].郑州: 信息工程大学, 2015 (Li Yongming.Regularized Kalman Filter and Its Application in Satellite Orbit Determination[D].Zhengzhou: Information Engineering University, 2015)
(  0) 0) |
| [8] |
杨元喜. 自适应动态导航定位[M]. 北京: 测绘出版社, 2006 (Yang Yuanxi. Adaptive Dynamic Navigation and Positioning[M]. Beijing: Surveying and Mapping Press, 2006)
(  0) 0) |
| [9] |
顾勇为.基于复共线性诊断的正则化方法及其在大地测量中的应用[D].郑州: 信息工程大学, 2010 (Gu Yongwei.Regularization Methods Based on Multicollinearity Diagnosis and Their Applications to Geodesy[D].Zhengzhou: Information Engineering University, 2010)
(  0) 0) |
| [10] |
韩松辉, 归庆明, 李建文, 等. 分布式自主定轨的岭型EKF算法[J]. 武汉大学学报:信息科学版, 2013, 38(4): 399-402 (Han Songhui, Gui Qingming, Li Jianwen. Ridge-Type EKF of Distributed Autonomous Orbit Determination[J]. Geomatics and Information Science of Wuhan University, 2013, 38(4): 399-402)
(  0) 0) |
| [11] |
韩松辉, 杜兰, 归庆明, 等. 诊断复共线性的特征分析法及其在GEO定轨中的应用[J]. 测绘学报, 2013, 42(1): 19-26 (Han Songhui, Du Lan, Gui Qingming, et al. Characteristics Analysis Approach for Multicollinearity Diagnosis and Its Applications in Orbit Determination of GEO Satellites[J]. Acta Geodaetica et Cartographioca Sinaica, 2013, 42(1): 19-26)
(  0) 0) |
| [12] |
王松桂. 线性模型的理论及其应用[M]. 合肥: 安徽教育出版社, 1987 (Wang Songgui. The Theory of Linear Model and Its Application[M]. Hefei: Anhui Education Press, 1987)
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38

