2. 武汉大学地球空间环境与大地测量教育部重点实验室,武汉市珞喻路129号,430079;
3. 武汉大学卫星导航定位技术研究中心,武汉市珞喻路129号,430079
研究表明,天线相位中心误差是GNSS高精度定位中不可忽视的一项误差源[1-2]。为了实现对该误差的精确改正,IGS提供了不定期更新的天线相位中心改正信息(称之为ANTEX文件)[3-4],但是这些改正信息目前只针对GPS和GLONASS发布[5-6],尚未有权威机构进行过北斗天线校正和发布相应的改正信息[7],这势必会影响和限制北斗系统的高精度应用。因此,在进行北斗高精度应用研究时,一些学者采取不考虑北斗天线相位中心改正,用GPS PCO代替、用GPS PCO与PCV代替等处理策略[8-13],但均没有就北斗相位中心改正给出明确的处理方法和可靠的理论依据。本文将对此展开详细研究和讨论。
笔者注意到,ANTEX文件中GPS和GLONASS所有天线对应两个频率的PCO都相同,IGS还建议用户在没有GLONASS天线相位中心改正的情况下可以用对应的GPS天线相位中心改正进行代替[3]。最新研究表明,用GPS的PCV(phase center variation)改正参数去代替对应GLONASS的PCV参数进行PPP解算,其高程方向偏差可由cm级提高到mm级,RMS能够提高73.4%[14];GLONASS各频率之间的PCV偏差在1 mm内,与GPS PCV的偏差为数mm[3]。文献[15]指出,GNSS天线在各频率带宽范围内具有稳定的相位中心(图 1),GLONASS与GPS对应的频率G1与L1、G2与L2较为接近,考虑到北斗与GPS两者对应的频率B1与L1、B2与L2也比较接近,猜测两者的相位中心应该也相近,是否也可以在北斗天线相位中心未知的情况下,用GPS天线相位中心改正代替相应频率(B1对应L1、B2对应L2)的北斗天线相位中心改正,进而提高北斗定位精度呢?针对此问题,本文从定位角度对其有效性、可行性等进行验证分析。

|
图 1 GNSS各系统频率带宽 Fig. 1 GNSS frequency plan |
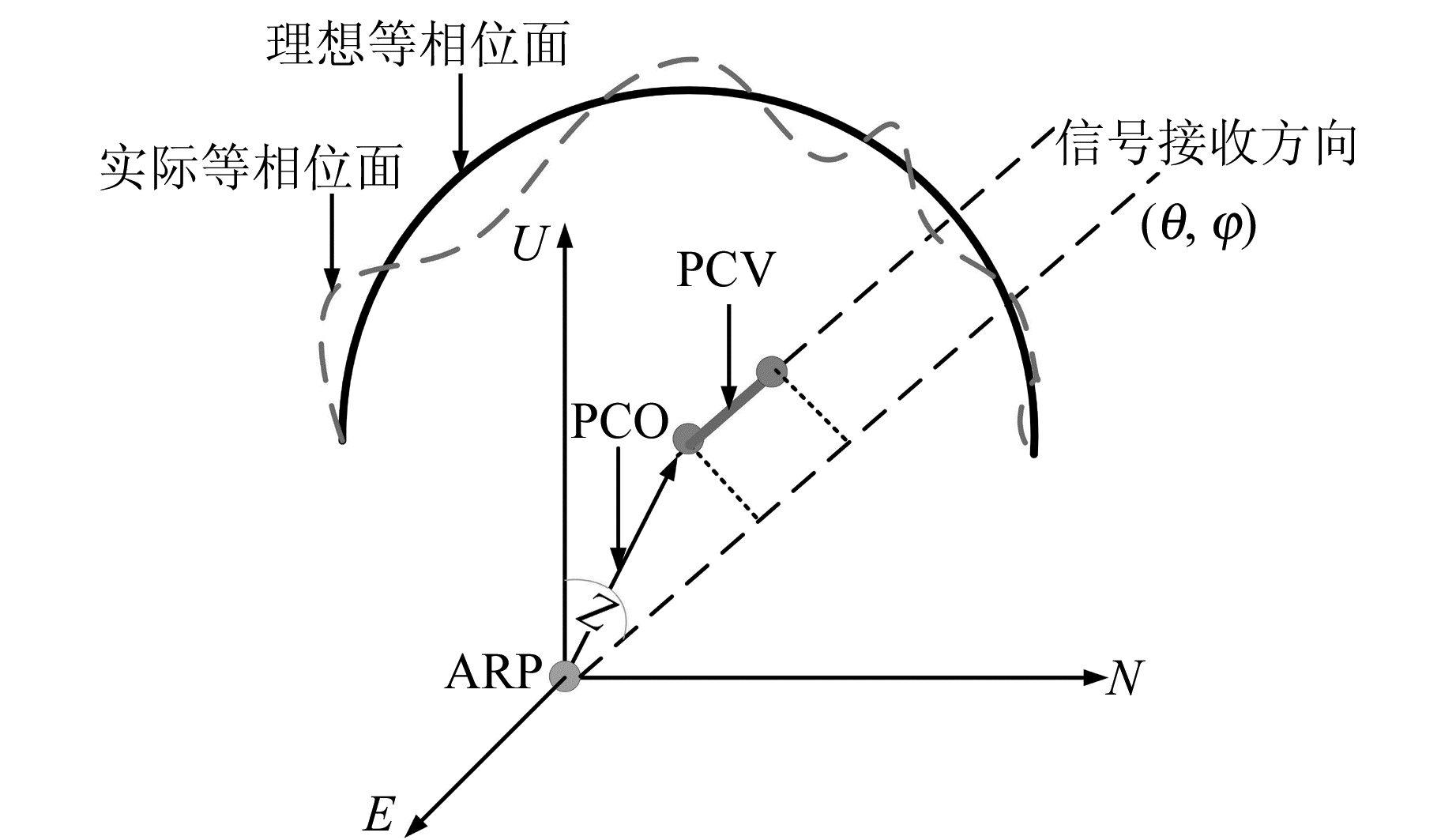
天线相位中心改正包括卫星端改正和接收机端改正(本文中如果没有特别说明时均指接收机端的改正)。如图 2所示[16],卫星和接收机天线相位中心改正由相位中心偏差(PCO)和相位中心变化(PCV)两部分组成,PCO为天线参考点到平均电气相位中心偏差,PCV为平均电气相位中心到随高度角和方位角变化的瞬时电气相位中心之间的变化量。PCO通常用天线本体三维坐标(E, N, U)表示,其中U方向为经过天线底面中心的竖直轴,N方向与指北方向重合,E方向与N和U方向构成左手系。PCV和PCO在E、N方向一般在mm级,PCO在U方向为cm到dm级。
|
图 2 天线相位中心示意图 Fig. 2 Antenna phase center |
图 3给出IGS14_1949天线表文件中共313款接收机天线的PCO各分量的分布情况。可以看出,PCO在水平方向偏差绝大多数都在-2~2 mm,总体上不会超过±10 mm;而在高程U方向上偏差均为正,绝大多数分布在50~120 mm,且分布范围较大。这说明对不同类型的天线而言,高程U方向的偏差远大于水平分量的偏差,且同一天线不同频率的PCO是有差异的。

|
图 3 IGS14_1949文件接收机天线PCO统计结果 Fig. 3 Analysis of receiver antenna PCOs in IGS14_1949.atx |
表 1给出的是TRM59800天线的PCO参数。可以看出,其PCO的特性和图 3中所有天线的特性是相似的,即水平方向偏差在1 mm以内,高程方向偏差在115 mm左右,GPS和GLONASS对应频率的PCO相同。
|
|
表 1 TRM59800 SCIS扼流圈天线的GPS/GLONASS PCO参数 Tab. 1 PCO paramters of GPS and GLONASS for the TRM59800 SCIS choke-ring antenna |
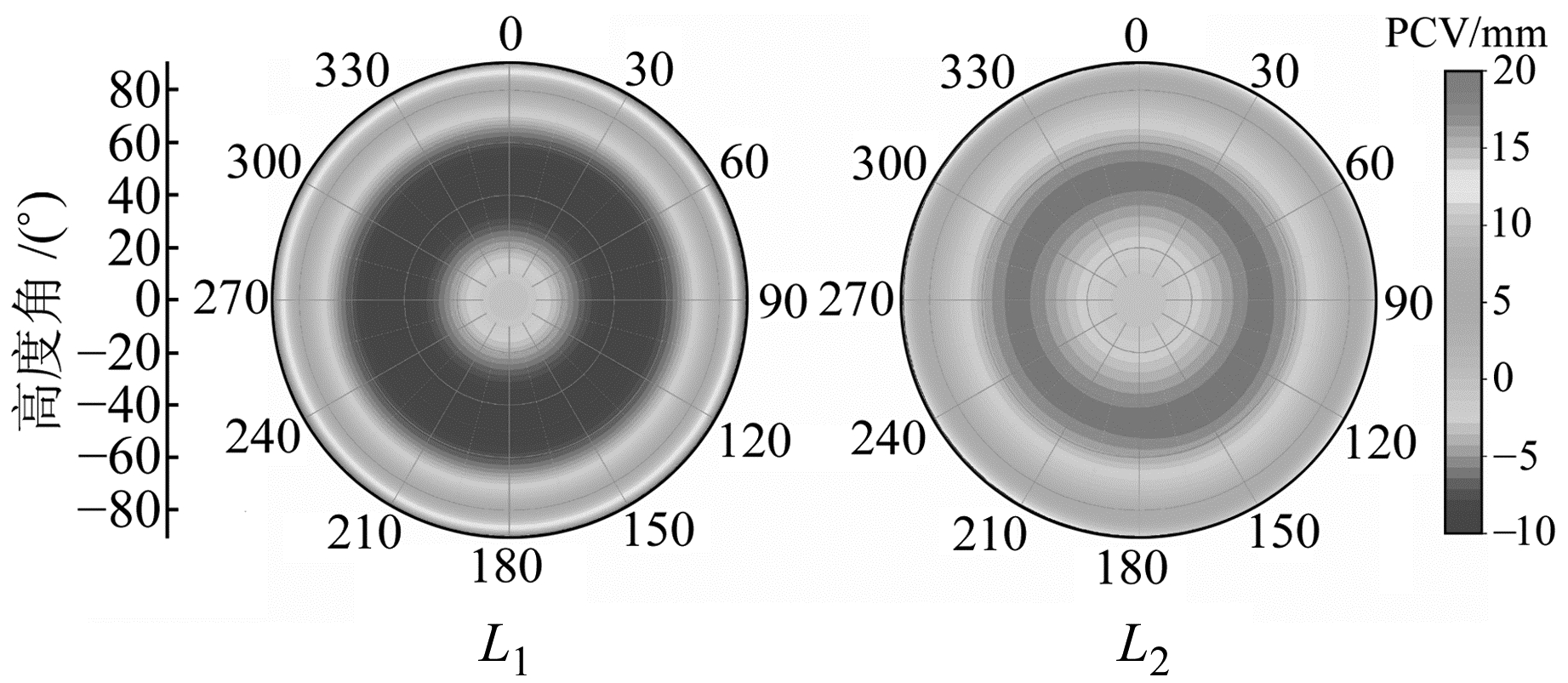
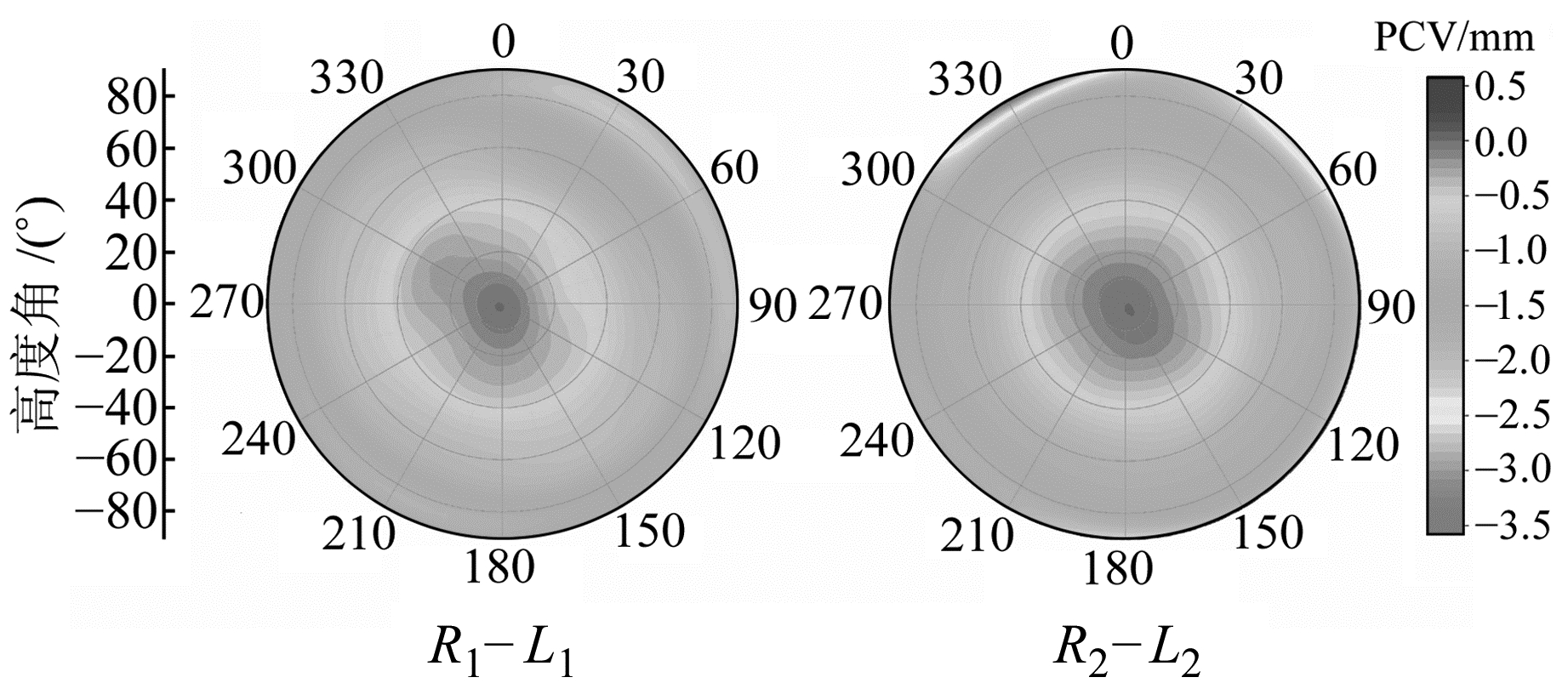
图 4为L1、L2 PCV图,可以看出,除了高度角10°以下的PCV达到1.5~2 cm外,其余均在1 cm内;PCV随高度角的变化较为明显,但是随方位角的变化并不明显。图 5是该款天线GPS减GLONASS PCV偏差分布,可以看出,两者对应频率的PCV相差数mm以内,其中R1与L1偏差绝对值不超过2.5 mm,R2与L2偏差绝对值不超过3.5 mm。
|
图 4 RM59800 SCIS扼流圈天线GPS PCV分布 Fig. 4 Antenna TRM59800 SCIS choke-ring PCV for GPS L1 and L2 |
|
图 5 TRM59800 SCIS扼流圈天线GPS与GLONASS PCV偏差分布 Fig. 5 Delta PCV between GPS and GLONASS of antenna TRM59800 SCIS choke-ring |
通过以上的天线相位中心的统计分析可以得出以下结论:
1) GPS PCO水平方向偏差在mm级,而高程分量偏差对于不同天线差异较大,其量级在cm级~1 dm,绝大多数集中在5~12 cm;PCV在高度角低于10°时可能会达到10~20 mm,但高于10°后均在mm级,且PCO高程分量偏差远大于PCV。因此,PCO的高程分量偏差是影响定位精度的最主要误差项。
2) 同款天线不同频率的GPS PCO与PCV均不相同,但GPS与GLONASS两者对应频率的PCO均相同,两者对应频率的PCV之间偏差为数mm,所以在缺少GLONASS相位中心参数时用GPS相应改正值进行代替是可行的。由此考虑,该处理方法对北斗也适用。
2 实验验证与结果分析为了分析IGS所发布的GPS天线相位改正信息是否有助于改善BDS的定位精度,对其定位参数有什么样的影响,影响有多大,本文分别从静态PPP和静态相对定位两个角度进行实验验证。
2.1 天线相位中心改正对GPS和北斗PPP的影响实验选取9个香港CORS站2017-06-05 (DOY156)的全天观测值,采样间隔为30 s,测站基本信息见表 2。PPP都为静态模式,均采用双频消电离层组合模型,待估参数为三维坐标、接收机钟差、对流层延迟误差。由于Bernese5.0不支持处理北斗的数据,所以GPS PPP采用Bernese5.0进行解算,BDS PPP采用RTKLIB进行解算。以Bernese5.0静态GPS PPP(PCC)单天解的结果作为参考真值。为验证上文分析内容,设计实验方案如表 3所示。
|
|
表 2 实验所用CORS站信息 Tab. 2 Information of CORS stations |
|
|
表 3 实验方案设计 Tab. 3 The experiment scheme |
图 6(a)~(f)分别是方案1~3按不同相位中心改正模式进行PPP解算与参考真值之间的偏差图。由于方案3中GPS计算方案与参考真值计算方案相同,所以图 6(e)各测站偏差均为0。对比图 6(a)、(c)、(e)可以看出,PCO和PCV对各测站GPS PPP水平方向的影响均为0~2 mm,对高程方向的影响因天线不同而呈现较大差异,Trimble两款天线的PCV对GPS PPP的影响达-2~-4 cm,显然这在高精度定位中必须考虑。对比图 6(b)、(d)、(f)可以看出,各方案BDS PPP水平方向偏差基本在2 cm内,U方向与天线类型有关,加入GPS PCO改正之后,Leica天线U方向偏差由15~20 cm减小到±4 cm内,Trimble天线略有改善,U方向偏差均在±3 cm内;加入PCV改正之后,Leica天线U方向基本没有变化,但Trimble两款天线U方向偏差均增加2~4 cm。

|
图 6 不同相位中心改正模式下的PPP偏差 Fig. 6 PPP biases with different phase center correction mode |
进行相位中心改正(PCO和PCV改正)之后的BDS和GPS PPP在水平方向的偏差基本在1 cm内,高程方向存在绝对值为2~4 cm的系统性偏差,引起偏差的原因可能是两者相位中心之间的差异、BDS轨道和钟差产品中的误差等,还需要进一步研究[5-6]。
2.2 天线相位中心改正对GPS和北斗相对定位的影响实验选取2017-07-18(DOY199)武汉大学测绘学院楼顶静态短基线数据,天线之间的基线长为数m,目的是消除或削弱与天线相位中心无关的其他误差的影响。实验设备配置见表 4。
|
|
表 4 实验测站所用设备信息 Tab. 4 Summary of equipments installed at each site |
本次实验的采样间隔为1 s,截止高度角设置为10°。实验过程中各天线均进行了整平且指北;同时,为便于分析,设计数据处理方案如表 5所示。
|
|
表 5 实验方案设计 Tab. 5 The experiment scheme |
基线解算均使用武汉大学研制的高精度GNSS动态定位软件KinPOS(V2.0)进行处理,将其单天静态解(PCC)作为参考真值,其他所有解算模式除相位中心改正方式不同外所有处理策略均相同。为方便起见,分别将基线SGG1-SGG2、SGG1-SGG3、SGG1-SGG4、SGG2-SGG3、SGG2-SGG4、SGG3-SGG4编号为1~6。
图 7(a)~(f)分别是方案4~6按不同相位中心改正模式进行基线解算与参考真值之间的偏差图,由于方案6中GPS解算策略与参考真值解算策略相同,所以图 7(e)中的各基线向量的偏差为0。对比图 7(a)、(c)、(e)可以看出,GPS各基线水平方向偏差均在2 mm以内,不加PCO和PCV改正,基线1~3在U方向偏差为-6 cm左右,基线4~6在U方向偏差在1 cm内;加入PCO改正后,各基线U方向偏差均在4 mm内,这说明PCV对基线U方向的影响在mm级。对比图 7(b)、(d)、(f)可以看出,BDS各基线水平方向基本在4 mm内,加入GPS PCO改正,基线1~3在U方向偏差由-6 cm改善到8 mm内,基线4~6在U方向偏差无明显变化但均在8 mm内。由表 4可知,当基线两端的天线PCO在U方向的值相差不大时,两者的偏差可以抵消大部分的误差影响,基线高程方向偏差较小;当两者相差较大时引起的基线高程方向偏差约为PCO的U方向之差,这与实际情况是相吻合的。加入PCV改正之后,水平方向几乎没有变化,高程方向偏差有0~4 mm的提高。

|
图 7 不同相位中心改正模式下基线解算偏差 Fig. 7 Baseline biases with different phase center correction modes |
加入相位中心改正(PCO和PCV改正)之后的BDS和GPS基线解算结果在水平方向的偏差基本在5 mm内,高程方向偏差在8 mm内。
3 结语本文讨论GNSS接收机天线相位中心模型及其参数特性,分析利用GPS天线相位中心改正参数代替BDS天线相位中心改正参数对PPP和基线解算精度的影响,得到如下结论:
1) 不同类型GNSS接收机天线的相位中心参数是不同的,其统计特性为:PCO水平分量在±2 mm以内,高程分量均为正,绝大多数分布在5~12 cm;PCV量级基本在mm级,在高度角低于10°时可能会达到1~2 cm;GLONASS与GPS对应频率的PCO均相同,PCV的差异在0~4 mm。
2) PCO对GPS和BDS PPP的高程方向影响可达cm级~1 dm,水平方向影响在0~2 mm;虽然PCV量级为mm级,但对PPP高程方向的影响可达cm级,所以在高精度PPP定位中,PCO和PCV改正都必须考虑。用GPS天线相位中心改正参数代替BDS相位中心改正参数进行PPP解算,其高程方向的偏差从1 dm减小到cm级。
3) 天线相位中心误差对GPS和BDS基线解算的影响与基线两端的天线有关。本文实验中,PCO可引起基线向量U方向6 cm左右的偏差,PCV的影响为数mm。用GPS相位中心改正参数代替BDS相位中心改正参数进行短基线解算,U方向精度从cm级提高到mm级,其中,PCO改善效果显著,PCV对其有0~4 mm的提高。
综上所述,在无法获得精确的BDS接收机天线相位中心改正参数的情况下,利用GPS天线相位中心改正参数代替BDS天线相位中心改正参数的策略是合理的、可行的,可以显著提高BDS精密定位的精度。
| [1] |
Araszkiewicz A, Völksen C. The Impact of the Antenna Phase Center Models on the Coordinates in the EUREF Permanent Network[J]. GPS Solutions, 2017, 21(2): 747-757 DOI:10.1007/s10291-016-0564-7
(  0) 0) |
| [2] |
李晓波, 王小亚, 任金卫. GNSS天线相位中心偏差与变化精确标定方法研究[J]. 天文学进展, 2012, 30(4): 501-517 (Li Xiaobo, Wang Xiaoya, Ren Jinwei. Research on Calibration Methods of GNSS Antenna Phase Center Offsets and Variations[J]. Progress in Astronomy, 2012, 30(4): 501-517)
(  0) 0) |
| [3] |
Schmid R, Dach R, Collilieux X, et al. Absolute IGS Antenna Phase Center Model IGS08.atx:Status and Potential Improvements[J]. Journal of Geodesy, 2016, 90(4): 343-364 DOI:10.1007/s00190-015-0876-3
(  0) 0) |
| [4] |
Schön S, Kersten T.Comparing Antenna Phase Center Corrections: Challenges, Concepts and Perspectives[C].IGS Analysis Workshop, 2014
(  0) 0) |
| [5] |
Montenbruck O, Schmid R, Mercier F, et al. GNSS Satellite Geometry and Attitude Models[J]. Advances in Space Research, 2015, 56(6): 1015-1029 DOI:10.1016/j.asr.2015.06.019
(  0) 0) |
| [6] |
IGS Working Group.IGS Antenna Files[DB].ftp://ftp.igs.org/pub/station/general/antenna_README.pdf.2016-05-03/2017-10-18
(  0) 0) |
| [7] |
马德强.GNSS接收机天线相位中心误差改正方法研究[D].西安: 长安大学, 2014 (Ma Deqiang.Study on the Correction Method of GNSS Receiver Antenna Phase Center Error[D].Xi'an: Chang'an University, 2014)
(  0) 0) |
| [8] |
Li M, Li W, Shi C, et al. Assessment of Precipitable Water Vapor Derived from Ground-Based Beidou Observations with Precise Point Positioning Approach[J]. Advances in Space Research, 2015, 55(1): 150-162 DOI:10.1016/j.asr.2014.10.010
(  0) 0) |
| [9] |
Li M, Qu L, Zhao Q, et al. Precise Point Positioning with the Beidou Navigation Satellite System[J]. Sensors, 2014, 14(1): 927-943 DOI:10.3390/s140100927
(  0) 0) |
| [10] |
Qu L, Zhao Q, Li M, et al.Precise Point Positioning Using Combined Beidou and GPS Observations[C].China Satellite Navigation Conference (CSNC), 2013
(  0) 0) |
| [11] |
Lou Y, Liu Y, Shi C, et al. Precise Orbit Determination of Beidou Constellation Based on BETS and MGEX Network[J]. Scientific Reports, 2015, 4(1): 4
(  0) 0) |
| [12] |
Lou Y, Zheng F, Gu S, et al. Multi-GNSS Precise Point Positioning with Raw Single-Frequency and Dual-Frequency Measurement Models[J]. GPS Solutions, 2016, 20(4): 849-862 DOI:10.1007/s10291-015-0495-8
(  0) 0) |
| [13] |
王峥, 周剑. GPS和BDS天线相位中心改正对基线结果的影响分析[J]. 大地测量与地球动力学, 2017, 37(3): 287-291 (Wang Zheng, Zhou Jian. Analysis of Influence from Antenna Phase Center Corrections of GPS and BDS on Baseline Results[J]. Journal of Geodesy and Geodynamics, 2017, 37(3): 287-291)
(  0) 0) |
| [14] |
Zhou F, Gu S, Chen W, et al. Comprehensive Assessment of Positioning and Zenith Delay Retrieval Using GPS+Glonass Precise Point Positioning[J]. Acta Geodynamica et Geomaterialia, 2017, 14(3): 317-326
(  0) 0) |
| [15] |
Popugaev A E, Wansch R. Multi-Band GNSS Antenna[M]. Berlin Heidelberg: Springer, 2011
(  0) 0) |
| [16] |
Görres B, Campbell J, Becker M, et al. Absolute Calibration of GPS Antennas:Laboratory Results and Comparison with Field and Robot Techniques[J]. GPS Solutions, 2006, 10(2): 136-145 DOI:10.1007/s10291-005-0015-3
(  0) 0) |
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, 129 Luoyu Road, Wuhan 430079, China;
3. GNSS Research Center, Wuhan University, 129 Luoyu Road, Wuhan 430079 China
 2018, Vol. 38
2018, Vol. 38


