通过对变形数据处理，作出合理分析并挖掘其物理规律，对边坡工程安全有效运行和人身安全有着重要的理论意义和应用价值。

当前边坡变形的预测方法较多，经历了从传统的数学统计方法到多尺度深入研究的发展过程。传统的数学统计方法有时间序列分析、混沌理论和灰色理论等。刘娜等^[1]通过对数据进行平稳化处理，建立时间序列模型，但需要大量实验数据且限定于短期预测；靖洪文等^[2]对原始数据进行优化重构，建立GM(1, 1)模型，但变形是一个受多因素影响的复杂非线性过程，仅传统的统计方法其预测精度受到一定限制。针对上述难题，基于神经网络具有非线性、良好泛化能力以及自适应性学习等特点，刘贺等^[3]建立了神经网络模型，预测精度得到提高，但由于神经网络模型存在易陷入局部最优、参数选择不确定性等缺陷，对边坡预测效果具有一定限制。近几年来，随着机器学习在边坡变形预测应用的快速发展，文献[4-5]利用支持向量机较好地解决了小样本、非线性和高维数边坡变形数据难题，建立的变形预测模型具有较好的鲁棒性、快速收敛和计算较简单等优点，但存在模型核函数受Mercer条件限制以及泛化能力较低等不足。由于LMD方法^[6-7]具有端点效应得到一定抑制、分解信号规律性强等优点，而RVM方法^[8]在泛化能力、模型稀疏性以及核函数不受Mercer条件限制等方面优于SVM方法，可将改进的LMD与RVM有效结合，建立改进的LMD-RVM预测模型。本文利用改进的LMD方法将变形信号分解成若干具有一定物理特征的变形分量，对处理数据建立相关向量机模型，通过遗传算法优化模型参数，累加分量预测模型，得到预测模型。通过实例精度指标分析，证实改进的LMD-RVM方法具有较高的预测精度。

1 LMD和RVM算法的改进 1.1 LMD算法的改进 1.1.1 LMD基本原理

局部均值分解(local mean decomposition, LMD)是由Smith在2005年提出的一种新的自适应非平稳信号处理方法。通过对信号进行分解，获得一系列具有一定物理特征的变形分量，每个变形分量由一个包络信号和一个纯调频信号相乘得到，由此可得到原始信号完整的时频分布情况。

求解信号x(t)所有局部极值点n_i，通过n_i求出局部均值函数m_i和局部包络函数a_i，对m_i和a_i进行滑动平均处理。滑动步长l为相邻极值点间最大距离d的1/3, 若相邻点的值相同，继续采用滑动平均方法直到任何相邻点不再相同，$ l = \frac{1}{3}{\rm{odd}}([{\bar d_i}]) = \frac{s}{3}$，对h₁₁(t)进行解调，可将h₁₁(t)除以a₁₁(t)得到s₁₁(t)。假定s₁₁(t)对应的局部包络函数满足s₁₂(t)=1，则s₁₁(t)是一个纯调频信号；反之，可对s₁₁(t)作为原始信号重复上述迭代过程，直到s_1n(t)是一个纯调频信号。但实际情况中，适当设置一个变动量δ，当达到1-δ≤a_1n(t)≤1+δ条件时，立即终止迭代。把PF₁(t)从x(t)中分离出来，可得一个新信号u₁(t)。重复上述过程，待得到单调函数u_k(t)为止：

$ \left\{ \begin{array}{l} {u_1}\left( t \right) = x\left( t \right) - {\rm{P}}{{\rm{F}}_1}\left( t \right)\\ {u_2}\left( t \right) = {u_1}\left( t \right) - {\rm{P}}{{\rm{F}}_2}\left( t \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {u_k}\left( t \right) = {u_{k - 1}}\left( t \right) - {\rm{P}}{{\rm{F}}_q}\left( t \right) \end{array} \right. $

(1)

信号x(t)可分解为：

$ x\left( t \right) = \mathop \sum \limits_{q = 1}^k {\rm{P}}{{\rm{F}}_q}\left( t \right) + {u_k}\left( t \right) $

(2)

1.1.2 LMD算法的改进

信号左右端点一般不是极值点，导致每个分量(PF)的筛选逐步向内进行传播，可能会引起分量信号失真。因此，对端点进行延拓显得尤为重要。鉴于相关向量机方法在对端点进行近似延拓时具有计算简单且计算端点极值点较接近近似点，通过相关向量机方法计算端点极值点，并服从最小二乘法(原函数为φ(x)，拟合函数γ(x)，使得$ \mathop \sum \limits_{i = 0}^n {\left[ {\varphi \left( x \right) - \gamma \left( x \right)} \right]^2}$的值最小)，通过计算端点处的函数值，可以把近似值作为端点极值点。

1.2 RVM算法的改进 1.2.1 RVM基本原理

相关向量机(relevance vector machine，RVM)是由Tipping于2000年提出的一种基于贝叶斯框架的核函数方法的概率学习模型，根据先验参数将不相关点进行移除，迭代过程中大部分参数的后验分布接近零，和预测值没有关联，非零参数所对应的点被称作相关向量。RVM在复杂系统拟合、图像处理、故障诊断和预测等领域具有广泛的应用价值。

设置训练样本集输入数据为{x_i, t_i}_i=1^N，因变量t_i相互独立且伴有高斯误差ε_i~N(0, σ²)。目标函数模型可以表示为t=y(x, w)+ε，相关向量机学习模型y(x, w)表示为$y\left( {x, w} \right) = \mathop \sum \limits_{i = 1}^N {w_i}K(x, {x_i}) + {w_0} $，其中w为权参数向量，K(x, x_i)为核函数，不需要满足Mercer定理条件的限制，训练样本数据集用N表示。学习相关向量机模型期间，似然边缘函数进行最大化算法是第Ⅱ类最大似然估计方法，故超参数向量α的边缘似然分布为p(t|α, σ²)=∫p(t|w, σ²)p(w|α)dw，其中超参数向量边缘似然服从p~N(0, R)，R=σ²E+ΦH^-1Φ^T。

最大化求解超参数向量边缘似然分布，通过设置迭代运算，计算超参数向量和高斯噪声误差，最后解得优化参数：

$ \alpha _i^{{\rm{opt}}} = \frac{{1 - {\alpha _i}{S_{i, i}}}}{{F_i^2}} $

(3)

$ {({\sigma ^2})^{{\rm{opt}}}} = \frac{{{{\left| {\left| {t - \mathit{\Phi }F} \right|} \right|}^2}}}{{N - \mathop \sum \limits_{i = 0}^N (1 - {\alpha _i}{S_{i, i}})}} $

(4)

式中，后验分布S的第i个权值对角元素为S_{i, i}，后验分布均值的期望值的第i个权参数为F_i，迭代更新得出超参数向量和误差向量。

因此，机器模型学习方法根据迭代公式进行不断更新，也需要及时更新后验分布均值和对应协方差，设定适量的迭代次数或者达到规定的收敛区间，迭代更新计算最后输出的结果。在目标函数训练结束之后，大部分超参数值趋于无穷大，对应权值为零，此时，删除基函数，小部分权值不为零的函数对应的向量被称为相关向量机^[9]。

1.2.2 RVM算法的改进

不同类型核函数具有各自特性，单一核函数已不能完整地反映函数数据的结构信息。通过采用多个核函数进行加权组合，其中局部核函数在非线性逼近状态上较强，全局核函数在泛化能力上有较好的表现，高斯核函数和多项式核函数分别在局部核函数与全局核函数应用广泛。根据两个不同类型核函数各自的优点进行加权组合，对映射的特征空间进行完善处理，可使模型预测精度效果有较大提高：

$ \begin{array}{l} K = \mu \exp \left( { - \frac{{||{x_i} - {x_j}|{|^2}}}{{{\psi ^2}}}} \right) + \\ \;\;\;\;\;\left( {1 - \mu } \right){\left[ {{x_i}{{\left( {\frac{{{x_j}}}{{{\chi ^2}}}} \right)}^{\rm{T}}} + 1} \right]^2} \end{array} $

(5)

式中，前部分为高斯核函数，μ、ψ为高斯核函数所占权重与核宽度；后部分为多项式核函数，χ为多项式核宽度，i、j为样本数据集输入向量，核函数参数为[μ, ψ, χ]。

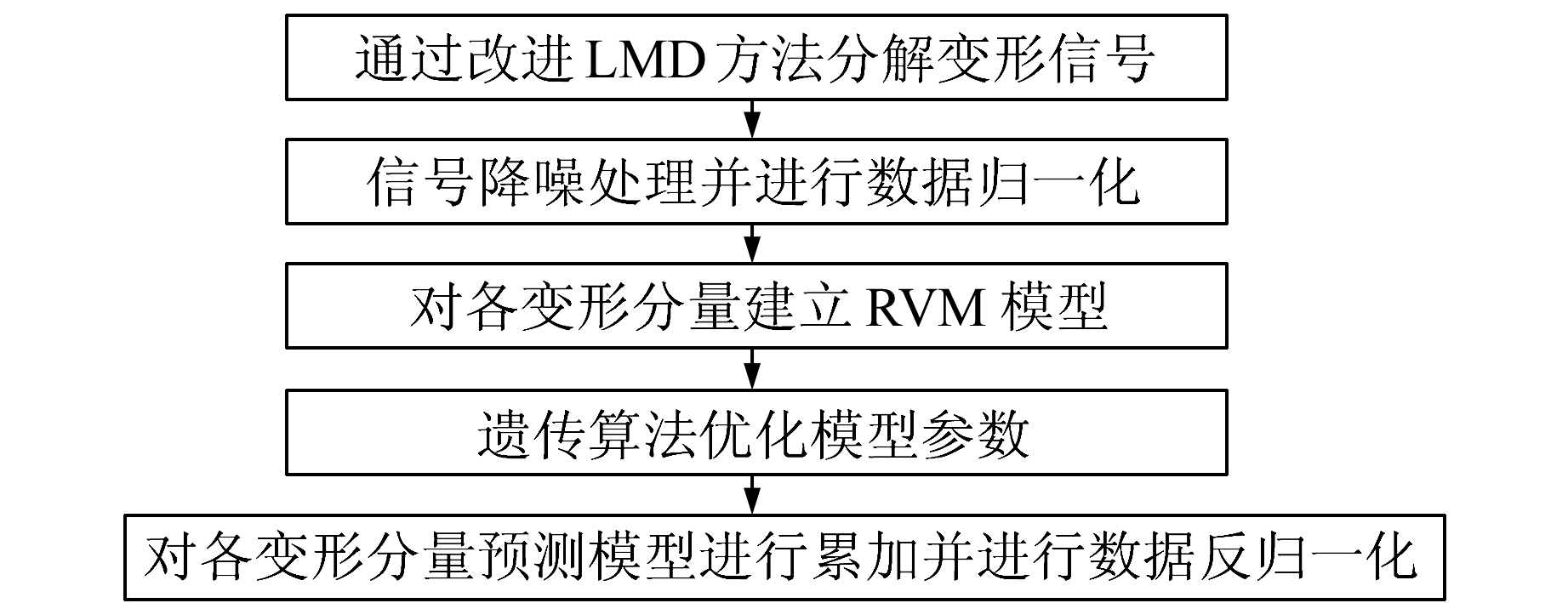
1.3 模型建立结构

通过对信号分解并建立模型，算法流程如图 1所示。

由图 1可知，变形信号通过改进LMD方法分解得到变形分量，进行信号降噪处理、数据归一化并建立RVM模型，利用遗传算法优化模型参数，最后对各变形分量预测模型进行累加并数据反归一化，得到变形预测模型。

2 基于改进LMD-RVM模型的大坝变形预测

本文实验数据为下库大坝监测数据。下库大坝的坝型属于重力碾压混凝土坝体。在大坝上布设正倒垂线，并布置3个监测点位，Y方向表示与大坝轴线垂直的方向，同时在坝体内安装18处电阻式温度计来测量坝体温度变化。对大坝的河床坝段坝顶的2^#观测点在2002-04-12~2004-06-25下库大坝时间(t/d)、水位(H/m)、温度(T/℃)和大坝位移量(Y)进行观测，数据通过Hermite插值法处理获取38期等时间间隔变形数据。根据近年来对大坝变形的研究，其影响因子是：时效分量取$\frac{t}{{100}} $、ln $ \frac{t}{{100}}$；水压因子取H、H²、H³；温度分量取sin(2πiT/365)、cos(2πiT/365)(其中i=1, 2)。

2.1 LMD处理大坝监测数据及小波阈值去噪

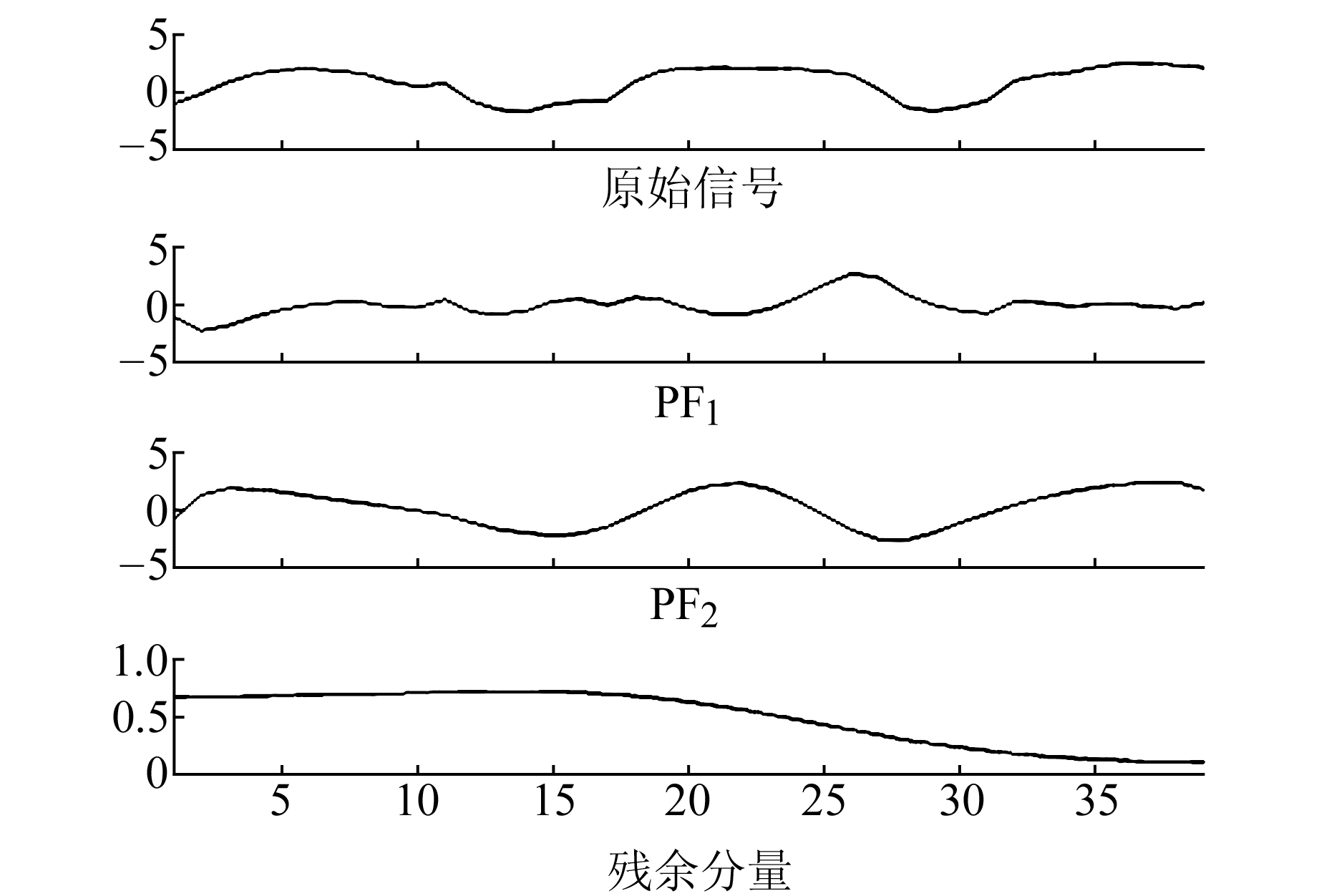
利用改进LMD分解38期大坝变形数据，获得PF₁、PF₂和残余分量3个变形分量(其中x(t)=PF₁+PF₂+PF₃), 如图 2所示。

由图 2可知，信号被分解为2个PF分量和1个残余分量。PF₁分量变化复杂、频率较高，可知主要受监测系统等因素影响；分量PF₂有比较明显的周期性变化，与温度分量变化有较大关系；残余分量主要受时效分量变化的影响，依照时间的推移，位移量趋势变化较单一^[10]。根据原始信号可知，分量PF₁和分量PF₂均含有高频成分，残余分量属于低频成分，一般认为噪声对低频成分影响很小^[11]，对挖掘信号的内部规律有进一步的提升。

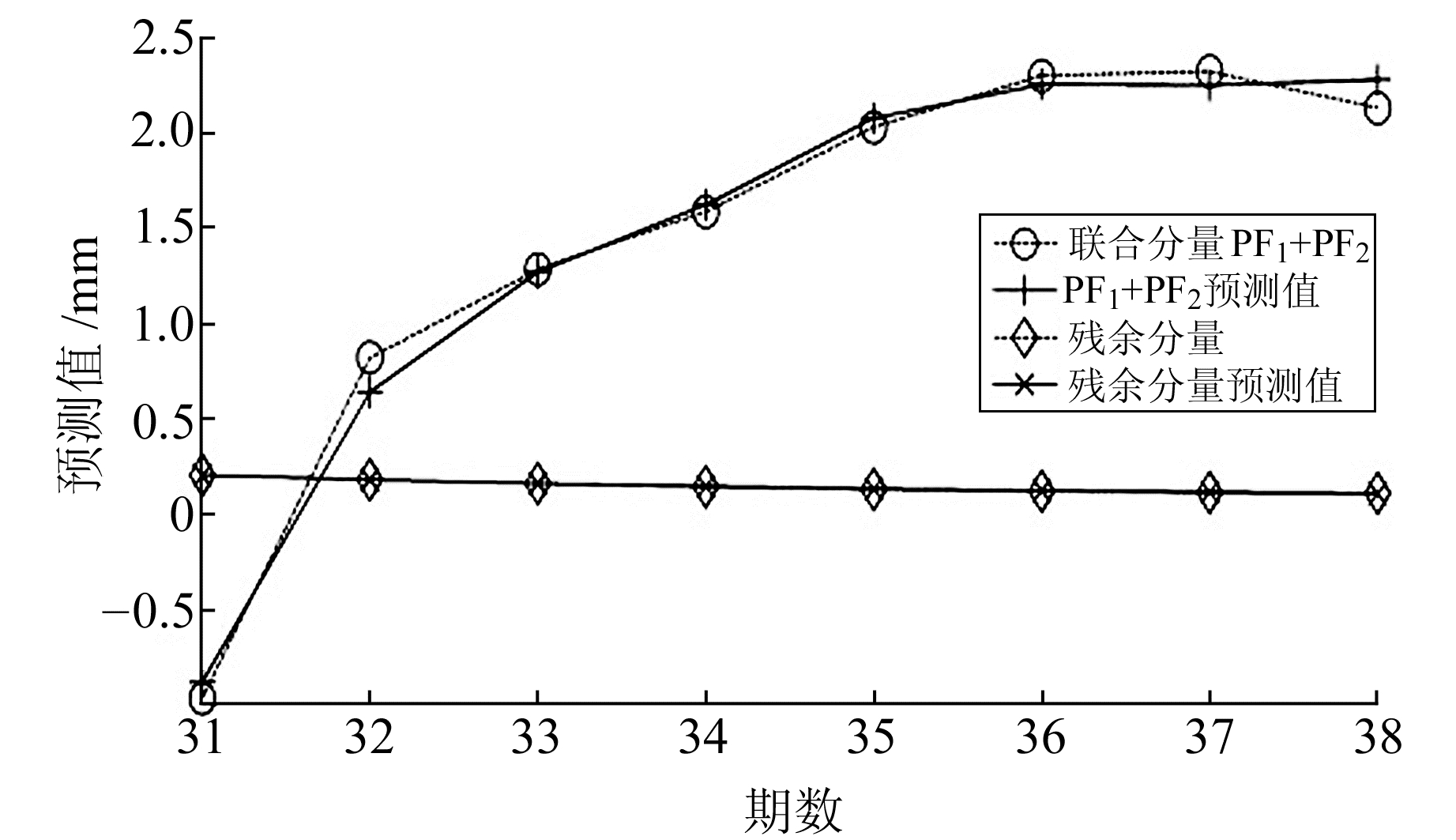
2.2 RVM模型预测结果

本文将前30期数据作为训练样本，分别建立RVM拟合模型，把31~38期数据作为模型的测试数据，用于评价模型的预测精度。本文是用遗传算法搜索最优参数，遗传算法参数设置原则及要求详见文献[12]，应用遗传算法优化训练模型参数运行到36代时算法收敛，将各变形分量预测模型叠加，最后得到大坝变形预测模型。各变形分量预测结果见图 3。

由图 3可知，残余分量呈现有规律的单调性，建立的模型预测精度较高，联合分量建立的模型少数预测精度一般，但整体预测效果较好，随着预测期数的增加预测精度较稳定，可知通过改进LMD方法分解的监测数据能有效处理复杂非平稳信号，RVM模型在处理小样本、贫信息问题时具有较大优势。

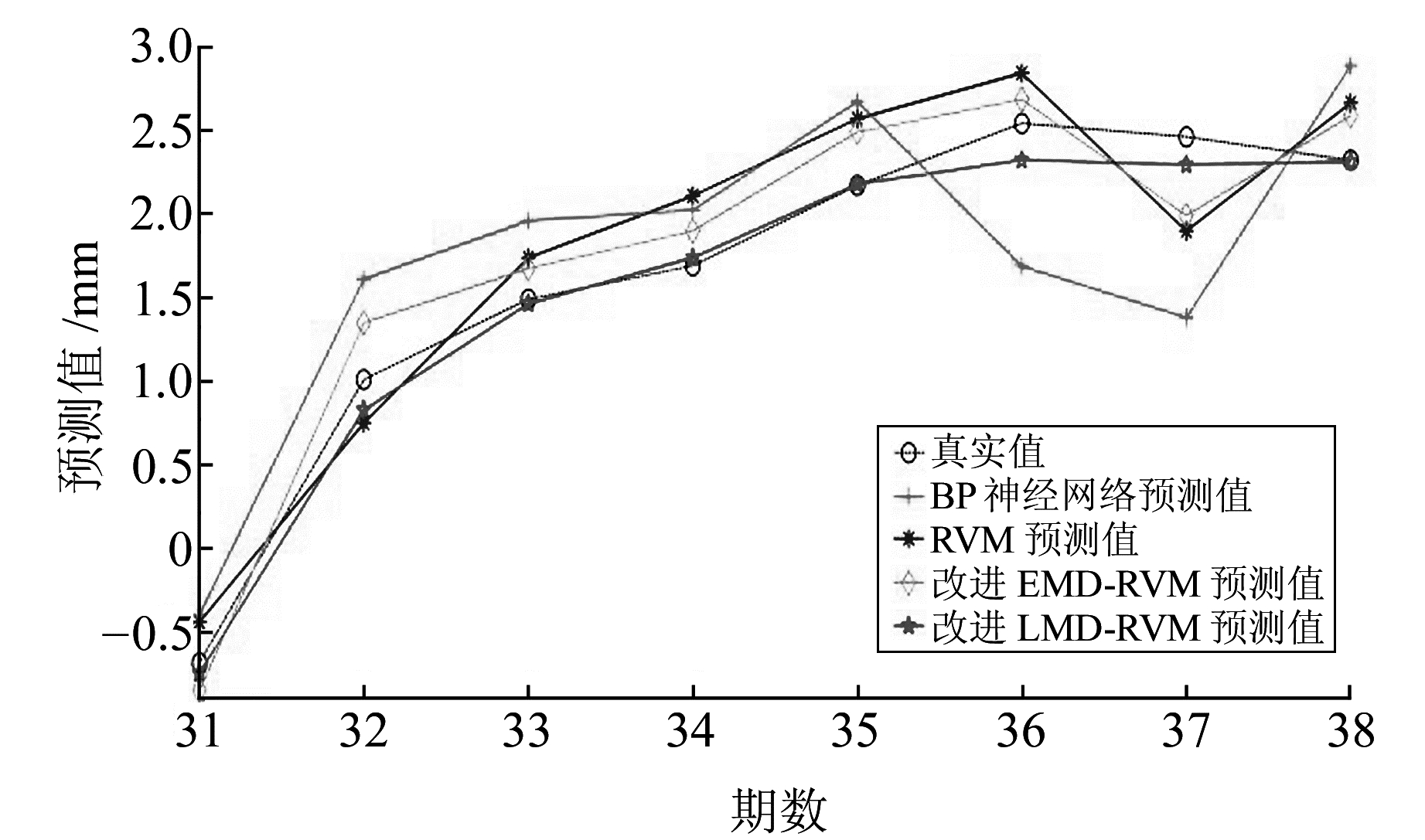
3 精度分析

通过实验可知，改进LMD-RVM方法在大坝变形预测方面具有较高的精度。为进一步证实该方法的预测效果，分别利用BP神经网络方法、RVM方法和改进EMD-RVM方法对其建立大坝变形预测模型，比较多种方法的预测效果，结果如图 4所示。

由图 4可知，BP神经网络方法预测结果还需改进，在处理小样本、贫信息方面存在不足之处；RVM方法预测能力存在一定的波动，有较大的改善空间；改进EMD-RVM方法在小样本预测方面具有一定优势，对预测效果有改善作用；改进LMD-RVM方法整体预测效果较好，在挖掘数据内部信息方面具有很大优势。

从图 5中可知，BP神经网络预测模型对多因素影响的复杂非线性难题的预测精度不理想，预测误差随着预测期数的增加而增大；RVM预测模型预测效果较平稳，但预测精度存在一定的限制；改进EMD-RVM预测模型预测精度有一定改善作用；改进LMD-RVM预测模型预测效果得到很大改善，随着预测期数的增加，预测精度不会出现太大波动。

为验证改进LMD-RVM方法的预测精度，将其预测结果与BP神经网络方法、RVM方法和改进EMD-RVM方法预测结果进行精度比较，采用平均相对误差、平均绝对误差及均方根误差精度评价指标，实验结果的精度指标见表 1。

由表 1可知，BP神经网络方法处理小样本、高度非线性问题有较多改进；RVM方法平均绝对误差和均方根误差得到较大改善，但平均相对误差仍较大，预测能力还有待提高；改进EMD-RVM方法多种精度指标值都有一定的改善；改进LMD-RVM方法预测结果与真实值的偏离很小，具有能更确切地反映预测准确度的优势，且多项精度指标值均小于其他预测方法，证实该方法在大坝变形预测上具有较好的预测精度。

4 结语

通过改进LMD方法分解大坝变形数据，建立RVM预测模型。通过实例结果与分析得出以下结论：

1) 通过改进LMD自适应分解非平稳信号获得多个具有一定物理特征的变形分量，能有效处理干扰因素对数据的影响，能适当减少模型结构的复杂程度且对挖掘数据内部规律有一定提升。

2) 建立RVM预测模型在处理小样本、贫信息及复杂非线性问题等方面具有很大优势，同时该方法求得的多项精度指标值均优于BP神经网络方法和RVM方法的预测结果，证实该方法具有较好的鲁棒性和较强的泛化能力，是一种预测精度较高的方法。