2. 中国地震局地球物理研究所,北京市民族大学南路5号,100081;
3. 中国地震局地震观测技术研究院,北京市民族大学南路5号,100081;
4. 中国地震局地震监测与减灾技术重点实验室,广州市先烈中路81号,510070
由于地震观测的需要,要求地震数据采集器具有很高的时间准确性和稳定性,并具有明确的系统特性,供地震记录数据使用者校正数据和恢复地动信号。
有些仪器生产商给出了其产品的时间准确性技术参数,例如北京港震仪器设备有限公司标称其EDAS-24GN数采在GPS同步状态下的系统时钟精度优于0.1 ms,在GPS信号缺失状态下的系统时钟漂移小于1 ms/d;而Reftek-130 s数采标称在GPS同步状态下的系统时钟精度为±10 μs,在GPS信号缺失状态下的系统时钟漂移在0~70 ℃、-20~0 ℃温度范围内分别为0.1×10-6、0.2×10-6。由于地震数据采集器作为商业产品并不提供内部时钟信号输出端口,用户直接测试其时钟精度是不可能的。美国SANDIA国家实验室(SNL)通过用地震数据采集器采集参考时钟源设备输出的分脉冲(PPM, pulse per minute)或时脉冲(PPH, pulse per hour)信号,然后分析记录数据的方法得出地震数采的相对时钟精度[1-3]。
地震计传递函数对地震记录数据的影响在学术界早就有深刻认识,地震计传递函数的测试方法和校正方法都有很全面、成熟的研究[4]。在地震数据采集器方面,由于其具有良好的系统特性,通常认为其对记录数据的影响与地震计的影响相比可以忽略,因此对地震数据采集器的测试和校正工作并不多见,SNL的测试报告[1-2]和技术报告[3]是目前作者查阅到的这方面最全面的工作。
目前国内对地震仪技术参数和性能的测试大多有成熟的规范[5],但对地震数据采集器时间服务精度的测试方法是不成熟的,无法测出优于ms级的时间误差。本文参考SNL的测试报告和技术报告,实现了对地震数据采集器时间服务精度的相对测试。由于用于测试的参考时钟方波串信号是时间确定的已知信号,作者进一步对记录数据与输入信号的频谱进行处理,实现了地震数据采集器的经验传递函数估计。作者利用相关测试方法实测了几个型号的地震数据采集器,结果发现,全国测震台网广泛使用的数据采集器之间可能存在对于时间精度要求高的研究来说不能接受的时间不一致性。
1 测试信号源特征Merchant和Hart[3]给出了SNL测试数采时间服务精度的具体方法要点。首先是按域值法识别时钟脉冲,并用适当的信号插值方法求取数采时间标识与参考点的时间差,以此作为该脉冲上升时刻的数采时间误差。Merchant和Hart[3]对所使用的PPM或PPH信号脉冲宽度没有作完全确定的要求,仅要求脉冲信号上升沿前后有足够长时间的有效低电平、高电平状态。根据Merchant和Hart[3]对信号插值算法的描述,他们要求的足够长时间是在40 sps(samples per second)采样率下上升沿前后各有至少5 s的有效低电平、高电平状态。
参考SNL的测试报告和技术报告[1-3],我们也采用PPM或PPH信号作为测试源信号。这是一种只有高、低电平两种状态的脉冲串信号,仅在整分或整小时时刻输出一个固定宽度的高电平脉冲,一般具有μs级的精度。IEEE发布的用于转换、脉冲及相关波形信号的测试标准[6]对此类信号的特征及检测方法、计算方法有详细描述,我们采用该测试标准来识别和处理时钟脉冲信号,此方法比Merchant和Hart[3]的波形上升沿域值搜索方法更具有普遍适应性。测试涉及的脉冲信号参数主要有状态电平、脉冲幅度、脉冲上升沿达到选定的参考点幅度时对应的时刻等。
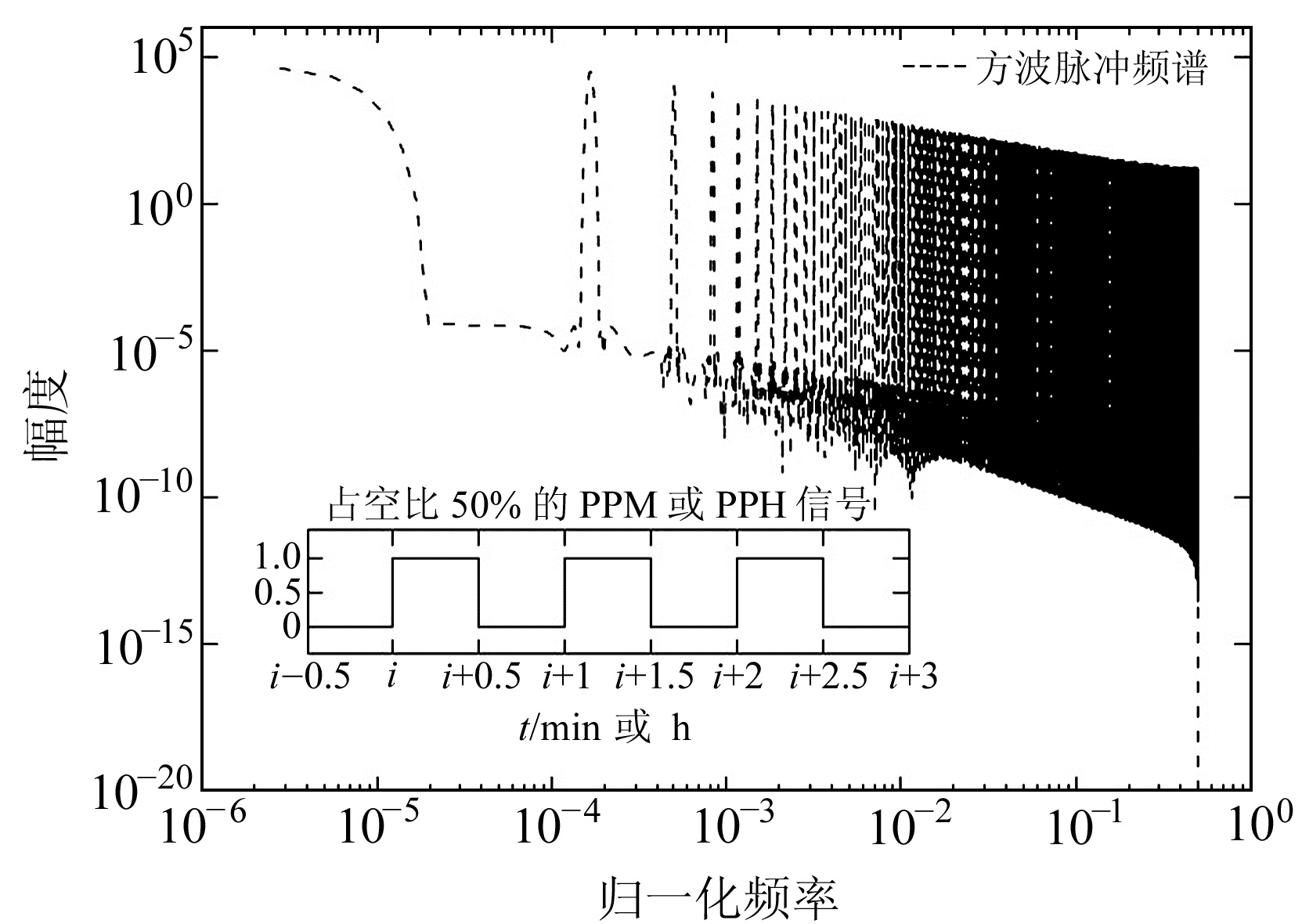
一般参考时钟源设备输出的PPM和PPH信号通常是宽度约为200~300 ms的窄脉冲,这对我们测试数据采集器的经验传递函数及时间精度是不够的,例如在我国台网常规使用的100 sps采样率下一个脉冲仅有20~30个采样点,10 sps下更是只有2~3个采样点,不足以按我们在后续章节描述的方法分析计算时钟脉冲参数。对于采样时间精度测试,须确保时钟脉冲的各态均有一定数量的采样点;而对于经验传递函数测试,需要知道确定的采集器输入信号,且该输入信号的能量应在采集器的整个观测频带有适当的分布,两种测试的具体方法将在后续章节详细描述。如果我们采用定制的参考时钟源设备,要求其输出的PPM和PPH信号均为占空比50%的方波串信号,则可能满足这两个方面的需求(PPH信号适用于低采样率下的测试)。图 1是占空比为50%的PPM或PPH信号及此种方波串信号的加窗频谱示意图。
|
图 1 占空比50%的PPM或PPH信号及其加窗频谱 Fig. 1 PPM or PPH signal with 50% duty cycle and its spectrum with taper applied |
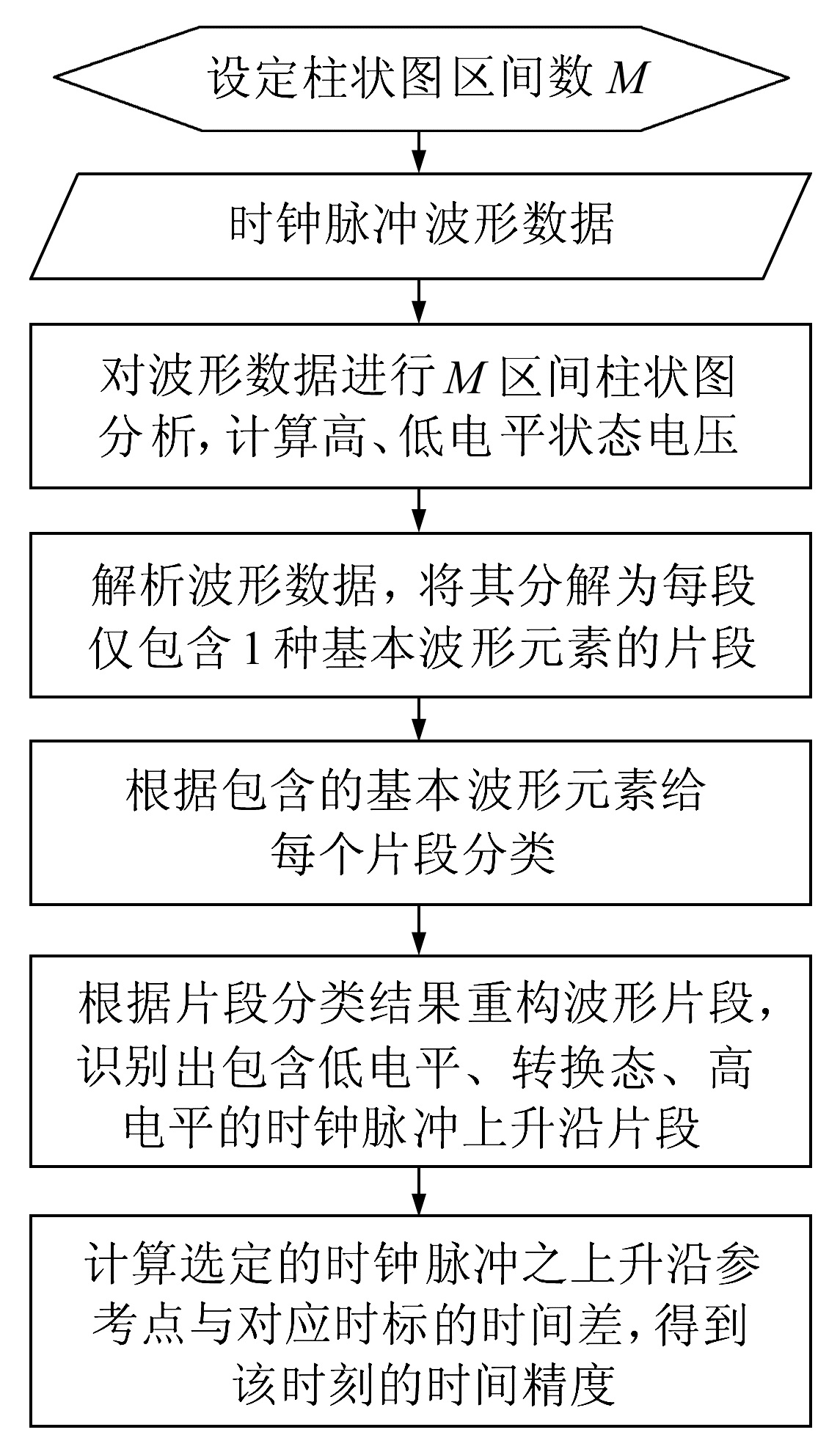
根据IEEE的测试方法[6],对记录的PPM或PPH信号进行识别并计算时钟脉冲对应时标的时间精度可归纳为图 2所示的流程。时钟脉冲识别的基本处理是作柱状图分析。柱状图是表达信号的幅度密度或出现频次的方式,柱状图区间数量M值的选取通常基于观测、实践或其他有意义的量[7]。时钟脉冲波形的基本元素包括某个基本水平(高/低电平)状态、转换状态、瞬态和端点态。根据柱状图分析结果计算各态电压平均值,分析信号状态的转换及达到稳定状态等多项参数需要为各状态设定抖动界限,各状态抖动界限的作用与Merchant和Hart[3]设置的波形上升沿电平域值有些相似。
|
图 2 时钟脉冲识别与时间精度计算流程 Fig. 2 Timing pulse identification and time tag accuracy calculation flow |
用参考时钟源的时钟脉冲检测采集器时间服务精度,即是要计算采集器给记录数据留下的时间标签相对时钟脉冲上升沿的时间差。由于采集器的采样率有限,时钟脉冲信号在经过相应采样率数字抽取滤波采样后,上升沿在采样数据点间的实际变化不是线性的。想要得到满足需要的时间精度结果,就要应用数字信号处理技术恢复时钟脉冲信号在对应带宽下的实际变化过程,这可以通过适当的信号内插算法实现。Merchant和Hart[3]介绍了通过时域和频域两种插值算法实现预期的10 μs级的数采时间误差估计。本文采用的信号内插算法是在频率域补零的方法[8]。使用信号内插提升采样率16倍后,我们认为信号在相邻采样点间的变化近似线性,可以在升采样后的相邻数据点间线性插值计算时间误差。
计算数据时间标签在时钟脉冲上升沿的时间误差需要指定一个参考点。在IEEE的测试标准[6]中有几个建议的幅度参考点,0%和100%幅度处主要用于建立脉冲波形的四边形参考波形,而50%电平这个参考点恰好与线性相位滤波器对阶跃信号滤波产生的延迟一致。图 3是用一个16抽头线性相位滤波器对阶跃信号作滤波结果阶跃起始位置的放大显示,按理论计算的滤波延迟[9]为(N-1)/2=7.5,取整得到7,也就是图中输出阶跃信号上升至阶跃幅度50%电平的位置。现代地震数据采集器的初始信号采集都具有较高的采样率,可通过适当抽取滤波器降低采样率得到最终的输出数据,因此最终的数据需要针对所作抽取滤波进行时间延迟校正。地震数据采集器通常具有线性相位抽取滤波器和最小相位抽取滤波器。最小相位滤波器产生的延迟与信号频率有关,而且没有普适的理论计算式。地震数据采集器的时间精度除与硬件电路有关外,也与数字抽取滤波器的延迟有关,最终输出数据的时间需要同时对硬件和数字抽取滤波器的延迟作校正。硬件的延迟和线性相位滤波器的延迟可以较准确地确定,但最小相位滤波器的延迟不好确定。因此选择具有确定性的线性相位滤波器的延迟位置作为计算时间误差的参考点是合适的,即时钟脉冲上升沿50%电平的位置。

|
图 3 线性相位滤波器阶跃响应实验 Fig. 3 An experimental step response of linear phase filter |
数采时间服务的稳定性包含两个方面,一个是在与参考时间源GPS同步状态下的稳定性,另一个是在GPS缺失状态下的稳定性。因此需要分别在GPS同步状态下和GPS缺失状态下连续测试数采在每个参考时钟脉冲上升沿的时间服务精度,以评估数采在两种不同状态下的时间服务稳定性。
3 经验传递函数测试方法前文所述用于测试数据采集器的时钟方波信号为占空比50%的PPM或PPH信号,因此在数据采集器时间系统与标准时间系统同步的情况下,这个输入信号是已知的。如果记输入的PPM或PPH信号频谱为U(ω),数据采集器记录的数据频谱为Y(ω),用记录数据的频谱与已知的输入信号频谱相除就得到了数据采集器的经验传递函数:
针对经验传递函数的估计可以采取一种加权的谱平滑算法[10]。具体方法是选取一个较窄的窗口函数Wγ(ξ),对输入、输出的自谱、互谱进行褶积处理:
| $ \tilde G({{\rm{e}}^{i{\omega _0}}}) = \frac{{\int_{ - \pi }^\pi {{W_\gamma }(\xi - {\omega _0})Y\left( \xi \right){U^*}\left( \xi \right){\rm{d}}\xi } }}{{\int_{ - \pi }^\pi {{W_\gamma }(\xi - {\omega _0}){{\left| {U\left( \xi \right)} \right|}^2}{\rm{d}}\xi } }} $ | (1) |
式中,U*(ξ)为U(ξ)的复共轭。分别记上式的分子、分母为
| $ {{\mathit{\hat \Phi }}_{yu}}\left( {{\omega _0}} \right) = \frac{1}{N}\sum\limits_{t = 1}^N {{w_\gamma }\left( t \right){c_{yu}}\left( t \right){{\rm{e}}^{ - j{\omega _0}t}}} $ | (2) |
| $ {{\mathit{\hat \Phi }}_{uu}}\left( {{\omega _0}} \right) = \frac{1}{N}\sum\limits_{t = 1}^N {{w_\gamma }\left( t \right){c_{uu}}\left( t \right){{\rm{e}}^{ - j{\omega _0}t}}} $ | (3) |
最后代入式(1)得到我们要的经验传递函数估计。
由于数采的最终输出数据经过滤波抽取,数据的时间延迟除数字滤波器的延迟外还存在抽取的延迟,但数字滤波器的延迟在数采记录数据时已作补偿,即该延迟的相位校正已包含在Y(ω)中,因此用式(1)得到的经验传递函数估计还需要对抽取产生的延迟进行相位校正。若抽取基数为D,即每D个输入数据产生1个输出数据,在此假设抽取的结果为D个输入数据的均值及样点时间在D个输入数据的中间是合理的。因此本文对抽取产生延迟的相位校正是-T/2,T为最终输出数据的采样时间间隔,即最终的经验传递函数估计是:
| $ \hat G({{\rm{e}}^{i{\omega _0}}}) = \frac{{{{\mathit{\hat \Phi }}_{yu}}\left( {{\omega _0}} \right)}}{{{{\mathit{\hat \Phi }}_{uu}}\left( {{\omega _0}} \right)}}{{\rm{e}}^{j{\omega _0}T/2}} $ | (4) |
作者用占空比为50%的参考时钟分脉冲信号测试了几种型号的地震数据采集器,包括它们在线性相位、最小相位滤波工作状态下的时间精度稳定性及经验传递函数。由于我国测震台网工作中的台站设备要求统一设置数采采样率为100 sps,我们在对这些数采测试时也使用100 sps的采样率。我们在文章前面已提到,参考时钟设备输出的PPM、PPH脉冲一般具有μs级精度,因此这里的测试结果多数只保留到μs值。
4.1 数采A在GPS同步状态下的时间精度稳定性该型号数采内部保存有约15 min间隔的工作时钟状态日志记录,刚好可以用来与实测时间精度作比较。我们对该数采的线性相位、最小相位滤波工作状态均作了不少于10 h的GPS同步时间精度测试。
图 4是数采A的测试结果,其中图 4(a)给出线性相位滤波工作状态测试中的单个分脉冲的详细结果,包含此段测试记录数据的起始时间、该记录波形为此段测试记录数据中的第几个分脉冲上升沿、该上升沿前后部分采样点值及升采样插值后的波形、四边形脉冲参考波形、该上升沿对应的分钟时标及时标相对该上升沿50%幅度水平处的时间差。图 4(b)给出最小相位滤波工作状态测试中的单个分脉冲的详细结果。图 4(c)是线性相位滤波工作状态的稳定性测试结果,是此段测试时间内全部分钟时标相对上升沿50%幅度的时间差变化图(底部横坐标和左侧纵坐标),并与数采日志中的时间误差数据(顶部横坐标和右侧纵坐标)进行比较,左右侧纵坐标的比例尺是一样的,使两种数据可以进行比较。图中也包含此段测试记录数据的起始时间、可识别分脉冲上升沿数及整段时间测试结果的3个统计结果:时标相对上升沿50%幅度的时间差平均值、对时间差平均值的最大偏差和标准偏差。图 4(d)则是最小相位滤波工作状态的稳定性测试结果。图 4(c)和4(d)均显示,将本文方法得到的测试结果与数采内部日志记录的时间误差相比较,时间差的相对变化值完全一致。图 4(a)和图 4(b)显示,数采A对数据的延迟时间校正不论是线性相位还是最小相位滤波均与本文的参考点选择不同。

|
图 4 数采A时间精度测试结果 Fig. 4 Time tag accuracy results of digitizer A |
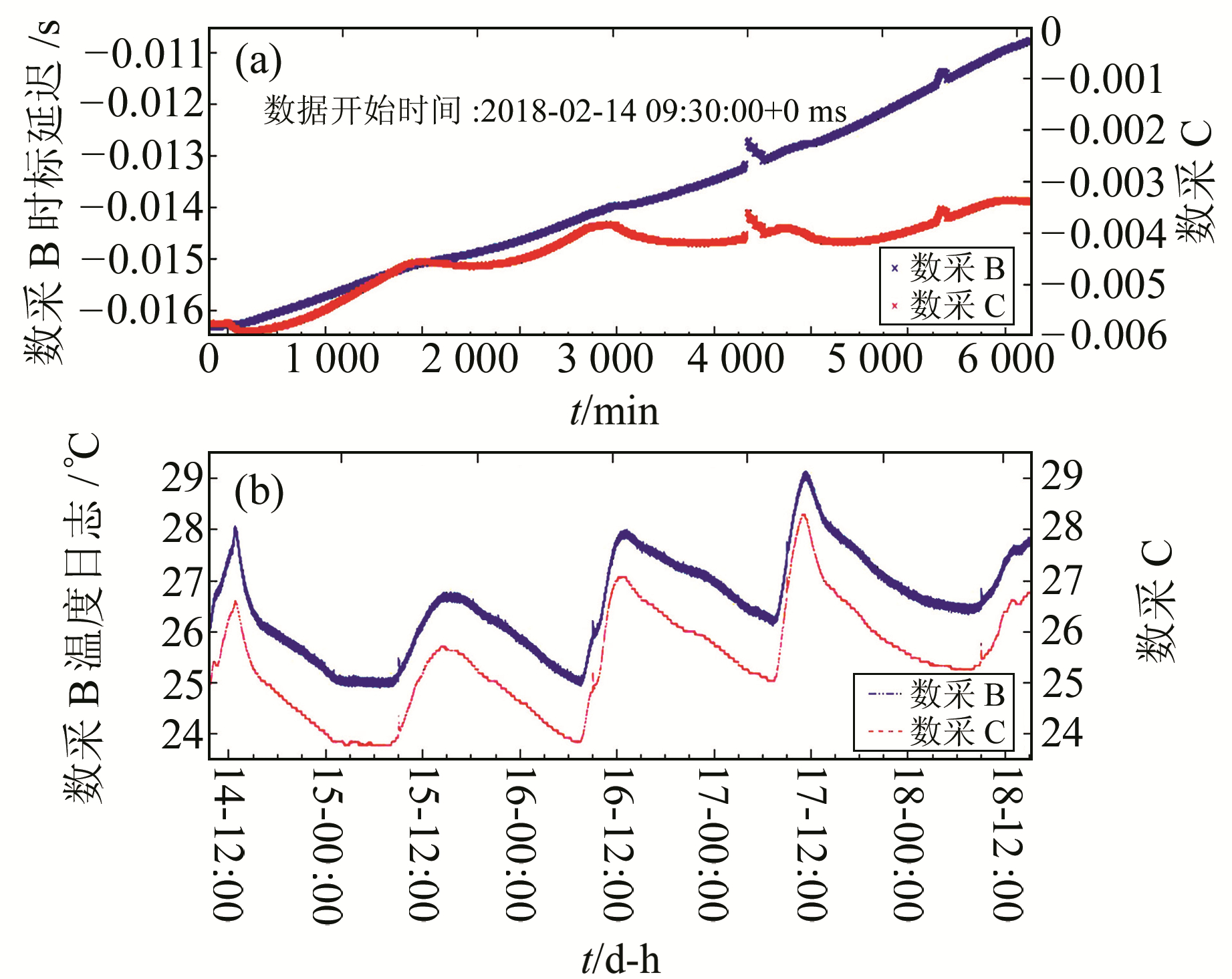
测试的数采B和C是同一型号不同生产批次的两台数采,有机箱内部温度监测信息。我们测试该型号数采的守时稳定性,并尝试了解其是否与环境温度变化有关。测试守时前先给数采接上GPS天线,待数采时间同步达到稳定状态后断开GPS天线,连续守时记录超过100 h。图 5(a)给出测试起始时间和两台数采工作的守时精度变化情况,图 5(b)则是相应时间段的数采机箱内部温度变化情况。两台数采机箱内温度数值有1 ℃的差别,但变化情况是一致的。从图 5看到,数采守时误差的变化趋势在中午气温接近最高时有较明显变化,但与温度的变化不完全一致,说明数采守时误差的变化存在非线性并可能与环境条件有一定关系,而且不同数采即使型号相同其守时变化的非线性也可以有明显的差别。
|
图 5 数采守时情况测试结果 Fig. 5 Time tag stability of digitizer without timing synchronization |
数采D测试时已连接GPS天线并同步达到稳定状态。我们测试了数采D的线性相位及最小相位两种工作状态,将测试结果与用厂家提供的滤波器系数、延迟时间校正参数计算的理论频率特性进行比较,理论频率特性用IRIS(incorporated research institutions for seismology)发布的evalresp-3.3.3程序计算。
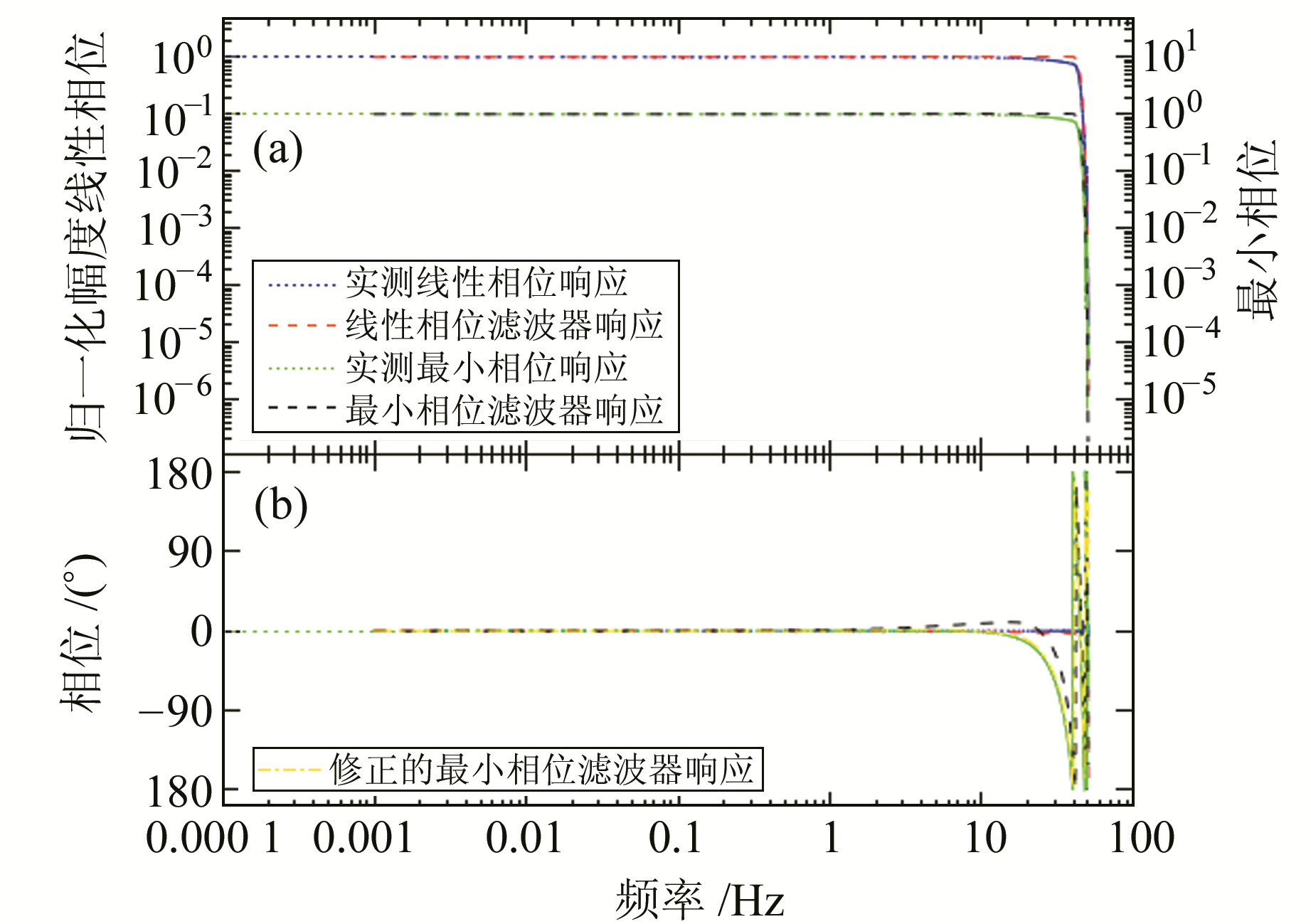
在测试数采A时发现,即使是在同步状态下数采的时间精度也是有抖动变化的,数采D也一样,时间抖动变化保持在μs量级。图 6是用该时段数据计算的经验传递函数频率特性及用于对比的理论特性。图 6显示,不论是在线性相位还是最小相位工作状态下,在频率高于10 Hz后实测的数采响应幅度均略低于用滤波器系数、延迟时间校正参数计算的理论响应,实测的相位特性线性相位响应与理论响应基本一致,而实测的最小相位响应与理论响应比较有明显的延迟。
|
图 6 数采D经验传递函数测试结果与计算的滤波器响应 Fig. 6 Estimated empirical transfer function of digitizer D, compared with calculated filter response |
从数采A的测试结果看出,采用本文方法测试的时间服务精度结果是相对的,数值与参考点的选取有关;而持续时钟脉冲串测试结果的连续变化值是可靠的,与数采自身的时钟误差日志一致。由于本文计算时间误差的过程基于柱状图分析时钟脉冲的高低电平,此过程的结果依柱状图区间的选取存在一些不确定性,但在柱状图区间选取确定下来后,脉冲分析的结果是确定的[7],这也是用本文方法测试持续时钟脉冲串结果连续变化值一致性、可靠性的保证。由于该方法依赖于参考点选取的相对性和柱状图区间选取带来的不确定性,测试结果时间误差的数值可能出现数10 μs甚至100 μs的不同,这点与Merchant和Hart[3]的方法相同。因此,受限于数采用户接口不能直接测试数采的硬件时钟电路,通过采集时钟脉冲的方法测试数采时间服务精度的结果不能从时间误差的数值判断一台数采的时间精确程度,但可以用系统时钟同步状态下的时间稳定性及同步失效状态下的守时能力对数采进行评价。
尽管地震数据采集器通常使用了高精度高稳定性的压控晶振以保证其时间系统的准确性,但本文对数采B和C的测试结果显示,当数采时钟系统与参考时间系统失去同步后,数采的守时误差不是线性变化的,还可能受环境因素(例如温度)的影响。而且不同数采间即使型号相同其守时能力也可能有很大不同(特别是在生产批次不同的情况下)。因此对于时间精度要求不同的应用情况,如果不能保证数采持续工作在与参考时间系统同步的状态下,记录数据的时间校正会有很大的困难。型号相同、生产批次也相同的数采是否会有好一些的守时一致性,这需要我们用更多的实验数据来评估。研究人员在缺乏PPM或PPH信号时,当然也可以在特定项目实施前对多套数采接统一的信号源(例如正弦波)进行比测,先同步数采时钟至稳定,后断开时钟源适当时间,评估数采间守时工作的一致性。
从数采D的测试结果中我们得到清晰的经验传递函数,并发现两个现象:
1) 实测的数采响应幅度在频率高于10 Hz后略低于用滤波器系数计算的理论响应,这有可能是系统在AD转换前的模拟电路的影响;而低通滤波拐点频率实测结果与理论计算结果一致。
2) 线性相位滤波器经验传递函数的实测结果显示,相位特性与厂家提供的系数及延迟校正数据的理论计算结果符合得较好,而最小相位滤波器经验传递函数的实测结果相位特性与相应的理论计算结果相比还有一些延迟。我们用evalresp-3.3.3程序再计算少校正2.54 ms的理论响应,将计算结果与原理论响应及实测响应的相位特性绘在一起,结果显示,修正的理论响应与实测的响应相符(图 6(b))。由此我们推测,可能是该数采对最小相位滤波的实际时间校正比厂家提供的校正量少了约2.54 ms。也就是说,我们实测评估的经验传递函数结果是符合实际的。
由于方法本身内在的不确定性,不能直接从测试结果的数值判断数采时间在数10 μs甚至100 μs的精确度,但在柱状图分析参数确定下来后,测试的结果是具有可比性的,包括数采时间精度的长期稳定性、守时稳定性、相对误差参考点的位置等。从本文测试的3种型号数采看,不同的数采再加上不同的抽取滤波方法,相互间的时间同步差别由于时间延迟校正参考点选取的不同可能达到ms甚至10 ms级别,在我们测试的采样率下就是1个采样点左右的差别。我们测试的数采包括在全国测震台网中有大量使用的型号,这样的时间差虽然对日常地震台网定位及速报影响不大,但对于时间一致性要求高的研究来说可能是不能接受的,例如地下细结构(包括走时和波形的反演、主动源探测)及震源破裂的研究。因此,时间一致性要求高的研究宜选择同型号数采、同抽取滤波方式的记录。确实不能选择完全同型号数采时可尝试在项目实施前对数采作时间同步状态下的一致性测试,可采取前面简介的守时一致性测试方法,为后续的项目数据处理提供时间一致性校正参考。
从数采D的经验传递函数测试结果可以看出,时间校正参考点的选取影响数采时间的一致性和实测的相位响应,如果数采生产商不提供时间校正参数或者提供的校正参数与实际不一致,对数字地震记录进行数采传递函数校正则可能产生震相相位异常。
致谢 感谢数采B厂家技术人员提供数采内部温度监测数据下载程序。
| [1] |
Kromer R P.Evaluation of the Kinemetrics/Quanterra Q330HR Remote Seismic System For IRIS/GSN[R]. Ground-Based Monitoring R and E Technology Report, 2006
(  0) 0) |
| [2] |
Kromer R P. Evaluation of the Refraction Technology RT130HR Remote Seismic System for IRIS/GSN[R]. Ground-Based Monitoring R and E Technology Report, 2006
(  0) 0) |
| [3] |
Merchant B J, Hart D M. Component Evaluation Testing and Analysis Algorithms[J]. Algorithms, 2011
(  0) 0) |
| [4] |
王广福. 地震观测系统的标定与检查[M]. 北京: 地震出版社, 1986 (Wang Guangfu. Calibration and Verification of Seismograph Systems[M]. Beijing: Seismological Press, 1986)
(  0) 0) |
| [5] |
中国地震局.测震台网专业设备入网管理办法(试行)──测震台网专业设备入网检测规程[S].2017 (China Earthquake Administration. Trial Regulations for Management of Instrument in Seismograph Network-Measurement Specification for Instrument of Seismograph Network[S]. 2017)
(  0) 0) |
| [6] |
IEEE Standard on Transitions, Pulses, and Related Waveforms[S].IEEE Std, 2011
(  0) 0) |
| [7] |
Solomon O M, Larson D R, Paulter N G. Comparison of Some Algorithms to Estimate the Low and High State Level of Pulses[C].IEEE Instrumentation and Measurement Technology Conference, Budapest, Hungary, 2001
(  0) 0) |
| [8] |
Stearns S D, David R A. Signal Processing Algorithms[M]. Prentice-Hall Inc, 1988
(  0) 0) |
| [9] |
Ifeachor E C, Jervis B W. 数字信号处理实践方法[M]. 第二版. 北京: 电子工业出版社, 2004 (Ifeachor E C, Jervis B W. Digital Signal Processing: A Practical Approach[M]. Second Edition. Beijing: Publishing House of Electronics Industry, 2004)
(  0) 0) |
| [10] |
Ljung L. System Identification Theory for the User(Second Edition)[M].Prentice Hall, 1999
(  0) 0) |
| [11] |
Jenkins G M, Watts D G. Spectral Analysis and Its Applications[M]. Holden-Day, San Francisco, 1968
(  0) 0) |
2. Institute of Geophysics, CEA, 5 South-Minzudaxue Road, Beijing 100081, China;
3. E-Institute of Earthquake Observation Technology, CEA, 5 South-Minzudaxue Road, Beijing 100081, China;
4. Key Laboratory of Earthquake Monitoring and Disaster Mitigation Technology of CEA, 81 Mid-Xianlie Road, Guangzhou 510070, China
 2018, Vol. 38
2018, Vol. 38

