2. 地理信息工程国家重点实验室,西安市雁塔路中段1号,710054;
3. 西安测绘研究所,西安市雁塔路中段1号,710054
目前,航空标量重力测量已成为获取地面重力测量难以到达地区的中短波地球重力场信息的主要手段[1-2]。根据比力测量系统的不同,航空标量重力测量系统一般分为平台式系统和捷联式系统,平台式系统已得到广泛应用,在不同的测量区域对于5 km的半波长分辨率精度可达1~5 mGal[1-4];捷联式系统较平台式系统具有体积小、重量轻、功耗低等优点,成为近年来重力仪领域的研究热点[5-8]。加拿大卡尔加里大学于20世纪90年代初率先开展了基于GNSS/SINS组合的重力标量测量(SISG)研究,文献[7]给出的SISG实验精度对于7 km半波长分辨率为2 mGal;文献[8]将其与平台式重力测量系统进行了比较,表明两者的一致性在移除线性偏差后为2~3 mGal。我国于2008年底研制出捷联式重力仪原理样机SGA-WZ01,基于该样机的实验数据开展了重力扰动估算方法的研究和验证[2, 5]。上述捷联式重力扰动估算大多采用类似于平台式的SISG算法,也有文献利用GNSS/SINS组合的15状态卡尔曼滤波方法估算重力扰动[3-4]。传统方法是以GNSS/SINS的位置、速度作为量测方程的观测量,估计惯性器件的误差并修正当地水平坐标系下的比力,利用直接求差法估算重力扰动矢量,其整个计算过程都在当地水平坐标系下进行;另一种新方法是将GNSS/SINS的加速度之差作为观测量,通过组合卡尔曼滤波估计惯性器件的误差,修正惯性坐标系下的比力。将重力扰动看成是随机误差的主要部分,从平差获得的残差中提取,整个计算过程都是在惯性坐标系下进行,相比传统方法模型简捷且精度相当。
1 数学模型 1.1 当地水平坐标系下重力扰动估计的数学模型及卡尔曼滤波算法 1.1.1 重力扰动估计的数学模型GNSS/SINS组合航空重力测量的基本原理是:从加速计测得的比力中扣除因载体运动等因素产生的扰动加速度,即可得到重力。其基本表达式为[9]:
| $ {\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{g}}^{\rm{n}}} = {{\mathit{\boldsymbol{\dot v}}}^{\rm{n}}} - \mathit{\boldsymbol{C}}_{\rm{b}}^{\rm{n}}{\mathit{\boldsymbol{f}}^{\rm{b}}} + \left( {2\mathit{\boldsymbol{\omega }}_{{\rm{ie}}}^{\rm{n}} + \mathit{\boldsymbol{\omega }}_{{\rm{en}}}^{\rm{n}}} \right){\mathit{\boldsymbol{v}}^{\rm{n}}} - {\mathit{\boldsymbol{\gamma }}^{\rm{n}}} $ | (1) |
式中,上角标n、b分别代表当地水平坐标系和载体坐标系;δgn为所求的重力扰动;vn、
为抑制惯性器件的误差随时间积累,提高重力扰动的估算精度,可利用基于位置、速度更新的卡尔曼滤波方法动态估计SINS的误差并及时修正。15状态参数包括SINS的位置、速度、姿态角误差以及陀螺漂移和加速计偏差,记为X1=[δr, δv, Ψ, bg, ba]T,其误差模型为[3-4]:
| $ {\rm{ \mathsf{ δ} }}\dot r = {\rm{ \mathsf{ δ} }}v $ | (2) |
| $ \begin{array}{*{20}{c}} {{\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{\dot v}} = \left[ {{\mathit{\boldsymbol{f}}^{\rm{n}}} \times } \right]\mathit{\boldsymbol{ \boldsymbol{\varPsi} }} + \mathit{\boldsymbol{C}}_{\rm{b}}^{\rm{n}}{\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{f}}^{\rm{b}}} - \left( {2\mathit{\boldsymbol{\omega }}_{{\rm{ie}}}^{\rm{n}} + \mathit{\boldsymbol{\omega }}_{{\rm{en}}}^{\rm{n}}} \right){\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{v}} - }\\ {\left( {2{\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{\omega }}_{{\rm{ie}}}^{\rm{n}} + {\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{\omega }}_{{\rm{en}}}^{\rm{n}}} \right) \times \mathit{\boldsymbol{v}} - {\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{g}}^{\rm{n}}}} \end{array} $ | (3) |
| $ \mathit{\boldsymbol{ \boldsymbol{\dot \varPsi} }} = - \mathit{\boldsymbol{\omega }}_{{\rm{in}}}^{\rm{n}} \times \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} + {\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{\omega }}_{{\rm{in}}}^{\rm{n}} - \mathit{\boldsymbol{C}}_{\rm{b}}^{\rm{n}}{\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{\omega }}_{{\rm{ib}}}^{\rm{b}} $ | (4) |
| $ {{\mathit{\boldsymbol{\dot b}}}_g} = 0 $ | (5) |
| $ {{\mathit{\boldsymbol{\dot b}}}_a} = 0 $ | (6) |
用式(2)~(6)构建卡尔曼滤波连续状态方程如下:
| $ {{\mathit{\boldsymbol{\dot X}}}_1} = {\mathit{\boldsymbol{F}}_1}{\mathit{\boldsymbol{X}}_1} + {\mathit{\boldsymbol{G}}_1}{\mathit{\boldsymbol{w}}_1} $ | (7) |
式中,F1、G1、w1依次为状态转换矩阵、噪声系数阵和过程白噪声向量,其中各矩阵元素可参考文献[2]。
以GNSS和SINS的位置、速度之差作为观测量,则卡尔曼滤波量测方程为[10]:
| $ {\mathit{\boldsymbol{Y}}_1} = {\mathit{\boldsymbol{H}}_1}{\mathit{\boldsymbol{X}}_1} + {\mathit{\boldsymbol{e}}_1} $ | (8) |
式中,观测量Y1=[rGNSSn- rSINSn vGNSSn- vGNSSn]T,H1为系数阵,e1为观测量白噪声。
1.2 惯性坐标系下卡尔曼滤波算法及重力扰动估计的数学模型 1.2.1 基于加速度更新的卡尔曼滤波算法由式(9)可知[11],惯性坐标系下加速计测量误差δai来源于两方面:一是加速度计测量误差δab引起的比力观测误差Cbiδab;二是姿态误差和比力耦合引起的误差项
| $ {\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{a}}^{\rm{i}}} = \mathit{\boldsymbol{C}}_{\rm{b}}^{\rm{i}}{\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{a}}^{\rm{b}}} + {{\mathit{\boldsymbol{\tilde a}}}^{\rm{i}}} \times {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^{\rm{i}}} $ | (9) |
| $ {{\mathit{\boldsymbol{ \boldsymbol{\dot \varPsi} }}}^{\rm{i}}} = - \mathit{\boldsymbol{C}}_{\rm{b}}^{\rm{i}}{\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{\omega }}_{{\rm{ib}}}^{\rm{b}} $ | (10) |
式中,上角标i表示惯性坐标系,Cbi为b系到i系的转换矩阵,Ψi为定向误差。
若式(9)、(10)中陀螺和加速度计的观测误差仅考虑零偏、刻度因子误差以及观测噪声,则针对SINS误差构建的卡尔曼滤波动态方程为[11-13]:
| $ \mathit{\boldsymbol{\dot s}} = {\mathit{\boldsymbol{F}}_2}\mathit{\boldsymbol{s}} + {\mathit{\boldsymbol{G}}_2}{\mathit{\boldsymbol{w}}_2} $ | (11) |
式中,F2为状态转换矩阵,G2为噪声系数阵,w2为噪声向量, 具体形式可参考文献[11]。
以GNSS/SINS的加速度之差作为观测量,则卡尔曼滤波的量测方程为[11]:
| $ \mathit{\boldsymbol{y}} + {\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{g}}^{\rm{i}}} = {\mathit{\boldsymbol{H}}_2}\mathit{\boldsymbol{s + }}{\mathit{\boldsymbol{e}}_2} $ | (12) |
式中,y为观测量,δgi为重力扰动,H2为量测方程的系数矩阵,e2为观测噪声向量,即
| $ {\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{g}}^{\rm{i}}} = {\mathit{\boldsymbol{g}}^{\rm{i}}} - {{\mathit{\boldsymbol{\bar \gamma }}}^{\rm{i}}} $ | (13) |
| $ {\mathit{\boldsymbol{H}}_2} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{C}}_{\rm{b}}^{\rm{i}}}&0&{\mathit{\boldsymbol{C}}_{\rm{b}}^{\rm{i}}{\rm{diag}}\left( {{{\mathit{\boldsymbol{\tilde a}}}^{\rm{b}}}} \right)}&0&{\left[ {{{\mathit{\boldsymbol{\tilde a}}}^{\rm{i}}} \times } \right]} \end{array}} \right] $ | (14) |
其中,gi、
用式(11)和(12)对卡尔曼滤波状态参数s进行动态估计。设状态参数的估值为
| $ \mathit{\boldsymbol{\hat y}} = {\mathit{\boldsymbol{H}}_2}\mathit{\boldsymbol{\hat s}} $ | (15) |
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{v}} = \mathit{\boldsymbol{y}} - \mathit{\boldsymbol{\hat y}} = - {\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{g}}^{\rm{i}}} - \left( {\mathit{\boldsymbol{C}}_{\rm{b}}^{\rm{i}}\left( {{\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{b}}_a} + } \right.} \right.}\\ {\left. {\left. {{\rm{diag}}\left( {{{\mathit{\boldsymbol{\tilde a}}}^{\rm{b}}}} \right){\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{k}}_a}} \right) + {{\mathit{\boldsymbol{\tilde a}}}^{\rm{i}}} \times {\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^{\rm{i}}}} \right\} + {\mathit{\boldsymbol{e}}_2}} \end{array} $ | (16) |
利用式(16)求得的外部观测量的残差值中,不仅包括重力扰动矢量,还有系统状态参数的真误差以及惯性传感器和载体运动加速度的残留噪声。经过上述处理,可以假定后3项误差相对于重力扰动矢量要小得多,故残差值可近似为重力扰动的估值,有:
| $ \mathit{\boldsymbol{v}} \approx - {\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{g}}^{\rm{i}}} $ | (17) |
在获得上述惯性坐标系下的重力扰动后,可以利用转换矩阵Cin得到当地水平坐标系下的重力扰动值。
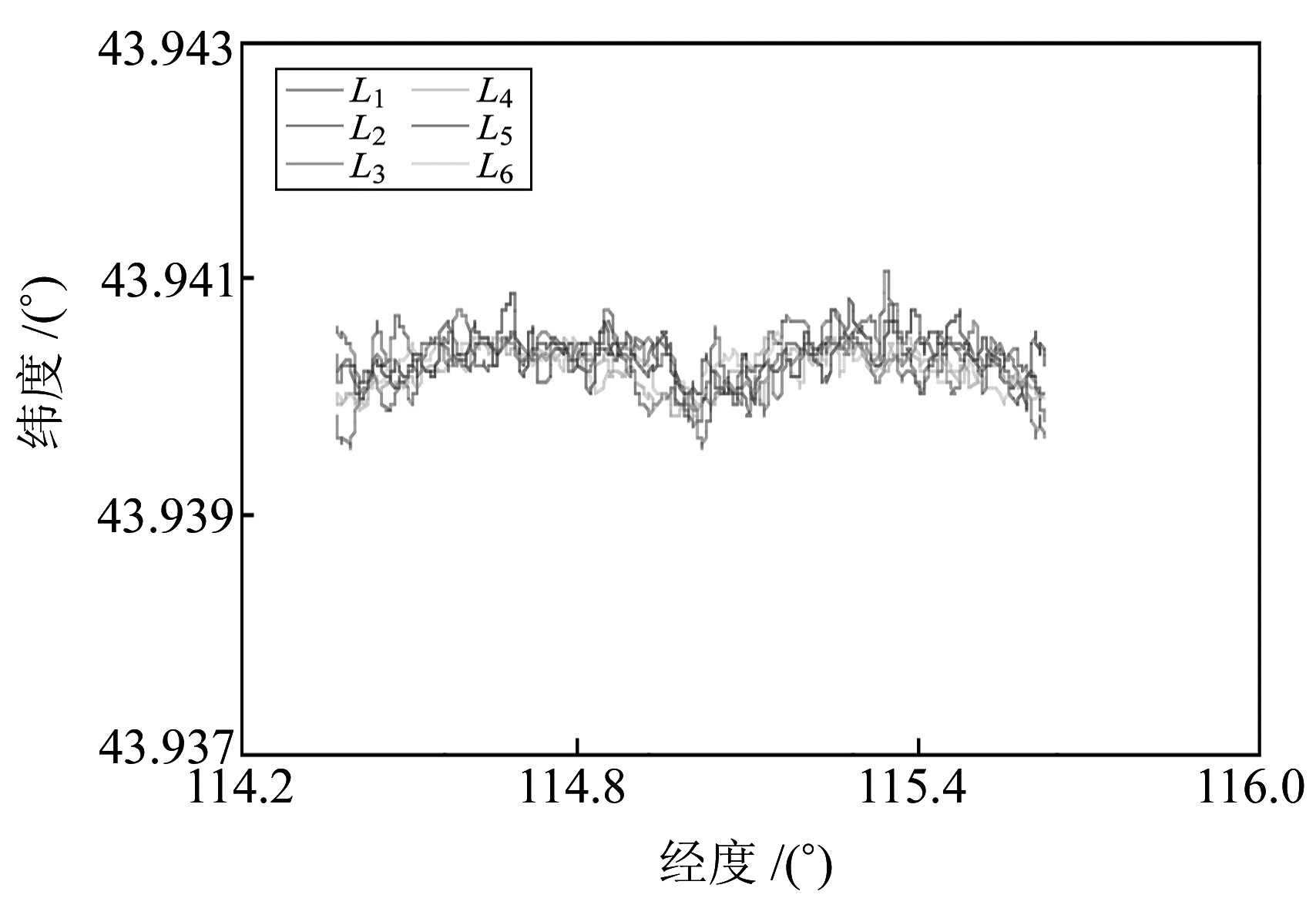
2 算例分析 2.1 实验数据来源所用GNSS/SINS原始观测数据来源于2015-06-15进行的某航空矢量重力测量实验。该次实验共计6条东西方向的重复测线,分别记为L1、L2、…、L6,如图 1所示。平均飞行速度为60 m/s,总计飞行约7.8 h。SINS原始数据采样率为200 Hz,GNSS数据采样率为2 Hz。
|
图 1 6条重复测线的飞行轨迹 Fig. 1 The flight path of the six repeatlines |
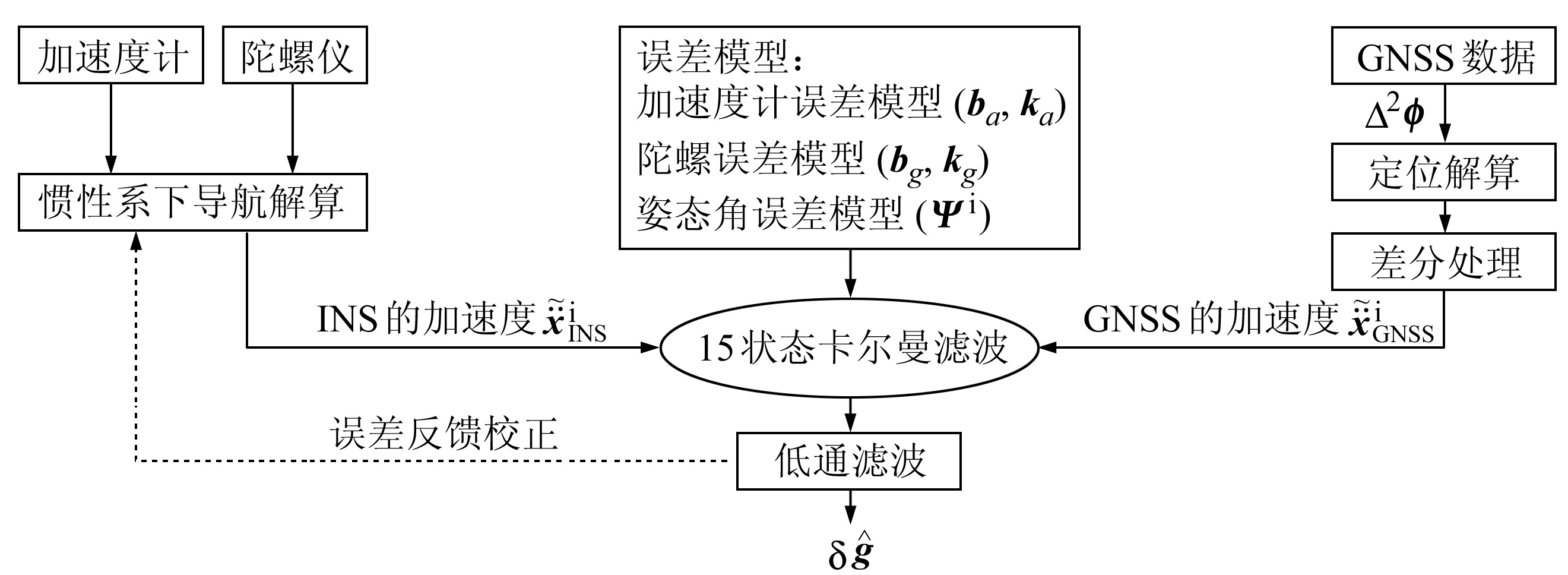
以惯性系下利用GNSS/SINS组合数据估算重力扰动为例,共包括4个部分,基本流程如图 2所示。当地水平坐标系下重力扰动的估计步骤见参考文献[2]。
|
图 2 基于加速度更新的重力扰动估算流程 Fig. 2 The schematic diagram of gravity disturbance estimation based on acceleration update |
1) 对SINS的原始观测数据进行导航解算,求出载体在惯性坐标系下的加速度
2) 对GNSS的载波相位观测值进行双差相位处理,获得GNSS位置或速度[14-15],再对位置时间序列或速度时间序列进行二次或一次差分运算,得到载体在当地坐标系下的运动加速度,并利用转换矩阵求出惯性坐标系下的加速度
3) 以GNSS的数据采样周期为滤波周期进行15状态卡尔曼滤波。状态参数初值均设为零,参数方差阵、噪声方差阵及外部观测值方差阵均为对角阵,其数值根据所用设备的性能指标设定,列于表 1。将惯性坐标系下GNSS和SINS加速度的差值作为观测量,用式(11)、式(12)对状态参数进行动态估计,并及时修正惯性器件的误差;用式(15)~(17)求出惯性坐标系下的重力扰动并将其转换到当地水平坐标系,结果如图 3(a)所示。
|
|
表 1 卡尔曼滤波器各参数初始中误差 Tab. 1 The error of Kalman filter initial parameters |
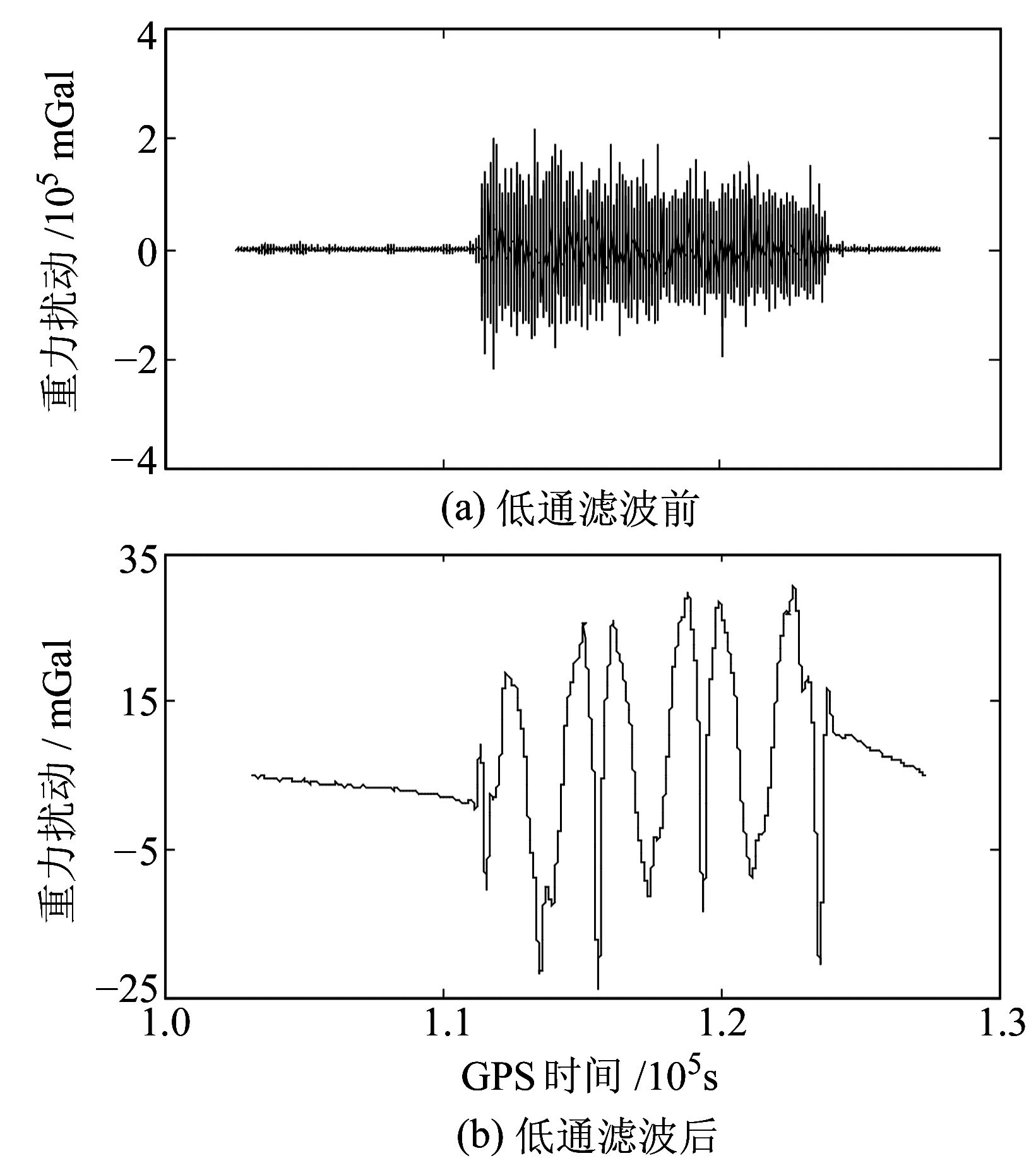
4) 上述卡尔曼滤波获得的重力扰动中含有许多高频噪声,需要采用低通滤波器进行降噪处理[16]。本文采用截止频率为0.004 Hz的巴特沃斯低通滤波器进行滤波处理,滤波后的重力扰动如图 3(b)所示,其半波长分辨率约为7.5 km。
|
图 3 低通滤波前后的重力扰动 Fig. 3 The gravity disturbance before and after low-pass filtering |
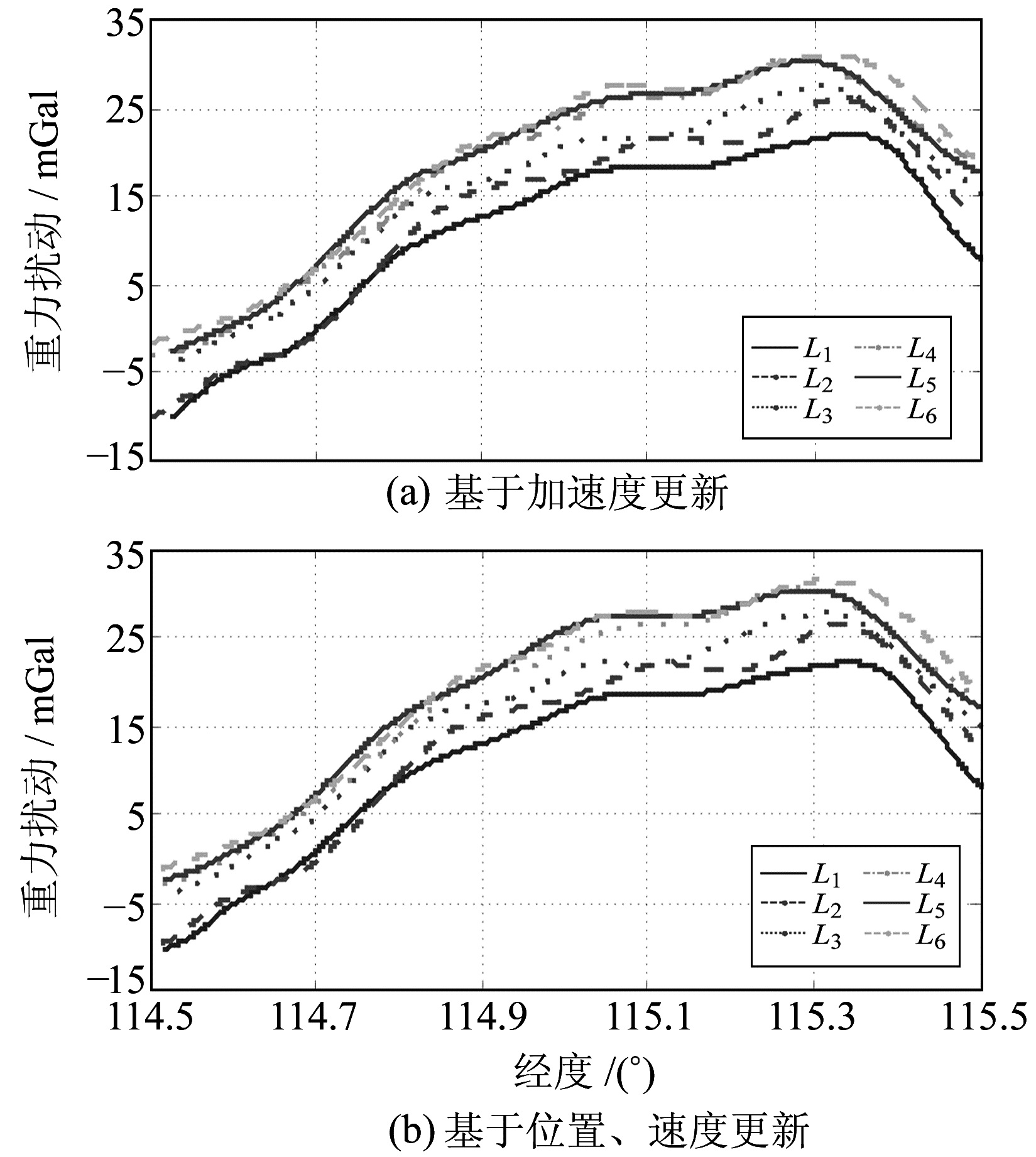
从如图 3(b)所示的全部重力扰动中分离出6条重复测线的重力扰动,如图 4(a)所示(方法1)。为便于比较,图 4(b)给出了当地水平坐标系下基于位置和速度更新得到的6条重复测线的重力扰动(方法2)。
|
图 4 重复测线的重力扰动 Fig. 4 The gravity disturbance of repeatlines |
由于测区没有外部重力参考值,以内符合精度公式评估重力扰动的精度:
| $ {\varepsilon _{ij}} = \pm \sqrt {\frac{{\sum\limits_{k = 1}^n {{\rm{ \mathsf{ δ} }}_k^2} }}{n}} ,(i = 1,2, \cdots ,5;j = i + 1, \cdots ,6) $ | (18) |
式中,εij为i、j两条重复测线的内符合精度,δk为重复测线第k个公共点处的重力扰动值之差,n为重复测线公共段观测点的数目。
表 2给出了方法1和方法2的重力扰动的内符合精度(标准差),可见其数值均小于2 mGal,惯性坐标系下重复测线重力扰动的估算精度与当地水平坐标系相当,平均标准差分别为1.21 mGal、1.27 mGal。对比式(7)、式(11)可知,惯性坐标系下卡尔曼滤波的状态方程比当地水平坐标系下要简单。此外,在GNSS/SINS组合卡尔曼滤波时,方法1只需要求出GNSS/SINS在惯性坐标系下的加速度,而方法2需要解出GNSS/SINS在当地水平坐标系下的加速度、速度、位置。与方法2相比,方法1更简捷。
|
|
表 2 重复测线重力扰动的内符合精度 Tab. 2 The internal accuracy of the gravity disturbance for repeat lines |
对于相同编号的测线,两种方法求出的重力扰动的差值统计于表 3,其中最大差值为1.81 mGal,差值标准差最大为0.74 mGal、平均值为0.65 mGal,表明两种方法具有较好的一致性。
|
|
表 3 两种方法求得的相同编号测线的重力扰动内符合精度 Tab. 3 The internal accuracy of the gravity disturbance using two methods for the lines of same number |
从图 4和表 2可以看出,两种方法所估计的重力扰动都存在系统性偏差,且随着时间的增加,L2~L6的重力扰动相对于起始测线L1的偏差逐渐增大,对于方法1,L6相对于L1的偏差均值为8.20 mGal。
将L1与L6之间的差值均值依时间等比例分配,内插出不同时刻的比力误差并进行修正,修正结果见图 5和表 4。可见,测线间的系统性偏差有明显减小。对比表 2和表 4,对于方法1,测线间的最大差值均值由8.20 mGal减小到2.70 mGal,平均内符合精度由1.21 mGal提高到1.06 mGal;对于方法2,测线间的最大差值均值由8.19 mGal减小到2.54 mGal,平均内符合精度由1.27 mGal提高到1.10 mGal。
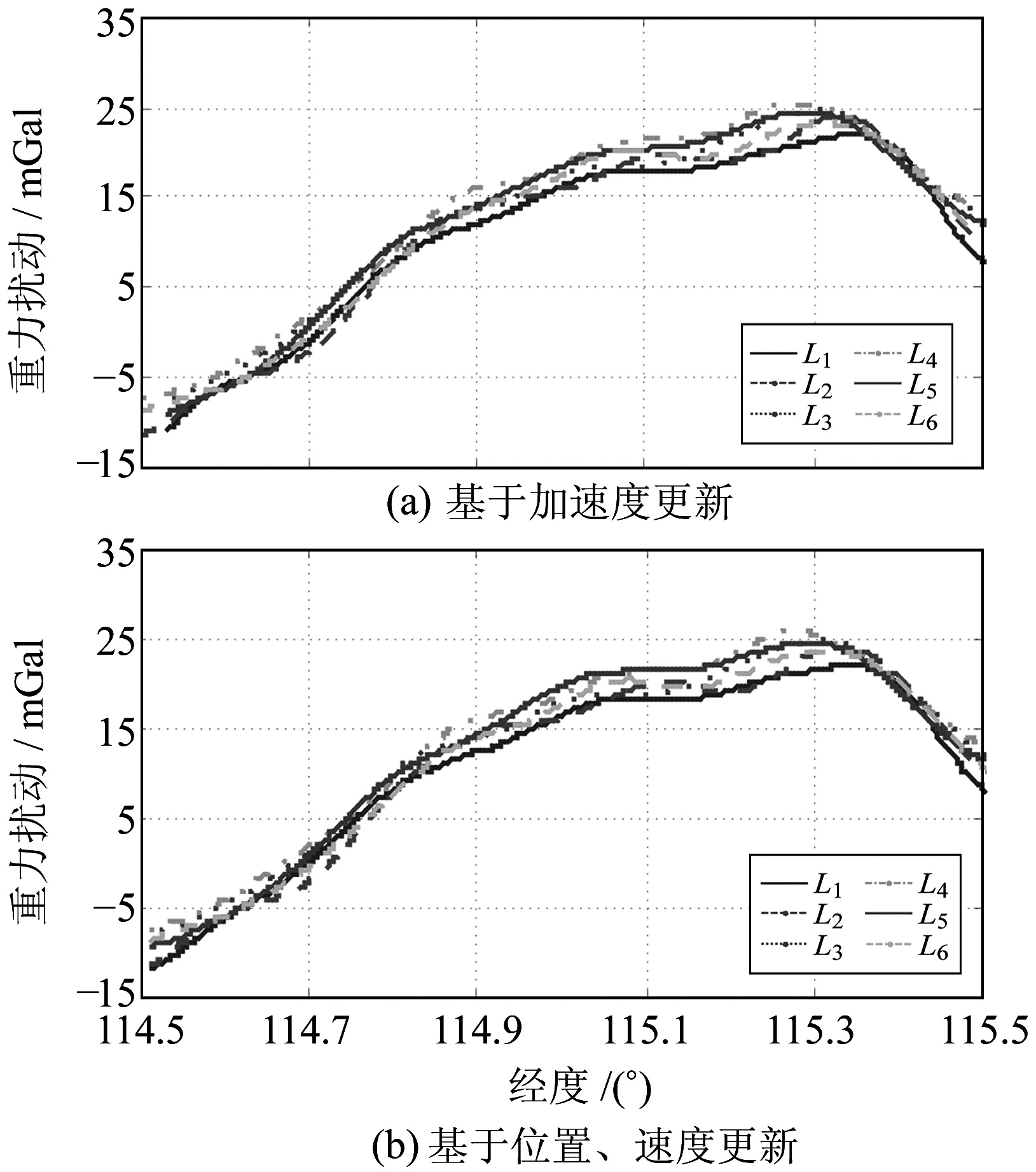
|
图 5 修正后6条重复测线的重力扰动 Fig. 5 The gravity disturbance of six repeat lines after correction |
|
|
表 4 修正后6条重复测线的重力扰动的内符合精度 Tab. 4 The internal accuracy of the gravity disturbance for the six repeat lines after correction |
本文对在惯性坐标系和当地水平坐标系下估算重力扰动的两种方法进行了比较,经过对实测数据的处理,得到如下结论:
1) 惯性坐标系下基于加速度更新的卡尔曼滤波算法(方法1)相比当地水平坐标系下基于位置、速度更新的卡尔曼滤波算法(方法2)模型便捷且重力扰动的估算精度相当,即在半波长分辨率为7.5 km时,6条重复测线的重力扰动之差的平均标准差分别为1.21 mGal、1.27 mGal。
2) 两种方法计算得到的重力扰动差值的标准差平均为0.65 mGal,表明二者具有较好的一致性。
3) 两种方法求得的重复测线上的重力扰动值都存在明显的系统误差,将测线间的最大平均差值按时间等比例分配进行线性修正后,重复测线间的系统偏差明显减小。
| [1] |
孙中苗.航空重力测量理论、方法及应用研究[D].郑州: 信息工程大学, 2004 (Sun Zhongmiao.Theory, Methods and Applications of Airborne Gravimetry[D].Zhengzhou: Information Engineering University, 2004) http://cdmd.cnki.com.cn/Article/CDMD-90008-2005030005.htm
(  0) 0) |
| [2] |
蔡劭琨.航空重力矢量测量及误差分离方法研究[D].长沙: 国防科学技术大学, 2014 (Cai Shaokun.The Research about Airborne Vector Gravimeter and Methods of Error Separation[D].Changsha: National University of Defense Technology, 2014)
(  0) 0) |
| [3] |
董绪荣, 张守信, 华仲春. GPS/INS组合导航定位及其应用[M]. 长沙: 国防科技大学出版社, 1998 (Dong Xurong, Zhang Shouxin, Hua Zhongchun. GPS/INS Integrated Navigation and Positioning and Its Application[M]. Changsha: National University of Defense Technology Press, 1998)
(  0) 0) |
| [4] |
吴富梅.GNSS/INS组合导航误差补偿与自适应滤波理论的拓展[D].郑州: 信息工程大学, 2010 (Wu Fumei.Error Compensation and Extension of Adaptive Filtering Theory in GNSS/INS Integrated Navigation[D].Zhengzhou: Information Engineering University, 2010) http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=chxb201103022
(  0) 0) |
| [5] |
张开东.基于SINS/DGPS的航空重力测量方法研究[D].长沙: 国防科学技术大学, 2007 (Zhang Kaidong.Research on the Methods of Airborne Gravimetry Based on SINS/DGPS[D].Changsha: National University of Defense Technology, 2007) http://cdmd.cnki.com.cn/Article/CDMD-90002-2008098727.htm
(  0) 0) |
| [6] |
Boedecker G.Configuration Optimization of Accelerometers for Strapdown Airborne Gravimeters[C].International Workshop on Airborne Gravity and the Polar Gravity Field, Kangerlussuaq, Greenland, 1998
(  0) 0) |
| [7] |
Wei M, Schwarz K P. Flight Test Results from a Strapdown Airborne Gravity System[J]. Journal of Geodesy, 1998, 72(6): 323-332 DOI:10.1007/s001900050171
(  0) 0) |
| [8] |
Glennie C, Schwarz K P. A Comparison and Analysis of Airborne Gravimetry Results from Two Strapdown Inertial/DGPS Systems[J]. Journal of Geodesy, 1999, 73(6): 311-321 DOI:10.1007/s001900050248
(  0) 0) |
| [9] |
柴华, 王勇, 王虎彪, 等. GNSS/SINS组合进行惯性重力测量误差分析[J]. 大地测量与地球动力学, 2011, 31(6): 73-78 (Chai Hua, Wang Yong, Wang Hubiao, et al. Error Analysis for Inertial Gravimetry by Use of GNSS/SINS Combination[J]. Journal of Geodesy and Geodynamics, 2011, 31(6): 73-78)
(  0) 0) |
| [10] |
Kwon J H.Airborne Vector Gravimetry Using GPS/INS[D]. Ohio: The Ohio State University, 2000
(  0) 0) |
| [11] |
Kwon J H, Jekeli C. A New Approach for Airborne Vector Gravimetry Using GPS/INS[J]. Journal of Geodesy, 2001, 74(10): 690-700 DOI:10.1007/s001900000130
(  0) 0) |
| [12] |
Senobari M S. New Results in Airborne Gravimetry Using Strapdown INS/DGPS[J]. Journal of Geodesy, 2010, 84(5): 277-291 DOI:10.1007/s00190-010-0366-6
(  0) 0) |
| [13] |
Li Xiaopeng. Strapdown INS/DGPS Airborne Gravimetry Tests in the Gulf of Mexico[J]. Journal of Geodesy, 2011, 85(9): 597-605 DOI:10.1007/s00190-011-0462-2
(  0) 0) |
| [14] |
应俊俊, 刘根友. 航空重力测量中利用GPS测定载体的速度和垂直加速度[J]. 大地测量与地球动力学, 2009, 28(5): 68-75 (Ying Junjun, Liu Genyou. Determination of Velocity and Vertical Acceleration in Airborne Gravimetry by Using GPS[J]. Journal of Geodesy and Geodynamics, 2009, 28(5): 68-75)
(  0) 0) |
| [15] |
肖云, 夏哲仁. 航空重力测量中载体加速度的确定[J]. 地球物理学报, 2013, 46(1): 62-67 (Xiao Yun, Xia Zheren. Determination of Moving Base Acceleration in Airborne Gravimetry[J]. Chinese Journal of Geophysics, 2013, 46(1): 62-67 DOI:10.3969/j.issn.1672-7940.2013.01.013)
(  0) 0) |
| [16] |
田颜锋, 李珊珊, 刘小刚, 等. 航空重力数据低通滤波处理及其功效分析[J]. 大地测量与地球动力学, 2009, 29(6): 130-134 (Tian Yangfeng, Li Shanshan, Liu Xiaogang, et al. Low-Pass Filter and It's Effective in Data Processing of Aerial Gravity Measurements[J]. Journal of Geodesy and Geodynamics, 2009, 29(6): 130-134)
(  0) 0) |
2. Xi'an Research Institute of Surveying and Mapping, 1 Mid-Yanta Road, Xi'an 710054, China;
3. School of Geology Engineering and Surveying, Chang'an University, 126 Yanta Road, Xi'an 710054, China
 2018, Vol. 38
2018, Vol. 38

