2. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室,武汉市徐东大街340号,430077;
3. 新疆维吾尔自治区地震局,乌鲁木齐市科学二街338号,830011
区域重力测量的主要目的之一是监测非潮汐重力场随时间的变化,研究地震孕育、发生和调整过程中重力场的时空变化特征。利用流动重力测量监测区域重力场变化,为有效提取地震前兆信息,首先需要建立合理的测网。区域重力网的网形结构对于重力网整体平差结果的可靠性起着至关重要的作用,良好的网形结构对于识别地震异常前兆信息和研究地震孕震机理等有积极作用。
我国的流动重力测量起步于1966年邢台地震后。20世纪80、90年代,随着高精度LCR-G型重力仪的全面推广,我国陆续在全国主要活动地震带上布设了区域重力监测网[1-2]。经过几十年的建设,流动重力测网不断完善、不断填补监测空白,已基本实现对全国主要地震监视防御区的全面监控[1]。根据流动重力测量的特点以及监测构造活动的需求,重力测网布设基本满足下面几点要求:1)测网应布设在地震活动区,通常应跨越主要构造单元与活动断裂带;2)测区交通便利,测点基础稳固,周围环境干扰小;3)测网尽可能布设成环,条件不允许时可布设成测线[3]。根据以上要求并结合测区实际情况,我国目前的流动重力测网已基本成熟,区域重力网基本都布设成相连的测环。然而,由于受到道路、交通以及恶劣气候等影响,实际观测时某些测段可能无法观测,导致实际观测路线无法闭合成环,从而形成支线,这必然会影响整网平差的结果。根据以往的观测经验,这种现象在实际观测过程中比较常见,如北天山测网在2016-05观测过程中由于道路不通致使测网中3个测段无法联测,导致测网中3个测环未闭合而形成了两个较长的支线。基于此,本文以北天山测网为例,探讨重力网中测环与支线对重力数据处理结果的影响。
1 流动重力测量及误差来源 1.1 流动重力测量流动重力测量包括基准点的绝对重力测量以及相邻测站间重力段差的相对重力联测。在狭义上,流动重力测量即是相对重力联测,它是利用相对重力仪按照一定的观测周期重复观测固定测点之间的重力差值[3]。目前,我国流动重力监测工作中应用较广泛的相对重力仪主要有LCR-G型、CG-5/6型以及Burris型等重力仪。
流动重力测量通常采用2~3台相对重力仪同时、同址施测,以检核仪器读数是否超限,保证观测质量的可靠性;联测时采用图 1所示的往返观测,即A→B→…→N→…→B→A的观测顺序,观测过程中如果仪器停放超过2 h,则在停放点重复观测,以消除仪器的静态零漂;每条测线一般当天闭合,最多可放宽到3 d。
|
图 1 相对重力联测示意图 Fig. 1 Schematic diagram of relativegravity observation |
相对重力观测容易受到环境变化以及仪器自身系统误差的影响。影响观测精度的主要误差来源包括[4]:
1) 系统误差。包括仪器的一次项格值系数误差、零漂改正误差、LCR-G型仪器的周期误差、Burris型重力仪及CG-5型重力仪的静电反馈误差等。其中仪器的一次项格值系数误差与零漂改正误差对观测精度影响最大。一次项格值系数误差可以通过基线场标定以及测区内绝对值标定减弱其影响,但无法完全消除;仪器的零点漂移通常采用观测周期内的线性零漂以及按闭合观测计算的分段线性零漂进行零漂改正,以减弱其误差影响。然而由于仪器零漂率的非线性特性以及闭合观测时间不固定,两种零漂计算方法都存在一定的局限性,无法完全消除其误差影响。
2) 偶然误差。由于观测员不同的观测技术及观测习惯引起的读数误差,属于偶然误差。按正常观测程序观测即可有效控制在误差允许范围内。
重力网平差一般采用观测段差作为平差元素,每个观测值都受到以上几个主要误差影响,测点的平差精度会不同程度地受到这些观测误差的影响。对于支线来说,根据误差传播定律,支线上第n个点的平差精度可以表示为
北天山地区是中国大陆构造运动最强烈、地震活动频度最高、强度最大的地区之一,作为我国的重要地震监测区,其流动重力测网每年的上下半年各观测一期[5-7]。北天山测网分别于2014年和2015年进行了两次优化改造,最终优化后的测网见图 2。自2015-08测网改造以后已经观测了4期数据,观测时间分别为2015-09、2016-05、2016-09和2017-05。其中2016-05(第2期)观测过程中由于道路不通,导致3个测段未联测(图 2中的3条蓝色虚线),在测区西部形成了两个较长的支线,测区西部未闭合成环,严重影响了平差结果的可靠性。
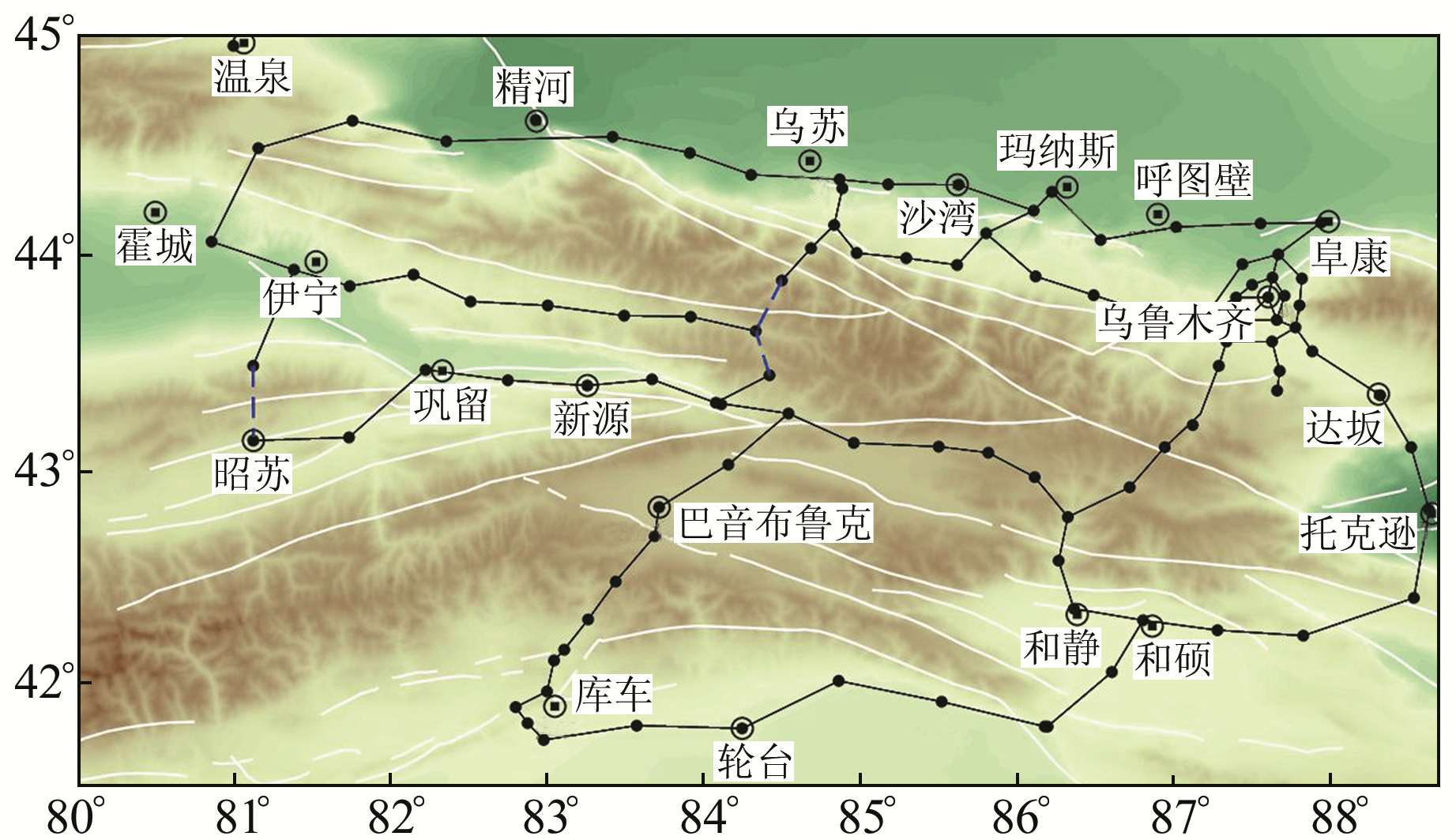
|
图 2 北天山重力测网路线 Fig. 2 Gravity monitoring network of northern Tianshan |
北天山测网内只有乌鲁木齐一个绝对点,不能满足该测网的基准控制需求,因此采用自由网平差对各期数据进行处理,然后归算到乌鲁木齐测点上,最后计算各期之间的差分重力变化。图 3是其他3期与第2期的差分重力变化图像(考虑到测网内测点分布不均,插值与滤波会造成一些虚假信息,为突出测点实际重力变化情况,在图中以箭头代表测点的重力变化量)。可以看出,其西部重力变化均呈显著异常,最大重力变化均在200 μGal以上;第2期与前后两期的重力变化明显反向,且量级相近。图 4给出了2015-09~2016-09的年重力变化与2016-09~2017-05的半年重力变化。与图 3相比,其重力变化量明显减小,属于正常重力变化,说明新增测点观测墩、测点周边环境以及季节性变化对测点重力变化影响较小,图 3的异常变化不是这些外界环境因素引起的。通过以上分析并结合第2期测网路线图可以看出,变化较大的测点是支线远端测点,由此判断,该异常变化可能是由于第2期测网不闭合导致该期平差结果不可靠,而不是真实的重力异常。

|
图 3 以2016-05为基准的北天山差分重力变化 Fig. 3 Differentiated gravity changes of northern Tianshan based on 2016-05 |
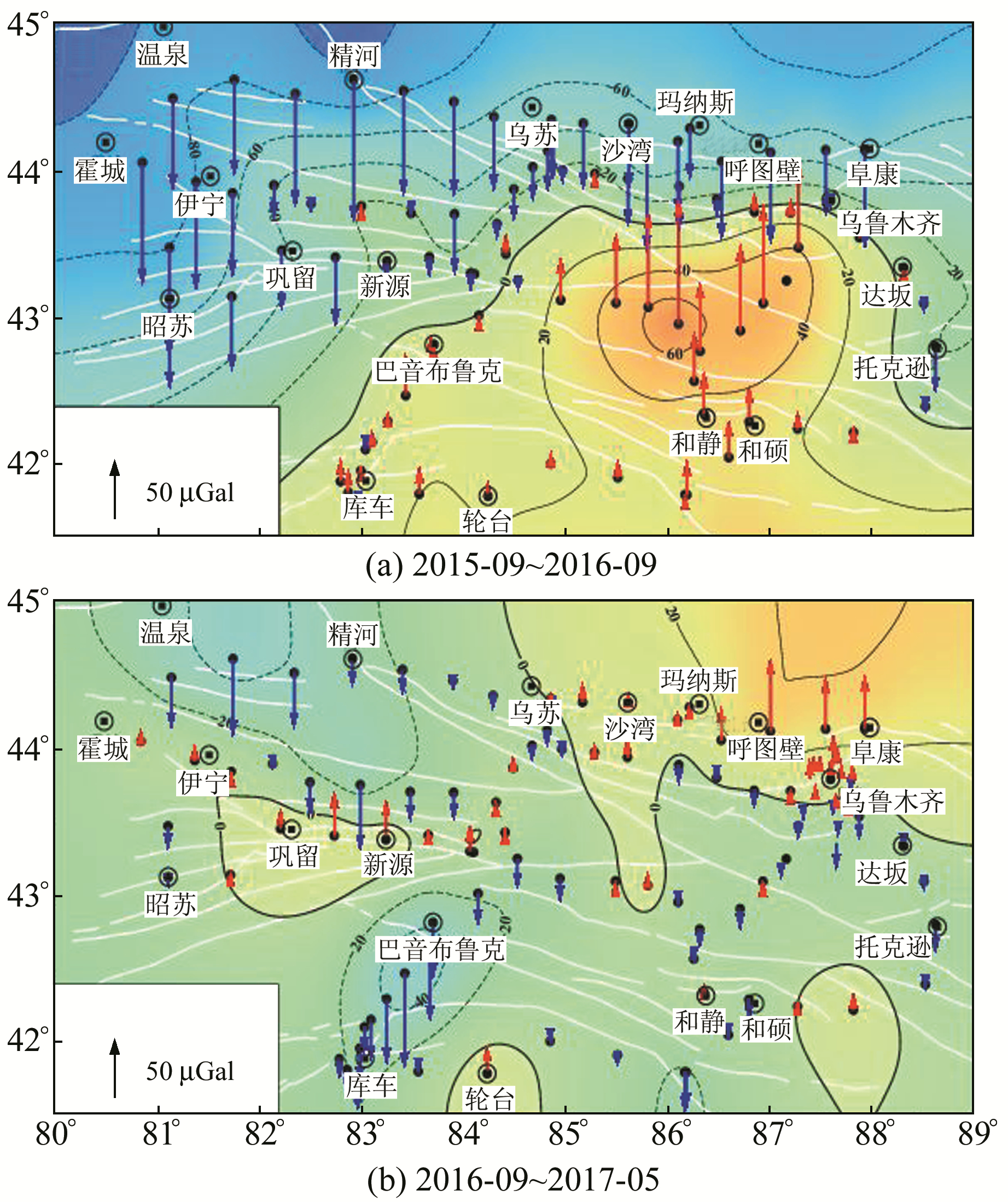
|
图 4 北天山其他3期差分重力变化(2016-05除外) Fig. 4 Differentiated gravity changes of northern Tianshan except 2016-05 |
为进一步判断支线上测点平差值的可靠性,计算测网内所有测点的平差精度(图 5),测点下方数字代表测点的平差精度值。可以看出,测区东部测环内的测点平差精度相近,精度较高,平差值较可靠;而测区西部两条长支线上的测点平差精度随支线方向迅速减小,表明随支线方向测点平差值的可靠性逐渐减小,末端测点平差结果不可靠。
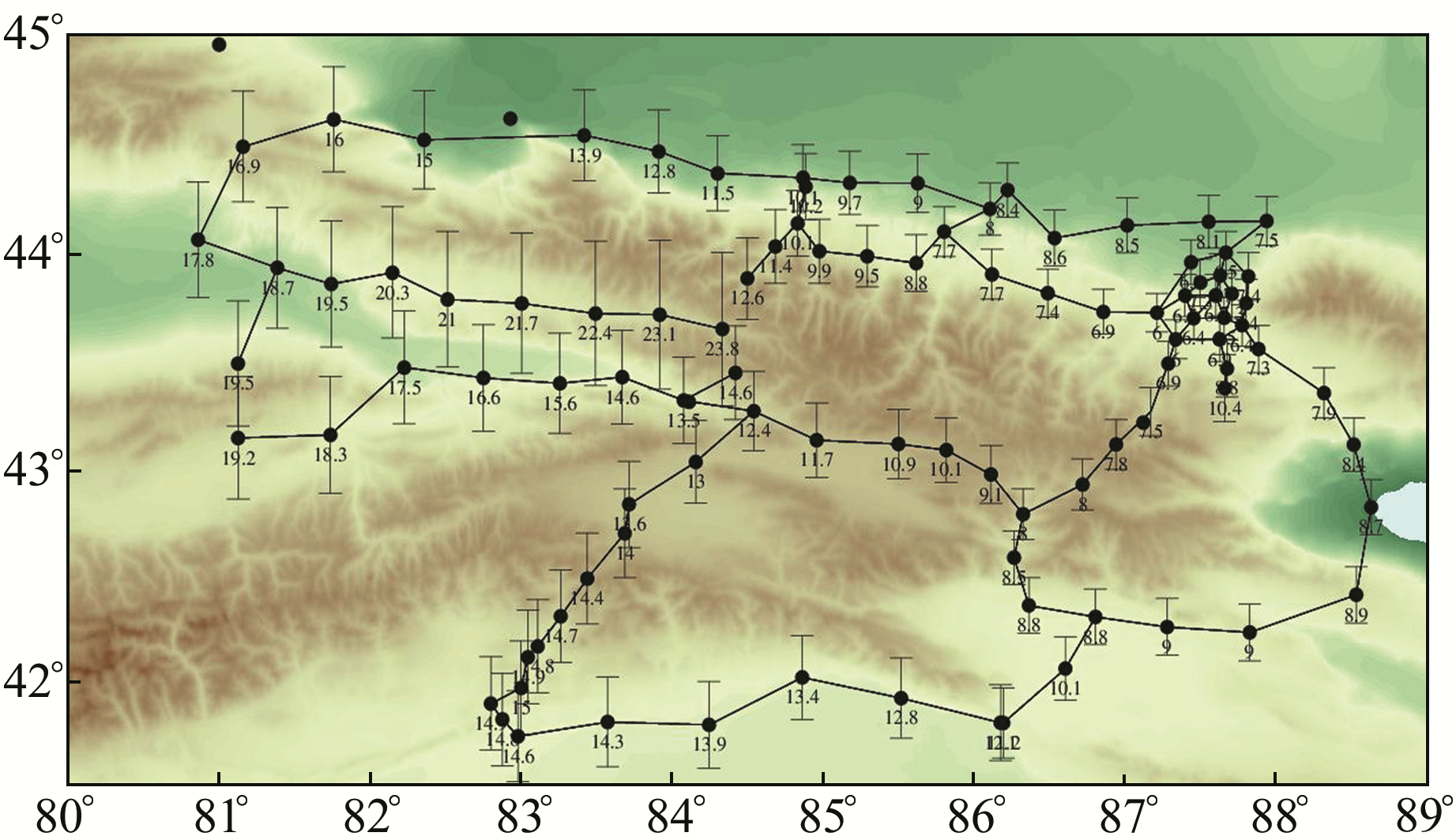
|
图 5 北天山测网第2期资料平差精度分布 Fig. 5 Adjustment accuracy distribution of the second gravity data set of northern Tianshan |
由于第2期有3个测段未联测,导致测网内形成两条长支线。考虑到长支线会严重影响测点的平差精度,为提高西部测点平差值的可靠性,利用第1期跟第3期中这3个测段的观测段差值作为第2期未联测测段的假设段差值,从而将两条测线相连组成测环。表 1给出了未联测的3个段差在前后两期的观测值变化。可以看出,3个段差值的变化均小于25 μGal,属于仪器观测误差范围以内。可以认为,这3个测段在前3期观测周期内无明显变化,遂利用前后两期的观测段差值的平均值作为第2期的观测段差值,将观测数据与这些替代段差值合称为合成数据。这些合成数据组成一个完整的测网,利用合成数据重新进行平差计算。
|
|
表 1 未联测测段在前后两期的段差值变化 Tab. 1 Variation of unmeasured gravity differences in before and after periods |
利用新的合成数据进行自由网平差并将重力值归算到乌鲁木齐测点,测点平差精度分布如图 6所示,图中蓝色虚线连接的测段为利用合成数据计算的测段。

|
图 6 北天山测网第2期合成数据的平差精度分布 Fig. 6 Adjustment accuracy distribution of the synthesis data set of northern Tianshan |
对比图 5与图 6的测点精度分布情况可以明显看出,利用合成数据消除支线影响以后,测区西部测点精度得到明显提高,测环内测点精度相近,有效消除了长支线误差累积的影响。为进一步验证平差结果的可靠性,计算相邻期次的差分重力变化,并将其视为修正后的重力变化图与原始的重力变化图进行比较。对比图 3与图 7修正前后差分重力变化图可以看出,利用合成数据修正后的重力变化明显小于修正前的重力变化,最大重力变化由260 μGal减小到60 μGal,其零值线位置也发生了明显变化,2016-12-08呼图壁地震与2017-08-09精河地震均发生在修正后的零值线附近。由图 7(b)、图 7(c)可以看出,呼图壁地震以后,震中南北两侧重力变化发生明显的反向,说明修正后的重力变化图像对最近两次地震都有很好的反映。由此说明,相比于测网中存在长支线,利用合成数据将长支线组成闭合环以后,测点平差值的可靠性得到明显提升。

|
图 7 合成数据修正后的差分动态重力变化 Fig. 7 Map of differentiated dynamic gravity changes using synthesis data |
通过对改造后的北天山测网的数据处理分析表明,测网中长支线的存在会严重影响整个测网的平差精度及结果的可靠性。如果实际作业过程中由于天气或者道路交通等因素无法联测某个测段,导致部分测环不闭合而形成长支线,应该第一时间进行补测,以避免长支线对整网平差的危害;如无法进行补测,在相邻期次段差值变化不大时可以考虑用相邻两期观测数据推算本期缺失的段差估值。因此,在重力变化结果分析过程中,如存在明显不合理的重力变化,首先要判断是否是观测数据和计算方法问题导致,不能直接归结为异常重力变化,如判断是由于网形不合理或者观测数据不可靠导致,应立即补测或者利用相邻两期的相关观测数据推算本期的理论观测数据,将支线连接成闭合环重新进行平差,这样可以有效地提高测网整体平差的可靠性,有利于获得可靠的重力场变化信息。
| [1] |
祝意青, 王庆良, 徐云马. 我国流动重力监测预报发展的思考[J]. 国际地震动态, 2008(9): 19-25 (Zhu Yiqing, Wang Qingliang, Xu Yunma. Thoughts on the Development of Earthquake Monitoring and Prediction in Mobile Gravity[J]. Recent Developments in World Seismology, 2008(9): 19-25 DOI:10.3969/j.issn.0253-4975.2008.09.004)
(  0) 0) |
| [2] |
郝洪涛.基于地表重力观测的地壳垂直运动和同震位错研究[D].北京: 中国科学院大学, 2015 (Hao Hongtao. Research on Vertical Displacement of Crust and Coseismic Gravity Change Based on Land Gravimetry[D]. Beijing: University of Chinese Academy of Sciences, 2015) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2853456
(  0) 0) |
| [3] |
国家地震局.地震重力测量规范[S].北京: 地震出版社, 1997 (State Seismological Bureau. Seismological Gravimetric Standard[S]. Beijing: Seismological Press, 1997)
(  0) 0) |
| [4] |
Lederer M. Accuracy of the Relative Gravity Measurement[J]. Acta Geodyn Geomater, 2009, 6(3): 383-390
(  0) 0) |
| [5] |
李杰, 王晓强, 谭凯, 等. 北天山现今活动构造的运动特征[J]. 大地测量与地球动力学, 2010, 30(6): 1-5 (Li Jie, Wang Xiaoqiang, Tan Kai, et al. Analysis of Movement Characters of Present-Day Active Tectonics of Northern Tianshan Region[J]. Journal of Geodesy and Geodynamics, 2010, 30(6): 1-5)
(  0) 0) |
| [6] |
刘代芹, 李杰, 王晓强, 等. 北天山中段近期重力场变化特征研究[J]. 地震工程学报, 2015, 37(4): 1001-1006 (Liu Daiqin, Li Jie, Wang Xiaoqiang, et al. Recent Variation Characteristics of Gravity Field in the Middle Segment of Northern Tianshan[J]. China Earthquake Engineering Journal, 2015, 37(4): 1001-1006 DOI:10.3969/j.issn.1000-0844.2015.04.1001)
(  0) 0) |
| [7] |
朱治国, 艾力夏提·玉山, 刘代芹, 等. 西天山地区重力场变化与地震研究[J]. 大地测量与地球动力学, 2017, 37(9): 903-907 (Zhu Zhiguo, Ailixiati Yushan, Liu Daiqin, et al. Variation of Gravity Field and Earthquake in the West Tianshan Area[J]. Journal of Geodesy and Geodynamics, 2017, 37(9): 903-907)
(  0) 0) |
2. State Key Laboratory of Geodesy and Earth's Dynamics, Institute of Geodesy and Geophysics, CAS, 340 Xudong Street, Wuhan 430077, China;
3. Earthquake Administration of Xinjiang Uyghur Autonomous Region, 338 Second-Kexue Street, Urumqi 830011, China
 2018, Vol. 38
2018, Vol. 38

