2. 流域生态与地理环境监测国家测绘地理信息局重点实验室,南昌市广兰大道418号,330013;
3. 云浮市国土资源和城乡规划管理局,广东省云浮市府前路11号,527300
在一些大型构件的实际测量数据处理过程中,经常遇到空间直线拟合问题[1]。由于空间直线的标准方程式
现有的空间直线拟合算法包括以下几种:文献[6]依据∑(Δxi2+Δyi2+Δzi2)=min的平差准则,利用拟合直线方向矢量与单位矢量的外积等于0,平差出拟合直线的方向矢量;文献[1]首先求解出与观测点组距离之和最小的平面,然后在此平面上采用LS进行直线拟合,此算法未顾及zi方向存在的误差,理论上不严谨;文献[3]利用空间直线的标准方程式建立EIV(errors-in-variables)模型,采用TLS求解拟合参数,但系数矩阵中的常数项也参与了误差分配,也不能保证重复元素有相同的改正数,这与实际理论不符;文献[7]和[8]采用混合结构总体最小二乘、结构总体最小二乘求解拟合参数,保证了系数矩阵中不同位置的重复元素得到了相同改正数,但求解过程较复杂。
本文首先对空间直线的标准方程进行变换,将标准方程转化成EIV模型;针对函数模型系数矩阵的特点,为了保证系数矩阵中重复元素具有相同改正数且只对有误差的元素进行改正,构建空间直线的PEIV模型[9](partial errors-in-variables models);最后提出基于PEIV模型的总体最小二乘空间直线拟合算法。
1 空间直线的EIV模型空间直线的标准方程为[10]:
| $ \frac{{x - {x_0}}}{l} = \frac{{y - {y_0}}}{m} = \frac{{z - {z_0}}}{n} $ | (1) |
式中,(l, m, n)为直线的方向矢量,(x0, y0, z0)为已知点。
式(1)变形为:
| $ \left\{ \begin{array}{l} x = \frac{l}{n}\left( {z - {z_0}} \right) + {x_0}\\ y = \frac{m}{n}\left( {z - {z_0}} \right) + {y_0} \end{array} \right. $ | (2) |
设
| $ \left\{ \begin{array}{l} x = az + b\\ y = dz + c \end{array} \right. $ | (3) |
式(3)写成矩阵形式可表示为:
| $ \left[ {\begin{array}{*{20}{c}} x\\ y \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} z&1&0&0\\ 0&0&1&z \end{array}} \right]{\left[ {\begin{array}{*{20}{c}} a&b&c&d \end{array}} \right]^{\rm{T}}} $ | (4) |
将式(4)改写成误差方程形式:
| $ {\mathit{\boldsymbol{e}}_Y} = \left( {\mathit{\boldsymbol{A}} + {\mathit{\boldsymbol{e}}_A}} \right)\mathit{\boldsymbol{\hat \beta }} - \mathit{\boldsymbol{Y}} $ | (5) |
式中,
式(5)的系数矩阵A中含有随机元素与常数元素,且随机元素在不同位置重复出现。理论上,重复元素应该有相同的改正数,常数元素的改正数为零。为满足上述条件,将式(5)的EIV模型转换为PEIV模型求解。
2.1 PEIV模型的构建PEIV模型是将系数矩阵中的随机元素与常数元素分离,其数学模型如下[9-10]。
1) 函数模型:
| $ \begin{array}{l} \mathit{\boldsymbol{Y}} = A\mathit{\boldsymbol{\hat \beta }} - {\mathit{\boldsymbol{e}}_Y} = \left( {{\mathit{\boldsymbol{\beta }}^{\rm{T}}} \otimes {\mathit{\boldsymbol{I}}_n}} \right)\left( {\mathit{\boldsymbol{h}} + \mathit{\boldsymbol{B\bar a}}} \right) - {\mathit{\boldsymbol{e}}_Y}\\ \mathit{\boldsymbol{a}} = \mathit{\boldsymbol{\bar a}} - {\mathit{\boldsymbol{e}}_a} \end{array} $ | (6) |
2) 随机模型:
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_Y}}\\ {{\mathit{\boldsymbol{e}}_a}} \end{array}} \right] \sim \left( {\left[ {\begin{array}{*{20}{c}} 0\\ 0 \end{array}} \right],\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Q}}_Y}}&0\\ 0&{{\mathit{\boldsymbol{Q}}_a}} \end{array}} \right]} \right) $ | (7) |
式中,B为构造的8n×t矩阵,t为系数矩阵A中随机元素的个数;a为系数矩阵A按列拉直后随机元素组成的t×1的列向量,a为其真值,ea为其对应的t×1的改正数;h是由系数矩阵A按列拉直后的零元素和常数元素所组成的8n×1列向量;QY、Qa分别是观测向量Y和列向量a的协因数阵。
针对空间直线拟合,PEIV模型中向量a的形式为:
| $ \mathit{\boldsymbol{a}} = {\left[ {\begin{array}{*{20}{c}} {{z_1}}&{{z_2}}& \cdots &{{z_n}} \end{array}} \right]^{\rm{T}}} $ | (8) |
B的形式为:
| $ \mathit{\boldsymbol{B}} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1}}&{{\mathit{\boldsymbol{B}}_2}}&{{\mathit{\boldsymbol{B}}_3}} \end{array}} \right]^{\rm{T}}} $ | (9) |
式中,B1= In⊗[1 0]T, B2=In⊗[0 0 0 0]T, B3=In⊗[0 1]T。
h的形式为:
| $ \mathit{\boldsymbol{h}} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{h}}_1}}&{{\mathit{\boldsymbol{h}}_2}}&{{\mathit{\boldsymbol{h}}_3}}&{{\mathit{\boldsymbol{h}}_4}} \end{array}} \right]^{\rm{T}}} $ | (10) |
式中,h1、h4均为1×2n的0向量,h2、h3分别为n个[1 0]T、[0 1]T向量组成的1×2n的列向量。
至此,将空间直线式(5)的EIV模型转换为式(6)的PEIV模型。
2.2 模型解算PEIV的函数模型中β和a均为待估参数。因此式(6)是非线性的,需对其进行线性化。将其在β = β0+Δβ、a=a0 +Δa处线性展开为[11]:
| $ \begin{array}{l} \mathit{\boldsymbol{Y}} = \left( {{\mathit{\boldsymbol{\beta }}^{{0^{\rm{T}}}}} \otimes {\mathit{\boldsymbol{I}}_{3n}}} \right)\left( {\mathit{\boldsymbol{h}} + \mathit{\boldsymbol{B}}{{\mathit{\boldsymbol{\bar a}}}^0}} \right) + \\ \;\;\Delta \mathit{\boldsymbol{\beta }}\left( {\mathit{\boldsymbol{h}} + \mathit{\boldsymbol{B}}{{\mathit{\boldsymbol{\bar a}}}^0}} \right) + \left( {{\mathit{\boldsymbol{\beta }}^{{0^{\rm{T}}}}} \otimes {\mathit{\boldsymbol{I}}_{3n}}} \right)\mathit{\boldsymbol{B}}\Delta \mathit{\boldsymbol{\bar a}} - {\mathit{\boldsymbol{e}}_Y}\\ \mathit{\boldsymbol{a}} = {{\mathit{\boldsymbol{\bar a}}}^0} + \Delta \mathit{\boldsymbol{\bar a}} - {\mathit{\boldsymbol{e}}_a} \end{array} $ | (11) |
表示为矩阵形式为:
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_Y}}\\ {{\mathit{\boldsymbol{e}}_a}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - {\rm{ve}}{{\rm{c}}^{ - 1}}\left( {\mathit{\boldsymbol{h}} + \mathit{\boldsymbol{B}}{{\mathit{\boldsymbol{\bar a}}}^0}} \right)}&{ - \left( {{\mathit{\boldsymbol{\beta }}^{{0^{\rm{T}}}}} \otimes {\mathit{\boldsymbol{I}}_{3n}}} \right)\mathit{\boldsymbol{B}}}\\ {\bf{0}}&{ - {\mathit{\boldsymbol{I}}_{3n}}} \end{array}} \right] \cdot }\\ {\left[ {\begin{array}{*{20}{c}} {\Delta \mathit{\boldsymbol{\beta }}}\\ {\Delta \mathit{\boldsymbol{\bar a}}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {\left( {{\mathit{\boldsymbol{\beta }}^{{0^{\rm{T}}}}} \otimes {\mathit{\boldsymbol{I}}_{3n}}} \right)\left( {\mathit{\boldsymbol{h}} + \mathit{\boldsymbol{B}}{{\mathit{\boldsymbol{\bar a}}}^0}} \right) - \mathit{\boldsymbol{Y}}}\\ {{{\mathit{\boldsymbol{\bar a}}}^0} - \mathit{\boldsymbol{a}}} \end{array}} \right]} \end{array} $ | (12) |
令
| $ \mathit{\boldsymbol{V}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_Y}}\\ {{\mathit{\boldsymbol{e}}_a}} \end{array}} \right],\mathit{\boldsymbol{X = }}\left[ {\begin{array}{*{20}{c}} {\Delta \mathit{\boldsymbol{\beta }}}\\ {\Delta \mathit{\boldsymbol{\bar a}}} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} {\left( {{\mathit{\boldsymbol{\beta }}^{{0^{\rm{T}}}}} \otimes {\mathit{\boldsymbol{I}}_{3n}}} \right)\left( {\mathit{\boldsymbol{h}} + \mathit{\boldsymbol{B}}{{\mathit{\boldsymbol{\bar a}}}^0}} \right) - \mathit{\boldsymbol{Y}}}\\ {{{\mathit{\boldsymbol{\bar a}}}^0} - \mathit{\boldsymbol{a}}} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{C = }}\left[ {\begin{array}{*{20}{c}} { - {\rm{ve}}{{\rm{c}}^{ - 1}}\left( {\mathit{\boldsymbol{h}} + \mathit{\boldsymbol{B}}{{\mathit{\boldsymbol{\bar a}}}^0}} \right)}&{ - \left( {{\mathit{\boldsymbol{\beta }}^{{0^{\rm{T}}}}} \otimes {\mathit{\boldsymbol{I}}_{3n}}} \right)\mathit{\boldsymbol{B}}}\\ {\bf{0}}&{ - {\mathit{\boldsymbol{I}}_{3n}}} \end{array}} \right] $ |
则式(12)可以简化为:
| $ \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{CX}} - \mathit{\boldsymbol{L}} $ | (13) |
式中,V是改正数,C是新构造的系数矩阵,X是拟合参数的改正数,L是待估参数的初值组成的常数向量, vec表示将矩阵按列拉直变换。
对式(13)采用VTQ-1V=min的平差准则求解,其中Q是观测向量Y和列向量a组成的协因数阵。
至此,基于PEIV模型的空间直线拟合转化为经典的最小二乘间接平差形式。与最小二乘间接平差不同的是,需要通过迭代计算拟合参数的最优解。参数估值的迭代公式为[12]:
| $ {\mathit{\boldsymbol{X}}_{i + 1}} = {\left( {\mathit{\boldsymbol{C}}_i^{\rm{T}}{\mathit{\boldsymbol{Q}}^{ - 1}}{\mathit{\boldsymbol{C}}_{\rm{i}}}} \right)^{ - 1}}\mathit{\boldsymbol{C}}_i^{\rm{T}}{\mathit{\boldsymbol{Q}}^{ - 1}}{\mathit{\boldsymbol{L}}_i} $ | (14) |
本文算法的具体计算步骤如下[14]。
1) 给出已知数据a、Y、h、QY、Qa以及收敛阈值ε;
2) 赋初值:β0=βLS,a0=a,根据式(13)建立迭代公式;
3) 根据式(13),并由Xi+1=(CiQ-1Ci)-1CiTQ-1Li计算Δβ和Δa,然后再根据βi+1= βi+Δβi、ai+1=ai+Δai更新β和a的值;
4) 重复步骤3),直到‖Xi+1-Xi‖2 < ε停止迭代,输出参数。
整个迭代计算过程与最小二乘间接平差类似,编程计算简便。
3 空间直线拟合精度评定指标对于空间直线拟合精度,可以利用各拟合点到拟合直线的距离和∑di、直线度[3]及参数平差值与真值的残差值Δ进行评定[6]。
1) 拟合点到拟合直线的距离公式为:
| $ {d_i} = \sqrt {\frac{{{{\left[ {m\left( {{x_i} - {x_0}} \right) - l\left( {{y_i} - {y_0}} \right)} \right]}^2} + {{\left[ {n\left( {{x_i} - {x_0}} \right) - l\left( {{z_i} - {z_0}} \right)} \right]}^2} + {{\left[ {n\left( {{y_i} - {y_0}} \right) - m\left( {{z_i} - {z_0}} \right)} \right]}^2}}}{{{l^2} + {m^2} + {n^2}}}} $ | (15) |
| $ \left. 2 \right)直线度 = \max \left( {{d_i}} \right) - \min \left( {{d_i}} \right) $ | (16) |
式中,di为第i个点到拟合直线的距离,i=1, 2, …, n。
3) 参数平差值与真值的残差值Δa、Δc可表示x=az+b和y=cz+d的斜率误差,Δb、Δd可表示相应的截距误差。
4 实例与分析表 1为空间直线拟合的一组实测数据[6]。ε取10-10,di为拟合点到拟合直线的距离。
|
|
表 1 空间直线实测数据 Tab. 1 Spatial straight line measured data |
根据§2.2迭代法的计算步骤,利用MATLAB编制程序进行空间直线拟合,求得
| $ \left\{ \begin{array}{l} x = 0.333\;248z + 2.002\;473\\ y = 0.666\;823z + 0.995\;786 \end{array} \right. $ | (17) |
由式(17)可以得到其中一个标准方程为:
| $ \frac{{x - 2.002\;473}}{{0.333\;248}} = \frac{{y - 0.995\;786}}{{0.666\;823}} = \frac{{z - 0}}{1} $ | (18) |
式中,方向矢量(l, m, n)为(0.333 248, 0.666 823, 1)。
分别采用文献[3]和[13]的总体最小二乘法(TLS)、文献[6]的残差平方和最小算法(残差平方和最小法)、混合总体最小二乘法(LS-TLS)及本文算法,根据式(15)计算拟合点到拟合直线的距离,结果如图 1所示,再求出距离和∑di如表 2所示;由式(17)计算上面4种算法的直线度,结果如表 2所示。
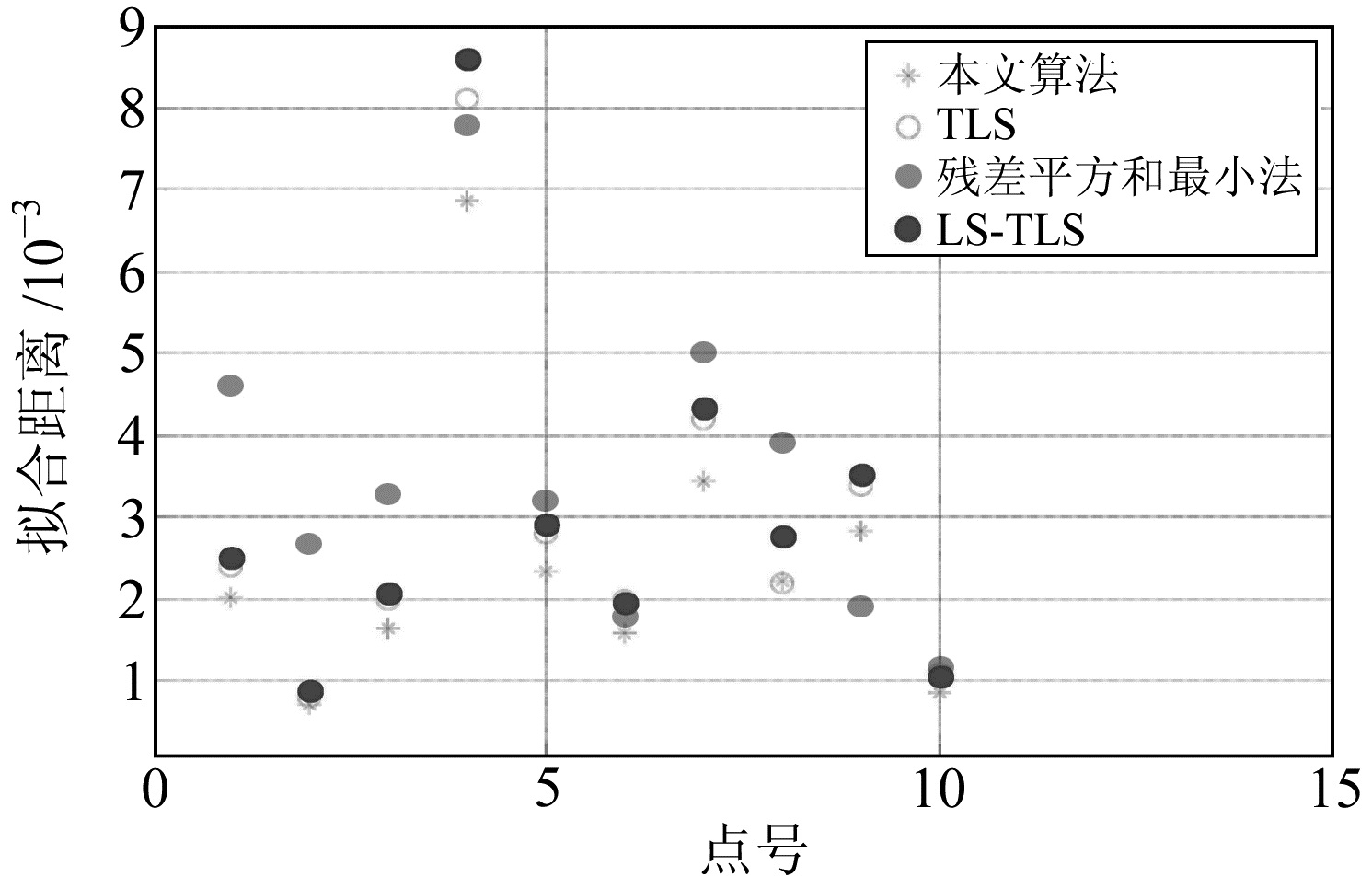
|
图 1 4种算法的拟合距离 Fig. 1 Fitting distance of four algorithms |
|
|
表 2 距离和与直线度 Tab. 2 Distance tolerance and straightness |
从图 1可以看出,本文算法的拟合距离值(星号)除了第9号点外均处于底部,说明本文算法拟合的空间直线与拟合点最接近。从表 2可以看出,本文算法的直线度为0.061,小于其他3种算法,说明本文算法求解的拟合距离更加稳定;本文算法的距离和最小为0.024 5,而距离和是反映拟合距离的总体水平,精度评价较直线度更有效,综合说明本文算法的拟合精度优于其他3种算法。
将已知拟合直线和TLS、LS-TLS、本文算法中求出的空间拟合直线的标准形式转化为参数形式,结果见表 3;比较各自参数值与真值的差值,计算结果见表 4。
|
|
表 3 各算法拟合空间直线的参数值 Tab. 3 The parameter values of fitting the space line with different algorithms |
|
|
表 4 各算法的参数值与真值的残差值 Tab. 4 Residual values between the parameter values and true values for each algorithm |
从表 3、表 4可以看出,本文算法求解的参数二范数‖(Δa, Δb, Δc, Δd)‖2最小,为10.151,说明本文算法求解的参数与真值最接近;本文算法的斜率误差‖(Δa, Δc)‖2较TLS、MSTLS分别减小了4.7%、3.7%,在高量级坐标值的笛卡尔坐标系中,x的数量级经常是107,可忽略截距误差的影响,而斜率误差影响巨大,斜率误差减少了660个单位(0.066×10-3×107)。因此,减少的斜率误差能够大幅改善空间直线的拟合效果,大大减少拟合误差带来的影响。
为进一步表明本文算法的有效性,分别求解TLS、LS-TLS、本文算法系数矩阵的改正数,计算结果如表 5(单位10-4)所示,改正数为0的未列出。
|
|
表 5 不同算法解算的系数矩阵改正数eA Tab. 5 The coefficient matrix correction eA with different algorithms |
从表 5可以看出,TLS法解算的系数矩阵的常数元素存在改正数,且重复元素的改正数不一致,与实际理论不符。LS-TLS法解算的系数矩阵重复随机元素改正数不一致,也与实际理论不符。而本文算法只对系数矩阵A中随机元素组成的a矩阵进行改正,所以保证了重复随机元素改正数一致、常数元素改正数为零,故本文模型相对严谨。本文算法解算的单位权方差为1.378 4×10-5,小于TLS、LS-TLS解算的2.778 3×10-5、1.785 9×10-5。综上说明,本文算法较TLS、LS-TLS更符合实际,空间直线拟合效果更优。
5 结语在使用EIV模型求解拟合参数时,系数矩阵中存在不含误差的常数项。采用总体最小二乘求解,系数矩阵中的常数项也参与了误差分配,不能保证重复元素有相同的改正数。混合总体最小二乘虽能保证系数矩阵常数元素的改正数为零,但不能保证重复元素有相同的改正数,这与实际不符。本文算法既保证了系数矩阵重复元素的改正数一致,常数元素的改正数为零,理论模型较为合理,且求解过程类似于经典最小二乘间接平差,编程计算简便。对空间直线的一组实测数据进行处理,并与其他文献的求解结果进行对比分析,验证了算法的可行性,且提高了拟合精度。
| [1] |
郭际明, 向巍, 尹洪斌. 空间直线拟合的无迭代算法[J]. 测绘通报, 2011(2): 24-25 (Guo Jiming, Xiang Wei, Yin Hongbin. No Iteration Algorithm for Spatial Straight Line Fitting[J]. Bulletin of Surveying and Mapping, 2011(2): 24-25)
(  0) 0) |
| [2] |
孔建, 姚宜斌, 吴寒. 整体最小二乘的迭代解法[J]. 武汉大学学报:信息科学版, 2010, 35(6): 711-714 (Kong Jian, Yao Yibin, Wu Han. Iterative Solutions of Whole Least Squares[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 711-714)
(  0) 0) |
| [3] |
姚宜斌, 黄书华, 孔建, 等. 空间直线拟合的整体最小二乘算法[J]. 武汉大学学报:信息科学版, 2014, 39(5): 571-574 (Yao Yibin, Huang Shuhua, Kong Jian, et al. Integral Least Squares Algorithm of Space Line Fitting[J]. Geomatics and Information Science of Wuhan University, 2014, 39(5): 571-574)
(  0) 0) |
| [4] |
王伟锋, 温耐. 空间直线拟合研究[J]. 许昌学院学报, 2010, 29(5): 37-39 (Wang Weifeng, Wen Nai. Spatial Straight Line Fitting[J]. Journal of Xuchang University, 2010, 29(5): 37-39 DOI:10.3969/j.issn.1671-9824.2010.05.011)
(  0) 0) |
| [5] |
Golub G H, Loan C. An Analysis of the Total Least Squares Problem[J]. SIAM Journal on Numerical Analysis, 1980, 17(6): 883-893
(  0) 0) |
| [6] |
陈基伟.工业测量数据拟合研究[D].上海: 同济大学, 2005 (Chen Jiwei. Industrial Measurement Data Fitting Study[D]. Shanghai: Tongji University, 2005)
(  0) 0) |
| [7] |
邓小渊, 鲁铁定, 常晓涛, 等. 空间直线拟合的混合结构总体最小二乘算法[J]. 测绘科学, 2016, 41(6): 1-4 (Deng Xiaoyuan, Lu Tieding, Chang Xiaotao, et al. General Least Squares Algorithm for Hybrid Structures with Spatial Line Fitting[J]. Science of Surveying and Mapping, 2016, 41(6): 1-4)
(  0) 0) |
| [8] |
汪奇生, 杨德宏, 杨腾飞. 空间直线的结构总体最小二乘拟合[J]. 大地测量与地球动力学, 2015, 35(3): 433-435 (Wang Qisheng, Yang Dehong, Yang Tengfei. Structural Least Squares Fitting for Spatial Straight Lines[J]. Journal of Geodesy and Geodynamics, 2015, 35(3): 433-435)
(  0) 0) |
| [9] |
Xu P, Liu J, Shi C. Total Least Squares Adjustment in Partial Errors-In-Variables Models: Algorithm and Statistical Analysis[J]. Journal of Geodesy, 2012, 86(8): 661-675 DOI:10.1007/s00190-012-0552-9
(  0) 0) |
| [10] |
同济大学数学系. 高等数学[M]. 上海: 高等教育出版社, 2010 (Department of Mathematics, Tongji University. Higher Mathematics[M]. Shanghai: Higher Education Press, 2010)
(  0) 0) |
| [11] |
汪奇生, 杨根新. Partial EIV模型参数估计新算法[J]. 测绘科学技术学报, 2016, 33(4): 341-345 (Wang Qisheng, Yang Genxin. New Algorithm for Parameter Estimation of Partial EIV Model[J]. Journal of Geomatics Science and Technology, 2016, 33(4): 341-345 DOI:10.3969/j.issn.1673-6338.2016.04.003)
(  0) 0) |
| [12] |
邱德超, 鲁铁定. 基于Partial EIV模型的三维坐标转换参数求解方法[J]. 江西科学, 2017, 35(3): 355-359 (Qiu Dechao, Lu Tieding. A Method of Solving Three-Dimensional Coordinate Transformation Parameters Based on Partial EIV Model[J]. Journal of Jiangxi Science, 2017, 35(3): 355-359)
(  0) 0) |
| [13] |
鲁铁定, 陶本藻, 周世健. 基于整体最小二乘法的线性回归建模和解法[J]. 武汉大学学报:信息科学版, 2008, 33(5): 504-507 (Lu Tieding, Tao Benzao, Zhou Shijian. Linear Regression Modeling and Solution Based on Global Least Squares[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 504-507)
(  0) 0) |
2. Key Laboratory of Watershed Ecology and Geographical Environment Monitoring, NASMG, 418 Guanglan Road, Nanchang 330013, China;
3. Land and Resources Planning Administration of Yunfu City, 11 Fuqian Road, Yunfu 527300, China
 2018, Vol. 38
2018, Vol. 38


