随着城市地下工程的飞速发展,深基坑工程也趋于更大、更深和更加复杂,深基坑支护的难度也愈加提升,同时深基坑变化趋势快,位移变化量随着基坑的开挖迅速变大,随着基坑逐渐加固稳定,基坑位移变形才趋于平缓,因此深基坑位移变形对周边建筑物环境的影响也越加广泛。如何精确地预报与有效地控制深基坑变形,对保障周边建筑、环境与人民的安全具有非常重要的意义。近年来,国内外专家学者对此展开深入的研究,提出了很多深基坑变形预测模型,并得到了有效的应用,如灰色模型、小波分析模型、神经网络、支持向量机等单一模型与组合模型[1-8]等。但由于深基坑组成结构的物理性质、外力作用的复杂性与自身的随机性,很难建立确定的模型预测其变形,因此通过分析基坑变形数据序列的本身结构和规律,建立动态变形预报模型,是推演其未来变形趋势的有效方法。最小二乘支持向量机(least square support vector machine,LSSVM)是在支持向量机的基础上发展起来的,它不仅具有支持向量机的优点,同时将支持向量机求解的二次规划问题转为求解线性方程组的问题,大大提高了求解效率,但其存在参数选择的随机性[9-10]。果蝇优化算法(fruit fly optimization algorithm,FOA)是一种基于果蝇觅食行为推演寻求全局最优化方法,具有算法易于实现、收敛速度快、全局寻优及参数设置少等特点,被广泛地应用于科学和工程领域[11-12]。
本文采用FOA来寻找LSSVM的最优参数组合,为增强数据序列的规律性,减小随机项的扰动,提出将相空间重构理论、灰色模型与最小二乘支持向量机(grey least square support vector machine,GLSSVM)组合的新方法进行基坑预测。首先应用相空间重构理论中的Cao法与互信息法确定数据序列的嵌入维数与延迟时间,重构时间序列,再采用灰色最小二乘支持向量机(GLSSVM)进行预测,并采用果蝇优化算法进行GLSSVM参数寻优,且与不同的预报模型进行对比分析,验证该模型的可行性与有效性。
1 基于相空间重构的FOA-GLSSVM变形预测模型理论 1.1 相空间重构理论Takens等[13]提出了相空间重构的思想,并证明当m≥2d+1时,可以找出一个在拓扑意义上与原系统等价的相空间,且其维数为d。对于边坡位移时间序列{xi, i=1, 2, …n},如果其嵌入维数为m和延迟时间为τ,则重构的相空间为:
| $ \begin{array}{*{20}{c}} {x\left( i \right) = \left\{ {x\left( i \right),x\left( {i + \tau } \right), \cdots ,x\left( {i + \left( {m - 1} \right)\tau } \right)} \right\}}\\ {i = 1,2 \cdots ,N - \left( {m - 1} \right)\tau } \end{array} $ | (1) |
式中,m为嵌入维数,τ为延迟时间,N为时间序列个数,x(i)为序列中的点。
相空间重构的关键在于嵌入维数m以及延迟时间τ的选择。目前,时间选取的方法主要有自相关函数法、复相关法、互信息法等。由于互信息法具有计算上的很大优势,因此本文选取互信息法确定重构相空间的延迟时间。空间嵌入维数的确定方法主要有几何不变量法、G-P法、虚假最邻近法(false neatest neighbors, FNN)、伪最邻近的改进方法——Cao方法、C-C法等,本文选取在FNN基础加以改进的Cao方法确定最小嵌入维数。
1.2 灰色最小二乘支持向量机理论(GLSSVM)已知变形体的原始观测序列{x10, x20, x30, …, xn0},利用灰色模型GM(1, 1)得到预测值
| $ f\left( x \right) = {\mathit{\boldsymbol{w}}^{\rm{T}}}\varphi \left( x \right) + b $ | (2) |
式中,φ(x)为映射函数,w为权值向量,b为偏差量。
由结构风险最小化原理,回归问题转化为:
| $ \left\{ \begin{array}{l} \min J\left( {\mathit{\boldsymbol{w}},e} \right) = \frac{1}{2}{\left\| \mathit{\boldsymbol{w}} \right\|^2} + \frac{\mathit{\boldsymbol{r}}}{2}\sum\limits_{i = 1}^l {e_i^2} \\ {\rm{s}}.\;{\rm{t}}\;{y_i} = {\mathit{\boldsymbol{w}}^{\rm{T}}}\varphi \left( {{x_i}} \right) + b + {\varepsilon _i}\left( {i = 1,2, \cdots ,l} \right) \end{array} \right. $ | (3) |
式中,r为正则化参数,εi为误差量,ei为松弛因子。构造其拉格朗日函数:
| $ \begin{array}{*{20}{c}} {L\left( {\mathit{\boldsymbol{w}},b,\varepsilon ,a} \right) = \frac{1}{2}{{\left\| \mathit{\boldsymbol{w}} \right\|}^2} + \frac{\mathit{\boldsymbol{r}}}{2}\sum\limits_{i = 1}^l {e_i^2} - }\\ {\sum\limits_{i = 1}^l {{a_i}\left( {{\mathit{\boldsymbol{w}}^{\rm{T}}}\varphi \left( {{x_i}} \right) + b + {\varepsilon _i} - {y_i}} \right)} } \end{array} $ | (4) |
式中,L(·)为拉格朗日函数,ai(i=1, 2, …, l)为拉格朗日乘子,通过KKT条件对其求偏导数可得线性方程组:
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} 1&1& \cdots &1\\ 1&{k\left( {{x_1},{x_1}} \right) + {\mathit{\boldsymbol{r}}^{ - 1}}\mathit{\boldsymbol{I}}}& \cdots &{k\left( {{x_i},{x_j}} \right)}\\ \vdots&\vdots&\ddots&\vdots \\ 1&{k\left( {{x_i},{x_j}} \right)}& \cdots &{k\left( {{x_i},{x_i}} \right) + {\mathit{\boldsymbol{r}}^{ - 1}}\mathit{\boldsymbol{I}}} \end{array}} \right]}\\ {\left[ {\begin{array}{*{20}{c}} b\\ {{a_1}}\\ \vdots \\ {{a_l}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0\\ {{y_1}}\\ \vdots \\ {{y_l}} \end{array}} \right]} \end{array} $ | (5) |
式中,y=[y1, y2, …, yl],I表示单位矩阵,ai(i=1, 2, …, l)表示拉格朗日乘子,k(xi, yi)表示核函数,其表达式为:
| $ k\left( {{x_i},{y_i}} \right) = \varphi \left( {{x_i}} \right)\varphi \left( {{x_j}} \right) $ | (6) |
求解可得LSSVM回归模型函数估计模型为:
| $ f\left( x \right) = \sum\limits_{i = 1}^l {{a_i}k\left( {{x_i},{y_i}} \right) + b} $ | (7) |
计算残差的预测值
| $ {{\tilde x}_1} = {{\tilde x}_0} + {{\tilde e}_1} $ | (8) |
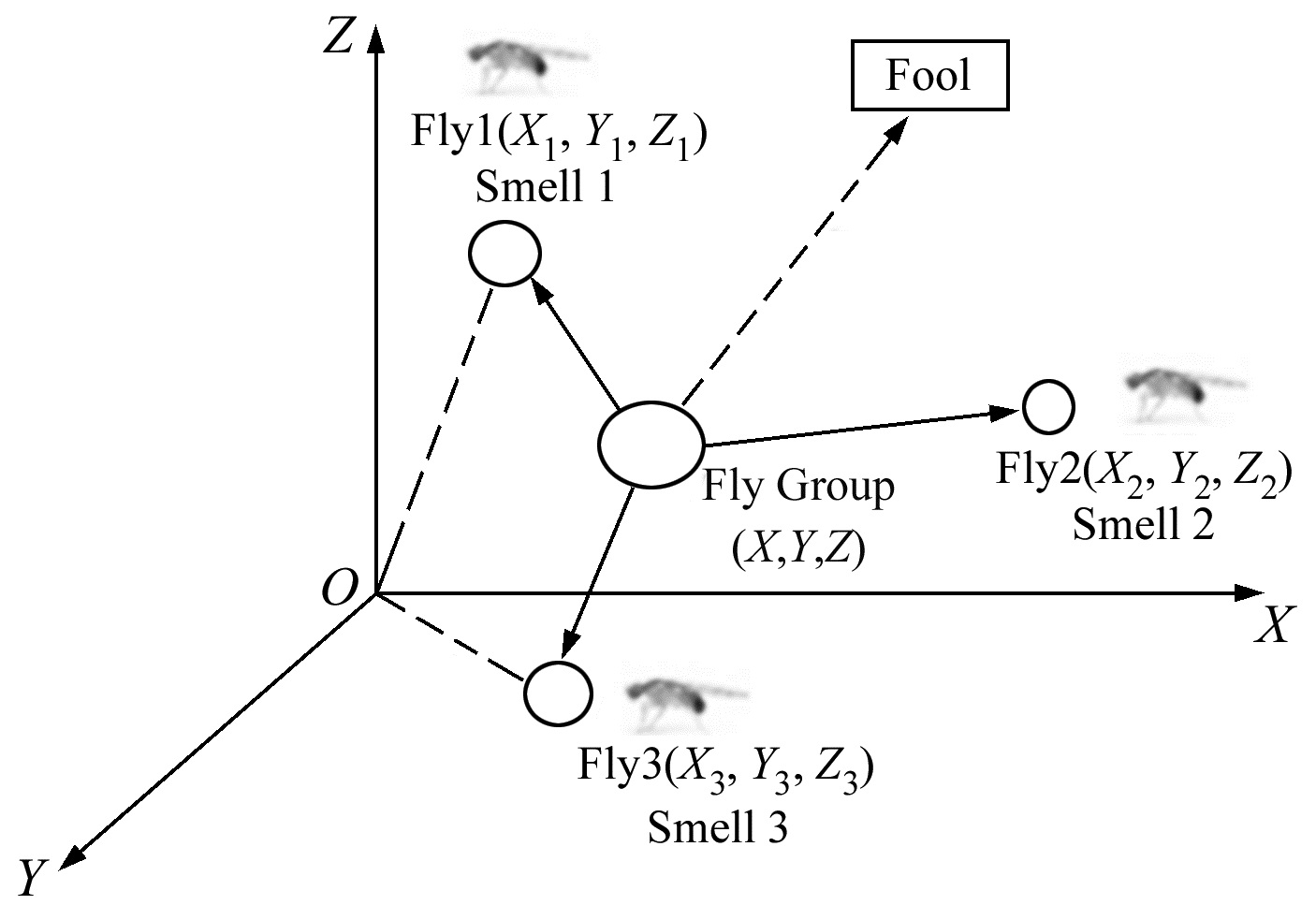
由于GLSSVM在核参数σ以及正则化参数C的选择上存在很大的随机性,因此应用FOA寻找GLSSVM的最优参数组合。果蝇算法搜寻GLSSVM的最佳参数组合的三维迭代寻优如图 1所示。
|
图 1 果蝇群体三维空间搜寻食物示意图 Fig. 1 The spatial search of food in the population of fruit fly |
果蝇优化算法(FOA)选择GLSSVM最优参数组合的具体步骤如下:
1) 初始设定果蝇群体的位置,随机设定果蝇群体的原始位置,设置果蝇群体的迭代次数以及种群规模。
2) 设定果蝇个体的飞行距离以及飞行的方向:
| $ \begin{array}{*{20}{c}} {{x_i} = {x_0} + {\rm{Random}}\;{\rm{Value}}}\\ {{y_i} = {y_0} + {\rm{Random}}\;{\rm{Value}}}\\ {{z_i} = {z_0} + {\rm{Random}}\;{\rm{Value}}} \end{array} $ | (9) |
3) 计算果蝇个体到坐标原点之间的距离(Dist),计算相应的味道浓度(S(i)),求出味道浓度的判定值:
| $ {\rm{Dist}} = \sqrt {x_i^2 + y_i^2 + z_i^2} ;S\left( i \right) = \frac{1}{{{\rm{Dist}}}} $ | (10) |
4) 设置GLSSVM的参数C与σ,进行GLSSVM训练集的计算,根据预测值计算味道浓度函数(Smell(i)),以GLSSVM的均方误差(RMSE)作为味道浓度的判定函数:
| $ {\rm{Smell}}\left( i \right) = \frac{1}{n}\sum\limits_{i = 1}^n {{{\left| {{\rm{predic}}{{\rm{t}}_i} - {y_i}} \right|}^2}} $ | (11) |
式中, predicti为预测值, yi为目标值。
5) 在果蝇群体中找出味道浓度最高位置上的果蝇个体:
| $ \left[ {{\rm{bestSmell}}\;{\rm{best}}} \right] = \min \left( {{\rm{Smell}}} \right) $ | (12) |
6) 保存最高浓度值S(best)以及相应的坐标位置(X_best, Y_best, Z_best),果蝇个体凭借视觉飞向此方向:
| $ \begin{array}{l} X{\rm{\_best}} = X\left( {{\rm{bestindex}},:} \right)\\ Y{\rm{\_axis}} = Y\left( {{\rm{bestindex}},:} \right)\\ Z{\rm{\_axis}} = Z\left( {{\rm{bestindex}},:} \right)\\ {\rm{best}}S = S\left( {{\rm{best}},:} \right)\\ {\rm{Smellbest}} = {\rm{bestSmell}} \end{array} $ | (13) |
7) 进入迭代寻优,并重复步骤2)~5),判断此时的味道浓度是否好于前一次迭代味道浓度,如果满足条件执行步骤6),否则继续执行循环迭代,直至达到最大迭代次数。将优化得到的最优参数组合输入到模型中进行预测。
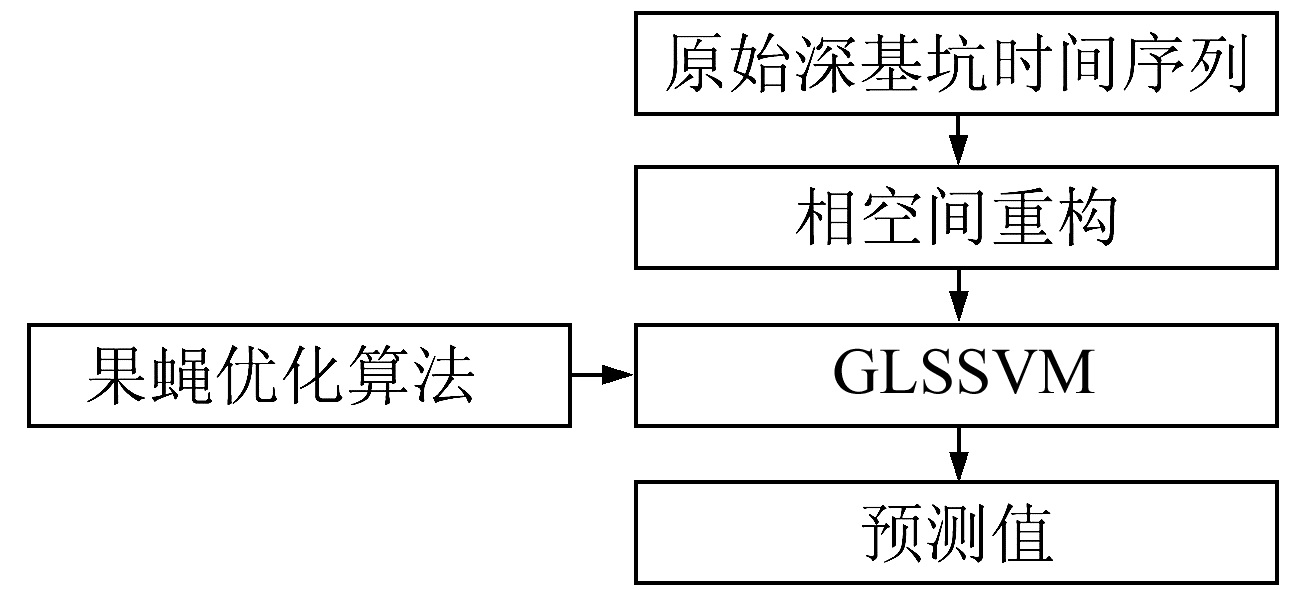
2 基于相空间重构的FOA-GLSSVM预测模型的流程设深基坑原始时间序列为{X(t), t=1, 2, …, m},采用相空间重构中的Cao法与互信息法确定该序列的嵌入维数m与延迟时间t,重新构造该序列。以前t期数据建立训练样本,剩余的后n-t期作为测试样本,建立FOA-GLSSVM预测模型,得到深基坑时间序列的预测值F={F1, F2, …, Fj}。模型预报的流程如图 2所示。
|
图 2 模型预测流程 Fig. 2 Flow chart of model prediction |
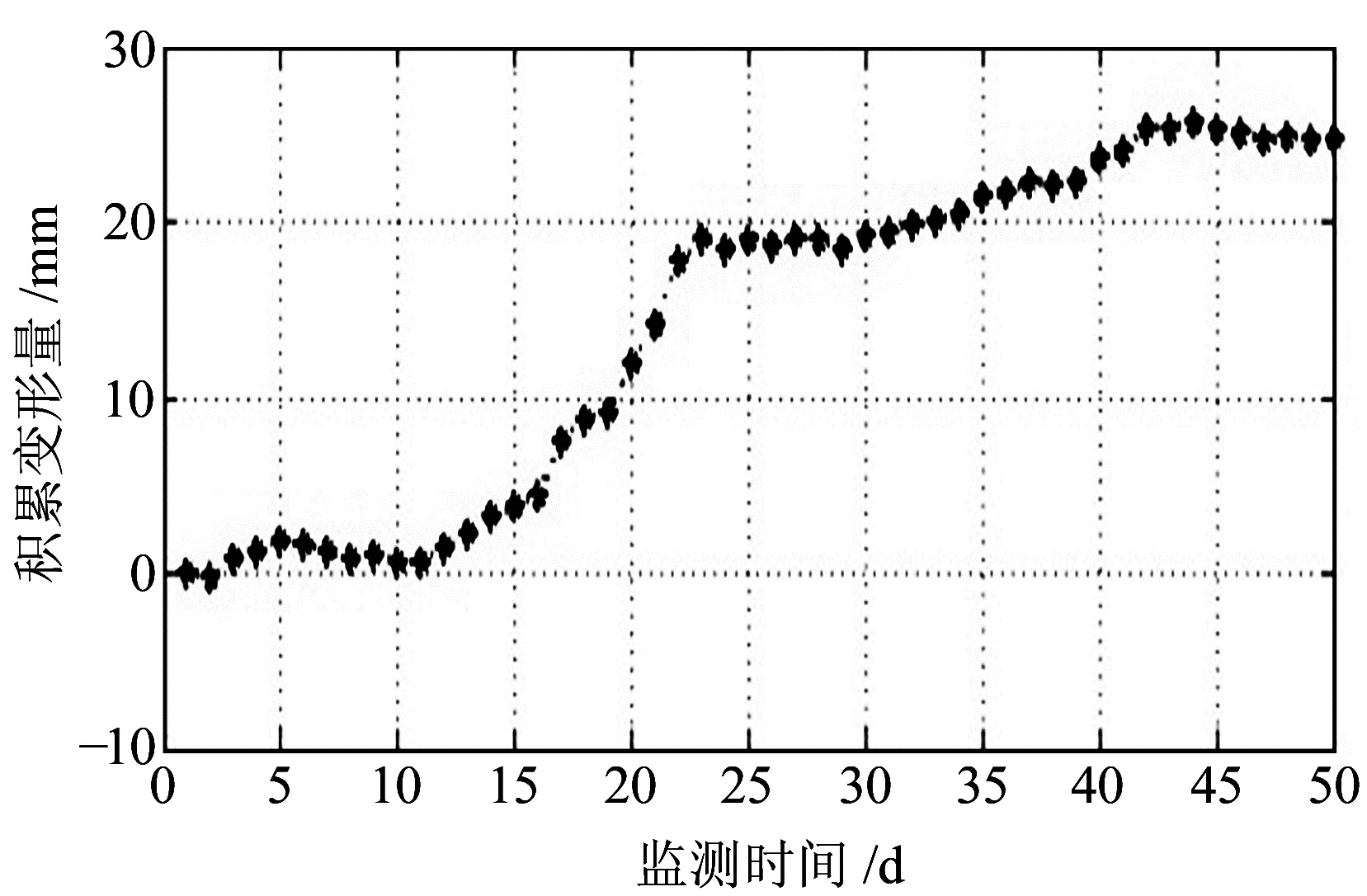
以华为总部A区北侧地下二层立体车库的深基坑围护桩桩顶S18号点的50期位移变化监测值作为模型训练与预测的样本。S18点位于基坑一侧的中部,位移变化值相对于其他监测点变化相对较大,在各监测点中变化较为突出,与基坑总体变化趋势一致,具有一定的代表性。以其前40期数据作为测试样本,剩余的10期数据作为预测样本,检查模型预测的有效性。S18点位位移变化曲线如图 3所示。
|
图 3 监测点的时间位移曲线 Fig. 3 Time displacement curve of monitoring point |
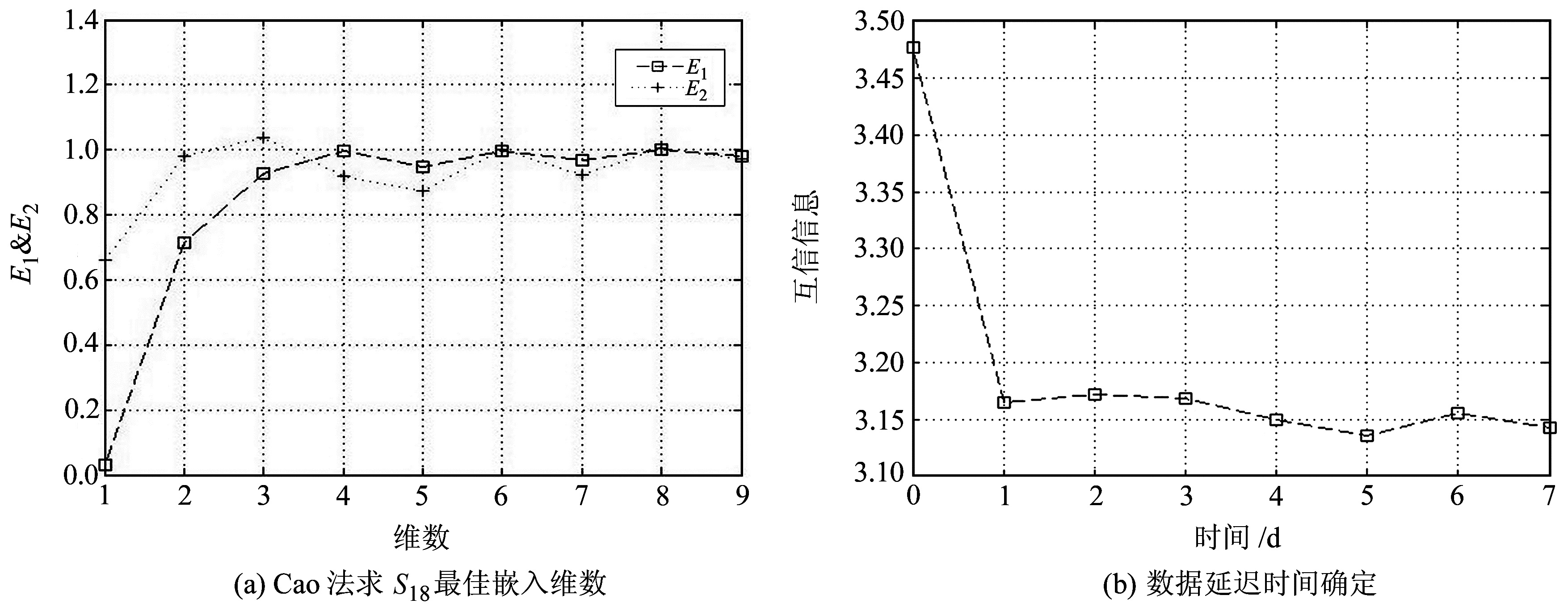
采用改进的虚假最邻近法与互信息法求取位移变化时间序列的嵌入维数以及延迟时间,图 4表示序列嵌入维数与延迟时间计算结果的变化趋势。当E1的值接近1并保持稳定,同时E2不为1时,此时即为最佳嵌入维数。互信息法是指互信息值达到第1个极值点时即为最佳延迟时间。因此由计算结果可知,此时最佳嵌入维数与延迟时间分别为m=4、τ=1。
|
图 4 嵌入维数与延迟时间计算结果 Fig. 4 Calculation results of embedding dimension and delay time |
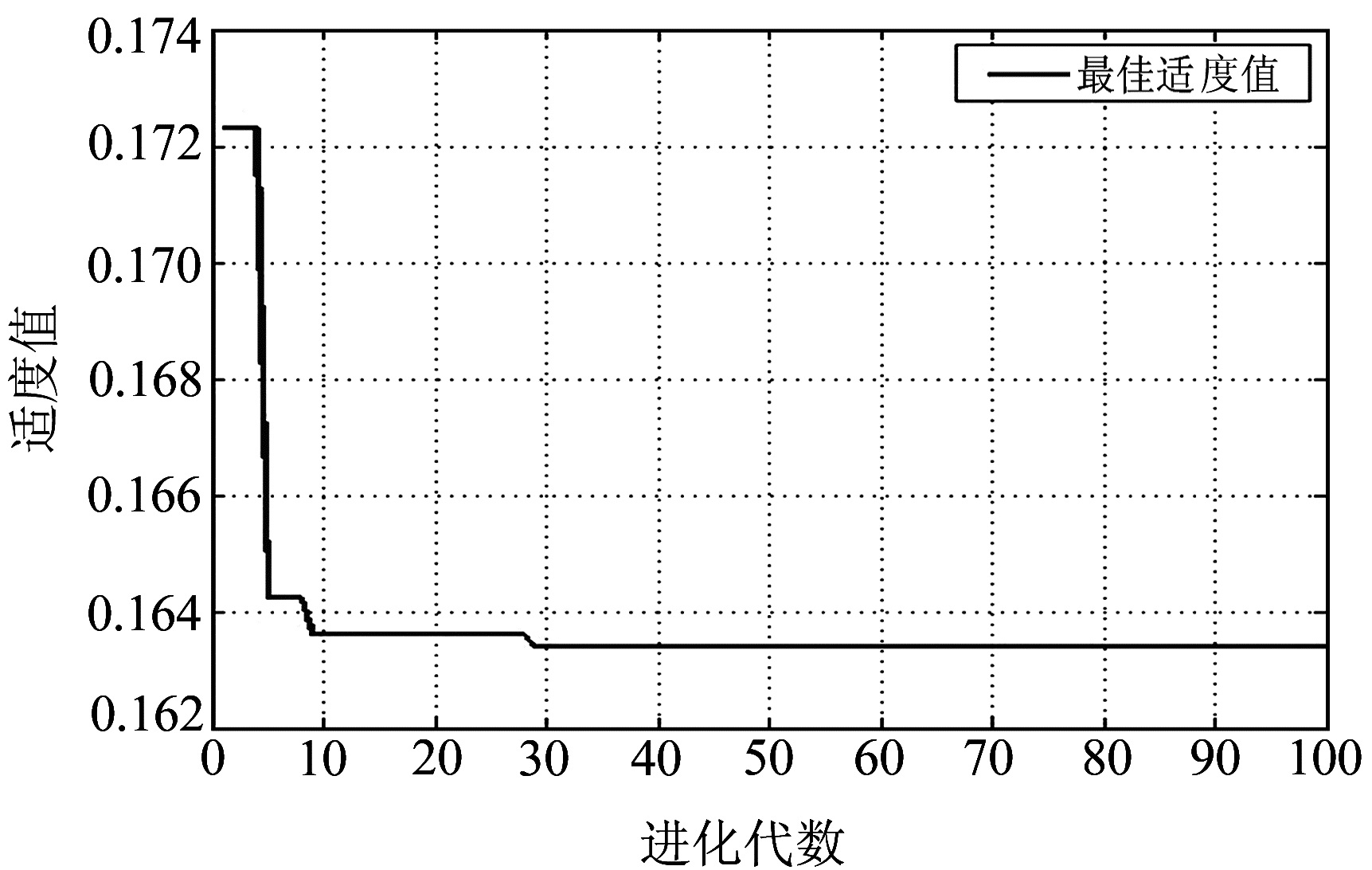
对FOA进行初始化参数设定,随机初始化设定果蝇群体位置为[0, 1],果蝇个体飞行方向与飞行距离为[-10, 10],果蝇种群规模为30,迭代次数100,以均方根误差作为算法的适度值函数。此时应用FOA对模型参数[C, σ]进行优化并建立预测模型,其寻优的适度值曲线变化如图 5所示。由图 5可知,模型在迭代计算28次时适度值曲线保持不变,此时得到最优的参数组合,即[C, σ]=[894.685 2, 0.108 5]。
|
图 5 FOA算法优化模型参数的适度值曲线 Fig. 5 FOA algorithm to optimize the model parameters of the fitness curve |
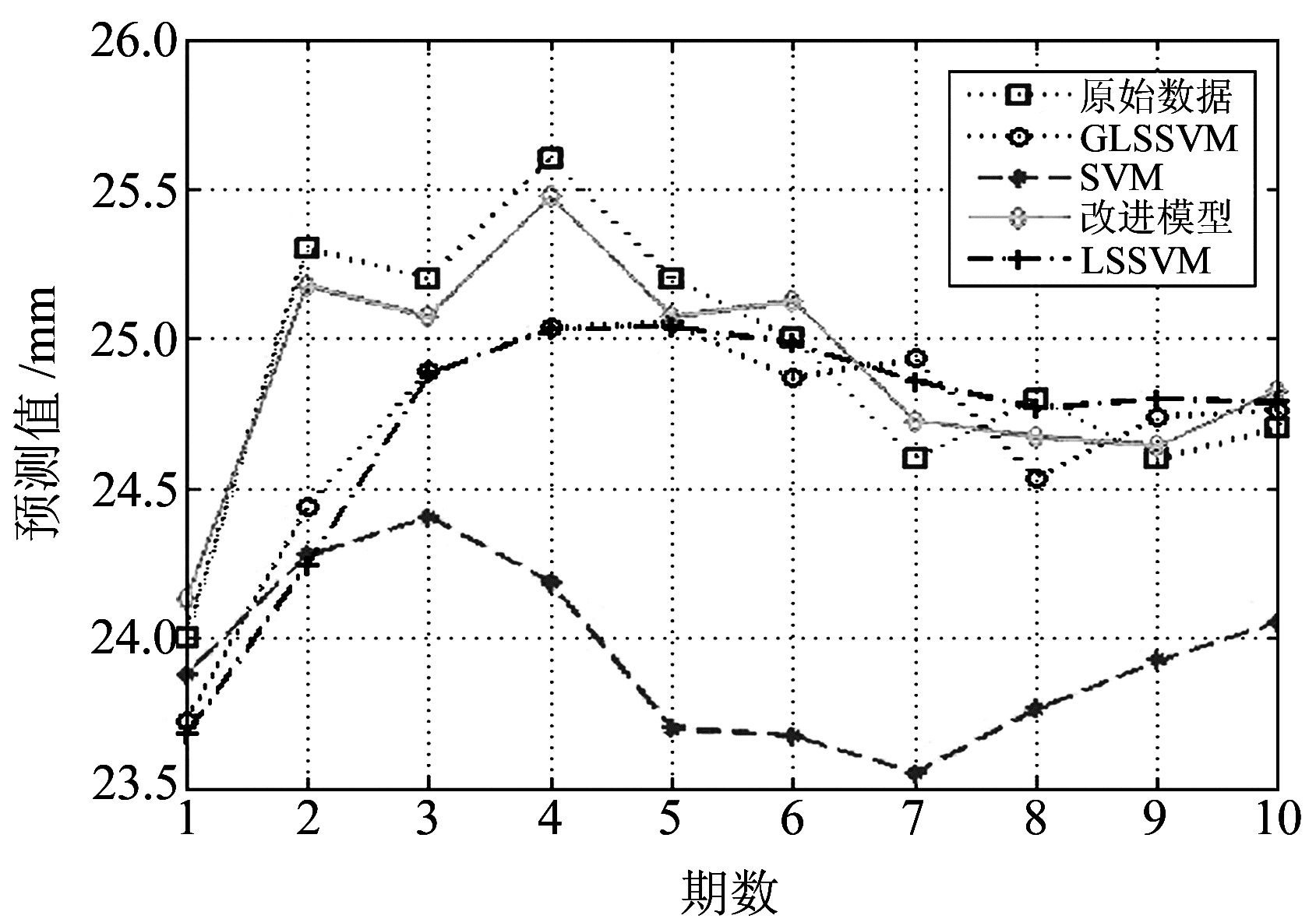
为了验证改进模型的精确性,本文与另外3种单一模型进行对比分析,并以方差、均方误差以及平均相对误差作为评定标准。各预测模型的计算结果如表 1所示,模型预测结果对比如图 6所示,精度评定如表 2所示。
|
|
表 1 不同模型预测值比较 Tab. 1 Comparison among different model predicted results |
|
图 6 模型预测值比较 Fig. 6 Comparison among results obtained by different model |
|
|
表 2 模型预测的精度评定 Tab. 2 Model fitting prediction evaluation value |
由表 1(单位mm)、表 2与图 6可知,改进模型在训练时模型训练充分、数据拟合程度较高,在预测数据与实测数据之间也相当吻合;在精度上以及稳定性上比其他预测模型更好,改进模型的最小预测误差为0.097,平均相对误差仅为0.47%,均方根误差仅为0.121。因此改进模型具有很高的可行性与可靠性,且基坑监测点的位移变化趋势总体上与基坑变形趋势一致,都是随着基坑的开挖变形迅速增大,随着基坑加固稳定变化逐步趋于稳定,因此改进模型具有很好的适应性。
4 结语1) 将相空间重构理论引入到单一变量数据序列的高维重构中,运用改进的虚假最邻近法与互信息法计算最佳维度与延迟时间,得到重构后的训练集样本与预测集,满足灰色最小二乘支持向量机数据高维度的需求。
2) 将果蝇优化算法、灰色模型与LSSVM模型进行有机结合,增加了数据序列的规律性,减小了误差影响;同时将果蝇优化算法用于模型最优参数组合的寻优中,有效地解决了模型参数选择随机性的问题,提高了模型预测的精度与稳定性。
3) 将模型应用于具体工程实例,并与单一预测模型进行对比分析,验证了模型具有一定的推广与泛化能力。
| [1] |
王强, 刘松玉, 童立元, 等. 灰色理论在深基坑支挡结构变形预测中应用[J]. 岩土工程学报, 2010, 32(2): 69-72 (Wang Qiang, Liu Songyu, Tong Liyuan, et al. Application of Grey Theory in Deformation Prediction of Retaining Structure of Deep Foundation Pit[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(2): 69-72)
(  0) 0) |
| [2] |
徐峰, 汪洋, 杜娟, 等. 基于时间序列分析的滑坡位移预测模型研究[J]. 岩石力学与工程学报, 2011, 30(4): 746-751 (Xu Feng, Wang Yang, Du Juan, et al. Study on Prediction Model of Landslide Displacement Based on Time Series Analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(4): 746-751)
(  0) 0) |
| [3] |
李龙, 高永涛, 吴顺川, 等. 综合改进BP神经网络在边坡稳定性预测中的应用[J]. 煤炭技术, 2015, 34(9): 202-205 (Li Long, Gao Yongtao, Wu Shunchuan, et al. Application of Comprehensive Improved BP Neural Network in Prediction of Slope Stability[J]. Coal Technology, 2015, 34(9): 202-205)
(  0) 0) |
| [4] |
潘国荣, 谷川. GMDH神经网络算法在变形预测中的应用[J]. 大地测量与地球动力学, 2008, 28(3): 54-58 (Pan Guorong, Gu Chuan. Application of GMDH Neural Network Algorithm in Deformation Prediction[J]. Journal of Geodesy and Geodynamics, 2008, 28(3): 54-58)
(  0) 0) |
| [5] |
范千, 花向红. 基于相空间重构与支持向量机预测滑坡位移的一种新方法[J]. 武汉大学学报:信息科学版, 2009, 34(2): 248-251 (Fan Qian, Hua Xianghong. A New Method for Predicting Landslide Displacement Based on Phase Space Reconstruction and Support Vector Machine[J]. Geomatics and Information Science of Wuhan University, 2009, 34(2): 248-251)
(  0) 0) |
| [6] |
Monfared M, Rasteger H, Kojabadi H M. A New Strategy for Wind Speed Forecasting Using Artificial Intelligent Methods[J]. Renewable Energy, 2009, 34(3): 845-848 DOI:10.1016/j.renene.2008.04.017
(  0) 0) |
| [7] |
Cortes C, Vapnik V. Support Vector Networks[J]. Machine Learning, 1995, 20(3): 273-297
(  0) 0) |
| [8] |
焦明连, 蒋廷臣. 基于小波分析的灰色预测模型在大坝安全监测中的应用[J]. 大地测量与地球动力学, 2009, 29(2): 115-117 (Jiao Minglian, Jiang Tingchen. Application of Grey Forecasting Model Based on Wavelet Analysis in Dam Safety Monitoring[J]. Journal of Geodesy and Geodynamics, 2009, 29(2): 115-117)
(  0) 0) |
| [9] |
杨帆, 谢洋洋. 基于LSSVM的区域卫星高程拟合模型[J]. 导航定位学报, 2017, 5(1): 100-103 (Yang Fan, Xie Yangyang. Regional Satellite Height Fitting Model Based on LSSVM[J]. Journal of Navigation and Positioning, 2017, 5(1): 100-103)
(  0) 0) |
| [10] |
谢洋洋, 杨帆, 俞凯. EEMD-PSOGSVM耦合模型在深基坑位移预测中的应用[J]. 大地测量与地球动力学, 2017, 37(6): 599-603 (Xie Yangyang, Yang Fan, Yu Kai. Application of EEMD-PSOGSVM Coupling Model in Displacement Prediction of Deep Foundation Pit[J]. Journal of Geodesy and Geodynamics, 2017, 37(6): 599-603)
(  0) 0) |
| [11] |
邹兵, 陈西宏, 薛伦生, 等. 果蝇优化算法优化灰色神经网络的卫星钟差预报[J]. 测绘科学, 2014, 39(9): 44-48 (Zou Bing, Chen Xihong, Xue Lunsheng, et al. Satellite Clock Error Prediction Based on Grey Neural Network Optimized by Fruit Fly Optimization Algorithm[J]. Science of Surveying and Mapping, 2014, 39(9): 44-48)
(  0) 0) |
| [12] |
潘文超.果蝇最佳化演算法[M].台北: 沧海书局, 2013 (Pan Wenchao. Fruit Fly Optimization Algorithm[M].Taibei: Tsang Hai Publishing, 2013)
(  0) 0) |
| [13] |
Takens F. Detecting Strange Attractors in Turbulence[M].Lecture Notes Math, 1981: 366-381
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38

