2. 中国测绘科学研究院,北京市莲花池西路28号,100830
自星载GPS定轨技术成功应用于TOPEX/Poseidon卫星[1]精密轨道确定(precision orbit determination,POD)任务,并通过如GRACE[2]、CHAMP[3]、GOCE[4]等多颗卫星的成功实验,因其高质量、高精度、全天候等特点,星载GPS定轨技术不仅成为低轨(low earth orbit,LEO)卫星POD的重要手段,而且这种利用卫星追踪卫星(satellite-to-satellite,SST)的模式在确立高精度全球重力场[3]等方面也具有重要意义。LEO卫星完成所承担的科学研究、实际应用等任务的前提,就是获取高精度的卫星轨道。随着GPS卫星精密星历、钟差等产品精度以及卫星相关硬件制造水平等方面的不断提高,LEO卫星轨道精度可达到cm级别[5-6]。
其中,天线相位中心偏差(phase center offset,PCO)和天线相位中心变化(PCV)是影响定轨精度的重要误差。低轨卫星搭载的GPS天线往往不是测地型天线,缺少相应的PCV信息,即使在卫星入轨前利用机器人或者微波暗室校正等方法[7]得到先验PCV模型,因卫星在轨后太空环境变化、质心移动等因素,先验模型与实际模型存在较大差异。忽视或者使用错误的PCV模型在POD过程中会产生系统误差,因此,在轨校正GPS天线相位中心变化是非常有必要的。Bruce[8]在Jason-1精密定轨中首次提出利用载波相位残差进行PCV改正;Montenbruck[7]对地面校正和利用载波相位残差校正PCV进行详细讨论,并在轨估计TerrsSAR-X和GRACE B卫星GPS天线的PCV模型发现,考虑PCV对精密定轨可提高mm级别,并建议在轨估计PCV时使用先验模型;Jäggi[9]则提出利用直接法和残差法估计PCV模型,通过模拟数据和实测数据分析了两种方法的优缺点;谷德峰[10]对国产实验3号卫星GPS天线PCV进行在轨估计,并讨论了残差法的可行性。此后国内外学者对GOCE[11]、SWARM[12]、HY2A[13]的GPS天线PCV模型利用直接法或残差法进行在轨估计,得到有益结论。
针对国产资源三号01星(ZY3-01)的精密定轨已有学者[14-15]进行相关研究,但均忽略PCV对该星精密定轨的影响。因此,本文利用该星的实测GPS数据,基于简化动力学定轨方法[14]和残差法[7-13],对ZY3-01星的GPS天线PCV模型进行在轨估计,并以重叠弧段对比、SLR检核等手段分析其对精密定轨的影响。
1 GPS接收机天线相位中心校正 1.1 GPS接收机天线相位中心模型GPS直接测量值为GPS卫星信号发射时刻天线瞬时相位中心和LEO卫星信号接收时刻天线瞬时相位中心的距离,而精密定轨在惯性系下需以LEO卫星质心为参考点,因此,需要对PCO和PCV进行改正。PCO、PCV均在天线固定参考坐标系(antenna-fixed system,AFS)下定义,AFS原点为几何参考点(antenna reference point,ARP);z轴正方向与机械系统轴相连,指向视准轴方向;y轴和x轴与卫星本体坐标系(satellite body system,SBS)相关,指向依据具体天线安装情况而定,本文选取的ZY3-01星AFS与SBS指向相同。方位角定义为一矢量在xoy平面内由+y轴旋转至+x轴的角度,高度角定义为该矢量和xoy平面的夹角。本文采用地面标定的PCO为固定值,重点探讨PCV校正对精密定轨的影响。
PCV主要与高度角α、方位角z及信号频率有关。设PCO矢量形式为Δr,则由PCO及PCV导致的改正到ARP的距离误差为[16]:
| $ \Delta \varphi \left( {\alpha, z} \right) = \Delta \boldsymbol{re} + {\rm{PCV}}\left( {\alpha, z} \right) $ | (1) |
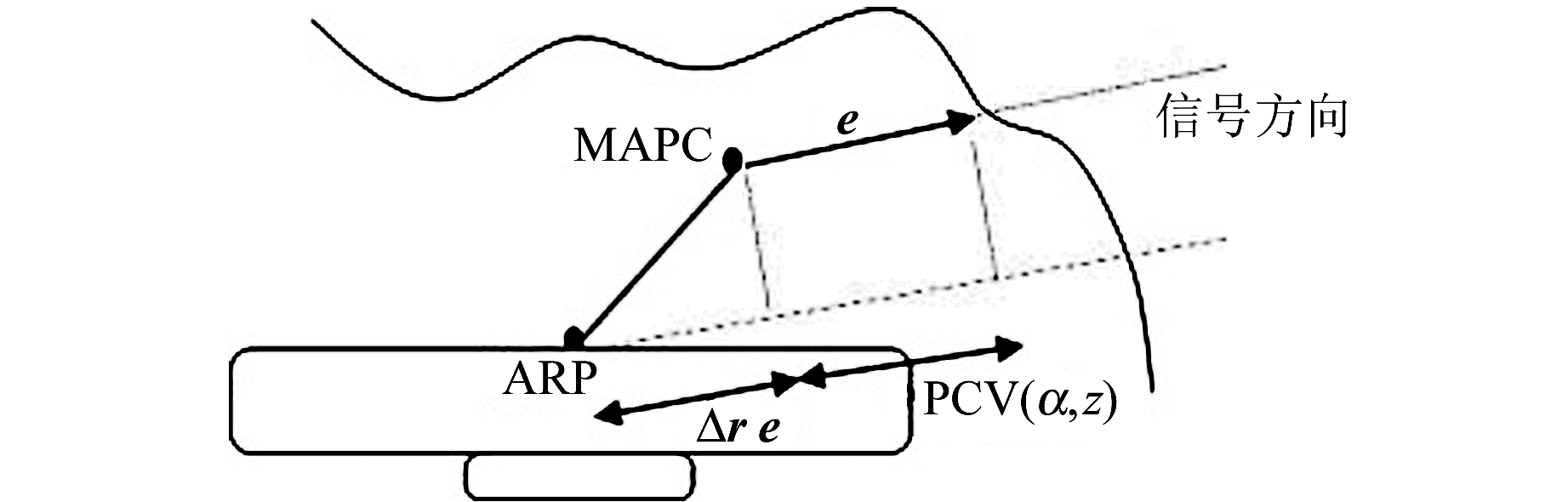
式中,Δr为平均相位中心(mean antenna phase center,MAPC)与ARP的偏差矢量,e为卫星信号入射方向的单位矢量(图 1)。
|
图 1 GPS接收机天线相位中心改正模型 Fig. 1 Model of GPS receiver antenna phase center correction |
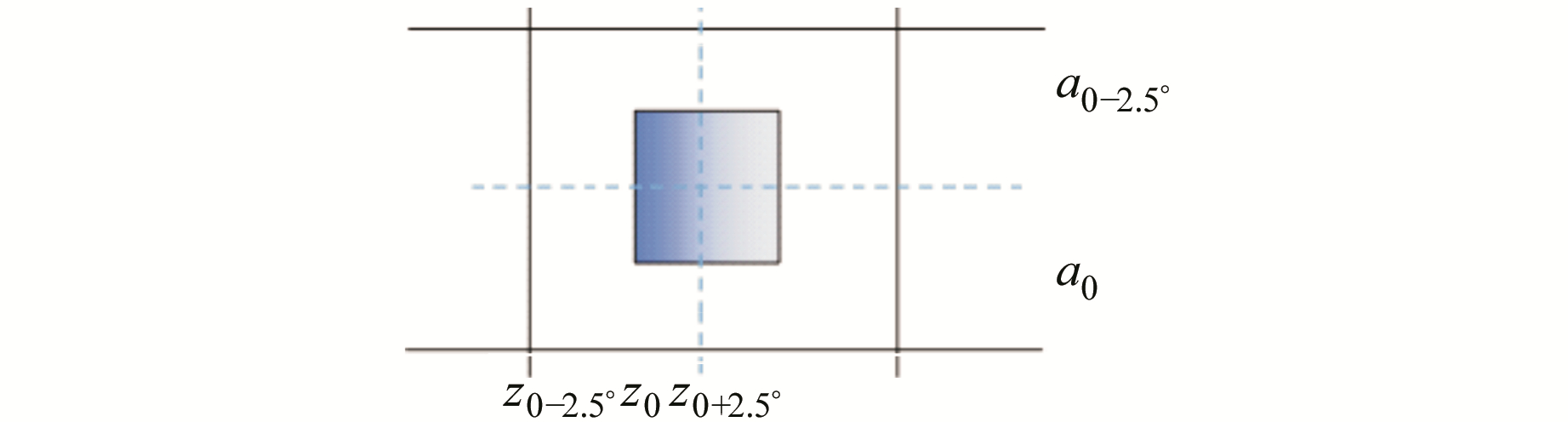
目前PCV模型的表示方法主要有球谐函数和分段线性函数。球谐函数表示方法物理意义明确,但计算量较大。与IGS发布的测地型天线ANTEX格式[16]的PCV表示方法相同,分段线性函数方法也将PCV表示为与图 2所示的与高度角、方位角相关的格网化的数值,该方法计算量小,实现容易,效果与球谐函数差异很小,所以本文采用分段线性函数表示PCV模型。设PCV模型由在高度角和方位角组成的网格图中的不同格网点组成,利用双线性插值公式即可得到所求对应方位角和高度角的PCV值。
|
图 2 残差法估计PCV模型 Fig. 2 Model of PCV estimation by residual method |
目前LEO卫星GPS天线PCV在轨估计主要有直接法和残差法。直接法[9]是将PCV视为未知参数,引入观测方程与其他动力学参数一起求解,该方法意义清晰,但计算量大且需要储存多天法方程一同解算,对计算机的储存能力和计算能力要求较高。残差法[7-8, 10-13]利用精密定轨后的载波观测值残差进行提取建模,从而建立最终的PCV模型,该方法计算简单,容易编程实现。本文采用残差法进行PCV估计。
为消除电离层一阶项影响,采取双频无电离层(ionosphere-free,IF)组合观测值,载波观测方程[10]为:
| $ \begin{array}{l} {L_{{\rm{IF}}}}^j\left( t \right) = \frac{{{f_1}^2}}{{{f_1}^2-{f_2}^2}}{L_1}^j\left( t \right)-{\rm{ }}\frac{{{f_2}^2}}{{{f_1}^2-{f_2}^2}}{L_2}^j\left( t \right) = \\ {\rho ^j}(t, {\tau ^j}) + c\;\delta t\left( t \right) + {b_{{\rm{IF}}}}^j + \delta {\rho _{{\rm{cor}}}}\left( t \right) + {\varepsilon _{{L_{{\rm{IF}}}}}}^j\left( t \right) \end{array} $ | (2) |
式中,下标IF表示无电离层组合,下标1、2表示不同频率载波,上标j表示第j颗卫星,τj是真实的信号传播时间,ρj(t, τj)是GPS卫星和LEO卫星各自质量中心的距离,δt是LEO卫星的钟差改正,bIFj是无电离层组合值模糊度,εjLIF是多路径、硬件噪声等未被模型化的误差,而δρcor是一系列的相关误差改正项:
| $ \begin{array}{l} \delta {\rho _{{\rm{cor}}}}\left( t \right) =-c\delta {\rho _{{\rm{clk}}}}(t, {\tau ^j}) + \delta {\rho _{{\rm{rel}}}}\left( t \right) + \\ \delta {\rho _{{\rm{GPS}}}}^j\left( t \right) + \delta {\rho _{{\rm{LEO, IF}}}}\left( t \right) \end{array} $ | (3) |
式中,δρclk是GPS卫星的钟差改正,δρrel是GPS卫星的相对论改正,δρGPSj是GPS卫星天线相位中心误差改正,δρLEO, IF则是LEO星载GPS天线的PCO误差改正。由于在定轨中引入了精密钟差、精密星历、GPS卫星的天线PCO及PCV(igs08.atx)、地面标定的LEO卫星星载GPS天线的PCO等相关改正,不考虑LEO星载GPS天线的PCV改正,可获取进行误差改正后的计算值ZIFj。所以载波相位观测值残差为:
| $ {\varphi _{{\rm{IF}}}}({e^j}) \approx {L_{{\rm{IF}}}}^j\left( t \right)-{Z_{{\rm{IF}}}}^j\left( t \right) $ | (4) |
经过上述改正,造成O-C(observation minus computation)差异的主要原因是未考虑LEO卫星PCV的影响,虽然PCV在定轨过程中会被钟差、模糊度等参数影响,但通过统计大量数据以及引入精密的改正模型,PCV误差大部分都残留在载波相位观测值残差中。
将LEO卫星天线空间划分为5°×5°的格网(图 2),获取的观测值残差将落入格网中,为获取[a0 z0]格网点处的PCV值,将落入[a0-2.5° z0-2.5°]、[a0+2.5° z0-2.5°]、[a0-2.5° z0+2.5°]、[a0+2.5° z0+2.5°]组成的阴影区域内所有的观测值残差值求取平均值,并视为[a0 z0]格网点处的PCV值。
当没有残差值落入时,为避免出现“空洞”,可将该点处的PCV值视为0,待有满足区域要求的残差值落入时再处理。在解算参数时,钟差、模糊度参数等会影响最终的观测值残差,因此需要多次迭代来尽可能消除该影响,本文是迭代3次获取最终的PCV模型。因PCV、PCO定义在天线固定坐标系下,需通过旋转矩阵将PCO、PCV转换至惯性系下,利用式(1)即可对测距信息进行改正。
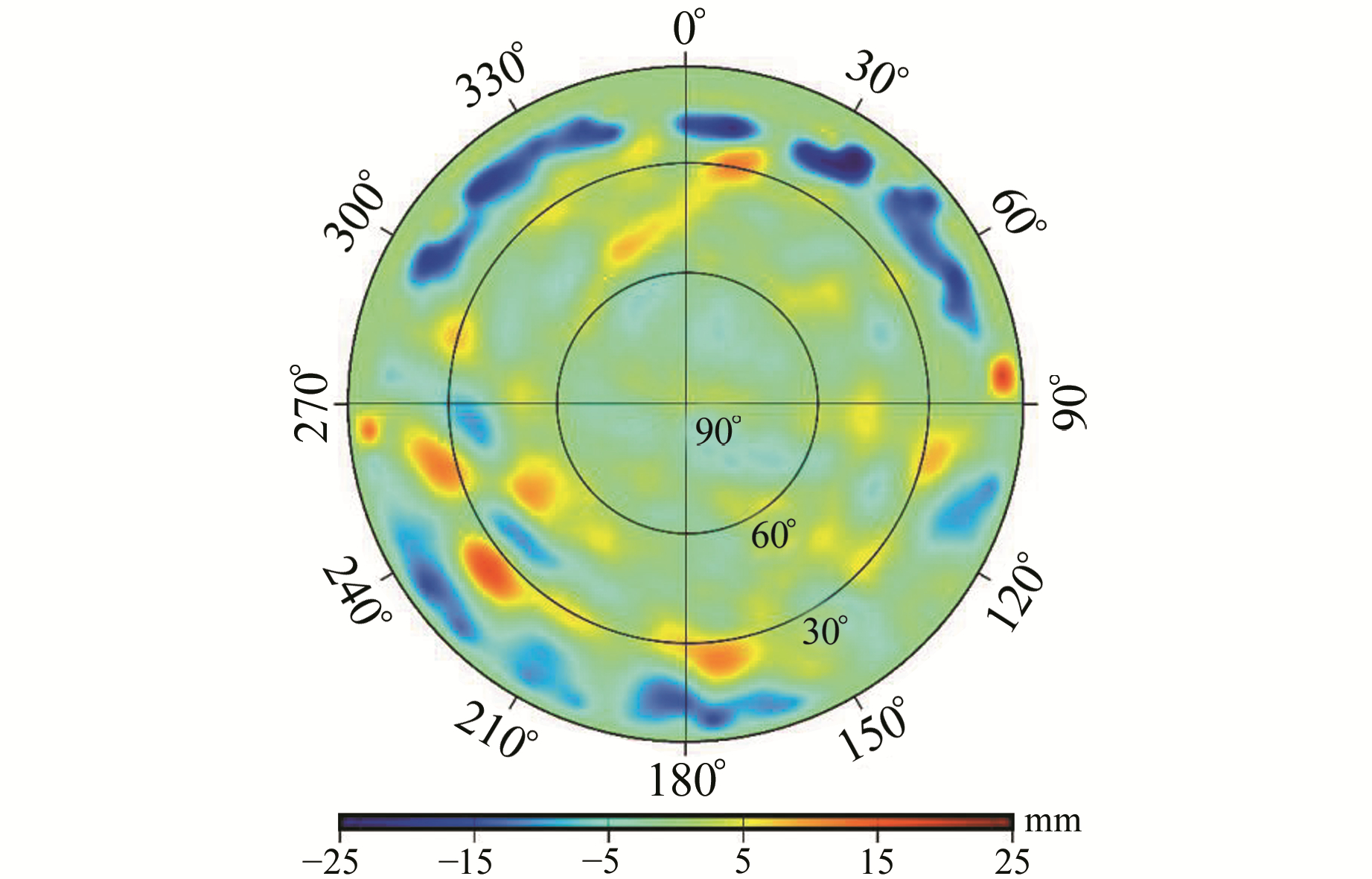
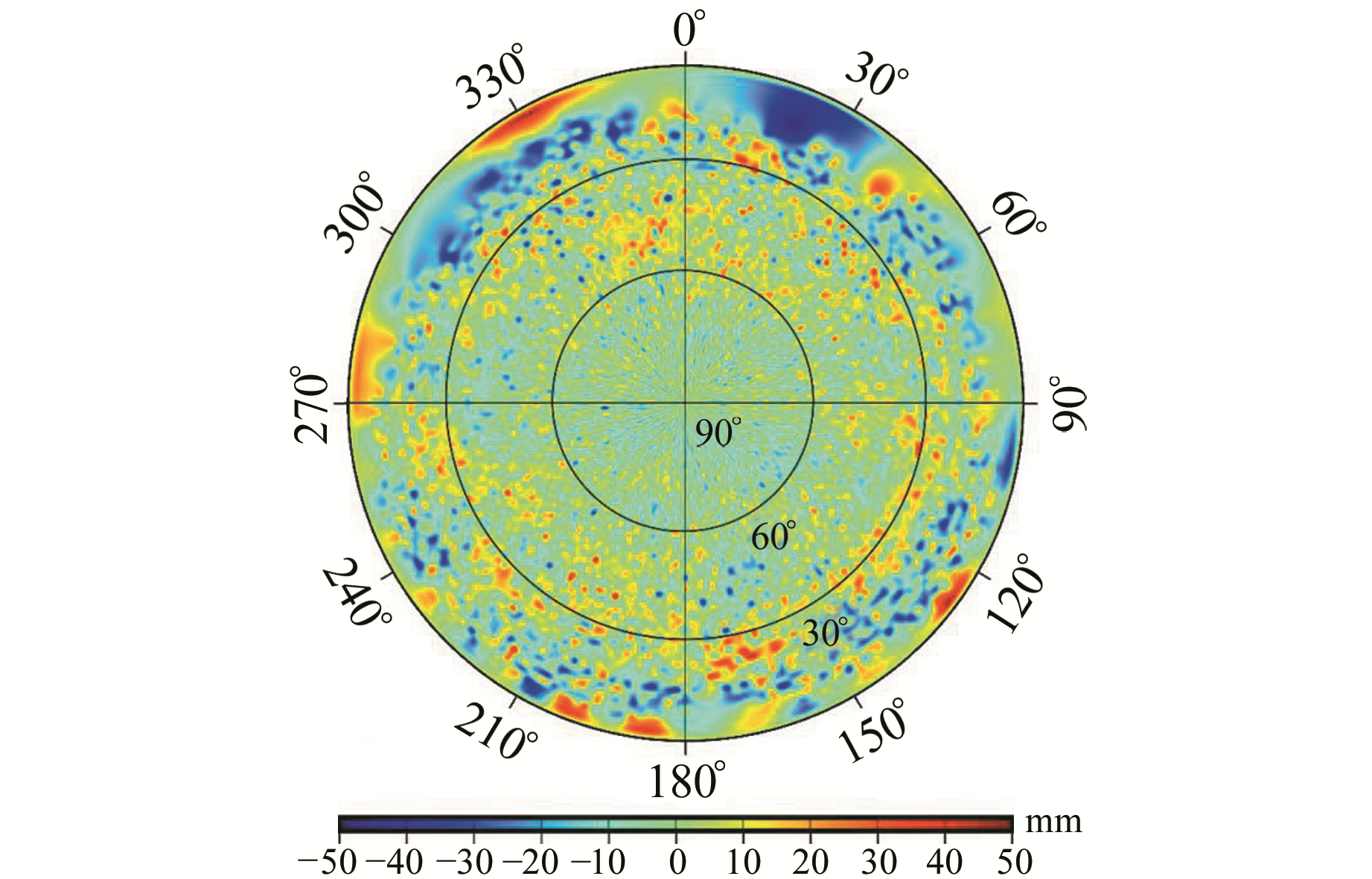
2 PCV对精密定轨的影响图 3展示了天线参考坐标系下ZY3-01星的GPS天线相位中心变化模型,分辨率为5°×5°(高度角×方位角)。分析可知,ZY3-01星的GPS天线PCV量级在-25 ~25 mm,极值为-34.42 mm和19.33 mm。极值点以及较大的PCV值均分布于较低的高度角(5°~30°),这主要是由于高度角过低时观测值精度较差。这也可以从图 4所示的观测值残差中看出,较大的观测值残差更多地分布在低高度角区域。
|
图 3 ZY3-01星的星载GPS天线相位中心变化模型 Fig. 3 ZY3-01 GPS spaceborne antenna PCV model |
|
图 4 ZY3-01星相位观测值残差 Fig. 4 Observation residuals for ZY3-01 |
重叠弧段对比是重要的内符合精度评估手段[17],选取30 h(或者其他定轨弧长)观测时段,每天00:00为开始观测时刻,前后有6 h重复计算轨道。重叠观测时段数据相同,定轨策略相同,理论上计算出的轨道应该相同,但是由于计算中各方面原因导致实际轨道并不相同,且这两段轨道通过两次独立解算得到,可认为这两段6 h重叠轨道不相关,因此,重叠轨道的RMS值是评价轨道内符合精度的重要指标。为减小边界效应的影响,在评估重叠轨道的精度时可取中间若干h的数据作为评估轨道精度的有效数据。本文采取重叠6 h,选取中间3 h数据的评价策略。
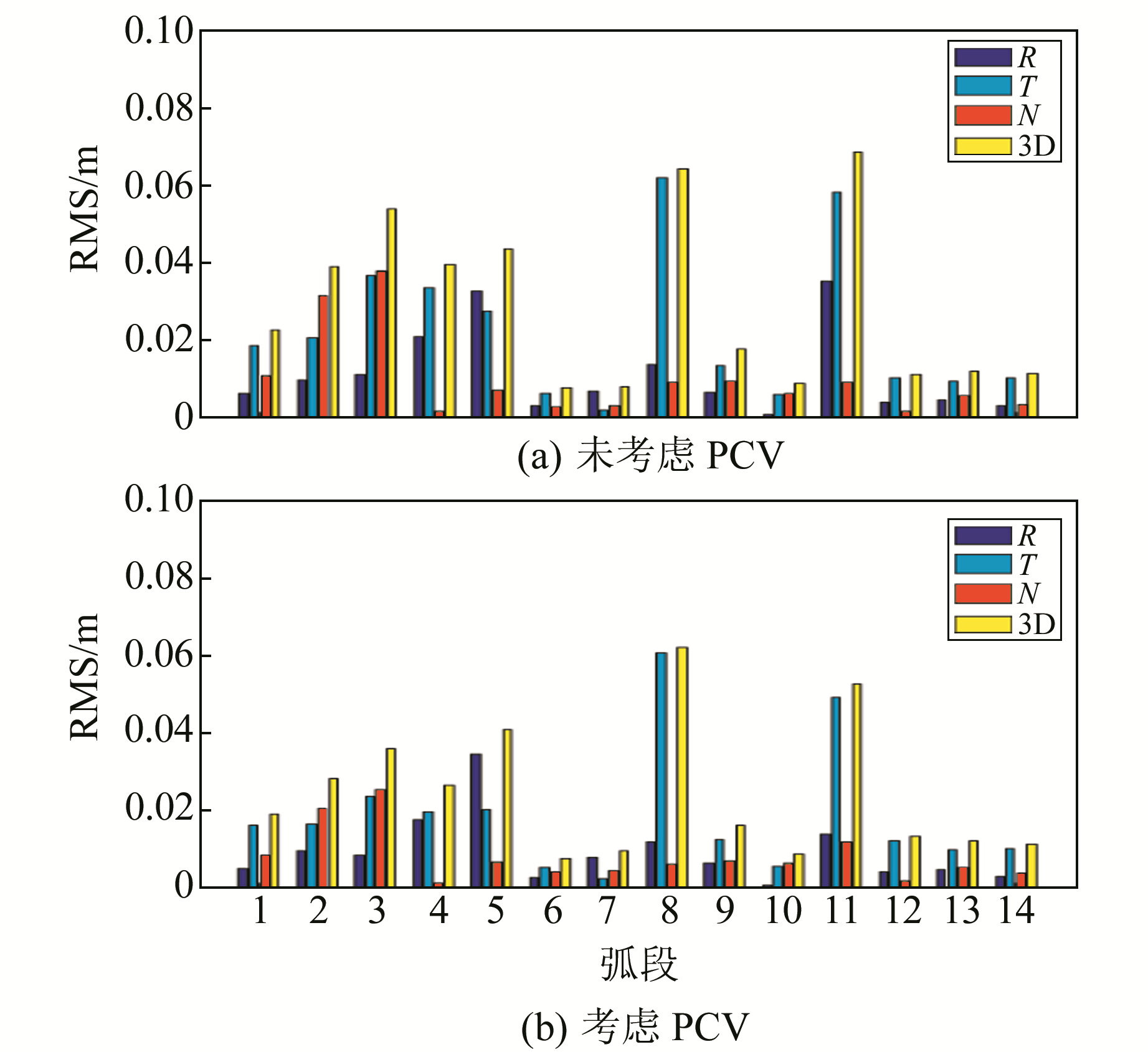
图 5反映了ZY3-01星2012-07-13~2012-07-27(年积日195~209)共14个重叠弧段在径向(R)、切向(T)、法向(N)以及三维位置(3D)的RMS值。通过分析,在未考虑PCV情况下,ZY3-01星在R、T、N、3D的重叠弧段RMS值平均为0.011 6 m、0.022 8 m、0.010 3m、0.029 6 m。在考虑本文所估计的PCV模型后,相应方向的重叠弧段RMS值分别为0.009 7 m、0.019 3 m、0.008 5 m、0.025 1 m,较未考虑PCV方案分别提高了16.4%(1.9 mm)、15.4%(3.5 mm)、17.5%(1.8 mm)、15.2%(4.5 mm)。综合分析来看,考虑PCV在ZY3-01星重叠弧段对比上,3个方向上有0.4 ~3.5 mm量级的精度提升,位置有4.5 mm的精度提升。可见,PCV影响是LEO卫星精密定轨中不可忽视的误差源,必须建立相应模型进行改正。
|
图 5 PCV对ZY3-01星重叠弧段对比的影响 Fig. 5 The influence of PCV for ZY3-01 orbit overlaps |
SLR作为重要的外符合精度检核手段,其测距精度可达到1 cm,作为低轨卫星定轨质量检核手段得到广泛的验证[17-19]。利用SLR数据检核定轨结果,实际上就是比较SLR直接测得的站星距离和星载GPS定轨结果反算的站星距,SLR残差即为两者站星距之差。为保证SLR检核可靠性,必须考虑SLR质心改正等各项改正。
ZY3-01星加入全球激光联测,在所选观测时段内(年积日195~209)选择观测质量较好的12个台站作为SLR数据来源,且SLR数据未设置截止高度角。
由图 6可见,在未考虑PCV情况下,ZY3-01星的SLR残差RMS值为0.059 2 m,轨道优于6 cm。通过考虑本文估计的PCV模型后,SLR残差的RMS值为0.058 0 m,较未考虑PCV情况提高了2.0% (1.2 mm)。文献[10]考虑GRACE卫星GPS天线PCV模型(量级:-10~10 mm),SLR检核RMS值较未考虑PCV模型提高了0.9 mm。文献[14]考虑SWARM卫星GPS天线PCV模型(量级:-20~20 mm),SLR检核RMS值较未考虑PCV模型提高了0.94 mm。文献[9]考虑TerrsSAR-X卫星GPS天线PCV模型(量级:-25~25 mm),SLR检核RMS值较未考虑PCV模型提高了1 mm。本文考虑ZY3-01卫星GPS天线PCV模型(量级:-25~25 mm),SLR检核RMS值较未考虑PCV模型提高了1.2 mm。文献[12]考虑GOCE卫星GPS天线PCV模型(量级:-30~30 mm),SLR检核RMS值较未考虑PCV模型提高了1.49 cm。可以看出,PCV量级越大,对于提高轨道精度效果越好。

|
图 6 PCV对ZY3-01星SLR残差的影响 Fig. 6 Influence of PCV on ZY3-01 SLR residuals |
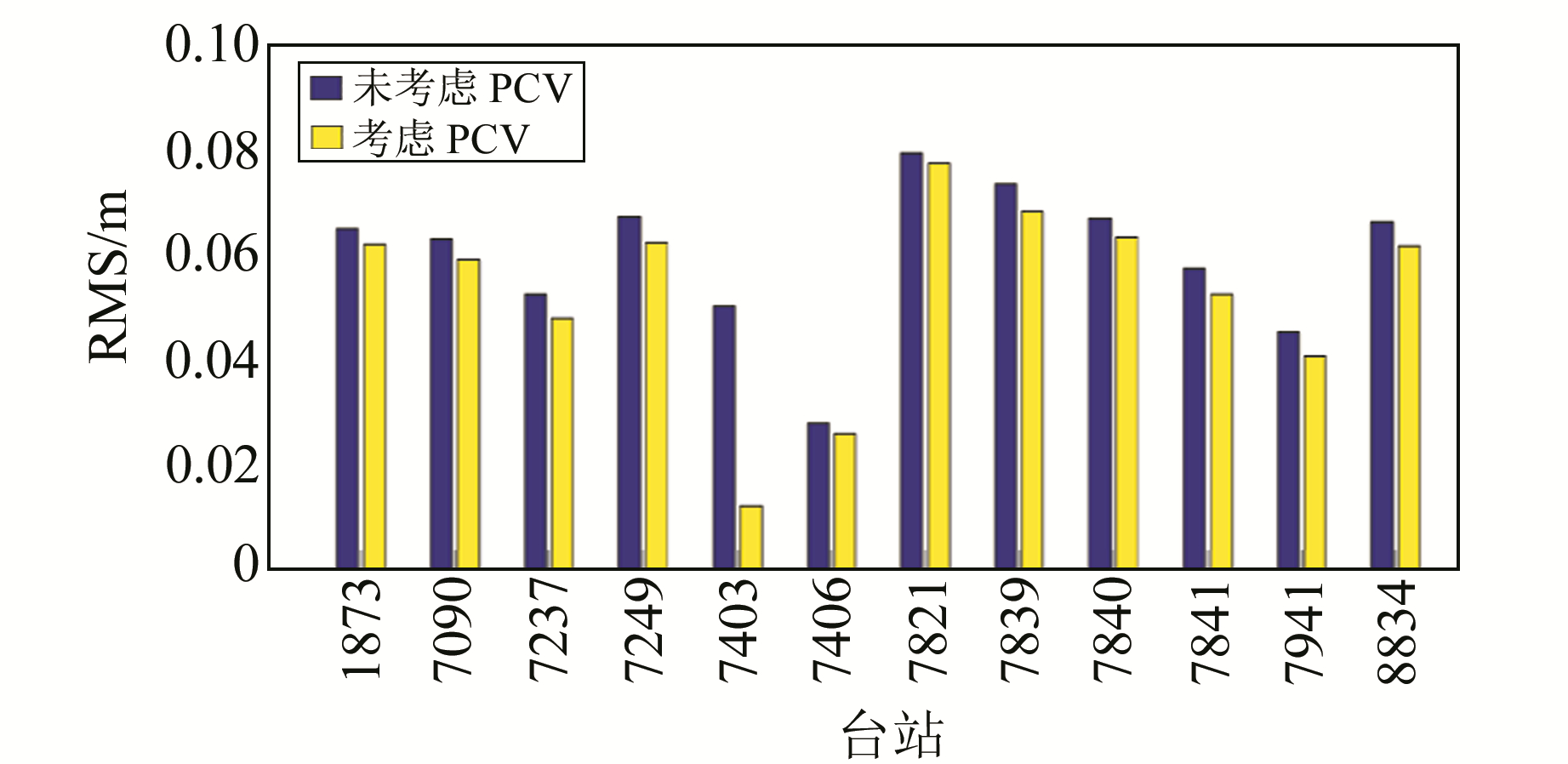
此外,为更加具体地分析PCV对精密定轨的影响,本文对每个观测台站的SLR残差RMS值进行统计(图 7,横坐标轴数字为台站编号)。经过分析,在考虑PCV影响后,ZY3-01星的观测台站的站星距残差RMS均有不同程度的精度提升,具体数据为4.6%(1 873,3.0 mm)、6.3%(7 090,4.4 mm)、8.9%(7 237,4.7 mm)、6.9%(7 249,4.6 mm)、76%(7 403,38.0 mm)、7%(7 406,2.0 mm)、2.6%(7 821,2.1 mm)、7.2%(7 839,5.3 mm)、5.2%(7 840,3.5 mm)、8.7%(7 841,5.0 mm)、9.8%(7 941,4.4 mm)、6.9%(8 834,4.6 mm)。
|
图 7 PCV对各SLR台站星站距残差的影响 Fig. 7 Influence of PCV on SLR stations residuals |
综合分析,通过考虑PCV影响,ZY3-01星各SLR台站的站星距残差RMS均有不同程度的精度提高,整体SLR检核结果有1.2 mm的提升,说明在SLR高精度测距的前提下,考虑PCV是提高精密定轨精度的一项重要措施。
3 结语本文阐述了LEO卫星GPS接收机天线相位中心改正模型以及所采用的残差法在轨估计PCV模型的基本原理和处理流程,利用我国国产ZY3-01星上搭载的国产GPS接收机上的实测GPS观测数据,基于简化动力学定轨后的载波相位观测值残差建立PCV模型,并分析了该误差源对精密定轨的影响。其中内符合精度方面,重叠弧段三维位置精度提高了4.5 mm;外符合精度方面,SLR检核站星距RMS提高了1.2 mm;各个SLR台站RMS值也有不同程度的精度提高。对比其他卫星,PCV量级越大,提高轨道精度(SLR检核)效果也越大。在未考虑PCV时定轨结果已达到cm级的基础上,考虑PCV对LEO卫星精密定轨仍有mm级别的精度提升,说明PCV是LEO卫星精密定轨中不可忽视的误差源,在我国以后的LEO卫星定轨任务中应当对此项误差源进行精密改正。
| [1] |
Yunck T P, Bertiger W I, Wu S C, et al. First Assessment of GPS-Based Reduced Dynamic Orbit Determination on TOPEX/Poseidon[J]. Geophysical Research Letters, 2013, 21(7): 541-544
(  0) 0) |
| [2] |
Tapley B D, Bettadpur S, Watkins M, et al. The Gravity Recovery and Climate Experiment: Mission Overview and Early Results[J]. Geophysical Research Letters, 2004, 31(9): 9607
(  0) 0) |
| [3] |
Reigber C, Lühr H, Schwintzer P. CHAMP Mission Status[J]. Advances in Space Research, 2002, 30(2): 129-134 DOI:10.1016/S0273-1177(02)00276-4
(  0) 0) |
| [4] |
Bock H, Jäggi A, Švehla D, et al. Precise Orbit Determination for the GOCE Satellite Using GPS[J]. Advances in Space Research, 2007, 39(10): 1638-1647 DOI:10.1016/j.asr.2007.02.053
(  0) 0) |
| [5] |
Luthcke S B, Zelensky N P, Rowlands D D, et al. The 1-Centimeter Orbit: Jason-1 Precision Orbit Determination Using GPS, SLR, DORIS, and Altimeter Data Special Issue: Jason-1 Calibration/Validation[J]. Marine Geodesy, 2003, 26(3-4): 399-421 DOI:10.1080/714044529
(  0) 0) |
| [6] |
Montenbruck O, Ramos-Bosch P. Precision Real-Time Navigation of LEO Satellites Using Global Positioning System Measurements[J]. GPS Solutions, 2008, 12(3): 187-198 DOI:10.1007/s10291-007-0080-x
(  0) 0) |
| [7] |
Montenbruck O, Garcia-Fernandez M, Yoon Y, et al. Antenna Phase Center Calibration for Precise Positioning of LEO Satellites[J]. GPS Solutions, 2009, 13(1): 23 DOI:10.1007/s10291-008-0094-z
(  0) 0) |
| [8] |
Haines B, Barsever Y, Bertiger W, et al. One-Centimeter Orbit Determination for Jason-1: New GPS-Based Strategies[J]. Marine Geodesy, 2004, 27(1-2): 299-318 DOI:10.1080/01490410490465300
(  0) 0) |
| [9] |
Jäggi A, Dach R, Montenbruck O, et al. Phase Center Modeling for LEO GPS Receiver Antennas and Its Impact on Precise Orbit Determination[J]. Journal of Geodesy, 2009, 83(12): 1145-1162 DOI:10.1007/s00190-009-0333-2
(  0) 0) |
| [10] |
Gu D F, Lai Y W, Liu J H, et al. Space Borne GPS Receiver Antenna Phase Center Offset and Variation Estimation for the Shiyan 3 Satellite[J]. Chinese Journal of Aeronautics, 2016, 29(5): 1335-1344 DOI:10.1016/j.cja.2016.08.016
(  0) 0) |
| [11] |
Bock H, Jäggi A, Meyer U, et al. Impact of GPS Antenna Phase Center Variations on Precise Orbits of the GOCE Satellite[J]. Advances in Space Research, 2011, 47(11): 1885-1893 DOI:10.1016/j.asr.2011.01.017
(  0) 0) |
| [12] |
Jose V D I, João E, Eelco D, et al. Precise Science Orbits for the Swarm Satellite Constellation[J]. Advances in Space Research, 2015, 56(6): 1042-1055 DOI:10.1016/j.asr.2015.06.002
(  0) 0) |
| [13] |
Jing G, Zhao Q L, Xiang G, et al. Quality Assessment of Onboard GPS Receiver and Its Combination with DORIS and SLR for Haiyang 2A Precise Orbit Determination[J]. Science China Earth Sciences, 2015, 58(1): 138-150 DOI:10.1007/s11430-014-4943-z
(  0) 0) |
| [14] |
赵春梅, 唐新明. 基于星载GPS的资源三号卫星精密定轨[J]. 宇航学报, 2013, 34(9): 1202-1206 (Zhao Chunmei, Tang Xinming. Precise Orbit Determination for the ZY-3 Satellite Mission Using GPS Receiver[J]. Journal of Astronautics, 2013, 34(9): 1202-1206 DOI:10.3873/j.issn.1000-1328.2013.09.004)
(  0) 0) |
| [15] |
龚学文, 王甫红. 海洋二号A与资源三号卫星星载GPS自主轨道确定[J]. 武汉大学学报:信息科学版, 2017, 42(3): 309-313 (Gong Xuewen, Wang Fuhong. Autonomous Orbit Determination of HY2A and ZY3 Missions Using Space-Borne GPS Measurements[J]. Geomatics & Information Science of Wuhan University, 2017, 42(3): 309-313)
(  0) 0) |
| [16] |
Dach R, Lutz S, Walser P, et al. Bernese GNSS Software Version 5. 2[M]. Switzerland: Astronomical Institute, University of Bern, 2015
(  0) 0) |
| [17] |
周晓青, 胡志刚, 张新远. 低轨卫星星载GNSS精密定轨的精度检核方法[J]. 武汉大学学报:信息科学版, 2010, 35(11): 1342-1345 (Zhou Xiaoqing, Hu Zhigang, Zhang Xinyuan. Discussion on POD Accuracy Evaluations for Satellite-Bone LEO Satellites[J]. Geomatics & Information Science of Wuhan University, 2010, 35(11): 1342-1345)
(  0) 0) |
| [18] |
秦显平, 焦文海, 程芦颖, 等. 利用SLR检核CHAMP卫星轨道[J]. 武汉大学学报:信息科学版, 2005, 30(1): 38-41 (Qin Xianping, Jiao Wenhai, Cheng Luying, et al. Evaluation of CHAMP Satellite Orbit with SLR Measurements[J]. Geomatics and Information Science of Wuhan University, 2005, 30(1): 38-41)
(  0) 0) |
| [19] |
衷路萍, 邹贤才, 吴林冲, 等. 利用SLR检核GOCE卫星精密轨道[J]. 大地测量与地球动力学, 2016, 36(8): 719-722 (Zhong Luping, Zou Xiancai, Wu Linchong, et al. Evaluation of GOCE Precise Orbit Using SLR[J]. Journal of Geodesy and Geodynamics, 2016, 36(8): 719-722)
(  0) 0) |
2. Chinese Academy of Surveying and Mapping, 28 West-Lianhuachi Road, Beijing 100830, China
 2018, Vol. 38
2018, Vol. 38

