2. 装备发展部军事代表局,北京市,100000;
3. 信息工程大学导航与空天目标工程学院,郑州市科学大道62号,450001
自从2005年第一颗Galileo卫星成功发射以来,国内外学者开始利用实测数据对Galileo的定位性能进行研究。文献[1-3]进行了Galileo标准单点定位(standard point positioning,SPP)的研究,文献[4-7]进行了Galileo精密单点定位(precise point positioning,PPP)的研究。然而,早期由于Galileo卫星较少,对其定位性能的研究主要集中在多系统组合方面,Galileo单系统定位的研究受到了极大的限制。
随着Galileo FOC卫星不断投入运行,Galileo单系统的定位性能也引起了广泛的关注。文献[8-9]利用9颗Galileo卫星(不包括GAL-201和GAL-202)进行了标准单点定位的研究。此外,文献[8]还利用11颗Galileo卫星进行了单系统静态精密单点定位的研究,取得了较好的定位精度。
但是,以上研究工作开展时,Galileo还未具备初始运行能力,最多只有11颗卫星参与定位解算。基于此,本文对当前Galileo单系统的单点定位性能进行评估。首先介绍Galileo星座的构成及现状;而后对GAL-201、GAL-202在标准单点定位中的作用进行验证,并评估了当前Galileo双频SPP的定位性能;最后对Galileo静态PPP的定位性能进行分析。
1 Galileo星座及现状[8-9]Galileo星座计划由30颗MEO卫星组成,分布在3个轨道平面上。其最初设计方案为“27+3”,即27颗工作星,3颗备份星;不过,目前已调整为“24+6”,即24颗工作星,6颗备份星。
截止到2017-07,欧盟已发射各类型的Galileo卫星共20颗,具体信息如表 1所示。
|
|
表 1 Galileo系统星座状态(2017-07) Tab. 1 Constellation status of Galileo system(2017-07) |
需要说明的是,GAL-201卫星(PRN:E18)和GAL-202卫星(PRN:E14)由于发射失利,导致两颗卫星未能进入预定轨道,现阶段二者均以椭圆轨道运行。此前,广播星历中并无相应的导航电文,这也是文献[8-9]未使用GAL-201、GAL-202进行SPP解算的原因。不过,目前发布的广播星历中已包含二者的导航电文。
2 Galileo定位性能评估 2.1 实验数据由上节叙述可知,在18颗在轨运行卫星当中,除GAL-104外,其余17颗卫星均已具备用于定位解算的条件。一些MGEX测站已开始接收全部18颗卫星的观测文件,并且MGEX的分析中心也发布了它们(除GAL-104)的精密星历与钟差产品,这些数据为本文的研究创造了条件。本文所用到的观测文件来自CHOF、KIRU、MAS1、MGUE、MAO0这5个MGEX跟踪站2017年DOY147的观测数据。这5个测站均可接收全部18颗Galileo卫星的信号,采样间隔为30 s。对于精密星历和钟差产品,采用GFZ分析中心发布的30 s精密钟差和5 min的精密星历。“坐标真值”采用snx文件中的IGS单天解。
2.2 Galileo双频标准单点定位 2.2.1 SPP模型及数据处理策略本文采用双频伪距消电离层组合观测值进行标准单点定位,在各项误差进行改正的基础上,其观测方程为:
| $ {{P}_{\text{IF}}}=m{{P}_{1}}+n{{P}_{5a}}=\rho +c\text{d}{{t}_{r}}+{{d}_{\text{trop}}}+{{\varepsilon }_{{{P}_{\text{IF}}}}} $ | (1) |
式中,m=f12/(f12-f5a2)、n=-f5a2/(f12-f5a2)表示消电离层组合系数,P1、P5a表示Galileo载波E1和E5a的伪距观测值,f1、f5a表示相应的频率,ρ表示站星几何距离,c表示光速,dtr表示接收机钟差,dtrop表示沿信号传播路径的对流层延迟,εPIF表示消电离层组合伪距观测值的测量噪声。
在进行标准单点定位时,高度角设置为7°,随机模型采用高度角模型。卫星轨道和卫星钟差由广播星历计算,相对论效应和地球自转效应进行模型改正,对流层延迟采用Saastamoinen模型改正,利用最小二乘法对三维位置坐标和接收机钟差进行参数估计[3]。同时,为了保证解的有效性,剔除所有PDOP值大于6的位置解[8]。
本文利用5个测站的观测数据和广播星历进行了两种方案的SPP解算。方案1为不包括GAL-201、GAL-202的标准单点定位,方案2为包含上述2颗卫星的标准单点定位。
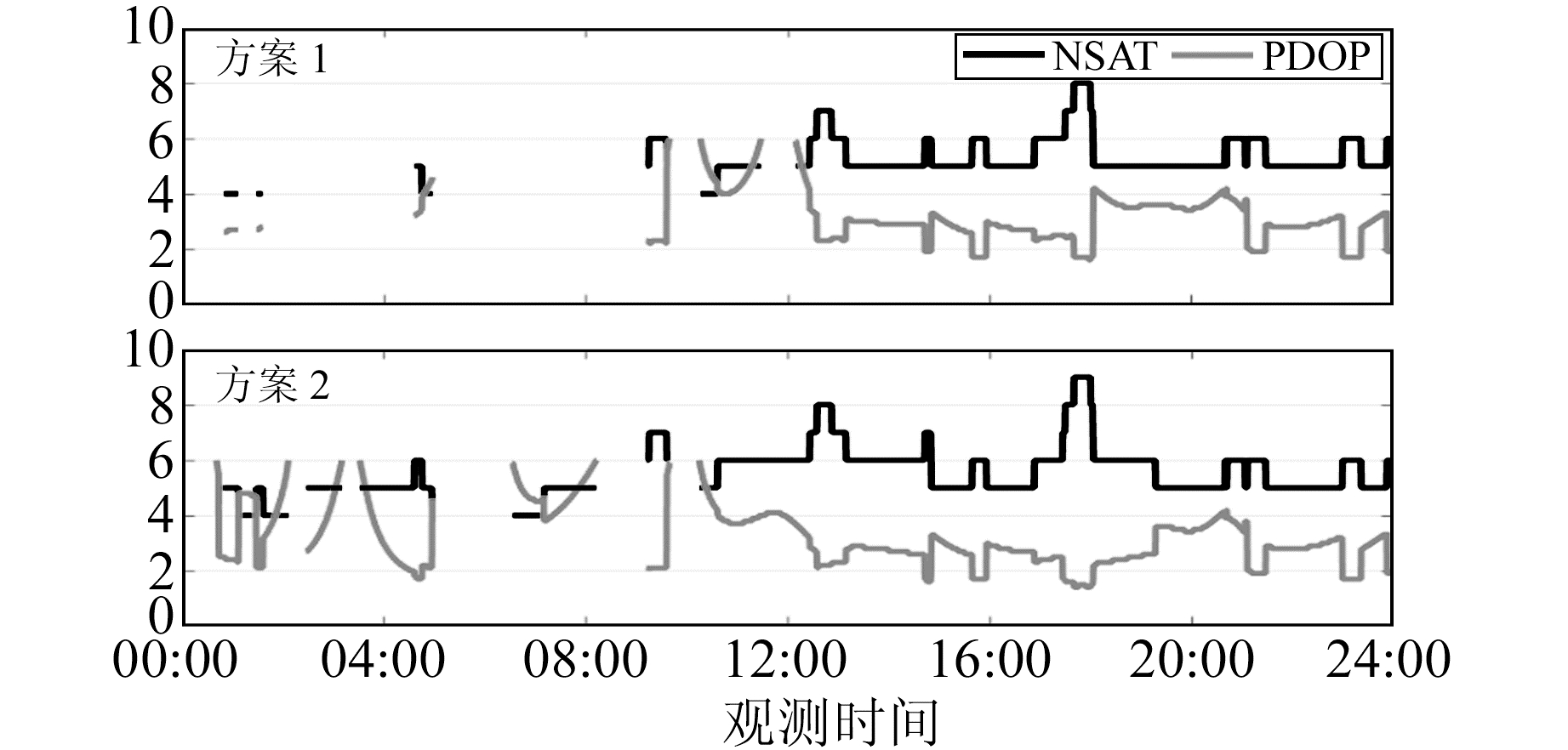
2.2.2 可见卫星数与PDOP值首先,以MGUE站为例,给出该站在观测时段内两种方案的可视卫星数(number of visible satellites, NSAT)和PDOP值,如图 1所示。可以看出,在观测时段内,方案1的可见卫星数为4~8颗,而方案2则在部分历元较方案1的可见卫星数增加1颗,这主要是由于引入了GAL-201或GAL-202。此外,部分方案1中未能显示NSAT和PDOP的历元处,在方案2中得以显示。
|
图 1 MGUE站可见卫星数目与PDOP值 Fig. 1 Visible satellite number and PDOP values at station MGUE |
表 2为5个测站的可视卫星数目和PDOP值的统计结果。可以看到,各测站方案2较方案1可视卫星数均有所增加,平均可达5.7颗;但是方案2较方案1的平均PDOP值并没有明显减小,二者均在2.9~3.4之间。这主要是因为GAL-201和GAL-202的引入,一方面使原本部分解算成功的历元获得更好的空间几何构型,进而减小了它们的PDOP值;另一方面使原本不能解算成功的历元得以成功解算,增加了统计样本数,但是这部分历元的PDOP值相对较大。两种因素的综合影响,使得方案2和方案1的平均PDOP值相差不大。
|
|
表 2 各测站平均可见卫星数目与PDOP平均值 Tab. 2 The average of visible satellite number and PDOP values at each station |
以IGS发布的单天解作为“真值”,将解算结果与“真值”作差,求得E、N、U 3个方向的坐标偏差。
对各测站当天的定位结果进行统计分析,表 3(单位m)给出位置误差的RMS具体统计信息。可以看出,两种方案的定位精度近乎相当,均可达到水平方向优于2 m、垂向优于4 m。
|
|
表 3 各测站SPP定位偏差RMS统计 Tab. 3 Statistics of RMS position bias of SPP at each station |
为了进一步分析两种方案的定位可用性,本文对定位可用率进行了统计[10]。表 4(单位%)给出了两种定位方案可用率的具体统计信息。相比于方案1,各测站方案2的可用率均有不同程度的提升,平均可用率由71.8%升至82.2%,提升了10.4%。
|
|
表 4 各测站两种方案的定位可用率 Tab. 4 The positioning availability rate of the two schemes for each station |
在精密单点定位中,双频消电离层组合观测值的观测方程为[11]:
| $ \left\{ \begin{array}{l} {P_{{\rm{IF}}}} = \rho + c{\rm{d}}{t_r} + {d_{{\rm{trop}}}} + {\varepsilon _{{P_{{\rm{IF}}}}}}\\ {\mathit{\Phi} _{{\rm{IF}}}} = \rho + c{\rm{d}}{t_r} + {d_{{\rm{trop}}}} + {\lambda _{{\rm{IF}}}}{N_{{\rm{IF}}}} + {\varepsilon _{{\mathit{\Phi} _{{\rm{IF}}}}}} \end{array} \right. $ | (2) |
式中,ΦIF表示消电离层组合载波相位观测值,NIF为消电离层组合模糊度,λIF为消电离层组合的载波波长,εΦIF表示消电离层组合伪距观测值的测量噪声。
在数据处理中,随机模型同样采用截止高度角为7°的高度角模型,利用精密星历和钟差计算卫星轨道和钟差。在数据预处理阶段,进行周跳和粗差探测[12-13];对于相对论效应、固体潮汐、地球自转效应、相位缠绕效应以及卫星、接收机PCO、PCV进行模型改正。对于对流层延迟,采用干延迟模型计算、湿延迟参数估计的方式进行修正。由于天线文件中缺少Galileo卫星的相关信息,未对Galileo卫星端进行PCO、PCV改正。采用Kalman滤波进行参数估计[14]。
为了验证Galileo PPP的定位性能,利用上述5个测站的观测数据分别进行Galileo PPP和GPS PPP两种模式的解算。同时,为了分析观测时长对Galileo PPP的影响,实验将观测数据分别以3 h、12 h、24 h作为一个观测时段进行解算。剔除个别数据质量差的观测时段后,对每个观测时段取最后100个历元的解算结果进行精度评定。
鉴于静态PPP有高精度的先验坐标值,实验将PDOP检验的限值设置为30。
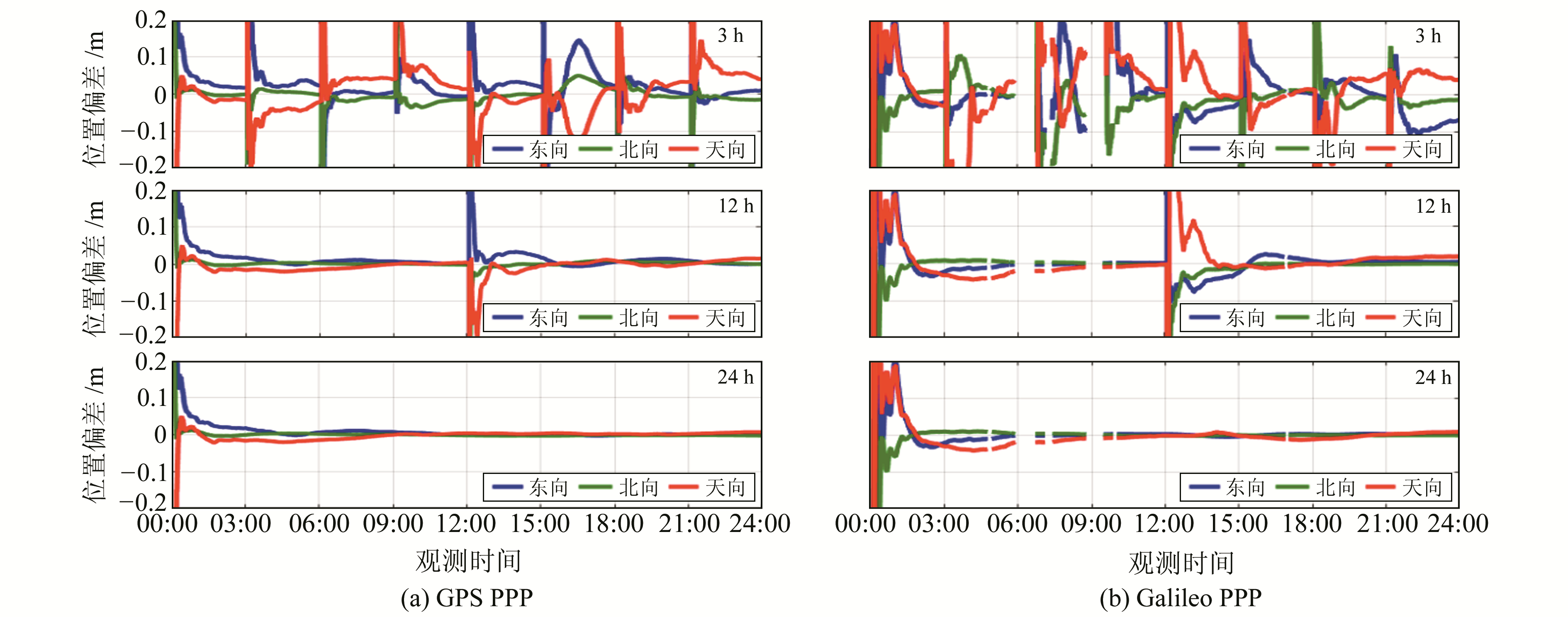
2.3.2 PPP定位精度分析首先,以MAS1站为例,依次给出观测时长为3 h、12 h、24 h的静态PPP位置偏差图,如图 2所示。可以看出,随着观测时间的增加,GPS、Galileo PPP的位置偏差逐渐减小,尽管Galileo PPP存在定位序列中断的情况,影响了收敛与定位精度,但当观测时间足够长时,仍可获得很好的位置精度。
|
图 2 MAS1站不同观测时长静态PPP位置偏差 Fig. 2 Position bias of static PPP at the station MAS1 for each time period |
表 5(单位cm)给出了不同观测时长各测站两种模式静态PPP时E、N、U各分量RMS偏差的统计结果。可以看出,在观测时长为3 h的情况下,Galileo PPP的水平精度优于5 cm、垂向精度优于7 cm,GPS PPP的水平精度优于2 cm、垂向精度优于3 cm,后者明显好于前者;而随着观测时长的增加,定位精度越来越好,当观测时长达到24 h时,Galileo PPP水平精度优于1 cm、垂向精度优于3 cm,已接近同等观测时长下GPS的定位精度。
|
|
表 5 Galileo PPP和GPS PPP各时段解的3个分量上的平均RMS Tab. 5 The average RMS of each time period solution in the east/north/up component for Galileo/GPS PPP |
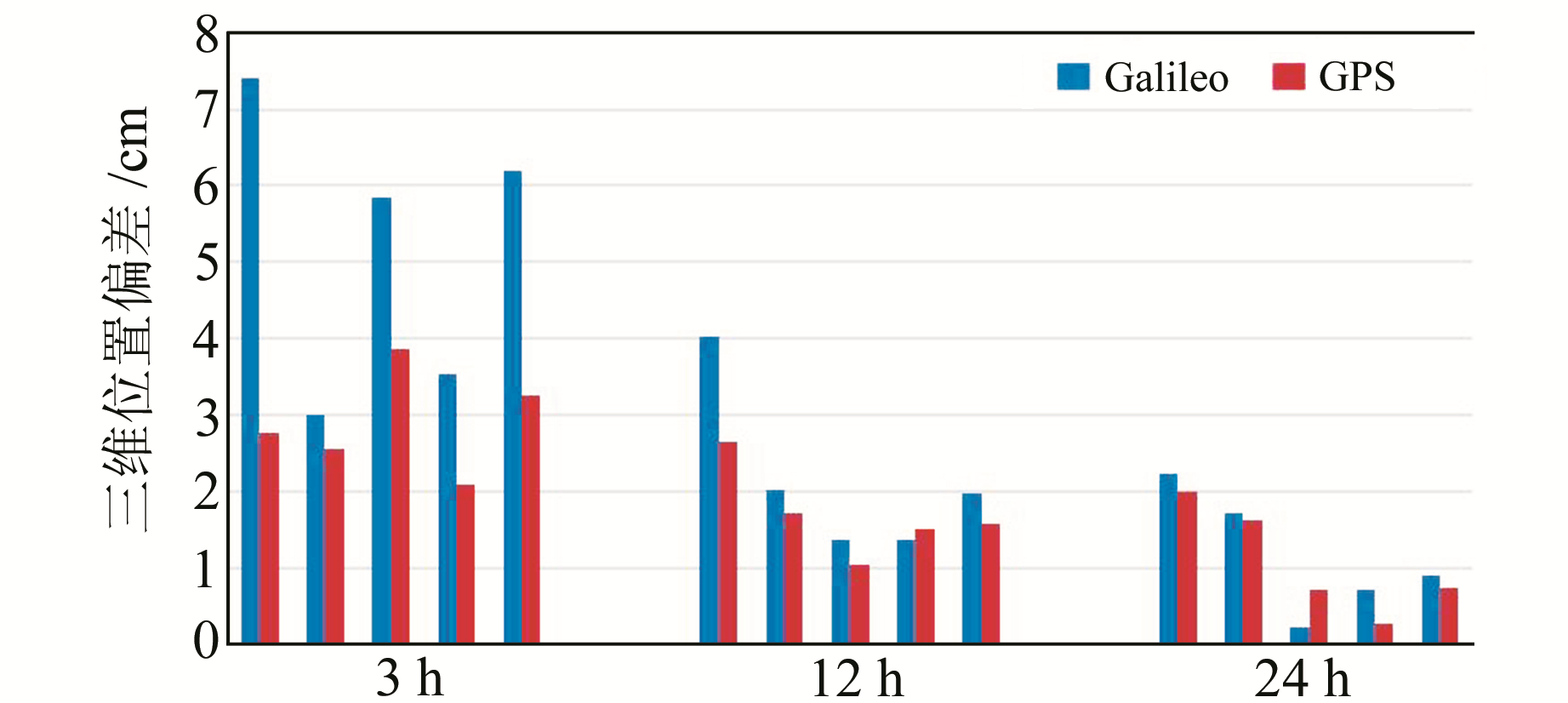
图 3给出了相应的三维位置偏差σ3D,表 6(单位cm)为具体统计信息。结合二者我们发现,当观测时长为3 h时,GPS PPP平均三维位置精度明显优于Galileo PPP。而随着观测时长的增加,两种模式PPP的σ3D逐渐减小,且二者之间的差距也越来越小,当观测时长为24 h时,Galileo与GPS PPP平均σ3D分别为1.16 cm和1.07 cm,二者几乎相当。这主要是因为相比于GPS,Galileo卫星较少,不但收敛较慢,还存在定位序列中断的情况,而且卫星端并未进行PCV、PCO改正,所以在观测时长较短时,定位精度较差,而随着观测时长的增加,逐渐收敛完全,所以精度不断提高且逼近GPS。
|
图 3 Galileo PPP和GPS PPP各时段解平均三维位置偏差 Fig. 3 The average three-dimensional positional deviation in each time period solution for Galileo/GPS PPP |
|
|
表 6 Galileo PPP和GPS PPP各时段解三维位置偏差的平均RMS Tab. 6 The average RMS of three-dimensional positional deviation in each time period solution for Galileo/GPS PPP |
Galileo卫星导航系统现已具备初始运行能力,开始提供初始服务。本文针对当前Galileo SPP和Galileo PPP的定位性能进行研究分析。通过5个MGEX跟踪站的观测数据进行定位实验,得到以下结论:
1) 目前,Galileo双频SPP可达到水平方向优于2 m、垂向优于4 m的定位精度。
2) 未进入预定轨道的Galileo卫星GAL-201、GAL-202的导航电文现可用于SPP解算,在引入二者之后,可以使平均定位可用率提升10%,达到80%以上并且保持上述的定位精度。
3) 在观测时长为3 h的情况下,Galileo PPP仅可达到水平方向优于5 cm、垂向优于7 cm的定位精度,与GPS PPP相差较大;但随着观测时长的增加,定位精度逐步提高,且与GPS的差距越来越小,当观测时长为24 h时,水平精度优于1 cm、垂向精度优于3 cm,其平均三维位置偏差与GPS近乎相当。
最后,需要指出的是,目前Galileo系统尚处于建设当中,未实现满星座运行,各种误差模型尚有待优化。随着Galileo系统建设的不断向前推进,其定位性能还会继续提升。
致谢 感谢李广杰老师对本文作者的支持与帮助。
| [1] |
Cao W, Hauschild A, Steigenberger P. Performance Evaluation of Integrated GPS/GIOVE Precise Point Positioning[C]. ION ITM 2010, San Diego, California, USA, 2010
(  0) 0) |
| [2] |
罗小敏, 蔡昌盛. GPS/Galileo组合单点定位精度分析[J]. 大地测量与地球动力学, 2013, 33(3): 136-140 (Luo Xiaomin, Cai Changsheng. Accuracy Assessment of Combined GPS/Galileo Single Point Positioning[J]. Journal of Geodesy and Geodynamics, 2013, 33(3): 136-140)
(  0) 0) |
| [3] |
Gioia C, Borio D, Angrisano A, et al. A Galileo IOV Assessment: Measurement and Position Domain[J]. GPS Solutions, 2015, 19(2): 187-199 DOI:10.1007/s10291-014-0379-3
(  0) 0) |
| [4] |
Langley R B, Banville S, Steigenberger P. First Results:Precise Positioning with Galileo Prototype Satellites[J]. GPS World, 2012, 23(9): 45-49
(  0) 0) |
| [5] |
Li X, Ge M, Dai X, et al. Accuracy and Reliability of Multi-GNSS Real-Time Precise Positioning: GPS, GLONASS, Beidou, and Galileo[J]. Journal of Geodesy, 2015, 89(6): 607-635 DOI:10.1007/s00190-015-0802-8
(  0) 0) |
| [6] |
任晓东, 张柯柯, 李星星, 等. Beidou、Galileo、GLONASS、GPS多系统融合精密单点[J]. 测绘学报, 2015, 44(12): 1307-1313 (Ren Xiaodong, Zhang Keke, Li Xingxing, et al. Precise Point Positioning with Multi-Constellation Satellite Systems:Beidou, Galileo, GLONASS, GPS[J]. Acta Geodaeticaet Cartographica Sinica, 2015, 44(12): 1307-1313)
(  0) 0) |
| [7] |
Chen J P, Zhangy Z, Wang J G, et al. A Simplified and Unified Model of Multi-GNSS Precise Point Positioning[J]. Advances in Space Research, 2015, 55(1): 125-134 DOI:10.1016/j.asr.2014.10.002
(  0) 0) |
| [8] |
Steigenberger P, Montenbruck O. Galileo Status: Orbits, Clocks, and Positioning[J]. GPS Solutions, 2017, 21(2): 319-331 DOI:10.1007/s10291-016-0566-5
(  0) 0) |
| [9] |
张琳, 曾子芳. 伽利略卫星导航系统的初步性能评估[J]. 中国惯性技术学报, 2017, 25(1): 91-96 (Zhang Lin, Zeng Zifang. Initial Assessment of Galileo Satellite Navigation System[J]. Journal of Chinese Inertial Technology, 2017, 25(1): 91-96)
(  0) 0) |
| [10] |
丁赫, 孙付平, 门葆红, 等. 多GNSS精密单点定位性能分析[J]. 测绘科学技术学报, 2016(1): 21-26 (Ding He, Sun Fuping, Men Baohong, et al. Performance Analysis of Multi-GNSS Precise Point Positioning[J]. Journal of Geomatics Science and Technology, 2016(1): 21-26)
(  0) 0) |
| [11] |
蔡昌盛. 多模GNSS融合精密单点定位理论与方法[M]. 北京: 科学出版社, 2017 (Cai Changsheng. The Theory and Method of Multi-GNSS Precise Point Positioning[M]. Beijing: Science Press, 2017)
(  0) 0) |
| [12] |
Blewitt G. An Auto Editing Algorithm for GPS Data[J]. Geophysical Research Letters, 1990, 17(3): 199-202 DOI:10.1029/GL017i003p00199
(  0) 0) |
| [13] |
张小红, 郭斐, 李盼, 等. GNSS精密单点定位中的实时质量控制[J]. 武汉大学学报:信息科学版, 2012, 37(8): 940-944 (Zhang Xiaohong, Guo Fei, Li Pan, et al. Real-Time Quality Control Procedure for GNSS Precise Point[J]. Geomatics and Information Science of Wuhan University, 2012, 37(8): 940-944)
(  0) 0) |
| [14] |
张小红, 左翔, 李盼, 等. BDS/GPS精密单点定位收敛时间与定位精度的比较[J]. 测绘学报, 2015, 44(3): 250-256 (Zhang Xiaohong, Zuo Xiang, Li Pan, et al. Convergence Time and Positioning Accuracy Combination between BDS and GPS Precise Point Positioning[J]. Acta Geodaetica et Carographica Sinica, 2015, 44(3): 250-256)
(  0) 0) |
2. Military Delegate Bureau of Equipment Development Department, Beijing 100000, China;
3. School of Navigation and Aerospace Engineering, Information Engineering University, 62 Kexue Road, Zhengzhou 450001, China
 2018, Vol. 38
2018, Vol. 38

