城市环境中运动载体接收GNSS信号会被频繁干扰和遮挡,RTK模糊度固定的效率相对开阔地区明显下降。GNSS RTK模糊度解算是高精度定位的前提,模糊度解算的成功率与观测卫星数、观测信号类型及数量、卫星几何结构、观测时间长度、观测值精度以及是否估计对流层或电离层参数等有关[1-2]。在单星座情况下,由于其GPS/BDS卫星观测数较少,单频RTK模糊度初始化时间需要十几min,定位效率和可靠性较低,导致GPS单频RTK难以推广,一般应用于定向、形变监测等具有外部辅助信息的领域。随着BDS和GLONASS系统逐渐完善,卫星数逐渐增多,多系统联合单频RTK高精度定位解算成为可能,并逐渐进入实用和推广阶段。加拿大Novatel公司推出了RT-2 LITE单频RTK接收机,基于GPS、GLONASS和SBAS等单频观测数据,可在1 min之内固定模糊度。基于此,本文分析一种顾及速度信息辅助模糊度固定、模糊度继承以及融合多普勒观测值的单频BDS/GPS RTK算法,并给出其算法模型;同时在JetBrains C++ IDE CLion平台上开发数据处理软件,通过该软件解算实测车载数据,分析BDS/GPS单频RTK算法的定位精度。
1 BDS/GPS单频RTK算法模型考虑到单频RTK滤波系统的稳健性,本文采用自适应Kalman滤波算法进行单频RTK解算。自适应Kalman滤波(adaptive Kalman filter)在利用GNSS测量数据进行滤波的同时,不断地由滤波本身去判断系统的动态特性是否有变化,对模型参数和噪声统计特性进行估计和修正,以改进滤波解算精度和缩小滤波的实际误差[3]。
1.1 系统模型在ECEF坐标系中表示接收机的位置坐标、速度,状态参数如下:
| $ \mathit{\boldsymbol{x}} = {\left( {\mathit{\boldsymbol{r}}_r^{\rm{T}},\mathit{\boldsymbol{v}}_r^{\rm{T}},c{\rm{d}}{{\mathit{\boldsymbol{\dot t}}}_r},\mathit{\boldsymbol{B}}_1^{\rm{T}}} \right)^{\rm{{\rm T}}}} $ | (1) |
式中,rr表示接收机三维坐标向量,vr表示接收机的速度向量,
接收机位置和速度参数采用如下动力学模型:
| $ {\left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{r}}_r}}\\ {{\mathit{\boldsymbol{v}}_r}} \end{array}} \right)_t} = \underbrace {\left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_{3 \times 3}}}&{{\mathit{\boldsymbol{I}}_{3 \times 3}}\tau }\\ {{{\bf{0}}_{3 \times 3}}}&{{\mathit{\boldsymbol{I}}_{3 \times 3}}} \end{array}} \right)}_{{\mathit{\boldsymbol{F}}_{11}}}{\left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{r}}_r}}\\ {{\mathit{\boldsymbol{v}}_r}} \end{array}} \right)_{t - 1}} $ | (2) |
式中,τ为GNSS观测历元间隔。
GNSS单频接收机钟差随时间的变化较为频繁,数值差异也较为明显。当伪距、载波相位和多普勒观测值进行组合解算时,需要估计接收机的钟差变率,同时可以将估计得到的接收机钟差变率值用于辅助卫星钟跳、接收机钟跳的探测。考虑滤波方程的稳健性,文中将接收机钟差变率建模为一阶高斯-马尔科夫过程:
| $ c{\rm{d}}{{\mathit{\boldsymbol{\ddot t}}}_r} = - \frac{1}{{{\tau _c}}}c{\rm{d}}{{\mathit{\boldsymbol{\dot t}}}_r} + \mathit{\boldsymbol{w}} $ | (3) |
式中,τc表示接收机时钟变率的一阶高斯-马尔科夫过程的相关时间,w为相应的驱动白噪声。状态转移方程为:
| $ {\left( {c{\rm{d}}{{\mathit{\boldsymbol{\dot t}}}_r}} \right)_t} \approx \underbrace {\exp \left( { - \frac{\tau }{{{\tau _c}}}} \right)}_{{\mathit{\boldsymbol{F}}_{22}}}{\left( {c{\rm{d}}{{\mathit{\boldsymbol{\dot t}}}_r}} \right)_{t - 1}} $ | (4) |
由于在城市环境中,GNSS信号受干扰和遮蔽较为严重,故将BDS和GPS模糊度参数建模为随机常数,增加滤波系统的稳定性:
| $ {\mathit{\boldsymbol{B}}_{1t}} = \underbrace {{\mathit{\boldsymbol{I}}_{m \times m}}}_{{\mathit{\boldsymbol{F}}_{33}}}{\mathit{\boldsymbol{B}}_{1t - 1}} $ | (5) |
式中,m表示当前历元与之前历元相同的双差参数个数,其他模糊度参数直接用先验值初始化。将式(2)、式(4)和式(5)写成矩阵形式:
| $ {\left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{r}}_r}}\\ {{\mathit{\boldsymbol{v}}_r}}\\ {c{\rm{d}}{{\mathit{\boldsymbol{\dot t}}}_r}}\\ {{\mathit{\boldsymbol{B}}_1}} \end{array}} \right)_t} = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_{11}}}&{}&{}\\ {}&{{\mathit{\boldsymbol{F}}_{22}}}&{}\\ {}&{}&{{\mathit{\boldsymbol{F}}_{33}}} \end{array}} \right){\left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{r}}_r}}\\ {{\mathit{\boldsymbol{v}}_r}}\\ {c{\rm{d}}{{\mathit{\boldsymbol{\dot t}}}_r}}\\ {{\mathit{\boldsymbol{B}}_1}} \end{array}} \right)_{t - 1}} $ | (6) |
BDS/GPS单频RTK利用流动站与基准站的伪距、载波相位和多普勒观测值组成双差观测值y =(Φ1T, P1T, D1T)T,以此更新滤波系统的量测方程h(x)=(hΦ, 1T, hP, 1T, hD, 1T)T。量测模型如式(7)所示:
| $ \begin{array}{*{20}{c}} {\left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{rb}^i}\\ {\mathit{\boldsymbol{P}}_{rb}^i}\\ {\mathit{\boldsymbol{D}}_{rb}^i} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\rho }}_{rb}^i + {\mathit{\boldsymbol{\lambda }}_{1 * }}\mathit{\boldsymbol{B}}_{rb}^i}\\ {\mathit{\boldsymbol{\rho }}_{rb}^i}\\ {\mathit{\boldsymbol{p}}_r^i} \end{array}} \right) \approx {{\left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\rho }}_{rb}^i + {\mathit{\boldsymbol{\lambda }}_{1 * }}\mathit{\boldsymbol{B}}_{rb}^i}\\ {\mathit{\boldsymbol{\rho }}_{rb}^i}\\ {\mathit{\boldsymbol{p}}_r^i} \end{array}} \right)}_0} + }\\ {\left( {\begin{array}{*{20}{c}} { - \mathit{\boldsymbol{E}}}&{\bf{0}}&{\bf{0}}&{{\mathit{\boldsymbol{\lambda }}_{1 * }}{\mathit{\boldsymbol{I}}_{m \times m}}}\\ { - \mathit{\boldsymbol{E}}}&{\bf{0}}&{\bf{0}}&{\bf{0}}\\ {{\mathit{\boldsymbol{H}}_D}}&{ - \mathit{\boldsymbol{E}}}&{\bf{1}}&{\bf{0}} \end{array}} \right){\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{x}}} \end{array} $ | (7) |
其中,
| $ \mathit{\boldsymbol{p}} = \mathit{\boldsymbol{\dot r}}_r^{\rm{s}} + c{\rm{d}}{{\mathit{\boldsymbol{\dot t}}}_r} - c{\rm{d}}\mathit{\boldsymbol{\dot T}} $ | (8) |
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot r}}_r^{\rm{s}} = \mathit{\boldsymbol{e}}_r^{{\rm{sT}}}\left( {{\mathit{\boldsymbol{v}}^{\rm{s}}}\left( {{\mathit{\boldsymbol{t}}^{\rm{s}}}} \right) - {\mathit{\boldsymbol{v}}_r}} \right) + }\\ {\frac{{{\mathit{\boldsymbol{w}}_e}}}{c}\left( {\mathit{\boldsymbol{v}}_y^s{x_r} + {y^{\rm{s}}}{\mathit{\boldsymbol{v}}_{x,r}} - \mathit{\boldsymbol{v}}_x^s{y_r} - {x^{\rm{s}}}{\mathit{\boldsymbol{v}}_{y,r}}} \right)} \end{array} $ | (9) |
式中,vs=(vxs, vys, vzs)和vr=(vx, r, vy, r, vz, r)分别表示卫星的运行速度和流动站接收机移动速度,e表示卫星与流动站接收机连线的单位向量,
城市环境中GNSS单频接收机测量噪声较大,需要充分利用之前历元模糊度参数的固定信息,以减少单频RTK观测量少及量测方程不稳定的影响。模糊度固定在很大程度上取决于伪距的测量精度,而单频接收机的伪距测量值噪声大,因此需要附加额外的约束防止伪距测量值破坏历元间模糊度连续性。当在k个历元之间没有周跳发生时,模糊度整数参数约束模型如下:
| $ \left( {\begin{array}{*{20}{c}} {\bf{0}}&{\bf{0}}&{\bf{0}}&{{\mathit{\boldsymbol{\lambda }}_{1 * }}}&{{\mathit{\boldsymbol{I}}_{m \times m}}} \end{array}} \right)\delta x = {\mathit{\boldsymbol{B}}_{t - k}} + {\mathit{\boldsymbol{v}}_b} $ | (10) |
式中,Bt-k表示当前历元的前k个历元中固定的模糊度参数,vb表示模糊度参数约束噪声。
1.4 随机模型| $ \sigma _{P/\mathit{\Phi }}^2 = \left\{ \begin{array}{l} {F_s}\left( {{a^2} + \frac{{{b^2}}}{{\sin e}}} \right) + C \times {10^{ - \frac{{C/N}}{{10}}}},{\rm{EL}} < {\rm{3}}{{\rm{0}}^ \circ }\\ {F_s}\left( {{a^2} + {b^2}} \right),{\rm{EL}} \ge {\rm{3}}{{\rm{0}}^ \circ } \end{array} \right. $ | (11) |
式中,Fs表示GPS与BDS相对权比关系,一般设置为1 :1.5;EL表示卫星高度角;当观测值为伪距时a=b=0.3 m,为载波相位时a=b=0.005 m。
| $ {\sigma _D} = \frac{{{\lambda ^ * }L}}{{2{\rm{ \mathsf{ π} }}T}}\sqrt {\frac{{4F{B_n}}}{{C/N}}\left( {1 + \frac{1}{{{T_D} \cdot C/N}}} \right)} $ | (12) |
式中,Bn为频环噪声带宽,TD一般设置为0.5 s,λ*表示BDS/GPS的B1/L1频率上的载波波长,F一般设置为1或者2,C/N表示卫星信号的信噪比。
2 BDS/GPS单频RTK模糊度固定BDS/GPS单频RTK模糊度固定算法模型如下[10]:
| $ \mathit{\boldsymbol{y}} = N\left( {Aa + Bb,{P_{yy}}} \right),a \in {\mathbb{Z}^n},b \in {\mathbb{R}^p} $ | (13) |
式中,y表示伪距、载波相位和多普勒观测值向量,a表示模糊度参数,b表示接收机位置坐标、速度、钟差变率等非模糊度参数,Pyy表示由自适应Kalman滤波解算得到的参数协方差矩阵的浮点解。
首先通过自适应Kalman滤波解算得到参数浮点解的协方差矩阵:
| $ \left( {\begin{array}{*{20}{c}} {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }\\ {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over b} } \end{array}} \right) \sim N\left( {\left[ {\begin{array}{*{20}{c}} a\\ b \end{array}} \right],\left[ {\begin{array}{*{20}{c}} {{P_{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }}}&{{P_{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over b} }}}\\ {{P_{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over b} \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }}}&{{P_{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over b} \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over b} }}} \end{array}} \right]} \right) $ | (14) |
根据模糊度参数的整数特性,存在一个映射关系
当采用
| $ {\rm{ratio}} = \frac{{{{\left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over a} }_2} - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} } \right)}^{\rm{T}}}\mathit{\boldsymbol{P}}_a^{ - 1}\left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over a} }_2} - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} } \right)}}{{{{\left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over a} }_1} - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} } \right)}^{\rm{T}}}\mathit{\boldsymbol{P}}_a^{ - 1}\left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over a} }_1} - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} } \right)}} > {\mathit{\boldsymbol{R}}_{{\rm{thres}}}} $ | (15) |
式中,ă1表示最优整数解,ă2表示次优整数解,Pă表示参数ă的协因数矩阵,Rthres是给定的阈值(由经验取得)。
一旦确定模糊度参数的整数解,便可以采用下式修正其余非模糊度参数,此时解算得到的非模糊度参数解为固定解:
| $ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over b} = \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over b} - {\mathit{\boldsymbol{P}}_{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over b} \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }}\mathit{\boldsymbol{P}}_{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} }^{ - 1}\left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over a} - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over a} } \right) $ | (16) |
考虑到在城市环境中,伪距和载波相位观测噪声较大,容易出现模糊度固定失败或错误的情况,因此还利用式(17)进一步判断:
| $ \frac{{{{\left( {\mathit{\boldsymbol{y}} - h\left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over a} }_2},{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over b} }_2}} \right)} \right)}^{\rm{T}}}\mathit{\boldsymbol{P}}_y^{ - 1}\left( {\mathit{\boldsymbol{y}} - h\left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over a} }_2},{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over b} }_2}} \right)} \right)}}{{{{\left( {\mathit{\boldsymbol{y}} - h\left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over a} }_1},{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over b} }_1}} \right)} \right)}^{\rm{T}}}\mathit{\boldsymbol{P}}_y^{ - 1}\left( {\mathit{\boldsymbol{y}} - h\left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over a} }_2},{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over b} }_2}} \right)} \right)}} > {{\mathit{\boldsymbol{R'}}}_{{\rm{thres}}}} $ | (17) |
式中,y表示伪距、载波相位和多普勒观测值向量,Py表示观测值y的协方差矩阵,R′thres表示给定的判断阈值,本文采用R′thres=5.0。
2.1 速度信息辅助模糊度固定BDS/GPS模糊度的固定在很大程度上取决于浮点解的精度。在城市环境中伪距和载波相位观测值的噪声较大,一般浮点解的精度在1.0 m左右,然而采用多普勒观测值估计接收机运动速度,其精度在0.1 m/s左右[12],当模糊度固定后,接收机运动速度精度也会有明显的提高。若充分利用速度信息以辅助模糊度参数的固定,则在一定程度上可以提高模糊度固定率。
首先给定速度信息辅助窗口{vt-Mt}的大小M(表示当前历元t的前M个模糊度已固定的历元数,一般M取为10),根据该窗口中各个历元的速度信息预估历元t的接收机位置坐标:
| $ \begin{array}{*{20}{c}} {{{\left( {{{\bar r}_r}} \right)}_t} = {{\left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over r} }_r}} \right)}_{t - M}} + }\\ {\sum\limits_{n = 1}^M {\left[ {v\left( {t - n + 1} \right) + v\left( {t - n} \right)} \right]\frac{{{T_n}}}{2}} } \end{array} $ | (18) |
式中,Tn表示历元t-n+1与t-n之间的时间间隔,当i历元为固定解时,v(i)等于该历元接收机速度的固定解;浮点解或单点解时,v(i)等于0。
预估的接收机位置坐标的方差为:
| $ \sigma _{{{\bar r}_r}}^2 = \sigma _{{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over r} }_{t - M}}}^2 + \sum\limits_{n = 1}^M {\left[ {\sigma _{v\left( {t - n + 1} \right)}^2 + \sigma _{v\left( {t - n} \right)}^2} \right]\frac{{T_n^2}}{4}} $ | (19) |
由式(18)和式(19)构成速度信息辅助方程如下:
| $ \left( {\begin{array}{*{20}{c}} 1&0&0&0 \end{array}} \right)\delta x = {\left( {{{\bar r}_r}} \right)_t} + v_r^ - $ | (20) |
式中,vr-表示速度信息辅助噪声。
2.2 模糊度继承策略在城市环境中,卫星信号受干扰和多路径影响较为严重,同时单频数据无法采用MW、GF等周跳探测方法。考虑到算法的稳健性,每一个历元均用MLABDA搜索模糊度,但在伪距噪声较大时,模糊度往往会搜索失败或固定率偏低。为降低上述情况对单频RTK解算性能的影响,本文提出一种模糊度继承策略,主要步骤如下。
1) 维持一个双差模糊度列表用于保存固定成功的双差模糊度(B, nFix, dH, Age),同时设置继承窗口大小K值、可信任继承阈值Q以及可继承时间限制Agemax(以s为单位)。其中,B表示模糊度; nFix表示的是模糊度固定次数,当模糊度固定时加1,反之减1;dH表示当前历元模糊度浮点解与列表中模糊度的差值; Age表示模糊度固定时间与当前时间的差值。K值和Q值的选取与测量噪声和速度有关,当测量噪声较大时,K取值较小,Q取值较大,本文采用Q=1.5,Agemax=3.0,并分析不同K值对单频RTK解算性能的影响。
2) 当MLAMBDA方法固定模糊度失败时,遍历列表查找满足条件(21)的双差模糊度:
| $ {n_{{\rm{Fix}}}} \ge K,{d_H} \ge Q,{\rm{Age}} \le {\rm{Ag}}{{\rm{e}}_{\max }} $ | (21) |
3) 采用式(17)计算非模糊度参数的固定解,并用式(16)和式(18)检验模糊度是否继承成功。若模糊度继承成功,则更新列表。
3 实验分析2017-07-13在武汉市区进行车载实验,设计路线包括林荫道、高楼建筑、高架桥、隔音墙等,其测试轨迹如图 1所示。测试中搭载了武汉迈普时空导航科技有限公司的战术级GNSS+INS组合导航系统POS310(陀螺零偏0.5°/h,加速度计零偏50 mGal);配置了高精度Trimble BD982 GNSS OEM板卡,接收机采样率为1 Hz;基准站采用Trimble Net R9接收机,架设在武汉大学教学实验大楼楼顶,基线长度为11.6~16.3 km。由于城市环境下GNSS RTK/INS紧组合可以大大提高系统的可靠性和定位精度,并提供连续的高精度导航定位结果,故本文将NovAtel商业软件Inertial Explorer 8.4的GNSS RTK/INS双频紧组合结果作为轨迹的参考真值,并使用其中的单频数据进行解算,以此分析BDS/GPS单频RTK的定位精度。

|
图 1 测试轨迹、典型场景以及GNSS接收机设备 Fig. 1 Vehicle trajectory, typical scenario and GNSS receiver equipment |
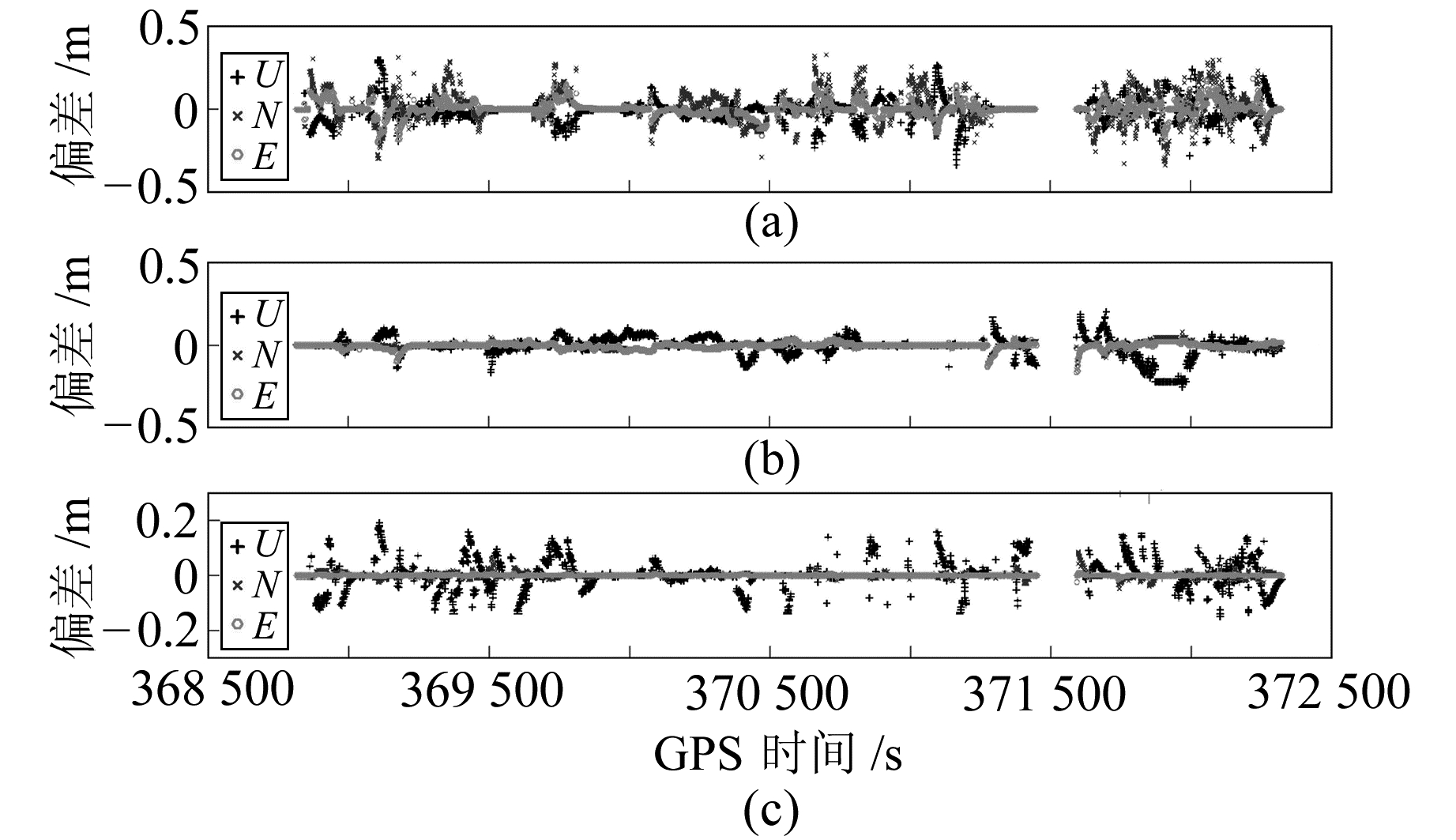
图 2(a)、图 2(b)、图 2(c)分别表示BDS、GPS、BDS+GPS模式解算得到的坐标序列与参考真值的E、N、U偏差序列,解算过程中使用速度信息辅助模糊度的固定以及模糊度继承策略。
|
图 2 GPS、BDS和BDS+GPS单频RTK解算坐标偏差 Fig. 2 E, N, U bias of GPS, BDS and BDS+GPS single-frequency RTK solution |
图 3表示GPS、BDS和BDS+GPS坐标序列与参考真值作比较得到的误差(E、N、U方向偏差值的平方根)统计图。从图 3可以看出,BDS+GPS联合解算单频RTK时,定位精度较BDS或GPS单独解算有较大的提高。

|
图 3 GPS、BDS和BDS/GPS单频RTK解算结果误差统计 Fig. 3 Error statistics of GPS, BDS and BDS+GPS single-frequency RTK solution |
分析速度信息辅助对BDS/GPS单频RTK定位精度的影响,解算过程采用模糊度继承策略(K=7,Q=1.5)。图 4(a)~(c)/(d)~(f)表示在有/无速度辅助信息辅助时,BDS、GPS和BDS+GPS单频RTK解算得到的坐标序列与参考真值之间的差异(E、N、U偏差值的平方根)。从图 4可以看出,无速度信息辅助时,模糊度固定率较低,与参考真值的偏差较大且波动也较为明显;有速度信息辅助时,模糊度固定率有所提高,且偏差值较小,变化也较为稳定。

|
图 4 有/无速度辅助信息辅助时BDS、GPS和BDS+GPS单频RTK解算结果坐标偏差序列 Fig. 4 Bias of BDS, GPS and BDS+GPS single-frequency RTK solution with/without aid-informations of speeds |
由此可见,速度信息辅助有助于提高BDS/GPS单频RTK模糊度固定率和解算定位精度。表 1中“FIXED”表示常规固定与模糊度继承固定对应固定解与参考真值偏差值的RMS,“FLOAT”表示浮点解与参考真值偏差值的RMS。
|
|
表 1 GPS、BDS和BDS+GPS单频RTK解算结果误差信息统计 Tab. 1 Error information statistics of GPS, BDS and BDS+GPS single-frequency RTK solution |
分析模糊度继承策略继承窗口大小K变化时对BDS/GPS单频RTK解算定位精度的影响:解算过程采用速度信息辅助模糊度的固定,模糊度MLAMBDA检测阈值RATIO设为3.0,截止高度角设置为15°,BDS+GPS联合单频RTK解算。表 2列出的是不同K值对应的BDS/GPS单频RTK解算结果的统计信息。从表 2中可以看出,BDS/GPS单频RTK解算固定解、模糊度继承固定解和浮点解坐标三维精度分别是5 cm、10 cm和35 cm左右。随着K值的增大,前两者所占比例随之降低,后者所占比例则随之增大。
|
|
表 2 不同K值对应的BDS/GPS单频RTK解算结果统计 Tab. 2 BDS/GPS single-frequency RTK solution results statistics corresponding to different K |
在城市环境中,由于GNSS信号受遮挡和干扰频繁,单频RTK动态定位时,模糊度固定效率偏低。本文采用一种附有整数参数约束的单频BDS/GPS RTK算法,并用速度信息和模糊度继承策略辅助模糊度固定。通过武汉市区自测车载实验验证分析表明,本文单频BDS/GPS RTK算法常规固定解、模糊度继承固定解和浮点解坐标三维精度可达5 cm、10 cm和35 cm左右。但是,对于较长时间的GNSS信号失锁和频繁干扰,单频BDS/GPS RTK仍无法提供cm级的定位结果,需要进一步研究其他传感器(里程计、惯性传感器、视觉传感器等)辅助单频RTK,以提高其在城市环境下的精密定位性能。
| [1] |
胡国荣, 欧吉坤. 改进的高动态GPS定位自适应卡尔曼滤波方法[J]. 测绘学报, 1999, 28(4): 290-294 (Hu Guorong, Ou Jikun. The Improved Method of Adaptive Kalman Filter for GPS High Kinematic Positioning[J]. Acta Geodaetica Cartographica Sinica, 1999, 28(4): 290-294 DOI:10.3321/j.issn:1001-1595.1999.04.003)
(  0) 0) |
| [2] |
何海波, 李金龙, 郭海荣, 等. 北斗/GPS双系统单频RTK模糊度解算性能分析[J]. 测绘科学与工程, 2014, 34(1): 50-54 (He Haibo, Li Jinlong, Guo Hairong, et al. Performance Analysis of Single-Frequency RTK Ambigutity Resolution Using Dual System Beidou/GPS[J]. Geomatics Science and Engineering, 2014, 34(1): 50-54)
(  0) 0) |
| [3] |
Chui C K, Chen G. Kalman Filtering with Real-Time Applications[M]. Springer-Verlag, 1987
(  0) 0) |
| [4] |
Zhao S, Cui X, Guan F, et al. A Kalman Filter-Based Short Baseline RTK Algorithm for Single-Frequency Combination of GPS and BDS[J]. Sensors, 2014, 14(8): 15415 DOI:10.3390/s140815415
(  0) 0) |
| [5] |
Elsobeiey M E. Stochastic Analysis of Low-Cost Single-Frequency GPS Receivers[J]. Positioning, 2016, 7(3): 91-100 DOI:10.4236/pos.2016.73009
(  0) 0) |
| [6] |
Odolinski R, Teunissen P J G. Low-Cost, High-Precision, Single-Frequency GPS-BDS RTK Positioning[J]. GPS Solutions, 2017, 21(1): 1-16 DOI:10.1007/s10291-016-0542-0
(  0) 0) |
| [7] |
Stempfhuber W. 3D-RTK Capability of Single GNSS Receivers[C]. ISPRS-International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2013
(  0) 0) |
| [8] |
Odolinski R, Teunissen P J G, Odijk D. Combined GPS, Beidou, Galileo, and QZSS Single-Epoch, Single-Frequency RTK Performance Analysis[C]. International Association of Geodesy Symposia, 2016
(  0) 0) |
| [9] |
Odolinski R, Teunissen P J G, Odijk D. Combined BDS, Galileo, QZSS and GPS Single-Frequency RTK[J]. GPS Solutions, 2015, 19(1): 151-163 DOI:10.1007/s10291-014-0376-6
(  0) 0) |
| [10] |
Takasu T, Yasuda A. Development of theLow-Cost RTK-GPS Receiver with an Open Source Program Package RTKLIB[C]. International Symposium on GPS/GNSS, South Korea, 2009
(  0) 0) |
| [11] |
Chang X W, Yang X, Zhou T. MLAMBDA: A Modified LAMBDA Method for Integer Least-Squares Estimation[J]. Journal of Geodesy, 2005, 79(9): 552-565 DOI:10.1007/s00190-005-0004-x
(  0) 0) |
| [12] |
Kubo N. Advantage of Velocity Measurements on Instantaneous RTK Positioning[J]. GPS Solutions, 2009, 13(4): 271-280 DOI:10.1007/s10291-009-0120-9
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38

