2. 国防科学技术大学机电工程与自动化学院,长沙市德雅路109号,410073
我国北斗卫星导航系统(BDS)目前正在全球系统建设阶段,预计会在2020年完全建成[1]。北斗卫星导航系统现在乃至将来都能提供正常的导航定位服务,然而用户接收机所处的应用环境却会使卫星导航的应用受到限制。我国土地辽阔,地形多样,随着城市化进程的加快,各处高楼林立,在这些场景中的应用条件完全超越了卫星导航系统最初的设计[2],卫星被遮挡会使卫星的截止仰角增大,卫星信号被反射会造成多路径效应,此时用户可能将无法正常使用导航定位服务,这对卫星导航系统来说是一个挑战。如若可以对上述应用场景进行效能评估,使用户对当前使用的导航定位服务有一个判断,在一定程度上能规避由定位异常带来的风险。
目前尚缺乏针对北斗卫星导航系统的有效的导航效能评估工具,对北斗终端的导航效能评估还停留在理想环境下关键指标的实验室测试或外场测试上,并没有面向典型应用的分析。而欧洲Galileo在其系统建成之前就已经推出了一款叫Polaris的软件。Polaris是一款在不同应用场景上对各种用户终端进行导航效能评估的软件,其在推广Galileo及提升Galileo服务性能等方面有重要贡献。对正在建设的北斗卫星导航系统来说,研究类似Polaris的基于应用场景的导航效能评估方法具有实用价值。
本文从模型的角度对北斗导航典型应用场景之一的山地应用场景进行构建,在此基础上提出效能评估的指标,经实验展示了具体山地场景中用户终端的效能评估结果,并对结果进行分析。
1 典型应用场景构建卫星系统导航定位依赖于直达导航信号LOS(line of sight),其在地表以下几乎不能发挥作用,即使在地面上也会面临各种因素的挑战,有学者把这类环境称为挑战性环境[3]。典型的挑战性环境有室内、隧道、城市峡谷、森林峡谷、陡峭山地等,在这些环境中容易出现导航定位精度恶化或者导航信号不连续的情况,使用户导航效能受到影响。因此本文提出典型应用场景构建的第一步是环境建模。
实际上,并不是挑战性环境中所有用户的导航定位都会受到不良影响,它还跟用户在具体时间的具体位置有关,故本文在环境模型基础上讨论了载体的轨迹模型。
导航定位还跟载体搭载的接收机类型有关,不同类型的接收机有不同的处理能力,自身产生的噪声也有差别。为了实现对多种用户终端的仿真,本文对终端接收机进行了参数化建模。
1.1 典型环境模型本文取山地环境为背景进行山地应用场景构建。山地环境模型可以分为空间环境模型和地面环境模型两部分[1]。目前,国内外针对空间环境模型的研究已较为成熟,故本文在实验中直接使用现有模型。因地面环境的复杂性,国内现有的BDS仿真软件中对地面环境的建模较为缺乏,本文基于山地环境,提出了从地形模型(遮挡模型)及多路径效应模型两方面构建地面环境的方法。
1.1.1 地形模型目前国内外对地形建模的研究普遍基于数字高程模型(digital elevation model,DEM)。DEM有4种表示模型[4]:不规则三角网模型、规则格网模型、等高线模型和层次地形模型,本文采用规则格网模型。具体构建过程如下。
1) 数据获取。从http://srtm.csi.cgiar.org/SELECTION/inputCoord.asp网站上可免费获取美国地质调查局提供的数据SRTM3,数据格式为. tiff。
2) 数据处理。.tiff格式的原始数据块大小为6 001×6 001个网格,共68.7 M,数据量大对计算机的处理性能要求很高,可以采用GIS处理软件(如Global Mapper、ArcGIS等)对数据进行裁剪,还可根据需要处理并导出为相应格式的DEM文件。一般DEM文件都包含参数和数据块两部分。
表 1是一个高程数据文件的参数列表。由于雷达阴影、回波延迟等因素难以避免[5],高程数据可能存在空值,默认用数值-9999代替。
|
|
表 1 高程数据文件的参数 Tab. 1 Parameters of elevation data file |
数据块比较简单,是具排列规律的高程矩阵。获取了经纬度高程,就可以构建地形环境。
1.1.2 多路径效应模型利用三角级数模型[6]对多路径效应进行建模:
| $ \begin{array}{*{20}{c}} {{M_{\rm{P}}}\left( {\theta ,\alpha } \right) = {a_1} + {a_2}\cos \theta + \sum\limits_{i = 1,j = 2i + 1}^N {\left\{ {{a_j}\cos \left( {i\alpha } \right) + } \right.} }\\ {\left. {{a_{j + 1}}\sin \left( {i\alpha } \right)} \right\} + {a_{2n + 3}}\cos \theta \cos \alpha } \end{array} $ | (1) |
式中,等号左边是多路径数据,可以由双频伪距观测值计算得到。θ是卫星仰角,α是卫星方位角,N是模型阶数,aj是需要求解的系数。
通过多个采样时刻的数据,可得观测方程:
| $ {\mathit{\boldsymbol{M}}_{\rm{P}}} = {\mathit{\boldsymbol{M}}_{{\rm{trigon}}}}\mathit{\boldsymbol{X}} $ | (2) |
式中,Mtrigon是模型系数,X是需求解的量。
以上过程存在因相邻采样时刻的高度角和方位角太过相似而引起的病态问题,采用岭估计[6]的方法解决:
| $ \mathit{\boldsymbol{X}} = {\left( {\mathit{\boldsymbol{M}}_{{\rm{trigon}}}^{\rm{T}}{\mathit{\boldsymbol{M}}_{{\rm{trigon}}}} + K\mathit{\boldsymbol{I}}} \right)^{ - 1}}\mathit{\boldsymbol{M}}_{{\rm{trigon}}}^{\rm{T}}{\mathit{\boldsymbol{M}}_{\rm{P}}} $ | (3) |
式中,K=1×10-9;I为单位矩阵,其维数与Mtrigon相同。
上述模型为静态模型。动态多路径效应模型的仿真非常复杂,目前没有统一的方法,SATNAV公司提出用高斯-马尔可夫模型来进行建模:
| $ {X_{k + 1}} = {{\rm{e}}^{ - \beta \left( {{t_{k + 1}} - {t_k}} \right)}}{X_k} + {w_k} $ | (4) |
式中,Xk是k时刻多路径效应误差;1/β是过程时间常数;wk是高斯白噪声的方差,可由多路径的方差σ2计算得到。
本文设多路径效应误差为服从马尔可夫模型的随机数,文献[6]分析卫星的多路径效应与卫星高度角的关系指出,随卫星高度角的增加,其多路径效应误差会减小,故本文根据卫星高度角对多路径效应进行不同程度的放大:卫星高度角为0°~5°,放大因子取2.5;卫星高度角为5°~10°,放大因子取2.0;卫星高度角为10°~15°,放大因子取1.5;卫星高度角为15°~75°,放大因子取1;卫星高度角为75°~90°,无多路径。
1.2 载体轨迹模型本文所构建的典型环境为山地环境,所以仅考虑地面载体。载体有静态和动态之分,静态载体轨迹模型在环境中就是一个静止的点,指定其坐标即可。因为考虑了地形因素,动态载体在山地的运动轨迹不能简单地用一个直线或者曲线方程来描述。
假设动态载体在CGCS2000坐标系下的起始点坐标为(B1,L1,H1),终点坐标为(B2,L2,H2),设载体的运动速度V不变,首先分析直线运动。
因为地球偏心率e极小,故计算中将地球看作球体。将已知数据代入球面余弦公式可得:
| $ \begin{array}{*{20}{c}} {\cos c = \cos \left( {{{90}^ \circ } - {B_2}} \right)\cos \left( {{{90}^ \circ } - {B_1}} \right) + }\\ {\sin \left( {{{90}^ \circ } - {B_2}} \right)\sin \left( {{{90}^ \circ } - {B_1}} \right)\cos \left( {{L_2} - {L_1}} \right)} \end{array} $ | (5) |
式中,c为起始点与球心的连线和终点与球心的连线之间的夹角。由三角函数基本公式可得:
| $ \sin c = \sqrt {1 - {{\cos }^2}c} $ | (6) |
求得正弦后将已知数据代入球面正弦公式并稍作变形,可得式(7):
| $ \sin A = \frac{{\sin \left( {{{90}^ \circ } - {B_2}} \right)\sin \left( {{L_2} - {L_1}} \right)}}{{\sin c}} $ | (7) |
A即为起始点到终点的航向角,相应的cosA为:
| $ \cos A = \frac{{\cos \left( {{{90}^ \circ } - {B_2}} \right) - \cos c\cos \left( {{{90}^ \circ } - {B_1}} \right)}}{{\sin c\sin \left( {{{90}^ \circ } - {B_2}} \right)}} $ | (8) |
则载体的运动轨迹方程为:
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {B\left( t \right)}\\ {L\left( t \right)}\\ {H\left( t \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{B_1}}\\ {{L_1}}\\ {\frac{{{H_1} + {H_2}}}{2}} \end{array}} \right] + }\\ {\left[ {\begin{array}{*{20}{c}} {V\left( {t - {t_1}} \right)\cos A/{I_{\rm{B}}}}\\ {V\left( {t - {t_1}} \right)\sin A/{I_{\rm{L}}}}\\ 0 \end{array}} \right]} \end{array} $ | (9) |
式中,IL和IB分别是经纬线的单位弧长,文献[7]给出了对于IL和IB较为精确的计算式:
| $ {I_{\rm{L}}} = 111\;132.8 - 559.5\cos \left( {2{B_1}} \right) + 1.1\cos \left( {4{B_1}} \right) $ | (10) |
| $ {I_{\rm{B}}} = \frac{{111\;319.5\cos {B_1}}}{{\sqrt {1 - {e^2}{{\sin }^2}{B_1}} }} $ | (11) |
当载体运动轨迹为曲线时,可将曲线分解成为多段直线,需获得每一小段直线的两个端点坐标,之后分段处理即可。
图 1中黑色部分是用上述方法模拟的动态载体运动轨迹。可以看出,生成的轨迹与地形可以很好地贴合。
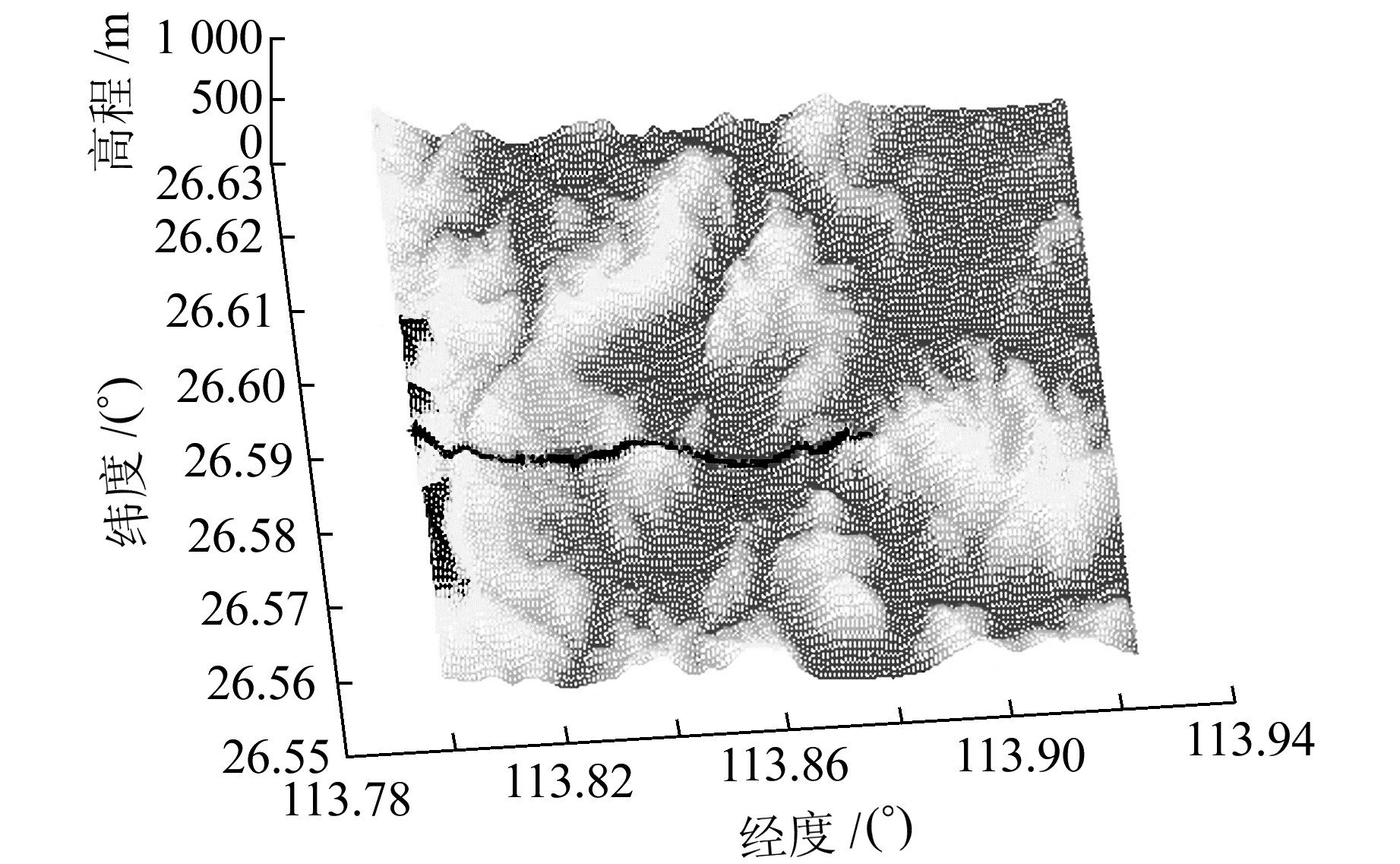
|
图 1 载体运动轨迹 Fig. 1 Moving tracks of carrier |
本文在北斗卫星导航系统下评估导航终端的效能,规定导航终端模型可设置的参数为频点数、通道数、接收机噪声,其中接收机噪声具有一定的随机性[8-9],可以用随机量来建模。
2 北斗导航效能评估方法用户使用卫星导航时最关心的就是能否定位,及若能定位其精度是否能满足服务指标要求。定位的基本条件是接收机能收到4颗及以上的可见卫星信号,定位精度在一定程度上也受可见卫星分布的影响,故首先需要在山地场景中对卫星可见性进行评估。
2.1 卫星可见性评估在山地场景中,卫星的截止高度角除受预设门限值限制外,还受到遮挡点的约束,需要对山地场景中遮挡点进行搜索。搜索时,需获得北斗卫星相对于用户接收机的高度角和方位角。
本文在构建地形环境模型时所用的高程数据是离散的,因此在方位角方向上不一定存在高程数据。对高程数据空缺的点采用邻近值替代的方法,即用离空缺点最近的规则网格上的点的高程来近似代替空缺点高程。
图 2给出了针对静态用户的遮挡点搜索流程。动态用户的遮挡点搜索过程与静态用户基本类似,只是其每一个仿真时刻的位置是变化的。

|
图 2 遮挡点搜索流程 Fig. 2 Flow chart of searching bar points |
定位误差的标准差计算公式为:
| $ {\sigma _{定位}} = {\rm{DOP}} \cdot {\sigma _{测量}} $ | (12) |
式中,DOP为精度因子,σ测量为用户等效距离误差(UERE,user equivalent range error)的标准差。
UERE与卫星误差、信号传播误差、接收机相关误差等因素有关,如果是既定的卫星导航系统和用户终端,其大小可以认为是确定的[10]。
在用户测量误差一定的条件下,DOP完全可以用来评估当前的定位精度。
DOP是由可见卫星的几何关系决定的,包含5个分量[2]。本文导航效能评估关心的是用户终端三维位置的定位偏差,故选用PDOP值来评估定位精度。
设站心坐标系下卫星n相对用户接收机的高度角和方位角分别为θn、αn,则几何矩阵G为:
| $ \mathit{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} { - \cos {\theta _1}\sin {\alpha _1}}&{ - \cos {\theta _1}\cos {\alpha _1}}&{ - \sin {\theta _1}}&1\\ { - \cos {\theta _2}\sin {\alpha _2}}&{ - \cos {\theta _2}\cos {\alpha _2}}&{ - \sin {\theta _2}}&1\\ \cdots&\cdots&\cdots&\cdots \\ { - \cos {\theta _n}\sin {\alpha _n}}&{ - \cos {\theta _n}\cos {\alpha _n}}&{ - \sin {\theta _n}}&1 \end{array}} \right] $ | (13) |
站心坐标系中的权系数矩阵H为:
| $ \mathit{\boldsymbol{H}} = {\left( {{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{G}}} \right)^{ - 1}} $ | (14) |
PDOP值为:
| $ {\rm{PDOP}} = \sqrt {{h_{11}} + {h_{22}} + {h_{33}}} $ | (15) |
式中,等号右边各参数为权系数矩阵H对角线元素。
3 实验结果与分析 3.1 应用场景仿真实验下载的数据块范围为25°~30°N、110°~115°E。最大高程值为1 890 m,最小高程值为44 m,属于典型的山地环境。在地形上指定了静态用户位置和动态用户轨迹,地形3D视图见图 3,静态、动态用户的相应场景参数设置如表 2、表 3。

|
图 3 山地地形的3D视图 Fig. 3 3D view of terrain environment |
|
|
表 2 静态用户应用场景参数 Tab. 2 Applying scene parameters of static user |
|
|
表 3 动态用户应用场景参数 Tab. 3 Applying scene parameters of dynamic user |
在以上场景中观测数据均由仿真生成,场景的空间环境采用由开源软件BDSim提供的模型。
3.2 导航效能分析对静态用户搭载的导航终端进行效能评估,可以知道该位置的定位服务是否能长时间满足使用需求。实验对指定静态用户1 d的定位误差进行分析,图 4是用户站心坐标系的定位误差,仿真时间段中不存在定位不成功的时刻,即可见卫星数目均大于等于4;图 5是该静态用户的可见星情况。
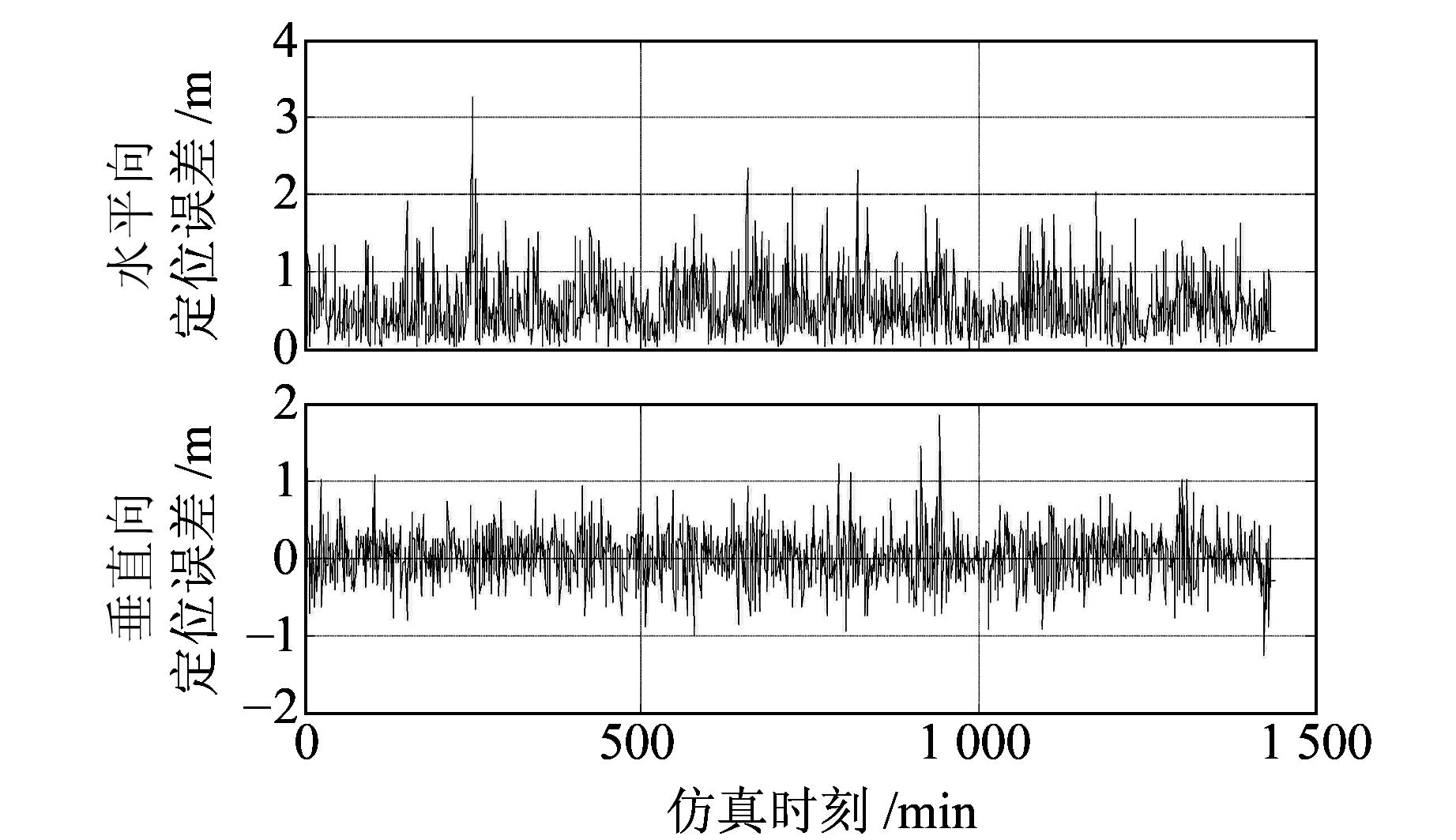
|
图 4 静态用户的定位误差 Fig. 4 Positioning error of static user |

|
图 5 静态用户的可见星数目 Fig. 5 Visible satellites' number of static user |
图 6是该静态用户的PDOP值。一般认为,PDOP < 6时,定位结果是可用的。由图 6可知,在仿真时间段内该静态用户的定位结果持续可用,导航效能不受影响。
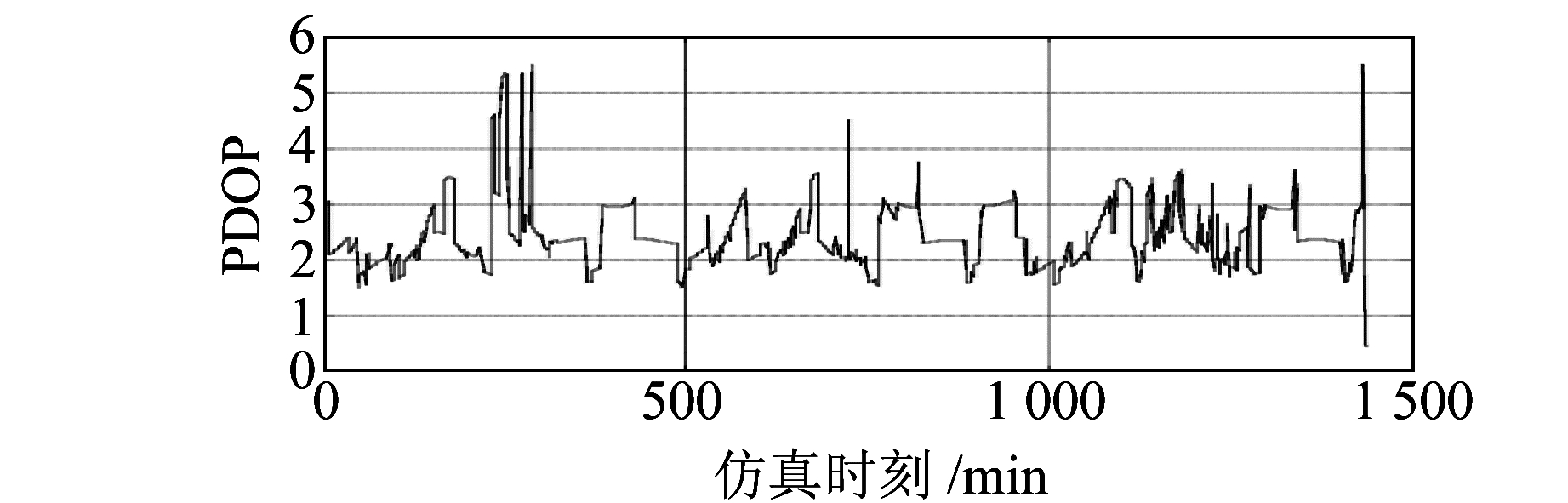
|
图 6 静态用户的PDOP值 Fig. 6 PDOP of static user |
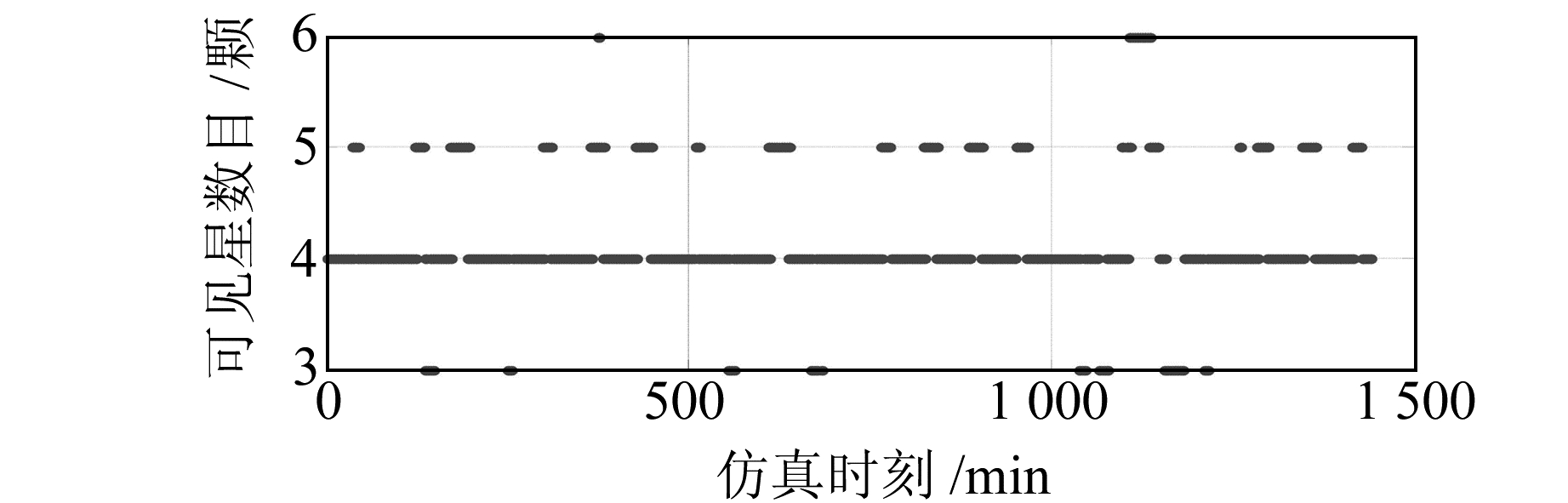
动态用户的评估过程与静态用户类似,不过在每一时刻获得的是不同位置的各项指标。动态用户终端的效能评估可用于路径规划。图 7是实验所构建动态用户1 d的定位误差,图 8是动态用户的可见星情况。图 8中存在可见星数目小于4的时刻,占整个仿真时段的5.2%,此时定位是无法解算的,故在图 7中没有体现。为突出细节,图 7对数据进行了尖峰平滑处理。
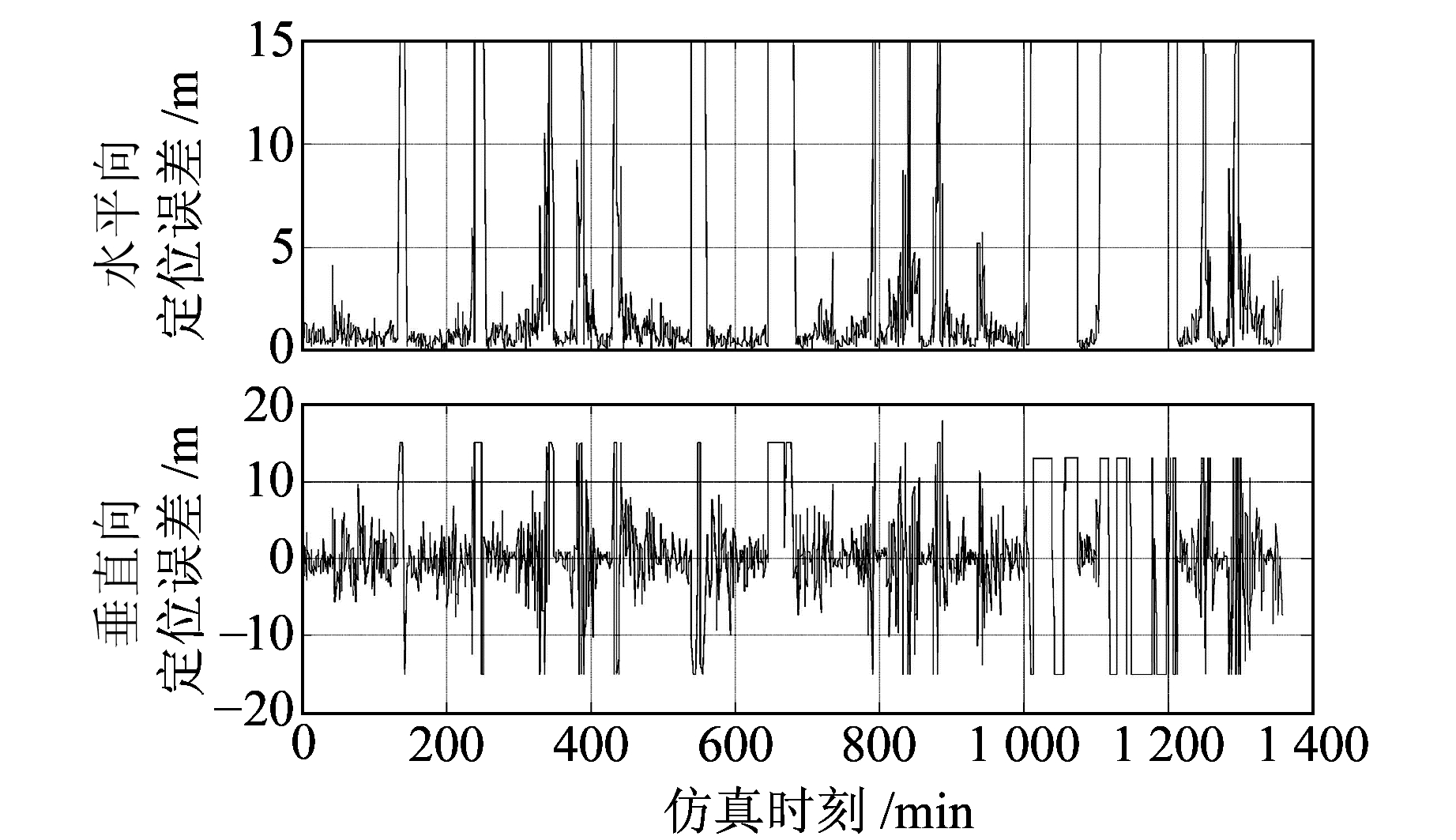
|
图 7 动态用户的定位误差 Fig. 7 Positioning error of dynamic user |
|
图 8 动态用户的可见星数目 Fig. 8 Visible satellites' number of dynamic user |
结合图 7和图 8可知,即使在可见星数目满足定位需求的条件下,定位误差有时也会出现很大的数值。表 4统计了该动态用户的PDOP值(小于6)和可见星(大于或等于4)的关系。
|
|
表 4 动态用户的PDOP统计 Tab. 4 Statistics of PDOP of dynamic user |
由表 4可知,只有可见星数为6颗时,PDOP < 6出现的概率是100%,其他均有不满足的情况,在这些时刻定位误差较大。
4 结语本文在构建较为真实的山地应用场景的基础上,对用户终端进行了效能评估。既有正常使用导航定位服务的情况,如实验构建的静态用户及动态用户的大部分时刻,又有导航效能受到影响的情况,如动态用户仿真中出现的可见星数目小于4及PDOP>6的时刻。对导航效能进行评估,有助于用户避免风险,提升用户体验。今后还可以拓展到更多场景(如城市、海洋、天空等),对更多的终端(如飞机、船舶等)进行效能分析,推出一整套的北斗卫星导航效能评估方法。这不仅有利于北斗卫星导航系统的推广和使用,也可以为北斗卫星导航系统的维护部门提供改善系统性能的依据。
| [1] |
杨俊. 卫星导航系统建模与仿真[M]. 北京: 科学出版社, 2016 (Yang Jun. Modeling and Simulation of Satellite Navigation System[M]. Beijing: Science Press, 2016)
(  0) 0) |
| [2] |
李作虎. 卫星导航系统性能监测及评估方法研究[D]. 郑州: 信息工程大学, 2012 (Li Zuohu. Research on Monitoring and Assessment of Satellite Navigation System Performance[D]. Zhengzhou: Information Engineering University, 2012)
(  0) 0) |
| [3] |
彭竞. 挑战性环境下卫星导航数据处理关键技术研究[D]. 长沙: 国防科学技术大学, 2013 (Peng Jing. Research on Data Processing Technology of Global Navigation Satellite System in the Challenging Environment[D]. Changsha: National University of Defense Technology, 2013)
(  0) 0) |
| [4] |
池聪伶. 三维地形可视域分析及显示技术的研究与实现[D]. 沈阳: 沈阳工业大学, 2009 (Chi Congling. Research and Implementation on 3D Terrain Viewsheds Analyze and Displaying Technology[D]. Shenyang: Shenyang University of Technology, 2009)
(  0) 0) |
| [5] |
黄朝安. SRTMDEM数据空洞插值填补方法对比分析[J]. 测绘与空间地理信息, 2011(4): 110-112 (Huang Chao'an. A Comparative Analysis to Interpolation Filling Method of the SRTMDEM Data[J]. Geomatics and Spatial Information Technology, 2011(4): 110-112 DOI:10.3969/j.issn.1672-5867.2011.04.034)
(  0) 0) |
| [6] |
张利云. 卫星导航地面监测站接收机的多路径效应分段仿真方法[J]. 大地测量与地球动力学, 2015, 35(1): 1-5 (Zhang Liyun. Simulation Modeling of Multipath Effect for Satellite Navigation Monitoring Station Receiver Based on a Segmentalization Technique[J]. Journal of Geodesy and Geodynamics, 2015, 35(1): 1-5)
(  0) 0) |
| [7] |
王鹏远. 复杂地形环境下可见星仿真分析[D]. 秦皇岛: 燕山大学, 2013 (Wang Pengyuan. Visible Star Simulation in Complex Terrain Environment[D]. Qinhuangdao: Yanshan University, 2013)
(  0) 0) |
| [8] |
刘荣. GPS接收机抗干扰性能仿真研究[J]. 无线电通信技术, 2014, 40(1): 58-64 (Liu Rong. Simulation Research on Anti-Jamming Performance of GPS Receiver[J]. Radio Communication Technology, 2014, 40(1): 58-64 DOI:10.3969/j.issn.1003-3114.2014.01.017)
(  0) 0) |
| [9] |
谢钢. GPS原理及接收机设计[M]. 北京: 电子工业出版社, 2009 (Xie Gang. Principles of GPS and Receiver Design[M]. Beijing: Publishing House of Electronics Industry, 2009)
(  0) 0) |
| [10] |
Gremers J G. Global Positioning System Standard Positioning Service Performance Standard[S]. Washington, 2008
(  0) 0) |
2. College of Mechatronics Engineering and Automation, National University of Defense Technology, 109 Deya Road, Changsha 410073, China
 2018, Vol. 38
2018, Vol. 38


