在GPS高精度实时动态变形监测中,通常采用相对定位方式获取观测站变形信息,接收机钟与卫星钟钟差等主要系统误差可以基本消除,且各测站之间距离较短,电离层延迟与对流层延迟造成的影响也可基本忽略,而多路径误差不能通过相对定位有效消除,便成为精密定位的主要误差源。由于多路径误差与观测站、周围环境以及卫星位置的几何关系有直接关系,而观测站变形量一般较小,周围环境大多变化缓慢或者基本不变,卫星运行周日重复,所以多路径误差通常表现出较强的周日重复性[1-3],采用一定的方法进行多路径误差建模,进而利用多路径误差的周日重复性,可以达到削弱多路径误差的目的。
国内外学者在多路径误差模型的构建方面进行了大量研究,其中,效果较为出色的是经验模式分解(empirical mode decomposition,EMD)。EMD最初由Huang等[4]于1998年提出并应用于信号处理,因其具有对时间序列自适应分解的特性,得到更广泛的关注。戴吾蛟等[5]利用其分解高斯白噪声得到本征模态分量,根据白噪声的能量密度与平均周期为常量的特性建立多路径误差模型,提出EMD滤波去噪方法。对于如何从EMD分解得到的模态分量中寻找多路径误差所在的模量范围,刘超等[6]利用基于标准化模量的累计均值的尺度提取方法建立多路径误差模型,并在实验中检验了新方法的有效性。EMD虽然在对时间序列的分解过程中有着较好的自适应性,但在应对信号中多路径误差间断性问题时会产生模态混叠现象,分解的模态分量并不能真实地反映信号中多路径误差的规律[7-8]。因此,出现了将高斯白噪声加入EMD待分解信号中进行多次分解,以克服模态混叠现象的集合经验模式分解(EEMD)。
EEMD虽然对模态混叠起到了一定的抑制作用,但由于多次加入的不同噪声导致模态分量数目不明确与分解不彻底[9-10]。因此,本文引入一种改进的集合经验模式分解(IEEMD)方法进行多路径误差建模,并针对尺度选择问题给出一种尺度选择方法,最后通过实测数据对新方法的准确性进行验证。
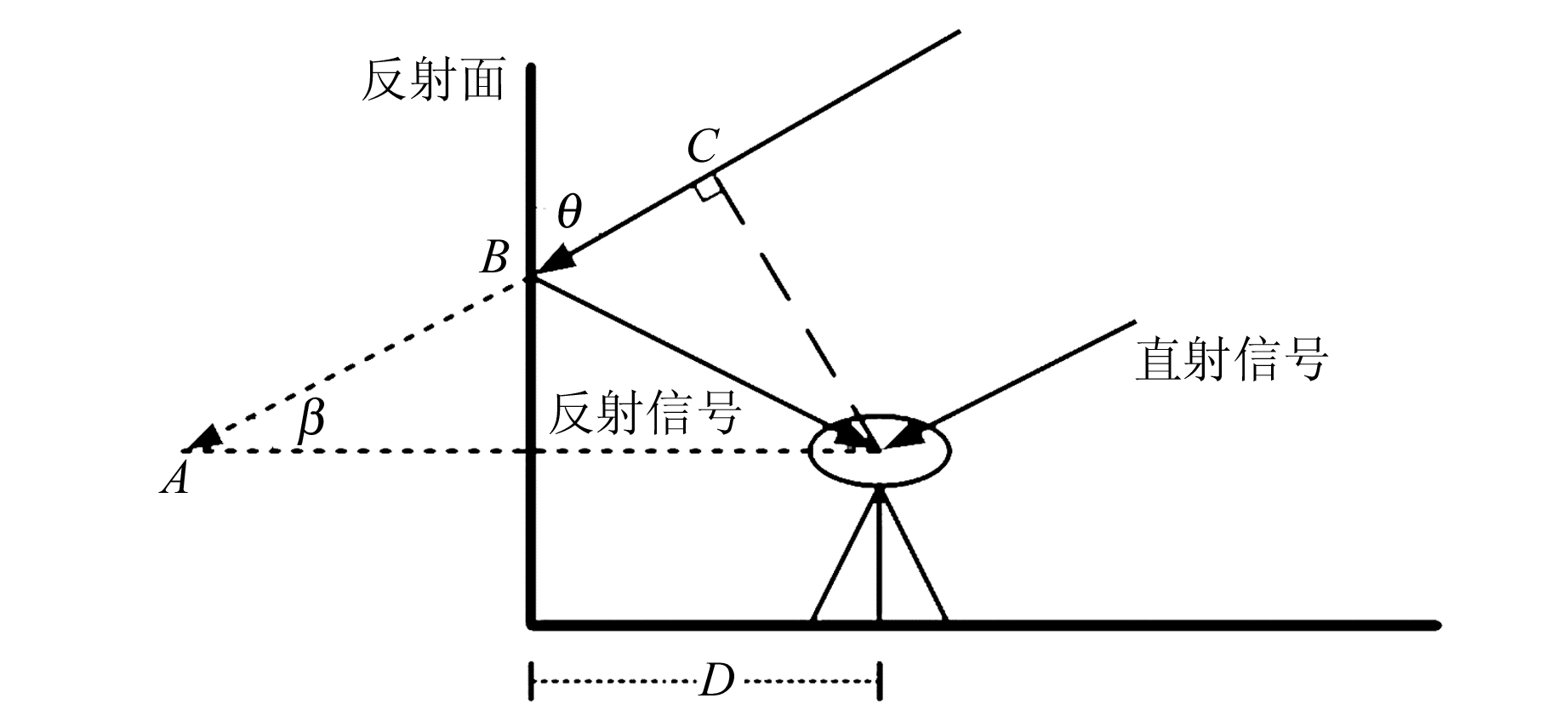
1 多路径误差与特性以单一反射信号的多路径误差为例(图 1)。测站环境造成的反射信号可表示为[3]:
|
图 1 单一反射信号多路径误差示意图 Fig. 1 Multipath error of single reflected signal |
| $ S = {\alpha _0}A\sin \left( {\tilde \omega t + {\Delta _0}} \right) $ | (1) |
式中,S表示多路径等效距离误差,即为AB与BC之和(图 1),且S=2Dcosβ,其中,D为接收机天线至反射面的垂直距离,β为卫星信号入射角,α0为反射面的反射系数,A为卫星信号振幅,ω为信号角频率,Δ0为反射信号引起的相位偏移量,且Δ0=4πD/λcosβ,其中λ为卫星信号的波长。当Δ0=π/4时,在L1载波上可产生最大约5 cm的多路径误差。
将相位偏移Δ0对偏移时间求导并除以2π,可以得到多路径误差的频率f与相位偏移Δ0的变化率之间的关系[3]。当接收机天线与反射面距离D较远时,多路径误差的频率f表现为高频,反之为低频。当距离达到50 m时,多路径误差基本不用考虑,因此多路径误差主要表现为低频。
由图 1可知,多路径误差主要由卫星、接收机和反射体三者的几何关系决定,而在进行动态变形监测的过程中,接收机位置与周围环境的变化较小或者保持不变,因此,多路径误差主要与观测卫星有关。由于GPS卫星运行周期为12个恒星时,所以连续2 d到达同一位置的时间理论上会提前236 s[2]。对于同一台接收机来说,相邻2 d测站环境不变,则多路径误差具有较强的相关性,相关性可以体现多路径误差的周日重复性。相关系数计算公式为:
| $ {\rho _{xy}}\left( l \right) = \frac{{{r_{xy}}\left( l \right)}}{{\sqrt {{r_{xx}}\left( 0 \right){r_{yy}}\left( 0 \right)} }} $ | (2) |
式中,rxx(0)与ryy(0)分别为x序列与y序列的方差;rxy(l)为x序列与延迟l历元的y序列的协方差:
| $ {r_{xy}}\left( l \right) = \frac{1}{n}\sum\limits_{i = 1}^n {x\left( n \right){y_l}\left( n \right)} $ | (3) |
式中,n为序列长度。
2 IEEMD方法 2.1 EEMD基本原理EEMD算法是利用噪声辅助分解的EMD算法。EMD算法的基本思想是,将复杂的信号看成是由一些互不相同、简单的、非正弦函数的信号分量构成[4]。根据这个特性,可以将复杂信号分解成从高频到低频的若干信号分量,即固有模态函数(intrinsic mode function,IMF)。
EMD分解的具体流程可参考文献[4]。若信号分解过程中存在异常事件,则会导致最终分解得到的某个模态分量中包含有不同的时间尺度,或者同一时间尺度分布在不同模态分量中的模态混叠现象[8]。
针对EMD的模态混叠,Wu等[8]提出在待分解信号中加入一定幅值的高斯白噪声,根据白噪声频谱分布均匀的特点,能将不同特征尺度下的分量自动分配到合适的尺度中。同时,运用白噪声零均值特性,加入多次白噪声后经过平均使噪声相互抵消,从而抑制甚至完全消除噪声的影响,并且得到经过平均后的各层模态分量。因此,EEMD的思想是一种叠加高斯白噪声的多次经验模式分解。
2.2 IEEMD基本原理与方法EEMD虽然对模态混叠起到了一定的抑制作用,但在低频分量部分多次平均后可能造成相邻模态分量出现重叠现象,造成分解模态分量个数不明确与分解不彻底的情况。因此本文引入一种改进的集合经验模式分解法IEEMD[9],具体分解步骤如下。
1) 在原始信号x(t)中分m次加入高斯白噪声n1m(t),对每一次加入白噪声后的输入信号进行EMD分解,对分解得到的第一层信号分量进行求平均,在输入信号中减去模态分量均值得到残余分量:
| $ {\rm{im}}{{{\rm{\tilde f}}}_1}\left( t \right) = \frac{1}{m}\sum\limits_{i = 1}^m {{\rm{imf}}_1^i\left( t \right)} $ | (4) |
| $ {r^1}\left( t \right) = {x_i}\left( t \right) - {\rm{im}}{{{\rm{\tilde f}}}_1}\left( t \right) $ | (5) |
式中,
2) 将残余分量r1(t)作为输入信号,分m次加入白噪声n2m(t)后,再次进行m次EMD分解得到
3) 对每一次分解得到的残余信号分量r(t)进行判断,如果不满足EMD分解的停止条件,则重复进行步骤1)与2),否则分解结束。将分解得到的每层模态分量与残余分量进行重构,可得到初始输入信号:
| $ x\left( t \right) = \sum\limits_{j = 1}^k {{\rm{im}}{{{\rm{\tilde f}}}_j}\left( t \right)} + {r^{k + 1}}\left( t \right) $ | (6) |
对于每一次分解加入的高斯白噪声ni(t),有:
| $ {n^i}\left( t \right) = {\beta _k}{E_i}\left( {{w^{\left( i \right)}}} \right) $ | (7) |
式中,k=0~m,i=1~m,w(i)表示第i次加入的高斯白噪声,βk表示加入噪声的幅值系数,Ei(w(i))表示对加入的噪声进行第i次EMD分解。为了在添加的噪声和残余信号分量中获得合适的信噪比,选择βk=εkstd(rk)来确定加入的噪声,即一个常量与残余分量标准差的乘积。噪声与信号之间的信噪比随着分解次数k的增加而增加,这是因为,在第k次加入的噪声的残差中(k>1),噪声的能量只是算法初始时加入噪声能量的一部分。依据这种思路,在算法中把β0按照一定设置,使ε0恰好为首次加入高斯白噪声与待分析信号之间最理想信噪比的倒数,把这个信噪比看成标准偏差的商,可以得到:
| $ {\beta _0} = {\varepsilon _0}{\rm{std}}\left( x \right)/{\rm{std}}\left( {E\left( {{w^{\left( i \right)}}} \right)} \right) $ | (8) |
选取合适的高斯白噪声的幅值系数β0以及执行EMD分解的次数m,通常认为加入噪声引起的分解误差在0.01以下时是合适的[9],当ε0取0.2、m取200时,即可满足上述要求。
2.3 IEEMD尺度分离方法经过EMD分解的高斯白噪声产生的一系列IMF分量的能量密度与其平均周期的乘积为常量const[8]。利用该特性,设计一种提取IMF分量的方法,具体步骤如下。
1) 加入高斯白噪声的待分解信号经过IEEMD分解后得到k个IMF分量,计算出每个IMF分量的const:
| $ {E_k} = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left[ {{A_k}\left( i \right)} \right]}^2}} $ | (9) |
| $ {{\bar T}_k} = \frac{{2N}}{{{\rm{Extr}}{{\rm{e}}_k}}} $ | (10) |
| $ {\rm{const}} = {E_k}{{\bar T}_k} $ | (11) |
式(9)~(11)中,Ek为第k个IMF分量的能量密度, N为第k个IMF分量的长度, Ak为第k个IMF分量的振幅, Tk为第k个IMF分量的平均周期, Extrek为极值点总数。
2) 计算提取尺度的判定系数Judk:
| $ {\rm{Ju}}{{\rm{d}}_k} = \frac{{k \times {\rm{cons}}{{\rm{t}}_k}}}{{\sum\limits_{i = 1}^k {{\rm{cons}}{{\rm{t}}_k}} }} - 1 $ | (12) |
当Judk≥1时,可以认为第k个IMF的const相对于前k-1个IMF的const的平均值以Judk倍增大,即前k-1个IMF的能量密度与平均周期之积为常量。由前文可知,这k-1个IMF分量作为噪声应当剔除,根据EMD的零点特性,残余分量符合趋势项表现出的线性趋势误差特性,在分量重构时也应去除,由剩下的IMF分量进行重构即可得到降噪后的多路径误差模型,这便是IEEMD构建多路径误差模型的原理。
2.4 IEEMD多路径误差建模与评价指标基于IEEMD的多路径误差模型,在每层模态分量的分解过程中,多次加入高斯白噪声求取模态分量均值,并根据高斯白噪声的能量密度与平均周期为常量的特性,设计尺度提取方法,进行多路径误差提取建模,然后利用多路径误差的周日重复性对后续的坐标序列进行恒星日滤波。具体数据处理流程如下。
1) 对于GPS动态变形监测观测数据进行单历元解算,求得测站点的三维动态坐标N、E、U方向的序列,作为IEEMD的输入信号。
2) 将坐标序列作为输入信号x(t),在x(t)中分200次加入均值为0、幅值系数常量为0.2的高斯白噪声进行EMD分解,将分解得到的模态分量进行平均得出
3) 计算高斯白噪声能量特性常数const,依据提取尺度的判定系数Judk确定多路径误差所处模态分量范围,提取符合条件的模态分量进行多路径误差模型的构建。
4) 计算相邻2 d多路径误差模型的相关系数,寻找相邻2 d多路径误差模型相关性最大时刻,在第2天的坐标序列中根据延迟理论剔除相关系数最大的多路径误差模型。
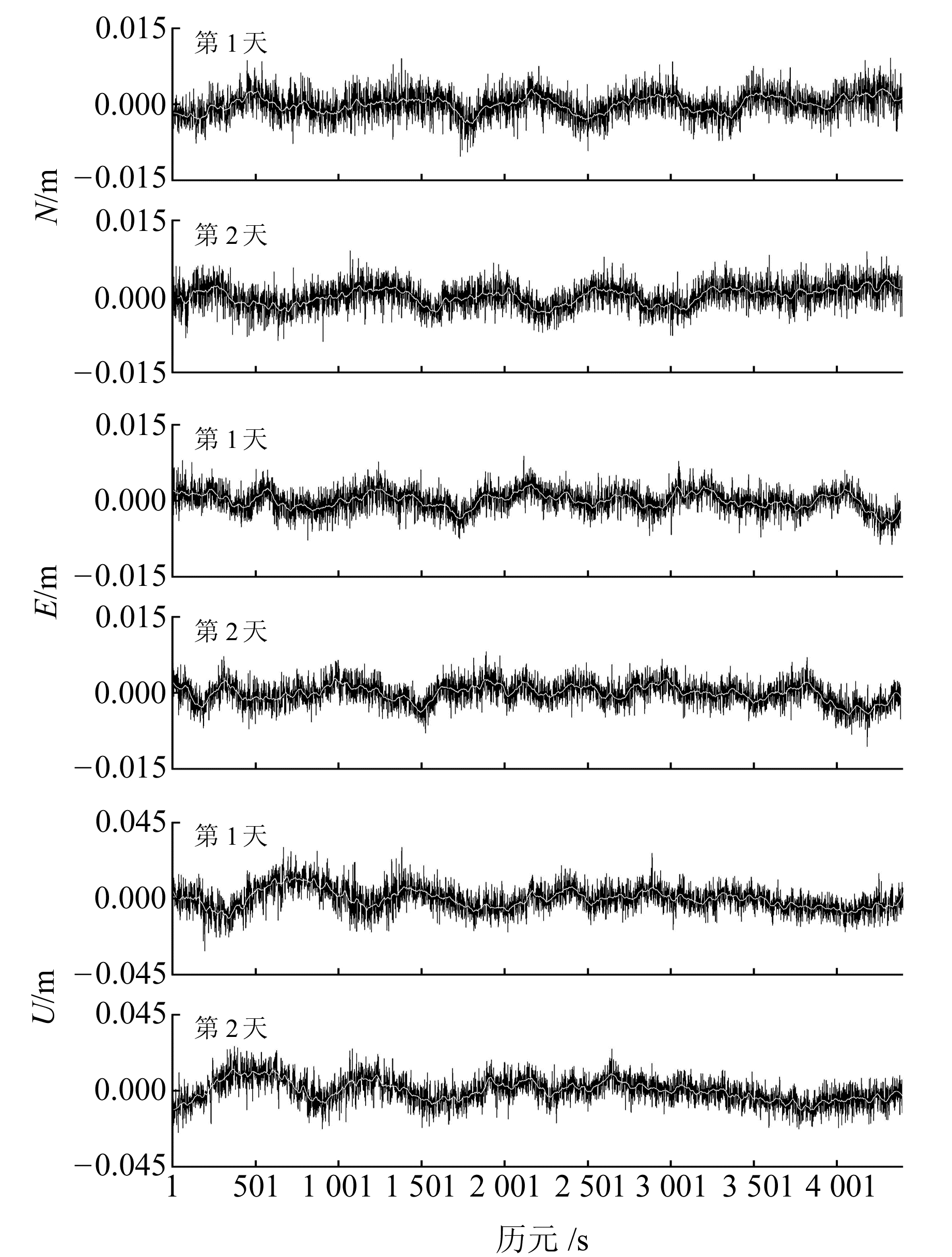
3 实验分析 3.1 数据采集与分析实验位于安徽理工大学某5楼顶,采用2台中海达V9接收机,构建长约43 m的基线,在2017-03-14~03-15相邻2 d的相同时段进行观测,采样间隔为1 s,卫星截止高度角10°,2 d天气状况均良好,微风,温度变化较小。接收机1东方向3 m有遮挡,接收机2北、西方向4 m有遮挡。以接收机1为固定站,接收机2为移动站进行单历元解算,得到三维动态坐标序列N、E、U方向坐标序列如图 2所示。图 2中将坐标序列以80个历元进行移动、平均,得到坐标序列趋势线(图中白色趋势线),可以看出,相邻2 d的坐标序列有几min的延迟,计算相同方向的坐标序列的相关系数大于0.65,说明相邻2 d的坐标序列具有很强的相关性。
|
图 2 相邻两天N、E、U方向坐标序列 Fig. 2 Coordinate series for two successive day |
为比较IEEMD与EEMD两种多路径误差建模的精度,设置一组EEMD实验进行对比。由于观测数据量较大,仅以E方向为例进行两种多路径误差模型的构建。对相邻2 d的E方向坐标序列分别进行IEEMD与EEMD多尺度分解,取第1天坐标序列分解结果为例进行分析。如图 3(单位10-3 m)所示,其中图 3(a)为第1天E方向坐标序列经IEEMD分解模态分量结果,分解得到9个模态分量与1个残余分量;图 3(b)为EEMD分解结果,得到10个模态分量与1个残余分量。计算imf9与imf10相减后序列标准差为0.311 cm,可知imf9与imf10频段重叠,模态分量个数不明确,分解并不彻底,而IEEMD分解得到的各个频段则因为在不同分解过程加入不同的高斯白噪声使得分解结果相较于EEMD效果要好。计算IEEMD分解提取尺度的判定系数,IEEMD与EEMD均是从尺度6开始Judk>1,按照高斯白噪声的能量密度与平均周期之积为常数的特性可以认为,前5个模态分量为高频的随机噪声,IEEMD从尺度6到尺度9为低频的多路径误差,EEMD从尺度6到尺度10为多路径误差。因此可以确定k为6提取多路径误差模型(图 4)。

|
图 3 第1天E方向坐标序列的IEEMD与EEMD分解结果 Fig. 3 Decomposition results of the time series of E direction in the first day using IEEMD and EEMD |

|
图 4 第1天E方向IEEMD与EEMD多路径误差模型 Fig. 4 Multipath error model between IEEMD and EEMD of E direction in the first day |
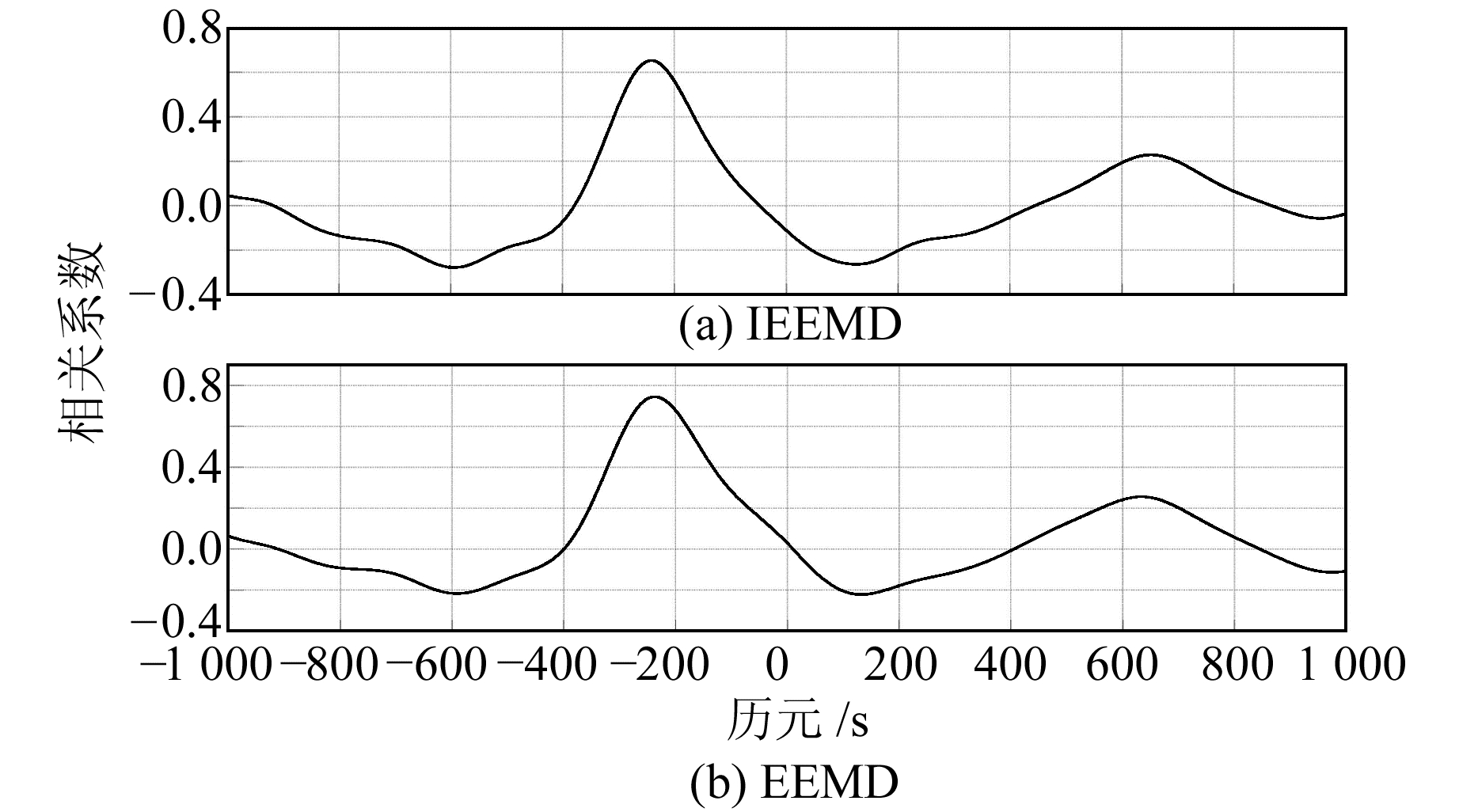
理论上,延迟l为-236 s时对应最大相关系数[2],采用式(3)计算的最大相关系数如图 5所示,在IEEMD中延迟为-239历元(-239 s)时,最大相关系数为0.65;EEMD中延迟为-243历元(-243 s),最大相关系数为0.73。两种方法所计算的延迟与理论值-236 s基本保持一致。在相邻2 d多路径误差模型的相关系数方面,IEEMD与EEMD相比小11%。
|
图 5 第1天E方向多路径误差模型的相关系数 Fig. 5 Cross-correlation of the multipath error models between two successive day of E direction in the first day |
利用多路径误差的周日重复性,提取第1天的多路径误差模型按照延迟理论值-236 s在第2天的坐标序列中进行剔除,图 6(a)与图 6(b)分别为经IEEMD与EEMD剔除理论相关系数最大多路径后的第2天N、E、U坐标序列,表 1中给出IEEMD与EEMD两种方法提取的第2天坐标序列消除多路径误差后的标准差与相关系数。两种方法均可以提取多路径误差模型对坐标序列进行改正,但IEEMD相较于EEMD效果更好。

|
图 6 剔除理论相关系数最大多路径后的第2天坐标序列 Fig. 6 Coordinate series after multipath error having the largest theoretical cross-correlation eliminated in the second day |
|
|
表 1 IEEMD与EEMD消除多路径误差对比 Tab. 1 Comparison of multipath error elimination effects between IEEMD and EEMD |
计算N、E、U方向IEEMD与EEMD所提取多路径误差模型的标准差,如表 2所示。第1天N、E、U方向IEEMD与EEMD提取的标准差相比分别减小3.25%、11.61%和8.38%;第2天N、E、U方向IEEMD与EEMD提取的标准差相比分别减小11.92%、11.80%与7.72%。可以看出,IEEMD相较于EEMD所提取的多路径误差模型精度较高。
|
|
表 2 IEEMD与EEMD提取多路径误差模型标准差对比 Tab. 2 Comparison of STD between IEEMD and EEMD for multipath error model extraction |
在GPS动态变形监测的多路径误差建模中,EEMD虽然可以解决由于观测过程中异常事件造成的模态混叠情况,但依然存在分解不彻底与模态分量数目不明确的问题。本文引入IEEMD算法,在EMD分解过程中多次加入自适应的高斯白噪声求取模态分量与残余分量,并对残余分量重复该过程直至分解结束, 然后设计一种自动提取尺度的方法提取多路径误差模型进行多路径误差的剔除。实验结果表明,与EEMD相比,该模型解决了EEMD分解不彻底与模态分量数目不明确的问题,通过相邻2 d多路径误差模型相关性计算可知,经IEEMD所提取的相邻2 d多路径误差模型相关性更强;通过计算两种模型去除多路径误差后的标准差可知,经过IEEMD剔除多路径误差后的N、E、U方向坐标序列稳定性相比EEMD均有提高,坐标序列精度得到提升,能够更有效地削弱多路径误差。
| [1] |
戴吾蛟, 丁晓利, 朱建军. GPS动态变形测量中的多路径效应特征研究[J]. 大地测量与地球动力学, 2008, 28(1): 65-71 (Dai Wujiao, Ding Xiaoli, Zhu Jianjun. Study on Multipath Effect in Structure Health Monitoring Using GPS[J]. Journal of Geodesy and Geodynamics, 2008, 28(1): 65-71)
(  0) 0) |
| [2] |
黄声享, 李沛鸿, 杨保岑, 等. GPS动态监测中多路径效应的规律性研究[J]. 武汉大学学报:信息科学版, 2005, 30(10): 877-880 (Huang Shengxiang, Li Peihong, Yang Baocen, et al. Study on the Characteristics of Multipath Effects in GPS Dynamic Deformation Monitoring[J]. Geomatics and Information Science of Wuhan University, 2005, 30(10): 877-880)
(  0) 0) |
| [3] |
袁林果, 黄丁发, 丁晓利, 等. GPS载波相位测量中的信号多路径效应影响研究[J]. 测绘学报, 2004, 33(3): 210-215 (Yuan Linguo, Huang Dingfa, Ding Xiaoli, et al. On the Influence of Signal Multipath Effects in GPS Carrier Phase Surveying[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(3): 210-215 DOI:10.3321/j.issn:1001-1595.2004.03.005)
(  0) 0) |
| [4] |
Huang N E, Shen Z, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[C]. Proc Roy Soc, London, 1998
(  0) 0) |
| [5] |
戴吾蛟, 丁晓利, 朱建军, 等. 基于经验模式分解的滤波去噪法及其在GPS多路径效应中的应用[J]. 测绘学报, 2006, 35(4): 321-327 (Dai Wujiao, Ding Xiaoli, Zhu Jianjun. EMD Filter Method and Its Application in GPS Multipath[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(4): 321-327 DOI:10.3321/j.issn:1001-1595.2006.04.005)
(  0) 0) |
| [6] |
刘超, 王坚, 胡洪, 等. 动态变形监测多路径实时修正模型研究[J]. 武汉大学学报:信息科学版, 2010, 35(4): 481-485 (Liu Chao, Wang Jian, Hu Hong, et al. Research on Real-Time Correcting Model of Multipath in GPS Dynamic Deformation Monitoring[J]. Geomatics and Information Science of Wuhan University, 2010, 35(4): 481-485)
(  0) 0) |
| [7] |
Wu Z H, Huang N E. Ensemble Empirical Mode Decomposition: A Noise Assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41
(  0) 0) |
| [8] |
Wu Z H, Huang N E. A Study of the Characteristics of White Noise Using the Empirical Mode Decomposition Method[C]. Proc Roy Soc, London, 2004
(  0) 0) |
| [9] |
Colominas M A, Schlotthauer G, Torres M E, et al. Noise-Assisted EMD Methods in Action[J]. Advances in Adaptive Data Analysis, 2012, 4(4): 1-11
(  0) 0) |
| [10] |
Colominas M A, Schlotthauer G, Torres M E. Improved Complete Ensemble EMD: A Suitable Tool for Biomedical Signal Processing[J]. Biomedical Signal Processing and Control, 2014, 14(1): 19-29
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38

