2. 山东省第一地质矿产勘查院,济南市二环东路4739号,250014
电磁波信号穿越电离层时会产生附加时间和距离延迟,造成误差。电离层是影响卫星导航系统精度、短波通信质量、电力传输安全的重要因素之一,因此有效获取电离层参数及电子密度剖面具有重要的科学研究意义[1]。
传统的电子密度探测方法包括电离层垂测仪和非相干散射雷达,但前者只能探测底部电离层,而后者造价高且数量稀少。经验模型如国际参考电离层IRI、Bent等模式预报误差较大,难以满足实际应用的需要[2]。GNSS掩星技术可用于大尺度电离层监测,但时间分辨率过低。近年来发展起来的GNSS电离层层析技术充分利用了总电子含量(total electron content, TEC)观测信息[3],但因其解算复杂、成本高昂,难以得到成熟应用。而随着GNSS获取VTEC的精度不断提高,利用单站VTEC数据反演电子密度剖面的方法逐渐引起国内外学者的重视。
本文利用单站GNSS VTEC数据反演测站上空电子密度,为获取更高精度的VTEC,考虑到常用的相位平滑伪距法易受平滑弧段长度以及与测站有关的误差影响[4],采用非组合精密单点定位(uncombined precise point positioning, UPPP)法进行单站电离层VTEC反演。在此基础上,提出用掩星观测数据约束电离层标高,结合Chapman模型和QPS模型分层反演,根据VTEC数据搜索最优的f0F2与hmF2参量,从而反演出近实时的测站上空电子密度剖面。本文解算了2016年不同季节4个GPS周的磁平静时期的观测数据,与IRI2016结果的比较显示, 利用本文方法反演的电子密度剖面结果更理想。
1 基于非组合PPP的单站电离层VTEC建模方法非组合PPP法采用GNSS双频原始观测值作为观测量,直接将站星间的电离层延迟作为未知参数估计。通过扩展卡尔曼滤波[4],共估计5类参数:测站坐标、接收机钟差、天顶对流层延迟、站星间斜电离层延迟以及模糊度参数[5]。
非组合PPP的电离层参数是先由伪距观测值计算初值,再通过滤波修正:
| $ I_{r,1}^s = \frac{{f_2^2}}{{f_2^2 - f_1^2}}\left[ {\left( {{P_1} - {P_2}} \right) - \left( {{b_R} + {b^s}} \right)} \right] $ | (1) |
式中,bR+bs为卫星与接收机组合硬件延迟,即系统硬件延迟,在1 d之内可以认为是个常量[6]。把系统硬件延迟作为待估参数引入观测方程,将其与电离层模型系数一并解出。
首先,系统硬件延迟的分离基于电离层单层模型[7]。在穿刺点处STEC转换为VTEC的投影函数可表示为:
| $ F\left( z \right) = \frac{{{\rm{STEC}}}}{{{\rm{VTEC}}}} = \frac{1}{{\sqrt {1 - {{\left( {\frac{{{R_e}\cos Z}}{{{R_e} + h}}} \right)}^2}} }} $ | (2) |
式中,Re为地球半径,h电离层薄层的高度,Z为测站处的卫星高度角。
而另一方面,穿刺点处的VTEC可以用区域电离层多项式模型进行拟合:
| $ {\rm{VTEC}}\left( {\varphi ,S} \right) = \sum\limits_{n = 0}^N {\sum\limits_{m = 0}^M {{E_{nm}}{{\left( {\varphi - {\varphi _0}} \right)}^n}{{\left( {S - {S_0}} \right)}^m}} } $ | (3) |
式中,φ、S分别为穿刺点的纬度、太阳时角;Emn为待求的多项式系数;(φ0, S0)为多项式模型的展开点;N、M表示模型最大阶数,通常N取1~2阶,M取2~4阶即可[8],本文将N和M均取为2。
因此,结合式(2)和式(3),便可得到求解系统硬件延迟的观测方程:
| $ {\mathit{\boldsymbol{\beta }}_s} = {\mathit{\boldsymbol{L}}_s} - F\left( z \right)\sum\limits_{i = 0}^m {\sum\limits_{j = 0}^n {{E_{mn}}{{\left( {\varphi - {\varphi _0}} \right)}^n}{{\left( {S - {S_0}} \right)}^m}} } $ | (4) |
式中,βs为待估的硬件延迟组合值,Ls表示未经校正的斜电离层延迟参数。可将式(4)写成:
| $ \mathit{\boldsymbol{AE}} + \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{\beta }}_s} = {L_s} + \varepsilon $ | (5) |
式中,A表示由(φ-φ0)n、(S-S0)m组成的参数,E表示待估的电离层模型系数,B表示系统硬件延迟参数的设计矩阵。取时段长度为1 h进行分段建模,对每一个卫星观测值,联立式(5)的观测方程,组成法方程:
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}}}&{{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PB}}}\\ {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PA}}}&{{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{E}}\\ {{\mathit{\boldsymbol{\beta }}_s}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{L}}_s}}\\ {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{L}}_s}} \end{array}} \right] $ | (6) |
按最小二乘法即可同时求解得到电离层模型系数与系统硬件延迟。
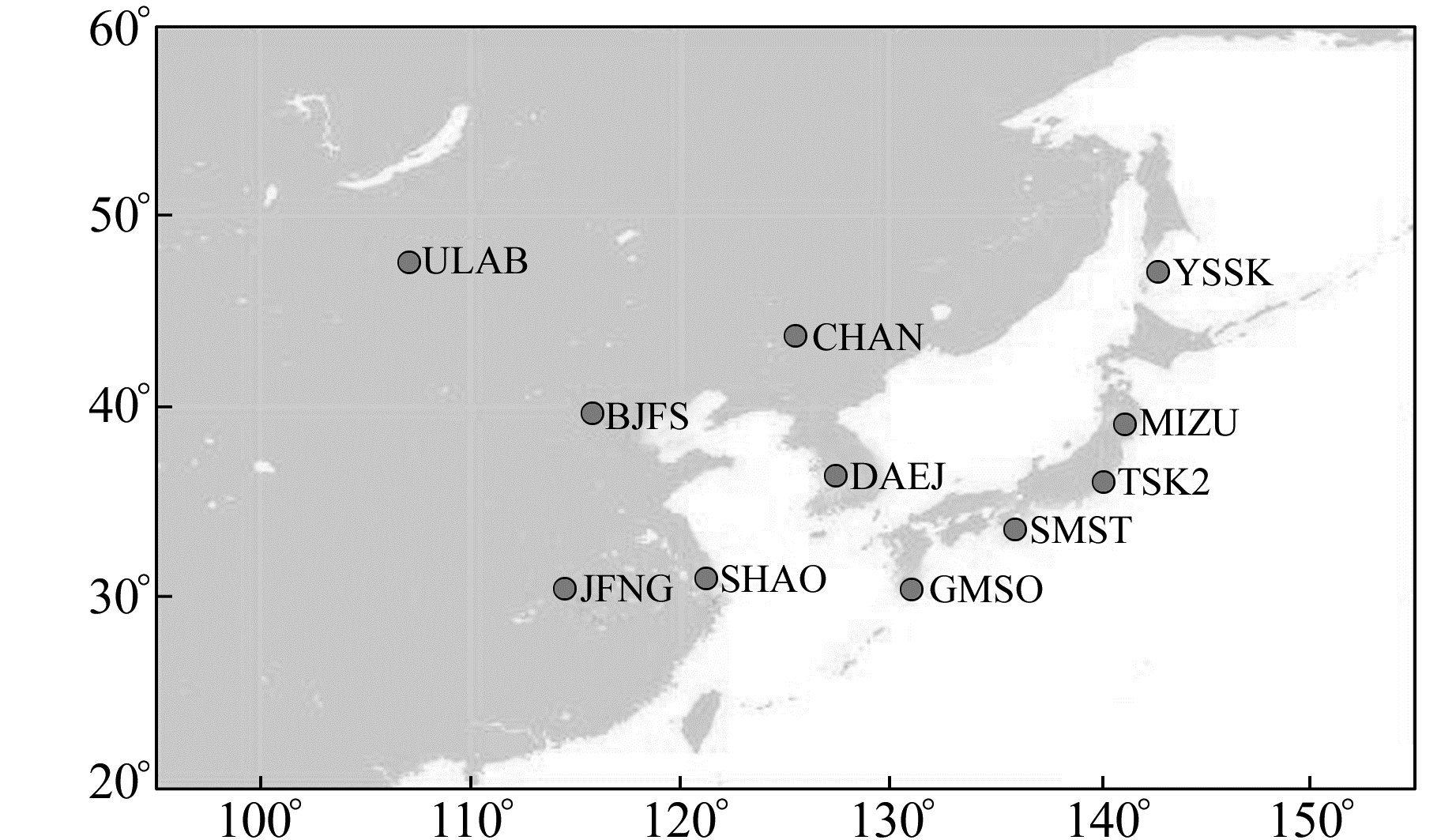
参与本文单站VTEC建模的IGS跟踪站共有11个,其分布如图 1所示。
|
图 1 IGS测站分布 Fig. 1 The distribution diagram of IGS stations |
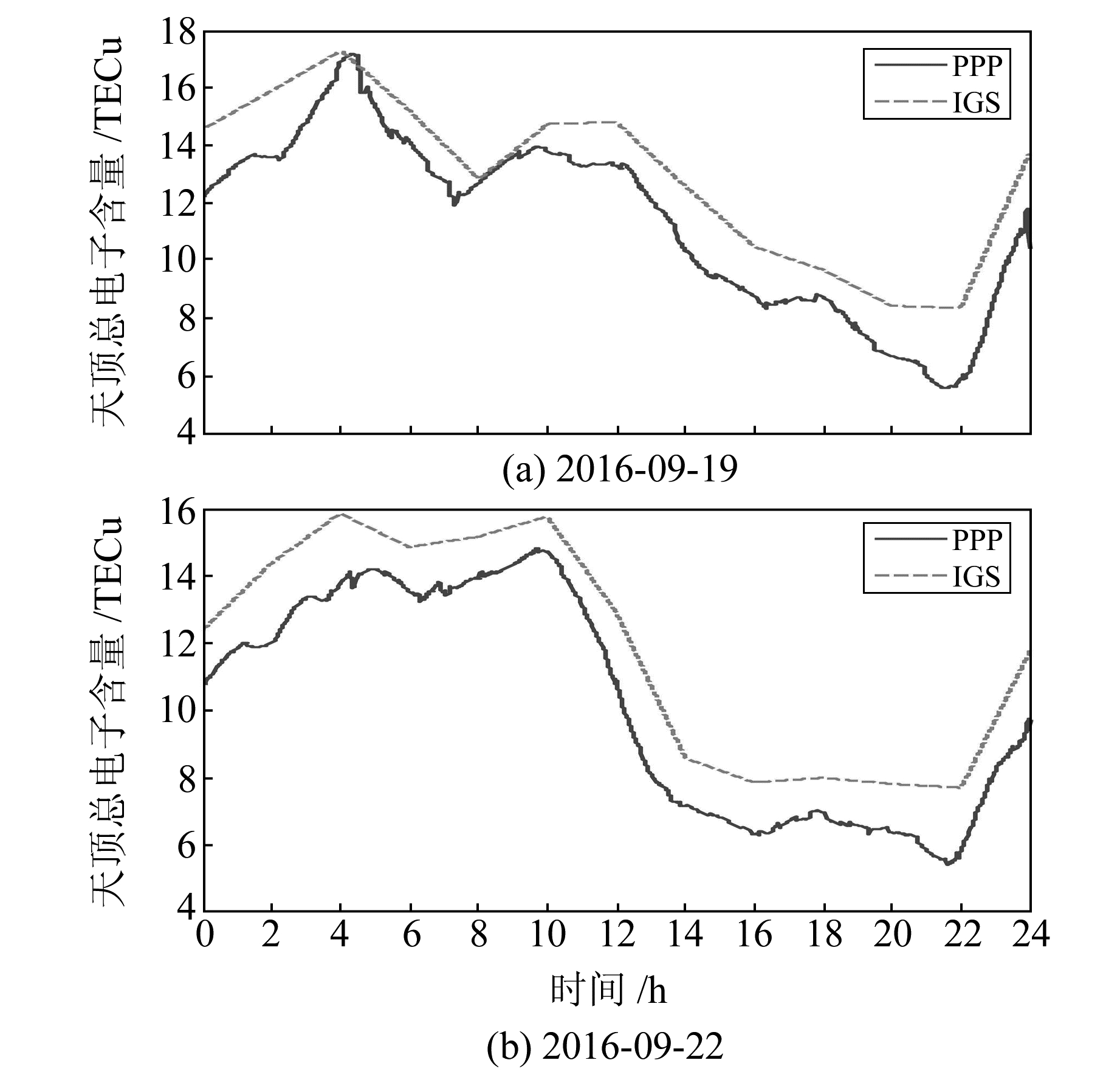
对北京站(BJFS)2016-09-18~24连续一周的数据进行试算。获取的测站VTEC与IGS电离层模型的对比示例如图 2所示,电离层区域建模的RMS日均值统计如表 1所示。图 2表明,本文计算的VTEC与IGS的结果有0~2 TECu的差异,整体变化趋势具有较强的一致性,可以近实时地监测电离层活动;由表 1可知,对于连续一周的单站电离层建模解算结果,RMS日均值不超过1 TECu。这说明非组合PPP估算的VTEC同时具有较高的精度和可靠性,可以应用于高精度的电离层电子密度剖面建模分析。
|
图 2 非组合PPP反演得到的VTEC Fig. 2 VTEC derived from uncombined PPP |
|
|
表 1 多项式电离层模型的RMS日均值(以BJFS站第1 915个GPS周为例) Tab. 1 Daily mean RMS of polynomial ionospheric modeling(The 1 915th GPS week, BJFS) |
建立电离层垂直剖面模型需要分别考虑E层、F1层和F2层。电离层TEC的绝大部分来自于F2层的贡献,底部的E层和F1层的贡献占比很小。可以用准抛物线QPS模型描述E层和F1层的电子密度[9]:
| $ {N_e} = \left\{ \begin{array}{l} \begin{array}{*{20}{c}} {{N_m}\left[ {1 - {{\left( {\frac{{r - {r_m}}}{{{r_m} - {r_b}}}} \right)}^2}{{\left( {\frac{{{r_b}}}{r}} \right)}^2}} \right],}\\ {{r_b} < r < {r_m}\left( {\frac{{{r_b}}}{{2{r_b} - {r_m}}}} \right)} \end{array}\\ 0,\;\;\;\;其他 \end{array} \right. $ | (7) |
式中,Nm与rm表示电子密度峰值及其所在地心高度,rb表示电离层底部的地心高度。
而关键层F2层的电子密度可以用Chapman模型来描述[10]:
| $ N\left( h \right) = {N_m}\exp \frac{1}{2}\left( {1 - y - {e^{ - y}}} \right) $ | (8) |
式中,Nm为F2层峰值电子密度,而约化高度为:
| $ y = \frac{{h - {h_m}}}{H} $ | (9) |
式中,hm代表F2层电子密度峰值所在高度;H表示电离层标高。因此Chapman模型的未知参量有3个:NmF2、hmF2和标高H。标高对于顶部电离层研究而言是一个非常重要的参数[11],其实测值可由COSMIC掩星数据提供。
COSMIC掩星数据可提供2~3 km垂直分辨率的电子密度剖面,可以代表掩星事件邻近时空电子密度剖面的真值,其精度已通过与电离层垂测仪数据的对比得到验证[12]。掩星数据由于时间分辨率限制,无法直接而持续准确地反映测站上空的电子密度,但能很好地反演电离层顶部信息。因此对于某一测站,结合邻近时空的掩星观测数据可以准确得到电离层标高。本文掩星数据来源于http://cdaac-www.cosmic.ucar.edu/cdaac中的ionPrf文件。
具体反演时,各电离层关键参数的初值由IRI2016模型确定。该模型在线版本的地址为https://omniweb.gsfc.nasa.gov/vitmo/iri2016_vitmo.html,直接输入参数就可以得到各种信息[13]。对于E层、F1层和F2层,分别有:
| $ \left\{ \begin{array}{l} {f_0}E = {f_0}{E_{{\rm{IRI}}}}\\ {h_m}E = {h_m}{E_{{\rm{IRI}}}}\\ {h_b}E = 90 \end{array} \right. $ | (10) |
| $ \left\{ \begin{array}{l} {f_0}{F_1} = {f_0}{F_{{\rm{1IRI}}}}\\ {h_m}{F_1} = {h_m}{F_{{\rm{1IRI}}}}\\ {h_b}{F_1} = {h_m}E \end{array} \right. $ | (11) |
| $ \left\{ \begin{array}{l} {f_0}{F_2} = \sqrt {\frac{{{\rm{VTEC}} \times {{10}^3}}}{{1.24 \times {\tau _{{\rm{IRI}}}}}}} \\ {h_m}{F_2} = {h_m}{F_{{\rm{2IRI}}}} \end{array} \right. $ | (12) |
式中,下标IRI代表该参量由IRI 2016模型获取。τIRI表示电离层板厚,其定义为:
| $ {\tau _{{\rm{IRI}}}} = \frac{{{\rm{TE}}{{\rm{C}}_{{\rm{IRI}}}}}}{{{N_m}{F_{{\rm{2IRI}}}}}} $ | (13) |
根据式(10)、式(11),E层和F1层的参数可由IRI模型确定;而对于关键的F2层,在由掩星数据分别限定电子密度峰值顶部和底部的标高后,基于电子密度线积分即为VTEC这一条件,搜索得到最优的f0F2与hmF2参数。由此获取完整的单站电离层电子密度垂直分布剖面。
3 反演结果与分析为评定本文反演方法的可靠性,从太阳活动中等年份2016年4个季节里3月、6月、9月和12月的最后一周中选取反演目标时刻进行实验。选取的基本条件是该时刻在测站附近存在掩星事件,以便作为真值进行比较。除此之外,按以下几个条件筛选数据:
1) 根据图 1中IGS跟踪站分布,掩星事件分布范围为东亚地区的28°~50°N、105°~145°E。
2) 掩星事件发生当日地磁Kp指数不超过4。
3) hmF2的范围应介于200~400 km之间,过高或过低则可能存在异常值,可通过电子密度剖面图验证。
4) 为保证强空间相关性,掩星事件在取得NmF2时掩星切点与邻近的IGS跟踪站的距离在600 km以内。
5) 由掩星数据获取标高实测值时,以目标时刻为中心,取前后一周内(不包含当天)、地方时相差2 h内的若干掩星事件的标高平均值。

|
图 3 CHAN测站电子密度剖面 Fig. 3 Electron density profile of CHAN station |

|
图 4 DAEJ测站电子密度剖面 Fig. 4 Electron density profile of DAEJ station |
|
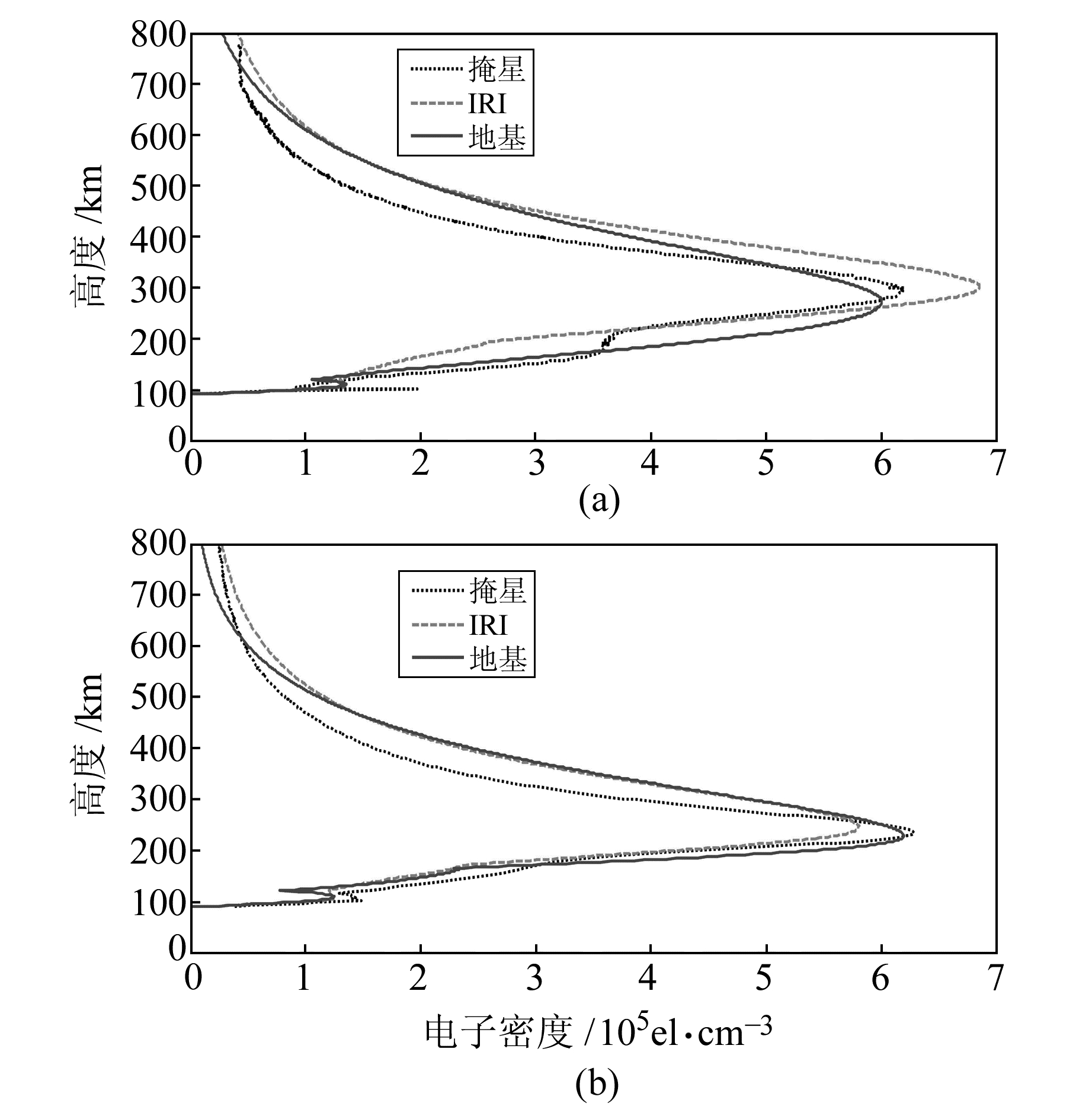
图 5 日本地区两个不同测站的电子密度剖面 Fig. 5 Electron density profile of two different stations in Japan |
图 3为同一测站(CHAN站)不同季节的电子密度反演结果。其中图 3(a)表示2016-03-31 12:15 LT的实验结果,图 3(b)表示2016-12-30 10:10 LT的实验结果。这一算例中,本文反演结果在电离层顶部比IRI模型更接近于掩星实测结果,但在电离层底部IRI模型略优于本文模型。两种方法均未能体现出F1层的存在。
图 4为同一测站(DAEJ站)同一季节不同时段的电子密度反演结果。其中图 4(a)表示2016-12-28 00:30 LT的实验结果,图 4(b)表示2016-12-28 11:15 LT的实验结果。反演的夜间结果相对于IRI模型在电离层顶部更优,而日间结果在底部更优。重要的是,本文结果明显取得了更为精确的NmF2与hmF2参数。
图 5为日本地区2个不同测站不同季节的电子密度反演结果。其中图 5(a)表示GMSD站2016-06-26 14:30 LT的实验结果,图 5(b)表示MIZU站2016-09-26 11:20 LT的实验结果。这一算例中GMSD站掩星数据出现E层异常,F1层的特征得以体现。但仅从剖面图难以判定本文结果与IRI模型的精度差异。
图 3~5的反演示例不足以对本文方法与IRI模型何者更优下一个定论。为进一步从整体上评价反演方法,以掩星实测数据为基准,对获取的所有hmF2和f0F2精度进行统计,对均方根误差(RMS)与绝对平均误差(MAE)的统计结果如表 2所示。
|
|
表 2 反演结果的精度评定 Tab. 2 Accuracy assessment of results |
表 2的统计结果表明,本文反演方法所获取的f0F2参数RMS为0.58 mHz,MAE为-0.11 mHz,均优于IRI2016模型的结果;而hmF2参数的RMS为28.77 km,MAE为-11.31 km,精度与IRI 2016模型相比也都略有提升,但仍有待进一步提高。
4 结语本文选取东亚地区11个IGS跟踪站,利用非组合PPP技术结合区域多项式模型获取了单站高精度VTEC。在此基础上,提出综合采用Chapman模型和QPS模型,以掩星实测电离层Chapman标高以及VTEC作为约束条件,反演得到测站上空近实时电离层电子密度剖面。计算2016年4个季节各一周的地磁平静时期数据,将反演计算得到的电子密度与IRI2016模型结果以及掩星实测结果进行对比,三者变化趋势高度一致;以掩星观测值为基准,经本文方法可以获得比IRI模型更为精确的电离层参数hmF2和f0F2。
标高对于电离层电子密度剖面建模具有重要意义。本文充分利用掩星标高实测数据,算法简便可行且保证反演精度,可近实时获取测站上空电子密度,对于单站区域电离层电子密度三维建模具有重要价值,但电离层顶部取固定标高时存在一定偏差,这也需要后续开展更加深入的工作。
| [1] |
欧明, 甄卫民, 张时生, 等. 一种融合天地基多源数据的电离层反演方法[J]. 电波科学学报, 2016, 31(4): 713-719 (Ou Ming, Zhen Weimin, Zhang Shisheng, et al. A Combined Ionosphere Inversion Methodby Data Fusion of Space and Ground-Based Multisource Observations[J]. Chinese Journal of Radio Science, 2016, 31(4): 713-719)
(  0) 0) |
| [2] |
刘琨, 赵振维, 康士峰. 利用单站地基GPS数据反演电离层电子密度[J]. 全球定位系统, 2008(6): 9-12 (Liu Kun, Zhao Zhenwei, Kang Shifeng. Retrieving the Electron Density Height Profile Using Single Ground-Based GPS Receiver[J]. GNSS World of China, 2008(6): 9-12 DOI:10.3969/j.issn.1008-9268.2008.06.003)
(  0) 0) |
| [3] |
刘三枝, 王解先, 李浩军. 基于CORS数据反演江苏上空电离层电子密度[J]. 测绘科学, 2013, 38(2): 47-49 (Liu Sanzhi, Wang Jiexian, Li Haojun, et al. Inversion of Ionospheric Electron Density over Jiangsu with CORS Data[J]. Science of Surveying and Mapping, 2013, 38(2): 47-49)
(  0) 0) |
| [4] |
张宝成, 欧吉坤, 袁运斌, 等. 利用非组合精密单点定位技术确定斜向电离层总电子含量和站星差分码偏差[J]. 测绘学报, 2011, 40(4): 447-453 (Zhang Baocheng, Ou Jikun, Yuan Yunbin, et al. Calibration of Slant Total Electron Content and Satellite-Receiver's Differential Code Biases with Uncombined Precise Point Positioning Technique[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 447-453)
(  0) 0) |
| [5] |
范磊, 钟世明, 李子申, 等. 跟踪站分布对非组合精密单点定位提取GPS卫星差分码偏差的影响[J]. 武汉大学学报:信息科学版, 2016, 41(3): 316-321 (Fan Lei, Zhong Shiming, Li Zishen, et al. Effect of Tracking Stations Distribution on the Estimation of Differential Code Biases by GPS Satellites Based on Uncombined Precise Point Positioning[J]. Geomatics and Information Science of Wuhan University, 2016, 41(3): 316-321)
(  0) 0) |
| [6] |
陈鹏, 陈家君. GPS/GLONASS融合的全球电离层格网模型结果分析[J]. 大地测量与地球动力学, 2014, 34(5): 70-74 (Chen Peng, Chen Jiajun. Analysis of Global Ionospheric Grid Model Integrated GPS /GLONASS[J]. Journal of Geodesy and Geodynamics, 2014, 34(5): 70-74)
(  0) 0) |
| [7] |
李文峰. 基于单站GNSS区域电离层延迟建模[D]. 青岛: 山东科技大学, 2014 (Li Wenfeng. Modeling Regional Ionosphere Delay Based on Single GNSS Station[D]. Qingdao: Shandong University of Science and Technology, 2014)
(  0) 0) |
| [8] |
刘长建. GNSS电离层建模方法与质量控制研究[D]. 郑州: 信息工程大学, 2011 (Liu Changjian. Study on Modeling Method and Model Quality Control of Ionosphere Based on GNSS[D]. Zhengzhou: Information Engineering University, 2011)
(  0) 0) |
| [9] |
Jiang C H. Reconstruction of the Vertical Electron Density Profile Based on Vertical TEC Using the Simulated Annealing Algorithm[J]. Advances in Space Research, 2016(57): 2167-2176
(  0) 0) |
| [10] |
刘伟, 郑作亚, 郭英, 等. 基于Chapman函数反演电离层电子密度[J]. 大地测量与地球动力学, 2013, 33(2): 120-122 (Liu Wei, Zheng Zuoya, Guo Ying, et al. Inversion of Ionospheric Electron Density Based on Chapman Function[J]. Journal of Geodesy and Geomatics, 2013, 33(2): 120-122)
(  0) 0) |
| [11] |
解海永, 宁百齐, 刘立波, 等. 北京地区电离层Chapman标高的统计分析[J]. 地球物理学报, 2014, 57(11): 3523-3531 (Xie Haiyong, Ning Baiqi, Liu Libo, et al. Statistical Analysis of the Ionospheric Chapman Scale Height at Beijing[J]. Chinese Journal of Geophysics, 2014, 57(11): 3523-3531 DOI:10.6038/cjg20141104)
(  0) 0) |
| [12] |
Guo P, Xu X, Zhang G X. Analysis of the Ionospheric Equivalent Slab Thickness Based on Ground-Based GPS/TEC and GPS/COSMIC RO Measurements[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2011(73): 839-846
(  0) 0) |
| [13] |
蔡超军. 利用GPS数据和IRI模型对比分析广州地区电离层TEC变化特性[D]. 广州: 华南理工大学, 2013 (Cai Chaojun. Comparative Analysis the Variation Characteristics of TEC over Guangzhou Region by Using GPS Data and IRI Model[D]. Guangzhou: South China University of Technology, 2013)
(  0) 0) |
2. No.1 Institute of Geology and Mineral Resources of Shandong Province, 4379 East-Erhuan Road, Jinan 250014, China
 2018, Vol. 38
2018, Vol. 38

