2. 中国卫星导航系统管理办公室测试评估研究中心,北京市,100094;
3. 中国科学院上海天文台,上海市南丹路80号,200030;
4. 河海大学地球科学与工程学院,南京市佛城西路8号,211100;
5. 同济大学测绘与地理信息学院,上海市四平路1239号,200092
对于卫星导航定位系统而言,电离层的影响严重削弱了卫星导航定位的精度和准确度,是卫星导航定位中的主要误差源[1]。采用电离层延迟模型可以有效地消除实时导航定位中电离层误差的影响,如现行的GPS系统广播星历中的电离层预报模型可以消除60%左右的延迟误差[2-3],而WAAS(wide area augmentation system)差分系统中格网电离层模型可以消除80%左右的电离层延迟误差[4-7]。我国现役北斗广域差分系统中的电离层延迟格网改正数计算采用的数据是监测站的伪距观测值,因此,格网改正数的精度直接受到伪距测量噪声的影响。虽然传统的相位平滑伪距法(如CNMC(code noise and multipath correction)算法)能够减小多径的影响[8],但是这类算法的有效性很大程度上依赖相位数据的连续性,当相位观测出现新的模糊度时,CNMC则需要重新收敛,导致一段时间内电离层延迟格网改正数解算精度降低。
针对这一问题,本文提出采用伪距相位综合算法,即利用伪距数据结合相位历元间差分数据综合解算电离层延迟格网改正数。利用GPS实测数据对该算法进行分析验证,比较分析采用伪距相位综合算法较单纯伪距法来实时计算站星斜路径方向的电离层延迟值的优越性,最后从实时生成的电离层格网内、外符合精度方面验证伪距相位综合算法的有效性。
1 GNSS双频电离层延迟改正对于双频GNSS的导航定位信号,其两个频率L1、L2上的伪距观测方程分别为:
| $ \left\{ \begin{array}{l} {P_1} = \rho + c\left( {\delta {t_{\rm{r}}} - \delta {t^{\rm{s}}}} \right) + {I_{{\rm{trop}}}} + {I_{\rm{1}}} + {B_1} + {\varepsilon _1}\\ {P_2} = \rho + c\left( {\delta {t_{\rm{r}}} - \delta {t^{\rm{s}}}} \right) + {I_{{\rm{trop}}}} + {I_{\rm{2}}} + {B_2} + {\varepsilon _2} \end{array} \right. $ | (1) |
式中,P1、P2分别为两个频点的伪距观测值;ρ为卫星至接收机的几何距离;c为光速;δtr为接收机钟差;δts为卫星钟差;Itrop为对流层延迟;B1、B2分别为两个频点上伪距观测量的卫星和接收机硬件延迟;ε1、ε2分别为两个频点的伪距观测噪声;I1、I2分别为两个频点的电离层延迟,其表达式为[9]:
| $ {I_i} = \frac{{40.3{\rm{TEC}}}}{{f_i^2}} $ | (2) |
式中,Ii为电离层延迟值,TEC为信号传播路径上的总电子含量,fi为信号频率。
由式(1)和式(2)可以得到由双频伪距观测值计算L1频率上的电离层延迟的表达式为:
| $ {I_1} = \frac{{f_2^2}}{{f_1^2 - f_2^2}}\left[ {\left( {{P_2} - {P_1}} \right) - \left( {{B_2} - {B_1}} \right)} \right] $ | (3) |
利用式(3)计算穿刺点处电离层延迟值,利用事先解算的硬件延迟偏差参数对相关误差进行改正,进而采用加权平均算法实时计算生成电离层延迟网格[9]。
2 伪距相位综合的电离层延迟解算算法第1步利用伪距解算电离层延迟的绝对值,第2步通过历元间差分获取电离层延迟历元间变化,第3步通过伪距相位综合解算电离层延迟。
2.1 相位差分获取电离层延迟历元间变化电离层延迟所采用的数据为观测站的伪距观测值,其计算精度受到伪距噪声的影响。为提高精度,可以采用高精度的相位观测值。同式(3)相似,任意测站对一颗卫星信号传播路径上L1频率的电离层延迟,亦可由双频载波相位观测值计算得到,其表达式为:
| $ \begin{array}{*{20}{c}} {{I_1} = \frac{{f_2^2}}{{f_1^2 - f_2^2}}\left[ {\left( {{\lambda _1}{\varphi _1} - {\lambda _2}{\varphi _2}} \right) + } \right.}\\ {\left. {\left( {{\lambda _1}{N_1} - {\lambda _2}{N_2}} \right) - \left( {{b_2} - {b_1}} \right)} \right]} \end{array} $ | (4) |
式中,λ1、λ2分别为两个频点的波长,φ1、φ2分别为两个频点的载波相位观测值,N1、N2分别为φ1、φ2的初始整周模糊度,b1、b2分别为两个频点上相位观测量的卫星和接收机硬件延迟。与式(3)相比,表达式中多了模糊度参数Ni。
采用以上观测模型,综合伪距和相位观测。相比伪距观测的数据处理,相位观测值包含了模糊度的处理。通常在实时逐历元处理模式下,模糊度的连续处理存在较长的收敛时间,此外在数据中断或者周跳的情况下,需要重新收敛。考虑到以上因素,采用对相邻历元的相位观测值作差分,可得到:
| $ \begin{array}{*{20}{c}} {\Delta I\left( {{t_{i - 1}},{t_i}} \right) = \frac{{f_2^2}}{{f_1^2 - f_2^2}}}\\ {\left[ {{\lambda _1}\Delta {\varphi _1}\left( {{t_{i - 1}},{t_i}} \right) - {\lambda _2}\Delta {\varphi _2}\left( {{t_{i - 1}},{t_i}} \right)} \right]} \end{array} $ | (5) |
从式(5)可以看出,通过历元间差分,硬件延迟以及模糊度等在历元间不变的参数得以消除。由于没有模糊度参数,以上方程解算不存在收敛性的问题,可采用与伪距一致的处理方法,获取电离层延迟在历元间的高精度变化值。采用以上模型,在数据丢失或者周跳的情况下,只会影响一个历元的处理。
2.2 伪距相位综合的电离层延迟计算模型式(3)解算的是电离层延迟绝对值,根据式(5)则可以得到电离层延迟的历元间的变化。定义历元ti基于伪距的电离层延迟为Ic, i,历元ti基于相位的电离层延迟变化为Iφ, i-Iφ, i-1。
在电离层延迟历元间变化结果中,只要已知其中任意一个历元的绝对值,所有与该历元一起形成连续观测的电离层延迟也就被确定,这在平差领域中可归结为基准问题。一种解决方法为:利用伪距的结果作为初值,当初值多余1个时,可以将伪距观测值作为虚拟观测值加权,最后采用最小二乘进行求解。将伪距结果作为实际参数的观测值,观测方程为:
| $ {{\hat I}_i} - {I_{c,i}} = {v_{c,i}} $ | (6) |
式中,
基于相位的历元间差分的结果同样作为虚拟观测值,观测方程为:
| $ \left( {{{\hat I}_i} - {{\hat I}_{i - 1}}} \right) - \left( {{{\hat I}_{\varphi ,i}} - {{\hat I}_{\varphi ,i - 1}}} \right) = {v_{\Delta \varphi ,i}} $ | (7) |
式中,
以每个历元的方差阵Pi作为权阵,对处理弧段的n个历元叠加,式(6)法方程的形式为:
| $ {\mathit{\boldsymbol{E}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_c}\mathit{\boldsymbol{E\hat I}} = {\mathit{\boldsymbol{E}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_c}{\mathit{\boldsymbol{I}}_c} $ | (8) |
式中,E为n×n的单位阵。式(7)法方程的形式为:
| $ {\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_\varphi }\mathit{\boldsymbol{A\hat I}} = {\mathit{\boldsymbol{E}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_\varphi }\Delta {\mathit{\boldsymbol{I}}_\varphi } $ | (9) |
在式(8)、式(9)中,A为式(7)对应的系数阵:
| $ \mathit{\boldsymbol{A}} = {\left[ {\begin{array}{*{20}{c}} { - 1}&1&0& \cdots &0&0\\ 0&{ - 1}&1& \cdots &0&0\\ \cdots&\cdots&\cdots&\cdots&\cdots&\cdots \\ \cdots&\cdots&\cdots&\cdots&\cdots&\cdots \\ 0&0&0& \cdots &{ - 1}&1 \end{array}} \right]_{\left( {n - 1} \right) \times n}} $ | (10) |
Pc和Pφ为伪距和相位的分块权矩阵,这里均取为单位阵。且有:
| $ \begin{array}{l} \mathit{\boldsymbol{\hat I}} = {\left( {\begin{array}{*{20}{c}} {{{\hat I}_1}}&{{{\hat I}_2}}& \cdots &{{{\hat I}_n}} \end{array}} \right)^{\rm{T}}}\\ {\mathit{\boldsymbol{I}}_c} = {\left( {\begin{array}{*{20}{c}} {{{\hat I}_{c,1}}}&{{{\hat I}_{c,2}}}& \cdots &{{{\hat I}_{c,n}}} \end{array}} \right)^{\rm{T}}}\\ \Delta {\mathit{\boldsymbol{I}}_\varphi } = {\left( {\begin{array}{*{20}{c}} {{I_{\varphi ,2}} - {I_{\varphi ,1}}}&{{I_{\varphi ,3}} - {I_{\varphi ,2}}}& \cdots &{{I_{\varphi ,n}} - {I_{\varphi ,n - 1}}} \end{array}} \right)^{\rm{T}}} \end{array} $ | (11) |
联合式(8)、式(9)就可以得到伪距相位综合的电离层延迟参数。由于解得的电离层延迟值为信号传播方向电离层延迟,所以可以采用三角投影函数得到穿刺点处天顶方向的电离层延迟值。其计算表达式为:
| $ {I_V} = {I_S}\cos Z' $ | (12) |
式中,IS为斜路径方向电离层延迟,IV为穿刺点处天顶方向电离层延迟,Z′为穿刺点处站星信号方向的天顶距。
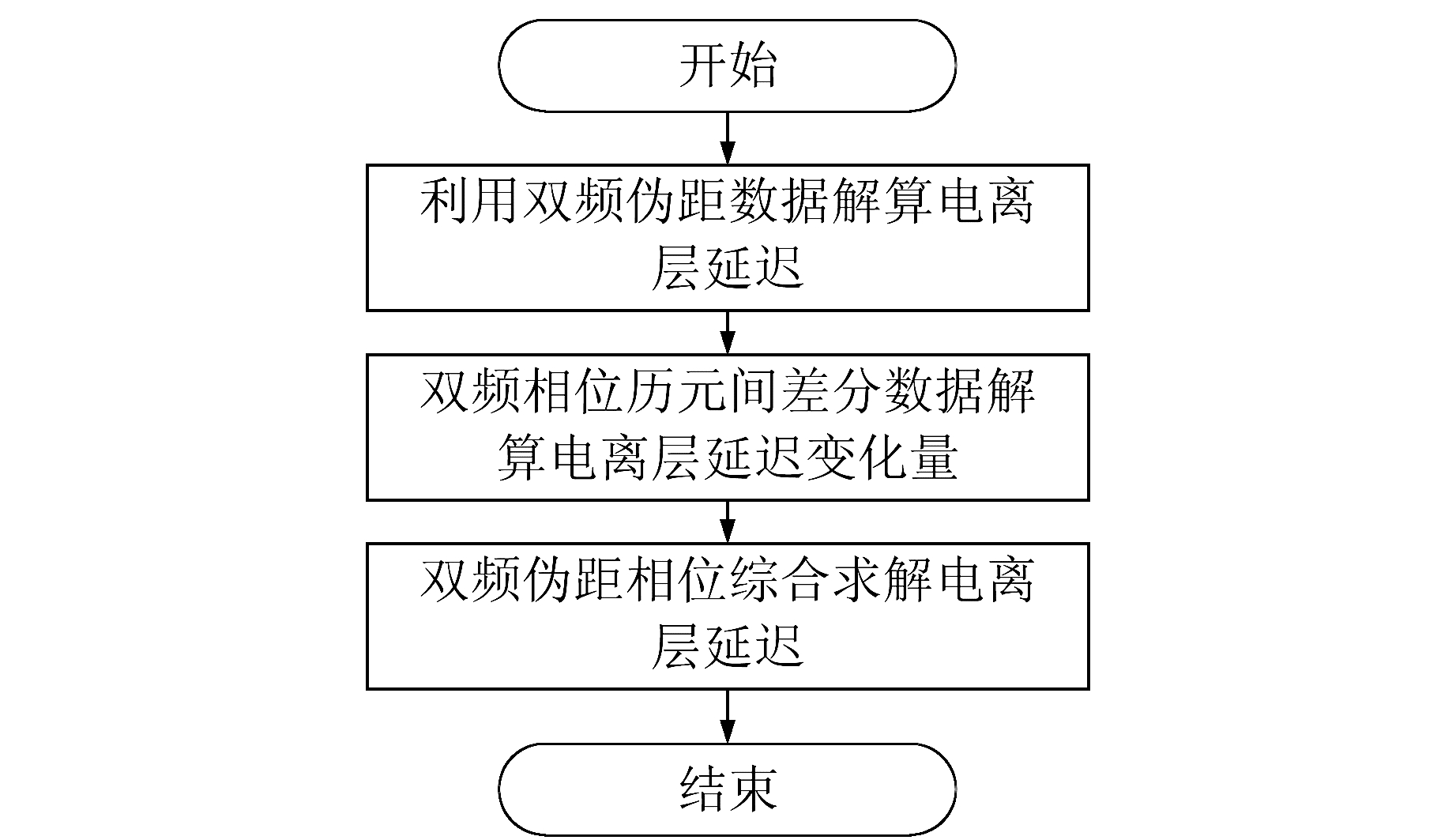
伪距相位综合的电离层延迟解算算法的具体流程见图 1。
|
图 1 伪距相位综合的电离层延迟解算算法流程 Fig. 1 The flow chart of the ionospheric delay solution algorithm based on pseudorange-phase synthesis |
根据格网点周围有效穿刺点电离层延迟,按照穿刺点与格网点的球面几何距离反比加权计算格网点的天顶方向电离层延迟,并考虑将电离层K8参数模型作为背景场,采用下式计算格网点延迟[6]:
| $ \begin{array}{l} {\rm{IGP\_dela}}{{\rm{y}}_j} = \\ \;\;\;\;\frac{{\sum\limits_{i = 1}^m {{w_i} \cdot {\rm{IPP\_dela}}{{\rm{y}}_i}} \cdot \frac{{{\rm{IGP\_Mode}}{{\rm{l}}_j}}}{{{\rm{IPP\_Mode}}{{\rm{l}}_i}}}}}{{\sum\limits_{i = 1}^m {{w_i}} }}\\ {w_i} = \frac{1}{{{d_{ij}}}}\\ {d_{ij}} = 6\;378.1 \cdot \arccos \left( {\sin {\varphi _j}\sin {\varphi _i} + } \right.\\ \;\;\;\left. {\cos {\varphi _j}\cos {\varphi _i}\cos \left( {{\lambda _j} - {\lambda _i}} \right)} \right) \end{array} $ | (13) |
式中,j为格网点编号,m为格网点周围的有效穿刺点个数;IGP_delayj为格网点处的电离层延迟,IPP_delayj为穿刺点处的电离层延迟,IGP_Modelj为格网点处根据K8参数计算得到的电离层延迟,IPP_Modeli为穿刺点处根据K8参数计算得到的电离层延迟;φi、φj分别为穿刺点和格网点的地理纬度,λi、λj分别为穿刺点和格网点的地理经度,dij为穿刺点与格网点之间的球面几何距离,权值wi取为距离的倒数。
3.2 电离层格网内、外符合精度使用A路数据(见§4)进行实时解算建立电离层格网,并对格网进行内符合精度评定,而B路数据(见§4)则可以用来进行格网的外符合精度评定。待解算出一组格网电离层天顶延迟后,可采用下式评估整个格网的内、外符合精度:
| $ {e_{{\rm{IPP}}}} = {I_{{\rm{IPP}}}} - {{\hat I}_{{\rm{IPP}}}},{\rm{RM}}{{\rm{S}}_{{\rm{in}}/{\rm{out}}}} = \sqrt {\sum\limits_{i = 1}^n {{{\left( {{e_{{\rm{IPP}}}}} \right)}^2}} /n} $ | (14) |
式中,IIPP为穿刺点处的电离层延迟值,
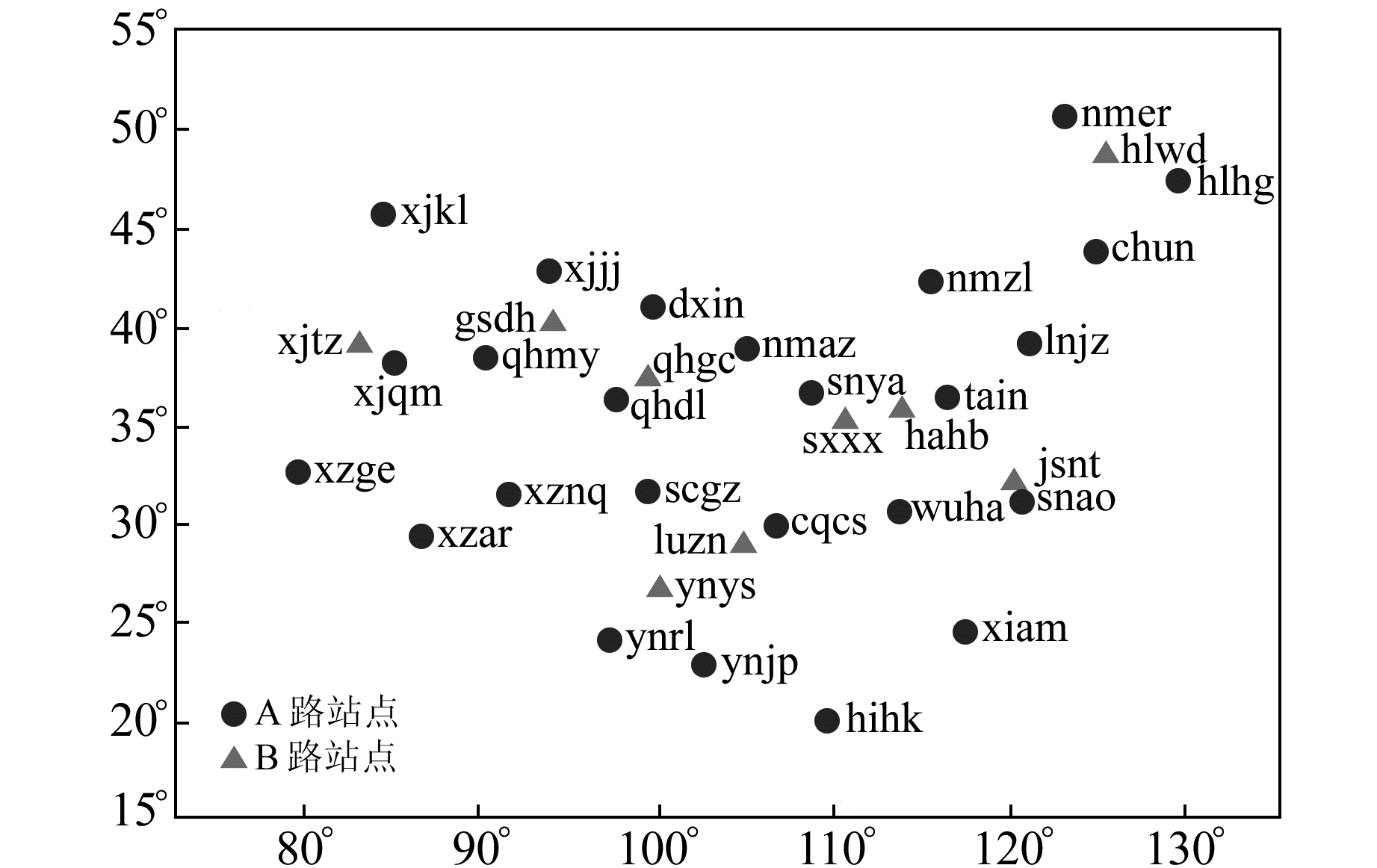
本文采用的GPS数据来自中国地壳运动观测网络(crustal movement observation network of China,CMONOC)数据,选择了25个遍布全国的台站作为A路数据,其点位分布如图 2中圆点所示;又选择了9个台站作为B路数据,其点位分布如图 2中三角形点所示。双频伪距相位的观测数据类型为C1、P2、L1、L2,采样率为30 s。本文对2012-06-30上述A路、B路的观测数据进行实时处理,截止高度角设为15°,电离层格网区域为70°~140°E、7.5°~55°N区域内纬度间隔2.5°和经度隔5°划分为320个格网点。图 3所示为A路数据某个历元时刻穿刺点分布,该历元所有的穿刺点基本覆盖了中国区域。
|
图 2 A路、B路所有站点的分布 Fig. 2 Distribution of station of A, B roads |

|
图 3 某历元时刻A路数据的穿刺点分布 Fig. 3 The IPP distribution of the data of A road at one epoch |
本文设计的电离层格网更新周期为3 min,伪距相位综合算法的处理弧段则取格网生成时间节点前9 min内的数据,将这些数据中每一站一星的数据作为一个处理单元,根据式(3)利用伪距观测值建立得到如式(6)的观测方程,根据式(5)利用相位数据进行历元间差分得到如式(7)的观测方程,最后联立法方程式(8)、式(9),采用最小二乘解算得出该处理弧段内每一站一星斜路径上的电离层延迟的时间序列。
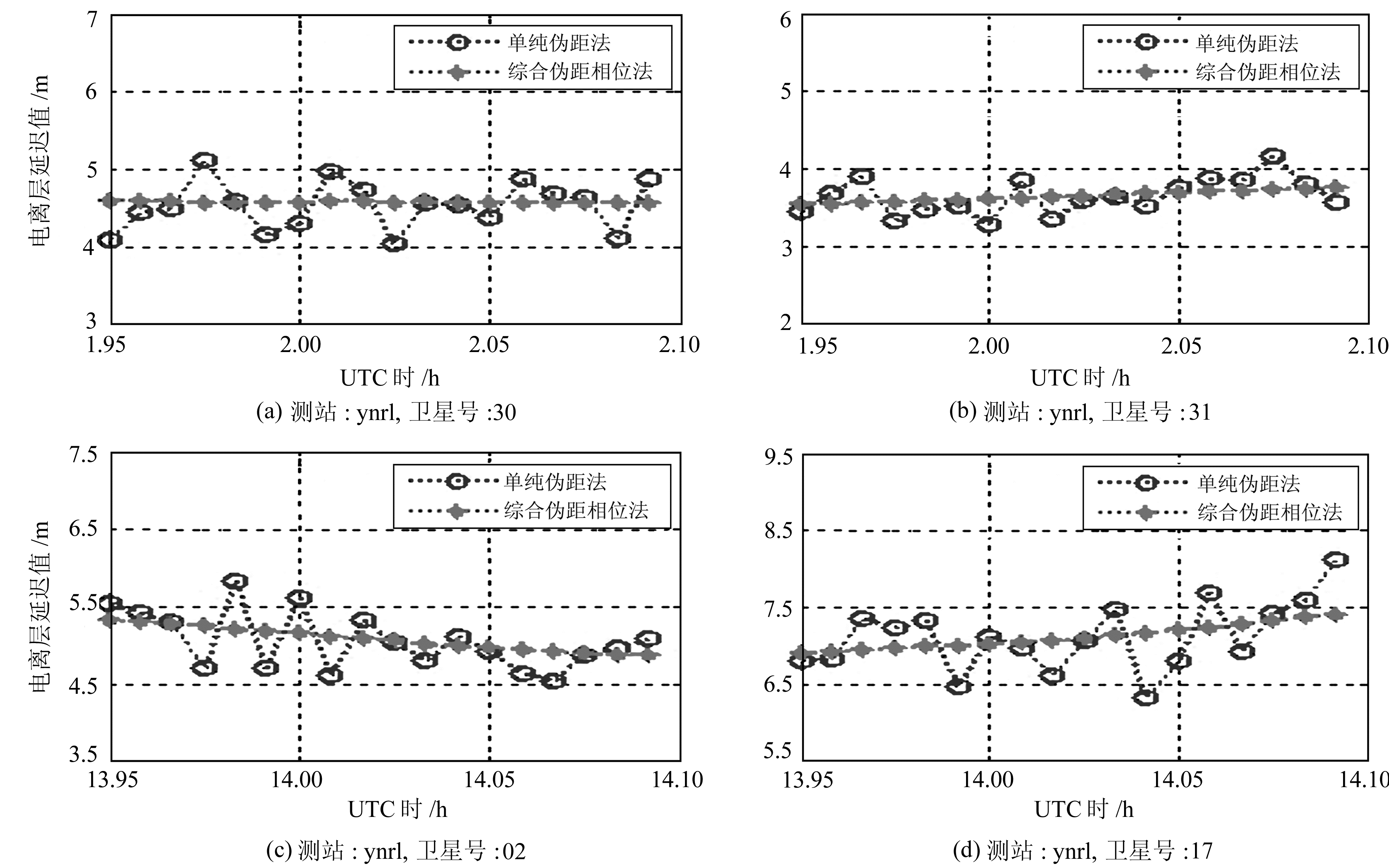
本文为以ynrl站为例,对任取的UTC 02:00左右的30号、31号卫星和在UTC 14:00左右的02号、17号卫星的观测数据,分别使用单纯伪距法和伪距相位综合算法解算站星斜路径方向电离层延迟的时间序列(图 4)。可以看出,单纯采用伪距计算出的电离层延迟值噪声很大,而采用综合伪距相位算法解算的电离层延迟值很平滑稳定,这得益于高精度的相位数据,若将后者视作真值则前者的噪声误差在±0.5 m左右内波动。所以采用综合伪距相位算法相较于使用单纯伪距能够获得精度更高、更稳定的实时电离层延迟值。
|
图 4 在处理弧段内采用单纯伪距法和综合伪距相位法计算的信号传播方向电离层延迟值比较 Fig. 4 Comparison of ionospheric delay in station-satellite direction in a processed arc using the pseudo-range method and the integrated pseudo-phase method |
使用A路数据采用单纯伪距法或伪距相位综合算法来实时解算站星斜路径电离层延迟值,再利用式(12)、式(13)便可以实现电离层格网点天顶电离层延迟的实时解算,每3 min生成一个电离层格网,全天共有480个格网。在用A路数据实时生成每个格网的同时,根据式(14)分别利用A路和B路实时数据对生成的格网进行内、外符合精度的评定。
图 5(a)、图 5(c)分别为采用两种方法实时解算生成的格网的内、外符合精度时间序列对比图,图 5(b)、图 5(d)分别为全天所有格网内、外符合精度提升百分比时间序列图。由图 5(a)可以看出,伪距相位综合算法较单纯伪距法对应格网的内符合精度有明显提高,其全天所有格网的内符合精度的平均值由0.446 m提高到0.312 m;由图 5(b)可以看出,几乎所有格网的内符合精度提高百分比都位于25%~35%之间,其平均提高30.2%;由图 5(c)可以看出,伪距相位综合算法较单纯伪距法对应格网的外符合精度亦有明显提高,其全天所有格网的外符合精度的平均值由0.404 m提高到0.293 m;由图 5(d)可以看出,绝大部分格网的外符合精度提高百分比位于15%~40%之间,虽然外符合精度提升百分比波动较大,但其平均提高亦能达到27.8%。

|
图 5 单纯伪距法和伪距相位综合算法的实时电离层延迟格网内、外符合精度对比 Fig. 5 The increased percentage of inner precision and the outer precision of all grids generated by using thepseudo-range method and integrated pseudo-phase method |
本文提出伪距数据结合相位历元间差分数据综合实时解算电离层延迟格网改正数,该算法不依赖相位数据连续性和不存在模糊度收敛问题。利用GPS实测数据对该算法进行分析验证,对在处理弧段内的每一站一星采用伪距相位综合算法和单纯伪距法计算出的电离层延迟值进行比较,结果表明,采用伪距相位综合算法可以大大减小伪距噪声且能获得平滑、稳定、精度更高的站星斜路径方向电离层延迟值。在此基础上,伪距相位综合算法相比单纯伪距法对应所有格网的内符合精度平均提高了30.2%;外符合精度平均提高了27.7%。
| [1] |
魏传军. 基于地基GNSS观测数据的电离层延迟改正研究[D]. 西安: 长安大学, 2014 (Wei Chuanjun. Study of Ionospheric Delay Correction Based on GNSS Observations[D]. Xi'an: Chang'an University, 2014)
(  0) 0) |
| [2] |
Geoffrey B. An Automatic Editing Algorithm for GPS Data[J]. Geophysical Research Letters, 1990, 17(3): 199-202 DOI:10.1029/GL017i003p00199
(  0) 0) |
| [3] |
黄兵杰, 柳林涛, 高光星, 等. 基于小波变换的GPS精密单点定位中的周跳探测[J]. 武汉大学学报:信息科学版, 2006, 31(6): 512-515 (Huang Bingjie, Liu Lintao, Gao Guangxing, et al. Cycle Slip Detection in GPS Precise Single Point Positioning Based on Wavelet Transform[J]. Information Science of Wuhan University, 2006, 31(6): 512-515)
(  0) 0) |
| [4] |
El-Arini M B, Conker R S, Albertson T W, et al. Comparison of Real-Time Ionospheric Algorithms for a GPS Wide-Area Augmentation System (WAAS)[J]. Navigation, 1994, 41(4): 393-414 DOI:10.1002/navi.1994.41.issue-4
(  0) 0) |
| [5] |
黄智, 袁洪, 万卫星. WAAS电离层网格改正算法在中国地区部分站点的试算精度[J]. 全球定位系统, 2003, 28(6): 5-10 (Huang Zhi, Yuan Hong, Wan Weixing. The WAAS Ionospheric Grid Correction Algorithm in the China Region Part of the Site's Trial Accuracy[J]. Global Positioning System, 2003, 28(6): 5-10 DOI:10.3969/j.issn.1008-9268.2003.06.002)
(  0) 0) |
| [6] |
Prasad N, Sarma A D. Ionospheric Time Delay Estimation using IDW Grid Model for GAGAN[J]. J Indian Geophys Union, 2004, 8(4)
(  0) 0) |
| [7] |
王永澄, 黄建宇. GPS广域增强系统的电离层延迟网格校正法[J]. 通信学报, 1998(12): 38-41 (Wang Yongcheng, Huang Jianyu. The Grid Ionospheric Delay Correction Method of GPS Wide-Area Augmentation System[J]. Journal of Communication, 1998(12): 38-41)
(  0) 0) |
| [8] |
曹月玲. Beidou区域导航系统广域差分及完好性监测研究[D]. 北京: 中国科学院大学, 2014 (Cao Yueling. Research on Wide Area Difference and Integrity Monitoring of Deidou Regional Navigation System[D]. Beijing: University of the Chinese Academy of Sciences, 2014)
(  0) 0) |
| [9] |
兰孝奇, 黄张裕, 李森, 等. GPS观测数据处理与应用[M]. 北京: 科学出版社, 2012 (Lan Xiaoqi, Huang Zhangyu, Li Sen, et al. GPS Observation Data Processing and Application[M]. Beijing: Science Press, 2012)
(  0) 0) |
| [10] |
詹先龙, 刘瑞华, 杨兆宁. 北斗系统格网电离层延迟算法研究[J]. 航天控制, 2012, 30(1): 15-19 (Zhan Xianlong, Liu Ruihua, Yang Zhaoning. The Algorithm of Beidou System Grid Ionospheric Delay[J]. Aerospace Control, 2012, 30(1): 15-19 DOI:10.3969/j.issn.1006-3242.2012.01.004)
(  0) 0) |
2. Test and Assessment Research Center, China Satellite Navigation Office, Beijing 100094, China;
3. Shanghai Astronomical Observatory, CAS, 80 Nandan Road, Shanghai 200030, China;
4. School of Earth Science and Engineering, Hohai University, 8 West-Focheng Road, Nanjing 211100, China;
5. College of Surveying and GEO-Informatics, Tongji University, 1239 Siping Road, Shanghai 200092, China
 2018, Vol. 38
2018, Vol. 38

