2. 江苏省资源环境信息工程重点实验室,江苏省徐州市大学路1号,221116
对流层延迟是GNSS定位导航的主要误差源之一[1-2]。天顶对流层延迟根据成因又可分为天顶静力学延迟(干延迟,ZHD)和天顶非静力学延迟(湿延迟,ZWD)[3]。在GNSS定位中,一般采用改正模型对其进行削弱。目前对流层改正模型主要分为依赖和不依赖实测气象参数两种。其中,需要实测气象参数的传统模型主要有Saastamoninen模型和Hopfield模型,该类模型若采用标准气象参数,改正效果不佳[4]。EGNOS模型不需要实测气象参数,其气象参数由提供值拟合得到,对某一区域长时间计算结果可反映该地区对流层的变化趋势。但气象条件变化剧烈时,其计算值与真实情况相差较大[5]。
本文对以上3种模型进行误差分析,结合气象观测仪器的测量误差及测站时空信息误差,得出各种误差对模型改正效果的影响。选定夏季与冬季特定日期,然后利用IGS提供的采样间隔为30 s的气象数据及采样间隔为5 min的ZTD参考值,结合自编的计算程序,对模型的精度进行系统的对比分析。
1 常用对流层延迟改正模型对流层延迟模型是在对气象资料分析和研究基础上,以地面气象条件作为参数,通过一定的算法,来近似地反映测站天顶方向上的信号延迟[6-7]。
1.1 Saastamoninen模型Saastamofnen模型(简称SA模型)的计算公式与相关字符含义详见参考文献[8-9]。
1.2 Hopfield模型Hopfield模型(简称HOP模型)是Hopfield[6, 10]在1969年利用全球18个台站一年的平均资料得到的。在对流层中,大气温度下降率假设成一个常数β=6.8 ℃/km,天顶干、湿延迟的表示方法详见参考文献[9]。
1.3 EGNOS模型EGNOS模型是欧盟“静止卫星导航覆盖系统”采用的对流层天顶延迟改正模型,该模型不需要实测气象数据[11]。参考文献[5]给出了所需气象参数的计算方法。
2 误差分析天顶对流层延迟的绝对误差会影响基线解的精度,造成的基线相对误差可表示为[12]:
| $ \frac{{\Delta l}}{L} = \frac{{{\delta _{{\rm{ZTD}}}}}}{{{R_{\rm{E}}}\sin {E_{\min }}}} $ | (1) |
造成的高程误差可表示为[13]:
| $ {\delta _H} = \frac{{{\delta _{{\rm{ZTD}}}}}}{{\sin {E_{\min }}}} $ | (2) |
式中,Δl、L分别为基线偏差和相应的基线长度,δZTD为对流层天顶延迟的绝对误差,RE为地球半径,Emin为卫星截止高度角,δH为对流层天顶延迟的绝对误差引起的高程误差。天顶延迟一般在2.5 m左右[12],如果不加以改正,则令δZTD=2.5 m,Emin取20°,基线相对误差约为1×10-6,且与基线长成正比,即基线越长,误差影响越大。根据式(2),同时造成约7 m的高程误差。
对流层改正模型是气象元素、测站高程及纬度的函数。根据误差传播率,对3种模型误差进行分析。由
| $ \sigma _{{\rm{SA}}}^2 = \sigma _{\rm{d}}^2 + \sigma _{\rm{w}}^2 $ | (3) |
可得SA模型的误差公式:
| $ \begin{array}{*{20}{c}} {\sigma _{{\rm{SA}}}^2 = {{\left( {\frac{{\partial {\delta _{{\rm{SA}}}}}}{{\partial P}}} \right)}^2}\sigma _P^2 + {{\left( {\frac{{\partial {\delta _{{\rm{SA}}}}}}{{\partial T}}} \right)}^2}\sigma _T^2 + {{\left( {\frac{{\partial {\delta _{{\rm{SA}}}}}}{{\partial \varphi }}} \right)}^2}\sigma _\varphi ^2 + }\\ {{{\left( {\frac{{\partial {\delta _{{\rm{SA}}}}}}{{\partial H}}} \right)}^2}\sigma _H^2 + {{\left( {\frac{{\partial {\delta _{{\rm{SA}}}}}}{{\partial {e_{\rm{w}}}}}} \right)}^2}\sigma _{{e_{\rm{w}}}}^2} \end{array} $ | (4) |
分别考虑干、湿延迟,可写作:
| $ \sigma _{{\rm{SA}}}^{{\rm{d2}}} = {\left( {\frac{{\partial \delta _{{\rm{SA}}}^d}}{{\partial P}}} \right)^2}\sigma _p^2 + {\left( {\frac{{\partial \delta _{{\rm{SA}}}^d}}{{\partial \varphi }}} \right)^2}\sigma _\varphi ^2 + {\left( {\frac{{\partial \delta _{{\rm{SA}}}^d}}{{\partial H}}} \right)^2}\sigma _H^2 $ | (5) |
| $ \begin{array}{*{20}{c}} {\sigma _{{\rm{SA}}}^{{\rm{w2}}} = {{\left( {\frac{{\partial \delta _{{\rm{SA}}}^{\rm{w}}}}{{\partial \varphi }}} \right)}^2}\sigma _\varphi ^2 + {{\left( {\frac{{\partial \delta _{{\rm{SA}}}^{\rm{w}}}}{{\partial H}}} \right)}^2}\sigma _H^2 + }\\ {{{\left( {\frac{{\partial \delta _{{\rm{SA}}}^{\rm{w}}}}{{\partial T}}} \right)}^2}\sigma _T^2 + {{\left( {\frac{{\partial \delta _{{\rm{SA}}}^{\rm{w}}}}{{\partial {e_{\rm{w}}}}}} \right)}^2}\sigma _{{e_{\rm{w}}}}^2} \end{array} $ | (6) |
其中,各模拟数据根据标准气象元素法求取。令测站高程H=500 m,纬度为39°N,根据标准气象元素法[14],有:
| $ \begin{array}{l} t = {t_0} - 0.006\;5h\\ p = {P_0}{\left( {1 - 0.000\;0266h} \right)^{5.225}}\\ {\rm{RH}} = {\rm{R}}{{\rm{H}}_0}\exp \left( { - 0.000\;639\;6h} \right) \end{array} $ | (7) |
式中,t0=20 ℃,P0=1 013.25 mbar,RH0=50%。
水气压公式为:
| $ \begin{array}{*{20}{c}} {{e_{\rm{w}}} = {\rm{RHexp}}\left( { - 37.246\;5 + } \right.}\\ {\left. {0.213\;166T - 0.000\;256\;908{T^2}} \right)} \end{array} $ | (8) |
计算得:P=944.79 mbar,T=289.91 K,RH=36.3%,H=500 m,ew=7 mbar,代入式(6)得:
| $ {\sigma _{{\rm{SA}}}} = \sqrt {0.002\;{{65}^2}\sigma _P^2 + 0.015\;{{65}^2}\sigma _\varphi ^2 + 0.000\;{{85}^2}\sigma _H^2 + 0.000\;{{28}^2}\sigma _T^2 + 0.011\;{{60}^2}\sigma _{{e_{\rm{w}}}}^2} $ | (9) |
分别考虑干、湿延迟可写作:
| $ \sigma _{{\rm{SA}}}^{\rm{d}} = \sqrt {0.002\;{{65}^2}\sigma _P^2 + 0.015\;{{16}^2}\sigma _\varphi ^2 + 0.000\;{{82}^2}\sigma _H^2} $ | (10) |
| $ \sigma _{{\rm{SA}}}^{\rm{w}} = \sqrt {0.000\;{{49}^2}\sigma _\varphi ^2 + 0.000\;{{03}^2}\sigma _H^2 + 0.000\;{{28}^2}\sigma _T^2 + 0.011\;{{60}^2}\sigma _{{e_{\rm{w}}}}^2} $ | (11) |
同理,HOP模型的误差公式为:
| $ \begin{array}{*{20}{c}} {\sigma _{{\rm{HOP}}}^{\rm{2}} = {{\left( {\frac{{\partial {\delta _{{\rm{HOP}}}}}}{{\partial P}}} \right)}^2}\sigma _P^2 + {{\left( {\frac{{\partial {\delta _{{\rm{HOP}}}}}}{{\partial {e_{\rm{W}}}}}} \right)}^2}\sigma _{{e_{\rm{W}}}}^2 + }\\ {{{\left( {\frac{{\partial {\delta _{{\rm{HOP}}}}}}{{\partial T}}} \right)}^2}\sigma _T^2 + {{\left( {\frac{{\partial {\delta _{{\rm{HOP}}}}}}{{\partial H}}} \right)}^2}\sigma _H^2} \end{array} $ | (12) |
分别考虑干、湿延迟, 可写作:
| $ \sigma _{{\rm{HOP}}}^{{\rm{d2}}} = {\left( {\frac{{\partial \delta _{\rm{d}}^z}}{{\partial P}}} \right)^2}\sigma _P^2 + {\left( {\frac{{\partial \delta _{\rm{d}}^z}}{{\partial T}}} \right)^2}\sigma _T^2 + {\left( {\frac{{\partial \delta _{\rm{d}}^z}}{{\partial H}}} \right)^2}\sigma _H^2 $ | (13) |
| $ \sigma _{{\rm{HOP}}}^{{\rm{w2}}} = {\left( {\frac{{\partial \delta _{\rm{w}}^z}}{{\partial {e_{\rm{w}}}}}} \right)^2}\sigma _{{e_{\rm{w}}}}^2 + {\left( {\frac{{\partial \delta _{\rm{w}}^z}}{{\partial T}}} \right)^2}\sigma _T^2 + {\left( {\frac{{\partial \delta _{\rm{w}}^z}}{{\partial H}}} \right)^2}\sigma _H^2 $ | (14) |
其中计算所需数值与SA模型相同,代入计算得:
| $ {\sigma _{{\rm{HOP}}}} = \sqrt {0.002\;{{26}^2}\sigma _P^2 + 0.000\;{{62}^2}\sigma _T^2 + 0.009\;{{32}^2}\sigma _{{e_{\rm{w}}}}^2 + 0.000\;{{056}^2}\sigma _H^2} $ | (15) |
分别考虑干、湿延迟可写作:
| $ \sigma _{{\rm{HOP}}}^{\rm{d}} = \sqrt {0.002\;{{26}^2}\sigma _P^2 + 0.000\;{{17}^2}\sigma _T^2 + 0.000\;{{05}^2}\sigma _H^2} $ | (16) |
| $ \sigma _{{\rm{HOP}}}^{\rm{w}} = \sqrt {0.009\;{{32}^2}\sigma _{{e_{\rm{w}}}}^2 + 0.000\;{{45}^2}\sigma _T^2 + 0.000\;{{006}^2}\sigma _H^2} $ | (17) |
由式(9)及式(15)可知,对于SA与HOP模型,气压与水气压测量误差对最终延迟量的求取影响最大,而高程及纬度误差占比较小,且实际测量精度较高,因此对延迟量影响很小。
根据式(9)及式(2)可知,5 mbar的气压测量误差,利用SA模型计算会造成13.25 mm的对流层延迟误差,最终造成3.8 cm的高程误差。同理,根据式(15)及式(2)可知,利用HOP模型计算会造成11.3 mm的对流层延迟误差,最终造成3.3 cm的高程误差。这与参考文献[15]得出的SA与HOP模型的计算值受气压影响较大的结论一致,故准确测量地面气压对对流层延迟改正十分重要,误差较大的气压测量值会对基线解算精度造成极大影响。
对于EGNOS模型,为了保证与SA模型和HOP模型相似的条件,令H=500 m,纬度为39°N,年积日为153,内插得到其他参数为:P=1 014.79 mbar,T=292.698 K,λ=3.025 43,β=0.005 927 9,ew=20.297 mbar,代入得:
| $ \begin{array}{*{20}{c}} {{\sigma _{{\rm{EGNOS}}}} = }\\ {\sqrt {0.002\;{{15}^2}\sigma _P^2 + 0.000\;{{84}^2}\sigma _T^2 + 0.031\;{{98}^2}\sigma _\lambda ^2 + 4.872\;{{43}^2}\sigma _\beta ^2 + 0.007\;{{84}^2}\sigma _{{e_{\rm{w}}}}^2 + 0.000\;{{002}^2}\sigma _H^2} } \end{array} $ | (18) |
分开考虑干、湿延迟,可写作:
| $ \sigma _{{\rm{EGNOS}}}^{\rm{d}} = \sqrt {0.002\;{{15}^2}\sigma _P^2 + 0.000\;{{43}^2}\sigma _T^2 + 4.323\;{{01}^2}\sigma _\beta ^2 + 0.000\;000\;{2^2}\sigma _H^2} $ | (19) |
| $ \sigma _{{\rm{EGNOS}}}^{\rm{w}} = \sqrt {0.00\;{{784}^2}\sigma _{{e_w}}^2 + 0.000\;{{41}^2}\sigma _T^2 + 0.031\;{{98}^2}\sigma _\lambda ^2 + 0.549\;{{42}^2}\sigma _\beta ^2} $ | (20) |
根据高精度气象观测站及高精度水准测量的技术指标,假定各项观测误差P=±0.3 mbar, T=±0.2 K, H=±1×10-3 m, ew=±2 mbar, φ=±1×10-4°,将各项误差代入,且不考虑模型系统误差的影响,求得气象和高程、纬度因素对SA模型造成的干延迟误差为7.9×10-4 m,湿延迟误差为2.3×10-2 m;对HOP模型造成的干延迟误差为6.7×10-4 m,湿延迟误差为1.8×10-2 m。可见,SA模型与HOP模型的改正效果受气象及测站位置误差影响的程度相当。上述误差对SA与HOP模型的干延迟造成mm级误差、湿延迟造成cm级误差,即湿延迟误差是主要的误差来源。且由于HOP模型简单,模型梯度与高度无关,是温度的函数[10],忽略对流层根据纬度和季节变化的特点,只定义了对流层顶的高度值[6],与SA模型相比,缺少纬度φ引起的误差项,造成其受气象元素和高程纬度因子的误差影响小于SA模型。
另外,设λ=±0.03、β=±0.03×10-3可得,气象和高程因素造成EGNOS模型的干延迟误差为7.6×10-4 m,湿延迟误差为1.5×10-2 m。EGNOS模型的气象值由内插得到,主要误差来自于根据测站纬度和观测年积日求得的模拟气象数据与实地气象数据的差异。由此可见,较准确的气象元素和测站位置信息,在不考虑模型本身存在的系统误差的条件下,3种模型都能对延迟进行有效的改正。然而,理论上的精度无法反映各模型的实际改正效果,根据地面气象资料有时也无法正确模拟对流层的气象状况,为了更直观地反映各模型的改正精度,需要利用实测气象资料导入各模型对具体测站的天顶延迟进行模拟计算[15]。
3 实例分析通过C++语言分别编译实现以上3种模型,对于SA模型与HOP模型所需的气象数据来自CDDIS发布的气象文件(.m),该气象文件来自IGS站并置的传感器,采样间隔为30 s,可认为与测站接收机处在同一气象条件下,不存在由高程差异和平面位置差异造成的气象观测误差。
对于EGNOS模型,无需实测气象数据,通过编译实现各参数的拟合,再导入公式进行计算。文献[16-17]针对各模型对国内相关测站1 a或2 a的计算结果进行了分析,并未充分利用时间间隔为5 mim的对流层延迟产品,因此,本文对各模型的质量评价从能否准确反映对流层延迟量的实时变化,模型计算精度与纬度、高程及季节的相关性展开。
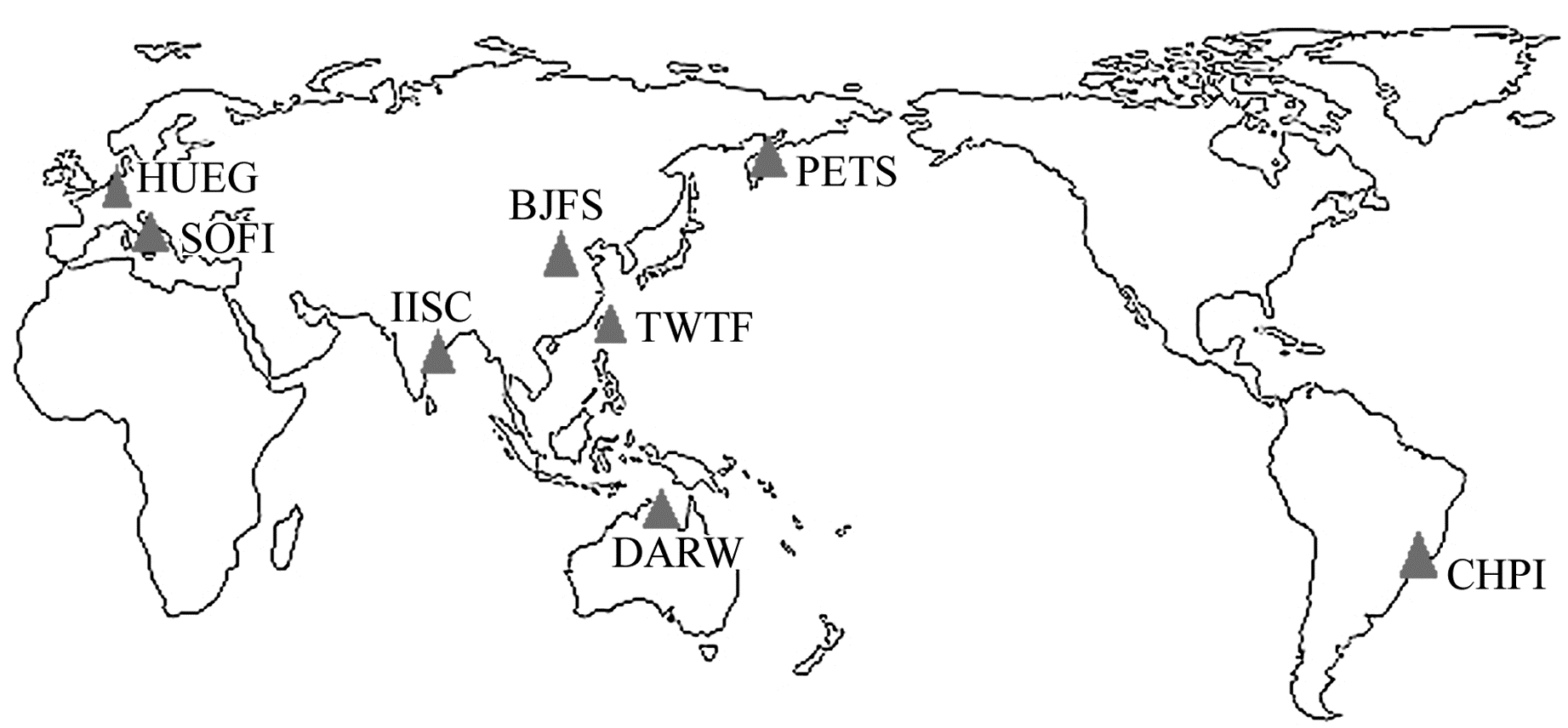
综合考虑测站的纬度与高程,同时兼顾该测站是否同时具有气象文件与ZTD参考值,有代表性地选取了表 1所示的测站,图 1为实验用测站的分布信息。
|
图 1 实验用IGS测站分布 Fig. 1 Distribution of IGS stations for experiment |
|
|
表 1 实验用IGS测站 Tab. 1 IGS stations for experiment |
考虑到夏、冬两季的气象差异,选用2016年年积日153(06-01)、336(12-01)的数据作为实验数据,其中TWTF测站同年当日没有气象数据,故选用2014年同日数据。EGNOS模型不采用实测气象数据,其计算结果每日为固定值,故不予成图。其中,SOFI测站计算误差超过1 m,将其剔除,未成图。
图 2、图 3分别表示SA与HOP模型年积日153、336的计算结果,表 2、表 3分别表示年积日153、336各模型的计算值与IGS提供的对流层产品之间的RMS。

|
图 2 模型ZTD计算结果(153日) Fig. 2 The ZTD results of model calculation (DOY=153) |

|
图 3 模型ZTD计算结果(336日) Fig. 3 The ZTD results of model calculation (DOY=336) |
|
|
表 2 153日各模型求得的ZTD与IGS参考值之间的RMS Tab. 2 The RMS of IGS references and the three models in 153th day |
|
|
表 3 336日各模型求得的ZTD与IGS参考值之间的RMS Tab. 3 The RMS of IGS references and the three models in 336th day |
1) 应用实测气象数据的SA及HOP模型能够较准确地反映ZTD的日变化趋势,且二者的结果较为接近。
2) 总体上SA模型计算值高于HOP模型,结果更接近ZTD参考值,其精度略高于HOP模型;相比HOP模型,SA模型系统误差较小。
3) SA与HOP模型的改正效果在气候变化平稳地区明显优于气候变化强烈的地区,例如在153日和336日,两个模型的改正效果在BJFS站明显优于TWTF站。
4) 3种模型在冬季的改正效果大多优于夏季。
5) 3种模型的改正误差随测站高程增加而明显增大,其中HOP模型的精度衰减最为显著。如336日纬度范围在20°以下时,随着测站高程的增加,HOP模型求得的ZTD与参考值之间的RMS明显升高。
6) 应用实测气象数据,SOFI测站SA与HOP模型均出现超过1 m的误差。该测站海拔在1 km以上,导致该现象出现的原因应是:根据地面气象数据,无法利用经验公式准确估计对流层的状况。
7) 对于EGNOS模型,由于各气象参数由内插求得,不能反映ZTD的实时变化情况,其改正效果在冬季明显优于夏季,但其气象参数较为准确,求得的ZTD与参考值差距不大,且在高纬度和高海拔地区表现优秀,这与模型较多考虑了位于高纬度高海拔的欧洲及北美地区的气象资料有关。
4 结语需要实测气象数据的SA与HOP模型能够较准确地反映ZTD的日变化趋势,SA模型的改正精度略高于HOP模型。因此,在实际应用中宜采用SA模型估计天顶延迟,作为高精度GNSS定位中所需的对流层延迟的先验值;EGNOS模型无需实测气象资料,在气象条件变化平稳地区可较准确地计算延迟量,该模型的气象元素是测站纬度和年积日的函数,可在无实测气象资料的条件下模拟任意地区对流层延迟的变化趋势。各模型求得的ZTD与IGS参考值之间的RMS均小于0.1 m,经模型改正后的ZTD残差仅会对定位精度造成cm级的影响,可满足GNSS的m级定位需求。
| [1] |
张双成, 张鹏飞, 范朋飞. GPS对流层改正模型的最新进展及对比分析[J]. 大地测量与地球动力学, 2012(2): 91-95 (Zhang Shuangcheng, Zhang Pengfei, Fan Pengfei. Recent Progress and Compative Analysis of Tropospheric Correction Models Based on GPS[J]. Journal of Geodesy and Geodynamics, 2012(2): 91-95)
(  0) 0) |
| [2] |
Liu J, Chen X, Sun J, et al. An Analysis of GPT2/GPT2w+ Saastamoinen Models for Estimating Zenith Tropospheric Delay over Asian Area[J]. Advances in Space Research, 2016, 59(3): 824-932
(  0) 0) |
| [3] |
姚宜斌, 何畅勇, 张豹, 等. 一种新的全球对流层天顶延迟模型GZTD[J]. 地球物理学报, 2013, 56(7): 2218-2227 (Yao Yibin, He Changyong, Zhang Bao, et al. A New Global Zenith Tropospheric Delay Model GZTD[J]. Chinese J Geophys, 2013, 56(7): 2218-2227)
(  0) 0) |
| [4] |
李薇, 袁运斌, 欧吉坤, 等. 全球对流层天顶延迟模型IGGtrop的建立与分析[J]. 科学通报, 2012, 57(15): 1317-1325 (Li Wei, Yuan Yunbin, Ou Jikun, et al. A New Global Zenith Tropospheric Delay Model IGGtrop for GNSS Applications[J]. Chinese Science Bulletin, 2012, 57(15): 1317-1325)
(  0) 0) |
| [5] |
汤中山, 吴良才. 三种对流层延迟模型的精度对比[J]. 测绘科学, 2017, 42(2): 11-13 (Tang Zhongshan, Wu Liangcai. Accuracy Comparison of Three Kinds of Tropospheric Delay Models[J]. Science of Surveying and Mapping, 2017, 42(2): 11-13)
(  0) 0) |
| [6] |
丁晓光. 对流层延迟改正在GPS数据处理中的应用与研究[D]. 西安: 长安大学, 2009 (Ding Xiaoguang. Research of Tropospheric Delay Model and Applications Based on the GPS Data Processing[D]. Xi'an: Chang'an University, 2009)
(  0) 0) |
| [7] |
姜卫平, 邹璇. 精密GPS定位中大气模型误差的研究与分析[J]. 武汉大学学报:信息科学版, 2008, 33(11): 1106-1109 (Jiang Weiping, Zou Xuan. On Error of Atmospheric Models in GPS Precise Positioning[J]. Geomatics and Information Science of Wuhan University, 2008, 33(11): 1106-1109)
(  0) 0) |
| [8] |
Saastamoinen J. Contributions to the Theory of Atmospheric Refraction[J]. Bulletin Geodesique, 1972, 105(1): 279-298
(  0) 0) |
| [9] |
曲伟菁, 朱文耀, 宋淑丽, 等. 三种对流层延迟改正模型精度评估[J]. 天文学报, 2008, 49(1): 113-122 (Qu Weiqian, Zhu Wenyao, Song Shuli. Accuracy of Three Kind of Tropospheric Delay Correction Models[J]. Acta Astronomica Sinica, 2008, 49(1): 113-122 DOI:10.3321/j.issn:0001-5245.2008.01.012)
(  0) 0) |
| [10] |
Hopfield H S. Two-Quartic Tropospheric Refractivity Profile for Correcting Satellite Data[J]. Journal of Geophysical Research, 1969, 74(18): 4487-4499 DOI:10.1029/JC074i018p04487
(  0) 0) |
| [11] |
黄良珂, 刘立龙, 周淼, 等. 亚洲地区EGNOS天顶对流层延迟模型的精度评估[J]. 大地测量与地球动力学, 2013, 33(4): 128-132 (Huang Liangke, Liu Lilong, Zhou Miao, et al. Precision Assessment of Zenith Tropospheric Delay Calculated from EGNOS Model over Asian Area[J]. Journal of Geodesy and Geodynamics, 2013, 33(4): 128-132)
(  0) 0) |
| [12] |
包海. GPS精密单点定位中对流层延迟改正模型的研究与分析[D]. 长沙: 中南大学, 2008 (Bao Hai. Research on the Model of Troposphere Delay Correction in GPS Precision Point Positioning[D]. Changsha: Central South University, 2008)
(  0) 0) |
| [13] |
Paul C, Richard L, James L. Limiting Factors in Tropospheric Propagation Delay Error Modelling for GPS Airborne Navigation[C]. Inst Navig 52nd Ann Meet, Massachusetts, 1996
(  0) 0) |
| [14] |
李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2005 (Li Zhenghang, Huang Jinsong. GPS Surveying and Data Processing[M]. Wuhan: Wuhan University Press, 2005)
(  0) 0) |
| [15] |
陈瑞琼, 刘娅, 李孝辉. 卫星导航系统中对流层改正模型分析[J]. 测绘通报, 2015(3): 12-36 (Chen Ruiqiong, Liu Ya, Li Xiaohui. Analysis of Tropospheric Correction Models in Navigation Satellite System[J]. Bulletin of Surveying and Mapping, 2015(3): 12-36)
(  0) 0) |
| [16] |
王君刚, 陈俊平, 王解先, 等. 对流层经验改正模型在中国区域的精度评估[J]. 武汉大学学报:信息科学版, 2016(12): 1656-1663 (Wang Jungang, Chen Junping, Wang Jiexian, et al. Assessment of Tropospheric Delay Correction Models over China[J]. Geomatics and Information Science of Wuhan University, 2016(12): 1656-1663)
(  0) 0) |
| [17] |
赵章明, 冯径, 洪亮. 卫星定位中对流层延迟模型对比分析[J]. 测绘通报, 2016(11): 18-21 (Zhao Zhangming, Feng Jing, Hong Liang, et al. Comparison and Analysis of Tropospheric Correction Models in Satellite Positioning[J]. Bulletin of Surveying and Mapping, 2016(11): 18-21)
(  0) 0) |
2. Jiangsu Key Laboratory of Resources and Environmental Information Engineering, 1 Daxue Road, Xuzhou 221116, China
 2018, Vol. 38
2018, Vol. 38

