在大地测量数据处理问题中，许多参数的先验信息往往被忽略，以致平差模型的不适定性无法减弱，获得的结果不唯一、不可靠。病态问题在大地测量中较为常见，一般将参数的某些先验信息加以等式或者不等式约束进行处理^[1-5]。病态问题常用的处理方法是岭估计^[6]和奇异值分解法^[7]。谢建等^[8]在研究等式约束对平差模型病态性消除或减弱的作用时，从一个新的角度出发，提出了消除部分参数，将等式约束病态问题转化为无约束问题的方法。王乐洋等^[9]运用虚拟观测法解决病态整体最小二乘算法，效果显著。

有时通过前期的数据处理已能大致确定参量的误差范围，如用误差椭圆表示点位误差。这些参数范围其实就是一种先验信息，可将其纳入平差模型进行求解。目前在测量平差领域，利用参数范围约束的理论尚不成熟，而实际工程应用中会遇到这类情形。针对此问题，本文提出一种带椭球约束的平差算法，给出参数求解的步骤，并用数值模拟实验和病态的测边网数据处理验证该算法的有效性，拓展现有的误差理论和研究方法。

1 带椭球约束的平差算法

对于一般的平差模型：

$ \left\{ \begin{array}{l} \mathit{\boldsymbol{L}} = \mathit{\boldsymbol{AX}} + \mathit{\boldsymbol{e}}\\ \mathit{\boldsymbol{e}} \sim \left( {0,{\sigma ^2}\mathit{\boldsymbol{Q}}} \right) \end{array} \right. $

(1)

式中，Q为协因数阵(Q=P^-1，P为权阵)，在线性条件下，Q_ii＞0，故存在唯一正定对称阵$ {\mathit{\boldsymbol{Q}}^{\frac{1}{2}}}$，使得Q=$ {\mathit{\boldsymbol{Q}}^{\frac{1}{2}}}{\mathit{\boldsymbol{Q}}^{\frac{1}{2}}}$。定义$ {\mathit{\boldsymbol{Q}}^{-\frac{1}{2}}}=({\mathit{\boldsymbol{Q}}^{\frac{1}{2}}})^{-1}$，并用$ {\mathit{\boldsymbol{Q}}^{-\frac{1}{2}}}$左乘L=AX+e等式两边，记$ \mathit{\boldsymbol{\tilde L}}{\rm{=}}{\mathit{\boldsymbol{Q}}^{-\frac{1}{2}}}\mathit{\boldsymbol{L}}{\rm{, }}\mathit{\boldsymbol{\tilde A}}{\rm{=}}{\mathit{\boldsymbol{Q}}^{-\frac{1}{2}}}\mathit{\boldsymbol{A}}$以及$ \mathit{\boldsymbol{\tilde e}}{\rm{=}}{\mathit{\boldsymbol{Q}}^{-\frac{1}{2}}}\mathit{\boldsymbol{e}}$，有：

$ \left\{ \begin{array}{l} \mathit{\boldsymbol{\tilde L}} = \mathit{\boldsymbol{\tilde AX}} + \mathit{\boldsymbol{\tilde e}}\\ \mathit{\boldsymbol{\tilde e}} \sim \left( {0,{\sigma ^2}\mathit{\boldsymbol{I}}} \right) \end{array} \right. $

(2)

对式(1)求最小二乘解，即$ \left\| {\mathit{\boldsymbol{\tilde L}}{\rm{ - }}\mathit{\boldsymbol{\tilde AX}}} \right\|^2$的最小值问题，等价于：

$ \begin{array}{*{20}{c}} {f\left( \mathit{\boldsymbol{X}} \right) = \min \left( {\left\| {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{AX}}} \right\|_P^2} \right) = }\\ {\min \left( {{{\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{AX}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{AX}}} \right)} \right)} \end{array} $

(3)

对式(1)解向量的每个分量加入如下约束：

$ \left| {{X_i}} \right| \le {r_i} $

(4)

可以认为式(4)是式(1)上所加的参数区间约束。另外对于区间不关于零点对称的情形，即l_i＜X_i＜u_i时，作如下变形：令c_i=$ {\frac{1}{2}}$(l_i+u_i)，r_i=$ {\frac{1}{2}}$(u_i-l_i)，原X_i用X_i-c_i替代，同时式(3)中观测向量L用L-Ac替代，这种情况下的解需要加上中心向量c。

对于加入式(4)约束的这类问题，可将其转化为不等式约束进行求解，而本文尝试用一种数理统计的新方法将式(4)进行变形：

$ \sum\limits_{i = 0}^n {{{\left( {\frac{{{X_i}}}{{{r_i}}}} \right)}^2}} \le n $

(5)

对任意i=1, 2, …, n，令m_i=$ \sqrt{\mathit{n}}{{\mathit{r}}_{\mathit{i}}} $，式(5)变为：

$ \sum\limits_{i = 0}^n {{{\left( {\frac{{{X_i}}}{{{m_i}}}} \right)}^2}} \le 1 $

(6)

写成矩阵形式：

$ {\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{MX}} \le 1 $

(7)

式中，$ \mathit{\boldsymbol{M}}{\rm{=diag}}\left( {\frac{1}{{\mathit{m}_1^2}}, \frac{1}{{\mathit{m}_2^2}}, \cdots , \frac{1}{{\mathit{m}_\mathit{n}^2}}} \right)$，式(7)即是由式(4)转化的椭球约束。综上，得到带椭球约束的平差模型：

$ \left\{ \begin{array}{l} \mathit{\boldsymbol{L}} = \mathit{\boldsymbol{AX}} + \mathit{\boldsymbol{e}},\mathit{\boldsymbol{e}} \sim \left( {0,{\sigma ^2}\mathit{\boldsymbol{Q}}} \right)\\ {\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{MX}} \le 1 \end{array} \right. $

(8)

下面解决模型(8)的参数求解问题：

1) 当f(X)的极小值满足X^TMX≤1时，则该极小值为问题的解；

2) 当f(X)的极小值使得X^TMX＞1时(在设计矩阵病态时，总会出现这种情况)，由式(7)可知，问题的约束解在椭球边界上取得，于是上述问题转化为在椭球面上求取最小二乘解的问题：

$ \left\{ \begin{array}{l} f\left( \mathit{\boldsymbol{X}} \right) = \min \left( {\left\| {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{AX}}} \right\|_P^2} \right) = \\ \;\;\;\;\min \left( {{{\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{AX}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{AX}}} \right)} \right)\\ {\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{MX}} = 1 \end{array} \right. $

(9)

对式(9)，使用拉格朗日乘数法得到：

$ \begin{array}{*{20}{c}} {F\left( {\mathit{\boldsymbol{X}},\lambda } \right) = }\\ {{{\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{AX}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{AX}}} \right) + \lambda \left( {{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{MX}} - 1} \right)} \end{array} $

(10)

式(10)两边分别对X和λ求偏导:

$ \frac{{\partial F\left( {\mathit{\boldsymbol{X}},\lambda } \right)}}{{\partial \mathit{\boldsymbol{X}}}} = - 2{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PL}} + 2{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PAX}} + 2\lambda \mathit{\boldsymbol{MX}} $

(11)

$ \frac{{\partial \mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{X}},\lambda } \right)}}{{\partial \lambda }} = {\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{MX}} - 1 $

(12)

令式(11)和(12)等于0，得到：

$ \left\{ \begin{array}{l} \left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}} + \lambda \mathit{\boldsymbol{M}}} \right)\mathit{\boldsymbol{X}} = {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PL}}\\ {\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{MX}} = 1 \end{array} \right. $

(13)

根据式(13)的第1式，有:

$ \mathit{\boldsymbol{X}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}} + \lambda \mathit{\boldsymbol{M}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PL}} $

(14)

但X^TMX＞1，存在正交矩阵S(即SS^T=I，I为单位阵)，使得：

$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PAS}} = \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} = {\rm{diag}}\left( {{a_1},{a_2}, \cdots ,{a_n}} \right),{a_i} > 0,}\\ {i = 1,2, \cdots ,n} \end{array} $

(15)

式(14)等价变为：

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{X}} = {{\left[ {{{\left( {{\mathit{\boldsymbol{S}}^{\rm{T}}}} \right)}^{ - 1}}{\mathit{\boldsymbol{S}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PAS}}{\mathit{\boldsymbol{S}}^{ - 1}} + {{\left( {{\mathit{\boldsymbol{S}}^{\rm{T}}}} \right)}^{ - 1}}{\mathit{\boldsymbol{S}}^{\rm{T}}}\lambda \mathit{\boldsymbol{MS}}{\mathit{\boldsymbol{S}}^{ - 1}}} \right]}^{ - 1}} \cdot }\\ {{\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{AS}}{\mathit{\boldsymbol{S}}^{\rm{T}}}{{\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}}} \right)}^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PL}} = }\\ {{{\left[ {{{\left( {{\mathit{\boldsymbol{S}}^{\rm{T}}}} \right)}^{ - 1}}\left( {{\mathit{\boldsymbol{S}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PAS}} + {\mathit{\boldsymbol{S}}^{\rm{T}}}\lambda \mathit{\boldsymbol{MS}}} \right){\mathit{\boldsymbol{S}}^{ - 1}}} \right]}^{ - 1}} \cdot }\\ {{\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{AS}}{\mathit{\boldsymbol{S}}^{\rm{T}}}{{\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}}} \right)}^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PL}}} \end{array} $

(16)

进而转化为:

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{X}} = \mathit{\boldsymbol{S}}{{\left( {{\mathit{\boldsymbol{S}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PAS}} + {\mathit{\boldsymbol{S}}^{\rm{T}}}\lambda \mathit{\boldsymbol{MS}}} \right)}^{ - 1}}{\mathit{\boldsymbol{S}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PAS}}{\mathit{\boldsymbol{S}}^{\rm{T}}} \cdot }\\ {{{\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}}} \right)}^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PL}} = \mathit{\boldsymbol{S}}{{\left( {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }} + {\mathit{\boldsymbol{S}}^{\rm{T}}}\lambda \mathit{\boldsymbol{MS}}} \right)}^{ - 1}}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{S}}^{\rm{T}}}{\mathit{\boldsymbol{b}}_{{\rm{LS}}}}} \end{array} $

(17)

式中，b_LS=(A^TPA)^-1A^TPL。

注意到，当M=I时，X=S(Λ+λI)^-1ΛS^Tb_LS=(A^TPA+λI)^-1A^TPL为通常的岭估计，但式(17)中的λ依赖于样本，不再是常数，故称之为广义型岭估计^[10]，属于自适应岭估计。下面介绍关于岭参数λ的求解方法。

根据式(13)中的第1式得λMX=A^TPL-A^TPAX，然后在等式两边左乘X^T，得到λX^TMX=A^TA^TPL - X^TA^TPAX。由于X^TMX=1，故：

$ \lambda = {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PL}} - {\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PAX}} $

(18)

结合式(17)可以看出，λ需要迭代求解。下面给出利用带椭球约束的平差算法的具体步骤：

1) 利用先验信息确定参数上下界u和l；

2) 中心化u和l，得到c和新观测向量L-Ac；

3) 利用求特征值和特征向量的方法得到S和Λ；

4) 设定λ的初值(如λ₀=0，λ₁=1)和限值e=10^-5；

5) 判断|λ_n+1-λ_n|＜e是否成立，若成立跳至7)，若不成立进行6)；

6) λ_n代入式(17)，得到X_n+1，然后将X_n+1代入式(18)，得到λ_n+1，回到5)；

7) 取出X_n+1，得到最终解X=X_n+1+c。

在上述步骤中，利用先验信息确定参数上下界u和l是实施椭球约束平差算法的前提和务必解决的问题，但由于先验信息本身存在较多的不确定性，在实际应用中大多采用经验模式来处理。本文在经验模式的基础上，针对具有前期数据处理结果以及经验信息的实例，给出确定参数上下界的方法和建议。

2 数值模拟实验

选取文献[11]中的一个例子进行实验：

$ \left[ {\begin{array}{*{20}{c}} 1&{\frac{1}{2}}&{\frac{1}{3}}&{\frac{1}{2}}\\ {\frac{1}{2}}&{\frac{1}{3}}&{\frac{1}{4}}&{\frac{1}{5}}\\ {\frac{1}{3}}&{\frac{1}{4}}&{\frac{1}{5}}&{\frac{1}{6}}\\ {\frac{1}{4}}&{\frac{1}{5}}&{\frac{1}{6}}&{\frac{1}{7}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_1}}\\ {{x_2}}\\ {{x_3}}\\ {{x_4}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{{25}}{{12}}}\\ {\frac{{77}}{{60}}}\\ {\frac{{19}}{{20}}}\\ {\frac{{319}}{{420}}} \end{array}} \right] $

其中，系数矩阵的条件数为1.55×10⁴，所以该线性方程组属于病态方程组。本例的精确解为$ {\mathit{\boldsymbol{\tilde x}}}$=[1 1 1 1]^T。当常数向量中加入微小误差时，得到L=[2.083 3 1.283 3 0.950 0 0.797 5]^T。先确定l=[0 0 0 0]^T，u=[2 2 2 2]^T，然后分别采用最小二乘法、岭估计、奇异值分解(SVD)、不等式约束以及椭球约束对本例参数进行求解，结果见表 1。

可以看到，由于系数矩阵的病态性，最小二乘解严重失真，‖$ \mathit{\boldsymbol{x}}{\rm{ - }}\mathit{\boldsymbol{\tilde x}}$‖高达201.860 3；不等式约束利用先验信息对参数构建不等式，这种外部约束虽然在一定程度上提高了解的精度，但并未实质改变平差模型的病态性；岭估计、SVD和椭球约束在本例中的应用都体现出高精度，但前2种算法并未考虑待求参数的先验信息，仅从数学的角度对平差模型的病态性进行改善，而本文提出的带椭球约束的平差算法将参数的先验信息纳入平差模型，再对平差模型的病态性进行改善的方法显然更符合实际，所求参数解的精度也较岭估计和SVD的精度更高。

除上述1组上下界外，另外选择4组上下界，同时计算参数解，结果见表 2。

从前3组上下界可以看出，中心向量均为c=[1 1 1 1]^T，这刚好与真值$ {\mathit{\boldsymbol{\tilde x}}}$=[1 1 1 1]^T一致。这3组上下界对应的实验结果反映出，中心向量越接近真值，参数范围越小(即上下界越接近)，解的精度越高；第1、4、5组结果说明，中心向量偏离真值的程度越大，解的精度越低。由此，给出椭球约束平差算法中参数范围选取的建议：在满足实际情况，符合先验信息提供的数据特征(参数的大致范围、参数误差等)的条件下，使参数上下界的中心向量越接近真值，且参数范围越小，运用带椭球约束的平差算法得到的解的精度越高。

3 病态测边网实验

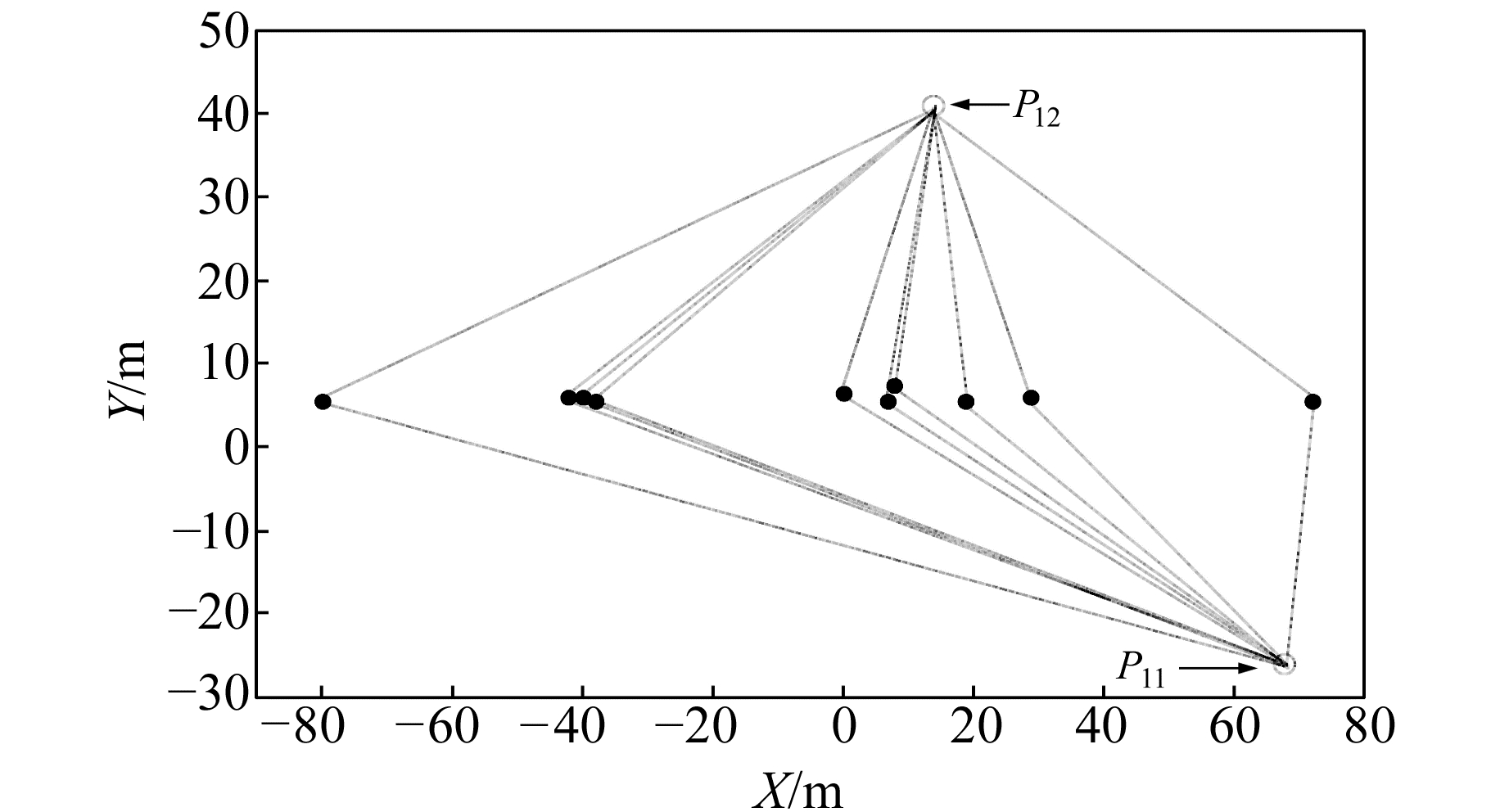
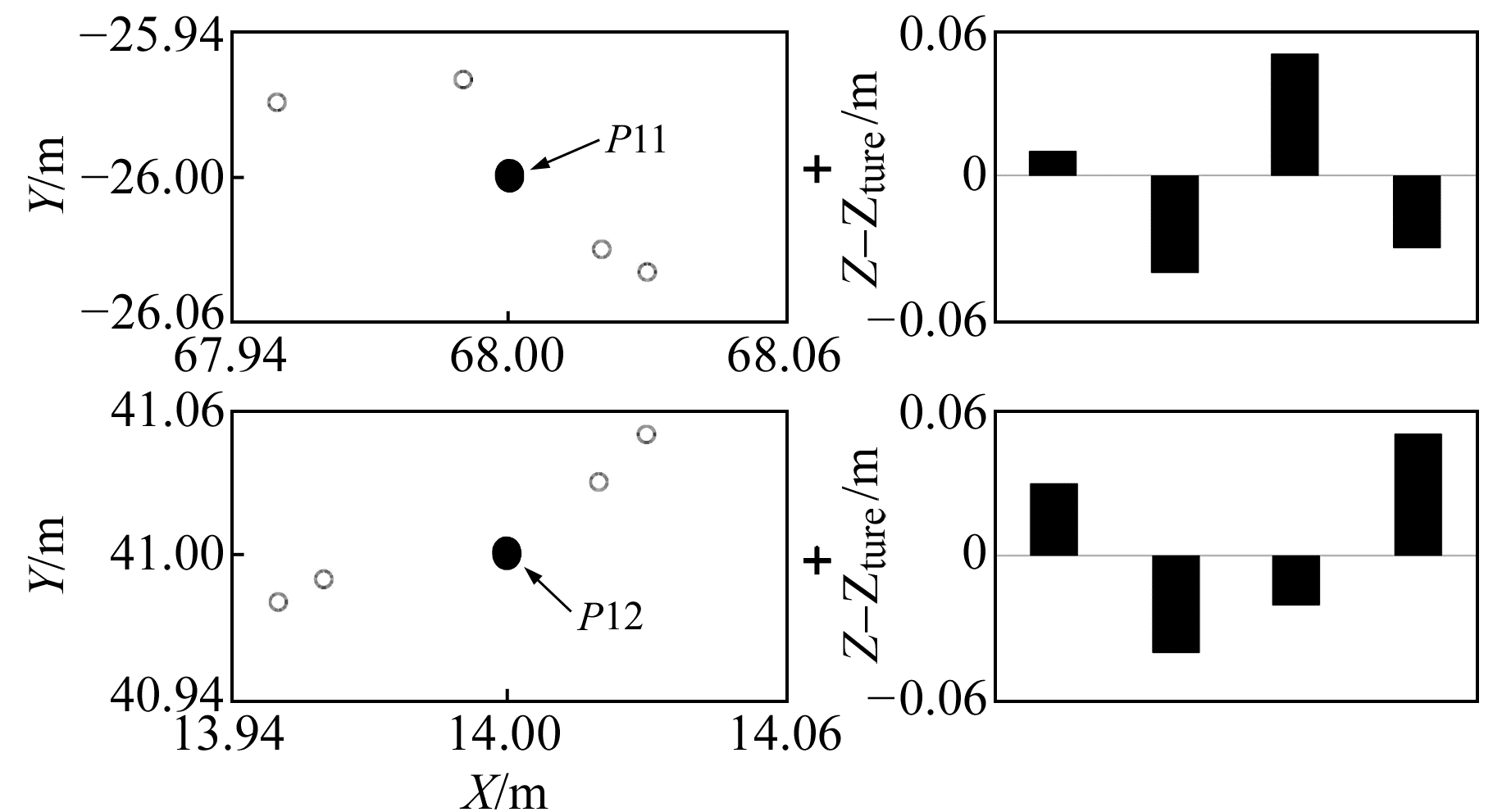
实验数据来源于文献[12]的测边网。图 1为该测边网，图中黑色实心点为10个已知点(三维坐标已知)，2个空心点(P₁₁，P₁₂)为待测点(真值为P₁₁=(68, -26, 9)，P₁₂=(14, 41, -11))，2个待测点间的观测距离为88.340 2 m，分别从已知点向待测点进行等精度测边，共计测边20条，观测数据见表 3。另外根据前几期观测结果(非同一测边网)，得到观测值与真值的分布情况(图 2，左侧图中的实心点为真值，空心点为前期观测值；右侧图表示前期高程方向观测值与真值之差)，用来确定点位变化范围。测边网平差时需要待测点的近似坐标，令P₁₁⁰=(68.01, -25.99, 8.98)，P₁₂⁰=(14.02, 40.99, -11.01)，同时根据先验信息并且按照数值模拟实验部分的参数范围选取建议，确定点位三维误差范围均为(-0.05, 0.05)，单位为m。

平差过程中发现，法方程系数阵的条件数为1.003 6×10⁵，说明该问题属于严重病态问题，最小二乘解会失真。根据点位三维误差范围提供的先验信息，运用上节介绍的带椭球约束的平差算法对待测点坐标进行求解。为了验证该算法的有效性，采用岭估计、奇异值分解以及不等式约束(罚函数法)对该问题进行解算。

实验结果见表 4，表中，‖ΔX‖=‖$ \mathit{\boldsymbol{X}}{\rm{ - }}\mathit{\boldsymbol{\tilde X}}$‖，其中X为计算值，$ \mathit{\boldsymbol{\tilde X}}$为待测点的坐标真值。由于本例中测边网网型的特殊性，导致构成的法方程系数矩阵条件数过大，可以看到最小二乘解已经失真，对应‖ΔX‖为3.316 m；不等式约束在本例中依然没有较好的作用，对参数解精度的提高量微乎其微，‖ΔX‖为3.041 m；使用奇异值分解和岭估计处理后，结果有了一定程度的改善，其中岭估计解更优，‖ΔX‖为0.115 m；本文使用带椭球约束的平差算法充分考虑了前期观测结果提供的先验信息，得到优于奇异值分解和岭估计的结果，‖ΔX‖仅为0.034 m。

4 结语

本文针对参数带有范围先验信息的情形，提出带椭球约束的平差算法，将这种先验信息纳入平差模型中，通过数值模拟实验和病态测边网的数据处理，得到以下结论：

1) 2个实验结果都证明了带椭球约束的平差算法能有效地改善病态解，这种算法与不等式约束最大的区别是：没有一种有效的方法能完全等价地将椭球约束转化为不等式。从系数矩阵的病态性出发，实验结果也体现出附加不等式约束对病态解的改善力度不大。

2) 岭估计和SVD主要从数学角度改善病态方程的解，一般的岭估计中岭参数为常数，本文算法中的岭参数随具体的椭球约束条件变化，而这个条件来自于先验信息，更符合实际情形。从实验结果来看，带椭球约束的平差算法所求解的精度也高于岭估计和SVD。