2. 广西空间信息与测绘重点实验室,桂林市雁山街319号,541006
无实测气象数据时,传统的ZTD估计模型精度会下降[1]。从2007年开始,IGS中心定期向用户提供PPP解算精度为1.5~5 mm、时间分辨率为5 min的ZTD产品[2],该产品精度较高,但其属于后处理数据,即时性不强,不利于实际应用。预测解算ZTD的研究较多,并取得了一定的成效[3-5]。近年来,许多学者将自回归移动平均模型(ARIMA)应用到电离层电子含量的预测中,并取得了较好的成果[6-7],而该模型在对流层预测中的应用却较少。ARIMA模型对非平稳序列具有较好的预测效果,且适用范围广,但容易在捕捉序列线性与非线性复合性特征时出现精度下降[8]。针对上述问题,本文提出一种基于集合经验模态分解(EEMD)和季节性自回归移动平均模型(SARIMA)的对流层延迟估计新方法。该方法首先使用EEMD对原始ZTD序列进行分解并生成n个IMF序列,然后对各IMF序列分别构建SARIMA参数进行预测,最终叠合预测结果以实现对对流层延迟的预测。最后,针对中国不同地区同季节和同地区不同季节的ZTD值进行预测分析,总结出EEMD-SARIMA模型的适用性规律,在一定程度上避免了偶然性。
1 模型介绍 1.1 集合经验模态分解(EEMD)理论EEMD是对经验模态分解(EMD)模型的改进[9]。EMD模型的实质是对信号序列中不同尺度的波形或趋势进行分解,产生一系列不同特征尺度的数据序列,并将每个序列定义为一个特征模态函数分量(intrinsic mode function,IMF)和一个残差(余量)序列。其中的所有IMF分量必须满足2个条件[10]:1)整个事件历程内,极值点的数目与过零点的数目相等,或最多相差1个;2)在任一时间点上,由局部极大值定义的上包络线和由局部极小值定义的下包络线的均值为0(信号关于时间轴局部对称)。
Wu等[11]为改正EMD方法中模态混叠的缺点,提出EEMD方法,其核心是在信号中引入高斯白噪声进行EMD分解,最后将多次分解的IMF总体平均定义为最终的IMF。这个方法避免了尺度混合问题,使IMF分量能保持自身的物理唯一性。EEMD算法中有2个重要的参数:白噪声幅值k (加入的白噪声占原始信号幅值标准差的比例)和重复进行EMD分解的总次数M,它们的确定方法暂无可使用的公式,多凭经验进行调整。EEMD的具体分析步骤见文献[11]。
1.2 季节性自回归移动平均模型(SARIMA)理论SARIMA模型是自回归移动平均模型(ARIMA)的改进,ARIMA是一个可以衡量内生变量及其滞后性与改变量关系的一个系统模型,是对移动平均模型(ARMA)的扩展[12]。
ARIMA (p, d, q)的实质是ARMA (p, q)的d阶单整(d次差分),该效果将一个非平稳的时间序列转化为平稳时间序列[13]。设φp(B)Xt=θq(B)εt为等时间间隔的ZTD序列,则可将ARMA (p, q)模型表示为:
| ${\varphi _p}\left( B \right){X_t} = {\theta _q}\left( B \right){\varepsilon _t} $ | (1) |
式中,B为滞后算子,εt为白噪声序列,φp(B)为p阶自回归系数多项式,定义其相应特征方程为φp(x),θq(B)为q阶滑动平均系数多项式,定义其相应特征方程为θq(x)。
当原ZTD序列{Xt}不平稳时,可考虑通过式(2)进行差分:
| $ {u_t} = {\nabla ^d}{y_t} = {\left( {1 - B} \right)^d}{y_t} $ | (2) |
式中,u为差分算子,d为差分阶数。{Xt}在经过d次差分后变为平稳序列,即可建立ARIMA (p, d, q)模型的一般形式:
| $ {\nabla ^d}{X_t} = \frac{{{\theta _q}\left( B \right)}}{{{\varphi _p}\left( B \right)}}{\varepsilon _t} $ | (3) |
式中,∇为差分符号,∇d=(1-B)d。
ARIMA (p, d, q)模型可以解决许多时间序列的拟合预测问题,但实际中有许多时间序列的变化具有明显的周期性特征,如气温、降雨、PM2.5等,这些时间序列的变化与其他季节性元素的变化之间存在极大的相关性,称之为季节性时间序列。由于时间序列的周期性变化,它们在不同周期内的同时期数据将处于一个相当的水平,此时可以恰当引入乘积季节性SARIMA (p, d, q)×(P, D, Q)模型[14]。当序列间的长期趋势、季节效应和随机波动间不是简单的相加关系时,可以使用ARIMA模型提取短期相关性,用周期步长为S的SARIMA模型提取季节周期性,再采用两者的乘积组合模型对ZTD序列进行预测,从而得到乘积季节模型的完整结构:
| $ {\nabla ^d}\nabla _S^D{X_t} = \frac{{{\theta _q}\left( B \right){\vartheta _Q}({B^S})}}{{{\varphi _p}\left( B \right){\varphi _P}({B^S})}}{\varepsilon _t} $ | (4) |
式中,D为季节性差分阶数,S为季节周期,∇S为差分符号,∇SD=(1-BS)d,φP(BS)为季节性P阶自回归系数多项式,ϑQ(BS)为季节性Q阶滑动平均系数多项式。下文均将该模型记为SARIMA (p, d, q)×((P, D, Q)模型。
2 EEMD-SARIMA模型构建EEMD-SARIMA模型的优势在于在对原始ZTD序列采用EEMD分解后,对不同频率特征的波形可以选择不同的p、d、q和P、D、Q参数,以更契合的参数寻优方式进行拟合预测。
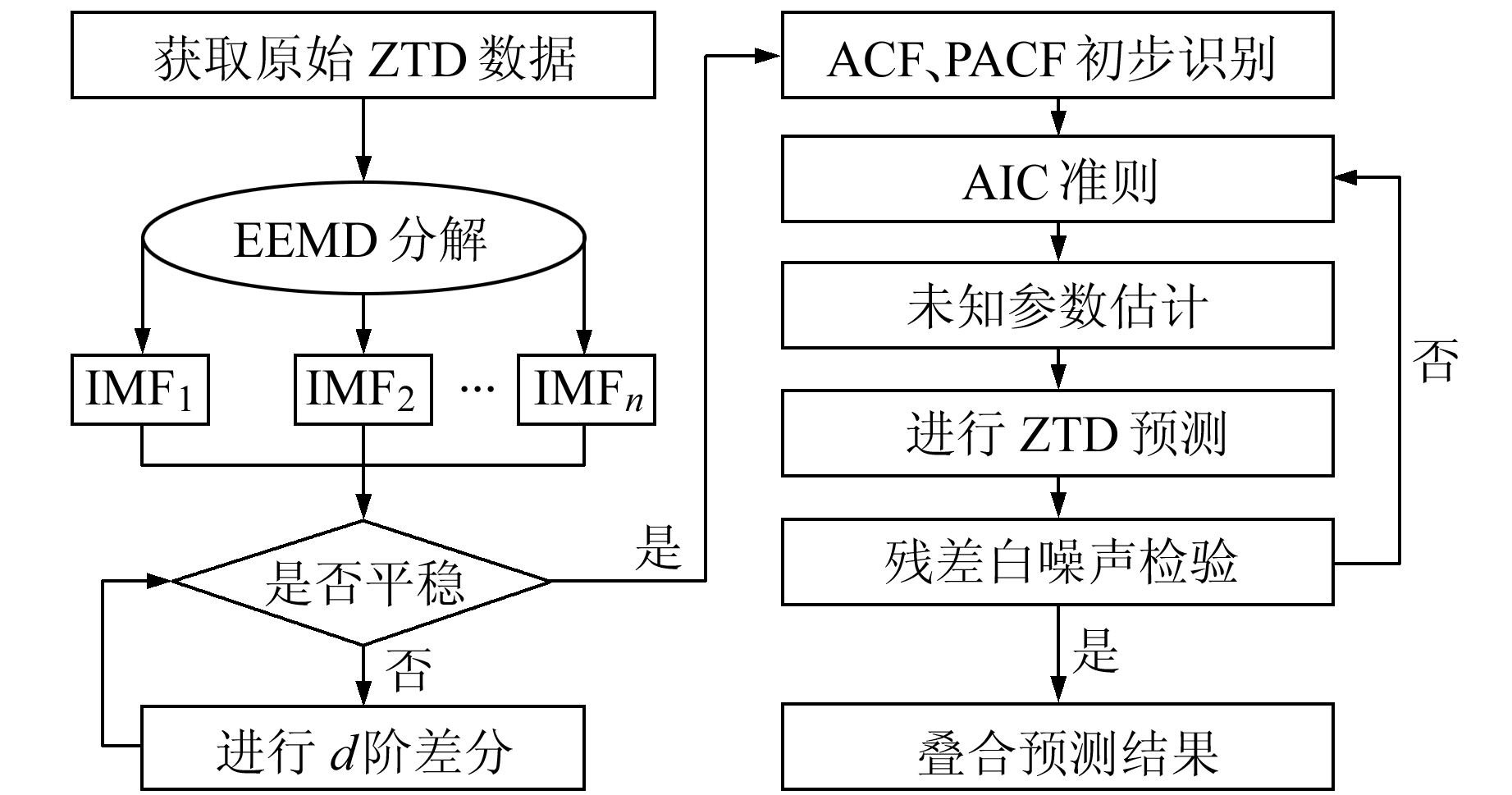
结合模型自身特点,按照如下步骤进行建模:1)对原ZTD序列进行集合经验模态分解,得到一系列不同频率的分量序列(IMF);2)通过ADF单位根检验判断IMF序列的平稳性并适当差分变换;3)考虑各IMF序列的自相关系数函数(ACF)与偏相关系数函数(PACF),对模型进行初步识别;4)通过赤池信息准则(AIC)和SBC准则确定最优模型参数;5)估计模型未知数,并通过参数的t统计量检验其显著性以及模型合理性;6)对ZTD序列进行预测,并检验残差序列是否为白噪声序列,若不满足,则返回步骤4);7)叠合各预测值得到最终结果。
EEMD-SARIMA模型进行ZTD预测的基本流程见图 1。
|
图 1 EEMD-SARIMA模型的ZTD预测流程 Fig. 1 The ZTD prediction flow chart of EEMD-SARIMA model |
选取IGS中心发布的长春站(CHAN)、上海佘山站(SHAO)和乌鲁木齐站(URMU)2016年的ZTD数据进行分析,原数据序列时间分辨率为5 min,经平均处理后使该数据时间分辨率变为1 h。实验中,仅选取该年4个季度的其中1个月的数据进行预测分析,并以此用于下文的季节性影响研究。选取的月份为每季度的季中月份(1月、4月、7月、10月),并以此月份来代表该季度(冬、春、夏、秋)。之后采用SARIMA和EEMD-SARIMA模型对它们进行预测分析,并评定其精度。预测分析原则为:选取该月前29 d作为拟合数据,并对未来24个逐小时的ZTD值进行预测。最后引入其他相关因子,通过控制变量法分别分析不同影响因子(季节、地理)对预测结果的影响。
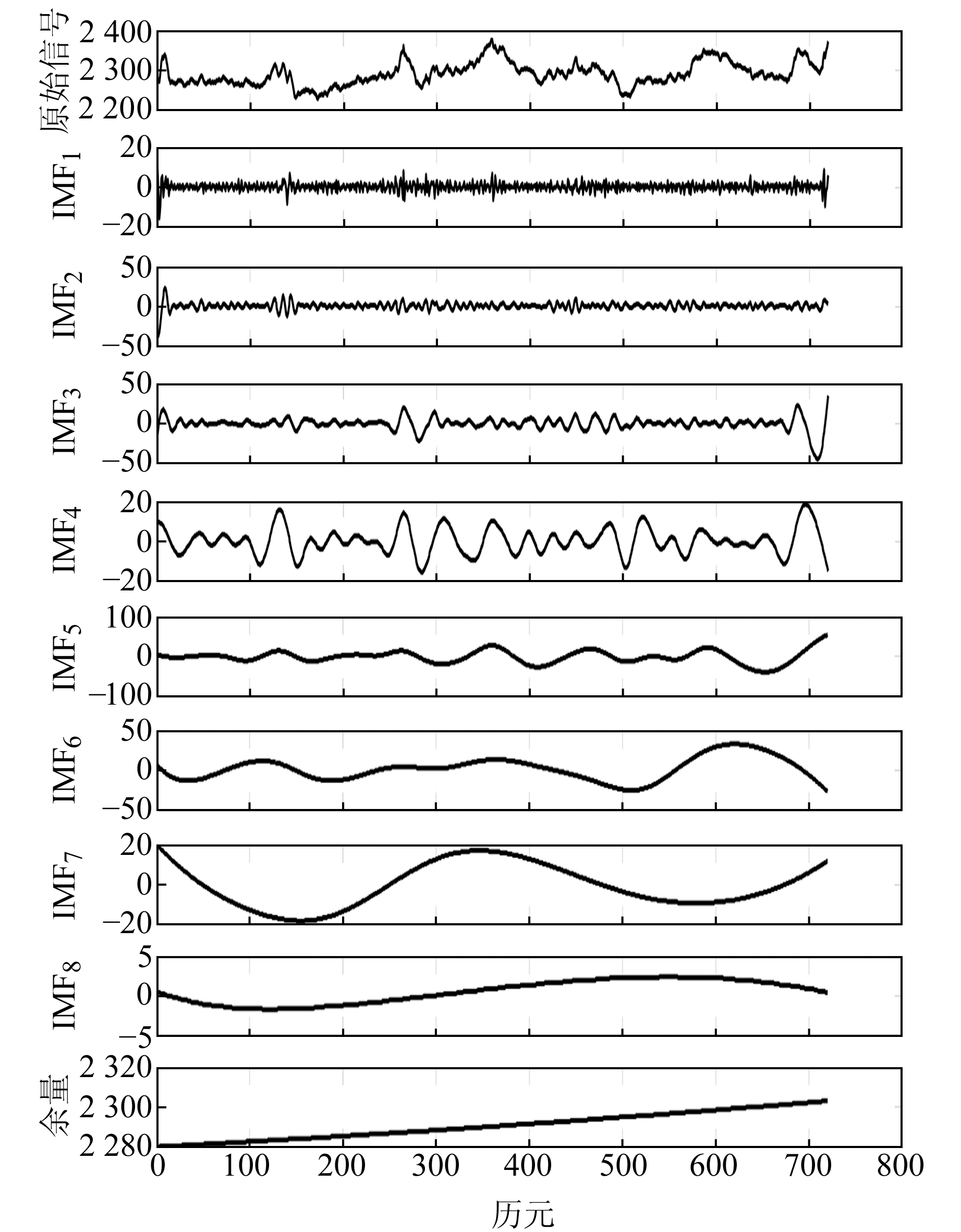
3个站2016年1月、4月、7月、10月的数据见图 2。对以上12个序列分别进行EEMD分解,并展示长春站1月原始ZTD序列分解后的IMF分量(图 3)。

|
图 2 各站点原始ZTD序列走势 Fig. 2 The trend of the original ZTD sequence of each station |
|
图 3 长春站2016-01 ZTD序列IMF分量图 Fig. 3 The IMF component of the ZTD sequence of January 2016 in Changchun |
将得到的各IMF序列与余量相叠合,理论上应得到原始ZTD序列,但由于模型误差,叠合后的结果往往与原始序列存在互差。为验证本次实验中的EEMD模型分解精度,采用式(7)计算新叠合序列与原始序列的平均相对误差(mean relative error,MRE)。结果表明,新叠合序列信息损失极小,可以满足后续分析的需求。新叠合序列与原始序列的MRE见表 1。
|
|
表 1 新叠合序列与原始序列间的MRE Tab. 1 The MRE between the new superposed sequence and the original sequence |
实现对各个ZTD分量序列的SARIMA模型构建后,选取前29 d的数据进行拟合分析,并对后24 h的数据进行预测。本文引入精度指标为:均方根误差(root mean square error,RMSE)、平均绝对误差(bias指标)(mean absolute error,MAE)、平均相对误差(mean relative error,MRE)、偏差(bias), 数学表达式分别为:
| $ {\rm{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{t = 1}^n {} {{({Y_t}{\rm{ - }}{{\hat Y}_t})}^2}} $ | (5) |
| $ {\rm{MAE}} = \frac{1}{n}\sum\limits_{t = 1}^n {} \left| {{Y_t}{\rm{ - }}{{\hat Y}_t}} \right| $ | (6) |
| $ {\rm{MRE}} = \frac{1}{n}\sum\limits_{t = 1}^n {} \left| {\frac{{{Y_t}{\rm{ - }}{{\hat Y}_t}}}{Y}} \right| $ | (7) |
| $ {\rm{bias}} = {{\hat Y}_t}{\rm{ - }}{Y_t} $ | (8) |
式中,Yt为原始数据值,
对数据进行预测分析,得到2个模型的预测精度,见表 2~5(单位mm)。分析表 2~5,得到以下结论:
|
|
表 2 2个模型预测成果RMSE对比 Tab. 2 RMSE of prediction results of two models |
|
|
表 3 2个模型预测成果MAE对比 Tab. 3 MAE of prediction results of two models |
|
|
表 4 2个模型预测成果MRE对比 Tab. 4 MRE of prediction results of two models |
|
|
表 5 2个模型预测成果平均bias对比 Tab. 5 Bias of prediction results of two models |
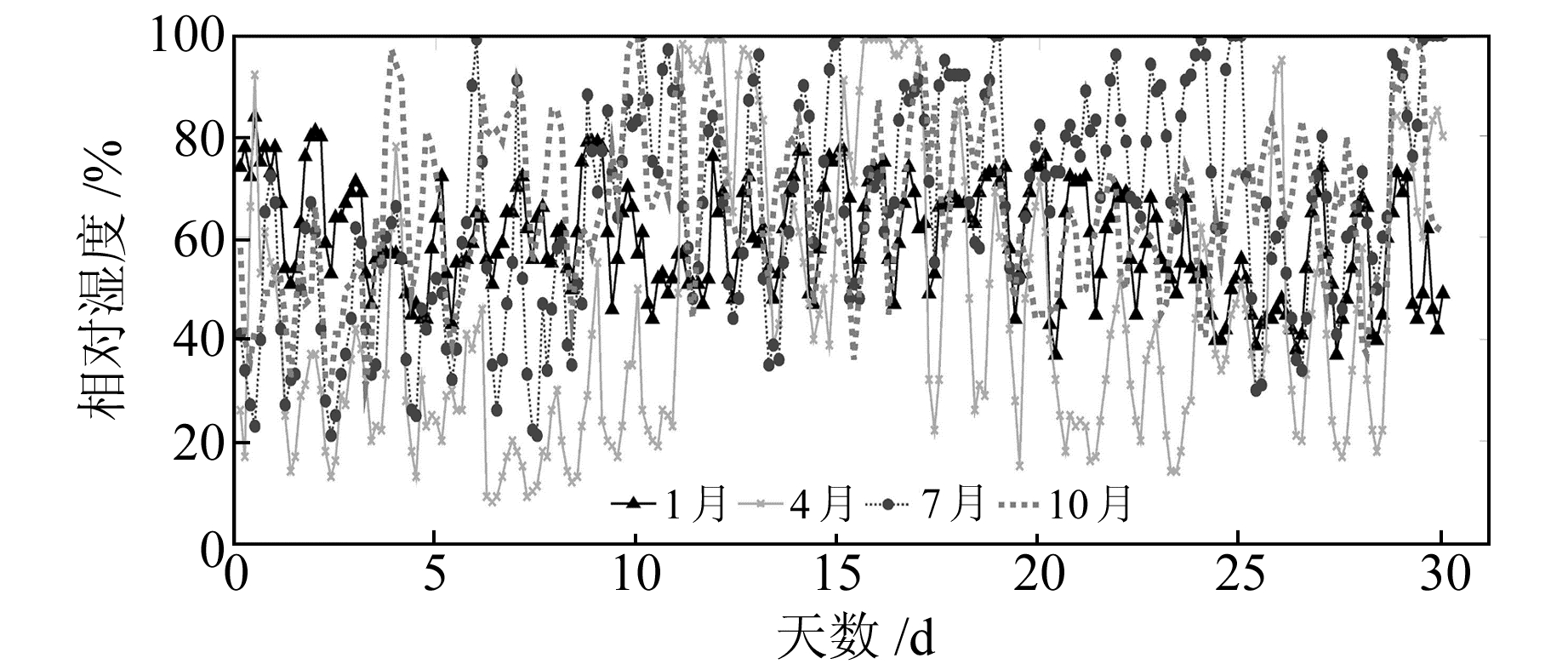
1) 由表 2所给出的4季预测精度可以判断,SARIMA模型对春、夏、秋季的预测精度偏低,3个地区的RMSE均值分别为30.23 mm、21.65 mm和36.28 mm,远低于冬季的4.27 mm,但对比上文所提及的模型,此精度仍属于较优的范畴。由于相对湿度与降雨量对对流层延迟影响较大,造成此结果的原因可能是冬季降雨较少,湿度变化相对平稳,故而对流层延迟的波动更小,序列更平稳,也更易于预测。图 4为长春4季相对湿度(数据采集于中国气象网)变化情况。由图 4可以发现,长春冬季相对湿度变化较其他季节更加平稳,虽然其他季节存在相对湿度较冬季更小的情况,但其长期变化极不平稳,有可能对对流层延迟变化产生非积极影响,符合上文推论。由于篇幅限制,气象因子对对流程延迟变化的具体作用方式此处不进行详细探讨。
|
图 4 长春站2016年4季相对湿度对比 Fig. 4 The comparison of station four seasons relative humidity of Changchun in 2016 |
2) 分析预测结果发现,EEMD-SARIMA模型相对原SARIMA模型的改进效果较好。特别是就春季而言,前者3个地区平均RMSE减小了83.56%,而秋季也减少了55.93%;就春季、冬季而言,3个地区平均预测精度(RMSE)达到了4.07 mm,而夏季、秋季为14.74 mm(此处不同季节精度差异较大,故仅取2个季节平均值)。
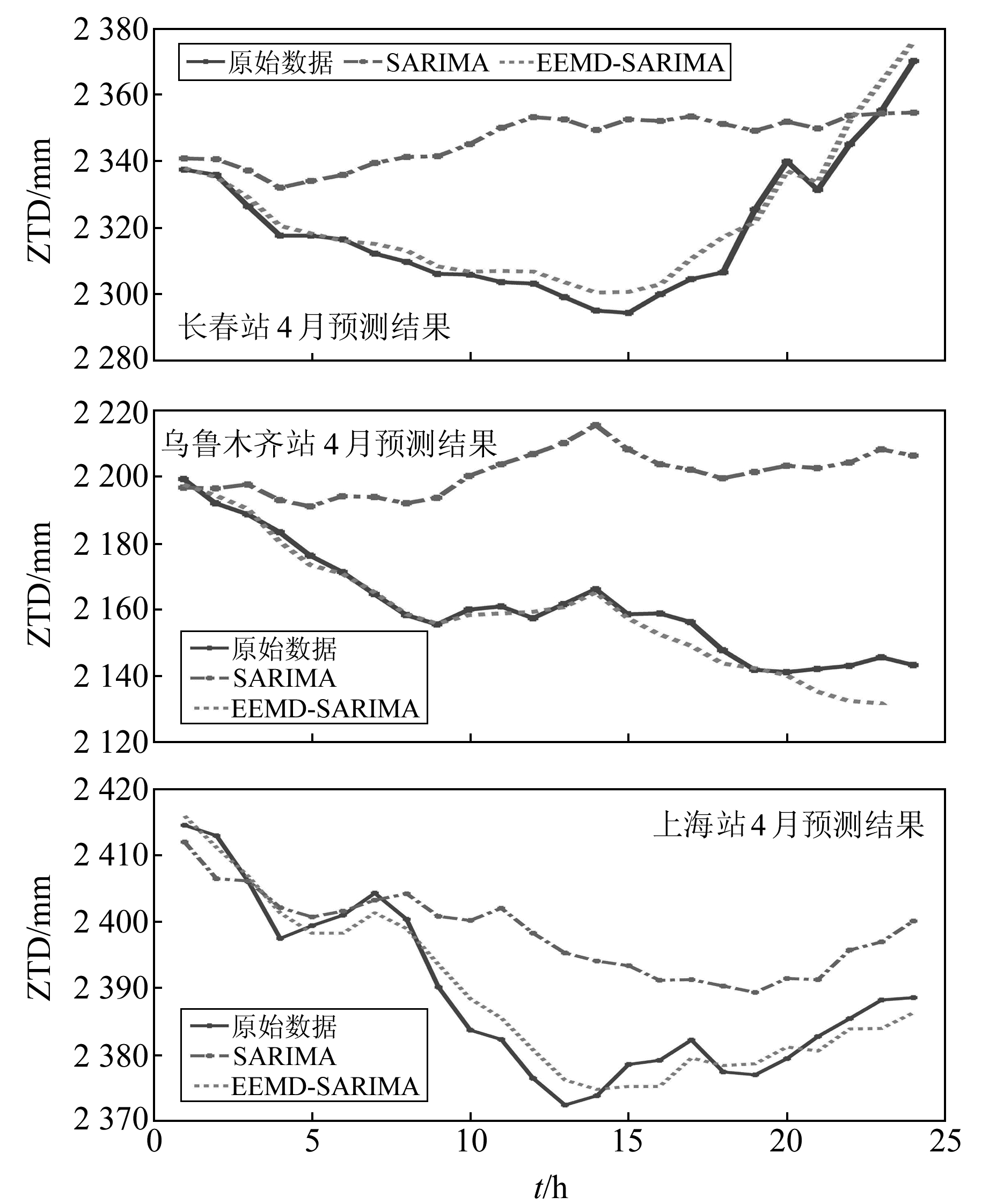
3) SARIMA模型面对个别ZTD变化波动较大的非平稳序列时,即使自身参数选择已为最优,仍会出现个别预测失效的情况,而EEMD-SARIMA模型可以很好地修复该缺陷。图 5为3个站点此类情况较为突出的4月份预测结果。以上3例中,SARIMA模型预测结果与原序列相关系数分别仅为43.5%、8.1%和62.4%,此时已基本属于预测失效,预测序列与原序列无相关性或相关性较小。而经模型改进后,预测结果与原序列相关系数分别为97.3%、97.0%和96.3%,属于高度相关。可以证明,在2个模型的参数选择接近最优的情况下,EEMD-SARIMA模型处理ZTD数据时较原模型具有更强的稳定性和适用性,能够很好地捕捉原序列中的运动趋势。
|
图 5 站点预测值分析 Fig. 5 The predictive value of individual station |
4) 从表 3可知,在多数情况下,改进模型预测残差占比不超过原序列的1%,仅占原值极小的一部分,故可以认为EEMD-SARIMA模型对ZTD数据具有很好的预测效果。
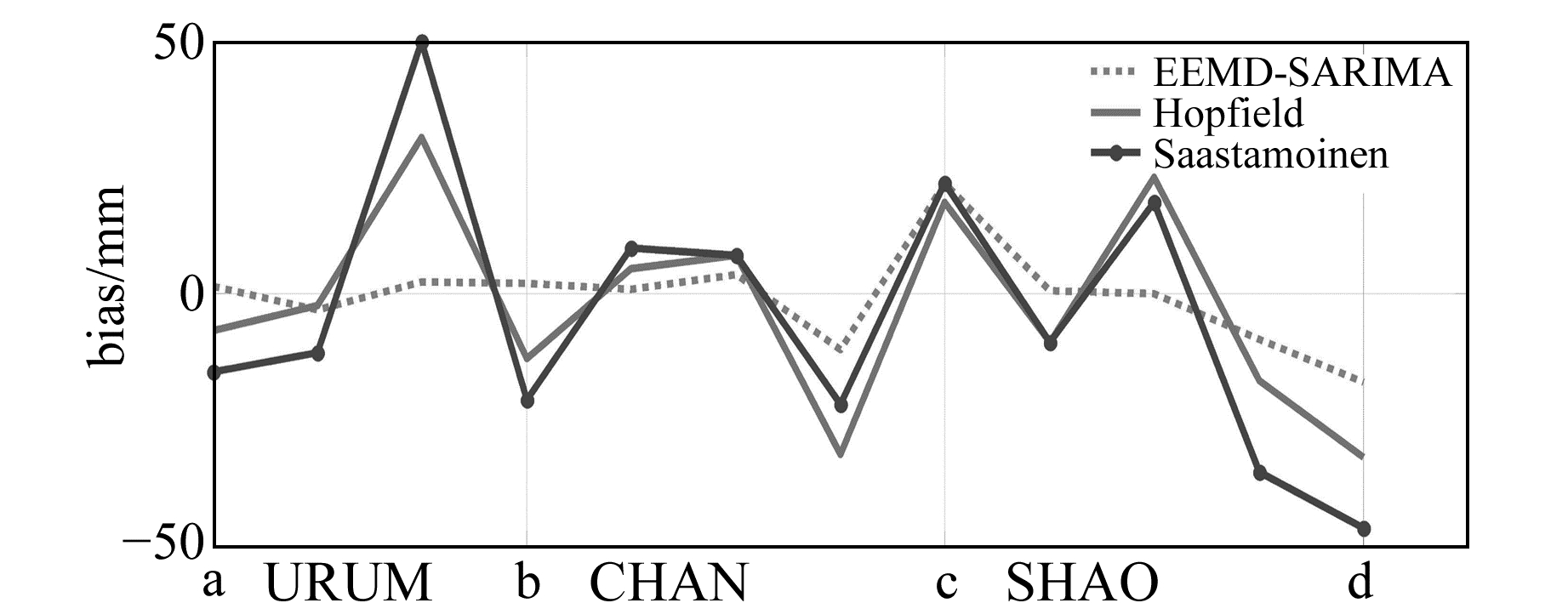
5) 将本文模型与Hopfield模型和Saastamoinen模型估计的ZTD偏差进行对比(图 6,其中a-b段为URUM站4个月的区段,b-c段为CHAN站,c-d段为SHAO站)。可直观地看到,本文模型估计效果更好。
|
图 6 与传统模型估计偏差对比 Fig. 6 The comparison of different models of bias |
本文综合分析了中国3个地区的ZTD变化,并分别以SARIMA和EEMD-SARIMA模型对3个地区4个季节的ZTD序列进行短期(24 h)预测。由于本文所选取的3个站点(长春、上海、乌鲁木齐)具有较大的经纬度差异,故而文章所得结论在一定程度上排除了偶然性。本文结论可总结如下:
1) SARIMA和EEMD-SARIMA模型对ZTD序列均有较好的预测效果,但面对个别波动较大的ZTD序列时,SARIMA模型会失效,预测结果与原序列失去相关性,但EEMD-SARIMA模型很好地修复了这个缺陷。
2) ZTD序列的变化具有较强的季节性特征,而本文分别针对不同季节的ZTD序列进行预测分析发现,SARIMA模型在冬季能够取得很好的预测效果,但其他季节容易失效;而EEMD-SARIMA模型在4季中均能获得较好的预测效果。
3) EEMD-SARIMA模型对ZTD序列的预测精度较高,且稳定性强、适用性好,具有较好的应用价值。
关于各种气象因子对ZTD序列的影响效果以及作用方式,则需要进一步研究。
| [1] |
曲伟菁, 朱文耀, 宋淑丽, 等. 三种对流层延迟改正模型精度评估[J]. 天文学报, 2008, 49(1): 113-122 (Qu Weijing, Zhu Wenyao, Song Shuli, et al. The Evaluation of Precision about Hopfield, Saastamoinen and EGNOS Tropospheric Delay Correction Model[J]. Acta Astronomica Sinica, 2008, 49(1): 113-122 DOI:10.3321/j.issn:0001-5245.2008.01.012)
(  0) 0) |
| [2] |
Byun S H, Bar-Sever Y E. A New Type of Tropospheric Zenith Path Delay Product of the International GNSS Service[J]. Journal of Geodesy, 2009, 83(3-4): 1-7 DOI:10.1007/s00190-008-0288-8
(  0) 0) |
| [3] |
王勇, 张立辉, 杨晶. 基于BP神经网络的对流层延迟预测研究[J]. 大地测量与地球动力学, 2011, 31(3): 134-137 (Wang Yong, Zhang Lihui, Yang Jing. Study on Prediction of Zenith Tropospheric Delay by Use of BP Neural Network[J]. Journal of Geodesy and Geodynamics, 2011, 31(3): 134-137)
(  0) 0) |
| [4] |
李剑锋, 王永前, 郭俊元. 预测模型在对流层延迟计算中的应用研究[J]. 测绘科学技术学报, 2015, 32(5): 450-454 (Li Jianfeng, Wang Yongqian, Guo Junyuan. Research on Tropospheric Delay Calculation with Prediction Model[J]. Journal of Geomatics Science and Technology, 2015, 32(5): 450-454 DOI:10.3969/j.issn.1673-6338.2015.05.003)
(  0) 0) |
| [5] |
吕慧珠, 黄文德, 闻德保. 一种基于频谱分析和AR补偿的对流层延迟预报模型[J]. 大地测量与地球动力学, 2015, 35(2): 283-286 (Lü Huizhu, Huang Wende, Wen Debao. A Tropospheric Delay Prediction Model Based on Spectrum Analysis and the AR Compensation[J]. Journal of Geodesy and Geodynamics, 2015, 35(2): 283-286)
(  0) 0) |
| [6] |
刘军, 柴洪洲, 刘先冬, 等. 基于ARIMA(p, 1, 1)的电离层预报模型[J]. 大地测量与地球动力学, 2010, 30(3): 79-82 (Liu Jun, Chai Hongzhou, Liu Xiandong, et al. A Prediction Model of Ionospheric Based on ARIMA(p, 1, 1)[J]. Journal of Geodesy and Geodynamics, 2010, 30(3): 79-82)
(  0) 0) |
| [7] |
刘立龙, 陈军, 黄良珂, 等. 基于小波-ARIMA电离层短期总电子含量预报预报模型[J]. 桂林理工大学学报, 2016, 36(2): 295-299 (Liu Lilong, Chen Jun, Huang Liangke, et al. TEC Forecast of Short-Term Ionosphere on Wavelet-ARIMA[J]. Journal of Guilin University of Technology, 2016, 36(2): 295-299)
(  0) 0) |
| [8] |
朱帮助, 林健. 基于ARIMA和LSSVM的非线性集成预测模型[J]. 数学实践与认知, 2009, 39(12): 34-40 (Zhu Bangzhu, Lin Jian. A Novel Nonlinear Ensemble Forecasting Model Incorporating ARIMA and LSSVM[J]. Mathematics in Practice and Theory, 2009, 39(12): 34-40)
(  0) 0) |
| [9] |
赵肖宇.基于EMD和EEMD的自适应光谱预处理方法及其应用研究[D].秦皇岛: 燕山大学, 2015 (Zhao Xiaoyu. Research and Application on Adaptive Spectra Preprocessing Methods Based on EMD and EEMD[D]. Qinhuangdao: Yanshan University, 2015) http://cdmd.cnki.com.cn/Article/CDMD-10216-1015901968.htm
(  0) 0) |
| [10] |
杨永锋, 吴亚锋. 经验模态分解在振动分析中的应用[M]. 北京: 国防工业出版社, 2013 (Yang Yongfeng, Wu Yafeng. Applications of Empirical Mode Decomposition in Vibration Analysis[M]. Beijing: National Defense Industry Press, 2013)
(  0) 0) |
| [11] |
Wu Z H, Huang N E. Ensemble Empirical Mode Decomposition :A Noise-Assisted Data Analysis Method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-14
(  0) 0) |
| [12] |
Zhang G P. Time Series Forecasting Using a Hybrid ARIMA and Neural Network Mode[J]. Neurocomputing, 2003, 50: 159-175 DOI:10.1016/S0925-2312(01)00702-0
(  0) 0) |
| [13] |
李子奈. 计量经济学[M]. 北京: 高等教育出版社, 2004 (Li Zinai. Econometrics[M]. Beijing: Higher Education Press, 2004)
(  0) 0) |
| [14] |
张婷. CPI的SARIMA模型与X-12季节调整模型对比预测分析[J]. 经济问题, 2014(12): 37-41 (Zhang Ting. Comparison of Predictive Analysis of CPI Based on SARIMA and X-12 Model[J]. Economic Problems, 2014(12): 37-41)
(  0) 0) |
2. Guangxi Key Laboratory of Spatial Information and Geomatics, 319 Yanshan Street, Guilin 541006, China
 2018, Vol. 38
2018, Vol. 38

