2. 中国矿业大学江苏省资源环境信息工程重点实验室,江苏省徐州市大学路1号,221116;
3. 西北农林科技大学水利与建筑工程学院,陕西省杨凌区渭惠路23号,712100
已有许多学者对广播星历的精度进行统计分析,其中对GPS星历的研究较多,对GLONASS、BDS,尤其是Galileo的研究较少[1-8]。本文以德国GFZ组织发布的精密星历作为参考真值,对4系统2017-02共28 d的导航文件信息进行精度分析,分别对比各个导航定位系统中不同类型卫星广播星历的经、切、法3个方向的精度以及导航文件中的卫星钟精度。
1 数据处理策略 1.1 卫星轨道计算理论GPS、BDS和Galileo均采用16参数模型,该模型包括1个参考时刻、6个对应参考时刻的开普勒轨道根数以及9个卫星轨道摄动修正参数。GPS、BDS的IGSO和GEO以及Galileo卫星广播星历的计算方法完全相同;BDS GEO卫星的轨道倾角很低,基本接近于0°,与其他类型的卫星计算方法有所区别。各系统的官方网站都公布了接口控制文件(ICD, interface control file),该文件对卫星固定时刻坐标的计算进行了详细介绍,本文不再赘述。
1.2 精密产品观测时刻参数计算方法精密产品均采用每隔固定时间输出一组参数,精密星历输出卫星坐标和钟差,精密钟差输出钟差估计的接收机钟差和卫星钟差,目前IGS精密星历一般不输出卫星速度,但可以通过坐标进行估计。为了保证插值精度,在采用15 min的精密星历内插5 min星历时,发现13阶插值精度最高,所以采用13阶的Lagrange插值法内插精密星历和精密钟差。为避免龙格现象在计算时刻对精度的影响,采用在前后多使用1 d精密产品的方法,保证任意插值时间都能处于插值数据的中间时刻。可以通过以下公式估计观测时刻的卫星坐标和钟差:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;X\left( t \right) = \sum\limits_{i = 0}^n {} X\left( {{t_i}} \right)\cdot\\ \frac{{(t - {t_0}) \cdots (t - {t_{i - 1}})(t - {t_{i + 1}}) \cdots (t - {t_n})}}{{({t_i} - {t_0}) \cdots ({t_i} - {t_{i - 1}})({t_i} - {t_{i + 1}}) \cdots ({t_i} - {t_n})}}{\rm{ }}\\ \;\;\;\;\;\;\;\;Y\left( t \right) = \sum\limits_{i = 0}^n {} Y({t_i})\cdot\\ \frac{{(t - {t_0}) \cdots (t - {t_{i - 1}})(t - {t_{i + 1}}) \cdots (t - {t_n})}}{{({t_i} - {t_0}) \cdots ({t_i} - {t_{i - 1}})({t_i} - {t_{i + 1}}) \cdots ({t_i} - {t_n})}}\\ \;\;\;\;\;\;\;\;Z\left( t \right) = \sum\limits_{i = 0}^n {} Z({t_i})\cdot\\ \frac{{(t - {t_0}) \cdots (t - {t_{i - 1}})(t - {t_{i + 1}}) \cdots (t - {t_n})}}{{({t_i} - {t_0}) \cdots ({t_i} - {t_{i - 1}})({t_i} - {t_{i + 1}}) \cdots ({t_i} - {t_n})}}\\ \;\;\;\;\;\;\;\;T\left( t \right) = \sum\limits_{i = 0}^n {} T({t_i})\cdot\\ \frac{{(t - {t_0}) \cdots (t - {t_{i - 1}})(t - {t_{i + 1}}) \cdots (t - {t_n})}}{{({t_i} - {t_0}) \cdots ({t_i} - {t_{i - 1}})({t_i} - {t_{i + 1}}) \cdots ({t_i} - {t_n})}} \end{array} $ |
式中,X(t)、Y(t)、Z(t)为观测时刻的卫星坐标,X(ti)、Y(ti)、Z(ti)为ti时刻精密星历文件中提供的卫星位置参数,T(t)为观测时刻的卫星钟差,T(ti)为ti时刻精密钟差文件中提供钟差信息,n为插值阶数,这里取13。
1.3 坐标系统和时间系统的统一4大导航定位系统的坐标原点和三轴指向均有微小差异。由于精密星历使用的坐标框架是ITRF2008,本文将4系统的坐标都转化到该框架下,但几个系统的差异很小,所以转化参数都非常小。平面坐标转化时采用四参数模型,三维立体转换时采用七参数模型,各系统之间的转换可以采用以下模型:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left[ \begin{array}{l} X\\ Y\\ Z \end{array} \right]_{{\rm{sy}}{{\rm{s}}_1}}} = \left[ \begin{array}{l} {\rm{d}}{X_0}\\ {\rm{d}}{Y_0}\\ {\rm{d}}{Z_0} \end{array} \right] + \\ (1 + {d_m})\left[ {\begin{array}{*{20}{c}} 1&{{\beta _z}}&{-{\beta _y}}\\ { - {\beta _z}}&1&{{\beta _x}}\\ {{\beta _y}}&{ - {\beta _x}}&1 \end{array} } \right]{\left[ \begin{array}{l} x\\ y\\ z \end{array} \right]_{{\rm{sy}}{{\rm{s}}_{\rm{2}}}}} \end{array} $ |
式中,等号右边第1项为两坐标系原点之间的平移量,dm为两坐标系之间的缩放尺度因子,βx、βy、βz为两坐标系之间的转化参数。
GPS使用GPS时,GLONASS使用含有跳秒改正的UTC(SU)时,BDS使用中国国家授时中心维持的BDS时,Galileo使用与国际原子时(TAI)保持偏差小于33 ns的连续时标。由于精密星历使用的是GPS时,所以将所有的时间都转化到GPS时[9-11]。
2 算例分析本文使用的广播星历是多系统融合的brdm星历,包含24 h四系统的广播星历以及钟差信息,使用的精密星历为德国GFZ组织(波茨坦地学研究中心)的gbm星历。该产品是对载波相位观测值事后处理进行定轨的结果,所以精密星历的轨道和钟差精度较高,GPS轨道精度优于2 cm,GLONASS优于3 cm,Galileo优于6 cm,BDS优于10 cm,钟差优于0.1 ns。而广播星历是伪距观测值定轨的结果,再对该结果进行预报,所以精密星历的精度远高于广播星历精度的3倍以上,即可以以精密产品作为参考真值。本文对比了广播星历2017-02-01~02-28四系统的卫星星历、钟差的残差,并给出各个系统SISRE值的变化曲线。
2.1 轨道和钟对比GPS选择3种卫星,分别为Ⅱ F G08、Ⅱ R-M G17和Ⅱ R G28号卫星,其中G08使用Cs钟,G17和G28使用Rb钟;GLONASS分别选择位于3个轨道面上的卫星R05、R13以及R17;Galileo选择一代E12和二代E24卫星;BDS选择位于不同轨道上的GEO卫星C03、IGSO卫星C09和MEO卫星C12。绘制出各个卫星在径向(R)、切向(A)、法向(C)上的误差和星历钟差(CLK)。各个系统代表卫星的星历和钟差残差见图 1~11。
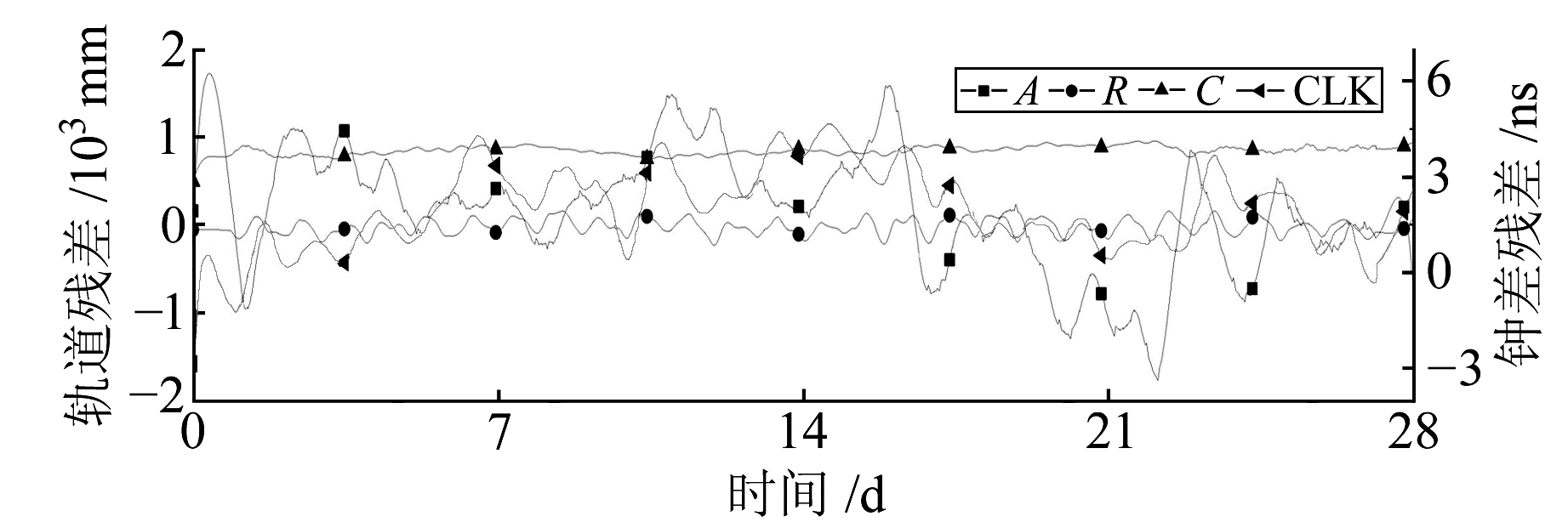
|
图 1 GPS G08轨道和钟残差 Fig. 1 The residual of GPS G08 orbit and clock offset |
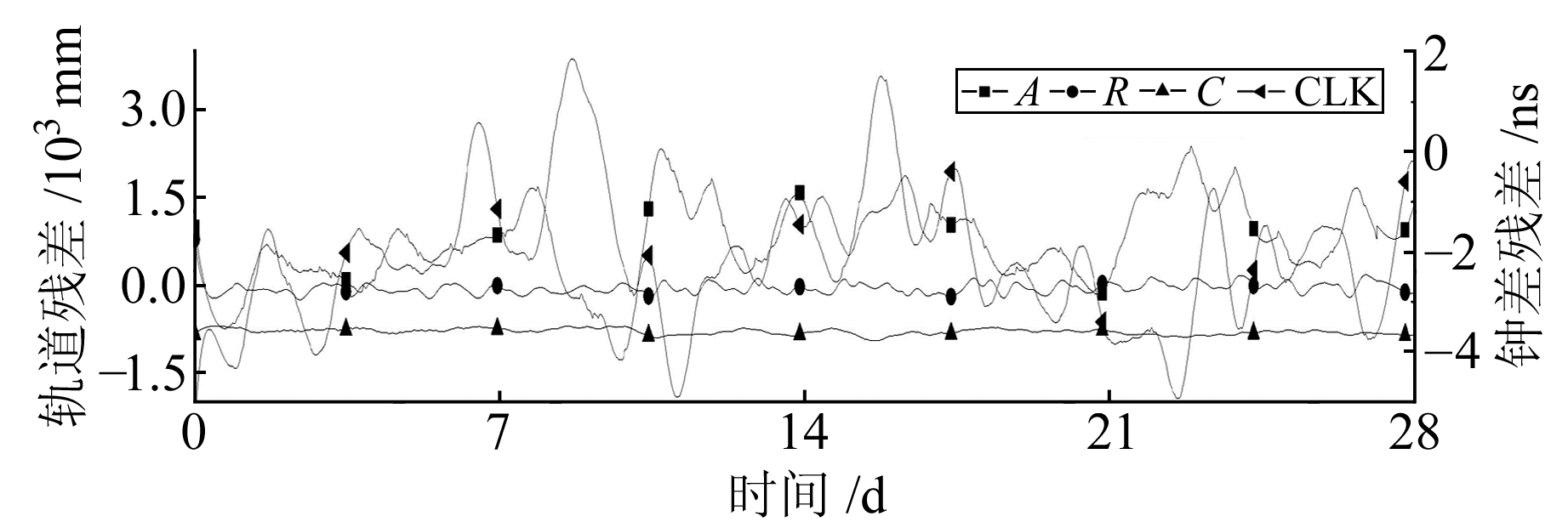
|
图 2 GPS G17轨道和钟残差 Fig. 2 The residual of GPS G17 orbit and clock offset |
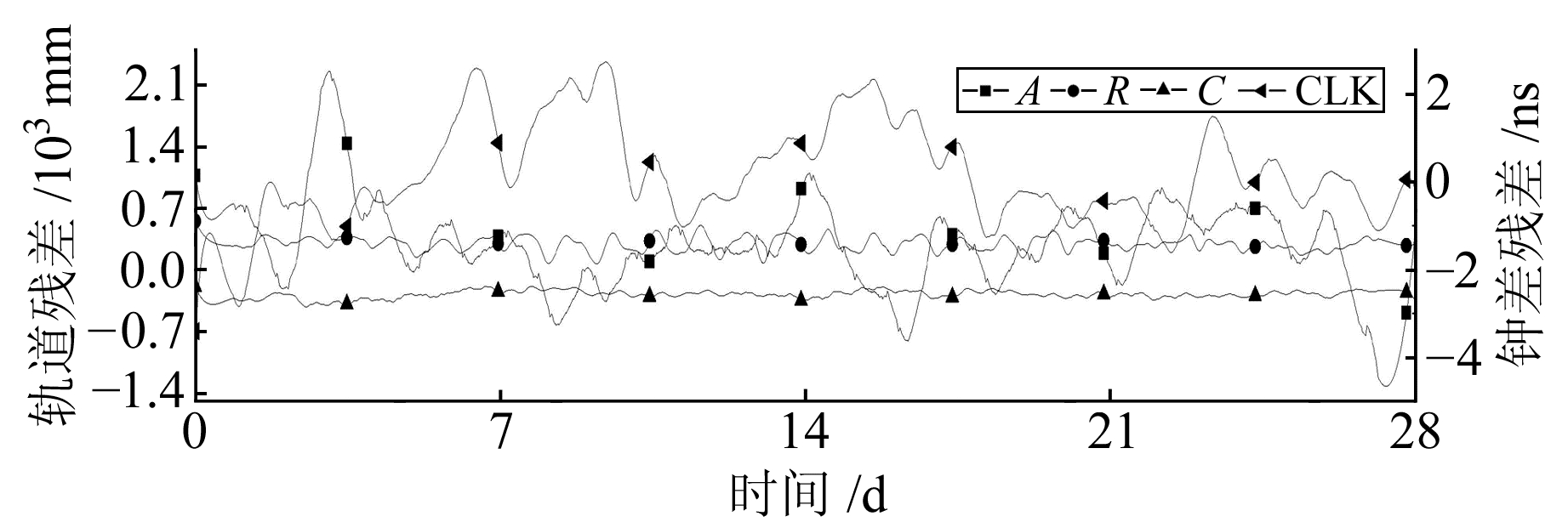
|
图 3 GPS G28轨道和钟残差 Fig. 3 The residual of GPS G28 orbit and clock offset |
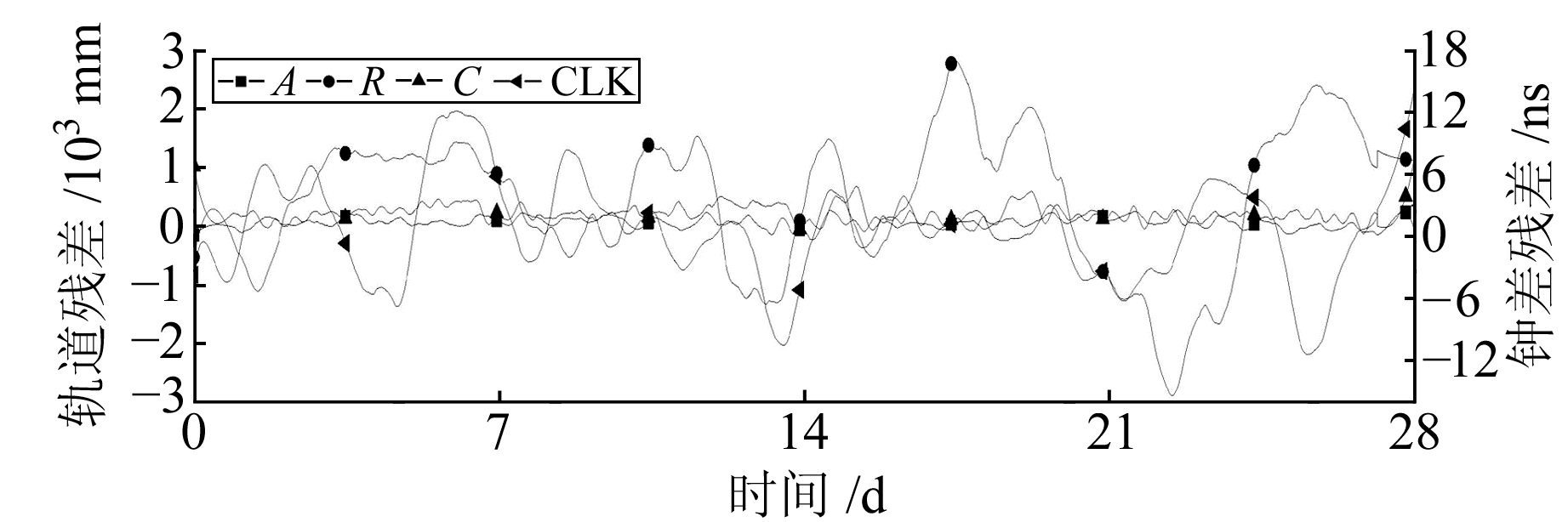
|
图 4 GLONASS R05轨道和钟残差 Fig. 4 The residual of GLONASS R05 orbit and clock offset |
|
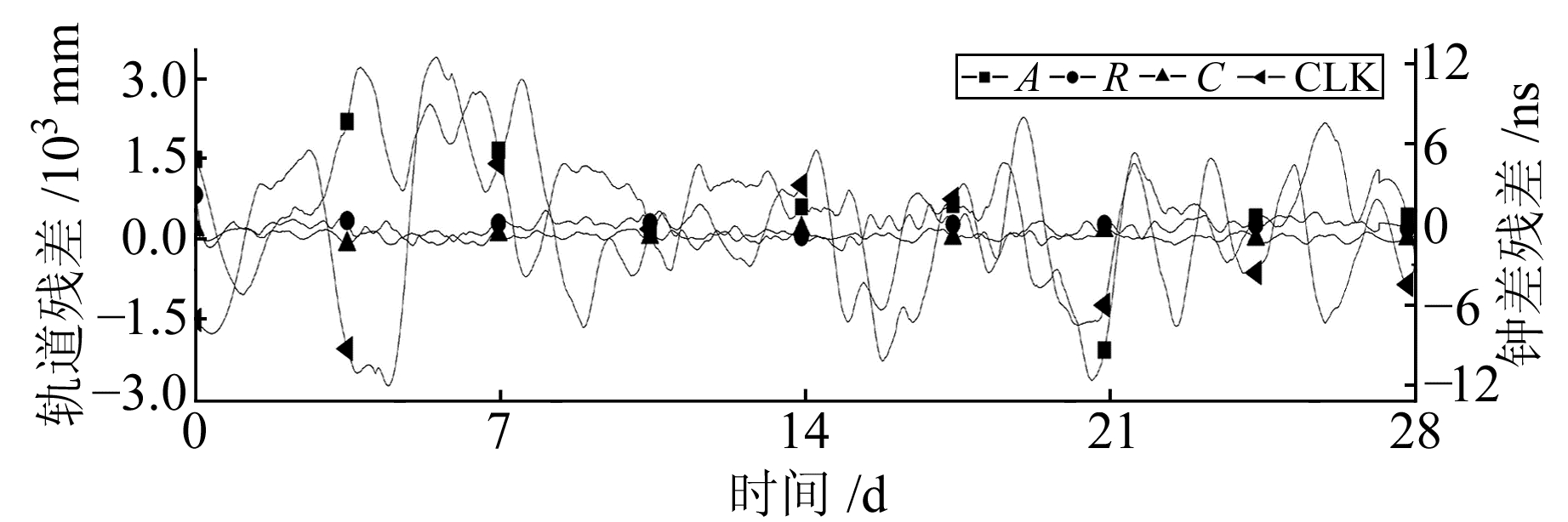
图 5 GLONASS R13轨道和钟残差 Fig. 5 The residual of GLONASS R13 orbit and clock offset |
|
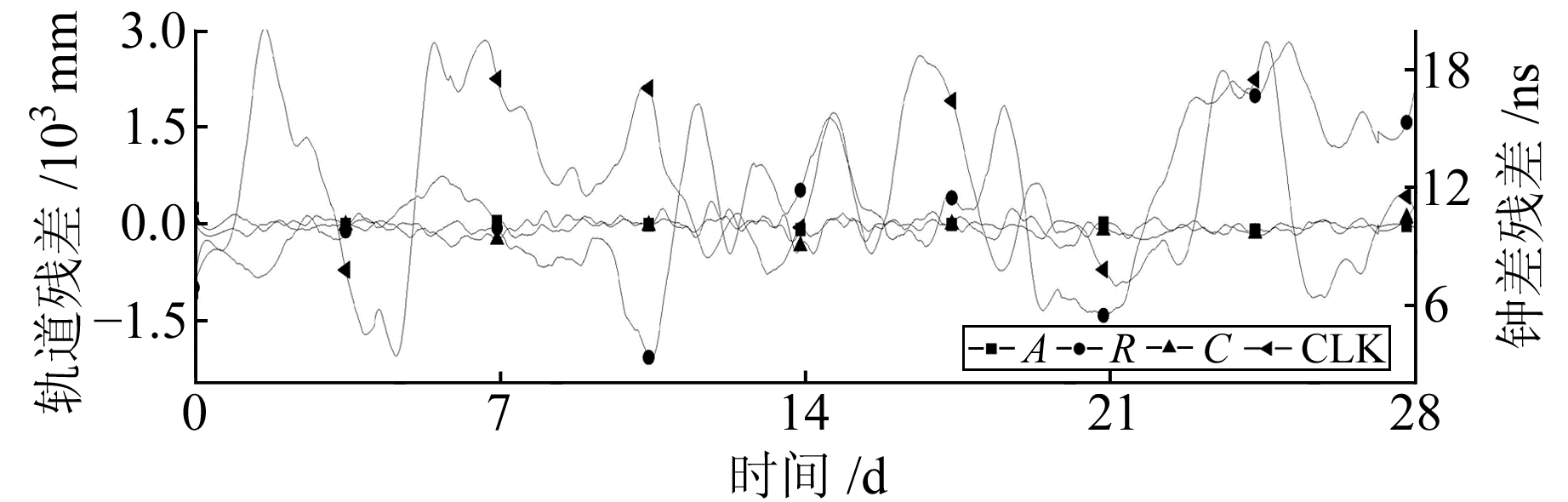
图 6 GLONASS R17轨道和钟残差 Fig. 6 The residual of GLONASS R17 orbit and clock offset |
|
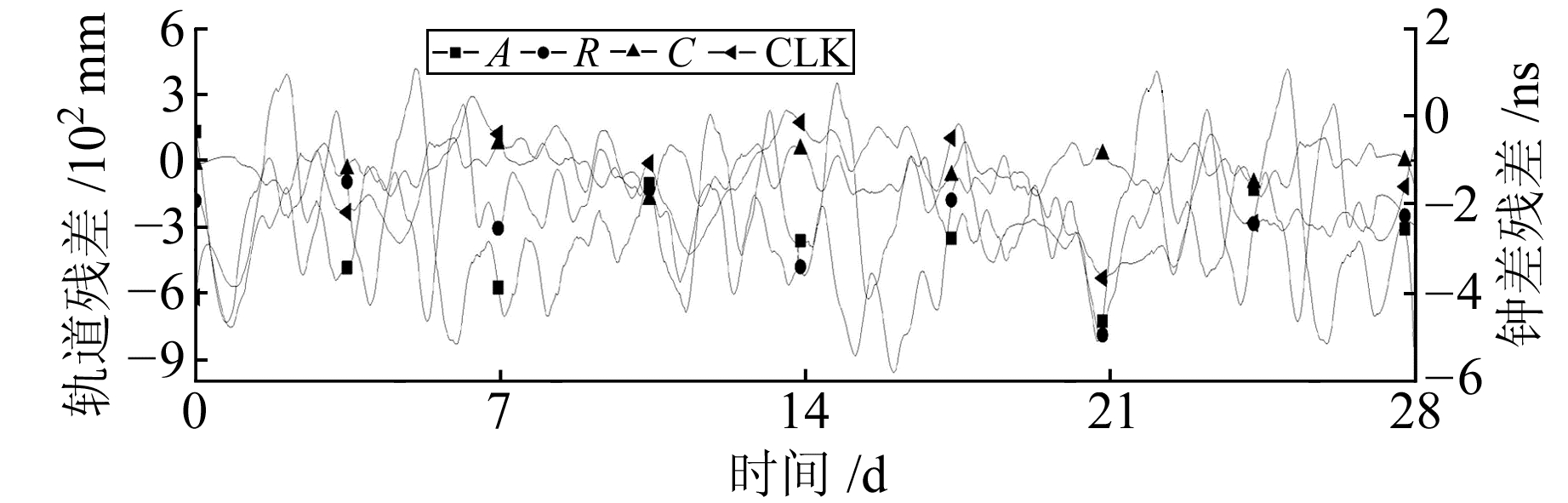
图 7 Galileo E12轨道和钟残差 Fig. 7 The residual of Galileo E12 orbit and clock offset |
|
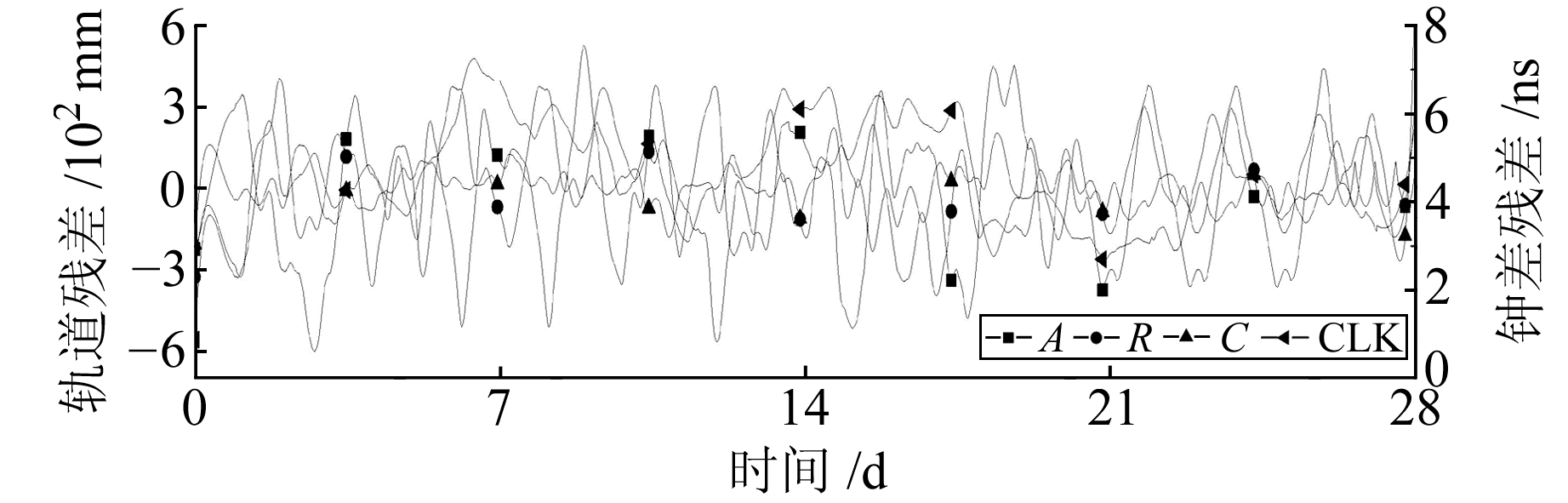
图 8 Galileo E24轨道和钟残差 Fig. 8 The residual of Galileo E24 orbit and clock offset |
|
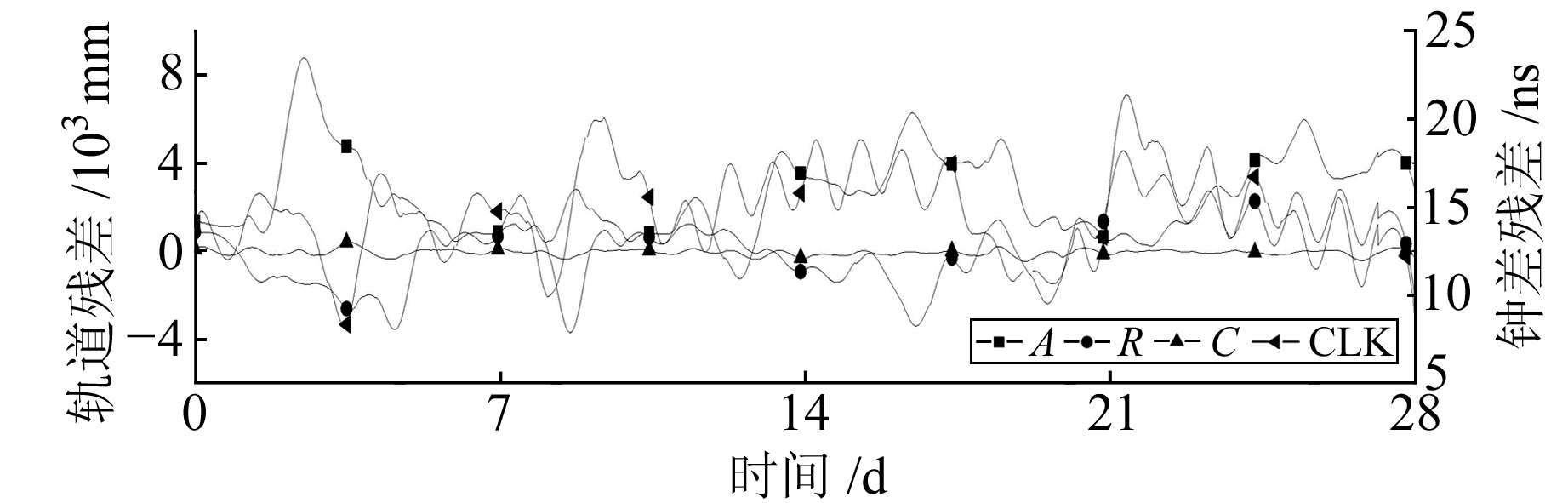
图 9 BDS GEO C03轨道和钟残差 Fig. 9 The residual of BDS GEO C03 orbit and clock offset |
|
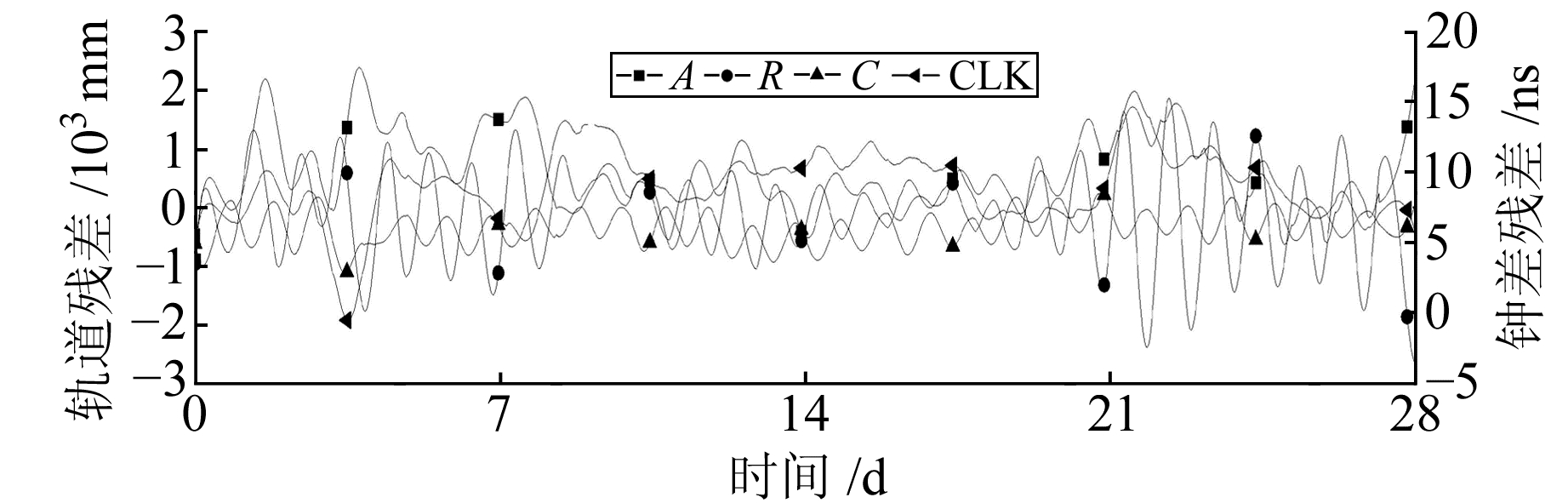
图 10 BDS IGSO C09轨道和钟残差 Fig. 10 The residual of BDS IGSO C09 orbit and clock offset |
|
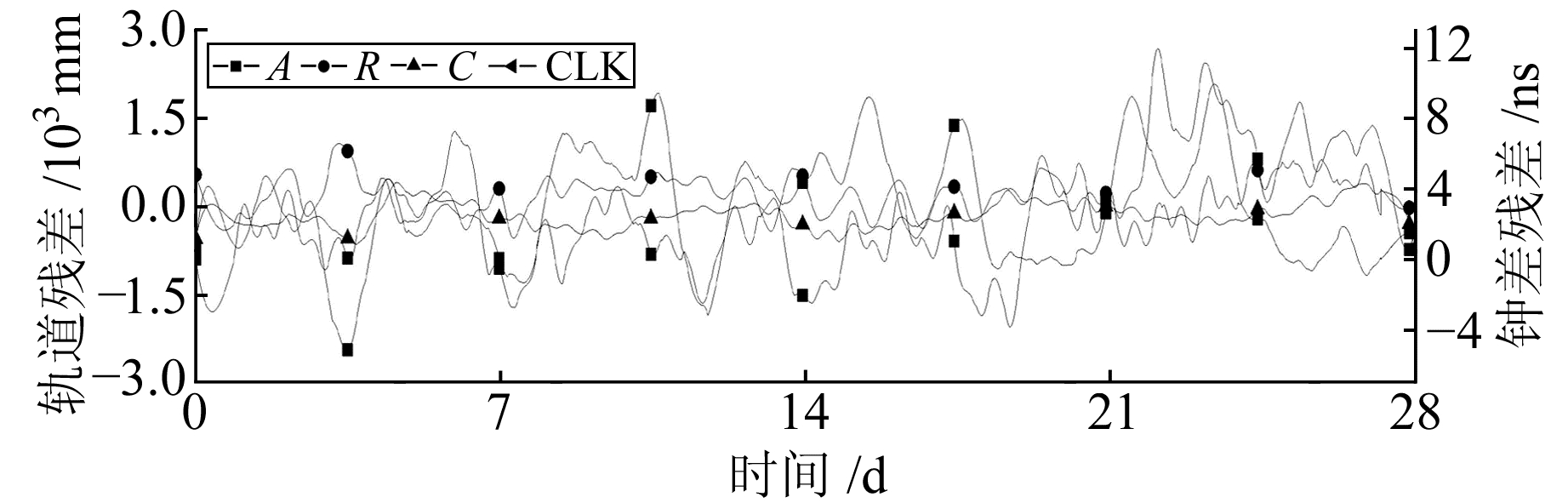
图 11 BDS IGSO C12轨道和钟残差 Fig. 11 The residual of BDS IGSO C12 orbit and clock offset |
根据以上的精度对比结果,统计各系统的切向、法向、径向以及钟差的标准差(表 1)。
|
|
表 1 各系统3个方向以及钟差的标准差 Tab. 1 The standard deviation of neck, tangential, normal direction and clock difference |
由表 1可知,在切向Galileo精度最高,其余依次为GLONASS、GPS、BDS;在径向GPS精度最高,其次为Galileo,BDS和GLONASS精度相当;在法向GPS精度最高,其余依次为Galileo、BDS、GLONASS;在3D方向Galileo精度最高,其余依次为GPS、GLONASS、BDS卫星。这是由于Galileo卫星的发射时间较短,卫星比较新,性能比较稳定;GPS属于比较成熟的系统,其监测站分布于全球,监测数据全球分布比较均匀,各个高校科研单位对其的研究都比较多,数据处理技术比较成熟,所以精度较高;俄罗斯为了减小GLONASS系统地面监测站分布不均的状况,采用激光测卫技术在一定程度上提高了卫星轨道精度。BDS卫星表现出GEO的广播星历轨道精度低于BDS其他卫星,但BDS的MEO和IGSO广播星历轨道和钟差精度已与GPS卫星基本相当。
各系统均表现出径向误差小于切向和法向,径向方向的偏差变化也比较平缓,同时切向和法向的波动基本相当。这是因为在使用地面观测得到的数据对GNSS卫星进行轨道确定时,由于导航定位卫星的空间分布状况,观测值对径向比其他2个方向更加敏感。
在钟差方面,GPS约为2 ns,BDS GEO约为14 ns,IGSO约为9 ns,MEO约为4 ns,GLONASS约为7 ns,Galileo约为3 ns。钟差的精度受卫星装备钟的影响非常明显,Rb原子钟的精度明显高于Cs原子钟,同时表现出新卫星的钟精度高于旧卫星。
2.2 卫星测距误差比较为了更加准确地判定4大系统广播星历的精度,估计各系统不同卫星的空间信号测距误差(SISRE)。该指标可以综合评价广播星历的星历误差和卫星精度,其计算公式为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{SISRE}} = \\ \sqrt {{{({p_1}\cdot R - c\cdot{\rm{CLK}})}^2} + {p_2}\cdot({A^2} + {C^2})} \end{array} $ |
式中,R、A、C为径向、切向、法向的误差(单位为m),CLK为广播星历的卫星钟差(单位为ns),p1和p2为各个方向的贡献因子(该值取决于卫星轨道的高度,对于GPS卫星,取p1=0.98,p2=0.141;对于GLONASS卫星,取p1=0.98,p2=0.149;对于Galileo卫星,取p1=0.98,p2=0.121;对于BDS的GEO和IGSO卫星,取p1=0.99,p2=1/127,对于BDS的MEO卫星,取p1=0.98,p2=1/54)。图 12~16为SISRE值的变化情况。
|
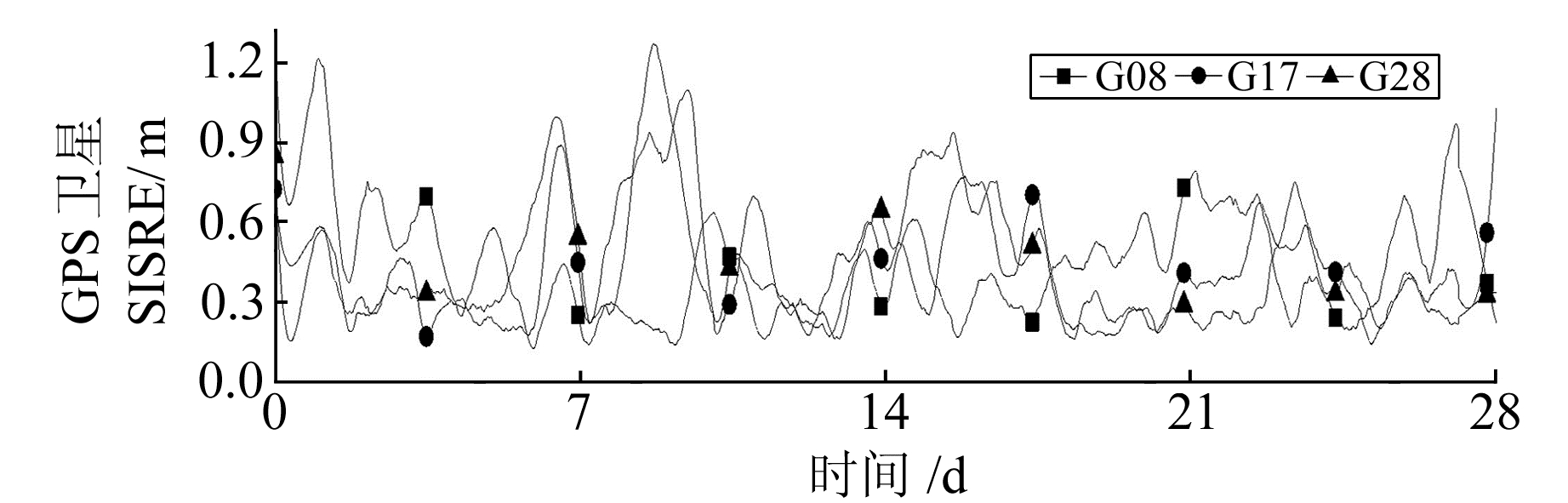
图 12 GPS G08、G17、G28卫星SISRE值变化 Fig. 12 The SISRE value change chart of GPS G08, G17, G28 satellite |
|
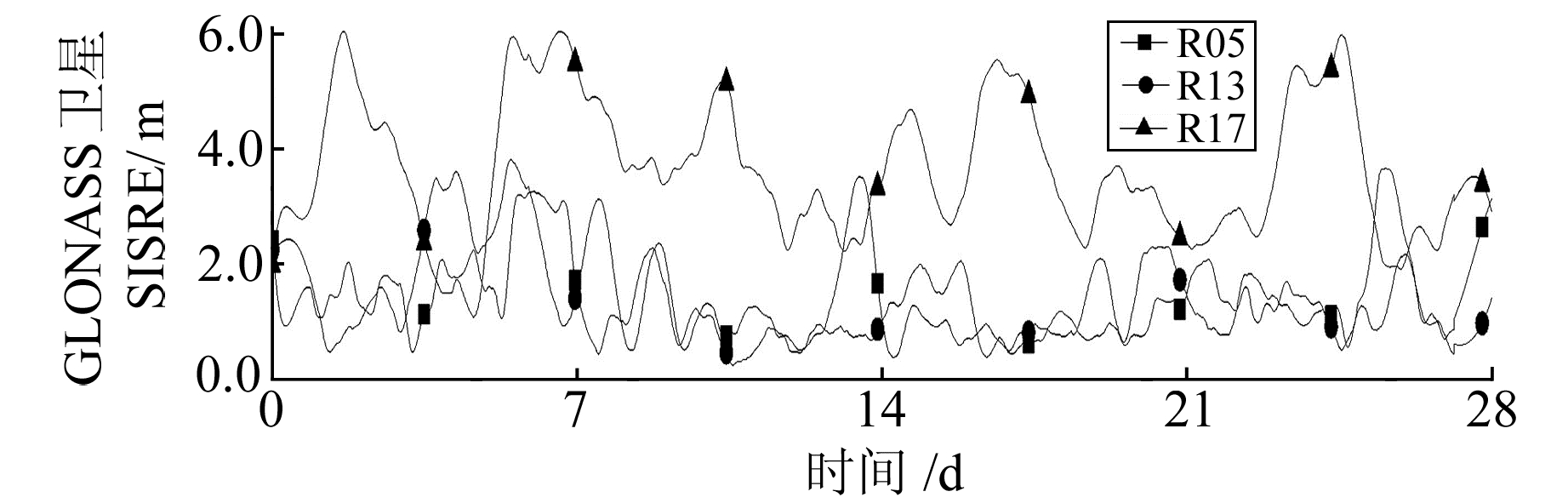
图 13 GLONASS R05、R13、R17卫星SISRE值变化 Fig. 13 The SISRE value change chart of GLONASS R05, R13, R17 satellite |
|
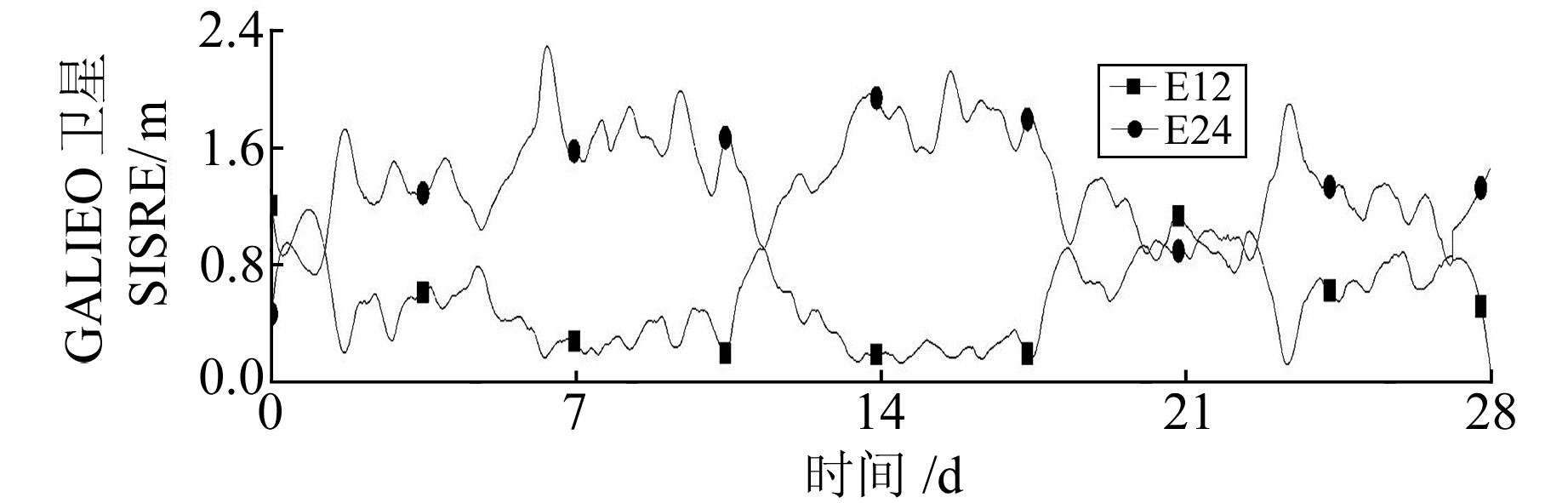
图 14 Galileo E12、E24卫星SISRE值变化 Fig. 14 The SISRE value change chart of Galileo E12, E24 satellite |

|
图 15 BDS C03、C09、C12卫星SISRE值变化 Fig. 15 The SISRE value change chart of BDS C03, C09, C12 satellite |
|
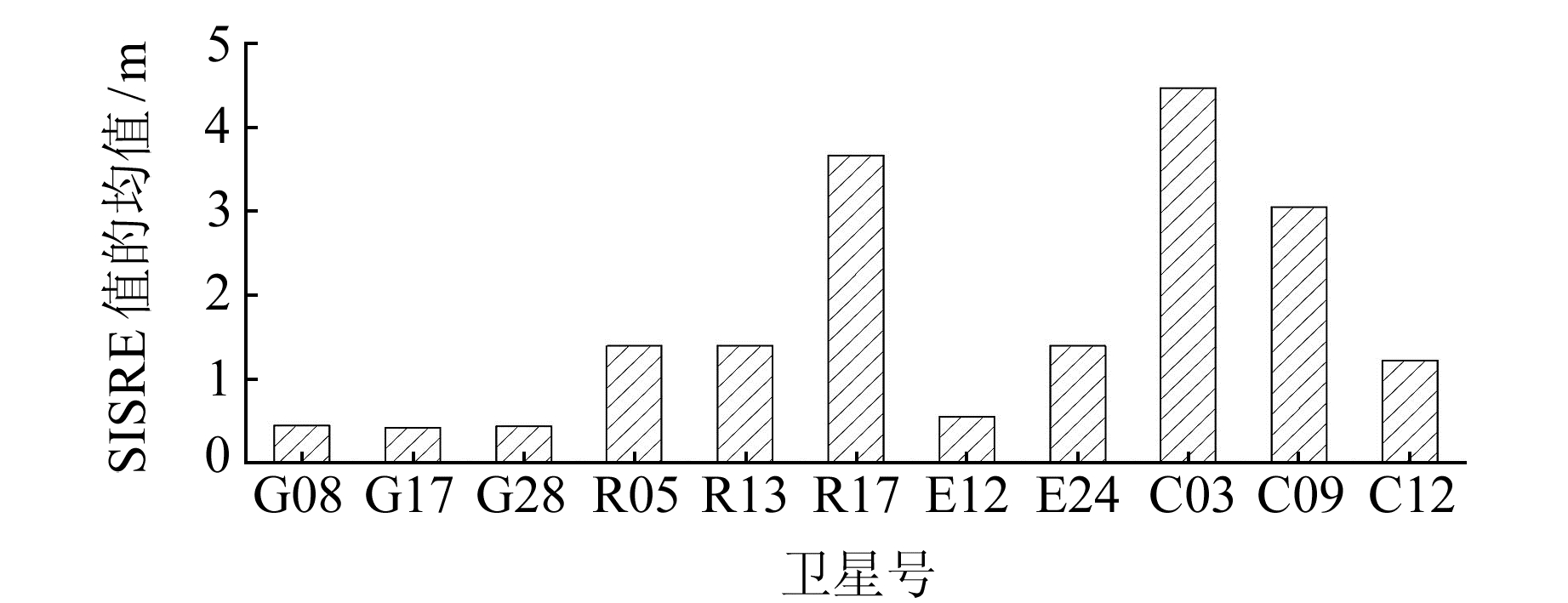
图 16 各个系统的空间信号测距误差均值 Fig. 16 The space signal ranging error of each system |
由图 12~16可知,GPS卫星广播星历的空间信号测距误差约为0.4 m,GLONASS约为2 m,Galileo约为1 m,BDS约为3 m。SISRE值主要取决于卫星3个方向轨道误差和卫星钟差的影响,GPS卫星的监测站全球分布较为均匀,所以对卫星的轨道和钟差预报都最为准确;而GLONASS卫星可能是由于频分多址的原因导致频率对卫星钟的影响较大,使得SISRE值变化较大;Galileo卫星均携带2台Rb钟和2台被动型氢钟,钟的卫星性和频率漂移率都比较好,这在一定程度上提高了该系统的SISRE值;而BDS在钟的设计参数和卫星轨道的设计等方面都和其他系统存在较大的差异,导致了北斗卫星的SISRE值较大。同时BDS和GLONASS卫星的SISRE精度随卫星的轨道改变表现出很大的不同,GLONASS卫星可能是由于地面测站分布的问题,而BDS是由于轨道不同,数据处理策略有所差异,导致卫星轨道精度也有所差异。
3 结语本文以gbm精密星历和钟差作为参考真值,对比了brdm广播星历2017-02-01~02-28的卫星轨道和钟差。结果表明,GPS轨道径向、切向、法向的精度为1 m、0.4 m、0.8 m左右,钟差约为2 ns,SISRE约为0.4 m;BDS不同类型的卫星表现出很大差异,其中GEO的径向、切向、法向精度分别为2 m、1.3 m、0.2 m左右,钟差约为14 ns,SISRE约为4.4 m,IGSO的径向、切向、法向精度为0.8 m、1.1m、0.4 m,钟差约为3 ns,SISRE约为3.0 m,MEO的径向、切向、法向精度为1.2 m、0.6 m、0.3 m,钟差约为3 ns,SISRE约为1.4 m;Galileo卫星的径向、切向、法向精度为0.3 m、0.3 m、0.2 m,钟差约为3 ns,SISRE约为1 m;GLONASS卫星的径向、切向、法向精度为0.4 m、1.0 m、0.4 m,钟差约为7 ns,SISRE约为2 m。BDS GEO卫星精度较低,而IGSO和MEO卫星已基本和GPS相当。
| [1] |
楼益栋, 刘万科, 张小红. GPS卫星星历的精度分析[J]. 测绘地理信息, 2003, 28(6): 4-6 (Lou Yidong, Liu Wanke, Zhang Xiaohong. Analysis on the Fitting Accuracy of Satellite Position Based on GPS Broadcast Ephemeris[J]. Journal of Geomatics, 2003, 28(6): 4-6)
(  0) 0) |
| [2] |
郭斐, 张小红, 李星星, 等. GPS系列卫星广播星历轨道和钟的精度分析[J]. 武汉大学学报:信息科学版, 2009, 34(5): 589-592 (Guo Fei, Zhang Xiaohong, Li Xingxing, et al. Precision Analysis on Orbit and Clock of GPS Satellites Broadcast Ephemeris[J]. Geomatics and Information Science of Wuhan University, 2009, 34(5): 589-592)
(  0) 0) |
| [3] |
帅平, 陈定昌, 江涌. GPS广播星历误差及其对导航定位精度的影响[J]. 数据采集与处理, 2004, 19(1): 107-110 (Shuai Ping, Chen Dingchang, Jiang Yong. Errors of GPS Broadcast Ephemerides and Their Effects on Navigation and Positioning Accuracy[J]. Journal of Data Acquisition and Processing, 2004, 19(1): 107-110 DOI:10.3969/j.issn.1004-9037.2004.01.023)
(  0) 0) |
| [4] |
郭际明, 孟祥广, 李宗华, 等. GLONASS卫星广播星历精度分析[J]. 大地测量与地球动力学, 2011, 31(1): 68-71 (Guo Jiming, Meng Xiangguang, Li Zonghua, et al. Accuracy Analysis of GLONASS Satellites Broadcast Ephemeris[J]. Journal of Geodesy and Geodynamics, 2011, 31(1): 68-71)
(  0) 0) |
| [5] |
王霞迎, 秘金钟, 张德成, 等. GPS广播星历位置、速度和钟差精度分析[J]. 大地测量与地球动力学, 2014, 34(3): 164-168 (Wang Xiaying, Bei Jinzhong, Zhang Decheng, et al. Analysis of Precision of Position Velocity and Clock of GPS Satellites Broadcast Ephemeris[J]. Journal of Geodesy and Geodynamics, 2014, 34(3): 164-168)
(  0) 0) |
| [6] |
谢小刚, 曾大治, 龙腾, 等. 北斗GEO卫星广播星历的直接拟合算法研究[J]. 华中科技大学学报:自然科学版, 2014(3): 14-18 (Xie Xiaogang, Zeng Dazhi, Long Teng, et al. Research on Broadcast Ephemeris Direct Fitting Algorithm of Beidou GEO Satellite[J]. Journal of Huazhong University of Science and Technology, 2014(3): 14-18)
(  0) 0) |
| [7] |
郭忠臣, 高井祥, 曹新运, 等. 北斗广播星历轨道及钟差精度分析[J]. 煤炭技术, 2015, 34(7): 113-116 (Guo Zhongchen, Gao Jingxiang, Cao Xinyun, et al. Accuracy Analysis on Orbit and Clock of BDS Satellites Broadcast Ephemeris[J]. Coal Technology, 2015, 34(7): 113-116)
(  0) 0) |
| [8] |
Kim M, Kim J. A Long-Term Analysis of the GPS Broadcast Orbit and Clock Error Variations[J]. Procedia Engineering, 2015, 99: 654-658 DOI:10.1016/j.proeng.2014.12.585
(  0) 0) |
| [9] |
刘庆元, 包海, 王虎, 等. GPS、GLONASS、Galileo三大系统间时间系统以及坐标系统的转换[J]. 测绘科学, 2008, 33(5): 13-15 (Liu Qingyuan, Bao Hai, Wang Hu, et al. Time Transformation and Coordinates Transformation among GPS、GLONASS and Galileo[J]. Science of Surveying & Mapping, 2008, 33(5): 13-15 DOI:10.3771/j.issn.1009-2307.2008.05.004)
(  0) 0) |
| [10] |
Wesson K D, Pesyna K M, Bhatti J A, et al. Opportunistic Frequency Stability Transfer for Extending the Coherence Time of GNSS Receiver Clocks[C]. ION GNSS Conference, Portland, 2010 https://www.ion.org/publications/abstract.cfm?articleID=9403
(  0) 0) |
| [11] |
李方超, 王浩, 高井祥, 等. 卫星截止高度角和系统组合对GNSS PPP精度影响研究[J]. 大地测量与地球动力学, 2017, 37(11): 1 150-1 155 (Li Fangchao, Wang Hao, Gao Jingxiang, et al. Influence of Elevation Masking Angle and System Integration on GNSS PPP Precision[J]. Journal of Geodesy and Geodynamics, 2017, 37(11): 1 150-1 155)
(  0) 0) |
2. Jiangsu Key Laboratory of Resources and Environmental Information Engineering, China University of Mining and Technology, 1 Daxue Road, Xuzhou 221116, China;
3. College of Water Resources and Architectural Engineering, Northwest A & F University, 23 Weihui Road, Yangling 712100, China
 2018, Vol. 38
2018, Vol. 38

