2. 西南交通大学地球科学与环境工程学院,成都市犀安路999号,611756
基于不同海潮模型的海潮负荷(ocean tide loading, OTL)位移建模对比研究较多[1-4],但针对中国沿海区域的研究有限。由晓文等[5]主要从潮波系数差异的角度分析海潮模型对中国沿海区域OTL位移的影响,验证了mm级的差异。由于现有海潮模型对水循环长周期效应的建模存在不足,OTL位移改正对测站表现的长周期运动会有影响[6],然而已有研究并未对该问题进行深入讨论。因此,本文尝试通过堆积功率谱对基于不同高频潮波参数的OTL改正后序列的周期信号进行对比分析,同时基于4种不同海潮模型的OTL改正结果,进一步讨论模型间差异对测站运动特性的影响,分析噪声特性、测站速度不确定度等方面的异同。
1 数据描述利用FES2004、EOT11a、TPXO7.2和Chinasea2010等4种海潮模型,对距中国海岸线200 km以内的23个CMONOC监测站的观测数据进行海潮负荷位移改正。23个测站的坐标时间序列均为ITRF2008框架下的GNSS单日解,其中XIAM和SHAO测站的序列跨度为2000~2016年,其他测站跨度为2010~2016年,且已去趋势[7]。海潮模型参数见表 1。
|
|
表 1 海潮模型 Tab. 1 Ocean tide models |
OTL位移计算实质是通过叠加各分潮波的影响得到总负荷位移,包括8个高频潮波:半日潮波M2、S2、N2和K2,周日潮波K1、O1、P1和Q1,以及长周期潮波Mm、Mf和Ssa。利用SPOTL软件[11]和Bos-Scherneck网站[12]计算得到EOT11a、TPXO7.2、Chinasea2010和FES2004等4个海潮模型在23个测站所在位置各潮波3个分量的振幅和格林尼治相位,格网间隔为0.25°×0.25°。其中,Chinasea2010模型是区域模型,区域以外选用FES2004模型进行融合计算。利用式(1)计算测站OTL位移3个分量ΔCk(k=1, 2, 3分别代表E、N和U分量)[13]:
| $ \Delta {C_k} = \sum\limits_{j = 1}^n {{f_i}{A_{k, j}}} \cos \left( {{\omega _j}t + {\chi _j}\left( {{t_0}} \right) + {\mu _j}-{\varphi _{k, j}}} \right) $ | (1) |
式中,Ak, j和φk, j为OTL位移振幅和相位, ωj和χj(t0)为潮波j的角频率和天文幅角初相,n为潮波数,除11个主潮波外,采用IERS协议2010推荐的最新海潮改正计算方法[14],将11个主潮汐分量应用样条插值法扩展成为342个小潮波,其模型精度达到0.1%[15]。
由于CMONOC发布的数据成果已经应用了FES2004模型海潮改正,本文先计算得到所选23个测站基于FES2004模型的OTL位移序列,将该改正还原,然后分别采用EOT11a,TPXO7.2和Chinasea2010模型对所得序列进行重新改正。
2.2 GNSS坐标时间序列频谱分析为了分析各海潮模型高频潮波对测站坐标序列周期信号的影响,使用Lomb-Scargle谱分析[16]对测站坐标序列进行时频变换,提取序列的周期信号进行对比。同时,为了有效地分离周日潮波和半日潮波对周期信号的影响,以FES2004模型为参考模型,将Chinasea2010、EOT11a和TPXO7.2模型的半日潮波参数和周日潮波参数分别替换FES2004模型相应的潮波参数。利用参数替换后的模型及FES2004模型分别得到23个测站的改正后序列,再计算得到各改正后序列的堆积功率谱,从而搜索并分析坐标序列中的周期信号的特征和变化。
2.3 GNSS坐标时间序列噪声分析早期的坐标时间序列噪声建模一般会预先指定谱指数κ,κ=0, -1, -2时分别代表白噪声(WN)、闪烁噪声(FN)和随机游走噪声(RWN),这3者及其组合是GNSS坐标序列的几种经典噪声模型。预先指定谱指数可以大大缩短计算耗时,但时间序列长度的限制、其他噪声的覆盖及其他因素的影响可能造成建模效果不佳。Williams[17]认为,同时估计噪声振幅和谱指数即白噪声+非整数谱指数幂律噪声(WN+PL),更有利于反映真实物理现象。
选取WN+FN、WN+RWN、WN+FN+RWN和WN+PL共4种噪声模型组合对23个测站坐标序列分别进行建模。由于OTL改正不能完全消除周年/半周年信号,因此在以上的噪声模型组合中均考虑周年、半周年信号。另外采用差分MLE快速估计方法[18]对以上4种噪声模型组合的优劣进行评价,该方法在计算效率与结果准确度方面均优于传统MLE方法,能表征测站的实际运动特征[19]。各噪声模型组合应用该方法可以得到极大似然对数值,数值越大代表模型越可靠,但该数值也随未知参数个数的增多而变大。因此,采用保守估计准则[20]来判断这4种模型组合的优劣:考虑到WN+PL模型比其他3种模型增加了对谱指数的估计,因此只有当前者MLE值比后者大2.6以上时,才认为该模型更优;其他3种模型所含未知参数个数相同,可直接比较MLE值。
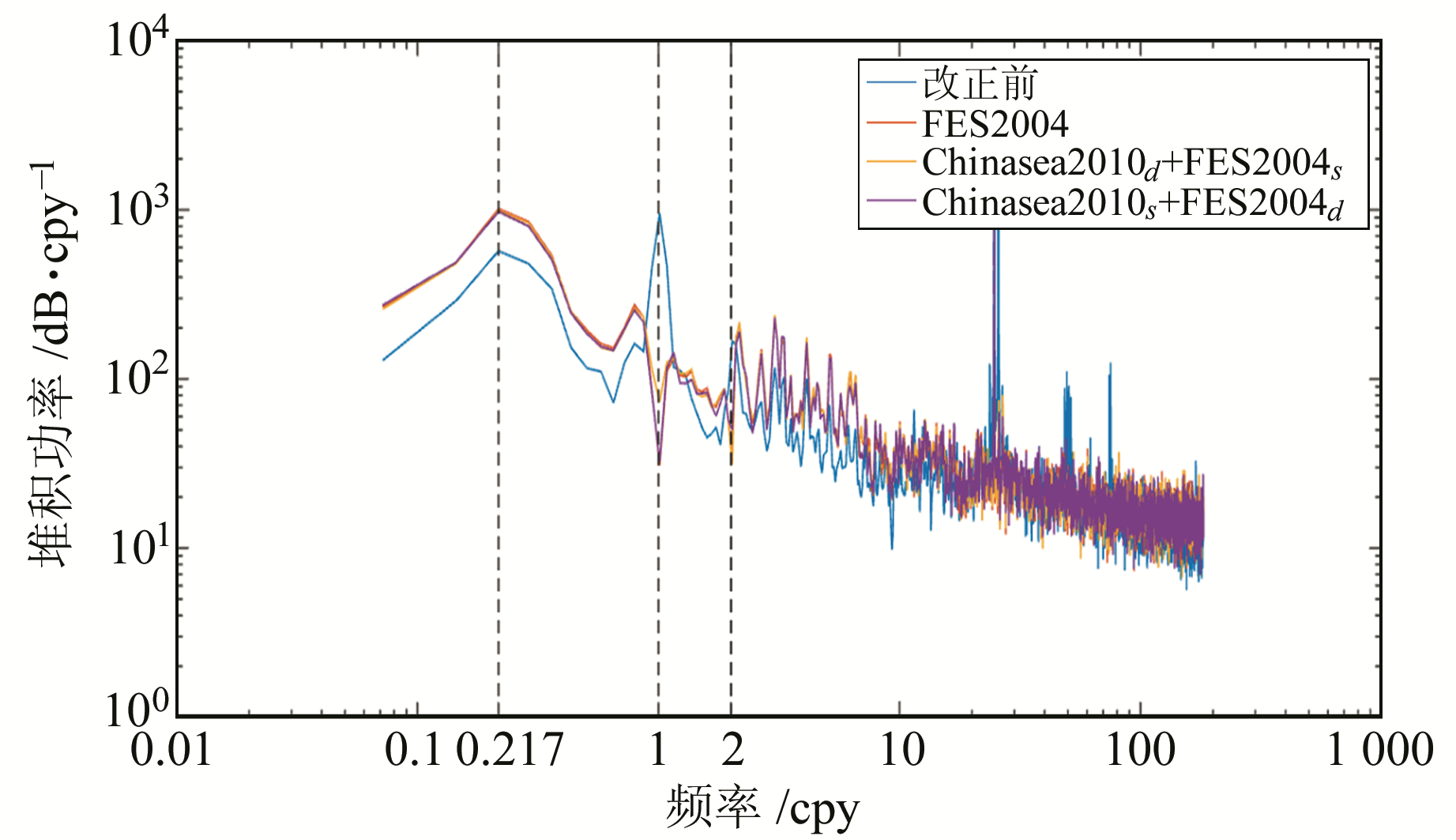
3 结果与讨论 3.1 周期信号量化分析将海潮模型X(Chinasea2010、EOT11a和TPXO7.2)的周日潮波参数替换为FES2004模型的周日潮波参数,得到Xs+FES2004d海潮模型组合,将X的半日潮波参数替换为FES2004模型的半日潮波参数,得到Xd+FES2004s海潮模型组合,即有Chinasea2010s+FES2004d、EOT11as+FES2004d、TPXO7.2s+FES2004d、Chinasea2010d+FES2004s、EOT11ad+FES2004s和TPXO7.2d+FES2004s共6种组合模型。由于OTL位移的U分量最为显著,仅讨论U分量。改正前坐标序列和基于以上6种组合模型及FES2004模型进行OTL改正后的坐标序列的堆积频谱见图 1~3。
|
图 1 基于潮波参数替换后的Chinasea2010海潮模型进行OTL改正前后序列堆积功率谱 Fig. 1 Stacked power spectra of the OTL corrected position time series using Chinasea2010 model with tide wave parameters replaced |
|
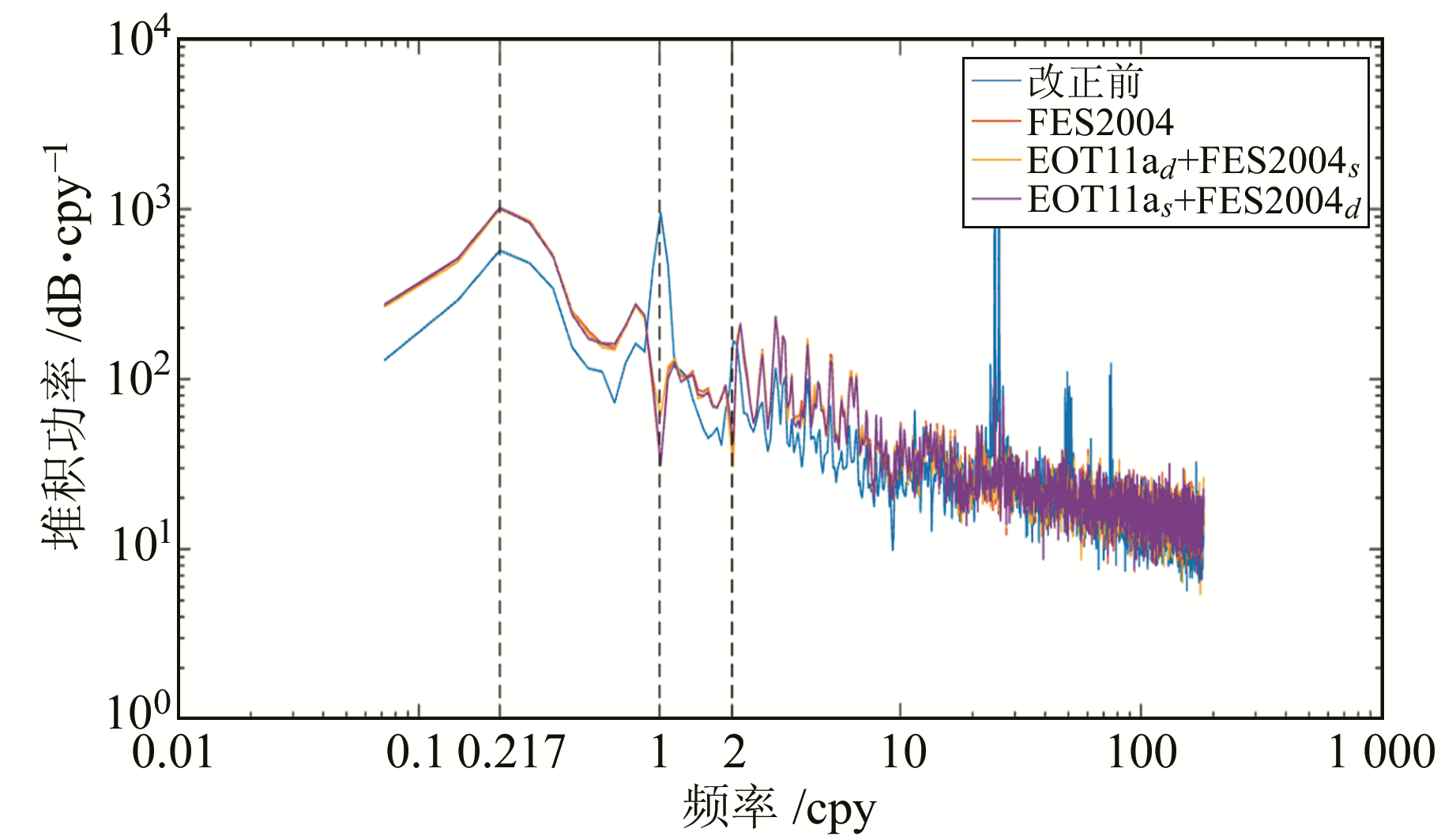
图 2 基于潮波参数替换后的EOT11a模型进行OTL改正前后序列堆积功率谱 Fig. 2 Stacked power spectra of the OTL corrected position time series using EOT11a model with tide wave parameters replaced tide wave parameters replaced |
|
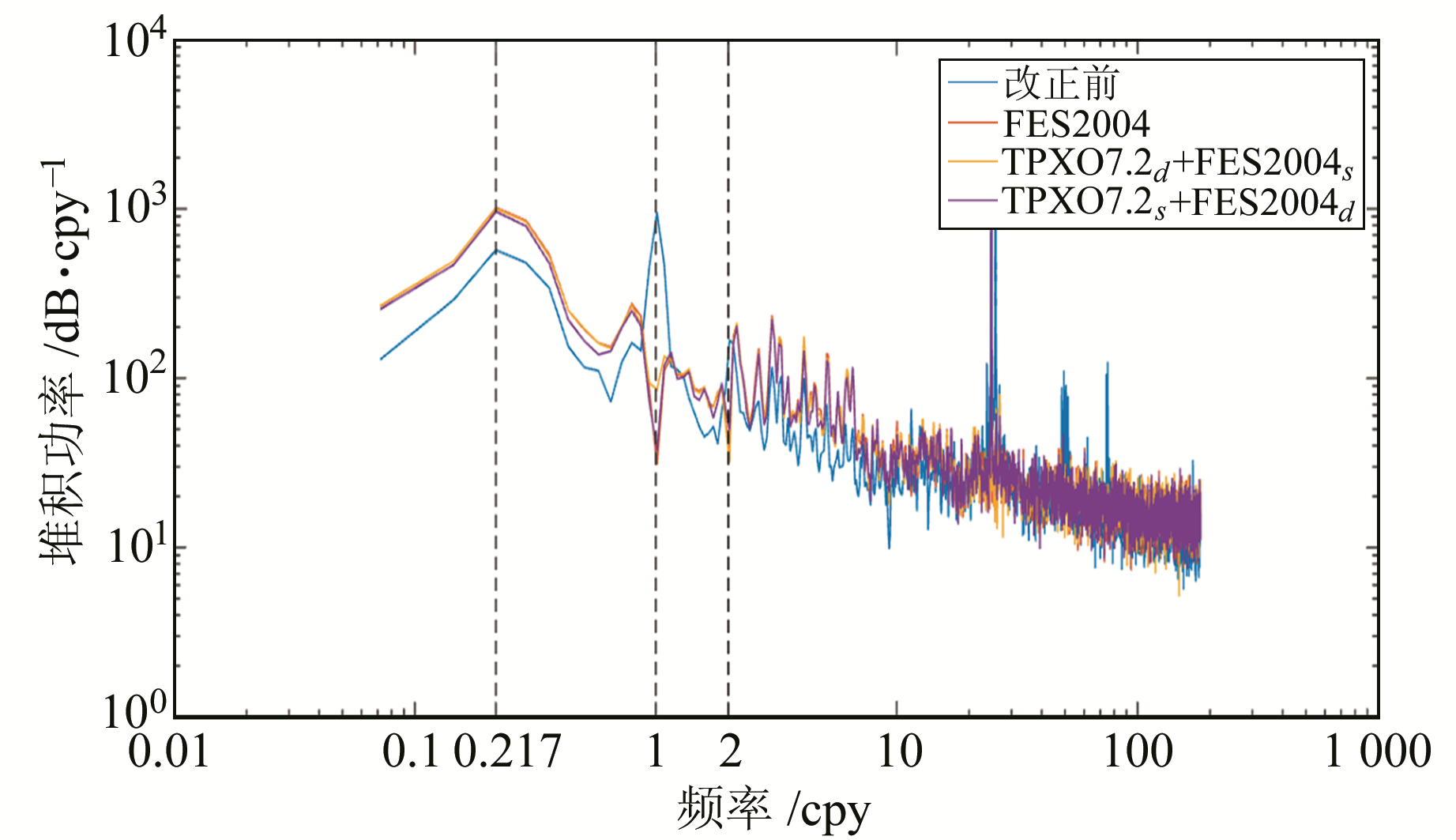
图 3 利用潮波参数替换后的TPXO7.2模型的OTL改正前后序列堆积功率谱 Fig. 3 Stacked power spectra of the OTL corrected position time series using TPXO7.2 model with tide wave parameters replaced |
从图 1~3可知,改正前的序列明显存在长周期信号、周年信号和半周年信号(0.217 cpy、1 cpy和2 cpy处);各种模型的改正结果均显示,周年信号和半周年信号得到显著削弱,而长周期信号功率增大,可见海潮负荷改正在一定程度上引入了长周期信号,在讨论测站长周期运动的研究中值得注意。
基于Chinasea2010d+FES2004s、EOT11ad+FES2004s和TPXO7.2d+FES2004s模型组合进行OTL改正后,长周期信号堆积功率分别增大73.1%、74.6%和75.2%,周年信号分别削弱94.2%、94.6%和94.5%,半周年信号分别削弱81.4%、82.0%和81.1%。基于Chinasea2010s+FES2004d、EOT11as+FES2004d和TPXO7.2s+FES2004d模型组合进行OTL改正后,长周期信号分别增大70.7%、77.8%和68.3%,周年信号分别削弱96.6%、96.7%和96.1%,半周年信号分别削弱70.3%、74.9%和70.7%。基于FES2004模型进行OTL改正后,长周期信号功率增大77.4%,周年信号削弱96.8%,半周年信号削弱80.0%。
Xd+FES2004s模型组合与FES2004模型的差异对海潮负荷位移改正后序列长周期信号、周年信号和半周年信号功率的影响分别达2.2%~4.3%、-2.6%~-2.1%和1.1%~2.0%;Xs+FES2004d模型组合与FES2004模型差异对海潮负荷位移改正后序列长周期信号、周年信号和半周年信号功率的影响分别达-0.5%~9.1%、-0.7% ~0.1%和-9.6%~-5.0%。基于Xd+ FES2004s的OTL改正对周年信号的削减程度比Xs+FES2004d小1.6%~2.4%,而对半周年信号的削减程度比Xs+FES2004d大7.0%~11.1%。
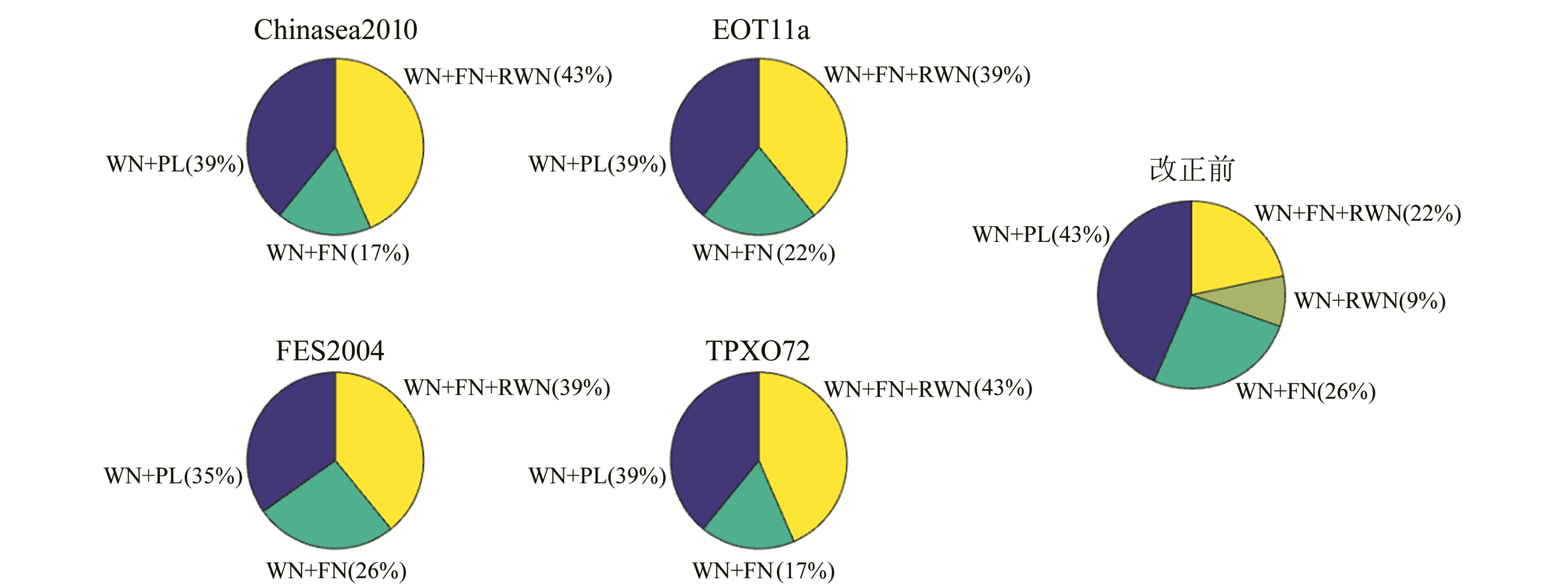
3.2 噪声特性分析 3.2.1 OTL改正对测站噪声模型的影响表 2给出了23个测站OTL位移改正前坐标时间序列及利用Chinasea2010、EOT11a、FES2004和TPXO7.2等4个海潮模型进行OTL位移改正后的坐标序列相应的最优噪声模型组合。图 4为23个测站OTL位移改正前后的最优噪声模型组合所占比例。
|
图 4 OTL位移改正前后的最优噪声模型所占比例 Fig. 4 Optimal noise model distribution of stations before and after OTL correction using different ocean tide models |
|
|
表 2 OTL改正前后的最优噪声模型组合 Tab. 2 Comparison of optimal noise model of stations before and after OTL correction |
从表 2可以看出,OTL改正后测站的最优噪声模型的变化因站而异,OTL改正噪声特性表现为WN+RWN的测站占9%,而改正后不存在该噪声特性的测站。图 4更直观地显示出,OTL改正后噪声特性表现为WN+FN+RWN的测站所占比例增大17%~21%,且不同海潮模型对噪声特性的影响有一定差异。
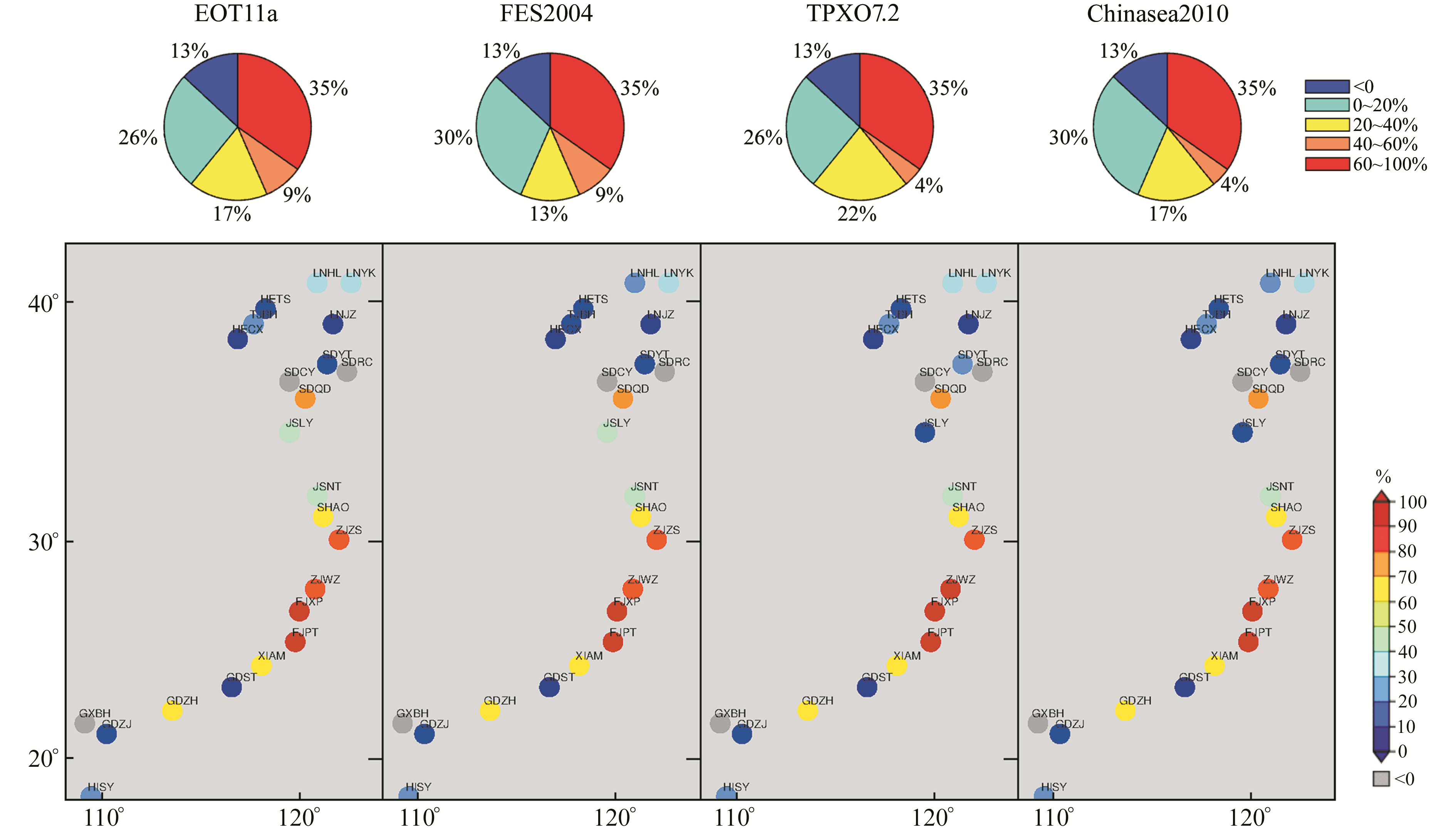
3.2.2 OTL改正对噪声振幅及测站速度不确定度的影响为进一步分析OTL改正对测站噪声量级的影响,对比WN+PL噪声模型组合的2种噪声振幅之和在改正前后的变化,见图 5。可以看出,4种模型均有35%的测站噪声振幅减小60%以上,30%左右的测站噪声振幅减小20%~40%,未改善的测站只有13%,且模型间差异不明显。
|
图 5 OTL位移改正前后WN和PL噪声振幅改善比例分布 Fig. 5 WN+PL amplitude reduction percentage before and after OTL correction using different ocean tide models |
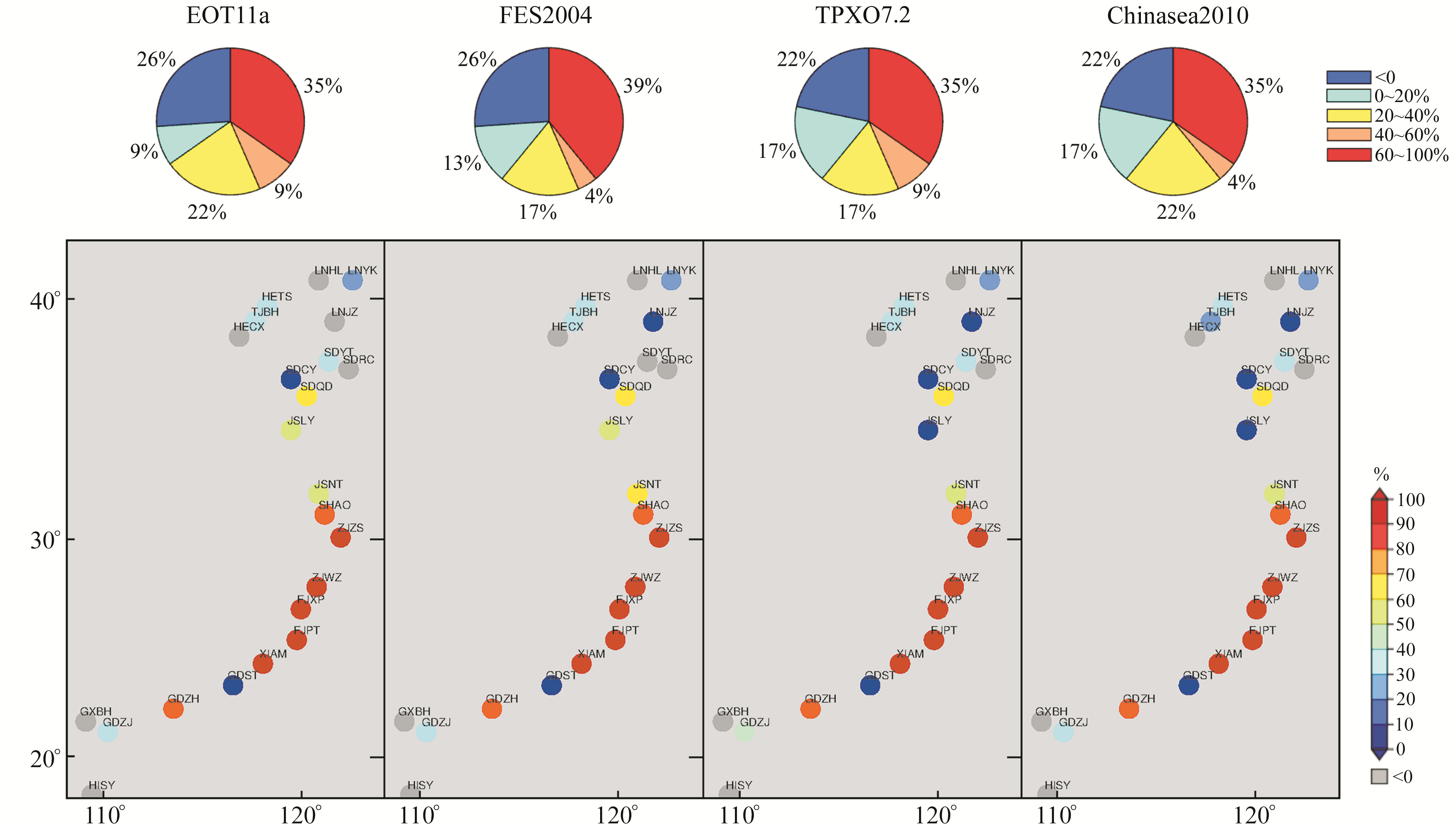
23个测站以最优噪声模型组合(表 2)建模得到的测站速度不确定度在OTL改正前后的改善幅度及其所占比例见图 6。可以看出,利用4种模型进行OTL改正后,均有超过70%的测站速度不确定度减小,削减幅度超过20%和60%的测站分别占65%和35%左右。其中基于FES2004模型的OTL改正效果最好,测站速度不确定度得到大幅改善的测站所占比例最大——39%的测站速度不确定度减小60%~98%;另外,还呈现出一定的空间分布规律,东海沿岸的测站相较于渤海沿岸等其他区域噪声振幅和测站速度不确定度的改善最为显著,说明东海沿岸的OTL改善效果最佳。
|
图 6 OTL改正前后测站速度不确定度改善比例分布 Fig. 6 Velocity uncertainty reduction percentage before and after OTL correction using different ocean tide models |
1) 海潮模型高频潮波参数的差异会引起OTL改正后周期信号功率的差异,尤其是长周期信号、周年信号和半周年信号。其中,EOT11a、TPXO7.2和Chinasea2010模型与FES2004模型间周日潮波参数的差异对海潮负荷位移改正后序列长周期信号、周年信号和半周年信号功率的影响分别达2.2%~4.3%、-2.6%~-2.1%和1.1%~2.0%;半日潮波参数差异对海潮负荷位移改正后序列长周期信号、周年信号和半周年信号功率的影响分别达-0.5%~9.1%、-0.7%~0.1%和-9.6%~-5.0%。
2) OTL改正对测站噪声模型的影响因区域而异,东海沿岸测站的改善效果比中国其他沿海区域显著。不同海潮模型对测站噪声模型的影响也有一定差别。总体上,利用不同海潮模型进行OTL改正后,噪声特性表现为WN+FN+RWN组合的测站所占比例均明显增大。利用Chinasea2010和TPXO7.2海潮模型进行OTL改正后,WN+FN+RWN模型组合所占比例最大,达43%。基于4个海潮模型的OTL改正对噪声振幅以及测站速度不确定度的影响总体上具有较好的一致性:35%左右的测站的噪声振幅得到60%以上的削减;测站速度不确定度削弱幅度超过20%和60%的测站分别占65%和35%左右。其中基于FES2004模型的OTL改正对测站速度不确定度的改善最大,39%的测站得到60%以上的改善。
| [1] |
Penna N T, King M A, Stewart M P. GPS Height Time Series: Short-Period Origins of Spurious Long-Period Signals[J]. Journal of Geophysical Research, 2007, 112(B2): 1074-1086
(  0) 0) |
| [2] |
Stammer D, Ray R D, Andersen O B, et al. Accuracy Assessment of Global Barotropic Ocean Tide Models[J]. Reviews of Geophysics, 2014, 52(3): 243-282 DOI:10.1002/2014RG000450
(  0) 0) |
| [3] |
汪一航, 方国洪, 魏泽勋, 等. 基于卫星高度计的全球大洋潮汐模式的准确度评估[J]. 地球科学进展, 2010, 25(4): 353-362 (Wang Yihang, Fang Guohong, Wei Zexun, et al. Accuracy Assessment of Global Ocean Tide Models Base on Satellite Altimetry[J]. Advances in Earth Science, 2010, 25(4): 353-362)
(  0) 0) |
| [4] |
张胜凯, 雷锦韬, 李斐. 全球海潮模型研究进展[J]. 地球科学进展, 2015, 30(5): 579-588 (Zhang Shengkai, Lei Jintao, Li Fei. Advances in Global Ocean Tide Models[J]. Advances in Earth Science, 2015, 30(5): 579-588)
(  0) 0) |
| [5] |
由晓文. 中国沿海地区海潮负荷位移建模[D]. 成都: 西南交通大学, 2016 (You Xiaowen. The Modeling of Ocean Tide Loading Displacements in the Coastal Area of China[D]. Chengdu: Southwest Jiaotong University, 2016)
(  0) 0) |
| [6] |
Riva R E M, Frederikse T, King M A, et al. Brief Communication: The Global Signature of Post-1900 Land Ice Wastage on Vertical Land Motion[J]. The Cryosphere, 2017, 11(3): 1-8
(  0) 0) |
| [7] |
中国地震局地震研究所. CMONOC基准站数据处理说明[Z]. 武汉, 2017 (Institute of Seismology, CEA. CMONOC Fiducial Stations Datum Processing Instructions[Z]. Wuhan, 2017)
(  0) 0) |
| [8] |
Lyard F, Lefevre F, Letellier T, et al. Modelling the Global Ocean Tides: Modern Insights from FES2004[J]. Ocean Dynamics, 2006, 56(5): 394-415
(  0) 0) |
| [9] |
Savcenko R, Bosch W. EOT11a-Global Empirical Ocean Tide Model from Multi-Mission Satellite Altimetry[R]. München, 2012
(  0) 0) |
| [10] |
Egbert G D, Erofeeva S Y. Efficient Inverse Modeling of Barotropic Ocean Tides[J]. Journal of Atmospheric & Oceanic Technology, 2002, 19(2): 183-204
(  0) 0) |
| [11] |
Agnew D C. SPOTL: Some Programs for Ocean-Tide Loading[R]. San Diego, 2012
(  0) 0) |
| [12] |
Scherneck H. Ocean Tide Loading Provider[EB/OL]. http://holt.oso.chalmers.se/loading/, 2017
(  0) 0) |
| [13] |
Mccarthy D D, Petit G. IERS Conventions 2010, Frankfurt am Main: Verlag des Bundesamts für Kartographie und Geodäsie[R]. IERS Technical Note, 2010
(  0) 0) |
| [14] |
Agnew D C. Hardisp. f yet again[EB/OL]. ftp://5.144.141.242/iers/convupdt/chapter7/add_info/report_hardisp.pdf, 2017
(  0) 0) |
| [15] |
Petit G, Luzum B. IERS Conventions (2010)[R]. Paris, 2010
(  0) 0) |
| [16] |
Press W H, Teukolsky S A, Vetterling W T, et al. Numerical Recipes in Fortran 77: The Art of Scientific Computing[M]. Cambridge: Cambridge University Press, 1992
(  0) 0) |
| [17] |
Williams S D P. Error Analysis of Continuous GPS Position Time Series[J]. Journal of Geophysical Research: Solid Earth, 2004, 109(B3)
(  0) 0) |
| [18] |
Bos M S, Fernandes R, Williams S, et al. Fast Error Analysis of Continuous GPS Observations[J]. Journal of Geodesy, 2008, 82(3): 157-166 DOI:10.1007/s00190-007-0165-x
(  0) 0) |
| [19] |
邓连生. GPS坐标时间序列中未模型化误差和环境负载的影响研究[D]. 武汉: 武汉大学, 2016 (Deng Liansheng. Research on Effects of Unmodeled Errors and Environmental Loading on GPS Coordinate Time Series[D]. Wuhan: Wuhan University, 2016)
(  0) 0) |
| [20] |
Langbein J. Noise in GPS Displacement Measurements from Southern California and Southern Nevada[J]. Journal of Geophysical Research: Atmospheres, 2008, 113(B5): 620-628
(  0) 0) |
2. Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University, 999 Xi'an Road, Chengdu 611756, China
 2018, Vol. 38
2018, Vol. 38

