重力潮汐是地球在日、月及近地行星引潮力的作用下产生的地球周期性形变,其最大幅度达到200 μGal, 是重力变化成分中最主要的部分。太阳和月亮的引潮力作用不但是固体潮汐的力源,也是海潮的驱动力。海潮和固体潮具有相同的力源,导致它们具有相同的频谱特征,因此不能用调和分析的方法直接把海潮从固体潮观测资料中分离出来。为了合理解释观测结果,从中得到固体潮和海潮的信息,必须将两者分开。重力潮汐残差中含有丰富的地球动力学信息,其主要贡献来自于全球和局部的海潮负荷效应。在全球大部分的区域内,海潮负荷达到重力潮汐振幅的1%~2%,沿海地区甚至可以达到3%~5%。
本文选取陆态网络青岛台站gPhone重力仪观测数据,首先利用Tsoft软件对各种干扰进行预处理,然后利用Eterna3.30软件求解重力固体潮各波群的潮汐参数(振幅因子和相位滞后)和精度估计值,最后利用全球海潮模型对主要潮波O1、K1和M2进行海潮负荷改正。
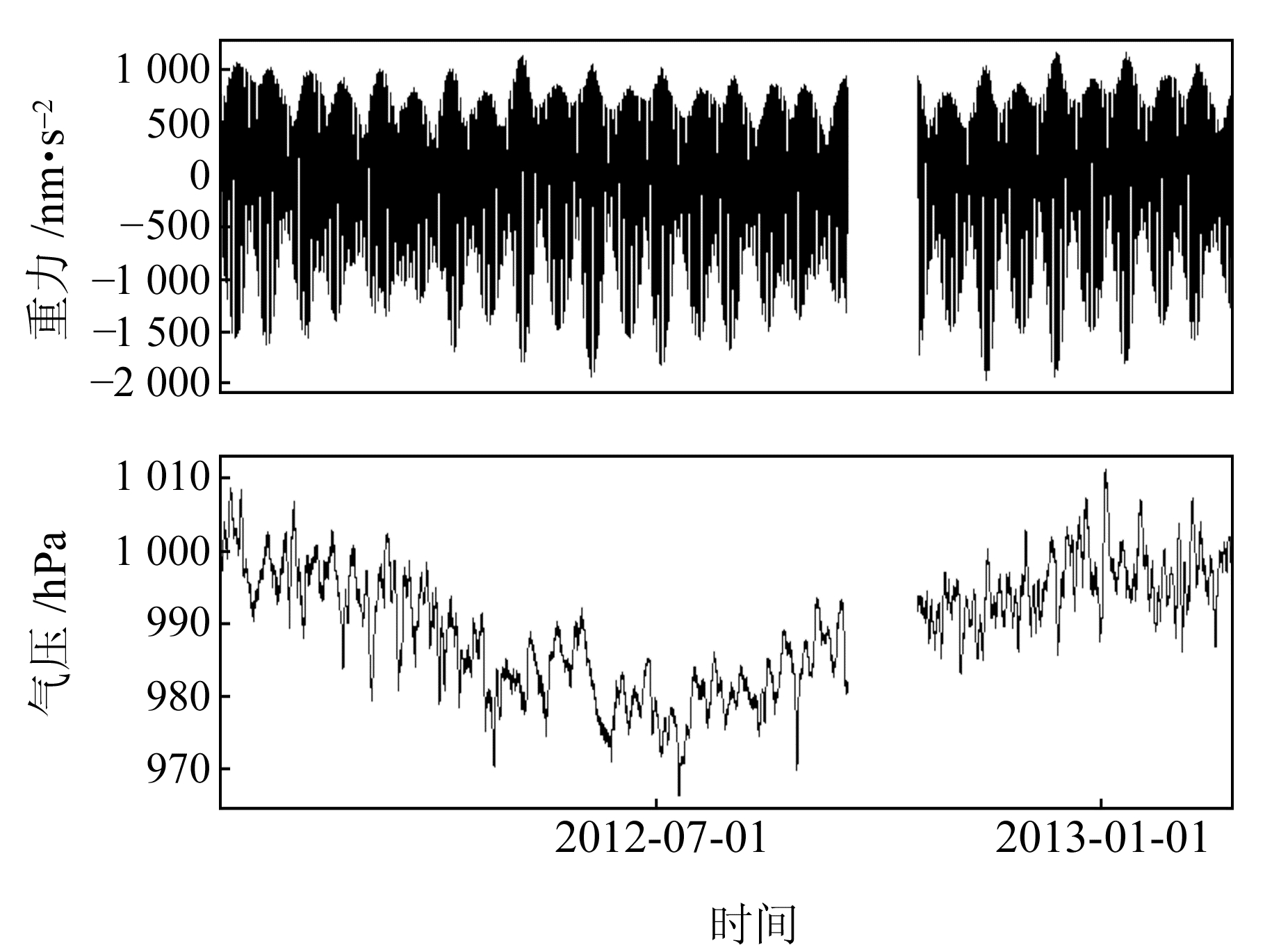
1 预处理及调和分析青岛台站连续重力观测数据时段为2012-01~2013-02,原始采样间隔为1 s,估算潮汐参数时,需要滤波成分钟数据再进行预处理,最终的调和分析一般是用小时采样的数据。目前大都采用国际地潮中心(ICET)推荐的降采样滤波器对原始数据进行降采样,得到观测数据的采样率为1 min,然后采用Tsoft软件[1]对数据进行预处理。数据预处理一般是在残差上进行,首先需要移除理论合成潮,根据标准大气导纳因子扣除大气效应,删除一些尖峰、突跳、仪器掉格和大地震等引起的错误数据,对由于仪器断电、故障等引起的间断采用线性插值或三次样条插值;然后,加上之前移除的理论合成潮和大气效应就可以得到预处理好的重力潮汐数据;最后,以480为窗口数、12 cpd为截止频率将分钟采样降为小时采样。降采样后的重力和气压数据如图 1所示, 由于仪器故障, 观测数据出现了一个大间断(2012-09-18~10-17)。
|
图 1 小时采样的重力和气压数据 Fig. 1 Hourly gravity and pressure data |
利用Eterna3.30[2]标准潮汐分析软件对青岛台站gPhone重力仪观测时间序列进行调和分析。Eterna3.30软件采用最小二乘方法估计潮汐参数,由于数据时间太短,不能用来确定长周期项,所以直接采用高通滤波去掉漂移。重力数据分析采用Tamura[3]给出的1 200个分波的高精度引潮位展开数值表,获得精度较高的重力潮汐参数(振幅因子、相位延迟和相应的误差估算),同时获得大气重力导纳值和零漂的切比雪夫多项式逼近系统。δth为Dehant等[4]提出的基于非流体静力平衡状态下的潮汐理论模型值,8个主要周日和半周日潮波的具体数值如表 1所示。由表 1可以看出,青岛地区观测振幅较大的是半日潮波M2、S2和周日潮波O1、K1,M2、S2振幅分别为49.021 μGal、22.807 μGal,O1、K1振幅分别为29.558 μGal、41.570 μGal,O1和M2振幅因子的相对精度分别为0.8%和1.1%,8个主要潮波的振幅因子的标准差均在2.6%之内,与理论潮汐模型值的差异也在3%之内。
|
|
表 1 青岛台站gPhone重力仪重力潮汐实测结果 Tab. 1 Gravity tide measurement results of gPhone gravimeter at Qingdao station |
海潮负荷效应计算一般使用Farrell[5]的经典负荷理论,并采用Agnew[6]提出的积分格林函数法将海潮与重力格林函数进行褶积积分,其计算公式为:
| $\begin{array}{l} L\left( {\theta, \lambda, t} \right) = {a^2}\int {\int {\rho H\left( {\theta ', \lambda ', t} \right)} } \cdot \\ G\left( \psi \right)S\left( A \right){\rm{sin}}\theta '{\rm{d}}\theta '{\rm{d}}\lambda ' = \\ {a^2}\int {\int {\rho H\left( {\psi, A, t} \right)} } G\left( \psi \right)S\left( A \right){\rm{sin}}\psi {\rm{d}}\psi {\rm{d}}A \end{array}$ | (1) |
式中,L(θ, λ, t)为某地点某时刻的海潮负荷,t为时间,θ和λ为计算点的余纬和经度,a为地球半径,ρ为海水密度,H(θ′, λ′, t)为瞬时潮高,θ′和λ′为负荷点的余纬和经度,G(ψ)为与角距有关的重力负荷格林函数,可由负荷勒夫数h和k的组合求得。
2.2 海潮模型现代化的全球海潮模型可分为经验模型和同化模型两大类。经验模型主要是基于卫星测高数据的累积,从中提取潮汐信息;同化模型则是以流体动力学为基础,将观测数据和数值模型相结合,以特定的标准和方法进行处理得到潮汐信息。表 2给出了本文使用的海潮模型名称和其统计特征。其中,FES2004模型同化了671个验潮站、337个T/P卫星交叉点数据和1 254个ERS-2卫星交叉点数据,在建模中计算负荷径向形变和重力位摄动,格网分辨率为0.125°。GOT系列模型是经验改正模型,GOT4.7全球海潮模型在南北纬66°以内的深海区域使用T/P数据,且在浅水和极地地区加入了GFO和ERS-1/2数据,以此来对全球海潮进行建模,并通过迭代方法计算负荷潮的影响。TPXO72atlas对T/P和Jason-1/2等卫星测高数据进行沿轨调和分析,模型在基于大洋区模型解的基础上结合沿海区域的高分辨率近海区域解,格网分辨率为0.25°。EOT系列模型是德国大地测量研究所研发的经验模型,EOT11a以FES2004模型作为参考,使用了1992~2010年的T/P、ERS-2、Jason-1/2和Envisat测高数据。DTU10全球海潮模型是丹麦技术大学基于FES2004建立的经验改正模型,格网分辨率为0.125°。NAO99b系列海潮模型由日本国家天文台建立,格网分辨率为0.5°。HAMTIDE11a全球海潮模型是由德国汉堡大学研发的正压同化模型,该模型基于广义反演方法,使用最小二乘法,可以直接将海潮模型和数据的不确定性降到最低,格网分辨率为0.125°。TPXO系列海潮模型是由美国俄勒冈州立大学建立的全球海潮模型,该模型使用二维正压流体动量方程,运用广义反演方法对卫星测高数据进行同化,并应用到正压潮能向斜压潮能转化的研究当中。其中DTU10、EOT11a和HAMTIDE11a为最新的全球海潮模型,空间分辨率为0.125°×0.125°。
|
|
表 2 8种海潮模型特征统计 Tab. 2 The features of eight global ocean tide models |
表 3给出了表 2中8种全球海潮模型计算的受海潮负荷影响最大的3个潮波(O1、K1、M2)的重力海潮负荷。
|
|
表 3 青岛台站主要潮波(O1,K1,M2)的重力海潮负荷 Tab. 3 The gravity tidal loading of the main tidal waves (O1, K1, M2) at Qingdao station |
由表 3看出,利用8个全球海潮模型算出的M2、O1、K1海潮负荷值分布在2.6~3.0 μGal之间,可见全球海潮模型之间的差异性不大。
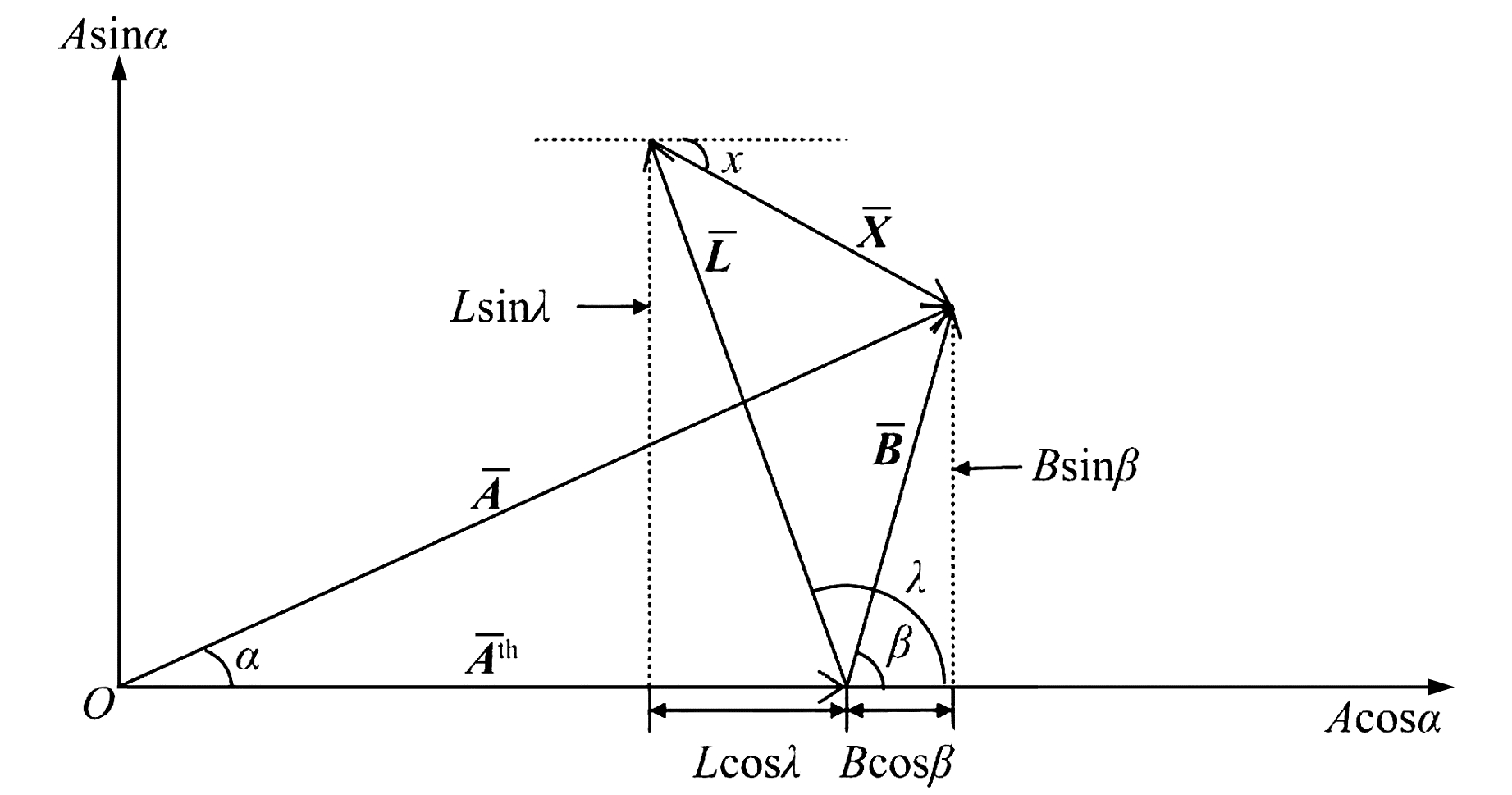
2.3 海潮负荷改正为了研究海潮负荷的影响,引进一个剩余残差矢量(图 2),矢量Ath为固体潮理论潮汐值,矢量A为固体潮观测潮汐值,海潮负荷矢量为L(振幅为L,相位为λ),固体潮汐观测残差矢量为B,固体潮剩余残差矢量为X(振幅为X,相位为χ)。它们有以下关系:
|
图 2 海潮负荷改正示意图 Fig. 2 Sketch of ocean tide loading correction |
| $\begin{array}{l} \boldsymbol{\bar B} = \boldsymbol{\bar A} - {{\boldsymbol{\bar A}}^{{\rm{th}}}}\\ \boldsymbol{\bar X} = \boldsymbol{\bar B} - \boldsymbol{\bar L} \end{array}$ | (2) |
固体潮观测值振幅和振幅因子分别为A、δ,理论振幅和振幅因子分别为Ath、δth, 它们之间有以下关系:
| $\frac{A}{\delta } = \frac{{{A^{{\rm{th}}}}}}{{{\delta ^{{\rm{th}}}}}}$ | (3) |
观测残差矢量的振幅和相位表达式为:
| $\begin{array}{l} B = {A^{{\rm{th}}}}\delta {\left[{1 + {{({\delta ^{{\rm{th}}}}/\delta )}^2}-2\left( {{\delta ^{{\rm{th}}}}/\delta } \right){\rm{cos}}\varphi } \right]^{1/2}}\\ \beta = {\rm{t}}{{\rm{g}}^{ - 1}}\left[{\delta {\rm{sin}}\varphi /\left( {\delta {\rm{cos}}\varphi-{\delta ^{{\rm{th}}}}} \right)} \right] \end{array}$ | (4) |
由式(4)求得的B和β加上由全球海潮模型算出的振幅L和相位λ,根据式(5)可计算得到经过海潮模型改正后剩余残差振幅Χ和相位χ:
| $\begin{array}{l} {\rm X} = {B^2} + {L^2} - 2BL{\rm{cos}}\left( {\beta - \lambda } \right)\\ \chi = {\rm{t}}{{\rm{g}}^{ - 1}}\left[{\left( {B{\rm{sin}}\beta-L{\rm{sin}}\lambda } \right)/\left( {B{\rm{cos}}\beta-L{\rm{cos}}\lambda } \right)} \right] \end{array}$ | (5) |
利用不同的全球海潮模型进行海潮负荷改正后,固体潮汐的剩余残差相对于观测残差有明显的减小。表 4给出了固体潮汐观测残差和经过全球海潮模型改正后的剩余残差。以半日潮波O1、K1和M2为例,观测残差分别为1.942 μGal、0.461 μGal和0.723 μGal,经过全球海潮模型改正后,剩余残差减小范围分别为1.205~1.484 μGal、0.115~0.165 μGal和0.239~0.410 μGal。可以看出,最终残差振幅明显减小,但与理论值比较仍然较大,主要原因可能是没有考虑区域海潮模型,也可能是数据预处理需要改进以及存在局部环境因素的影响。
|
|
表 4 海潮负荷改正前后的青岛台站重力观测残差和剩余残差 Tab. 4 Observation residuals and final residuals of tidal gravity before and after ocean loading correction |
表 5给出了由全球海潮模型改正后O1、K1和M2的振幅因子。可见,除了M2潮波,O1和K1潮波的振幅因子均有不同程度的下降,和理论模型之间的差异均保持在1%之内,说明了海潮负荷改正的有效性。M2潮波振幅因子没有减小,可能是由于没有考虑区域海潮模型改正。
|
|
表 5 海潮改正后的振幅因子 Tab. 5 Amplitude factor after correction of ocean tide loading |
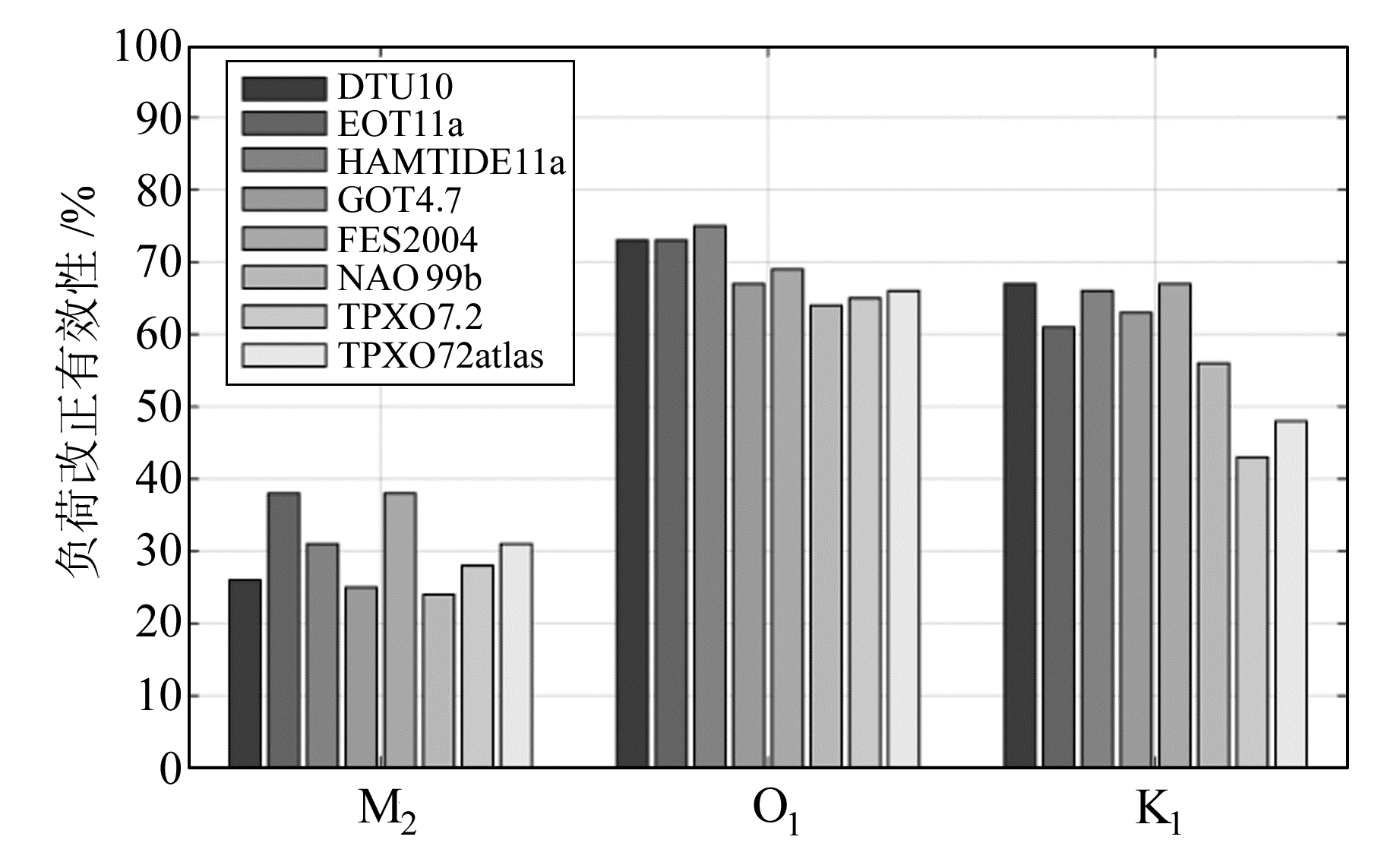
图 3给出了采用8个全球海潮模型进行海潮负荷改正后, M2、O1和K1潮波负荷改正的有效性(观测残差矢量振幅减去剩余残差振幅再除以观测残差振幅)。可见,M2潮波负荷改正的有效性为25%~38%,O1潮波为64%~75%,K1潮波为43%~67%,TPXO7.2模型K1潮波改正效果较好,对于M2和O1潮波,NAO99b模型最好。
|
图 3 8个海潮模型计算的K1、O1和M2潮波的海潮负荷改正有效性 Fig. 3 Loading effect efficiency for main constituents (K1、O1 and M2) estimated by eight different models |
本文基于8个全球海潮模型分析青岛台站受海潮负荷的影响,并对观测结果进行海潮负荷改正,对比分析海潮模型在青岛台站的适用性,得出以下结论:
1) 3个主要潮波的振幅因子的标准差精度均在3%之内,调和分析精度较高。
2) 3个主要潮波的海潮负荷振幅范围为2.6~3.0 μGal,从海潮负荷的振幅数值来看,M2潮波最大,O1潮波和K2潮波次之。8个全球海潮模型算出的主要潮波的振幅差异很小,相位差异稍大。由全球海潮模型改正后,O1和K1潮波的振幅因子均有不同程度的下降,和理论模型之间的差异均保持在1%之内。
3) 应用8个海潮模型进行海潮改正,观测残差振幅改正的有效性大致分布在30% ~75%,利用海潮负荷改正后的残差矢量计算出的振幅因子和相位,除了M2潮波以外,O1和K1潮波振幅因子均出现不同程度的下降,且均与理论潮汐模型值差异在1%之内。如果用近海海潮模型osu.chinasea.2010及NAO.99Jb进行修正,可以进一步提高青岛台站海潮负荷改正的有效性。
致谢 感谢中国大陆环境监测网络提供的重力数据和中科院测量与地球物理研究所陈晓东副研究员在重力数据处理中给予的帮助!
| [1] |
Camp M V, Vauterin P. Tsoft: Graphical and Interactive Software for the Analysis of Time Series and Earth Tides[J]. Computers and Geoscience, 2005, 31(5): 631-640 DOI:10.1016/j.cageo.2004.11.015
(  0) 0) |
| [2] |
Wenzel H G. The Nanogal Software: Data Processing Package ETERNA 3.3[J]. Bull Inf Marées Terrestr, 1996, 124: 9425-9439
(  0) 0) |
| [3] |
Tamura Y. A Harmonic Development of the Tidal Generating Potential[J]. Bull Inf Marées Terrestres, 1987, 99: 6813-6815
(  0) 0) |
| [4] |
Dehant V, Defraigne P, Wahr J. Tides for a Convective Earth[J]. J Geophys Res, 1999, 104(B1): 1035-1058 DOI:10.1029/1998JB900051
(  0) 0) |
| [5] |
Farrell W E. Deformation of the Earth by Surface Loads[J]. Rev Geophys Space Phys, 1972, 10(3): 761-797 DOI:10.1029/RG010i003p00761
(  0) 0) |
| [6] |
Agnew D C. NLOADF: A Program for Computing Ocean-Tide Loading[J]. J Geophys Res, 1997, 102(B3): 5109-5110 DOI:10.1029/96JB03458
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38


