航空重力观测值为空中获取的中高频地球重力场信号,而地球科学领域的诸多应用,如Stokes积分、Hotine积分等,都需要重力数据在地球表面或大地水准面上,因此将空中获取的重力观测值向下延拓到地表或大地水准面上,是航空重力测量数据处理的重要内容之一。
向下延拓属于不适定问题,若采用的延拓方法不适合,会放大航空重力数据中的高频噪声,从而扭曲延拓解。向下延拓方法中应用最为广泛的是逆Poisson积分法,但逆Poisson积分法需要引入正则化处理才能得到稳定可靠的延拓解。常用的正则化方法包括Tikhonov正则化、岭估计、广义岭估计、迭代法、滤波等。航空矢量重力测量获取的是扰动重力的3个分量,其中垂直分量为重力扰动或重力异常,其余为水平分量。理论上重力矢量水平分量向下延拓原理与垂直分量类似,但研究较少,且由于一些技术原因,目前获取的水平分量在精度上不如垂直分量,仅为6~8 mGal[1],如何将航线高度上低信噪比的水平分量向下延拓到地表或大地水准面上是一个亟待解决的问题。本文引入频域输入输出系统(input output system),以不同噪声水平的航空矢量重力观测值作为输入,比较分析单输入单输出系统(single-input single-output system,SISOS)和双输入单输出系统(double-input single-output system, DISOS)对水平分量向下延拓的效果,以此来验证输入输出理论应用于航空矢量重力水平分量向下延拓的可靠性和有效性。
1 输入输出法常用于地球重力场数据融合处理[2-6]的输入输出法的基本思想是将传统的最小二乘配置法转换到频率域中,避免空域中大型矩阵的求逆计算,从而减少数据储存空间及其硬件消耗,提高程序运行速度。根据输入输出端口的不同,可分为单输入单输出、单输入多输出、多输入单输出和多输入多输出等系统,本文仅讨论单输入单输出和双输入单输出系统。
1.1 单输入单输出系统图 1为单输入单输出系统SISOS,在空域和频域中可分别表示为:

|
图 1 单输入单输出系统 Fig. 1 Single-input single-output system |
| $ \boldsymbol{y} = \boldsymbol{bx}'{\rm{ + }}\boldsymbol{e} $ | (1) |
| $ \boldsymbol{Y} = \boldsymbol{BX} + \boldsymbol{E} $ | (2) |
式中,y为输出信号, e为输出误差, b为转换矩阵, x′ = x + n,x为输入信号,n为输入噪声, Y、B、X、E分别为y、b、x′、e的傅里叶变换。逆Poisson积分的FFT快速算法可理解为单输入单输出系统的一种应用[7]。以东向分量的向下延拓为例,输入为航线高度上的东向分量δgx(R+H),输出为大地水准面上的东向分量δgx(R),代入式(2)得:
| $ {F_2}\left\{ {\delta {g_x}(R)} \right\} = {{\rm{e}}^{2\pi Hq}}S(q){F_2}\left\{ {\delta {g_x}(R + H)} \right\}{\rm{ + }}E $ | (3) |
式中,H为航线高度, R为地球平均半径, F2为二维傅立叶变换算子,
| $ S(q) = \frac{1}{{1 + {{(kq)}^4}}} $ | (4) |
式中,k为滤波参数,且k>0。
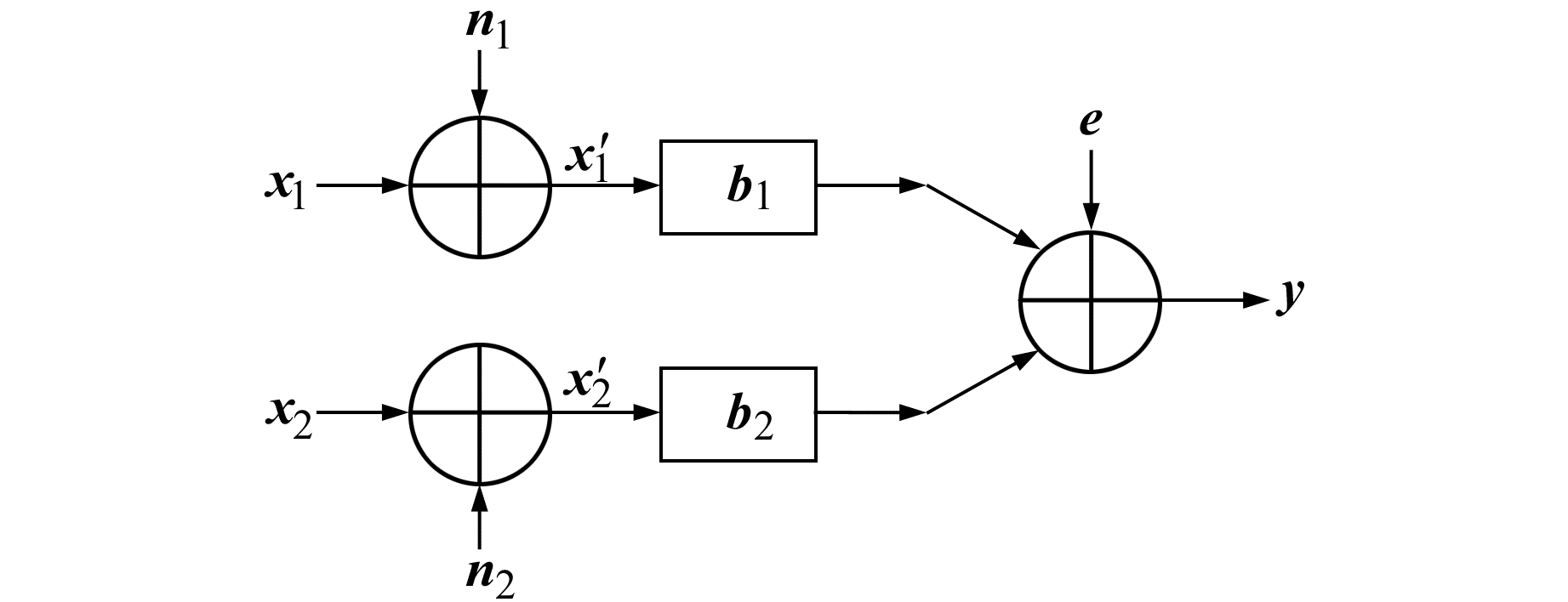
1.2 双输入单输出系统图 2为双输入单输出系统DISOS,在空域和频域中可分别表示为:
|
图 2 双输入单输出系统 Fig. 2 Double-input single-output system |
| $ \boldsymbol{y} = {\boldsymbol{b}_1}{\boldsymbol{x}'_1} + {\boldsymbol{b}_2}{\boldsymbol{x}'_2} + \boldsymbol{e} $ | (5) |
| $ \boldsymbol{Y} = {\boldsymbol{B}_1}{\boldsymbol{X}_1} + {\boldsymbol{B}_2}{\boldsymbol{X}_2} + \boldsymbol{E} $ | (6) |
式中,x′1= x1+ n1,x′2= x2+ n2,x1、x2为输入信号,n1、n2为对应的输入噪声, b1、b2为转换矩阵, X1、X2、Y、B1、B2、E分别为x′1、x′2、y、b1、b2、e的二维傅里叶变换。设噪声与信号之间不相关,以航线高度处的东向分量δgx(R+H)和垂向分量观测值δgz(R+H)为输入,以大地水准面上的重力矢量东向分量延拓值δgx(R)为输出,代入式(6)可得:
| $ \begin{array}{l} {F_2}\left\{ {\delta {g_x}(R)} \right\} = {{\hat B}_1}{F_2}\left\{ {\delta {g_x}(R + H)} \right\} + \\ {{\hat B}_2}{F_2}\left\{ {\delta {g_z}(R + H)} \right\}{\rm{ + }}E \end{array} $ | (7) |
其中,
| $ \left\{ \begin{array}{l} {{\hat B}_1} = {{\rm{e}}^{2\pi Hq}}S(q){R_1}\\ {{\hat B}_2} = {{\rm{e}}^{2\pi Hq}}S(q){R_2} \end{array} \right. $ | (8) |
式中,R1、R2为融合算子:
| $ \left\{ \begin{array}{l} {R_1} = \frac{{\left( {{P_{22}} + {P_{{n_2}{n_2}}}} \right){P_{11}}-{P_{21}}{P_{12}}}}{{\left( {{P_{11}} + {P_{{n_1}{n_1}}}} \right)\left( {{P_{22}} + {P_{{n_2}{n_2}}}} \right)-{{\left| {{P_{12}}} \right|}^2}}}\\ {R_2} = \frac{{\left( {{P_{11}} + {P_{{n_1}{n_1}}}} \right){P_{12}}-{P_{12}}{P_{11}}}}{{\left( {{P_{11}} + {P_{{n_1}{n_1}}}} \right)\left( {{P_{22}} + {P_{{n_2}{n_2}}}} \right) - {{\left| {{P_{12}}} \right|}^2}}} \end{array} \right. $ | (9) |
式中,P11、P22、Pn1n1、Pn2n2分别为δgx(R+H)、δgz(R+H)及对应的输入噪声的自相关功率谱密度函数, P12=P21*为δgx(R+H)、δgz(R+H)之间的互相关功率谱密度函数。
对于格网数据,一般采用直接法计算功率谱密度函数。以式(7)为例,首先通过FFT将航空重力数据转换至频率域,再采用式(10)计算功率谱密度函数:
| $ {P_{12}} = \frac{1}{{{T_x}}}\frac{1}{{{T_{\rm{z}}}}}\left\{ {{F_2}\left\{ {\delta {g_x}(R + H)} \right\}{F_2}\left\{ {\delta {g_z}(R + H)} \right\}} \right\} $ | (10) |
式中,Tx、Tz分别为输入数据在x、z方向的长度。
在频域输入输出法中,可认为观测数据的噪声是已知的,如以航空重力观测值为输入,则噪声的标准差为交叉点平差之后观测值的精度[8]。
2 模拟实验及分析基于2 160阶的EGM2008地球重力场模型得到不同航线高度处的扰动重力矢量水平分量和垂向分量模拟观测值,因篇幅所限,仅以水平分量中的东向分量为例进行分析。空中数据点范围为经度[107°, 110°]、纬度[30°, 33°],格网间隔为2.5′×2.5′,为减小边界效应的影响,地面计算点的范围为经度[107.5°, 109.5°]、纬度[30.5°, 32.5]°。表 1给出了航线高度(正高)分别为2 km、3 km、4 km、5 km时模拟数据的相关统计信息。依据文献[9]的研究结果,向下延拓的积分半径选为1°。延拓过程采用移去-恢复技术:延拓前,先从观测值中移去根据2~120阶EGM2008计算的航线高度处的参考值,从而得到残余重力观测值,然后将残余重力观测值向下延拓至大地水准面,再恢复2~120阶EGM2008计算得到的大地水准面上的参考值。以大地水准面上2 160阶EGM2008计算得到的东向分量作为真值,并以其与大地水准面上延拓值的差值的RMS来评价向下延拓的数学模型和计算方法。
|
|
表 1 模拟观测值统计 Tab. 1 Statistics of simulated gravity observations |
为了验证东向分量的向下延拓效果,设计2种延拓方案:1)在模拟生成的重力矢量东向分量和垂向分量中均加入数学期望为0、标准差为1.5 mGal的高斯白噪声;2)在东向分量和垂向分量中加入数学期望为0、标准差分别为1.5 mGal和6 mGal的高斯白噪声,采用式(3)和式(7)分别将2种噪声水平的东向分量向下延拓到大地水准面上。
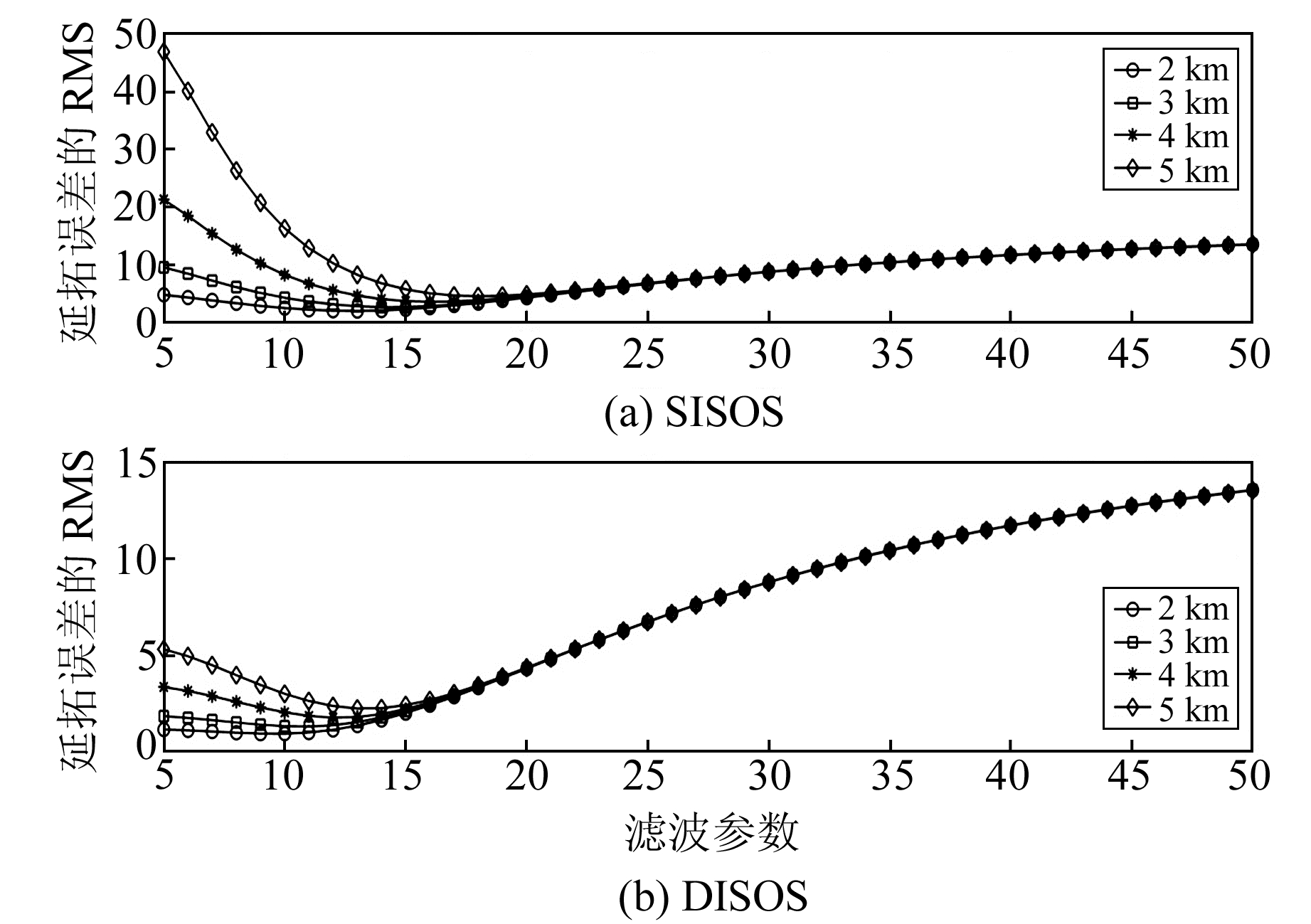
方案1的延拓结果见表 2和图 3。可以看出,东向分量的延拓结果与滤波参数的选取有关。当地面存在检校数据时,可将延拓值与检校数据比较,当二者差值的RMS最小时可确定最优滤波参数;当地面检校数据较少甚至没有时,最优滤波参数可采用L曲线法、广义交叉检验GCV等方法确定。本文为模拟实验,大地水准面上的检校数据可采用重力场模型计算得到,因此采用前者来确定最优滤波参数。分别选择最优滤波参数时,SISOS延拓误差的均方根由2.048(H=2 km)增加为4.608(H=5 km),而DISOS延拓误差的均方根由0.919(H=2 km)增加为2.222(H=5 km)。以上延拓结果也表明,当东向分量的精度与垂直分量相当时,2种输入输出法都能实现东向分量的稳定向下延拓;当延拓高度相同时,DISOS的向下延拓效果更为可靠。
|
图 3 方案1中东向分量的向下延拓误差与滤波参数的关系 Fig. 3 Relation between continued errors of east component and filter parameter in scheme 1 |
|
|
表 2 方案1的向下延拓误差统计 Tab. 2 Statistics of continued errors in scheme 1 |
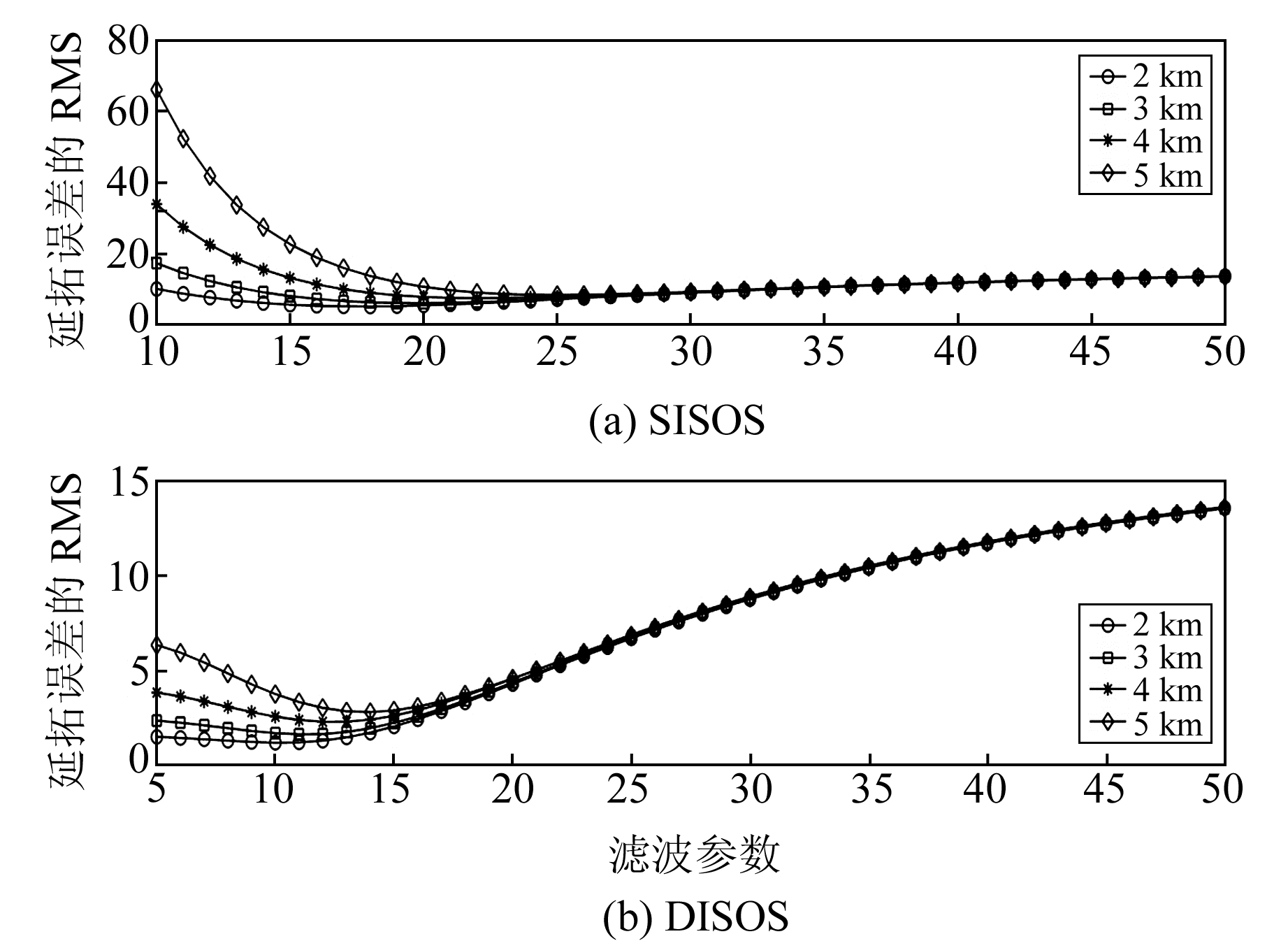
表 3和图 4(a)表明,航线高度上东向分量中白噪声的标准差为6 mGal时,采用SISOS向下延拓,延拓误差的RMS与观测数据中噪声的标准差相当。这表明SISOS能在一定程度上抑制噪声的放大,即使航线高度为5 km时,延拓过程对噪声的放大倍数仅为(8.334-6)/6=0.389。但由于航线高度上东向分量的信噪比相对较低,因此延拓解出现严重扭曲而失真,这说明SISOS不具备低信噪比情况下的稳定向下延拓能力。表 3与图 4(b)给出了航线高度上东向分量中白噪声的标准差为6 mGal时DISOS的延拓结果。可以看出,DISOS能实现低信噪比情况水平分量的稳定向下延拓,且随着航线高度的增加,延拓误差的RMS增大幅度较为平缓。当H=5 km时,延拓误差的RMS最大,约为2.82 mGal。与SISOS相比,DISOS大幅提高了延拓精度,这是因为DISOS以高精度的垂直分量为辅助,通过频域数据融合压制了东向分量中的高频噪声,改善了低信噪比情况下东向分量的延拓结果。
|
图 4 方案2中滤波参数与东向分量向下延拓误差的关系 Fig. 4 Relation between continued errors of east component and filter parameter in scheme 2 |
|
|
表 3 方案2东向分量的向下延拓误差统计 Tab. 3 Statistics of continued errors of east component in scheme 2 |
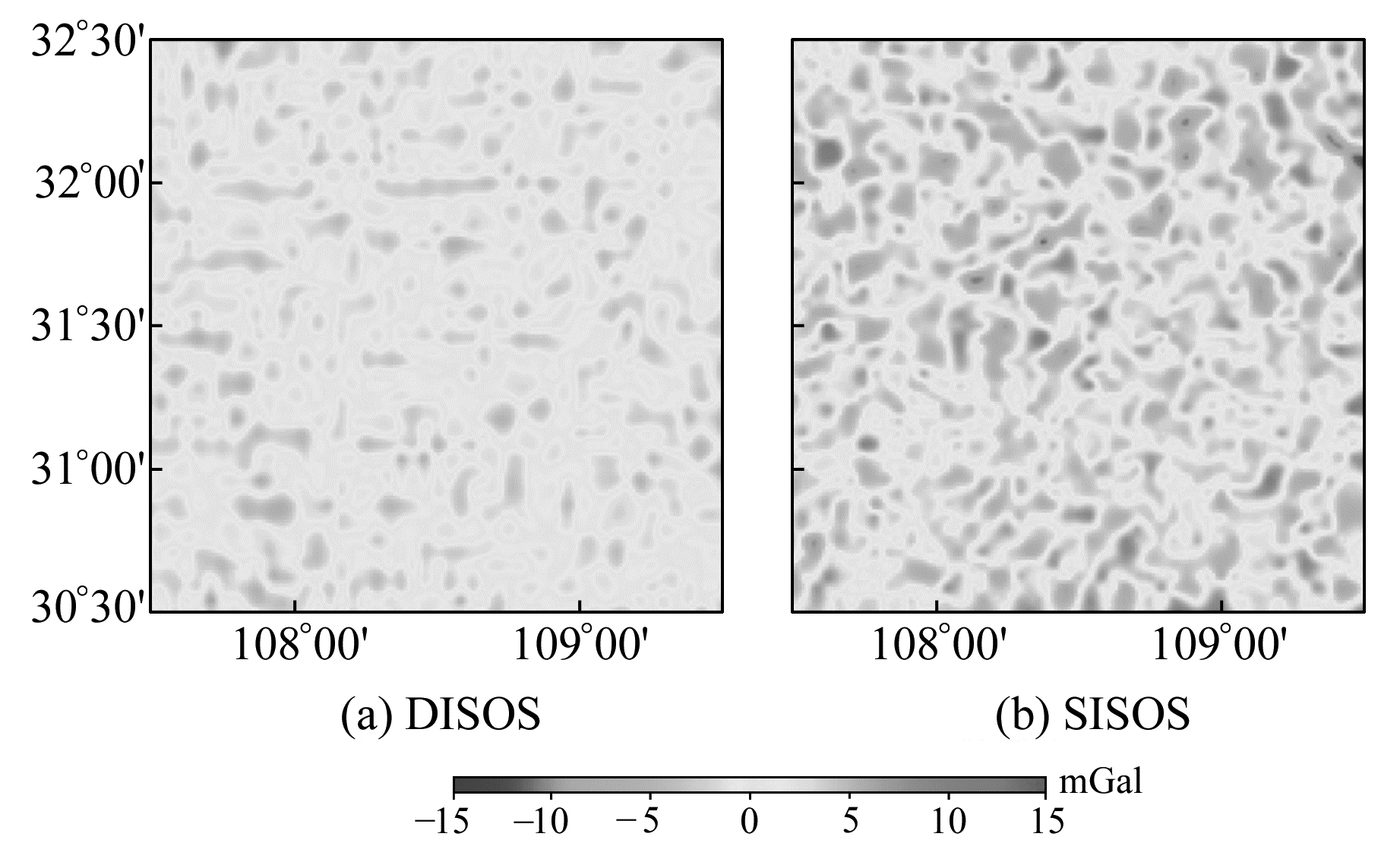
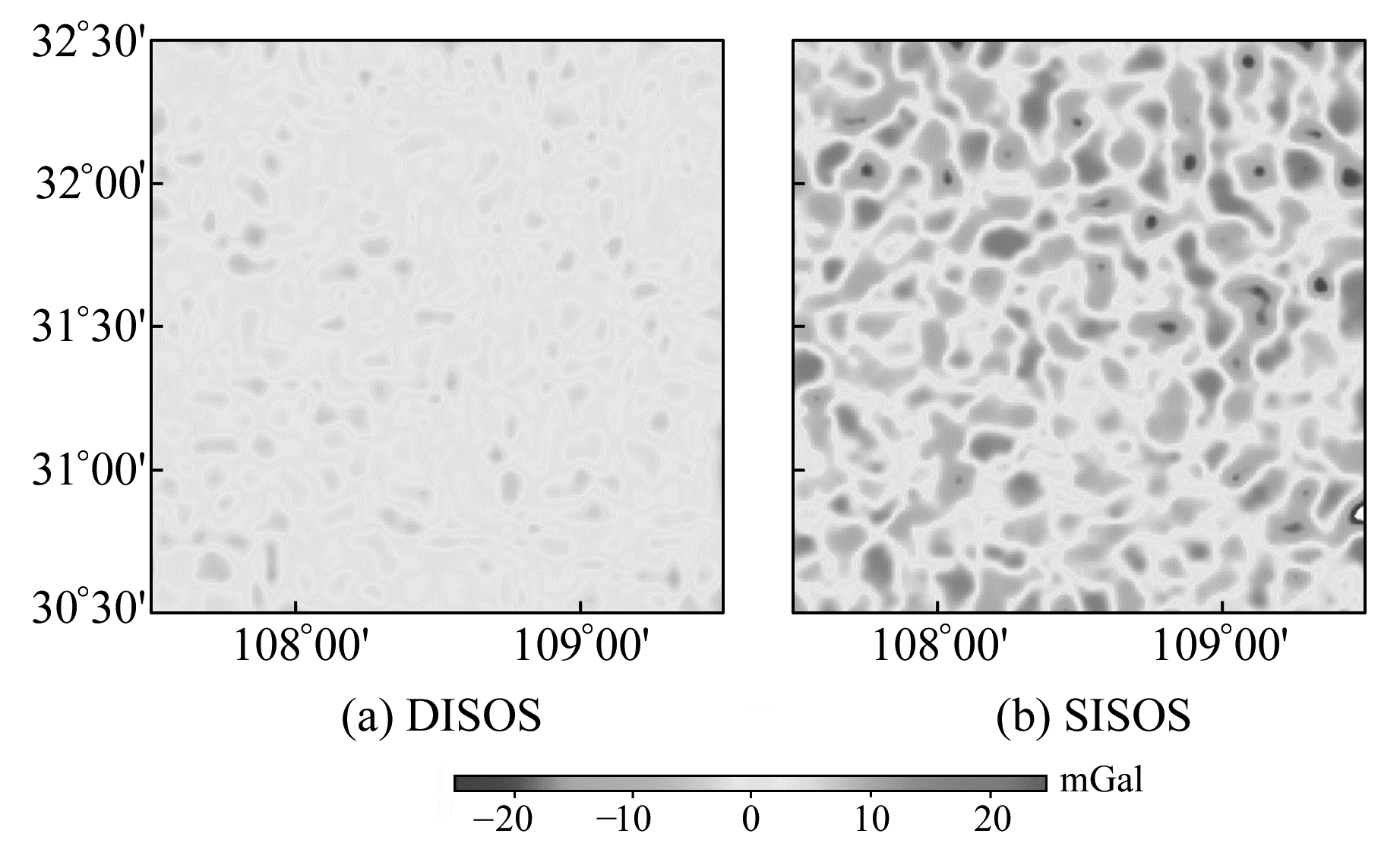
图 5和6分别给出了延拓高度为4 km,东向分量中噪声的标准差分别为1.5 mGal和6 mGal时,采用SISOS和DISOS后延拓误差的空间分布。不难发现,SISOS延拓误差的极值点较多,延拓效果较差;相比之下,DISOS的延拓误差均在±10 mGal以内,且几乎没有误差极值点,延拓结果稳定可靠。综合以上实验结果说明,DISOS可以有效地抑制高频噪声,实现东向分量的稳定向下延拓,优于SISOS,且当东向分量信噪比较低时优势更为明显。
|
图 5 方案1中延拓误差的空间分布 Fig. 5 Distribution of continued errors in scheme 1 |
|
图 6 方案2中延拓误差的空间分布 Fig. 6 Distribution of continued errors in scheme 2 |
本文以重力矢量东向分量为例,采用输入输出系统,基于模拟数据研究了航空矢量重力水平分量的向下延拓。结果表明,当重力矢量水平分量与垂直分量的精度一致时,SISOS和DISOS均能实现水平分量的稳定向下延拓;当东向分量的信噪比较低时,SISOS的延拓结果较差,而DISOS能大幅提高东向分量的向下延拓精度。北向水平分量的向下延拓与东向分量类似,因篇幅限制并未列出其结果。
本文仅考虑了观测值含有白噪声的情况,后续工作将进一步研究有色噪声情况下水平分量的向下延拓。
| [1] |
Kwon J H. Airborne Vector Gravimetry Using GPS/INS[D]. Ohio: Ohio State University, 2000
(  0) 0) |
| [2] |
Sideris M G. On the Use of Heterogeneous Noise Data in Spectral Gravity Field Modeling Methods[J]. Journal of Geodesy, 1996, 70(8): 470-479 DOI:10.1007/BF00863619
(  0) 0) |
| [3] |
Wu L M. Spectral Methods for Post Processing of Airborne Vector Gravity Data[D]. Calgary : University of Calgary, 1996
(  0) 0) |
| [4] |
Tziavos I N, Sideris M G, Forsberg R. Combined Satellite Altimetry and Shipborne Gravimetry Data Processing[J]. Marine Geodesy, 1998, 21(4): 299-317 DOI:10.1080/01490419809388144
(  0) 0) |
| [5] |
宁津生, 李金文, 晁定波. 各向异性局部重力场计算的谱方法[J]. 武汉测绘科技大学学报, 1998, 23(3): 227-229 (Ning Jinsheng, Li Jinwen, Chao Dingbo. The Spectral Methods for Computation of Non-Isotropic Local Gravity Field[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1998, 23(3): 227-229 DOI:10.3321/j.issn:1671-8860.1998.03.010)
(  0) 0) |
| [6] |
崔立鲁. 频域输入输出法及其在大地水准面精化中的应用研究[D]. 武汉: 武汉大学, 2008( (Cui Lilu. Frequency Domain Input and Output System Theory and Its Application in the Precise Determination of Geoid[D]. Wuhan: Wuhan University, 2008))
(  0) 0) |
| [7] |
周波阳, 罗志才, 许闯, 等. 航空重力数据向下延拓的FFT快速算法[J]. 大地测量与地球动力学, 2013, 33(1): 64-68 (Zhou Boyang, Luo Zhicai, Xu Chuang, et al. Comparison among Fast Fourier Transform Algorithms for Downward Continuation of Airborne Gravity Data[J]. Journal of Geodesy and Geodynamics, 2013, 33(1): 64-68)
(  0) 0) |
| [8] |
Hwang C, Hsiao Y S, Shih H C, et al. Geodetic and Geophysical Results from a Taiwan Airborne Gravity Survey: Data Reduction and Accuracy Assessment[J]. Journal of Geophysical Research: Solid Earth, 2007, 112(B4)
(  0) 0) |
| [9] |
欧阳永忠, 邓凯亮, 黄谟涛, 等. 重力异常延拓计算积分半径的选取及远区效应[J]. 海洋测绘, 2011, 31(4): 5-7 (Ouyang Yongzhong, Deng Kailiang, Huang Motao, et al. The Choice of Integral Radius and It's Far-Zone Effects in the Continuation of the Gravity Anomaly[J]. Hydrographic Surveying and Charting, 2011, 31(4): 5-7 DOI:10.3969/j.issn.1671-3044.2011.04.002)
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38

