2. 中科院测量与地球物理研究所,武汉市徐东大街340号,430071;
3. 中国人民解放军95957部队,广州市,510610;
4. 天津城建大学地质与测绘学院,天津市津静路26号,300384
地表观测到的重力异常场是地下不同深度层地质源异常的叠加,从总异常场中分离出单个地质源在观测面上的位场信息十分困难,但却是重力反演及解释工作中一项非常重要的任务[1-2]。为了定性区分地下不同深度及尺度的地质源在观测面上产生的位场信息,通常用区域场(regional)表示那些埋藏相对较深、尺度较大的地质源产生的位场,用剩余场(residual)表示局部的近地表质量在观测面上产生的位场[3]。区域场和剩余场的分离方法主要可概括为4类:1)图形类平滑法,该方法出现较早,计算速度慢且无法实现自动处理,区域场信息的提取主要依赖于研究人员的经验来完成,具有很强的主观性;2)频谱类方法[4-5],通过在频率域中区分区域场与剩余场占据的不同波段来进行位场分离,计算速度快,相对于图形类方法大大降低了解算过程的主观性,然而当区域场与剩余场信号频域发生重叠时,分离不完全;3)多项式拟合方法[6-7],该方法的前提是假设多项式曲面能够对区域场信号进行充分有效的拟合,区域场的平滑程度可以根据多项式的阶次来进行控制,利用低阶多项式模拟平滑,但区域位场不规则时,容易出现拟合的区域场信号发生扭曲的现象;4)剥离类方法(stripping method)[8-9],通过详尽的地质构造信息反演地质源模型,进而构建局部场或区域场信号,然后从总位场中减去建模得到的信号完成最终的位场分离。该方法几乎不会扭曲提取的异常场形状,也不受区域场和剩余场频谱重叠的影响,但实际观测中,缺乏研究区域充分的地质构造信息往往限制了该类方法的使用。此外,位场分离的方法还有很多,如位场延拓滤波法、最小曲率法、Kriging法、熵参数法、梯度测深法和Morlet变换法、插值切割法、优选滤波法和三维主成分分析法等[10-14]。
本文在多项式拟合算法的基础上,改进多项式拟合观测数据求取区域场的解算过程,通过加权迭代并引入深度分离思想[12]进行川滇地区重力数据的位场分离实验,并与基于插值切割位场分离算法的结果和川滇地区地质构造图进行对比分析。
1 方法原理 1.1 区域场异常的确定位场分离算法的基本思想是先求得区域场异常,然后根据总异常场与区域场的差值解算得到剩余异常场,即
| $ \begin{array}{l} {G_{^{{\rm{measure}}}}}\left( {{x_i}, {y_j}} \right) = {G_{^{{\rm{region}}}}}\left( {{x_i}, {y_j}} \right) + {G_{^{{\rm{residual}}}}}\left( {{x_i}, {y_j}} \right)\\ = f\left( {{G_{^{\rm{measure}}}}\left( {{x_i}, {y_j}} \right)} \right) + {G_{^{{\rm{residual}}}}}\left( {{x_i}, {y_j}} \right) \end{array} $ | (1) |
式中,Gmeasure和Gregion、Gresidual分别为重力总异常场、区域场异常和剩余场异常,i=1, 2, …, N, j=1, 2, …, M, N、M为研究区域x方向和y方向上的数据个数,f(Gmeasure(xi, yj))为对重力总异常场观测值进行某种函数操作(如频谱滤波、多项式拟合、小波变换、主成分分析等),可获得相应深度的区域场异常。
本文基于多项式拟合算法来解算研究范围的区域场异常,选择双线性鞍状函数(bilinear saddle function)作为多项式拟合函数[10],即
| $ P\left( {{x_i}, {y_j}} \right) = a + b{x_i} + c{y_j} + d{x_i}{y_j} $ | (2) |
式中,a、b、c、d为拟合系数,P(xi, yj)为根据坐标(xi, yj)拟合得到的值。
1.2 地质源深度的确定确定异常场信号与其对应的地质源深度主要有2种手段。在频谱分析理论中,基于统计假设可以得到异常信号功率谱与地质源平均深度之间的关系[15]:
| $ \left\langle {E\left( k \right)} \right\rangle = 4\pi {M^2}\left\langle {{{\rm{e}}^{-2hk}}} \right\rangle \left\langle {1-{{\rm{e}}^{-tk}}} \right\rangle \left\langle {{S^2}\left( k \right)} \right\rangle $ | (3) |
式中,〈〉表示总体平均,M为电磁矩/单位体积,h为地质源顶部的深度,t为地质源的厚度,k为径向圆频率,S(k)为地质源水平尺寸因子。
研究发现,地质源信号功率谱的大小主要由深度因子〈e-2hk〉控制,而伸展因子〈1-e-tk〉及水平因子〈S2(k)〉对功率谱的影响相对较小,特别是在低频波段。因此,功率谱可以简化为:
| $ E\left( r \right) \approx A{{\rm{e}}^{-2\bar hk}} $ | (4) |
对数形式为:
| $ \ln \left( {E\left( r \right)} \right) \approx - 2\bar hk + {\rm{ }}A' = - 4\pi \bar hk' + A' $ | (5) |
式中,A和A′为常系数,h为地质源的平均深度,k′为空间波数。
实际计算中,在以径向波数为横轴、功率谱的对数为纵轴的关系图中,对功率谱进行分段线性拟合,则某段频谱范围最佳拟合直线的斜率就表示地质源相应的平均深度[13, 15]。在后面的模型实验中解算了组合模型总重力异常场的径向平均功率谱对数与径向频率的关系(文中未列),发现采用谱分析方法分段拟合的地质源平均深度是相对固定的,因此本文拟采用另一种更为灵活的确定分离位场对应地下地质源深度的方法。
徐世浙等[12]根据大量模型实验和实际资料的应用效果统计分析认为,切割半径r得到的区域位场可近似代表深度r以上的地层产生的重力场。本文将该思想进行扩展,基于滑动窗口对观测总位场进行分区操作,利用低阶二维多项式对滑动窗口内的观测点数据进行拟合,拟合值的加权迭代值作为当前滑动窗口内中心点的区域场值,整个研究区域内的解算结果代表深度为滑动窗口尺寸大小的地层在地表观测面产生的重力区域场,进而剩余位场就是观测重力位场与计算区域位场的差值。基于不同尺寸的滑动窗口解算得到的位场的差值,就表示特定深度地层在观测面上产生的位场值。
为了区分滑动窗口内不同的观测点值对解算的区域场的贡献大小,对二维多项式拟合后的各计算点值进行加权处理。在滑动窗口内,中心点位于窗口的中心,窗口内除中心点外,其他点称为外围点,外围点到中心点的“点距”定义为S(x轴方向点距记为dx,y轴方向点距记为dy,
| $ \begin{array}{l} \omega \left( {{x_i}, {y_j}} \right) = {k_1}{r^{{k_2}-1}}\mathit{\Delta} \frac{1}{S} = \\ {k_1}{r^{{k_{^2}}-1}}\mathit{\Delta} \frac{1}{{\sqrt {{d_x}^2 + {d_y}^2} }} \end{array} $ | (6) |
式中,dx、dy分别为x轴方向和y轴方向观测点距离中心点的距离,Δ为观测数据的数据间隔,k1、k2为经验参数,用来控制滑动窗口内中心点与各外围点的权重分配,根据实验结果,这里选择k1=k2∈(0.075, 0.125)。
中心点拟合值的权函数为:
| $ \omega \left( {{x_c}, {y_c}} \right) = 1-\sum\limits_{i \ne c, j \ne c}^{{N_w}} {\omega \left( {{x_i}, {y_j}} \right)} $ | (7) |
式中,(xc, yc)为滑动窗口内的中心点坐标。
结合式(6)、(7)发现,这样定权的优势在于随着窗口尺寸的增大,滑动窗内中心点之外的点权重分配的比例会增加,在一定程度上有助于获取更大尺寸及埋深的地质源在观测面上的区域场。
该窗口内位于中心点坐标上的区域值为:
| $ \begin{array}{l} {G_{{\rm{Region}}}}^{\left( {\rm{1}} \right)}\left( {{x_c}, {y_c}} \right) = \\ {\rm{sum}}\left( {{G^{{\rm{fit}}}}\left( {{x_i}, {y_j}} \right) \cdot \omega \left( {{x_i}, {y_j}} \right)} \right) \end{array} $ | (8) |
式中,sum表示对窗口内的计算值进行求和,上标(1)表示第1次解算出的区域场值。对解算到的区域场进行迭代操作,直至满足终止条件:
| $ \mathop {\lim }\limits_{k \to N} \frac{{\partial {\rm{median}}\left( {G_{{\mathop{\rm Re}\nolimits} {\rm{gion}}}^{\left( k \right)}} \right)}}{{\partial k}} \le \varepsilon $ | (9) |
式中,median表示中位数算子,
为了检验算法的应用效果,在100 km×100 km×50 km(长×宽×深)的空间范围内设计一组理论棱柱模型,其中浅层模型由5个形状不同的棱柱模型组成,对应产生的重力场作为局部场或剩余场;深层模型由一个尺寸较大的棱柱体构成,对应产生的重力场作为区域场,总重力位场包含剩余场和区域场数据。模型组合相对位置见图 1,相关参数见表 1,模型组在观测面产生的重力场数据见图 2。
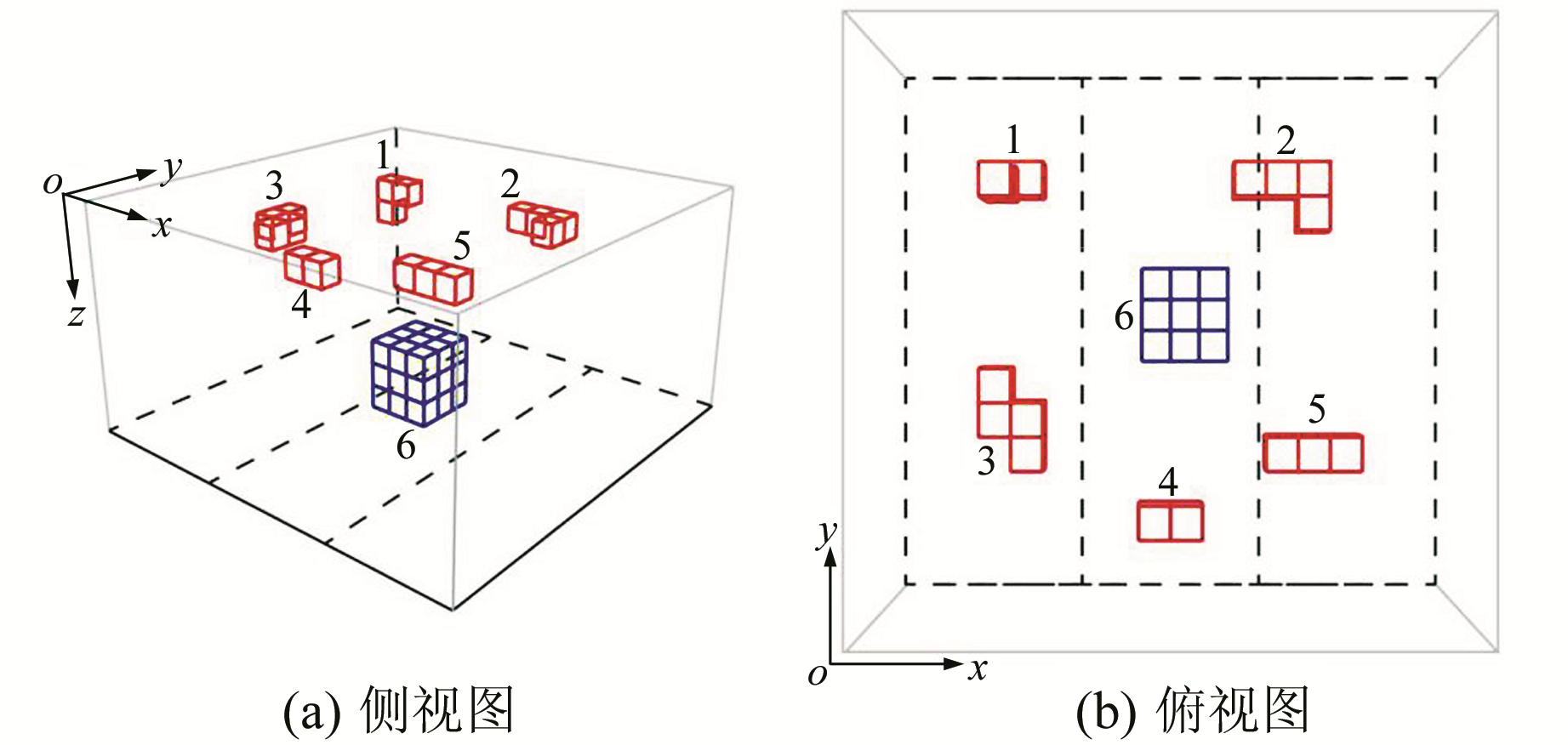
|
图 1 组合模型示意图 Fig. 1 Sketch maps of synthetic models |
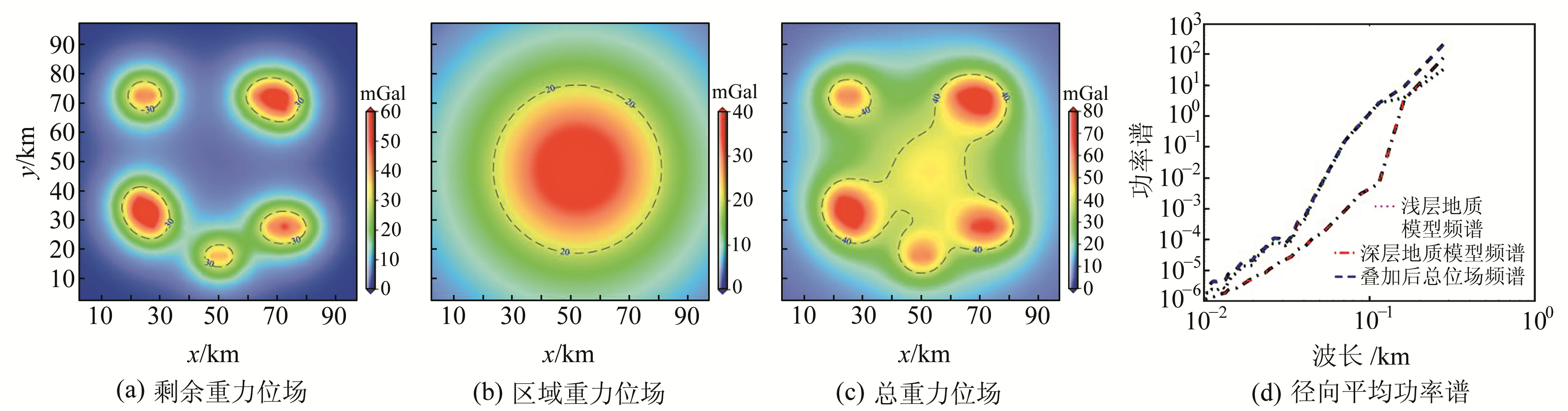
|
图 2 模型组合产生的重力位场及径向平均功率谱 Fig. 2 Gravity field of synthetic models and radially averaged power spectrum of the field |
|
|
表 1 产生区域重力场与剩余重力场的模型组合参数 Tab. 1 Parameters of synthetic models which generating regional field and residual field |
图 2(a)是浅层地质组合模型在地表观测面上的重力异常信息,图 2(b)是深层地质模型在地表观测面上的重力异常信息,图 2(c)是叠加后的总重力位场效应。可以看出,叠加后的重力位场已经难以直观地区分出深层地质模型的位场信号,地表观测到的位场信息主要由浅层位场控制,这也符合大多数实际情况。图 2(d)是各层位场及总重力位场的径向平均功率谱。可以看出,大于0.15 km波长(低频)的是深部模型代表的区域场占优,而小于0.15 km波长(中高频)的是浅部模型代表的局部异常场占优,但在实际位场数据中,大多数情况下并没有明显的截断频率用来区分不同深度的异常频谱。
利用低阶二维多项式拟合和加权迭代算法,对不同深度模型叠加后的位场进行垂向分离,分离深度依据滑动窗口尺寸来定义,选择的窗口尺寸大小以2.5 km为间隔,范围为17.5 ~27.5 km以及45 km,代表各次的分离深度,分离后的区域位场和剩余位场结果见图 3。可以看出,在分离区间范围内(17.5~27.5 km),分离深度越浅,对深部模型所反映的重力位场影响越小,分离得到的区域场异常越明显;反之,分离深度越深,即分离深度靠近深部地质源埋深时,分离得到的区域场异常信号减弱,造成部分区域场信号叠加到浅部地质源模型所反映的剩余场异常中。当切割深度与模型组合下边界深度重合时(图 3(i)和3(l)的分离深度为45 km,而深部模型的设计埋深是30~45 km),已经无法分离出相应深部地质源(深部模型代表的区域场异常)在观测面上的重力异常,只能得到剩余异常与区域异常混合的结果,类似于总重力异常位场,这也说明选择的滑动窗尺寸作为位场分离深度的合理性。因此,本文方法是通过先分离出深部地质源代表的区域场异常,然后再得到浅部地质源在观测面的剩余重力异常。
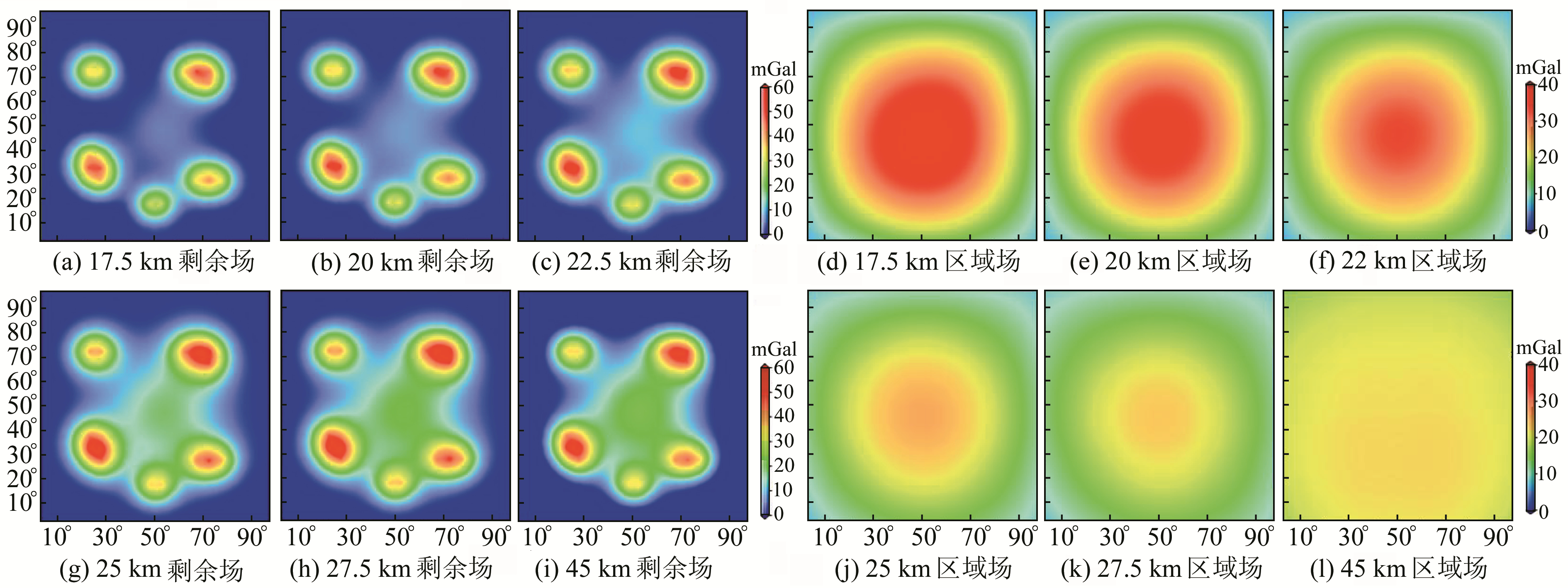
|
图 3 分离得到的各深度层区域场异常和剩余场异常 Fig. 3 Regional field and residual field at different depth |
基于二维多项式拟合及加权迭代算法,对川滇地区实测重力异常数据进行位场分离,探索并分析该区域中地壳地质构造特征。该实测重力异常数据依托于中国地震局中国综合地球物理场项目和中国大陆构造环境监测网络2014年的流动重力测量任务,观测时采用2台CG-5型相对重力仪(仪器测量精度优于10 μGal)进行联测作业,作业流程严格遵守重力测量规范;同时以观测网中的部分基准点重力绝对值作为控制点,对测区所有观测点进行整体经典平差,得到统一起算基准下的重力变化,平差后的重力点值平均精度优于15 μGal。
图 4(a)为研究区域的地形图,地形高程自西向东呈下降趋势,高值区位于研究区域的西北角,低值区位于研究区域的东北角,红色实线表示该研究区域内的断裂带分布。图 4(b)为研究区域的重力异常场分布图(图中黑色圆点为测点位置)。可以看到,区域内异常分布自西向东呈增大趋势,其中重力异常低值区位于研究区西北角(对应地形高程高值区),而异常高值区则位于研究区域东北角(对应地形高程低值区),整个区域内重力异常变化范围为0~1 100 mGal。
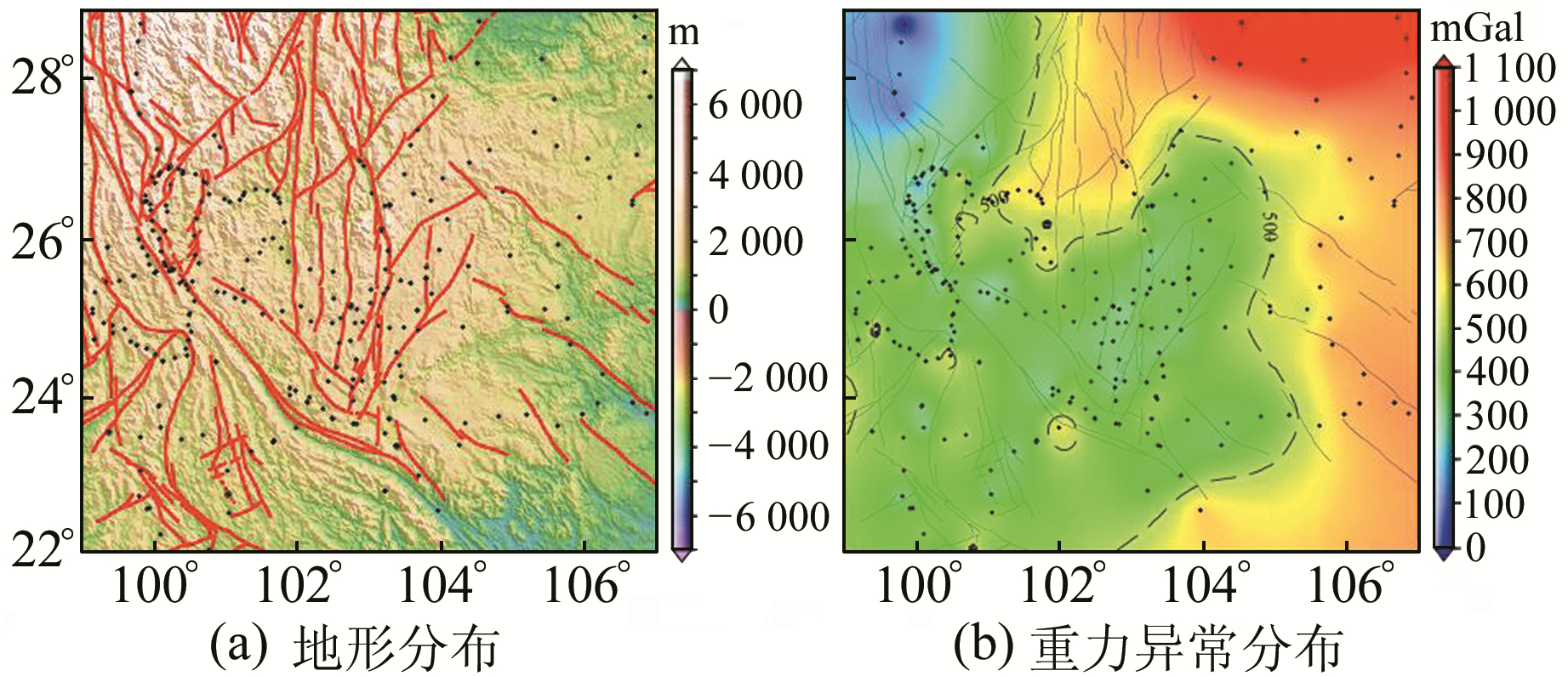
|
图 4 川滇研究区域的地形和重力异常分布 Fig. 4 DEM and gravity anomaly of Sichuan-Yunnan region |
以0.1°(约11.10 km)为分离深度区间,基于多项式拟合-加权迭代算法和插值切割算法对研究区分别进行11.10 km、22.20 km、33.30 km和44.40 km共4个深度层的区域位场和剩余位场分离操作,2种算法结果见图 5和6。对比图 5和图 6发现,2种算法在各深度层都获得了较为一致的剩余场异常和区域场异常分布。但当分离深度变大时,对比图 5(f)和6(f)、图 5(h)和6(h)可以看到,基于插值切割算法得到的位场分离区域场结果出现了类似“噪声”的扰动信号(图 6(f)和6(h)中等值线下端呈锯齿状),这会在一定程度上影响对解算得到的剩余场信号的解释和判断(图 6(e)和6(g)也出现了与经向和纬向相平行的扰动信号);而本文提出的方法得到的区域场结果则更为平缓和圆滑(图 5(f)和5(h)),这也符合对区域场异常特征的定性和直观认识。
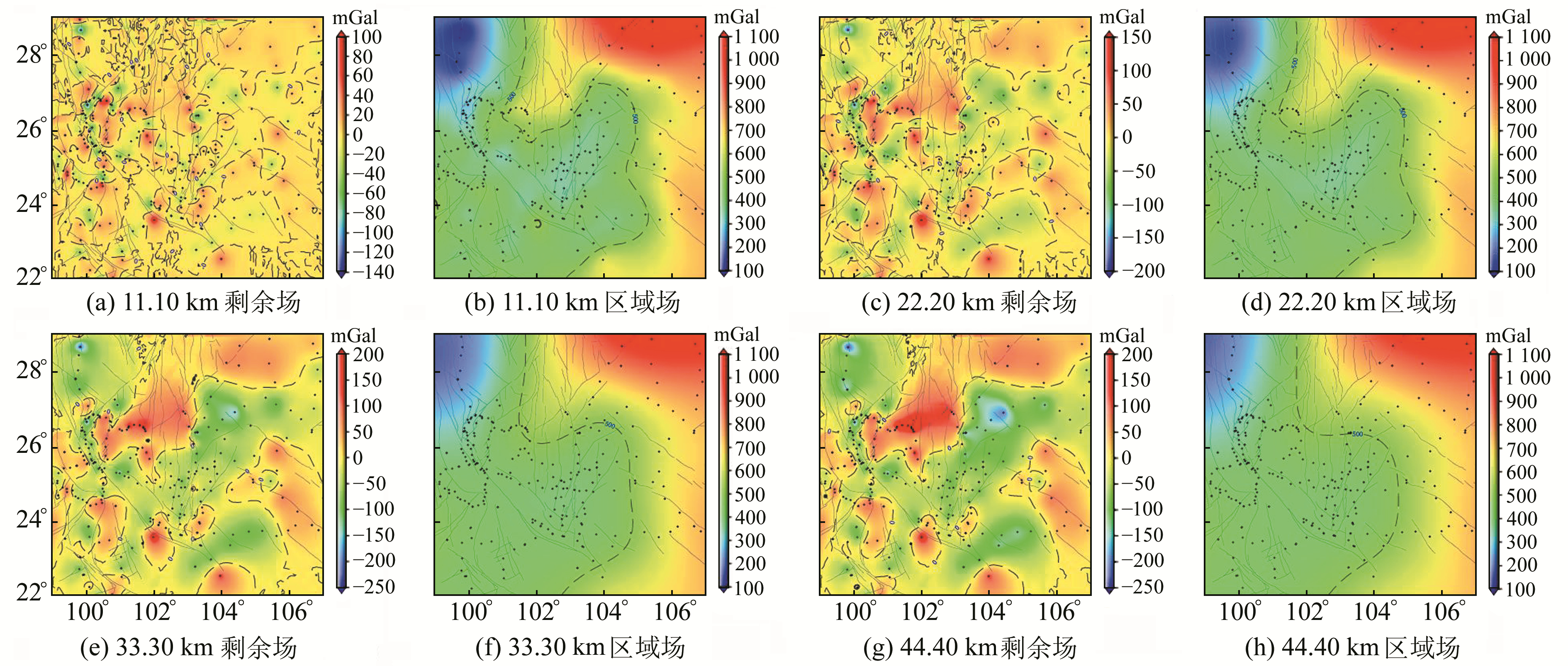
|
图 5 基于二维低阶多项式拟合-加权迭代法得到的川滇重力位场分离结果 Fig. 5 Gravity field separation results of Sichuan-Yunnan derived from 2D low-order polynomial fitting and weighting iterative algorithm |
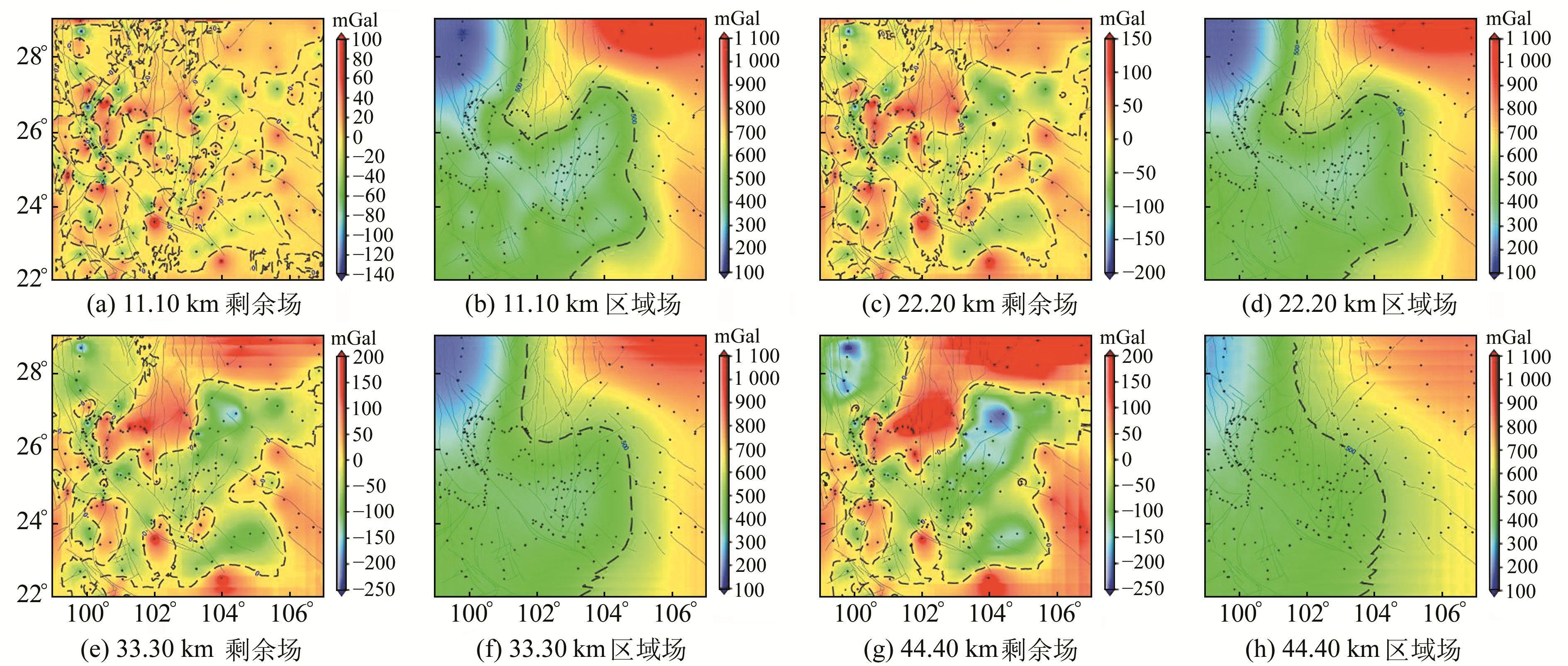
|
图 6 基于插值切割法得到的川滇重力位场分离结果 Fig. 6 Gravity field separation results of Sichuan-Yunnan derived from interpolation-cutting algorithm |
为进一步分析本文提出算法的位场分离结果的合理性,将分离得到的中地壳深度剩余场异常分布(22.20 km,对应图 5(c))与滇西地区地质构造图及中地壳密度扰动平面图[16]的结果进行对比,见图 7(图 7(a)的黑色实线对应图 7(c)中的几条主要边界断裂)。图 7(c)为滇西区域地质构造略图[16], 该区域位于中国扬子克拉通和印度克拉通之间,大地构造上属于中新生代古特提斯洋和特提斯洋封闭形成的大陆碰撞带,包含印支和缅马地块有密切亲缘关系的多个小地块[16]。对比图 7(a)和7(c)发现,本文分离得到的区域中部剩余场正异常(红色,即图 7(a)中标注数字“1”的区域附近)可能与滇西区域构造图中的前震旦纪克拉通及华力西构造带盖层沉积具有一定的位置对应关系;区域下部(即图 7(a)中标注数字“2”的区域附近,沿L断裂带)对应图 7(c)中的花岗岩类构造,但由于该区域测点分布较为稀疏,异常特征没有表现出明显的条带状分布;区域中R断裂的东南段(即图 7(a)中标注数字“3”的区域附近)可能对应该区域印支构造带超镁铁岩类地质构造分布特征。同时,在区域的上部由于没有足够的测点分布,分离得到的位场也无法有效地反映出该区域的地质构造信息。对比图 7(a)和7(b)发现,分离得到的滇西中地壳深度范围(22.20 km)剩余场异常分布与杨文采等[16]的中地壳密度扰动平面图(24.16 km)在典型地质构造分布上具有较为一致的特征。

|
图 7 分离得到的滇西中地壳深度剩余场异常与地质构造图及密度扰动分布的比较 Fig. 7 Residual anomalies of west Yunnan with median crustal depth, the density disturbance and simplified tectonic map |
本文利用基于双线性鞍状函数(bilinear saddle function)的2D多项式拟合及加权迭代算法对重力异常数据进行不同深度层源的位场分离。川滇地区实测重力异常数据的解算证明了本文提出的算法可以有效地给出研究区域内不同深度的位场分离结果。同时,为了验证算法给出结果的可靠性,解算了基于插值切割算法的相同范围的位场分离结果。通过对比发现,2种算法得到的各分离深度区域场及剩余场异常均具有相似的分布特征。此外,通过比较滇西地区中地壳已有的密度扰动反演结果和本文分离得到的中地壳深度剩余场异常以及该区域的地质构造图,发现本文算法得到的结果与杨文采等[16]得到的密度扰动平面图在滇西地区测点分布较为密集的地区具有较为一致的分布特征。另外,参考该区域的地质构造图可以看到,分离得到的剩余场异常与特定的地质结构具有高度的对应关系,从而验证了本文算法的有效性。
在利用多项式拟合算法进行位场分离时,假设的前提条件是多项式曲面能够对区域场信号进行充分有效的拟合。在某些复杂地质构造区,当剩余场异常与区域场异常在深度上强相关时,无论是常规的还是改进的多项式拟合算法都会在不同程度上扭曲区域场异常的形状,导致获得的目标地质源所反映的剩余场异常分布不够准确。解决上述问题并联合其他算法获得更为可靠、一致性好的位场分离结果,有利于地质结构精细反演和解释等方面的研究探索。
| [1] |
Boschetti F, Therond V, Hornby P. Feature Removal and Isolation in Potential Field Data[J]. Geophysical Journal International, 2004, 159(3): 833-841 DOI:10.1111/gji.2004.159.issue-3
(  0) 0) |
| [2] |
Nabighian M N, Ander M E, Grauch V J S, et al. Historical Development of the Gravity Method in Exploration[J]. Geophysics, 2005, 70(6): 63-89 DOI:10.1190/1.2133785
(  0) 0) |
| [3] |
Griffin W R. Residual Gravity in Theory and Practice[J]. Geophysics, 1949, 14(1): 39-56 DOI:10.1190/1.1437506
(  0) 0) |
| [4] |
Fedi M, Quarta T. Wavelet Analysis for the Regional-Residual and Local Separation of Potential Field Anomalies[J]. Geophysical Prospecting, 1998, 46(5): 507-525 DOI:10.1046/j.1365-2478.1998.00105.x
(  0) 0) |
| [5] |
Ulrych T J. Effect of Wavelength Filtering on the Shape of the Residual Anomaly[J]. Geophysics, 1968, 33(6): 1015-1018 DOI:10.1190/1.1439979
(  0) 0) |
| [6] |
Beltrao J F, Silva J B C, Costa J C. Robust Polynomial Fitting Method for Regional Gravity Estimation[J]. Geophysics, 1991, 56(1): 80-89 DOI:10.1190/1.1442960
(  0) 0) |
| [7] |
Ojo S B, Kangkolo R. Shortcomings in the Determination of Regional Fields by Polynomial Fitting: A Simple Solution[J]. Journal of Applied Geophysics, 1997, 36(4): 205-212 DOI:10.1016/S0926-9851(96)00043-2
(  0) 0) |
| [8] |
Mads J M, Henrik O, Carsten P, et al. Gravity Field Separation and Mapping of Buried Quaternary Valleys in Lolland Denmark Using Old Geophysical Data[J]. Journal of Geodynamics, 2007, 43(2): 330-337 DOI:10.1016/j.jog.2006.09.021
(  0) 0) |
| [9] |
Li Y, Oldenburg D W. Separation of Regional and Residual Magnetic Field Data[J]. Geophysics, 1998, 63(2): 431-439 DOI:10.1190/1.1444343
(  0) 0) |
| [10] |
Al-Zoubi A, Eppelbaum L, Abueladas A, et al. Removing Regional Trends in Microgravity in Complex Environments: Testing on 3D Model and Field Investigations in the Eastern Dead Sea Coast (Jordan)[J]. International Journal of Geophysics, 2013
(  0) 0) |
| [11] |
Martínez-Moreno F J, Galindo-Zaldívar J, Pedrera A, et al. Regional and Residual Anomaly Separation in Microgravity Maps for Cave Detection: The Case Study of Gruta de las Maravillas (SW Spain)[J]. Journal of Applied Geophysics, 2015, 114: 1-11 DOI:10.1016/j.jappgeo.2015.01.001
(  0) 0) |
| [12] |
徐世浙, 余海龙, 李海侠, 等. 基于位场分离与延拓的视密度反演[J]. 地球物理学报, 2009, 52(6): 1592-1598 (Xu Shizhe, Yu Hailong, Li Haixia, et al. The Inversion of Apparent Density Based on the Separation and Continuation of Potential Field[J]. Chinese J Geophys, 2009, 52(6): 1592-1598 DOI:10.3969/j.issn.0001-5733.2009.06.021)
(  0) 0) |
| [13] |
Guo L H, Meng X H, Chen Z X, et al. Preferential Filtering for Gravity Anomaly Separation[J]. Computers & Geosciences, 2013, 51: 247-254
(  0) 0) |
| [14] |
Zhang L L, Hao T Y, Jiang W W. Separation of Potential Field Data Using 3-D Principal Component Analysis and Textural Analysis[J]. Geophysical Journal International, 2009, 179(3): 1397-1413 DOI:10.1111/gji.2009.179.issue-3
(  0) 0) |
| [15] |
Xu Y, Hao T Y, Li Z W, et al. Regional Gravity Anomaly Separation Using Wavelet Transform and Spectrum Analysis[J]. Journal of Geophysics and Engineering, 2009, 6(3): 279-287 DOI:10.1088/1742-2132/6/3/007
(  0) 0) |
| [16] |
杨文采, 侯遵泽, 于常青. 滇西地壳三维密度结构及其大地构造含义[J]. 地球物理学报, 2015, 58(11): 3902-3916 (Yang Wencai, Hou Zunze, Yu Changqing. 3D Crustal Density Structure of West Yunnan and Its Tectonic Implications[J]. Chinese J Geophys, 2015, 58(11): 3902-3916)
(  0) 0) |
2. Institute of Geodesy and Geophysics, CAS, 340 Xudong Street, Wuhan 430077, China;
3. 95957 Troops of PLA, Guangzhou 510610, China;
4. School of Geology and Geomatics, Tianjin Chengjian University, 26 Jinjing Road, Tianjin 300384, China
 2018, Vol. 38
2018, Vol. 38

