2015-04-25尼泊尔首都加德满都西北方向约80 km(廓尔喀县)处发生强烈地震,矩震级为MW7.9,震源深度约15 km[1],05-12在主震东南地区发生7级以上余震[2]。此次地震发生在主喜马拉雅推挤(main Himalayan thrust,MHT)断裂上,受到印度板块与欧亚板块陆-陆挤压碰撞,该地区曾多次发生大地震[2]。本次地震导致主喜马拉雅推挤断裂破裂,形成一个沿走向150 km、倾向50 km的破裂区域[3]。
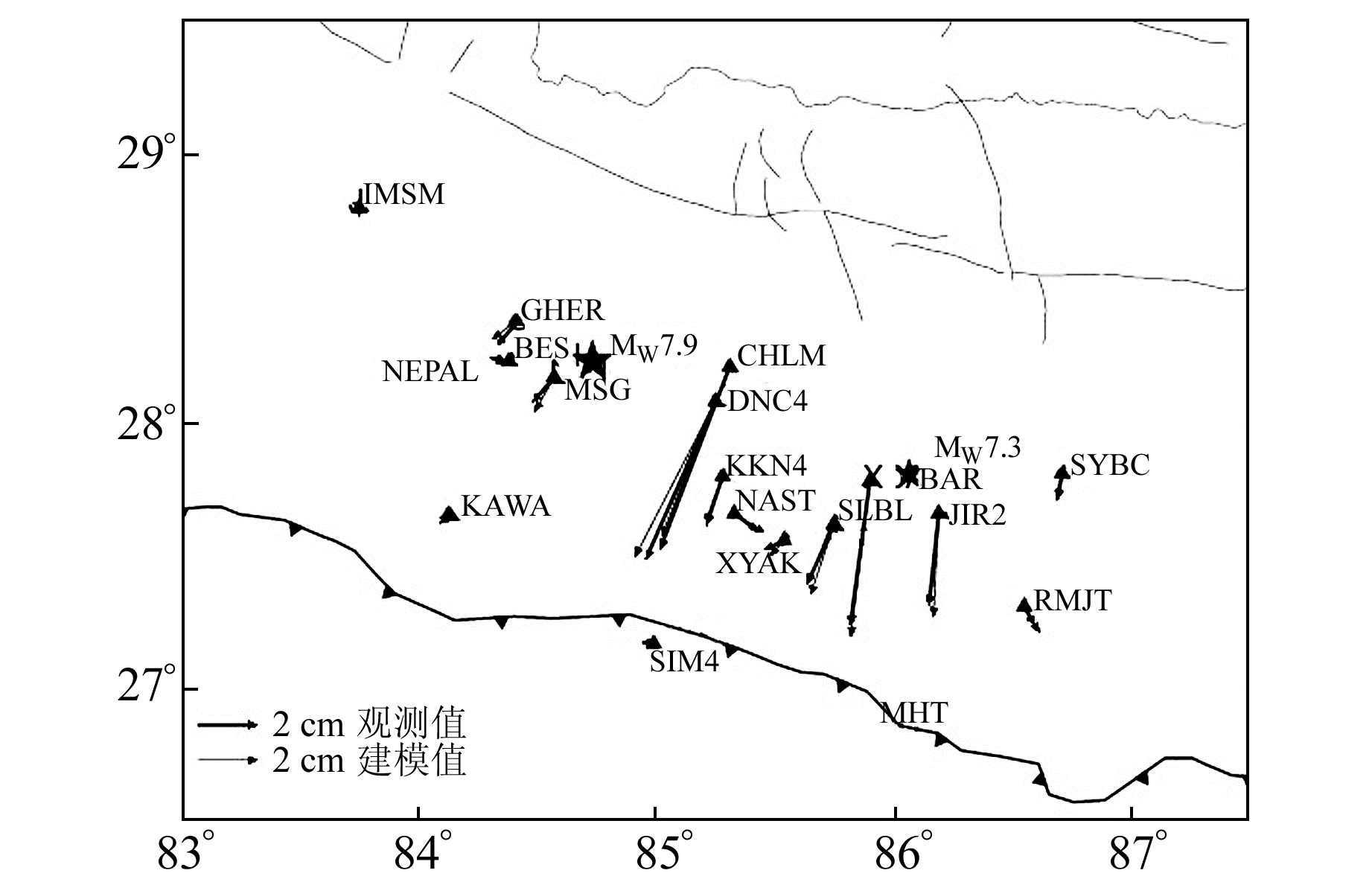
现代大地测量技术,尤其是GPS和InSAR,为尼泊尔地区地震的发生机理、地震灾害评估提供了可靠依据[4-5]。布设在尼泊尔地区的GPS连续运行参考站(图 1, 细向量为建模值,粗向量为观测值,五角星分别为主震(MW7.9)与最大余震(MW7.3)震中位置)记录了此次地震震后阶段高时空分辨率的形变信息,为震后形变研究提供了有效的观测约束。大地测量及地质调查的研究表明,该地震是一次以逆冲为主,兼具少量右旋走滑运动的低倾角事件,且破裂未露出地表[1, 6]。GPS观测数据表明,地震引起了大范围同震和震后形变,较明显的同震滑动主要分布在10~15 km深处,由于浅层孕震区仍未破裂,加德满都地区仍面临着较大的地震风险[7]。
|
图 1 尼泊尔廓尔喀地震震后位移场 Fig. 1 Postseismic deformation field of the 2015 MW7.9 Gorkha earthquake |
大的构造地震通常伴随着明显的震后变形,在时间上可持续几十a,在空间上可延伸到几千km。对于尼泊尔地震震后效应的研究,目前主要集中在早期的余滑,也有少量学者利用大地测量约束(GPS和InSAR)研究了震后余滑。Sreejith等[5]利用早期GPS和InSAR观测的震后位移(4~88 d)发现,早期震后地面抬升和下沉与同震方向相反。Gualandi等[3]利用震后7个月余滑,得出震后位移变化服从对数衰减模式。本文基于Okada位错理论[8],通过加权最小二乘滤波提取GPS震后位移时间序列,采用主成分反演方法[9](PCAIM)研究此次地震震后断层滑动时空变化特性[9]。
1 数据来源在这次地震之前,加利福尼亚地震研究所、尼泊尔矿业和地质部、尼泊尔科学技术学院、中央华盛顿大学、加德满都大学等[3]不同机构在震中附近布设了大量的GPS连续运行参考站,获得了大量的地壳形变观测资料。所有GPS参考站数据可以从UNAVCO网站(http://www.unavco.org/)下载。本文使用美国内华达州大学大地测量实验室发布的GPS位移时间序列产品(http://geodesy.unr.edu/),具体解算策略参考网站中解算策略文件(http://geodesy.unr.edu/gps/ngl.acn.txt)。选用距离震中500 km以内、时间范围为2010-01-01~2016-10-08的16个GPS参考站位移时间序列进行分析(表 1)。
|
|
表 1 震后位移场 Tab. 1 Postseismic deformation field |
GPS位移时间序列主要包括3个部分的信号源:反映构造运动的地壳形变信号,如震前、同震、震后变形;地表圈层引起的季节性变化(如陆地水储量变化);由仪器或天线变更引起的阶跃。为了得到地震引起的变形信号,采用加权最小二乘拟合的方法估计位移时间序列各部分信号:
| $\begin{array}{l} y({t_i}) = {y_0} + v{t_i} + A\sin (2\pi {t_i}) + B\cos (2\pi {t_i}) + C\sin (4\pi {t_i}) + D\cos (4\pi {t_i})\\ {\rm{ }}\sum\limits_{j = 1}^k {{O_j}H({t_i} - t{o_j})} + \sum\limits_{j = 1}^m {H({t_j} - t{q_j})} ({c_j} + {p_j}\ln (1 + \frac{{{t_i} - t{q_j}}}{{\tau _j^{\log }}}) + {\varepsilon _i} \end{array}$ | (1) |
式中,ti为历元数,v为线性趋势项,反映长期构造运动,A、B、C、D分别为正余弦函数振幅,O为由不同原因导致的点位突变(如由仪器或天线变更引起的位移或由某些未知的原因引起的点位变化等[10-11]),c、p、τlog分别为同震阶跃项、震后对数振幅、对数松弛时间,k、m分别为非震和地震引起的阶跃的个数,εi为误差项。提取震后形变的步骤如下:
1) 去除粗差,修补阶跃项。分别将E、N、U方向中误差超过20 mm、20 mm、40 mm的数据去除,将拟合残差大于4倍均方根误差作为粗差予以剔除,改正由于仪器设备更换和地震引起的阶跃。
2) 速度场内插。对于震后安装或震前数据较少的GPS站点,可根据研究区域震间速度场数据改正这些测站的长期构造运动。根据尼泊尔地区的震间形变信息,采用VISR (velocity interpolation for strain rate)算法[12]内插这些站点的震间速度场。
3) 确定震后弛豫时间。在去除时间序列的线性趋势项和季节性信号后,选取断层附近观测时间较长的站点,采用对数函数拟合的方法,通过加权均方根误差和最小搜索得到此次地震松弛时间为70 d。
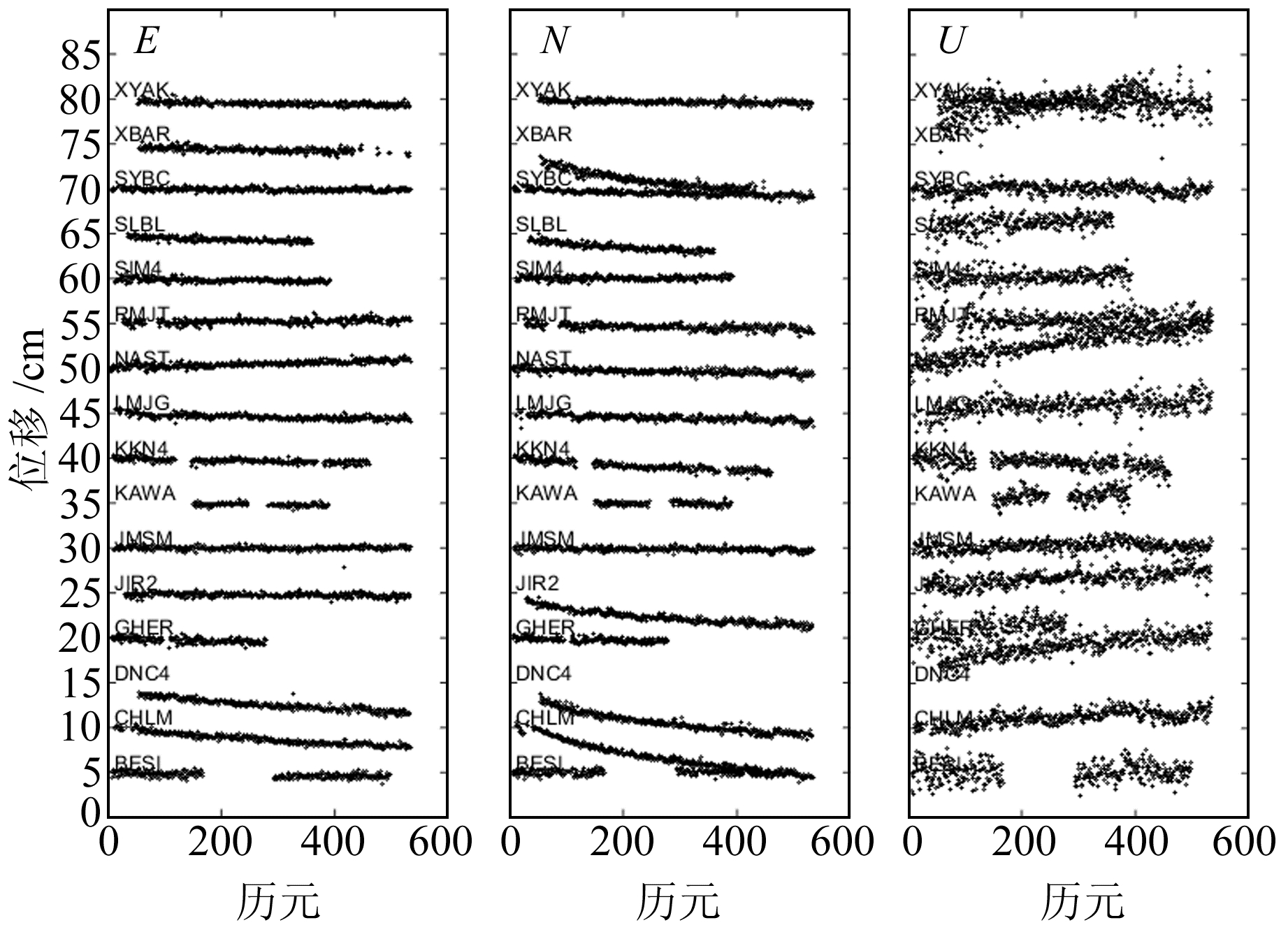
1.2 震后形变场通过加权最小二乘方法及速度场内插的方法得到所有站点的季节性信号、线性趋势项以及由多种原因引起的点位突变的估计值。将站点位移时间序列扣除这些预测值,得到高信噪比的震后形变数据。图 2为16个近场震后时间序列。可以看出,东西方向形变较小,南北方向形变较大,且整体继续向南运动。观测的震后总位移如表 1所示,最大震后地表水平位移发生在CHLM和DNC4两个站,分别达到6.49 cm、5.75 cm,方向西南。最大余震附近的XBAR站朝南西方向的震后位移也达到4.82 cm。
|
图 2 去除长期趋势项、季节项及点位突变项的震后位移时间序列 Fig. 2 Post-seismic coordinate time series with linear trend, co-seismic offset and seasonal variations removed |
本文使用加州理工学院开发的主成分反演程序PCAIM[9]分析断层表面震后余滑的时空分布特征。该方法采用均匀弹性半空间位错模型反演断层滑动分布,将近场位移信号通过主成分方法(PCA)分解为n个主分量,然后利用主成分的空间分量线性反演断层滑动,该方法无需任何先验信息(滑移速度、最大滑移量和滑移特征等)。PCAIM震后滑动反演主要包含PCA分解,确定主成分数量,使用空间特征向量进行线性反演和线性重构滑动分布。
2.1 PCA分解 2.1.1 基本理论假设一个GPS区域网有m个基准站,进行了n天观测,则位移时间序列可写成3m×n的时间序列矩阵X3m×n(每一个基准站有N、E、U 3个方向)。为了保证每个时间序列为零均值,按式(2)对矩阵进行中心化。利用奇异值分解的方法将位移时间序列分解成相互正交的空间特征向量和相对应的时间函数[9], 见式(3)。
| $ \boldsymbol{X}(i, j) = {\boldsymbol{X}_0}(i, j)-\frac{{\sum\limits_{k = 1}^m {{\boldsymbol{X}_0}(i, k)} }}{m} $ | (2) |
| $ {\boldsymbol{X}_{3m \times n}} = {\boldsymbol{U}_{3m \times 3m}}{\boldsymbol{S}_{3m \times n}}{\boldsymbol{V}_{n \times n}} $ | (3) |
式中,与基准站有关的第i个空间特征向量与时间相关的第i个时间函数分量可分别表示为Ui和Vi。
PCA分解得到的高阶主分量通常表示的是整网不相关噪声和小范围站点的局部形变。因此,PCA分解采用低阶主分量重新构造时间序列,从而达到空间滤波的目的[9],提高数据的信噪比。假设原始数据矩阵X,选择前r个主分量重构时间序列,则有:
| $ \boldsymbol{X} \approx {\boldsymbol{X}_r} = {\boldsymbol{U}_r}{\boldsymbol{S}_r}\boldsymbol{V}_r^t $ | (4) |
式中,Ur、Vr分别是U、V的前r列,Sr为S的r×r子矩阵。
为了确定主成分个数,采用前n个主成分的累积贡献率确定主成分个数。假设第i个主成分的特征值为λi,则前n个主成分的累积贡献率P可由式(5)计算得到:
| $ P = \sum\limits_{i = 1}^{3m} {{\lambda _i}} /\sum\limits_{i = 1}^n {{\lambda _i}} $ | (5) |
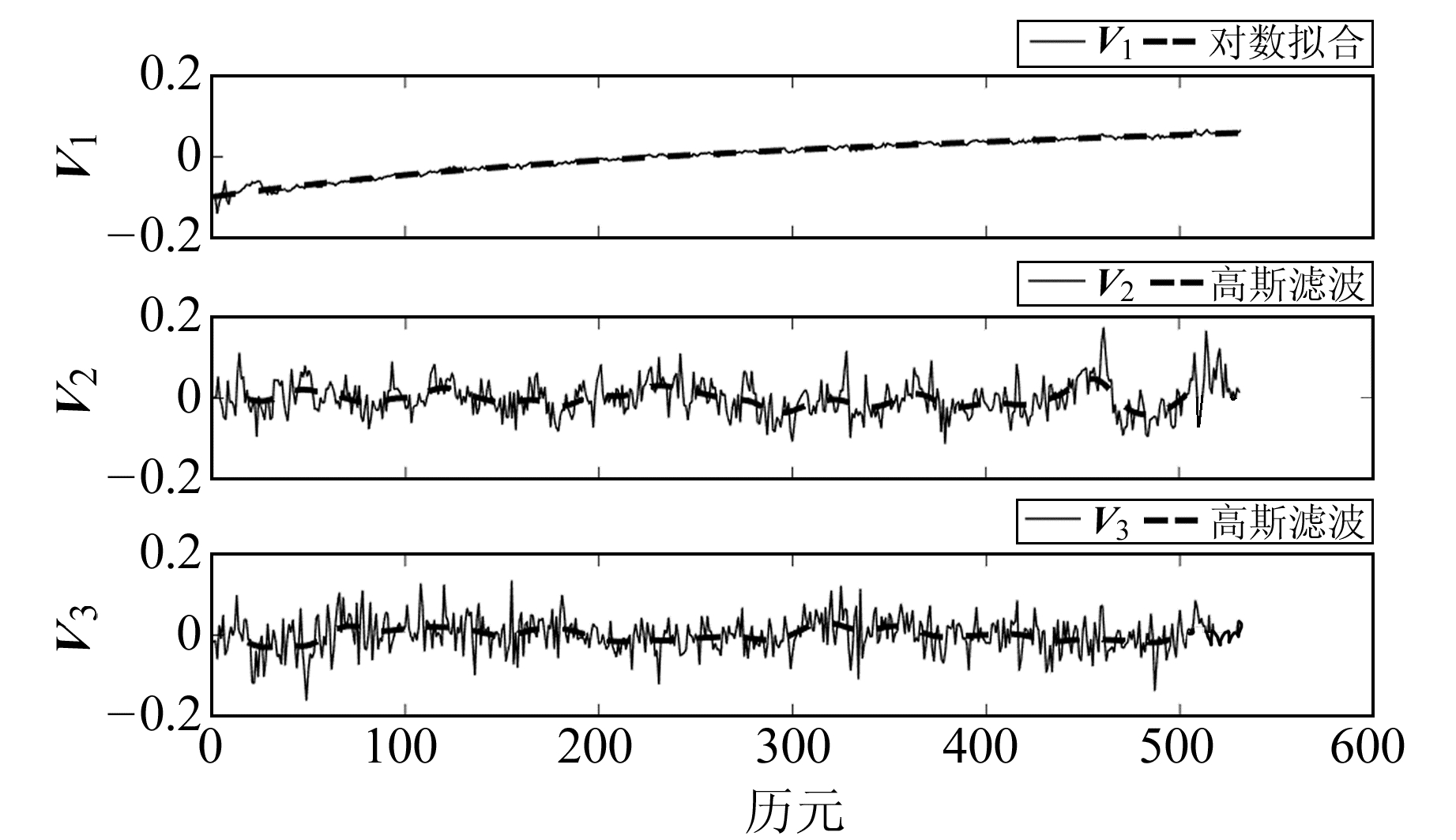
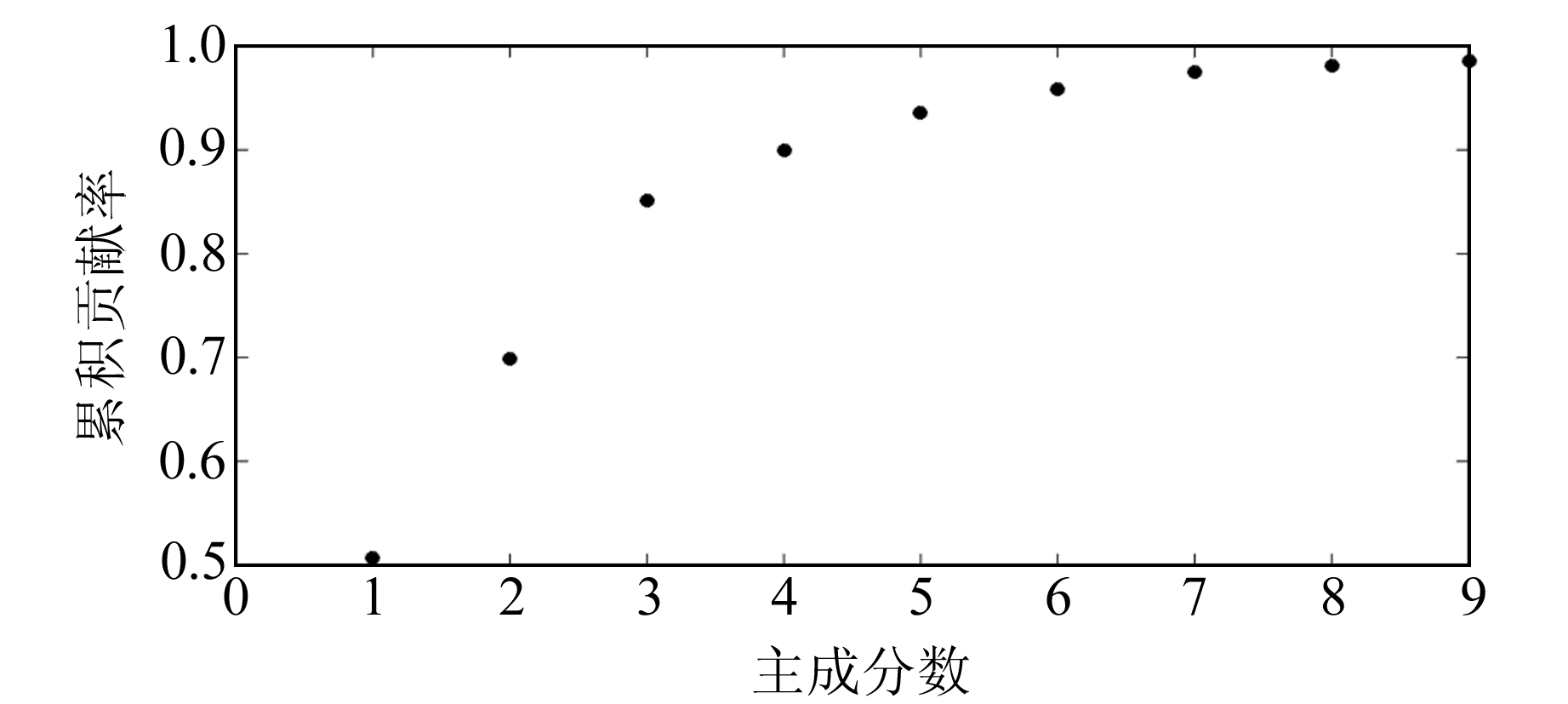
选用近场16个GPS站点的数据进行主成分分解,前3个主成分的时间函数如图 3所示(黑色实线表示滤波前数据,V1中黑色曲线表示对数拟合数据,V2、V3黑色曲线表示高斯平滑滤波后数据)。第一主成分V1在震后早期主要受到2015-05-12 MW7.3余震的影响,产生明显的波动,但整体呈现对数衰减模式,反映了震后余滑的整体运动趋势[13],第二、三主成分黑色曲线采用高斯平滑滤波方法[14-15]。前9个主成分的累积贡献率如图 4所示。可以看出,前3个主成分累积贡献率约为85%,反映了整个研究区域的变形信息。因此,只选用前3个主成分进行震后断层滑动反演。
|
图 3 时间特征向量V1、V2、V3 Fig. 3 Emporal eigenvectors V1, V2 and V3 |
|
图 4 前9个主成分的累积贡献率 Fig. 4 Cumulative contribution rate of the first nine principal components |
本文选用前3个主成分,使用PCAIM方法研究震区断层滑动分布。根据已有的研究成果及断层几何参数[1, 16-17],构建单一的断层几何模型。考虑到滑动的不均匀性,将断层表面离散成25×20=500个子断层,每个子断层空间尺度为20 km×14 km。主要对每个子断层走向和倾向滑动反演,得到最终的空间滑动分布,6个断层参数如表 2所示。
|
|
表 2 断层参数 Tab. 2 Parameters of fault geometry |
通过震后位移时间序列分析发现,震后位移有明显的向南运动趋势,与MHT(喜马拉雅推挤断裂带)区域余滑方向完全吻合。利用PCAIM方法,结合PCA分解得到的空间特征向量和对应的时间函数,通过静态反演的方法得到断层滑动随时间的演变。反演过程中,采用变化滑动角(0~360°),平滑因子γ=1 000,假设地壳为均匀介质,刚性模量为30 GPa,泊松比为0.25。格林函数采用Okada位错模型[8]计算,式(6)是利用每个空间特征向量Ui线性反演得到每个空间分量的断层滑移Li,整个滑移时空分布为Slipcum,可用式(7)计算得到。为了得到更加合理的结果,利用拉普拉斯平滑(式(8))对震后余滑进行约束[9]。
| $ {\boldsymbol{U}_i} = {\boldsymbol{G}_\alpha }{\boldsymbol{L}_i} $ | (6) |
| $ {\rm{Sli}}{{\rm{p}}_{{\rm{cum}}}} = \sum\limits_{i = 1}^r {{\boldsymbol{L}_i}{\boldsymbol{S}_i}\boldsymbol{V}_i^{\rm{T}}} $ | (7) |
| $ \begin{array}{l} \boldsymbol{F} = {\sum\limits_{k = 1}^{3m} {([{\boldsymbol{G}_\alpha }\;\;{\boldsymbol{L}_i}](k) -{\boldsymbol{U}_i}(k))} ^2}{\rm{ + }}\\ \;\;\;\;\;\;\;\;\;\;\frac{1}{{{\gamma ^2}}}||\Delta {\boldsymbol{L}_i}|{|^2} \end{array} $ | (8) |
式中,Ui为第i个主成分的空间特征向量,Gα为断层为α的位错格林函数,Li为第i个主滑动量(行表示子断层在走向和倾向上的滑动量,列表示历元数),γ对断层面空间滑动进行平滑约束,Δ为拉普拉斯算子,Δ=(∂2/∂x2)+(∂2/∂y2),m为子断层个数,S和V分别为特征值和时间函数。
3 断层滑动反演结果根据GPS震后位移时间序列和确定的几何断层模型,利用PCAIM反演方法得到的断层滑动分布及地表震后形变场如图 1所示。东西、南北和垂直(E、N、U)方向的平均偏差分别为4 mm、8 mm、11 mm。最大震后地表位移发生在主震震中东方向约100 km处的CHLM和DNC4两个站,分别达到6.37 cm、5.80 cm,方向西南。最大余震附近的XBAR站朝西南方向的震后位移也达到4.80 cm。观测值与模拟值相关系数达98%。
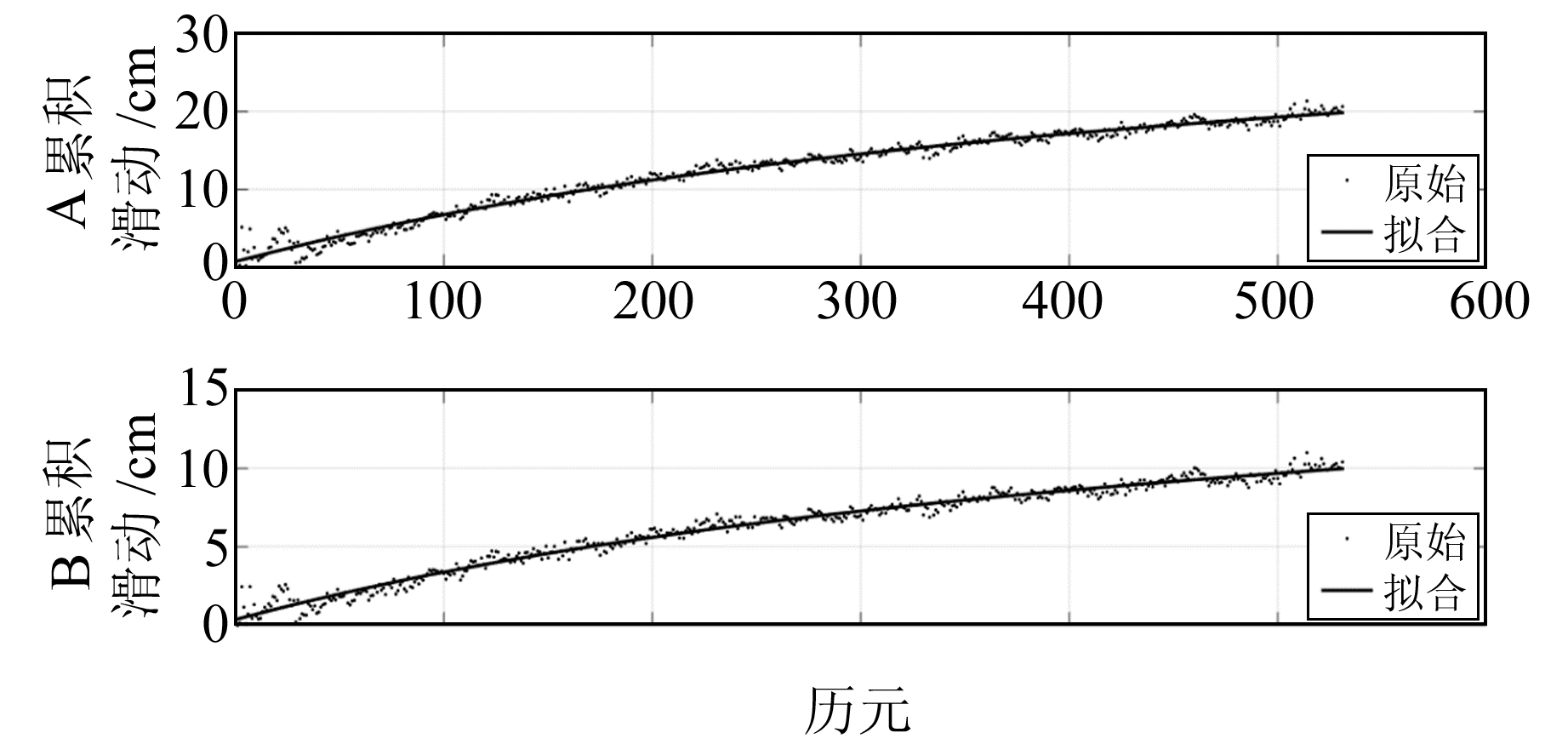
Jiang等[18]通过GPS数据得到的同震断层滑动以及本文所得余滑滑动结果如图 5(a)、5(b)所示。可以看出,同震断层滑动最大值为5.7 m,深度约为12 km, 滑动主要分布在10~20 km深处。余滑主要位于主震破裂面的北部区域,滑动值超过5 cm,浅层区域滑动量相对较小。断层滑动存在2个滑动峰值区域(区域A、B),滑动最大值分别为20.6 cm、10.4 cm,深度分别为26.7 km、7.3 km。余滑滑动相比于同震滑动具有滑动范围更广、主要滑动区域较深的特点。通过图 6可以得出2个峰值区域滑动随时间变化服从对数衰减模式,且在2015-05-12 MW7.3余震发生时刻出现较明显的波动。

|
图 5 同震和断层滑动分布[18] Fig. 5 Coseismic slip model and distribution of the fault slip |
|
图 6 峰值区域A(上)、B(下)滑动量随时间的变化(黑线为对数函数拟合曲线) Fig. 6 Peak area A, B slip with time changes |
本文选取剪切模量μ=30 GPa,整个断层面平均滑动量约为4.4 cm,得到余滑释放的地震矩为M0=3.36×1020 N·m,矩震级约为MW7.6。
4 结语本文主要利用GPS位移时间序列,基于Okada弹性半空间位错理论,采用主成分反演方法(PCAIM)研究尼泊尔2015年廊尔喀地震震后断层滑动时空分布。结果表明:
1) 地表最大震后位移位于CHLM和DNC4两个站,分别达到6.37 cm、5.80 cm,方向西南。最大余震附近的XBAR站朝西南方向的震后位移也达到4.80 cm。观测值与模型预测值相关系数达98%。
2) 震后滑动随时间的变化服从对数衰减模式,且在2015-05-12 MW7.3余震历元附近发生较为明显的波动。
3) 余滑主要分布在主震破裂带北部区域,存在2个滑动峰值区域(区域A、B),滑动最大值分别为20.6 cm、10.4 cm,深度分别为26.7 km、7.3 km,平均滑动量为4.4 cm。
4) 反演所得余滑释放的地震矩为3.36×1020 N·m,相应的矩震级约为MW7.6。
| [1] |
赵斌, 杜瑞林, 张锐, 等. GPS测定的尼泊尔MW7.9和MW7.3级地震同震形变场[J]. 科学通报, 2015, 60(28-29): 2758-2764 (Zhao Bin, Du Ruilin, Zhang Rui, et al. Co-Seismic Displacements Associated with the 2015 Nepal MW7.9 Earthquake and MW7.3 Aftershock Constrained by Global Positioning System Measurements[J]. Chinese Science Bulletin, 2015, 60(28-29): 2758-2764)
(  0) 0) |
| [2] |
张贝, 程惠红, 石耀霖. 2015年4月25日尼泊尔MS8.1大地震的同震效应[J]. 地球物理学报, 2015, 58(5): 1794-1803 (Zhang Bei, Cheng Huihong, Shi Yaolin. Calculation of the Co-seismic Effect of MS8.1 Earthquake, Apirl 25, 2015, Nepal[J]. Chinese J Geophys, 2015, 58(5): 1794-1803)
(  0) 0) |
| [3] |
Gualandi A, Avouac J P, Galetzka J, et al. Pre-and Post-Seismic Deformation Related to the 2015, MW7.8 Gorkha Earthquake, Nepal[J]. Tectonophysics, 2016, 670: 714-715
(  0) 0) |
| [4] |
Wang K, Fialko Y. Slip Model of the 2015 MW7.8 Gorkha (Nepal) Earthquake from Inversions of ALOS-2 and GPS Data[J]. Geophysical Research Letters, 2015, 42(18): 7452-7458 DOI:10.1002/2015GL065201
(  0) 0) |
| [5] |
Sreejith K M, Sunil P S, Agrawal R, et al. Coseismic and Early Postseismic Deformation Due to the 25 April 2015, MW7.8 Gorkha, Nepal, Earthquake from InSAR and GPS Measurements[J]. Geophysical Research Letters, 2016, 43(7): 3360-3168 DOI:10.1002/2016GL067926
(  0) 0) |
| [6] |
Feng G C, Li Z W, Shan X J, et al. Geodetic Model of the 2015 April 25 MW7.8 Gorkha Nepal Earthquake and MW7.3 Aftershock Estimated from InSAR and GPS Data[J]. Geophysical Journal International, 2015, 203(2): 896-900 DOI:10.1093/gji/ggv335
(  0) 0) |
| [7] |
Wu Y Q, Jiang Z S, Liang H B, et al. Coseismic Deformations of the 2015 MW7.8 Gorkha Earthquake and Interseismic Strain Accumulation in the Himalayan Tectonic Belt and Tibetan Plateau[J]. Tectonophysics, 2016, 670: 144-154 DOI:10.1016/j.tecto.2015.12.028
(  0) 0) |
| [8] |
Okada Y. Surface Deformation Due to Shear and Tensile Faults in a Half-Space[J]. Bulletin of the Seismological Society of America, 1985, 75(4): 1135-1154
(  0) 0) |
| [9] |
Kositsky A P, Avouac J P. Inverting Geodetic Time Series with a Principal Component Analysis-Based Inversion Method[J]. Journal of Geophysical Research: Solid Earth, 2010, 115(B3)
(  0) 0) |
| [10] |
Yuan L G, Ding X L, Chen W, et al. Characteristics of Daily Position Time Series from the Hong Kong GPS Fiducial Network[J]. Chinese Journal of Geophysics, 2008, 51(5): 976-990 DOI:10.1002/cjg2.v51.5
(  0) 0) |
| [11] |
Dong D, Fang P, Bock Y, et al. Spatiotemporal Filtering Using Principal Component Analysis and Karhunen-Loeve Expansion Approaches for Regional GPS Network Analysis[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B3)
(  0) 0) |
| [12] |
Shen Z K, Wang M, Zeng Y H, et al. Optimal Interpolation of Spatially Discretized Geodetic Data[J]. Bulletin of the Seismological Society of America, 2015, 105(4): 2117-2127 DOI:10.1785/0120140247
(  0) 0) |
| [13] |
方颖, 张晶, 江在森, 等. 用跨断层形变资料分析鲜水河断裂西北段的运动特征[J]. 地球物理学报, 2015, 58(5): 1645-1653 (Fang Ying, Zhang Jing, Jiang Zaisen, et al. Movement Characteristics of the Northwest Segment of the Xianshuihe Fault Zone Derived from Cross-Fault Deformation Data[J]. Chinese J Geophys, 2015, 58(5): 1645-1653)
(  0) 0) |
| [14] |
Gualandi A, Serpelloni E, Belardinelli M E. Space-Time Evolution of Crustal Deformation Related to the MW6.3, 2009 L'Aquila Earthquake (Central Italy) from Principal Component Analysis Inversion of GPS Position Time-Series[J]. Geophysical Journal International, 2014, 197(1): 174-191 DOI:10.1093/gji/ggt522
(  0) 0) |
| [15] |
Perfettini H, Avouac J P, Tavera H, et al. Seismic and Aseismic Slip on the Central Peru Megathrust[J]. Nature, 2010, 465(7 294): 78
(  0) 0) |
| [16] |
Hayes G P, Briggs R W, Barnhart W D, et al. Rapid Characterization of the 2015 MW7.8 Gorkha, Nepal, Earthquake Sequence and Its Seismotectonic Context[J]. Seismological Research Letters, 2015, 86(6): 1557-1567 DOI:10.1785/0220150145
(  0) 0) |
| [17] |
张勇, 许力生, 陈运泰. 2015年尼泊尔MW7.9地震破裂过程:快速反演与初步联合反演[J]. 地球物理学报, 2015, 58(5): 1804-1811 (Zhang Yong, Xu Lisheng, Chen Yuntai. Rupture Precess of the 2015 Nepal MW7.9 Earthquake: Fast Inversion and Preliminary Joint Inversion[J]. Chinese J Geophys, 2015, 58(5): 1804-1811)
(  0) 0) |
| [18] |
Jiang Z S, Yuan L G, Huang D F, et al. Postseismic Deformation Associated with the 2015 MW7.8 Gorkha Earthquake, Nepal: Investigating Ongoing Afterslip and Constraining Crustal Rheology[J]. Journal of Asian Earth Sciences, 2018, 156: 1-10 DOI:10.1016/j.jseaes.2017.12.039
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38


