由于测量技术的局限性和环境因素,测量结果必然存在误差,这种误差有时甚至是不确定的。当利用这种含有不确定性的量构造误差方程时,其系数阵也必然包含不确定性,从而导致最小二乘解不够精确甚至病态[1-3]。研究者针对观测向量和系数阵都含有误差的情况,提出用总体最小二乘法(TLS)解决[4-12]。王乐洋等[4]考虑到系数矩阵可能包含随机误差和固定误差的情形,利用TLS算法将坐标转换的EIV模型推广到Partial-EIV模型。杨娟等[5]针对GPS高程拟合模型中的不确定性,提出稳健的总体最小二乘算法,解决了含有误差的控制点坐标对模型参数求解有影响的问题。考虑到总体最小二乘平差模型将不确定性(误差)同时融入观测矩阵和系数阵,可能导致系数阵过度修正[13],有研究者引入不确定度来限制不确定性[14-15]。目前,应用不确定度理论减小平差模型中不确定性的方法,仍是研究热点。如宋迎春等[14]将不确定度作为参数融入函数模型,利用残差最大不确定度达到最小的平差准则(min-max准则),采用迭代算法解算不确定性平差模型,但对不确定度的选择却没有提出有效的方法。本文针对不确定性平差模型(ULS)中关键的不确定度选择问题,提出用类L曲线法处理,并将其应用于位错理论,对位错参数进行反演。为了体现算法的有效性,同时运用最小二乘(LS)和总体最小二乘反演位错参数,通过比较LS、TLS和ULS的反演结果分析ULS的稳定性和优越性。
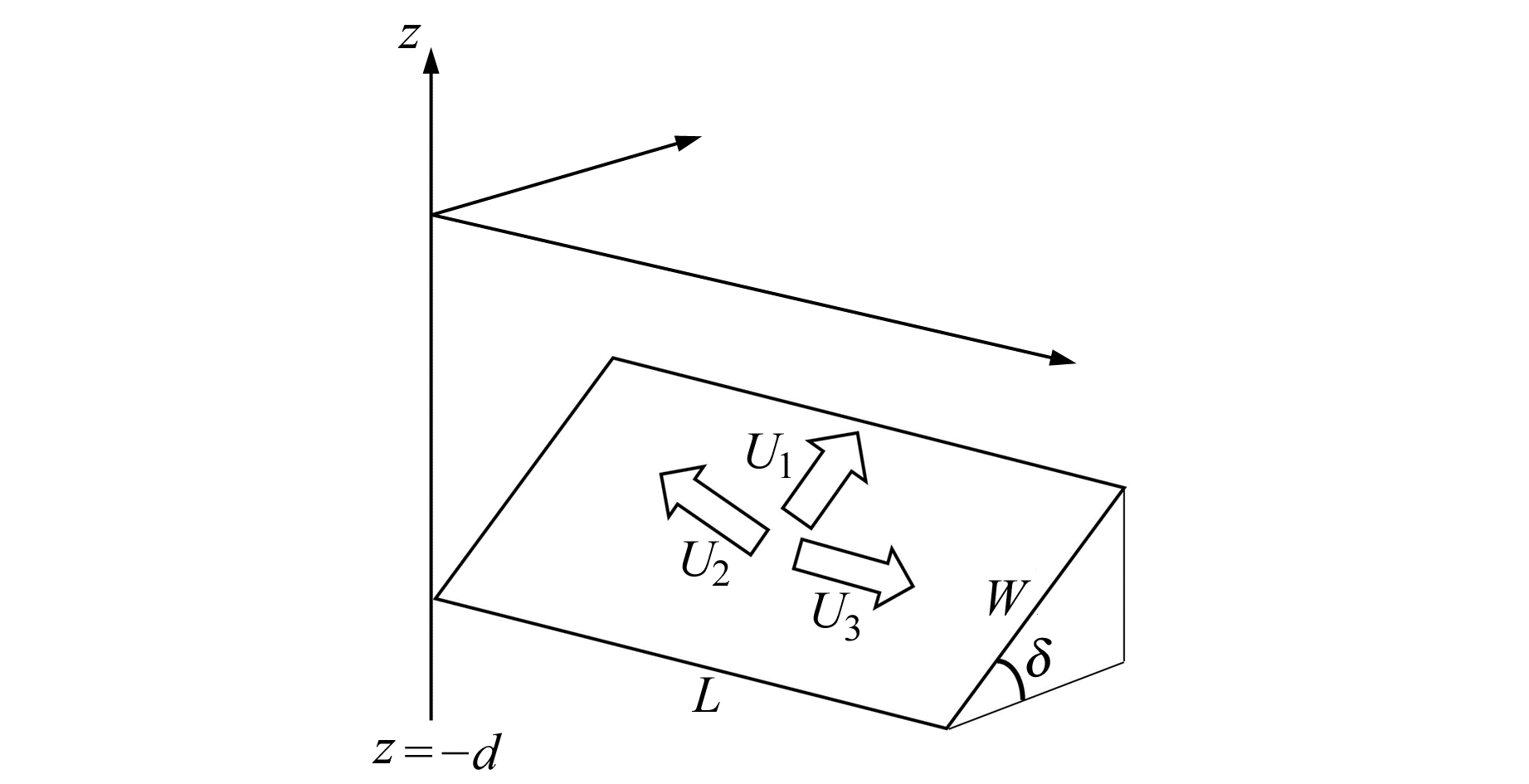
1 位错模型Steketee在1958年首次用位错模型描述地球物理学中的断层运动。本文利用三维位错与地表变形量构建函数模型。如果将断层分为若干段,则可用图 1所示的矩形位错模型近似描述。图示是倾角为δ的断层的下盘,以地面断层走向和地面的垂线方向分别建立x轴、z轴,垂直于xz平面建立y轴,空心箭头表示断层上点的走滑、倾滑和张裂分量(U1 U2 U3),L、W和d分别表示断层的半长度、宽度和深度。根据文献[16],走滑分量U1引起的地表位移表示为:
| $ {u_{{x_1}}} = - \frac{{{U_1}}}{{2\pi }}\left[ {\frac{{\xi q}}{{R\left( {R + q} \right)}} + {{\tan }^{ - 1}}\frac{{\xi \eta }}{{qR}} + {I_1}\sin \sigma } \right]\left. {} \right\| $ | (1) |
| $ {u_{{y_1}}} = - \frac{{{U_1}}}{{2\pi }}\left[ {\frac{{\tilde yq}}{{R\left( {R + \eta } \right)}} + \frac{{q\cos \sigma }}{{R + \eta }} + {I_2}\sin \sigma } \right]\left. {} \right\| $ | (2) |
| $ {u_{{z_1}}} = - \frac{{{U_1}}}{{2\pi }}\left[ {\frac{{\tilde dq}}{{R\left( {R + \eta } \right)}} + \frac{{q\sin \sigma }}{{R + \eta }} + {I_4}\sin \sigma } \right]\left. {} \right\| $ | (3) |
|
图 1 矩形位错模型 Fig. 1 Rectangular dislocation model |
倾滑分量U2引起的地表位移表示为:
| $ {u_{{x_2}}} = - \frac{{{U_2}}}{{2\pi }}\left[ {\frac{q}{R} - {I_3}\sin \sigma \cos \sigma } \right]\left. {} \right\| $ | (4) |
| $ \begin{array}{l} \;\;\;\;\;\;\;{u_{{y_2}}} = - \frac{{{U_2}}}{{2\pi }}\left[ {\frac{{\tilde yq}}{{R\left( {R + \xi } \right)}} + } \right.\\ \left. {\cos \sigma {{\tan }^{ - 1}}\frac{{\xi \eta }}{{qR}} - {I_1}\sin \sigma \cos \sigma } \right]\left. {} \right\| \end{array} $ | (5) |
| $ \begin{array}{l} \;\;\;\;\;\;{u_{{z_2}}} = - \frac{{{U_2}}}{{2\pi }}\left[ {\frac{{\tilde dq}}{{R\left( {R + \xi } \right)}} + } \right.\\ \left. {\sin \sigma {{\tan }^{ - 1}}\frac{{\xi \eta }}{{qR}} - {I_5}\sin \sigma \cos \sigma } \right]\left. {} \right\| \end{array} $ | (6) |
张裂分量U3引起的地表位移表示为:
| $ {u_{{x_3}}} = \frac{{{U_3}}}{{2\pi }}\left[ {\frac{{{q^2}}}{{R\left( {R + \eta } \right)}} - {I_3}{{\sin }^2}\sigma } \right]\left. {} \right\| $ | (7) |
| $ \begin{array}{l} {u_{{y_3}}} = \frac{{{U_3}}}{{2\pi }}\left\{ {\frac{{ - \tilde dq}}{{R\left( {R + \xi } \right)}} - \sin \sigma } \right.\left[ {\frac{{\xi q}}{{R\left( {R + \eta } \right)}} - } \right.\\ \left. {\left. {\;\;\;\;\;\;\;\;\;\;\;{{\tan }^{ - 1}}\frac{{\xi \eta }}{{qR}}} \right] - {I_1}{{\sin }^2}\sigma } \right\}\left. {} \right\| \end{array} $ | (8) |
| $ \begin{array}{l} {u_{{z_3}}} = \frac{{{U_3}}}{{2\pi }}\left\{ {\frac{{\tilde yq}}{{R\left( {R + \xi } \right)}} - \cos \sigma } \right.\left[ {\frac{{\xi q}}{{R\left( {R + \eta } \right)}} - } \right.\\ \left. {\left. {\;\;\;\;\;\;\;\;\;\;\;\;\;{{\tan }^{ - 1}}\frac{{\xi \eta }}{{qR}}} \right] - {I_5}{{\sin }^2}\sigma } \right\}\left. {} \right\| \end{array} $ | (9) |
其中,
| $ \left\{ {\begin{array}{*{20}{l}} {p = y\cos \sigma + d\sin \sigma , q = y\sin \sigma - d\cos \sigma }\\ {}\\ {\tilde y = \eta \cos \sigma + q\sin \sigma , \tilde d = \eta \sin \sigma - q\cos \sigma }\\ {}\\ {{R^2} = {\xi ^2} + {p^2} + {q^2} = {\xi ^2} + {{\tilde y}^2} + {{\tilde d}^2}} \end{array}} \right. $ | (10) |
Ii(i=1, 2, …, 5)表达式较复杂,此处不再赘述,具体可参考文献[16]。
式(1)~(9)中双竖线定义的运算如下:
| $ \begin{array}{l} f\left( {\xi , \eta } \right) = f\left( {x + L, p} \right) - f\left( {x + L, p - W} \right) - \\ \;\;\;\;\;\;\;f\left( {x - L, p} \right) + f\left( {x - L, p - W} \right)\left. {} \right\| \end{array} $ | (11) |
式中,(x, y)为地表变形点在局部坐标系下的坐标,(ξ, η)为断面上质点在局部坐标系下的坐标。断层三维运动在地表局部断层坐标系中表示为:
| $ \left\{ \begin{array}{l} {u_x} = {u_{{x_1}}} + {u_{{x_2}}} + {u_{{x_3}}}\\ {u_y} = {u_{{y_1}}} + {u_{{y_2}}} + {u_{{y_3}}}\\ {u_z} = {u_{{z_1}}} + {u_{{z_2}}} + {u_{{z_3}}} \end{array} \right. $ | (12) |
上式也可以写成矩阵形式L = AX,X = (U1 U2 U3)T。根据X =(ATPA)-1ATPL(P为单位阵)得到位错模型中的三参数(走滑、倾滑和张裂)。
2 类L曲线法获取不确定平差模型(ULS)的不确定度位错模型中,局部坐标系坐标(x, y)含有不确定性,代入式(11)和(12)后得到的设计矩阵A也含有不确定性ΔA。同样,地表三维位移(ux、uy、uz)也含有不确定,于是观测矩阵L就含有不确定性ΔL。带不确定性的平差模型为[13]:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{L}} + \Delta \mathit{\boldsymbol{L}} = \left( {\mathit{\boldsymbol{A}} + {\rm{\Delta }}\mathit{\boldsymbol{A}}} \right)\mathit{\boldsymbol{X}}}\\ {{{\left\| {\Delta \mathit{\boldsymbol{A}}} \right\|}_2} \le \alpha {{\begin{array}{*{20}{c}} , &{\left\| {\Delta \mathit{\boldsymbol{L}}} \right\|} \end{array}}_2} \le \beta } \end{array}} \right. $ | (13) |
式中,α和β为不确定度。在带不确定性的平差模型中,α和β已知。最小二乘平差不考虑系数矩阵的不确定性(即ΔA=0),而观测向量的不确定性未知,故在总体最小二乘平差中,系数矩阵和观测向量的不确定性都是未知的。
对ΔA和ΔL的不确定性进行参数估计。根据min-max平差准则,让残差的最大不确定性最小:
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{\hat X} \begin{array}{*{20}{c}} {}&{\mathop {\max }\limits_{{{\left\| {\Delta A} \right\|}_2} \le \alpha {{\begin{array}{*{20}{c}} , &{\left\| {\Delta L} \right\|} \end{array}}_2} \le \beta } } \end{array}}\\ {\left\{ {{{\left\| {\left( {\mathit{\boldsymbol{L}} + \Delta \mathit{\boldsymbol{L}}} \right) - \left( {\mathit{\boldsymbol{A}} + \Delta \mathit{\boldsymbol{A}}} \right)\mathit{\boldsymbol{\hat X}}} \right\|}_2}} \right\}} \end{array} $ | (14) |
其中,
| $ f\left( {\mathit{\boldsymbol{\hat X}}} \right) = {\left\| {\mathit{\boldsymbol{A\hat X}} - \mathit{\boldsymbol{L}}} \right\|_2} + \alpha {\left\| {\mathit{\boldsymbol{\hat X}}} \right\|_2} + \beta $ | (15) |
| $ \begin{array}{l} \frac{{\partial f\left( {\mathit{\boldsymbol{\hat X}}} \right)}}{{\partial \mathit{\boldsymbol{\hat X}}}} = \frac{1}{{{{\left\| {\mathit{\boldsymbol{A\hat X}} - \mathit{\boldsymbol{L}}} \right\|}_2}}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\left( {\mathit{\boldsymbol{A\hat X}} - \mathit{\boldsymbol{L}}} \right) + \frac{\alpha }{{{{\left\| {\mathit{\boldsymbol{\hat X}}} \right\|}_2}}}\mathit{\boldsymbol{\hat X}} = \\ \;\;\;\;\;\;\;\;\;\frac{1}{{{{\left\| {\mathit{\boldsymbol{A\hat X}} - \mathit{\boldsymbol{L}}} \right\|}_2}}}\left( {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}} + \mu \mathit{\boldsymbol{I}}} \right)\mathit{\boldsymbol{\hat X}} - {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}}} \right) \end{array} $ | (16) |
式中,μ为正实数:
| $ \mu = \alpha \frac{{{{\left\| {\mathit{\boldsymbol{A\hat X}} - \mathit{\boldsymbol{L}}} \right\|}_2}}}{{{{\left\| {\mathit{\boldsymbol{\hat X}}} \right\|}_2}}} $ | (17) |
令
| $ \mathit{\boldsymbol{\hat X}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}} + \mu \mathit{\boldsymbol{I}}} \right)^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{L}} $ | (18) |
其中,I是单位阵。先将设计矩阵A进行SVD分解,即
| $ \mu = \alpha \frac{{\sqrt {\left\| {{\mathit{\boldsymbol{L}}_2}} \right\|_2^2 + {\mu ^2}\left\| {{{\left( {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^2} + \mu \mathit{\boldsymbol{I}}} \right)}^{ - 1}}{\mathit{\boldsymbol{L}}_1}} \right\|_2^2} }}{{{{\left\| {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}{{\left( {{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^2} + \mu \mathit{\boldsymbol{I}}} \right)}^{ - 1}}{\mathit{\boldsymbol{L}}_1}} \right\|}_2}}} $ | (19) |
其中,
μ是关于α的迭代函数,α的选取会影响到岭参数μ求解的准确性。由迭代式也可以看到,每一个α都会对应一个终止迭代时的μ。文献[14]对于不确定度α的选定是依靠计算2-范数‖ΔA‖2,选择稍大于‖ΔA‖2的常量作为α,但在多数情况下ΔA是未知的,即使ΔA已知也不能保证ΔAX=ΔL。
a) 当ΔA=0且ΔL=0时,有L = AX;
b) 当ΔA=0而ΔL≠0时,有L+ΔL=AXLS,XLS即最小二乘解;
c) 当ΔA≠0且ΔL≠0时,有L+ΔL=(A+ΔA)XULS。
如果能保证ΔAX=ΔL,则XULS=X。本文提出利用类L曲线法确定α,即选定一系列α值(α>0),由μ的迭代函数确定终止迭代时的μ,然后代入式(18)得到XULS。以α为横坐标、‖XULS-X‖2为纵坐标作曲线,选择使XULS最接近X的α,此时XULS也是最优值,近似满足ΔAX=ΔL。在ΔAX=ΔL条件下,α并不一定是稍大于‖ΔA‖2的值。在实际中无法获取X的真值
假设一断裂带的参数如表 1所示。
|
|
表 1 断裂带参数 Tab. 1 Parameters of fault zone |
利用式(12)可以计算断层上任意点在地表局部断层坐标系的三维位移量,如表 2所示。
|
|
表 2 断层上12个点的位移 Tab. 2 Displacements of 12 points on fault |
在表 2中的坐标(x, y)中分别加入0.1 m、0.01 m和0.001 m的误差,在三维位移量上加上0.1 mm的随机误差,计算得到‖L-
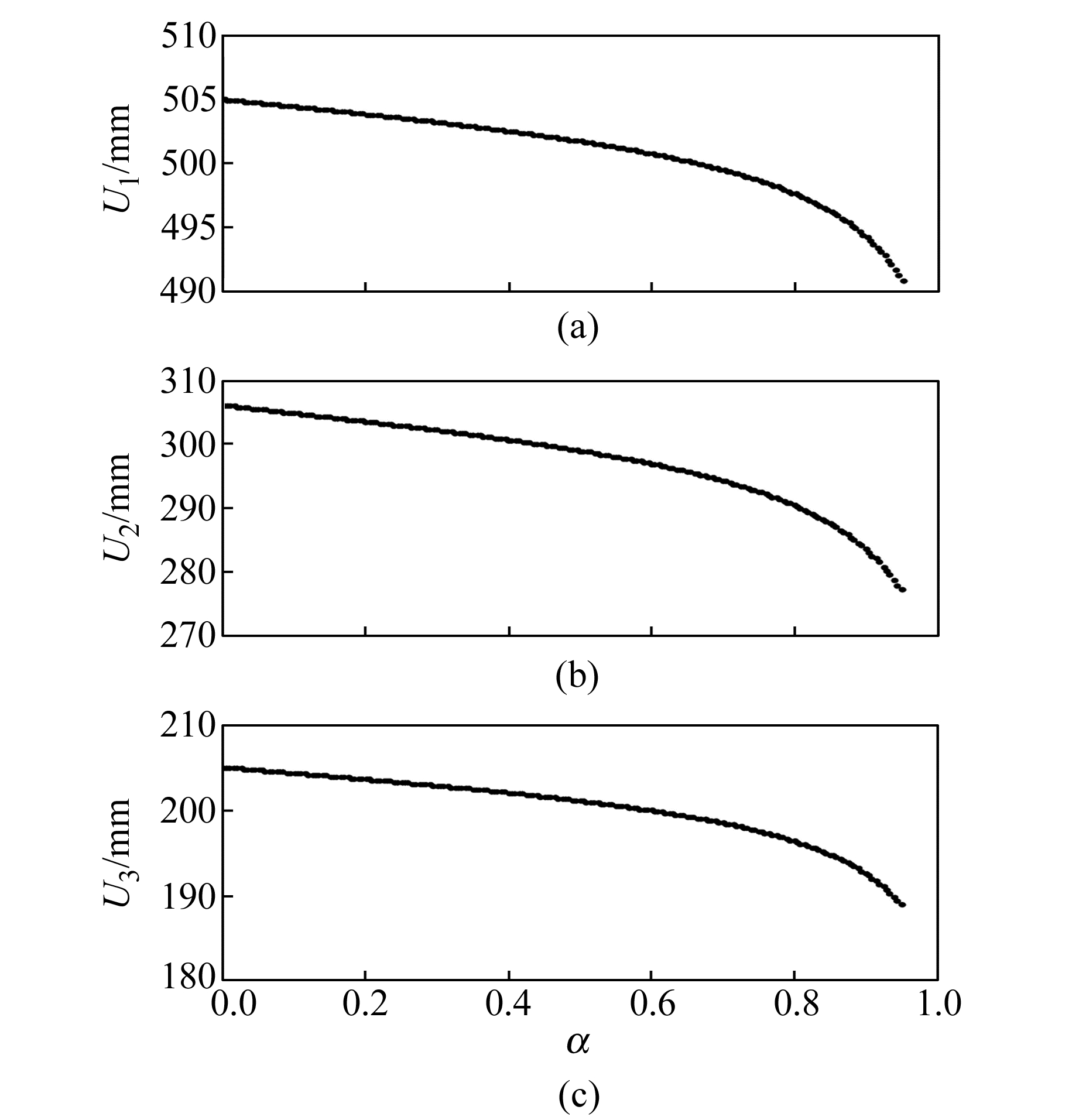
以坐标(x, y)中含有0.01 m误差为例进行说明。选取一系列α,根据不确定性平差算法得到解XULS的分量图(图 2)。需要在图 2上选取各分量的“最稳定值”。具体操作步骤为:以图 2(a)中U1分量为例,从这些离散点构成的曲线起点开始,拉取一条尽量与多点重合或靠近的直线(图 3中的倾斜虚线),当这条直线与分量曲线分离时,选取分离的临界值(图 3中α=0.2对应的分量值)作为“最稳定值”。同理,U2、U3分别在α取0.23和0.18时有“最稳定值”,然后将得到的(U1 U2 U3)作为X进行下一步类L曲线法确定α的操作。需要说明的是,估值X的获取受人为因素影响,但类L曲线法会对其进行修正。表 3为不同误差量级下X及其每个分量对应的α。
|
图 2 不同α计算参数解各分量的值 Fig. 2 Components of result calculated by different α |

|
图 3 最平缓点的选择 Fig. 3 Selection of the flattest point |
|
|
表 3 不同误差量级下的近似真值 Tab. 3 Approximate true value of error under different order of magnitude |
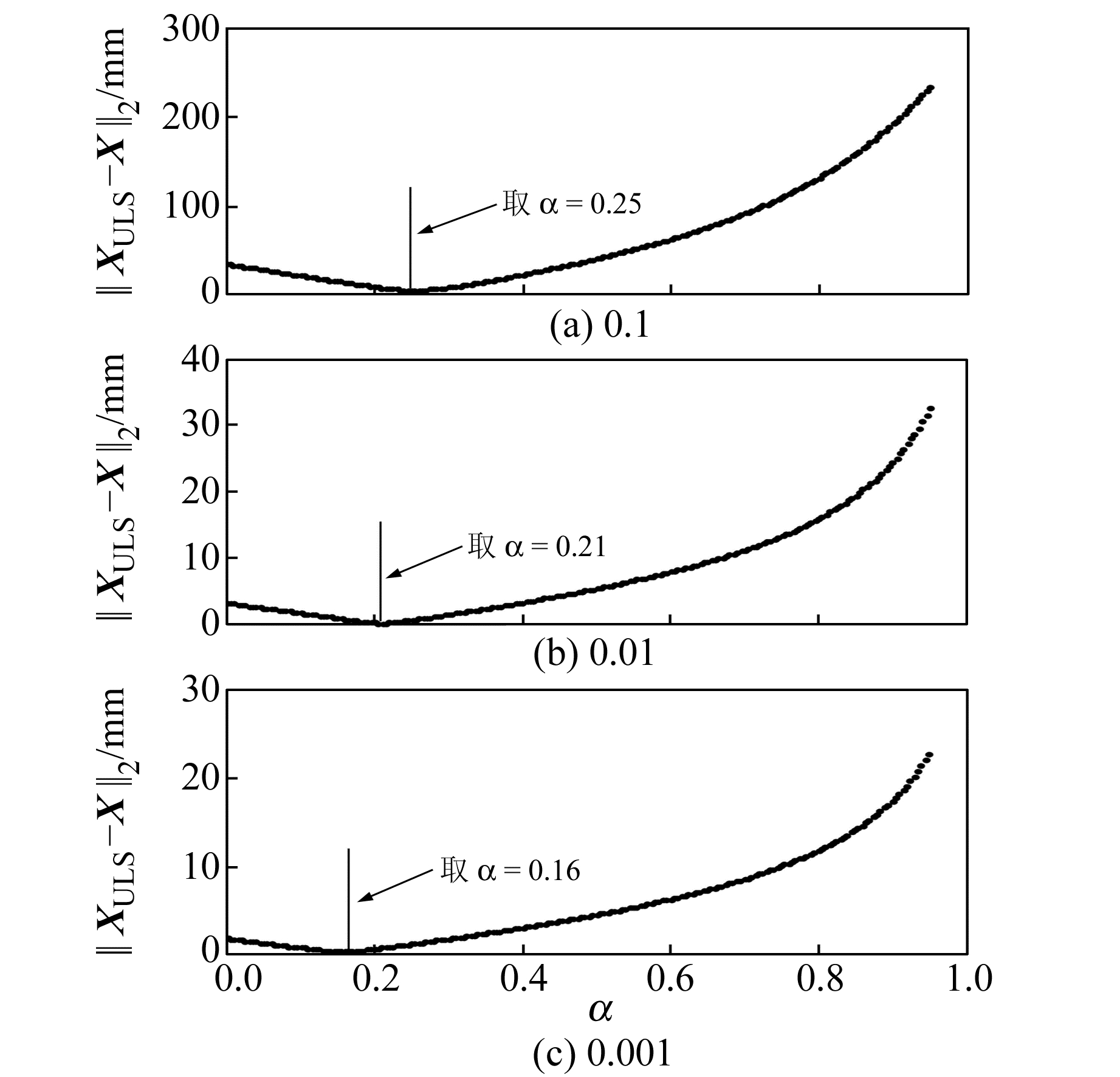
根据上述确定估值X的方法,可以得到3种误差量级干扰下的X,利用类L曲线法寻找使‖XULS-X‖2最小的α,进一步修正X,得到带不确定性的平差最优解XULS。如图 4,当坐标中分别混有0.1 m、0.01 m和0.001 m误差时,α分别取0.25、0.21和0.16,能使‖XULS-X‖2最小。
|
图 4 不同量级误差下α的选取 Fig. 4 Selection of α according to error under different order of magnitude |
表 4是根据LS、TLS和ULS分别反演位错参数的结果(表中
|
|
表 4 LS、TLS和ULS求解位错参数 Tab. 4 Dislocation parameters calculated by LS, TLS and ULS |
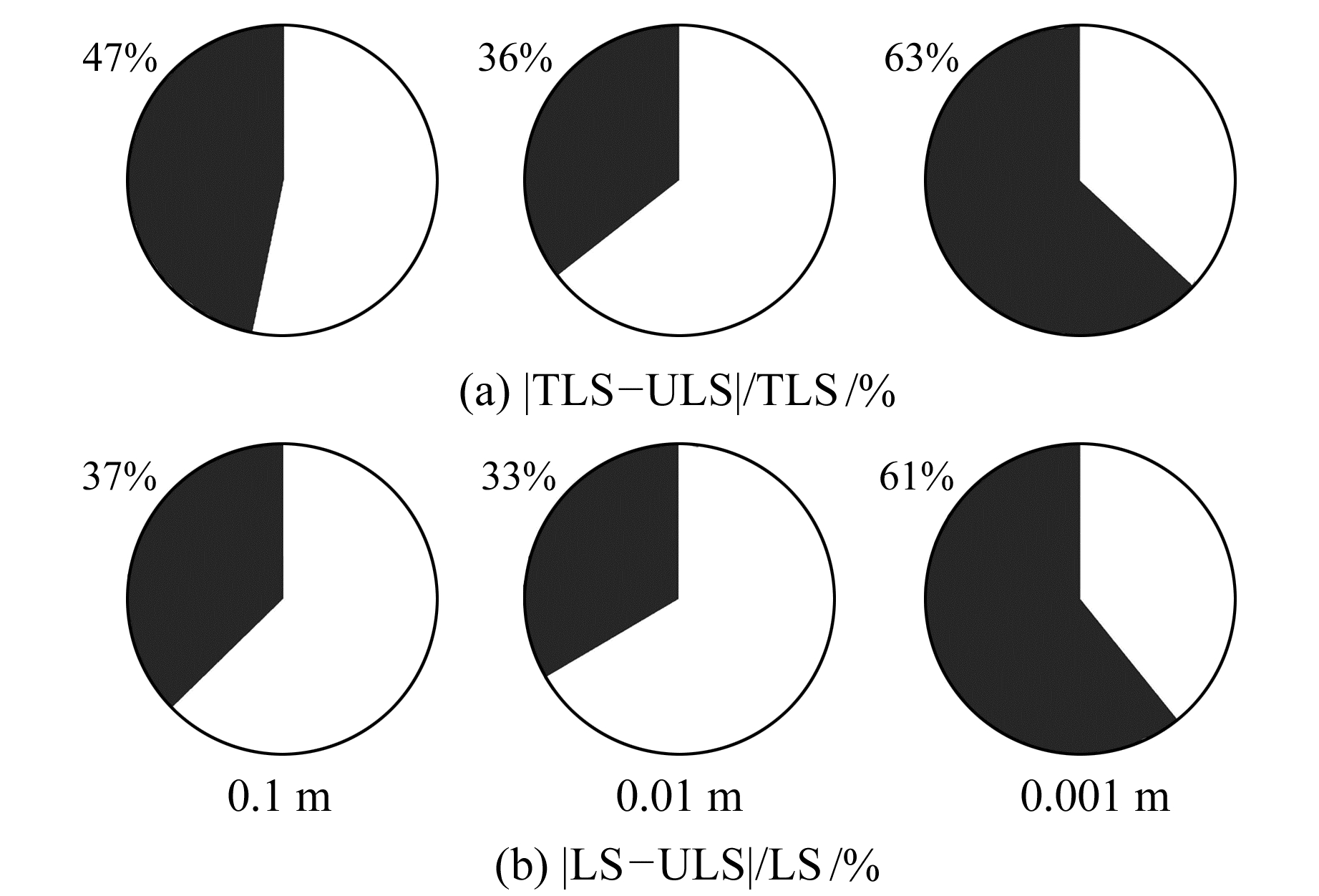
|
图 5 ULS结果较LS和TLS精度提高的百分比 Fig. 5 Increased percentage in precision of ULS's results compared with the results of TLS and LS |
从表 5也可以看到,TLS解精度最差,是因为TLS同时考虑系数矩阵和观测向量的不确定性,但没有对这种不确定性进行限制,导致系数矩阵过度修正。当系数矩阵中混有较大不确定性时,过度修正系数矩阵的不确定性,让其缩小,根据TLS的平差准则min(ΔLTLSTΔLTLS+ΔATLSTΔATLS),一部分不确定性转移到LTLS中,使观测向量中不确定性增大,如表 5中所示,TLS求出的‖ΔATLS‖2非常小,而‖ΔLTLS‖2较大。
|
|
表 5 TLS和ULS中不确定性的大小 Tab. 5 Magnitude of uncertainty calculated by TLS and ULS |
构造误差方程求解位错模型的三维位错参数时,因为系数矩阵和观测向量同时包含不确定性,导致最小二乘解失真。而带不确定性的平差算法(ULS)通过限制不确定度,利用min-max准则,可以提高参数解算的准确性。本文针对ULS算法中不确定度选择问题,提出类L曲线法,在系数矩阵包含不同量级误差情况下,同时采用LS、TLS以及ULS求解三维位错参数。结果表明,ULS解在较大误差干扰下仍然保持一定的稳定性,优于LS和TLS。随着误差级别的降低,虽然ULS对失真解的改善程度降低,但结果依然优于LS和TLS。尤其是当误差量级为0.001 m时,ULS结果较LS和TLS改善程度分别为61%和63%,体现了ULS算法的有效性和优越性。
| [1] |
谢建, 朱建军. 等式约束病态模型的正则化解及其统计性质[J]. 武汉大学学报:信息科学版, 2013, 38(12): 1440-1444 (Xie Jian, Zhu Jianjun. A Regularized Solution and Statistical Properties of Ill-Posed Problem with Equality Constraints[J]. Geomatics and Information Science of Wuhan University, 2013, 38(12): 1440-1444)
(  0) 0) |
| [2] |
谢建, 朱建军. 等式约束对病态问题的影响及约束正则化方法[J]. 武汉大学学报:信息科学版, 2015, 40(10): 1344-1348 (Xie Jian, Zhu Jianjun. Influence of Equality Constraints on Ill-Conditioned Problems and Constrained Regularization Method[J]. Geomatics and Information Science of Wuhan University, 2015, 40(10): 1344-1348)
(  0) 0) |
| [3] |
王乐洋, 于冬冬. 病态总体最小二乘问题的虚拟观测解法[J]. 测绘学报, 2014, 43(6): 575-581 (Wang Leyang, Yu Dongdong. Virtual Observation Method to Ill-Posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6): 575-581)
(  0) 0) |
| [4] |
王乐洋, 郑玄威, 申兴林, 等. 坐标转换Partial-EIV总体最小二乘方法[J]. 测绘工程, 2015, 24(12): 12-16 (Wang Leyang, Zheng Xuanwei, Shen Xinglin, et al. Partial-EIV Total Least Squares Method for Coordinate Transformation[J]. Engineering of Surveying and Mapping, 2015, 24(12): 12-16 DOI:10.3969/j.issn.1006-7949.2015.12.003)
(  0) 0) |
| [5] |
杨娟, 陶叶青. GPS高程异常拟合的稳健总体最小二乘算法[J]. 大地测量与地球动力学, 2014, 34(5): 130-133 (Yang Juan, Tao Yeqing. A Solution of GPS Elevation Anomaly Fitting Based on Robust Total Least Squares[J]. Journal of Geodesy and Geodynamics, 2014, 34(5): 130-133)
(  0) 0) |
| [6] |
Markovsky I, Huffel S. Overview of Total Least-Squares Methods[J]. Signal Processing, 2007, 87(10): 2283-2302 DOI:10.1016/j.sigpro.2007.04.004
(  0) 0) |
| [7] |
Schaffrin B, Wieser A. On Weighted Total Least-Squares Adjustment for Linear Regression[J]. Journal of Geodesy, 2008, 82(7): 415-421 DOI:10.1007/s00190-007-0190-9
(  0) 0) |
| [8] |
陈玮娴, 陈义, 袁庆, 等. 加权总体最小二乘在三维激光标靶拟合中的应用[J]. 大地测量与地球动力学, 2010, 30(5): 90-96 (Chen Weixian, Chen Yi, Yuan Qing, et al. Application of Weighted Total Least Squares to Target Fitting of Three-Dimensional Laser Scanning[J]. Journal of Geodesy and Geodynamics, 2010, 30(5): 90-96)
(  0) 0) |
| [9] |
王乐洋. 地壳应变参数反演的总体最小二乘方法[J]. 大地测量与地球动力学, 2013, 33(3): 106-110 (Wang Leyang. Inversion of Crustal Strain Parameters Based on Total Least Squares[J]. Journal of Geodesy and Geodynamics, 2013, 33(3): 106-110)
(  0) 0) |
| [10] |
Beck A, Ben-Tal A. On the Solution of the Tikhonov Regularization of the Total Least Squares Problem[J]. SIAM Journal on Optimization, 2006, 17(1): 98-118 DOI:10.1137/050624418
(  0) 0) |
| [11] |
余岸竹, 姜挺, 郭文月, 等. 总体最小二乘用于线阵卫星遥感影像光束法平差解算[J]. 测绘学报, 2016, 45(4): 442-449 (Yu Anzhu, Jiang Ting, Guo Wenyue, et al. Bundle Adjustment for Satellite Linear Array Images Based on Total Least Squares[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 442-449 DOI:10.11947/j.AGCS.2016.20150354)
(  0) 0) |
| [12] |
陈义, 陆珏. 以三维坐标转换为例解算稳健总体最小二乘方法[J]. 测绘学报, 2012, 41(5): 715-722 (Chen Yi, Lu Jue. Performing 3D Similarity Transformation by Robust Total Least Squares[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 715-722)
(  0) 0) |
| [13] |
宋迎春, 金昊, 崔先强. 带有不确定性的观测数据平差解算方法[J]. 武汉大学学报:信息科学版, 2014, 39(7): 788-792 (Song Yingchun, Jin Hao, Cui Xianqiang. Adjustment Algorithm about Observation Data with Uncertainty[J]. Geomatics and Information Science of Wuhan University, 2014, 39(7): 788-792)
(  0) 0) |
| [14] |
宋迎春, 谢雪梅, 陈晓林. 不确定性平差模型的平差准则与解算方法[J]. 测绘学报, 2015, 44(2): 135-141 (Song Yingchun, Xie Xuemei, Chen Xiaolin. Adjustment Criterion and Algorithm in Adjustment Model with Uncertainty[J]. Acta Geodaetica et Cartogra phica Sinica, 2015, 44(2): 135-141 DOI:10.11947/j.AGCS.2015.20130213)
(  0) 0) |
| [15] |
邹渤, 宋迎春, 唐争气, 等. 沉降观测AR模型的不确定性平差算法[J]. 大地测量与地球动力学, 2016, 36(8): 686-688 (Zou Bo, Song Yingchun, Tang Zhengqi, et al. Adjustment Algorithm on AR Model with Uncertain in Settlement Observation[J]. Journal of Geodesy and Geodynamics, 2016, 36(8): 686-688)
(  0) 0) |
| [16] |
Okada Y. Surface Deformation Due to Shear and Tensile Faults in a Half-Space[J]. Bulletin of the Seismological Society of America, 1985, 92(2): 1018-1040
(  0) 0) |
 2018, Vol. 38
2018, Vol. 38

