2. 海军海洋环境研究所, 天津市友谊路40号, 300061
海洋磁异常资料是描述海洋地磁场分布特征的主要信息[1],但无论是船载磁力测量还是航空磁力测量,获取的资料往往是描述距离磁源一定高度观测面上的磁场信息,而观测面以外距离磁源不同高度的磁场分布特征仍是未知的。经典场论中的重磁位场解析延拓理论为解决该问题提供了途径[2]。
在位场延拓方法中,向下延拓是典型的不适定反问题。位场向下延拓的方法分直接法和迭代法[3]。直接法主要是针对向下延拓算子的改造,常用的有维纳滤波法[3-6]和Tikhonov正则化方法[7-8];迭代法中有代表性的是积分迭代法[9-10],该方法虽然实现了位场20倍点距向下延拓,但未解决延拓算子对高频噪声的放大作用,当数据中含有高频噪声时,延拓结果发散。对此,常用的方法是在延拓前采用快速傅里叶变换(FFT)平滑法对数据中的高频噪声进行平滑处理[11-12],但数据中的噪声水平一般是未知的,平滑系数无法确定,系数选择过小则噪声不能有效消除,选择过大则高频磁异常数据可能被平滑掉。小波阈值去噪法是一种简单有效的去噪方法[13]。于波等[14-15]最早将小波阈值法用于海洋磁力测量数据消噪,实现了高频噪声及真实磁异常的有效分离,但对如何选取合适的阈值没有进一步讨论。本文针对迭代法在磁场向下延拓时易受高频噪声影响的问题,引入二维小波自适应阈值去噪法,通过估计数据中的噪声方差,在不同小波分解阶层中设定自适应阈值,在进行频域迭代向下延拓前对数据去噪,并通过理论模型试验与实测数据计算比较该方法与FFT平滑法对磁场频域迭代向下延拓结果的影响。
1 二维小波自适应阈值去噪法在海洋磁力测量中,因仪器噪声及海洋环境的动态影响,磁测数据不可避免地存在噪声信息。如果直接用含有噪声的数据进行磁空间背景场构建,将大大降低磁空间背景场的精度,并使用户将噪声作为磁异常进行判读。
根据小波阈值去噪思想,决定去噪性能的因素有3方面:小波母函数选择,阈值估计及阈值函数选取。考虑到磁异常信号变化较平缓与光滑,本文在理论模型试验与实例计算中均选择振荡较小、对称性及紧支撑性较好的Haar小波为小波母函数。
1.1 自适应阈值估计方法阈值选取是小波去噪中较关键的一步,如果阈值选择过小,去噪处理后的数据中仍有噪声存在;选择过大,则数据中的真实异常会被去除。Donoho等[13]给出一种固定阈值计算公式,在图像去噪处理中取得较好效果。本文引入自适应阈值估计方法来实现噪声和真实磁异常的分离。该方法具体原理如下。
设含有加性高斯白噪声的磁异常数据y为:
| $ y = x + n $ | (1) |
式中,x为无噪声磁异常,其方差为σx2;n为服从正态分布的高斯白噪声,方差为σn2,且x与n之间相互独立。因此,有:
| $ \sigma _y^2 = \sigma _x^2 + \sigma _n^2 $ | (2) |
Chang根据Bayes准则,在Bayes风险最小的条件下得到理想阈值的经验公式[16]:
| $ \hat t = \sigma _n^2/{\sigma _x} $ | (3) |
式中,
| $ \hat \sigma _n^2 = \frac{{{\rm{Median}}\left( {\left| {{Y_{i, j}}} \right|} \right)}}{{0.6745}}, {Y_{i, j}} \in {\rm{H}}{{\rm{H}}_1} $ | (4) |
式中,Median为取中值运算符,Yi, j为小波系数,HH1为小波分解得到的高频子带。
Chang提出的Bayes萎缩阈值估计法虽能根据数据噪声水平设定合适的阈值来去除高频噪声,但其只能在某一小波分解层中设定阈值去噪,而其他小波子带中仍有残留噪声。为此,Kaur等[17]在Bayes萎缩理想阈值基础上乘一个尺度参数β,使每一个小波分解层中均计算一个阈值,大大提高了去噪效果。各层的阈值计算公式为:
| $ {T_j} = \frac{{{\beta _j}\hat \sigma _n^2}}{{{\sigma _x}}} $ | (5) |
式中,Tj为第j层所确定的阈值;βj为尺度参数,其计算式为:
| $ {\beta _j} = {2^{ - j}}\sqrt {\log \left( {\frac{{{L_k}}}{J}} \right)} $ | (6) |
式中,j=1, …, J,Lk为第k级子带长度,J为分解总层数。随着j的改变,每一级的尺度参数β会自适应改变,从而实现了阈值的自适应估计。
1.2 改进的软阈值函数小波阈值函数主要有硬阈值函数与软阈值函数。硬阈值函数在阈值点处不连续,重构时容易导致数据失真;软阈值函数虽然连续,但选取的小波系数与分解的小波系数存在一定的偏差,直接影响重构信号的精度。本文采用一种改进的软阈值函数[18],其定义如下:
| $ X = \left\{ \begin{array}{l} {\rm{sgn}}\left( Y \right)\left( {\left| Y \right| \cdot \left( {1 - {{\left( {\frac{{{T_j}}}{Y}} \right)}^2}} \right)} \right), \;\;\;\left| Y \right| \ge {T_j}\\ 0, \left| Y \right| < {T_j} \end{array} \right. $ | (7) |
式中,Y为小波变换得到的小波系数,X为经阈值函数选取的小波系数,sgn为符号函数,Tj为第j层所确定的阈值。
可以证明,对于大于阈值Tj的小波分解系数Y,当Y逐渐增大时,选取的小波系数X逐渐接近小波分解系数Y,这在一定程度上克服了软阈值函数分解与重构时小波系数存在恒定偏差的问题,提高了信号重构精度。
1.3 二维小波自适应阈值去噪步骤结合海洋磁场数据中真实磁异常与噪声的特点,在频域迭代向下延拓前,采用二维小波自适应阈值法去除数据中的高频噪声,具体步骤见图 1。

|
图 1 二维小波自适应阈值去噪流程 Fig. 1 The flow chart of two-dimensional wavelet adaptive threshold denoising method |
为了验证二维小波自适应阈值的去噪效果,设计球体磁异常理论模型试验。测区范围为-2 000 m≤x≤2 000 m,-2 000 m≤y≤2 000 m,网格点距为50 m×50 m。以测区中心为原点,z轴向上为正建立坐标系,5个球体埋深均在-300 m~-200 m,观测高度z=200 m。球体磁异常理论计算值见图 2(a)。向理论值中分别加入标准差σn=0.01Tmean、0.02Tmean、0.05Tmean、0.1Tmean的高斯白噪声作为含不同观测噪声的仿真测量值,其中Tmean为理论磁异常的绝对均值,经统计知,Tmean=15.62 nT。加入标准差σn=0.05Tmean后的仿真观测资料见图 2(b)。

|
图 2 球体组合模型磁异常等值线(单位:nT) Fig. 2 Magnetic anomaly contour map of the sphere model |
分别采用二维小波自适应阈值法与FFT平滑法对含不同噪声的球体磁异常数据进行去噪,并计算去噪前后的信噪比(SNR)及2种方法的去噪均方误差(MSE)作为去噪效果的评价指标,其中信噪比的计算式为:
| $ {\rm{SNR}} = 10 \cdot \lg \left[ {\frac{{\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{T_x}{{\left( {i, j} \right)}^2}} } }}{{\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{\left( {{T_y}\left( {i, j} \right) - {T_x}\left( {i, j} \right)} \right)}^2}} } }}} \right] $ | (8) |
式中,SNR为信噪比,是衡量信号中噪声水平的物理量,单位dB;Tx为无噪声数据,Ty为含噪磁异常数据,M、N均为网格点数。去噪均方误差MSE为:
| $ {\rm{MSE}} = \sqrt {\frac{1}{{MN}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {({T_d}(i, j) - } } {T_x}(i, j){)^2}} $ | (9) |
式中,Td为去噪后磁异常数据。
采用FFT平滑法去噪时,需将去噪结果与真值多次比较来确定最佳平滑系数。经多次试验,当数据中含σn=0.01Tmean、0.02Tmean、0.05Tmean、0.10Tmean噪声时,FFT平滑法选择的最佳平滑系数分别为1、2、3、3。而二维小波自适应阈值法通过估计数据中噪声标准差来设定阈值,实现自适应去噪过程,效率大大提高。图 2(c)、(d)分别给出当观测数据中含标准差σn=0.05Tmean噪声时,FFT平滑去噪后及小波自适应阈值去噪后的磁异常图。将2种方法的去噪结果分别与理论值(图 2(a))对比可知,小波自适应阈值去噪结果更光滑且与理论值更接近。进一步统计2种方法在不同噪声条件下的信噪比及去噪误差,见表 1。
|
|
表 1 自适应阈值与FFT平滑去噪误差统计 Tab. 1 Denoising error statistics of adaptive threshold and FFT smooth method |
由表 1可知:1)在不同噪声条件下,自适应阈值估计的噪声标准差与试验加入的噪声标准差十分接近,说明自适应阈值法可以较好地估计出数据中的噪声;2)比较2种方法去噪前后的信噪比可知,在不同噪声水平下,2种方法去噪后信噪比均明显提高,而自适应阈值法较FFT平滑法的信噪比提高更多,说明自适应法去噪结果中剩余噪声更少,去噪效果更好;3)对比2种方法的去噪均方误差可知,不同噪声条件下,自适应阈值法的去噪均方误差均小于FFT平滑法,即自适应阈值去噪结果与理论值更接近。
2.2 实例计算选取某次船载磁力测量资料,测区范围10 km×10 km,主测线南北向布设,测线间距为500 m。磁测数据经常规改正(磁测点位置改正、日变改正、船磁改正、正常场校正)后进行网格化处理,共生成201×201个磁异常点,网格间距为50 m×50 m。将其视为0 m高度磁异常,磁异常等值线分布见图 3(a)。将成果数据向上延拓500 m(10倍点距)视为航磁测量资料。
|
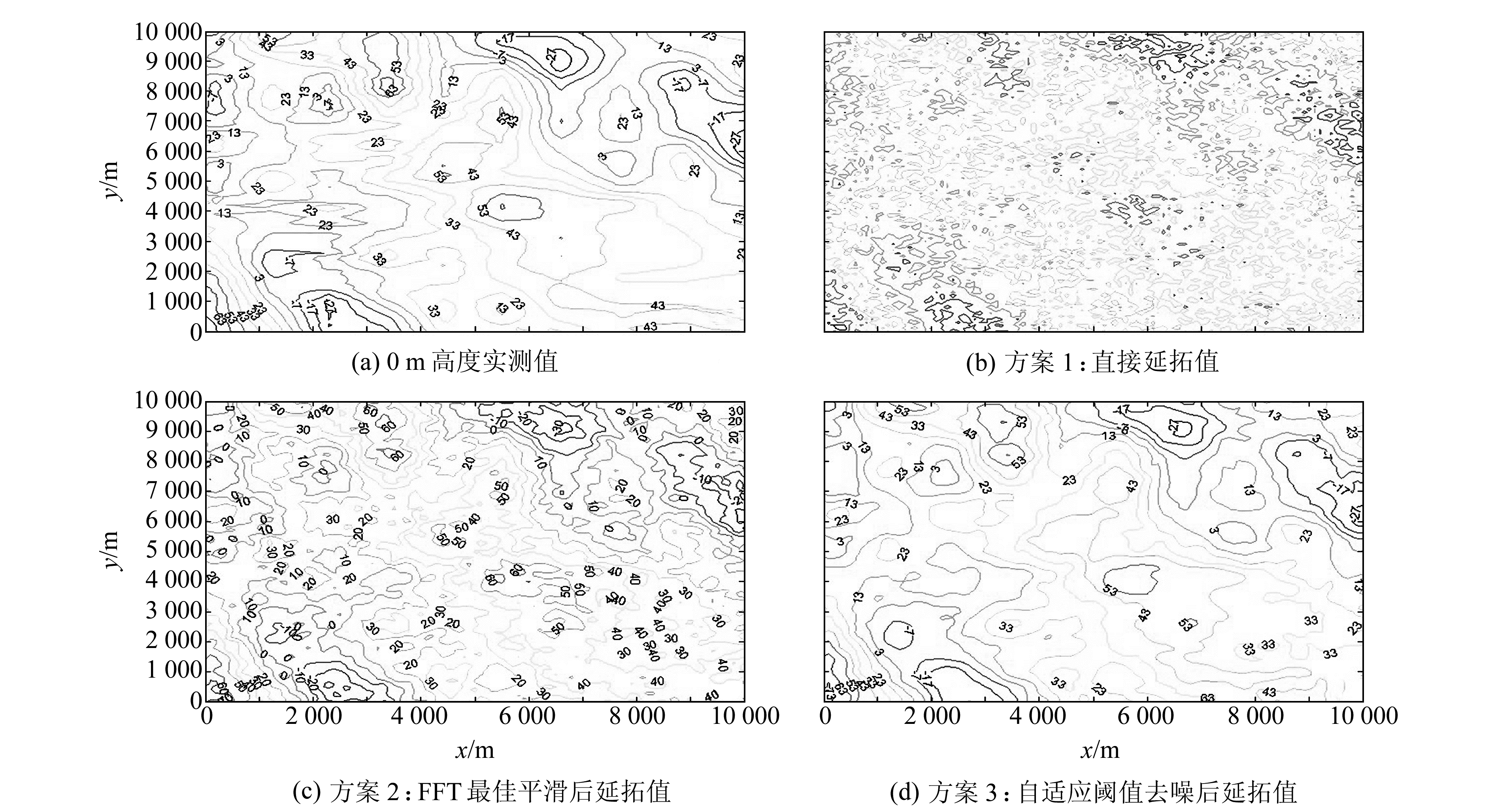
图 3 含σn=0.2 nT噪声数据(500 m高度)下延到0 m后结果对比(单位:nT) Fig. 3 The contrast figure of downward continuation calculated by different schemes |
考虑到磁场数据向上延拓会对噪声有一定的平滑作用,为此在向上延拓得到的航磁数据中加入噪声干扰。高精度的航磁测量精度要求是1 nT[19],为此,向航磁数据中(500 m高度)加入均值为0、标准差σn分别为0.2 nT、0.5 nT、1.0 nT的高斯白噪声。
为了检验自适应阈值法在磁场频域迭代向下延拓中对高频噪声的抑制效果,本文采用3种方案将500 m高度含不同噪声水平的磁异常数据向下延拓到0 m。
方案1:直接采用频率域向下延拓迭代法将500 m高度含不同噪声水平的数据延拓到0 m;
方案2:先采用FFT平滑法对500 m高度数据去噪,然后再采用频域迭代法延拓到0 m;
方案3:先用二维小波自适应阈值法对不同噪声水平数据去噪,再用频域迭代法延拓到0 m。
图 3为0 m高度实测值及3种方案延拓结果的等值线,等值线间隔均为10 nT。比较图 3(b)与3(a)可见,方案1延拓结果因延拓算子对数据中高频噪声的放大作用,随着迭代次数的累加导致延拓结果发散;比较图 3(c)与3(a)可见,方案2延拓结果虽与实测值总体趋势相似,但因FFT平滑法去噪效果较差,数据中仍残留部分噪声,并在向下延拓时被放大导致延拓结果与实测值偏差较大;而比较图 3(d)与3(a)可见,采用小波自适应阈值法去噪后,其延拓结果的磁异常等值线图总体趋势及数值与实测值均较接近,说明小波自适应阈值去噪法对磁异常的频域迭代向下延拓结果有明显改善,验证了方法的有效性。
进一步从数值统计上验证自适应阈值去噪法在迭代向下延拓中的应用效果。将3种方案的延拓结果与0 m高度实测值进行对比,并计算延拓均方误差及相对误差作为3种方案延拓效果的评价指标:
| $ {\rm{RMSE}} = \sqrt {\frac{1}{{mn}}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {({T_c}(i, j) - } } {T_t}(i, j){)^2}} $ | (10) |
| $ {R_e} = \frac{{{{\left\| {{T_c} - {T_t}} \right\|}_2}}}{{{{\left\| {{T_t}} \right\|}_2}}} \times 100\% $ | (11) |
式中,RMSE为延拓均方误差,表示延拓结果与实测值的偏离程度;Re为延拓相对误差,表示延拓偏差在实测值中所占比重;Tc为延拓计算值;Tt为0 m高度实测值;m为网格化后测线数,n为网格化后测点数。
需要注意的是,因试验采用的500 m高度数据是由0 m数据向上延拓得到的,向上延拓虽然计算精度较高,但其低通滤波的平滑作用必然会滤除实测数据中的高频信息,再将500 m高度零噪声数据直接向下延拓到0 m高度,此时得到的延拓误差则是频域迭代延拓算法的计算误差,而非高频噪声引起的误差。为此,本文在比较FFT平滑法与自适应阈值去噪法对向下延拓结果的改善效果时,去除迭代延拓算法的计算误差,只比较2种方法通过抑制高频噪声而减小延拓误差的效果。表 2给出了3种方案延拓误差统计情况。
|
|
表 2 按不同方案计算的向下延拓误差统计 Tab. 2 Statistics of downward continuation error calculated by different schemes |
由表 2知,方案1在噪声标准差σn=0 nT时计算的延拓均方误差及相对误差分别为1.31 nT、3.12%,即视为频域迭代延拓算法的计算误差,其他含不同噪声水平数据按3种方案计算的延拓误差均为扣除延拓算法计算误差后得到的由噪声引起的误差。
如果按方案1实施后与零噪声延拓误差相比,当观测资料中含标准差为σn=0.2 nT的噪声时,延拓均方误差与相对误差较无噪声时分别增大了3.40 nT和1.33%;而当噪声标准差为σn=1.0 nT时,延拓均方误差与相对误差分别增大了21.09 nT和16.15%,说明噪声对延拓结果影响较大,此时延拓结果不可信。如果按方案2与3实施后,得到的延拓误差与方案1相比明显降低,且不同噪声条件下方案3的延拓误差均比方案2小,进一步说明二维小波自适应阈值去噪法在磁异常向下延拓时可以有效改善因高频噪声引起的延拓误差,且效果明显优于FFT平滑法。
另外,由表 2还可以看出,频域迭代延拓算法本身的计算误差比较大,在实际计算中不能忽略。如何改进延拓算法,降低算法本身的计算误差,对于磁场数据向下延拓是非常重要的,这也是下一步研究的重点。
3 结语针对海洋磁力测量资料向下延拓时数据中的高频噪声易被延拓算子放大,导致延拓结果发散的问题,采用二维小波自适应阈值法在延拓前对数据去噪,并在理论模型试验与实测资料计算中将该方法与FFT平滑法进行比较,对其在磁场频域迭代向下延拓算法中的作用进行验证。研究结果表明:
1)无论数据中含有较小噪声还是较大噪声,自适应阈值法都可以较好地估计数据中的噪声标准差,且去噪效果都优于FFT平滑法。
2) 利用频域迭代向下延拓时,采用二维小波自适应阈值法可有效提高延拓结果精度,且效果明显优于FFT平滑法。该法可以有效改善频域迭代向下延拓结果,为三维磁空间背景场模型构建提供基础。
值得注意的是,小波自适应阈值去噪法虽然可有效降低因噪声引起的延拓误差,但却无法降低延拓算法本身的计算误差,相比于噪声引起的延拓误差是不可忽视的,需进一步提高延拓算法的准确性。
| [1] |
边刚, 夏伟, 金绍华, 等. 海洋磁力测量数据处理方法及其应用研究[M]. 北京: 测绘出版社, 2015 (Bian Gang, Xia Wei, Jin Shaohua, et al. Marine Magnetic Survey Data Processing and Its Application[M]. Beijing: Surveying and Mapping Press, 2015)
(  0) 0) |
| [2] |
陈龙伟. 面向地磁导航的位场延拓空间域算法研究[D]. 长沙: 国防科学技术大学, 2013 (Chen Longwei. Research on Spatial Domain Numerical Methods for Potential Field Continuation in Geomagnetic Navigation[D]. Changsha: National University of Defense Technology, 2013)
(  0) 0) |
| [3] |
曾小牛, 刘代志, 李夕海, 等. 位场向下延拓的改进迭代维纳滤波法[J]. 地球物理学报, 2014, 57(6): 1958-1967 (Zeng Xiaoniu, Liu Daizhi, Li Xihai, et al. An Improved Iterative Wiener Filter for Downward Continuation of Potential Fields[J]. Chinese J Geophys, 2014, 57(6): 1958-1967 DOI:10.6038/cjg20140626)
(  0) 0) |
| [4] |
Clarke G K. Optimum Second-Derivative and Downward Continuation Filters[J]. Geophysics, 1969, 34(3): 424-437 DOI:10.1190/1.1440020
(  0) 0) |
| [5] |
Pawlowski R S. Preferential Continuation for Potential Field Anomaly Enhancement[J]. Geophysics, 1995, 60(2): 390-398 DOI:10.1190/1.1443775
(  0) 0) |
| [6] |
张辉, 陈龙伟, 任治新, 等. 位场向下延拓迭代法收敛性分析及稳健向下延拓方法研究[J]. 地球物理学报, 2009, 52(4): 1107-1113 (Zhang Hui, Chen Longwei, Ren Zhixin, et al. Analysis on Convergence of Iteration Method for Potential Fields Downward Continuation and Research on Robust Downward Continuation Method[J]. Chinese J Geophys, 2009, 52(4): 1107-1113)
(  0) 0) |
| [7] |
梁锦文. 位场向下延拓的正则化方法[J]. 地球物理学报, 1989, 32(5): 600-608 (Liang Jinwen. Downward Continuation of Regularization Methods for Potential Fields[J]. Chinese J Geophys, 1989, 32(5): 600-608)
(  0) 0) |
| [8] |
Abedi M, Gholami A, Norouzi G H. A Stable Downward Continuation of Airborne Magnetic Data:A Case Study for Mineral Prospectivity Mapping in Central Iran[J]. Computers & Geosciences, 2013, 52: 269-280
(  0) 0) |
| [9] |
徐世浙. 位场延拓的积分-迭代法[J]. 地球物理学报, 2006, 49(4): 1176-1182 (Xu Shizhe. The Integraliteration Method for Continuation of Potential Fields[J]. Chinese J Geophys, 2006, 49(4): 1176-1182)
(  0) 0) |
| [10] |
刘东甲, 洪天求, 贾志海, 等. 位场向下延拓的波数域迭代法及其收敛性[J]. 地球物理学报, 2009, 52(6): 1599-1605 (Liu Dongjia, Hong Tianqiu, Jia Zhihai, et al. Wave Number of Domain Iteration Method for Downward Continuation of Potential Fields and Its Convergence[J]. Chinese J Geophys, 2009, 52(6): 1599-1605)
(  0) 0) |
| [11] |
于波, 翟国君, 刘雁春, 等. 噪声对磁场向下延拓迭代法的计算误差影响分析[J]. 地球物理学报, 2009, 52(8): 2182-2188 (Yu Bo, Zhai Guojun, Liu Yanchun, et al. Analysis of Noise Effect on the Calculation Error of Downward Continuation with Iteration Method[J]. Chinese J Geophys, 2009, 52(8): 2182-2188)
(  0) 0) |
| [12] |
陈龙伟, 徐世浙, 胡小平, 等. 位场向下延拓的迭代最小二乘法[J]. 地球物理学进展, 2011, 26(3): 894-901 (Chen Longwei, Xu Shizhe, Hu Xiaoping, et al. The Iterative Least Square Method for Downward Continuation of Potential Fields[J]. Progress in Geophys, 2011, 26(3): 894-901)
(  0) 0) |
| [13] |
Donoho D L, Johnstone J M. Adapting to Unknown Smoothness via Wavelet Shrinkage[J]. Journal of the America Statistical Association, 1995, 90(432): 1200-1224 DOI:10.1080/01621459.1995.10476626
(  0) 0) |
| [14] |
于波, 翟国君, 刘雁春, 等. 基于小波阈值的海洋磁力测量数据消噪方法[J]. 测绘科学, 2009, 34(5): 89-91 (Yu Bo, Zhai Guojun, Liu Yanchun, et al. Data Denoising Based on Wavelet Threshold in Marine Magnetic Survey[J]. Science of Surveying and Mapping, 2009, 34(5): 89-91)
(  0) 0) |
| [15] |
于波, 翟国君, 刘雁春, 等. 一种海洋磁力测量降噪的有效方法[J]. 测绘科学技术学报, 2009, 26(3): 200-203 (Yu Bo, Zhai Guojun, Liu Yanchun, et al. A Novel Method for De-nosing in Marine Magnetic Survey[J]. Journal of Geomatics Science and Technology, 2009, 26(3): 200-203)
(  0) 0) |
| [16] |
Chang S G, Yu B, Vetterli M. Adaptive Wavelet Thresholding for Image Denoising and Compression[J]. IEEE Transactions on Image Processing, 2000, 9(9): 1532-1546 DOI:10.1109/83.862633
(  0) 0) |
| [17] |
Kaur L, Gupta S, Chauhan R C. Image Denoising Using Wavelet Thresholding[J]. IEEE Image Processing, 2002, 9: 1522-1530
(  0) 0) |
| [18] |
张小燕, 吐尔洪江·阿布都克力木. 小波变换的阈值图像去噪算法改进[J]. 计算机技术与发展, 2017, 27(3): 81-84 (Zhang Xiaoyan, Turghunjan Abdukirim. Improvement of Threshold Image Denoising Algorithm with Wavelet Transform[J]. Computer Technology and Development, 2017, 27(3): 81-84)
(  0) 0) |
| [19] |
DZ/T 0142-2010. 航空磁测技术规范[S]. 北京: 中华人民共和国国土资源部, 2010 (DZ/T 0142-2010. Criterion of Aeromagnetic Survey[S]. Beijing: Ministry of Land and Resources of the People's Republic of China, 2010)
(  0) 0) |
2. Naval Institute of Marine Environment, 40 Youyi Road, Tianjin 300061, China
 2018, Vol. 38
2018, Vol. 38

