2. 武汉大学精密工程与工业测量国家测绘地理信息局重点实验室, 武汉市珞喻路129号, 430079;
3. 辽宁省交通高等专科学校, 沈阳市沈北路102号, 110122
选权迭代法对观测值中的多个粗差具有迭代降权的作用,从而减弱粗差对参数估值的影响[1]。但当观测值存在系统性的模型误差时,选权迭代法将无法识别。半参数模型通过引入非参数,克服了经典参数回归模型的局限性,能够有效分离系统误差和偶然误差,是一种非常理想的数据处理方法[2]。但当观测数据中含有多个显著性粗差时,系统误差的估值会受到影响,进而降低参数分量估值的精度。
滑坡形变是一个不确定、复杂的非线性过程,观测值中除包含偶然误差,也可能受到粗差和系统误差的综合影响[3]。半参数回归模型是参数模型和非参数模型的混合模型,较参数线性模型有更强的适应性,通过选权迭代法的补充改进,将平差改正数不断迭代参与权阵的重构,进而重新解算回归系数,可以削弱粗差和系统误差的影响。
1 半参数回归模型建立 1.1 补偿最小二乘原理下的半参数模型在经典间接平差模型中,通常假定观测误差Δ是期望为0的偶然误差,即除去观测误差,观测值L可表示为未知参数x的函数。若模型不准确,或观测值中有系统误差,则基于最小二乘准则的间接平差公式并不能严格成立,而改写为[2, 4]:
| $ \mathop {\mathit{\boldsymbol{L}}}\limits_{n \times 1} = \mathop {\mathit{\boldsymbol{B}}}\limits_{n \times t} \mathop {\mathit{\boldsymbol{x}}}\limits_{t \times 1} + \mathop {\mathit{\boldsymbol{s}}}\limits_{n \times 1} + \mathop {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}}\limits_{n \times 1} $ | (1) |
式中,L为观测值向量,B为列满秩系数矩阵,x为参数估值向量,Δ为偶然误差向量,s =[s1 s2 … sn]是一个描述模型误差或系统误差的n维未知向量。观测方程中既有参数分量又有非参数分量,故式(1)称为半参数模型[5]。其误差方程为:
| $ \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{B\hat x}} + \mathit{\boldsymbol{\hat s}} - \mathit{\boldsymbol{L}} $ | (2) |
根据补偿最小二乘原理:
| $ {\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{PV}} + \alpha {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{Rs}} = \min $ | (3) |
式中,R是一个适当给定的正定矩阵,称为正则化矩阵;二次型sTRs反映对向量s的某种度量;α是一个对V和s起平衡作用的纯量因子,称为平滑因子。这时, 可把平差问题归结为一个条件极值问题[5]。由拉格朗日乘数法构造函数:
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = {\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{PV}} + \alpha {{\mathit{\boldsymbol{\hat s}}}^{\rm{T}}}\mathit{\boldsymbol{R\hat s}} + 2{\mathit{\boldsymbol{K}}^{\rm{T}}}\left( {\mathit{\boldsymbol{B\hat x}} + \mathit{\boldsymbol{\hat s}} - \mathit{\boldsymbol{L}} - \mathit{\boldsymbol{V}}} \right) $ | (4) |
分别令
| $ \mathit{\boldsymbol{K}} = \mathit{\boldsymbol{PV}},\mathit{\boldsymbol{K}} = - \alpha \mathit{\boldsymbol{R\hat s}},{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{K}} = 0 $ | (5) |
综合式(1)~式(5)可得法方程:
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}}}&{{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}}\\ {\mathit{\boldsymbol{PB}}}&{\mathit{\boldsymbol{P}} - \alpha \mathit{\boldsymbol{R}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat x}}}\\ {\mathit{\boldsymbol{\hat s}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PL}}}\\ {\mathit{\boldsymbol{PL}}} \end{array}} \right] $ | (6) |
令N=BTPB,显然N可逆。令M=P+αR-PBN-1BTP,则由法方程可得:
| $ \mathit{\boldsymbol{\hat x}} = {\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PL}} - {\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P\hat s}} $ | (7) |
| $ \mathit{\boldsymbol{\hat s}} = {\mathit{\boldsymbol{M}}^{ - 1}}\left( {\mathit{\boldsymbol{P}} - \mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}} \right)\mathit{\boldsymbol{L}} $ | (8) |
这样,通过式(8)、式(7)及式(2)就可计算非参数分量的估值
正则化矩阵的选取有自然样条函数法、时间序列法、距离法等[2, 4]。在滑坡形变拟合与预测中,由于误差与时间存在很大关系,本文选用时间序列法[6]。
在半参数模型中,如果观测值是在时刻t1,t2…tn得到的一个时间序列,且相邻时刻的模型误差si与si+1差别不大,则可取相邻两观测点系统误差之差的平方和为二次型[5],即
| $ \mathit{\boldsymbol{R}} = {\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{G}} $ | (9) |
其中,
因R秩亏,需再增加一个约束条件。若假设s呈周期性变化,且观测值个数多,分布较均匀,则可令
| $ {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{\hat s}} = 0,\mathit{\boldsymbol{e}} = \left[ {\begin{array}{*{20}{c}} 1&1& \cdots &1 \end{array}} \right]_n^{\rm{T}} $ | (10) |
同样,可构造拉格朗日函数:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = {\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{PV}} + \alpha {{\mathit{\boldsymbol{\hat s}}}^{\rm{T}}}\mathit{\boldsymbol{R\hat s}} + }\\ {2{\mathit{\boldsymbol{K}}^{\rm{T}}}\left( {\mathit{\boldsymbol{B\hat x}} + \mathit{\boldsymbol{\hat s}} - \mathit{\boldsymbol{L}} - \mathit{\boldsymbol{V}}} \right) + 2\gamma {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{\hat s}}} \end{array} $ | (11) |
由上述公式,可得如下基于时间序列法的参数与非参数分量估计结果:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{W}} = \mathit{\boldsymbol{P}} - \mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}\\ \gamma = {\mathit{\boldsymbol{e}}^{\rm{T}}}{\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{WL}}/{\mathit{\boldsymbol{e}}^{\rm{T}}}{\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{e}}\\ \mathit{\boldsymbol{\hat s}} = {\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{WL}} - \gamma {\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{e}}\\ \mathit{\boldsymbol{\hat x}} = {\mathit{\boldsymbol{N}}^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{\hat s}}} \right) \end{array} \right. $ | (12) |
其中,平滑因子α是一个重要的待定参数,起到拟合和光滑的平衡作用,选取是否得当对估计量的影响很大。常用的选取方法有信噪比值法、L曲线法、交叉核实法及广义交叉核实法[2, 4],本文采用文献[7]中的L曲线法[7]。
2 选权迭代法半参数回归下的滑坡数据处理方法 2.1 系数矩阵的构造对临江库区滑坡进行监测,一般采取多因子共同监测模式,包括平面位移、高程、地下水位、长江水位、降雨量、内部应力等[3, 8]。将这些监测因子(包括时间)构造为系数矩阵,再通过多项式回归(参数回归)或半参数回归得到回归方程的参数估值。
以临江滑坡监测为例,设L为某监测点的位移形变值,t为时间因子,c为长江水位,r为降雨量,w为此监测点处地下水位。在建立预测模型时,可近似认为L由t、c、r、w共同决定。若回归方程取至2次,并加入常数项系数,即可构造如式(13)所示的系数矩阵。其中先对t、c、r、w进行标准化处理,即减去因子序列平均值,再除以标准差,以消除系数矩阵的病态现象[9]。
| $ \mathop {\mathit{\boldsymbol{B}}}\limits_{n \times 15} = \left[ {\begin{array}{*{20}{c}} 1&{{t_1}}&{{c_1}}&{{r_1}}&{{w_1}}&{t_1^2}&{c_1^2}&{r_1^2}&{w_1^2}&{{t_1}{c_1}}&{{t_1}{r_1}}&{{t_1}{w_1}}&{{c_1}{r_1}}&{{c_1}{w_1}}&{{r_1}{w_1}}\\ 1&{{t_2}}&{{c_2}}&{{r_2}}&{{w_2}}&{t_2^2}&{c_2^2}&{r_2^2}&{w_2^2}&{{t_2}{c_2}}&{{t_2}{r_2}}&{{t_2}{w_2}}&{{c_2}{r_2}}&{{c_2}{w_2}}&{{r_2}{w_2}}\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots \\ 1&{{t_n}}&{{c_n}}&{{r_n}}&{{w_n}}&{t_n^2}&{c_n^2}&{r_n^2}&{w_n^2}&{{t_n}{c_n}}&{{t_n}{r_n}}&{{t_n}{w_n}}&{{c_n}{r_n}}&{{c_n}{w_n}}&{{r_n}{w_n}} \end{array}} \right] $ | (13) |
在进行滑坡位移预测时,可直接由实时监测因子构造系数向量,代入回归方程,即可得到位移估值。
2.2 权阵重构在基于间接平差的参数回归中,参数估值可以表示为:
| $ {{\mathit{\boldsymbol{\hat x}}}_{{\rm{pr}}}} = {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PB}}} \right)^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{PL}} $ | (14) |
若单纯地取单位阵作为权值,将无法体现观测值误差,进而导致粗差对回归结果的影响显著。在观测值误差未知而无法定权的情况下,可采取选权迭代法进行权阵重构,步骤如下。
1) 利用单位权阵进行初次半参数回归计算,若所得参数分量估值为
| $ \mathop {\mathit{\boldsymbol{V}}}\limits_{n \times 1} = \mathit{\boldsymbol{B}}{{\mathit{\boldsymbol{\hat x}}}_{{\rm{spr}}}} - \mathit{\boldsymbol{L}} $ | (15) |
2) 令单位权中误差为
| $ w\left( v \right) = \left\{ {\begin{array}{*{20}{c}} {1,}&{\left| v \right| < 1.5{\sigma _0}}\\ {\frac{{1.5{\sigma _0}}}{{\left| v \right|}},}&{1.5{\sigma _0} \le \left| v \right| < 2.5{\sigma _0}}\\ {0,}&{\left| v \right| \ge 2.5{\sigma _0}} \end{array}} \right. $ | (16) |
则重构的权阵可表示为如下的对角矩阵:
| $ \mathop {\mathit{\boldsymbol{P}}}\limits_{n \times n} = {\rm{diag}}\left( {\begin{array}{*{20}{c}} {w\left( {{v_1}} \right)}&{w\left( {{v_2}} \right)}& \cdots &{w\left( {{v_n}} \right)} \end{array}} \right) $ | (17) |
3) 利用重构的权阵,按照步骤1)、2)重新进行半参数回归迭代解算,直至第k次与第k+1次所得参数估值之差的绝对值小于选定的阈值,则停止迭代。
利用选权迭代法对半参数回归结果重新定权、解算,可同时将系统误差和粗差提取至非参数分量
为说明选权迭代法的半参数模型的拟合效果,构造线性模型Y= Bx,x =[2 5]T,B=(bij)200×2,bi1=i/40,bi2=(i/40)2,系统误差为s=(si)200×1,其中si=10sin(iπ/50),i=1, 2, 3…200,偶然误差Δ~N(0,1),并随机构造粗差向量g。在不加入系统误差s即L =Y+ Δ + g情况下,由经典间接平差法(参数回归)得到的参数估值为
同时加入系统误差和粗差后,观测值可表示为L =Y+s+ Δ + g,得到各方法参数估值为
|
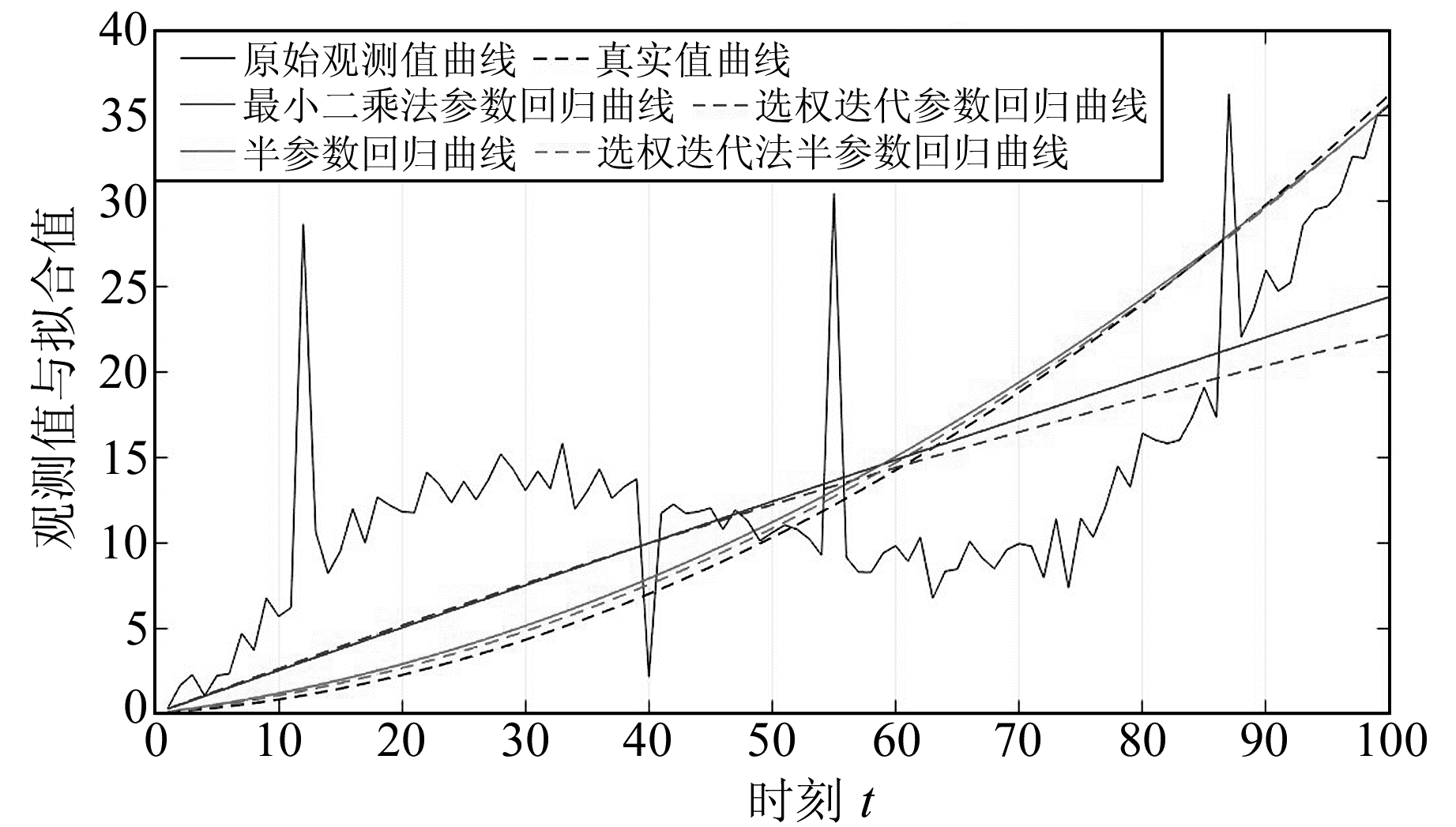
图 1 观测值与各模型拟合值曲线 Fig. 1 The curve of observation values and fitting values of each model |
|
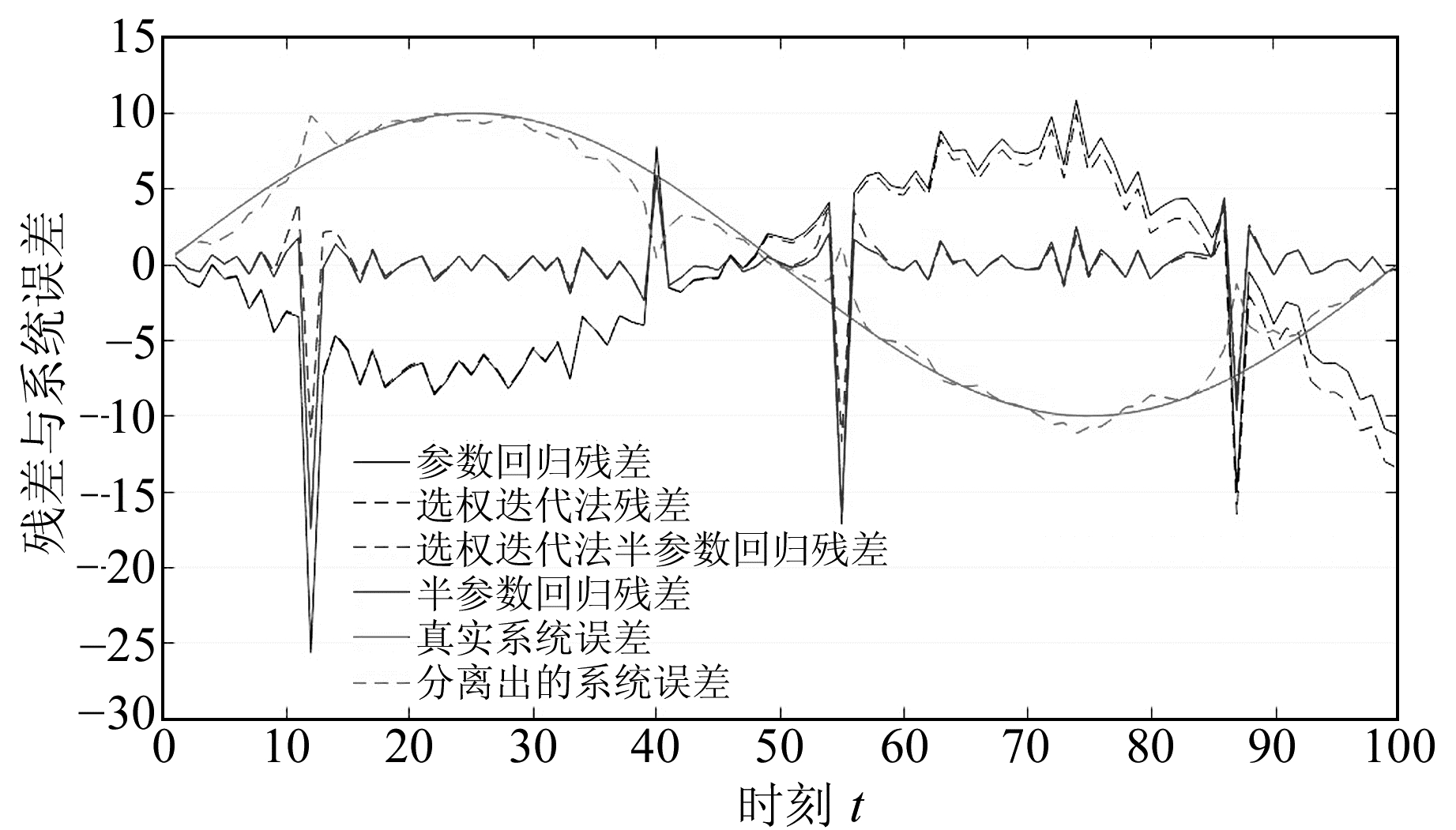
图 2 各模型回归残差比较 Fig. 2 Comparison of regression residual of each model |
由图 1可见,加入选权迭代法的半参数模型的回归拟合效果,在含有系统误差及显著粗差的观测量中比单纯的选权迭代法和半参数回归要好,这是由于通过权阵的不断重构,对粗差进行降权处理,同时利用半参数模型的优势将系统误差分离出来,提高了参数估值的精度。从残差图中可以发现,选权迭代法下的半参数回归模型将观测值中的系统误差和粗差同时提取至非参数分量中,其残差相比其他方法更小,更具有随机性。
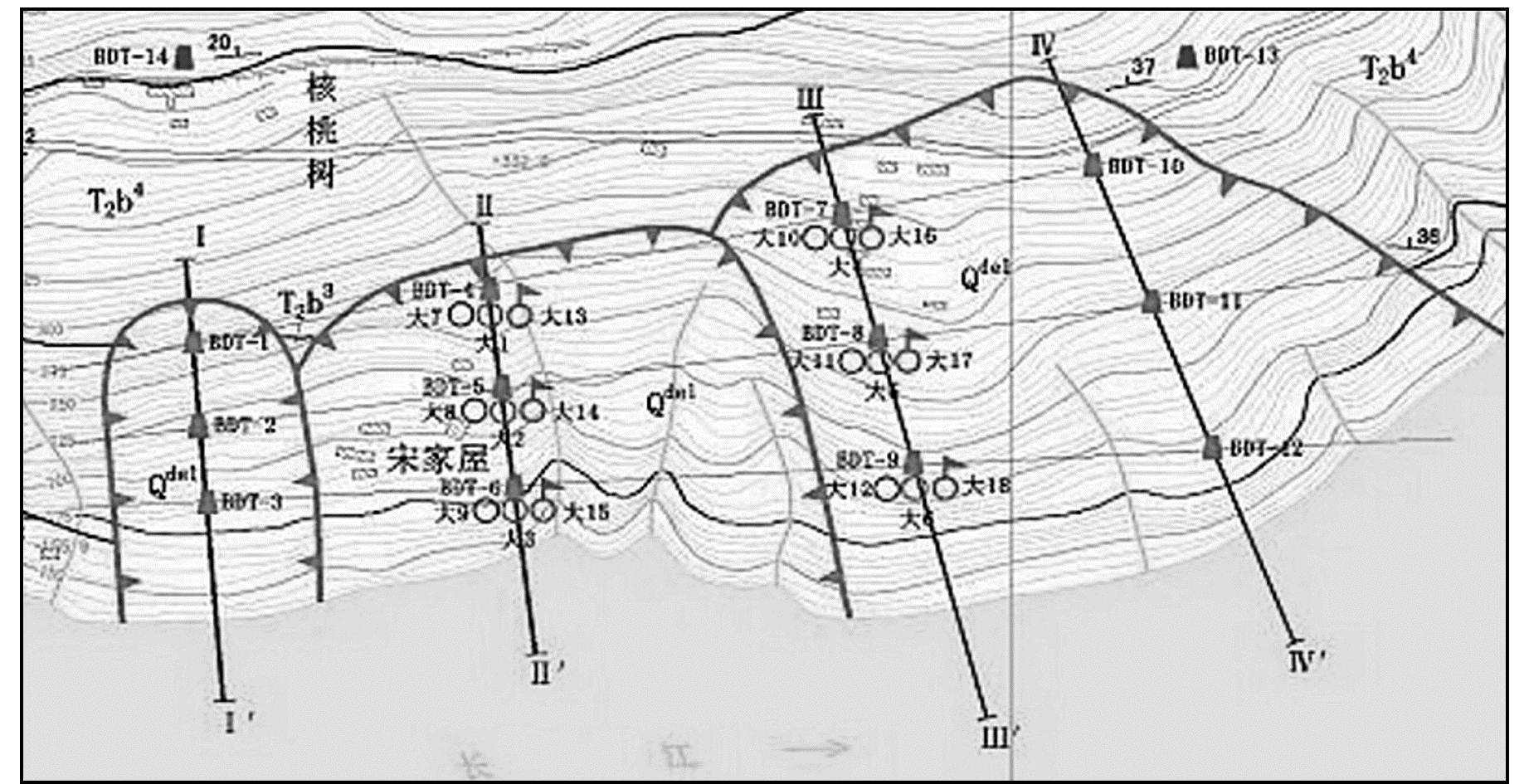
4 工程实例 4.1 滑坡监测数据的选取位于重庆市奉节县的大坪滑坡纵长380 m,宽1 200 m,平均厚度63 m,总体积3 150×104 m3,后缘高程365 m,前缘部分滑体淹没于水下。图 3为大坪滑坡监测点布置示意图,滑坡整体处于缓慢滑移状态。
|
图 3 大坪滑坡监测点平面布设图 Fig. 3 Layout of monitoring points in Daping landslide |
选取滑坡段2007-04~2009-10 BDT-5和BDT-6监测点北向位移作为观测值(36组),监测因子包括长江水位、监测点处地下水位和降雨量,其中位移监测值中的系统误差可能来源于库区环境变化和测量仪器本身导致的周期性误差。由式(13)构造系数矩阵,分别利用多项式回归(参数回归,PR)、选权迭代法(WIPR)、半参数回归(SPR)以及选权迭代法的半参数回归(WISPR),对位移观测值进行拟合和预测,以2009-11~2010-04的8期位移数据作为预测值精度检核依据。
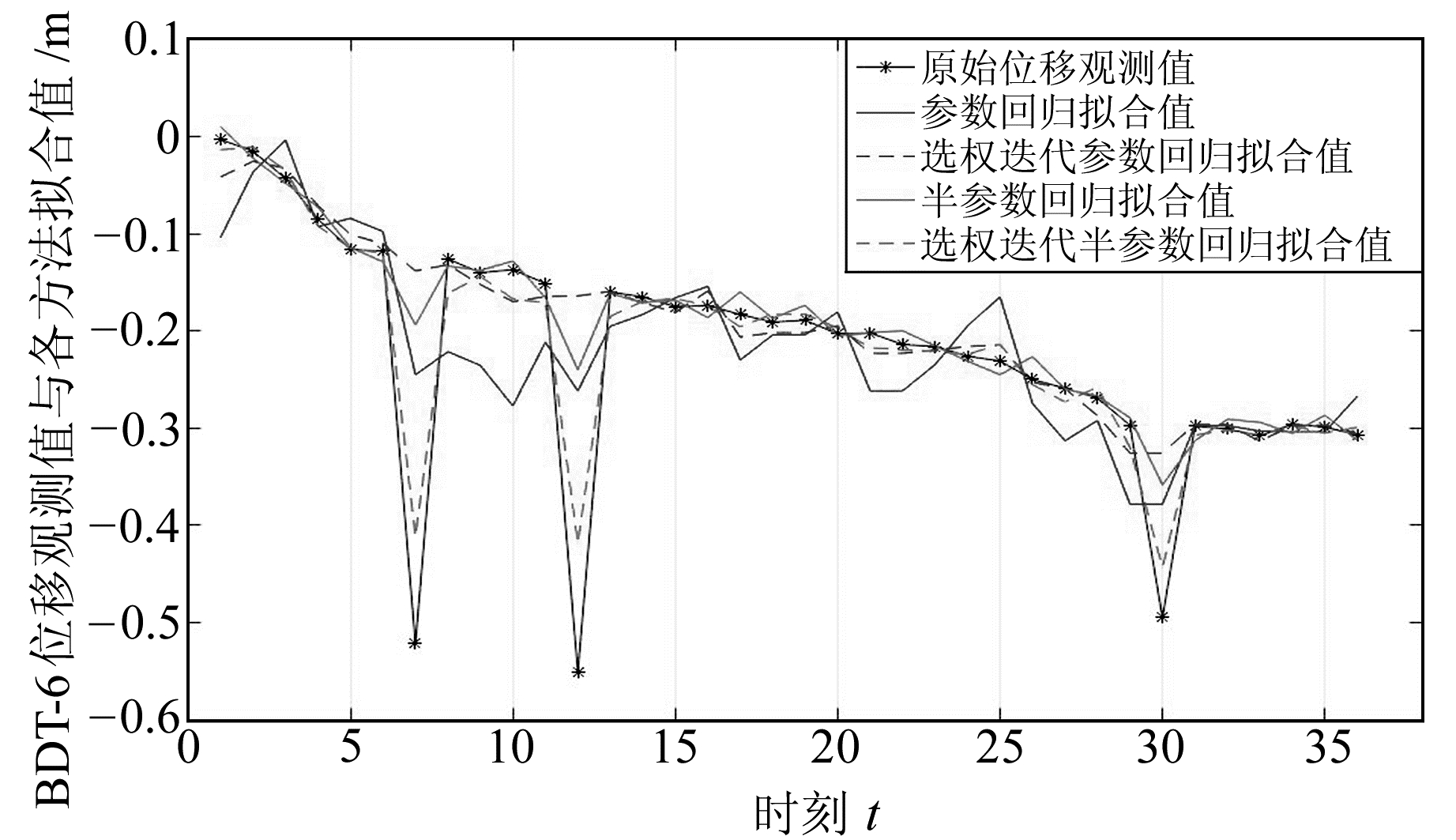
4.2 预测结果及分析经计算,4种方法拟合的残差平方和如表 1所示,BDT-6监测点北向位移的回归拟合效果如图 4所示,其中序列7、12、30处为监测点受到人为移动而导致的观测粗差。图 5和图 6分别为BDT-5与BDT-6北向位移预测曲线,表 2(单位cm)、表 3(单位cm)为两监测点各模型预测误差的比较。
|
|
表 1 各方法拟合残差统计 Tab. 1 The fitting residual statistics of each method |
|
图 4 BDT-6监测点北向位移拟合效果比较 Fig. 4 Comparison of fitting effect of north displacement of BDT-6 |

|
图 5 BDT-5北向位移预测值比较 Fig. 5 Comparison of predicted values of north displacement of BDT-5 |
|
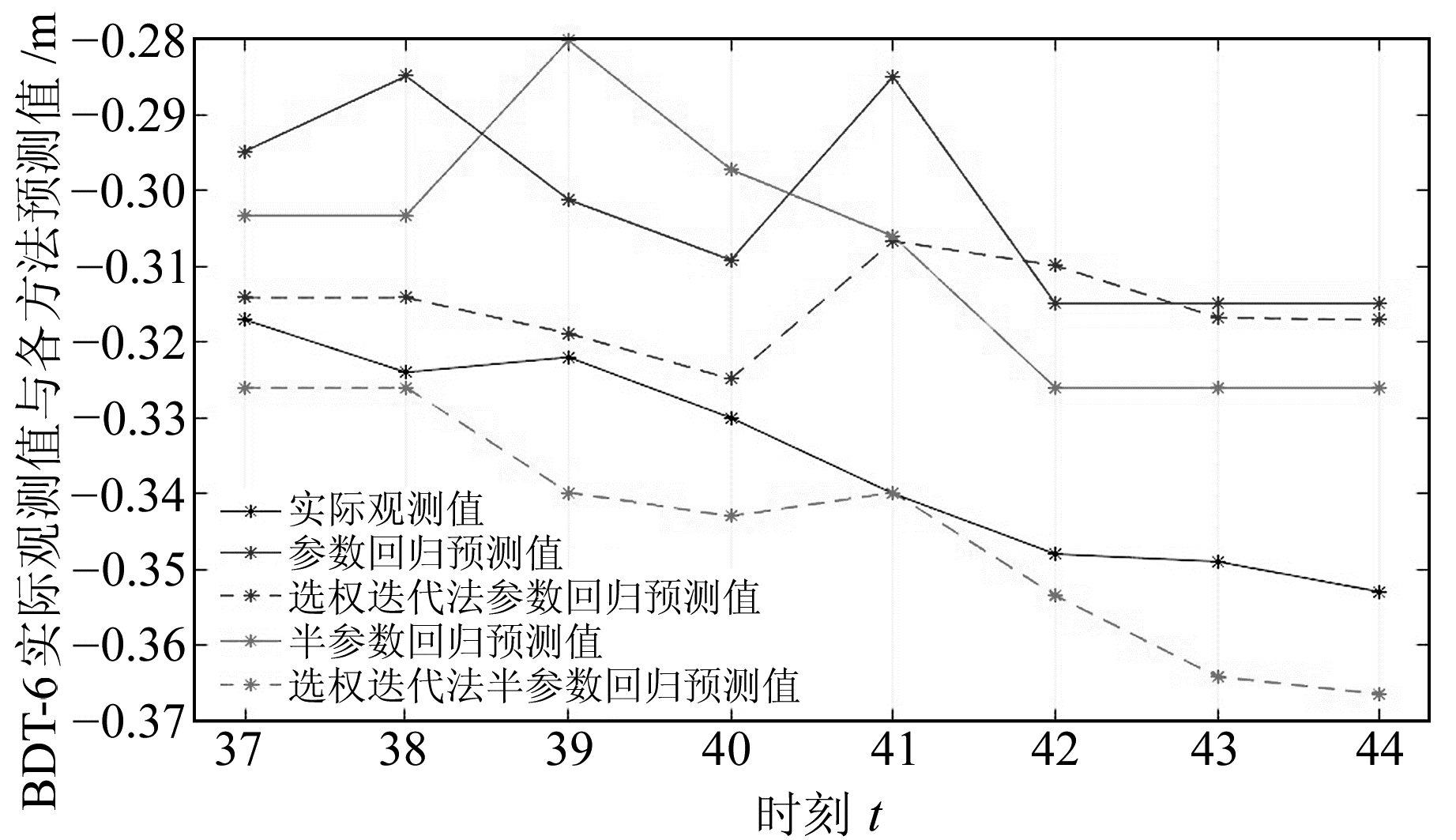
图 6 BDT-6北向位移预测值比较 Fig. 6 Comparison of predicted values of north displacement of BDT-6 |
|
|
表 2 BDT-5位移预测残差比较 Tab. 2 Comparison of residual in BDT-5 displacement prediction |
|
|
表 3 BDT-6位移预测残差比较 Tab. 3 Comparison of residual in BDT-6 displacement prediction |
由图 4可知,当位移观测值中含有系统误差(或非参数分量)和多个粗差时,PR和WIPR因没有考虑系统误差而导致曲线呈现系统性的拟合偏差,而SPR对显著性的粗差识别不够充分,表现在图中粗差处拟合效果远低于WISPR模型。结合表 1可以看出,WISPR模型的拟合残差平方和最小,更能体现实际形变的变化规律。
由预测曲线和预测残差比较可知,WISPR模型的位移预测效果最好,其次是WIPR模型。这是由于该监测点处位移观测值中的粗差相对于系统误差的影响更为显著,突出了选权迭代法对粗差的降权作用。WISPR模型的BDT-5北向位移预测残差最大为12.44 cm,BDT-6处的最大残差为1.79 cm,这是由于BDT-5监测点位于远离江面的山腰处,受长江水位的影响较小,在进行参数计算时,长江水位因子的变化影响了参数的真实估值。
可见,选权迭代法的半参数回归模型有效地兼顾了观测值中的系统误差和粗差,其在大坪滑坡位移监测数据拟合和预测中的效果要优于单纯的选权迭代法和半参数回归模型,且预测相对精度满足滑坡预测精度要求,可以用于三峡库区滑坡监测数据的处理和预测。
5 结语当监测数据中含有未参数化的系统误差与粗差时,常规的最小二乘平差很难发现,经典的半参数模型对显著粗差的识别能力也较弱。本文通过权阵重构建立选权迭代法下的半参数回归模型,将测量数据中的粗差和系统误差同时提取出来,提高了参数估值的精度。并以大坪滑坡为例,验证了该方法的优越性,为滑坡变形预测提供借鉴。此外,本文在影响因子矩阵和选权迭代法中权因子的选取上的讨论比较粗浅,还需要对系数矩阵和最优权因子的选取方法进行深入探讨。
| [1] |
张勤, 张菊清, 岳东杰, 等. 近代测量数据处理与应用[M]. 北京: 测绘出版社, 2011 (Zhang Qin, Zhang Juqing, Yue Dongjie, et al. Advanced Theory and Application of Surveying Data[M]. Beijing: Surveying and Mapping Press, 2011)
(  0) 0) |
| [2] |
丁士俊. 测量数据的建模和半参数估计[D]. 武汉: 武汉大学, 2005 (Ding Shijun. Survey Data Modeling and Semiparametric Estmating[D]. Wuhan: Wuhan University, 2005)
(  0) 0) |
| [3] |
段伟国, 孙世国, 刘玉福. 滑坡预测技术发展概论[J]. 北方工业大学学报, 2008, 20(1): 90-94 (Duan Weiguo, Sun Shiguo, Liu Yufu. Advances and Trends of Landslide Prediction[J]. J North China Univ of Tech, 2008, 20(1): 90-94)
(  0) 0) |
| [4] |
潘雄. 半参数模型的估计理论及其应用[D]. 武汉: 武汉大学, 2005 (Pan Xiong. The Estimation Theory and Application Research in Semi-Parametric Model[D]. Wuhan: Wuhan University, 2005)
(  0) 0) |
| [5] |
孙海燕, 吴云. 半参数回归与模型精化[J]. 武汉大学学报:信息科学版, 2002, 27(2): 172-174 (Sun Haiyan, Wu Yun. Semi-paraetric Regression and Model Refining[J]. Geomatics and Information Science of Wuhan University, 2002, 27(2): 172-174)
(  0) 0) |
| [6] |
高宁. 半参数GM(1, 1)模型参数辨识及滑坡变形预测[J]. 辽宁工程技术大学学报:自然科学版, 2016, 35(3): 326-331 (Gao Ning. Identification of Parameters of Semi-Parametric GM(1, 1) and Its Application in landslide Deformation Prediction[J]. Journal of Liaoning Technical University:Natural Science, 2016, 35(3): 326-331)
(  0) 0) |
| [7] |
王振杰, 欧吉坤, 曲国庆, 等. 用L-曲线法确定半参数模型中的平滑因子[J]. 武汉大学学报:信息科学版, 2004, 29(7): 651-653 (Wang Zhenjie, Ou Jikun, Qu Guoqing, et al. Determining the Smoothing Parameter in Semi-Parametric Model Using L-Curve Method[J]. Geomatics and Information Science of Wuhan University, 2004, 29(7): 651-653)
(  0) 0) |
| [8] |
黄声享, 尹晖, 蒋征. 变形监测数据处理[M]. 武汉: 武汉大学出版社, 2003 (Huang Shengxiang, Yin Hui, Jiang Zheng. Deformation Monitoring Data Processing[M]. Wuhan: Wuhan University Press, 2003)
(  0) 0) |
| [9] |
丁士俊, 陶本藻. 半参数模型及其在形变分析中的应用[J]. 测绘科学, 2004, 29(5): 38-40 (Ding Shijun, Tao Benzao. Semi-parametric Model and Application of Deformation Analysis[J]. Science of Surveying and Mapping, 2004, 29(5): 38-40)
(  0) 0) |
| [10] |
周江文. 经典误差理论与抗差估计[J]. 测绘学报, 1989, 18(2): 115-120 (Zhou Jiangwen. Classical Theory of Errors and Robust Estimation[J]. Acta Geodaetica et Cartographica Sinica, 1989, 18(2): 115-120)
(  0) 0) |
| [11] |
陈西强, 黄张裕. 抗差估计的选权迭代法分析与比较[J]. 测绘工程, 2010, 19(4): 8-11 (Chen Xiqiang, Huang Zhangyu. Analysis and Comparison of the Selecting Weight Iteration Method in Resistance Robust Estimation[J]. Engineering of Surveying and Mapping, 2010, 19(4): 8-11)
(  0) 0) |
| [12] |
王奉伟, 周世健, 周清, 等. 选权迭代法残差初值求解方法比较[J]. 测绘科学, 2015, 40(8): 18-21 (Wang Fengwei, Zhou Shijian, Zhou Qing, et al. Comparisons between Three Methods Initial Residuals Problem of Selecting Weight Iteration Method[J]. Science of Surveying and Mapping, 2015, 40(8): 18-21)
(  0) 0) |
| [13] |
Gao J T, Tong H, Wolff R C L. Adaptive Orthogonal Series Estimation in Additive Stochastic Regression Models[J]. Statistica Sinica, 2002, 12: 409-428
(  0) 0) |
| [14] |
丁士俊, 陶本藻. 半参数回归与平差模型[J]. 大地测量与地球动力学, 2003, 23(4): 111-114 (Ding Shijun, Tao Benzao. Semi-parametric Regression and Adjustment Models[J]. Journal of Geodesy and Geodynamics, 2003, 23(4): 111-114)
(  0) 0) |
| [15] |
徐波, 高井祥, 李增科, 等. 基于选权迭代的总体最小二乘算法在三维坐标转换中的应用[J]. 大地测量与地球动力学, 2015, 35(4): 693-696 (Xu Bo, Gao Jingxiang, Li Zengke, et al. The Application of the Total Least Squares Algorithm based on Reweighting Iteration to the Conversion of Three-Dimensional Coordinates[J]. Journal of Geodesy and Geodynamics, 2015, 35(4): 693-696)
(  0) 0) |
2. Key Laboratory of Precise Engineering and Industry Surveying of NASMG, Wuhan University, 129 Luoyu Road, Wuhan 430079, China;
3. Liaoning College of Communication, 102 Shenbei Road, Shenyang 110122, China
 2018, Vol. 38
2018, Vol. 38


