2. 国家卫星定位系统工程技术研究中心, 武汉市珞喻路129号, 430079
在短距离范围内采用GNSS相对观测模式可以很好地消除卫星轨道误差、卫星钟误差以及大气时延等公共误差,但很难通过站间作差方式消除与测站环境密切相关的多路径误差。载波多路径主要与测站附近反射面的信号反射系数、频率和入射角有关,其大小最大可达波长的1/4[1-2]。国内外对削弱多路径效应的研究主要集中在抗多路径天线及信号处理层面的抑径算法[3-5]和高精度GNSS数据处理算法两方面。
研究表明,GPS信号以一定的入射角经反射面形成的多路径误差的典型周期为120~2 400 s[6]。综合考虑导航卫星的空间运动及其相对稳定的回归周期,地面反射环境对静态测站引起的多路径在时间序列上具有明显的恒星日周期特性[7]。利用这一特性,对连续多天的GPS解算结果在坐标值域进行恒星日滤波,能够有效削弱多路径的影响,提高定位精度[1-2]。多路径在坐标值域的周期性影响是参与坐标解算的各个卫星信号对测站周期性影响的叠加。当GPS、Beidou、Galileo多系统联合定位时,由于卫星回归周期差异较大,导致坐标域的多路径周期比单系统的卫星回归周期更长,不利于利用较短观测时段消除多路径,而应该在观测值域对各系统卫星单独进行多路径建模[8-9]。为此,本文首先研究BDS、GPS等各类卫星的回归周期特性并推导相应的计算公式,然后探讨如何在观测值域利用双差观测值残差分离单星单差(站间单差)多路径的建模方法,最后利用实测BDS和GPS实时变形监测数据评估基于观测值域的多路径建模方法的精度。
1 GNSS回归周期计算方法本文使用广播星历计算卫星的回归周期。根据开普勒第三定律,卫星的平均角速度(顾及修正量)[10]为:
| $ n = \frac{{2\pi }}{T} = {a^{ - \frac{3}{2}}}{\mu ^{\frac{1}{2}}} + {n_c} $ | (1) |
式中,a为卫星椭圆轨道半长轴;nc为平均角速度修正量;μ为地球引力常数,各个卫星系统所定义的值可能有差异;T为某系统卫星的轨道周期(恒星日)。参数a和nc可直接从卫星播发的广播星历中获取。设地球自转周期为Te(1恒星日),若存在[11]
| $ T/{T_e} = p/q $ | (2) |
则称Tq或者Tep为回归周期。其中,p和q是互为质数的整数,在考虑摄动因素时需作近似处理。由于地球在自转的同时还绕太阳公转(周期约为365.256 4平太阳日),因此地球自转周期时长用平太阳时(UTC)表示:
| $ {T_e} = 86400 \times \frac{{365.2564}}{{365.2564 + 1}} \approx 86164.0996\;{\rm{s}} $ | (3) |
顾及式(2)和式(3),可采用试探法计算出p和q,进而得到GNSS主流导航系统的卫星回归周期计算公式(GLONASS需要进一步转换星历计算a值,本文不作讨论),见表 1。
|
|
表 1 BDS、GPS和Galileo系统卫星回归周期 Tab. 1 The revisiting orbital period of BDS, GPS and Galileo |
由表 1可知,BDS、GPS和Galileo由于设计轨道的长半轴差异较大,导致各个系统卫星的回归周期差异非常明显。BDS的GEO和IGSO卫星具有相同的轨道周期且与地球自转周期相同,即p/q=1/1;而MEO卫星轨道运行13周正好是地球自转7周所需时间(p/q=7/13),可据此推断其回归周期约7 d,但会提前约7×(86 400-86 164)=1 650 s。同理,GPS卫星需运行2周才能满足其星下点轨迹正好重合(p/q=1/2),而Galileo需要17周(p/q=10/17)。实际应用中,各种摄动力的影响会导致Tq与Tep计算的回归周期存在数秒至几十秒的差异,此时应按表 1中Tq计算回归周期时长,按86 400 p-Tq计算周期提前量。实测数据表明,同一卫星系统各个卫星的回归周期略有差异,并且同一卫星不同时段的回归周期也存在几秒到几十秒的波动[9],特别是BDS的GEO卫星。
2 观测值域多路径误差建模基于恒星日回归周期的多路径滤波算法在坐标值域和观测值域都有应用[1-2, 8-9]。考虑到基于载波的相对定位方法仍是mm级定位的主要手段,本文主要讨论基于站间单差观测值域的多路径误差建模。这主要基于两点考虑:1)就静态观测模式而言,站间单差残留的多路径误差周期仅与单星回归周期有关,各类卫星可按各自回归周期进行独立处理,避免在坐标值域内由于多类卫星的混合造成混合多路径周期过长的问题;2)消除多路径后的单差观测值能够任意两两组合形成双差观测值,与参考星的选择无关,方便后续实时相对定位的解算。
在历元时刻t,测站1和2(中短基线)对GNSS单星i作差得站间单差观测方程[15]:
| $ \begin{array}{l} {\rm{SD}}_{1, 2}^i\left( {\rm{t}} \right) = \rho _{1, 2}^i - c{R_{1, 2}} + \lambda N_{1, 2}^i + \\ \;\;\;\;\;\;\;\;M_{1, 2}^i + \varepsilon _{1, 2}^i, {\rm{}}i = 1, n \end{array} $ | (4) |
式中,ρ、R、N、M、ε分别是卫地几何距离、接收机钟差、载波模糊度、多路径误差和观测值噪声,c、λ、n分别是光速、单个频率波长和同一历元参与解算的卫星数。选择参考星r,对式(4)组成双差:
| $ {\rm{DD}}_{1, 2}^{i, r}\left( {\rm{t}} \right) = {\rm{SD}}_{1, 2}^i\left( {\rm{t}} \right) - {\rm{SD}}_{1, 2}^r\left( t \right) $ | (5) |
| $ N_{1, 2}^{i, r} = N_{1, 2}^i - N_{1, 2}^r $ | (6) |
式中,DD1, 2i, r为i星与参考星r组成的双差观测值。将已知基线坐标、固定后的双差模糊度式(6)代入式(4),所得到的卫星单差残差除残余多路径外,还含有公共项R1, 2和N1, 2r。该公共项的大小随历元不断变化,但不影响由式(5)确定的双差残差。因此为方便后续分析,常常采用重心基准法[10]消除同一历元所有卫星单差的公共部分(扣除均值),则新的卫星单差残差之和为:
| $ \begin{array}{l} \mathop \sum \limits_{i = 1}^n \widetilde {{\rm{SD}}_{1, 2}^i\left( t \right)} = \mathop \sum \limits_{i = 1}^n {\rm{SD}}_{1, 2}^i\left( t \right) - \\ \;\;\;\;\;n \cdot \frac{1}{n}\mathop \sum \limits_{i = 1}^n {\rm{SD}}_{1, 2}^i\left( t \right) = 0 \end{array} $ | (7) |
新的站间单差之差
| $ \begin{array}{l} \widetilde {{\rm{SD}}_{1, 2}^r\left( t \right) = }\frac{1}{{n - 1}}\left( {\mathop \sum \limits_{i = 1}^{n - 1} \widetilde {SD_{1, 2}^i\left( t \right)} - } \right.\\ \left. {\mathop \sum \limits_{i = 1}^{n - 1} DD_{1, 2}^{i, r}\left( t \right)} \right) = - \frac{1}{n}\mathop \sum \limits_{i = 1}^{n - 1} DD_{1, 2}^{i, r}\left( t \right) \end{array} $ | (8) |
根据式(5)、式(8)可计算出重心基准意义下的各颗卫星站间单差残差值。在观测值域提取单差载波多路径修正模型需注意两点:1)各个卫星建议连续观测一个完整的回归周期,比如北斗GEO/IGSO需要连续观测1 d,MEO连续观测7 d。2)为了减少观测值噪声的影响,建议在提取单差载波多路径之前利用小波算法作消噪处理。基于观测值域的恒星日滤波消多路径误差算法流程为:首先在前一个回归周期内利用已知基线坐标(也可利用长时间静态解)进行基线强约束条件下的相对定位解算;然后按式(5)~(8)从模糊度固定后的双差残差中分离出各个卫星单差残差时间序列;再进行小波去噪处理,得到各个卫星单差载波模糊度多路径时间序列修正模型,在下个回归周期对应历元将路径作为系统误差直接从线性化的单差载波观测值残差中消除;在新的回归周期内(当前历元)利用广播星历计算各个卫星回归周期间隔,与前一个回归周期进行匹配提取相应的载波多路径修改正值并对当前历元单差载波残差进行修正;最后,使用修正后的单差载波观测值进行实时相对定位(其余算法流程与修正前的实时相对定位算法流程相同),得到多路径修正后的实时坐标,见图 1。

|
图 1 观测值域恒星日滤波算法流程 Fig. 1 The flow of sidereal filtering algorithm based on the observation domain |
本文采集数据时选择直线长度约85 m的短基线,基准站位于武汉大学信息学部实验大楼楼顶,流动站位于测绘学院。基线两端采用同类天线并进行定向处理以消除天线相位中心误差对定位的影响;电离层和对流程误差采用模型改正,双差模糊度采用LAMBDA算法固定。使用Trimble R9多模接收机,能够采集和分析BDS和GPS观测数据(由于Galileo卫星数较少,未作深入分析)。数据处理方面,对RTKLIB软件进行扩展,实现本文讨论的基于观测值域的多路径消除算法。连续采集14 d观测数据(2017年DOY195~208),覆盖单星回归周期最长达7 d的BDS MEO所需的最短时间。基于最后7 d数据对GPS、BDS和GPS+BDS联合实时定位的多路径修正效果进行分析和讨论。为不失一般性,本文仅分析GPS单频L1和BDS B1观测数据。
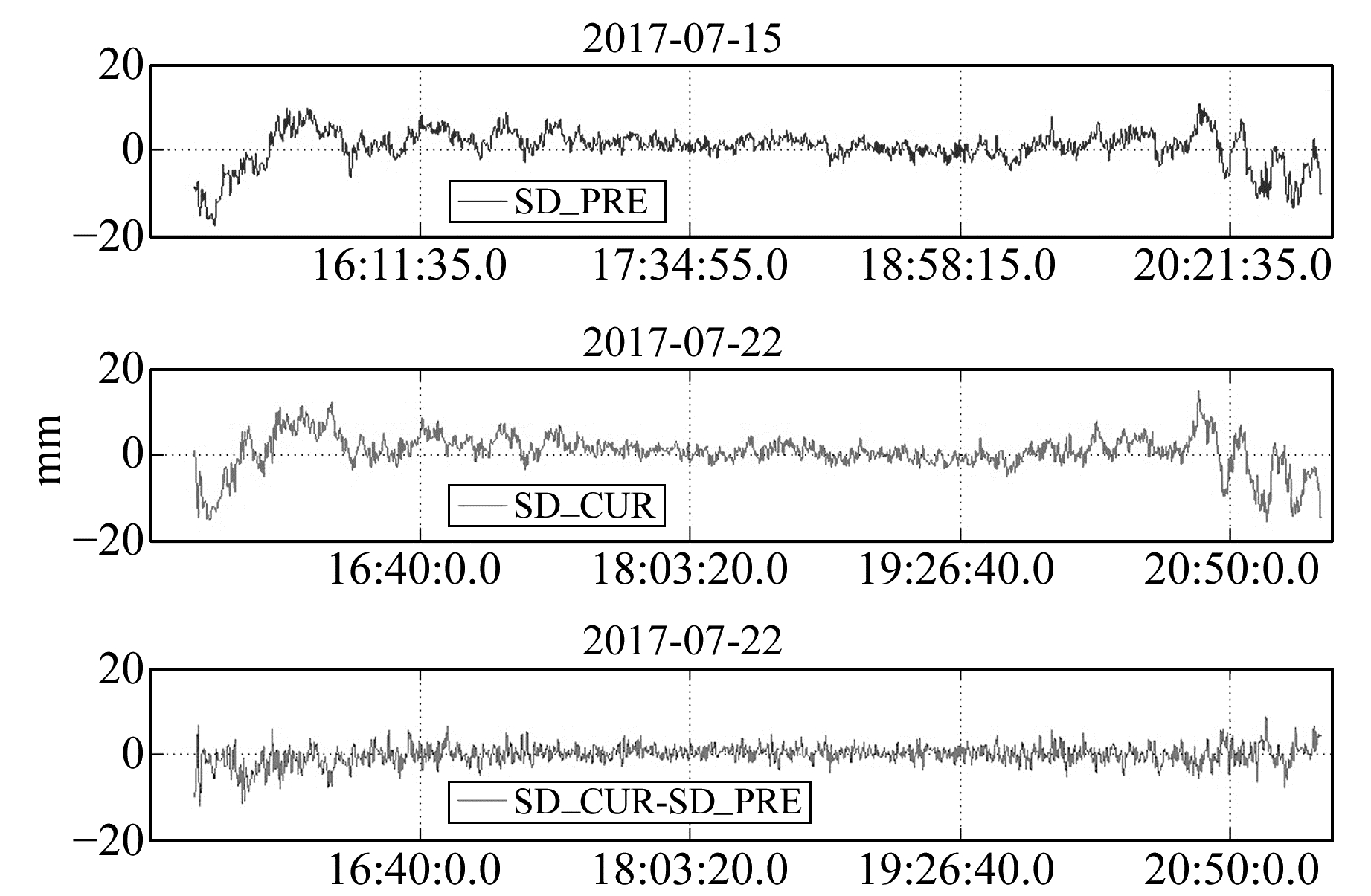
图 2是固定基线坐标和模糊度后计算的BDS卫星C14站间单差残差时间序列。该图显示,相邻回归周期的C14单差载波残差时间序列存在明显相似的变化趋势(图 2上部和中部子图),其相关系数达到0.79。这种系统性偏差主要由多路径效应引起。将相邻周期同一卫星载波单差残差对应时刻相减(C14提前量约1 705 s),可大大削弱多路径误差的影响(图 2下部子图)。
|
图 2 BDS C14相邻回归周期的单差残差时间序列 Fig. 2 The single-differenced residuals of two adjacent revisiting periods for C14 |
由于卫星在星下点回归周期上与测站及周边环境在空间上具有高度相似性,导致多路径也呈现出与卫星回归周期一致的周期性变化。表 2统计了同一卫星(GPS G03和BDS C02)连续多个回归周期间隔之间的相关系数, 结果表明:1)不同回归周期间隔的多路径误差仍然体现出强相关,G03与C02卫星前后多个回归周期之间的相关系数大部分在0.7以上,其他卫星结论亦相近。因此,在实际应用中可以建立一个按照回归周期为单位的载波单差多路径修正模型数据库,如果相邻回归周期由于某种原因没有观测数据可用,则可以采用相应的历史多路径修正模型进行修正。2)回归周期间隔越近,多路径误差相关性越高。理论上,同一颗卫星的回归周期应该相同,但由于受地球非球形摄动、太阳光压和潮汐等摄动影响,同一卫星相邻回归周期的卫星位置并不重合,会出现几十m到几十km的几何距离误差。尽管如此,BDS IGSO和MEO卫星相邻回归周期的提前量变化一般不超过2 s/周,而GEO卫星的波动较大,最大可达10 s/周(限于篇幅未列出)。
|
|
表 2 G03(右上)和C02(左下)回归周期间相关系数 Tab. 2 The correlation coefficient of revisiting periods for G03 (upper right) and C02 (bottom left) |
图 3给出了年积日202的BDS、GPS以及GPS+BDS联合定位未使用和使用基于观测值域的多路径误差修正模型的定位结果。坐标参考值采用7 d GPS L1定位静态解的平均值(三维RMS优于1.2 mm)。图 3表明,即使本文使用的短基线仅为85 m,但双差残余多路径误差仍对定位有明显的系统性影响。考虑或不考虑多路径修正,对GPS东方向、北方向分量的定位结果没有产生明显的系统性偏差,但使用多路径误差修正的定位结果离散度更小。相比较而言,BDS未考虑多路径误差修正时,东方向产生明显偏离,而考虑多路径修正后东方向的定位结果明显改善。这很可能跟BDS当前特殊星座和测站相对位置(环境)有关,5颗GEO卫星相对地面变化较小,造成多路径效应以近似常量的形式影响载波测量值,且5颗IGSO卫星的变化也比MEO慢得多,而MEO卫星参与解算的卫星较少,最终导致多路径对定位产生较大的系统性偏差(文献[16]报道卫星星上多路径误差在短基线双差模式下消除)。这种偏差也影响到BDS与GPS的联合定位精度。相比东方向和北方向,高程方向未考虑多路径模型改正时除标准差较大外,整体上存在比较明显的系统性偏差。

|
图 3 年积日202实时动态定位结果(深色线为修正前坐标结果,浅色线为修正后坐标结果) Fig. 3 The real-time kinematic positioning results of DOY 202 |
表 3统计了年积日202~208共7 d的解算结果,其中RMS、RMS_M分别表示考虑多路径模型改正前后的均方根统计值。采用多路径模型改正前后,BDS平均定位精度在东、北、高方向由3.59 mm、3.94 mm、17.43 mm提高至1.97 mm、2.39 mm、7.76 mm,分别提升45%、39%、55%;GPS则提高至1.98 mm、2.41 mm、6.01 mm,分别提升41%、41%、58%。而BDS+GPS定位精度最高,由2.45 mm、2.3 mm、11.33 mm提高到1.49 mm, 1.51 mm, 4.77 mm,分别提升39%、34%、49%。整体而言,修正多路径误差后,基线解在时间序列上的系统性偏差明显削弱,三维定位精度达到mm级。
|
|
表 3 年积日202~208实时动态定位结果改正效果 Tab. 3 The real-time kinematic positioning results of DOY 202~208 |
本文分析了多类卫星的轨道回归周期特性并推导相应公式,研究基于观测值域的多路径误差建模方法,利用BDS/GPS短基线观测数据对算法的改正效果进行分析,得到如下结论:
1) 各类卫星的回归周期跟其轨道高度密切相关。尽管各类卫星保持相对稳定,但由于卫星轨道的渐变与轨道机动,同一卫星系统各个卫星的回归周期略有差异,且同一卫星相邻回归周期也存在几s到几十s的波动。
2) 实验表明,GPS+BDS实时联合定位精度最高,GPS与BDS比较接近,但整体上基于观测值域多路径误差修正方法能够有效抑制载波多路径对GNSS实时定位的影响,可使BDS、GPS及GPS+BDS平均定位精度在北、东和高程方向分别提高约42%、38%和54%,达到mm级的三维实时定位精度。本文仅研究了观测值域多路径误差修正方法在GPS和BDS中的应用,但该方法对Galileo和GLONASS同样适用,在高精度GNSS实时变形监测中具有较高的参考价值。
| [1] |
刘丹, 解强, 张鑫, 等. 北京冬季雾霾频发期VOCs源解析及健康风险评价[J]. 环境科学, 2016, 37(10): 3693-3701 (Liu D, Xie Q, Zhang X, et al. Source apportionment and health risk assessment of VOCs during the haze period in the winter in Beijing[J]. Environmental Science, 2016, 37(10): 3693-3701)
(  0) 0) |
| [2] |
Gee I L, Sollars C J. Ambient air levels of volatile organic compounds in Latin American and Asian cities[J]. Chemosphere, 1998, 36(11): 2497-2506 DOI:10.1016/S0045-6535(97)10217-X
(  0) 0) |
| [3] |
王铁宇, 李奇锋, 吕永龙. 我国VOCs的排放特征及控制对策研究[J]. 环境科学, 2013, 34(12): 4756-4763 (Wang T Y, Li Q F, Lü Y L. Characteristics and countermeasures of volatile organic compounds (VOCs) emission in China[J]. Environmental Science, 2013, 34(12): 4756-4763)
(  0) 0) |
| [4] |
王伯光, 张远航, 邵敏. 珠江三角洲大气环境VOCs的时空分布特征[J]. 环境科学, 2004, 25(S1): 7-15 (Wang B G, Zhang Y H, Shao M. Special and temporal distribution character of VOCs in the ambient air of Peal River Delta region[J]. Environmental Science, 2004, 25(S1): 7-15)
(  0) 0) |
| [5] |
吴方堃, 王跃思, 安俊琳, 等. 北京奥运时段VOCs浓度变化、臭氧产生潜势及来源分析研究[J]. 环境科学, 2010, 31(1): 10-16 (Wu F K, Wang Y S, An J L, et al. Study on concentration, ozone production potential and sources of VOCs in the atmosphere of Beijing during Olympics period[J]. Environmental Science, 2010, 31(1): 10-16)
(  0) 0) |
| [6] |
王倩, 陈长虹, 王红丽, 等. 上海市秋季大气VOCs对二次有机气溶胶的生成贡献及来源研究[J]. 环境科学, 2013, 34(2): 424-433 (Wang Q, Chen C H, Wang H L, et al. Forming potential of secondary organic aerosols and sources apportionment of VOCs in autumn of Shanghai, China[J]. Environmental Science, 2013, 34(2): 424-433)
(  0) 0) |
| [7] |
全国城市空气质量实时发布平台[EB/OL]. http://106.37.208.233:20035, 2018-01-01.
(  0) 0) |
| [8] |
Huang C, Chen C H, Li L, et al. The study of emission inventory on anthropogenic air pollutants and VOC species in the Yangtze River Delta region, China[J]. Atmospheric Chemistry and Physics Discussions, 2011, 11(1): 951-983 DOI:10.5194/acpd-11-951-2011
(  0) 0) |
| [9] |
孙杰, 王跃思, 吴方堃, 等. 唐山市和北京市夏秋季节大气VOCs组成及浓度变化[J]. 环境科学, 2010, 31(7): 1438-1443 (Sun J, Wang Y S, Wu F K, et al. Concentration and change of VOCs in summer and autumn in Tangshan[J]. Environmental Science, 2010, 31(7): 1438-1443)
(  0) 0) |
| [10] |
周裕敏, 郝郑平, 王海林. 北京城乡结合地空气中挥发性有机物健康风险评价[J]. 环境科学, 2011, 32(12): 3566-3570 (Zhou Y M, Hao Z P, Wang H L. Health risk assessment of atmospheric volatile organic compounds in urban-rural juncture belt area[J]. Environmental Science, 2011, 32(12): 3566-3570)
(  0) 0) |
| [11] |
Kim E, Hopke P K, Edgerton E S. Source identification of Atlanta aerosol by positive matrix factorization[J]. Journal of the Air & Waste Management Association, 2003, 53(6): 731-739
(  0) 0) |
| [12] |
周静博, 任毅斌, 洪纲, 等. 利用SPAMS研究石家庄市冬季连续灰霾天气的污染特征及成因[J]. 环境科学, 2015, 36(11): 3972-3980 (Zhou J B, Ren Y B, Hong G, et al. Characteristics and formation mechanism of a multi-day haze in the winter of Shijiazhuang using a single particle aerosol mass spectrometer (SPAMS)[J]. Environmental Science, 2015, 36(11): 3972-3980)
(  0) 0) |
| [13] |
温彦平, 闫雨龙, 李丽娟, 等. 太原市夏季挥发性有机物污染特征及来源分析[J]. 太原理工大学学报, 2016, 47(3): 331-336 (Wen Y P, Yan Y L, Li L J, et al. Pollution characteristic and source analysis of volatile organic compounds in summer in Taiyuan[J]. Journal of Taiyuan University of Technology, 2016, 47(3): 331-336)
(  0) 0) |
| [14] |
李丽娟. 朔州市城区大气挥发性有机物的特征研究及来源分析[D]. 太原: 太原理工大学, 2015. (Li L J. A preliminary study on characteristics and source of volatile organic compounds in the urban area of Shuozhou[D]. Taiyuan: Taiyuan University of Technology, 2015.)
(  0) 0) |
| [15] |
李雷, 李红, 王学中, 等. 广州市中心城区环境空气中挥发性有机物的污染特征与健康风险评价[J]. 环境科学, 2013, 34(12): 4558-4564 (Li L, Li H, Wang X Z, et al. Pollution characteristics and health risk assessment of atmospheric VOCs in the downtown area of Guangzhou, China[J]. Environmental Science, 2013, 34(12): 4558-4564)
(  0) 0) |
| [16] |
李娜. 济南市环境空气中VOCs组分特征及转化规律研究[D]. 济南: 山东建筑大学, 2014.
(  0) 0) |
| [17] |
Tang J H, Chan L Y, Chan C Y, et al. Characteristics and diurnal variations of NMHCs at urban, suburban, and rural sites in the Pearl River Delta and a remote site in South China[J]. Atmospheric Environment, 2007, 41(38): 8620-8632 DOI:10.1016/j.atmosenv.2007.07.029
(  0) 0) |
| [18] |
Perry R, Gee I L. Vehicle emissions in relation to fuel composition[J]. Science of the Total Environment, 1995, 169(1-3): 149-156 DOI:10.1016/0048-9697(95)04643-F
(  0) 0) |
| [19] |
Scheff P A, Wadden R A. Receptor modeling of volatile organic compounds. 1. Emission inventory and validation[J]. Environmental Science & Technology, 1993, 27(4): 617-625
(  0) 0) |
| [20] |
Andreae M O, Merlet P. Emission of trace gases and aerosols from biomass burning[J]. Global Biogeochemical Cycles, 2001, 15(4): 955-966 DOI:10.1029/2000GB001382
(  0) 0) |
| [21] |
Brocco D, Fratarcangeli R, Lepore L, et al. Determination of aromatic hydrocarbons in urban air of Rome[J]. Atmospheric Environment, 1997, 31(4): 557-566 DOI:10.1016/S1352-2310(96)00226-9
(  0) 0) |
| [22] |
dos Santos C Y M, de Almeida Azevedo D, de Aquino Neto F R. Atmospheric distribution of organic compounds from urban areas near a coal-fired power station[J]. Atmospheric Environment, 2004, 38(9): 1247-1257 DOI:10.1016/j.atmosenv.2003.11.026
(  0) 0) |
| [23] |
Barletta B, Meinardi S, Rowland F S, et al. Volatile organic compounds in 43 Chinese cities[J]. Atmospheric Environment, 2005, 39(32): 5979-5990 DOI:10.1016/j.atmosenv.2005.06.029
(  0) 0) |
| [24] |
Liu Y, Shao M, Zhang J, et al. Distributions and source apportionment of ambient volatile organic compounds in Beijing city, China[J]. Journal of Environmental Science and Health, Part A:Toxic/hazardous Substances and Environmental Engineering, 2005, 40(10): 1843-1860 DOI:10.1080/10934520500182842
(  0) 0) |
| [25] |
Jobson B T, Parrish D D, Goldan P, et al. Spatial and temporal variability of nonmethane hydrocarbon mixing ratios and their relation to photochemical lifetime[J]. Journal of Geophysical Research, 1998, 103(D11): 13557-13567 DOI:10.1029/97JD01715
(  0) 0) |
| [26] |
Liu Y, Shao M, Fu L L, et al. Source profiles of volatile organic compounds (VOCs) measured in China:Part Ⅰ[J]. Atmospheric Environment, 2008, 42(25): 6247-6260 DOI:10.1016/j.atmosenv.2008.01.070
(  0) 0) |
| [27] |
Norris G, Vedantham R. EPA positive matrix factorization (PMF) 3. 0 fundamentals and user guide[R]. USA: EPA, 2008.
(  0) 0) |
| [28] |
魏巍, 王书肖, 郝吉明. 中国涂料应用过程挥发性有机物的排放计算及未来发展趋势预测[J]. 环境科学, 2009, 30(10): 2809-2815 (Wei W, Wang S X, Hao J M. Estimation and forecast of volatile organic compounds emitted from paint uses in China[J]. Environmental Science, 2009, 30(10): 2809-2815 DOI:10.3321/j.issn:0250-3301.2009.10.001)
(  0) 0) |
| [29] |
Yuan B, Shao M, Lu S H, et al. Source profiles of volatile organic compounds associated with solvent use in Beijing, China[J]. Atmospheric Environment, 2010, 44(15): 1919-1926 DOI:10.1016/j.atmosenv.2010.02.014
(  0) 0) |
| [30] |
Yan Y L, Yang C, Peng L, et al. Emission characteristics of volatile organic compounds from coal-, coal gangue-, and biomass-fired power plants in China[J]. Atmospheric Environment, 2016, 143: 261-269 DOI:10.1016/j.atmosenv.2016.08.052
(  0) 0) |
| [31] |
王志辉, 张树宇, 陆思华, 等. 北京地区植物VOCs排放速率的测定[J]. 环境科学, 2003, 24(2): 7-12 (Wang Z H, Zhang S Y, Lu S H, et al. Screenings of 23 plant species in Beijing for volatile organic compound emissions[J]. Environmental Science, 2003, 24(2): 7-12)
(  0) 0) |
| [32] |
谢军飞, 李延明. 植物源挥发性有机化合物排放清单的研究进展[J]. 环境科学, 2013, 34(12): 4779-4786 (Xie J F, Li Y M. Research advances on volatile organic compounds emission inventory of plants[J]. Environmental Science, 2013, 34(12): 4779-4786)
(  0) 0) |
| [33] |
Guenther A, Geron C, Pierce T, et al. Natural emissions of non-methane volatile organic compounds, carbon monoxide, and oxides of nitrogen from North America[J]. Atmospheric Environment, 2000, 34(12-14): 2205-2230 DOI:10.1016/S1352-2310(99)00465-3
(  0) 0) |
| [34] |
张玉欣, 安俊琳, 林旭, 等. 南京北郊冬季挥发性有机物来源解析及苯系物健康评估[J]. 环境科学, 2017, 38(1): 1-12 (Zhang Y X, An J L, Lin X, et al. Source apportionment of volatile organic compounds and health assessment of benzene series in northern suburb of Nanjing in winter[J]. Environmental Science, 2017, 38(1): 1-12)
(  0) 0) |
| [35] |
Jorquera H, Rappenglück B. Receptor modeling of ambient VOC at Santiago, Chile[J]. Atmospheric Environment, 2004, 38(25): 4243-4263 DOI:10.1016/j.atmosenv.2004.04.030
(  0) 0) |
| [36] |
Draxler R R, Hess G D. An overview of the HYSPLIT-4 modelling system for trajectories, dispersion and deposition[J]. Australian Meteorological Magazine, 1998, 47(4): 295-308
(  0) 0) |
| [37] |
Yu S C, Mathur R, Kang D W, et al. A study of the ozone formation by ensemble back trajectory-process analysis using the Eta-CMAQ forecast model over the northeastern U.S. during the 2004 ICARTT period[J]. Atmospheric Environment, 2009, 43(2): 355-363 DOI:10.1016/j.atmosenv.2008.09.079
(  0) 0) |
| [38] |
Carter W P L. Development of ozone reactivity scales for volatile organic compounds[J]. Air & Waste, 1994, 44(7): 881-899
(  0) 0) |
| [39] |
Grosjean D. In situ organic aerosol formation during a smog episode:Estimated production and chemical functionality[J]. Atmospheric Environment, 1992, 26(6): 953-963 DOI:10.1016/0960-1686(92)90027-I
(  0) 0) |
| [40] |
Grosjean D, Seinfeld J H. Parameterization of the formation potential of secondary organic aerosols[J]. Atmospheric Environment, 1989, 23(8): 1733-1747 DOI:10.1016/0004-6981(89)90058-9
(  0) 0) |
2. National Engineering Center for Satellite Positioning System, 129 Luoyu Road, Wuhan 430079, China
 2018, Vol. 38
2018, Vol. 38

